线性规划应用举例及软件
线性规划的应用及计算机求解

金融投资
在金融投资领域,如何合理配置资产以实现最大收益或最小风险是投资者关注的问题。线性规划可以用于制定最优的资产配 置方案,考虑风险和收益的平衡,以实现投资效益的最大化。
例如,一个养老基金可以使用线性规划来配置股票、债券和现金等资产,以实现长期稳定的收益并控制风险。
农业优化
在农业生产中,如何合理安排种植、养殖等 生产活动以达到最优的经济效益是农业经营 者关注的问题。线性规划可以用于解决农业 生产的优化问题,考虑土地、水资源、劳动 力等资源的限制,通过调整生产结构实现农 业生产的效益最大化。
其中,单纯形法是最常用的一种,它 通过迭代的方法逐步逼近最优解,直 到找到最优解或确定无解为止。
02
线性规划的应用领域
生产计划
生产计划是企业运营管理中的重要环节,线性规划可以用于制定最优的生产计划,以最小化生产成本 或最大化利润为目标,考虑生产能力、市场需求、产品组合等因素,通过调整生产资源的配置,实现 生产效益的最大化。
金融投ห้องสมุดไป่ตู้优化案例
总结词
金融投资优化
数学模型
目标函数通常是最大化预期收益或最小化 风险,约束条件包括投资限额、资产种类
限制等。
详细描述
线性规划在金融投资优化中具有实际应用 价值,通过合理配置投资组合,降低投资 风险,提高投资收益。
求解方法
使用计算机求解线性规划问题,常用的算 法有单纯形法、椭球法等。
资源分配优化案例
总结词 详细描述 数学模型 求解方法
资源分配优化
线性规划在资源分配优化中起到关键作用,通过合理分配有限 资源,实现资源利用的最大化,提高资源效益。
目标函数通常是最小化总成本或最大化总效益,约束条件包括 资源限制、需求约束等。
线性规划Lindo软件-整数规划

定制化不足
对于特定领域的整数规划问题, 可能需要针对具体问题对软件进 行定制化开发。
未来研究的方向与展望
算法改进
随着计算技术的发展,未来可以进一步优化 Lindo软件的算法,提高求解速度和精度。
扩展应用领域
随着整数规划问题的多样化,未来可以进一步拓展 Lindo软件的应用领域,如金融、物流、能源等领 域。
整数规划的求解方法
分支定界法
通过不断分割可行解空间和排除不可行解空 间来逼近最优解。
割平面法
通过逐步构建整数解来逼近最优解,适用于 小规模问题。
回溯法
通过添加割平面来缩小可行解空间,最终找 到最优解。
Lindo软件求解法
使用Lindo软件进行整数规划求解,具有高效 、稳定、易操作等优点。
04
使用Lindo软件进行整数规划
在求解结果查看界面中,可以查看问题的最优解、最优值、变量取值等信 息。
可以使用软件提供的图表功能,绘制变量取值与目标函数之间的关系图, 以便更好地理解问题的解。
05
案例分析
案例一:简单的整数规划问题
问题描述
01
考虑一个简单的整数规划问题,目标是最小化目标函数,同时
满足一系列线性约束条件。
解决方案
• 易用性:用户界面友好,操作简单,无需复杂的编程知识 即可使用。
Lindo软件在整数规划中的优势与限制
依赖性
Lindo软件的功能和性能高度依赖 于计算机硬件配置,高性能计算 机是求解大规模问题的必要条件。
模型限制
对于某些特殊类型的整数规划问 题,如非凸或非线性问题,Lindo 软件的求解效果可能有限。
在约束条件设置界面中,根据问题数据设置相 应的约束条件,如“less than”、“equal to”或“greater than”。
线性规划应用案例分析

线性规划应用案例分析线性规划是一种在数学和运营管理中常见的优化技术。
它涉及到在一组线性不等式约束下,最大化或最小化一个线性目标函数。
这种技术可以应用于许多不同的领域,包括供应链管理、资源分配、投资组合优化等。
本文将探讨几个线性规划应用案例,以展示其在实际问题中的应用和价值。
某制造公司需要计划生产三种产品,每种产品都需要不同的原材料和生产时间。
公司的目标是最大化利润,但同时也受到原材料限制、生产能力限制以及每种产品市场需求限制的约束。
通过使用线性规划,该公司能够找到最优的生产计划,即在满足所有约束条件下,最大化利润。
某物流公司需要计划将货物从多个产地运输到多个目的地。
公司的目标是最小化运输成本,但同时也受到运输能力、货物量和目的地需求的约束。
通过使用线性规划,该公司能够找到最优的运输方案,即在满足所有约束条件下,最小化运输成本。
某投资公司需要将其资金分配给多个不同的投资项目。
每个项目都有不同的预期回报率和风险水平。
公司的目标是最大化回报率,同时也要保证投资风险在可接受的范围内。
通过使用线性规划,该公司能够找到最优的投资组合,即在满足所有约束条件下,最大化回报率。
这些案例展示了线性规划在实践中的应用。
然而,线性规划的应用远不止这些,它还可以用于诸如资源分配、时间表制定、路线规划等问题。
线性规划是一种强大的工具,可以帮助决策者解决复杂的问题并找到最优解决方案。
线性规划是一种广泛应用的数学优化技术,适用于在多种资源限制下寻求最优解。
这种技术涉及到各种领域,包括工业、商业、运输、农业、金融等,目的是在给定条件下最大化或最小化线性目标函数。
下面我们将详细讨论线性规划的应用。
线性规划是一种求解最优化问题的数学方法。
它的基本思想是在一定的约束条件下,通过线性方程组的求解,求得目标函数的最优解。
这里的约束条件通常表现为一组线性不等式或等式,而目标函数则通常表示为变量的线性函数。
工业生产:在工业生产中,线性规划可以用于生产计划、物料调配、人力资源分配等方面。
线性规划的实际应用举例

线性规划的实际应用举例为了便于同学们掌握线性规划的一般理论和方法,本文拟就简单的线性规划(即两个变量的线性规划)的实际应用举例加以说明。
1 物资调运中的线性规划问题例1 A,B两仓库各有编织袋50万个和30万个,由于抗洪抢险的需要,现需调运40万个到甲地,20万个到乙地。
已知从A仓库调运到甲、乙两地的运费分别为120元/万个、180元/万个;从B仓库调运到甲、乙两地的运费分别为100元/万个、150元/万个。
问如何调运,能使总运费最小?总运费的最小值是多少?解:设从A仓库调运x万个到甲地,y万个到乙地,总运费记为z元。
那么需从B仓库调运40-x万个到甲地,调运20-y万个到乙地。
从而有z=120x+180y+100(40-x)+150·(20-y)=20x+30y+7000。
作出以上不等式组所表示的平面区域(图1),即可行域。
令z'=z-7000=20x+30y.作直线l:20x+30y=0,把直线l向右上方平移至l l的位置时,直线经过可行域上的点M(30,0),且与原点距离最小,即x=30,y=0时,z'=20x+30y取得最小值,从而z=z'+7000=20x+30y+7000亦取得最小值,z min=20×30+30×0+7000=7600(元)。
答:从A仓库调运30万个到甲地,从B仓库调运10万个到甲地,20万个到乙地,可使总运费最小,且总运费的最小值为7600元。
2 产品安排中的线性规划问题例2某饲料厂生产甲、乙两种品牌的饲料,已知生产甲种饲料1吨需耗玉米0.4吨,麦麸0.2吨,其余添加剂O.4吨;生产乙种饲料1吨需耗玉米0.5吨,麦麸0.3吨,其余添加剂0.2吨。
每1吨甲种饲料的利润是400元,每1吨乙种饲料的利润是500元。
可供饲料厂生产的玉米供应量不超过600吨,麦麸供应量不超过500吨,添加剂供应量不超过300吨。
问甲、乙两种饲料应各生产多少吨(取整数),能使利润总额达到最大?最大利润是多少?分析:将已知数据列成下表1。
线性规划在实际生活中的应用(多种方法求解,MATLAB,lingo,winQSB,含灵敏度分析)
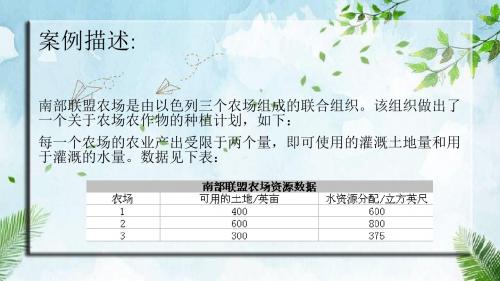
2.每一个农场的水量分布 3X1+2X4+X7≤600 3X2+2X5+X8≤800 3X3+2X6+X9≤375
每一种作物的总种植量
X1+X2+X3≤600 X4+X5+X6≤500 X7+X8+X9≤325 非负约束 Xi≥0 , i=1,2,……9
fval =
-633333.333333211
四、Excel
最优值的选择
四种计算工具计算出来的最优值相同,但最优解,即每个农场所种农作 物的量不同,考虑到实际生活中的人力成本以及不同农作物的管理难度 等,我们决定将WinQSB(Excel)的结果作为最优解来施行
结论:
农场种植最优种植方案如下:
计算机求解过程步骤
一、WinQSB
步骤1.生成表格 步骤2.输入数据
步骤3.求解结果
输出分析:
最优解为(0, 133.33,125, 300, 200, 0, 0, 0,0) 最优值为Z=633333.334.
二、Lingo
Max=1000*(X1+X2+X3)+750*(X4+X5+X6)+250*(X7+X8+X9); X1+X4+X7<=400; X2+X5+X8<=600; X3+X6+X9<=300; 3*X1+2*X4+X7<=600; 3*X2+2*X5+X8<=800; 3*X3+2*X6+X9<=375; X1+X2+X3<=600; X4+X5+X6<=500; X7+X8+X9<=325; Xi>0(i=1,2,...,9)
线性规划的应用

线性规划的应用1. 简介线性规划是一种数学优化方法,用于解决线性约束条件下的最优化问题。
它在各个领域都有广泛的应用,包括生产计划、资源分配、投资组合、运输问题等。
本文将介绍线性规划的基本概念和应用领域,并以一个实际案例来说明其具体应用。
2. 基本概念2.1 目标函数在线性规划中,我们需要最大化或最小化的目标称为目标函数。
目标函数通常是一个线性函数,表示决策变量的加权和。
2.2 约束条件约束条件是限制决策变量取值范围的条件。
线性规划的约束条件通常是一组线性等式或不等式。
2.3 决策变量决策变量是我们要求解的问题中的未知数,它们的取值将影响目标函数的值。
3. 应用领域3.1 生产计划线性规划可以用于优化生产计划,以最大化产出或最小化成本。
例如,一个工厂需要决定每种产品的生产数量,以最大化总利润。
我们可以将每种产品的利润作为目标函数,将生产数量的约束条件表示为线性等式或不等式。
3.2 资源分配线性规划可以帮助我们合理分配有限资源,以达到最优效益。
例如,一个公司需要决定如何分配有限的人力资源和资金,以最大化销售额。
我们可以将销售额作为目标函数,将人力资源和资金的约束条件表示为线性等式或不等式。
3.3 投资组合线性规划可以用于优化投资组合,以最大化收益或最小化风险。
例如,一个投资者需要决定如何分配资金到不同的投资标的,以最大化投资组合的收益。
我们可以将投资组合的收益作为目标函数,将资金分配的约束条件表示为线性等式或不等式。
3.4 运输问题线性规划可以解决运输问题,以最小化运输成本或最大化运输量。
例如,一个物流公司需要决定如何安排货物的运输路线和运输量,以最小化运输成本。
我们可以将运输成本作为目标函数,将货物的供应和需求、运输路线的约束条件表示为线性等式或不等式。
4. 案例分析假设某公司生产两种产品A和B,每天的生产时间为8小时。
产品A每单位利润为100元,产品B每单位利润为150元。
产品A的生产时间为1小时,产品B的生产时间为2小时。
线性规划应用案例

市场营销应用案例一:媒体选择在媒体选择中应用线性规划的目的在于帮助市场营销经理将固定的广告预算分配到各种广告媒体上,可能的媒体包括报纸、杂志、电台、电视和直接邮件。
在这些媒体中应用线性规划,目的是要使宣传范围、频率和质量最大化。
对于应用中的约束条件通常源于对公司政策、合同要求及媒体的可用性。
在下面的应用中,我们将介绍如何应用线性规划这一工具来建立模型进而解决媒体选择问题。
REL发展公司正在私人湖边开发一个环湖社区。
湖边地带和住宅的主要市场是距离开发区100英里以内的所有中上收入的家庭。
REL公司已经聘请BP&J 来设计宣传活动。
考虑到可能的广告媒体和要覆盖的市场,BP&J建议将第一个月的广告局限于5种媒体。
在第一个月末,BP&J将依据本月的结果再次评估它的广告策略。
BP&J已经收集到了关于受众数量、广告单价、各种媒体一定周期内可用的最大次数以及评定5种媒体各自宣传质量的数据。
质量评定是通过宣传质量单位来衡量的。
宣传质量单位是一种用于衡量在各个媒体中一次广告的相对价值的标准,它建立于BP&J在广告业中的经验,将众多因素考虑在内,如受众层次(年龄、收入和受众受教育的程度)、呈现的形象和广告的质量。
表4-1列出了收集到的这些信息。
表4-1 REL发展公司可选的广告媒体REL发展公司提供给BP&J第一个月广告活动的预算是30000美元。
而且,REL公司对BP&J如何分配这些资金设置了如下限制:至少要使用10次电视广告,达到的受众至少要有50000人,并且电视广告的费用不得超过18000美元。
应当推荐何种广告媒体选择计划呢?案例二:市场调查公司开展市场营销调查以了解消费者个性特点、态度以及偏好。
专门提供此种信息的市场营销调查公司,经常为客户机构开展实际调查。
市场营销调查公司提供的典型服务包括涉及计划、开展市场调查、分析收集数据、提供总结报告和对客户提出意见。
第五节 线性规划建模举例

第五节线性规划建模举例线性规划是一种操作研究的数学方法,广泛应用于商业、经济、工程领域中的优化问题。
线性规划建模是将实际问题描述为线性规划模型的过程。
本节将介绍几个线性规划建模的典型例子。
例1:混合饲料配方问题某饲料厂要生产一种混合饲料,需包括以下六种饲料成分:大豆粉、面粉、玉米、鱼粉、鸡粉、牛粉,并且要求这种混合饲料包含不少于25%的蛋白质和不多于15%的纤维素。
每吨饲料的生产成本和含量如下:| 饲料成分 | 成本(元/吨) | 蛋白质含量(%) | 纤维素含量(%) || -------- | ------------- | -------------- | -------------- || 大豆粉 | 200 | 45 | 10 || 面粉 | 100 | 10 | 2 || 玉米 | 150 | 8 | 5 || 鱼粉 | 300 | 60 | 0 || 鸡粉 | 280 | 50 | 2 || 牛粉 | 320 | 70 | 5 |问如何使得生产的混合饲料成本最小,同时满足蛋白质含量不少于25%和纤维素含量不超过15%的要求。
自变量:混合饲料中每种成分的含量。
目标函数:最小化混合饲料的成本。
约束条件:1. 蛋白质含量不少于25%:0.45×x1 + 0.1×x2 + 0.08×x3 + 0.6×x4 + 0.5×x5 + 0.7×x6 ≥ 0.25。
2. 纤维素含量不超过15%:0.1×x1 + 0.02×x2 + 0.05×x3 + 0×x4 + 0.02×x5 + 0.05×x6 ≤ 0.15。
3. 非负性:x1, x2, x3, x4, x5, x6 ≥ 0。
其中,x1,x2,x3,x4,x5,x6 分别表示大豆粉、面粉、玉米、鱼粉、鸡粉和牛粉的含量,单位为吨。
线性规划方法及其应用

05
线性规划方法优缺点分析
优点分析
有效处理多变量问题
线性规划能够同时处理多个决策变量,通过 优化算法寻找最优解。
直观易懂的数学模型
线性规划在各个领域都有广泛的应用,如生 产计划、资源分配、运输问题等。
广泛应用
线性规划的数学模型相对简单,易于理解和 应用。
可求解大规模问题
随着计算机技术的发展,线性规划可以求解 大规模的问题,满足实际应用的需求。
复杂约束处理
研究如何处理包含复杂约束条件的线性规划问题,提高求解效率和 准确性。
不确定性问题建模
针对包含不确定性因素的线性规划问题,发展有效的建模和求解方 法。
应用领域拓展
探索线性规划方法在更多领域(如机器学习、大数据分析等)的应用 潜力,推动相关领域的理论和技术创新。
感谢您的观看
THANKS
3
考虑不确定性
将不确定性因素引入资源分配问题中,通过线性 规划求解鲁棒性强的资源分配策略,以应对潜在 的风险和变化。
04
线性规划软件介绍
MATLAB软件介绍
1
MATLAB是一款由MathWorks公司开发的数学 计算软件,广泛应用于算法开发、数据可视化、 数据分析以及数值计算等领域。
2
MATLAB提供了丰富的工具箱,其中包括优化工 具箱(Optimization Toolbox),可用于解决线 性规划问题。
线性规划方法及其应用
目录
• 线性规划基本概念 • 线性规划方法 • 线性规划应用举例 • 线性规划软件介绍 • 线性规划方法优缺点分析 • 线性规划方法发展趋势与展望
01
线性规划基本概念
定义与特点
定义:线性规划是一种数学方法,用于 优化一组线性不等式约束下的线性目标 函数。
线性规划 实际案例

线性规划实际案例
线性规划(LinearProgramming)是一种模型化工具,它可以帮
助我们更好地解决有限资源最大化利用的计算问题。
线性规划可以找出给定问题的最优解,这使得其在商业决策中受到越来越多的重视。
本文将介绍线性规划的一些实际案例,并阐述其优势以及在商业决策中的应用。
首先,我们从最简单的线性规划开始讨论。
在一组普通工作面前,线性规划可以让我们避免“最小化最大值”方面的问题,从而更容易找出最佳解决方案。
例如,假设我们正在解决以下简单的问题:有两种产品A和B,要在有限的资源内生产尽可能多的产品,并获得最大的利润。
在这种情况下,我们可以使用简单的线性规划,通过计算生产各种产品所消耗的资源,并将此类资源最大化利用以获得最大利润,最终找到最优解决方案。
其次,我们可以将线性规划作为其他更复杂问题的解决方案。
例如,我们可以使用线性规划来求解众多变量相互影响之间的最优解决方案。
它可以解决各种复杂的组合优化问题,例如投资组合优化、产品组合优化、成本优化等。
另外,它也可以用来解决货币及其它各种金融上的优化问题。
最后,线性规划可以用来解决各种决策问题。
例如,对于一个商业决策,管理者往往希望尽可能地实现最大的预期价值,以及尽可能最小的风险,这也是线性规划的一个典型应用场景。
同样,我们也可以使用线性规划来进行企业资源调度、供应链调度等各种决策,最终
获得最佳的结果。
综上所述,线性规划可以应用于众多场景,其优势是可以快速找出最优解决方案,在商业决策中可以起到非常有效的作用。
以上是本文介绍的关于线性规划实际案例,欢迎各位读者积极探索这一领域,为商业决策及其它工作增加价值。
运用Lingo进行线性规划求解(实例)

LINGO
支持多种线性规划算法,包括单纯形法、网络算法等。
要点二
Gurobi
主要采用高级优化算法,如分支定界法、动态规划等。
LINGO与Gurobi的比较
LINGO
支持各种类型的约束条件,包括整数约束、非线性约束 等。
Gurobi
特别擅长处理大规模、非线性问题,但对线性问题的处 理能力稍弱。
LINGO
界面简洁,建模语言直观,易于学习和掌握。
Excel
需要结合多个函数和工具进行建模,对于复杂问题操作相对繁琐。
LINGO与Excel的比较
LINGO
针对优化问题进行了优化,求解速度 较快,精度较高。
Excel
求解速度较慢,对于大规模问题可能 无法得到满意的结果。
LINGO与Gurobi的比较
LINGO软件特点
高效求解
LINGO采用先进的求解算法,能够快速求解大规 模线性规划问题。
灵活建模
LINGO支持多种建模语言,用户可以根据需要选 择合适的语言进行建模。
图形界面
LINGO提供直观的图形界面,方便用户进行模型 设计和结果查看。
LINGO软件应用领域
生产计划
LINGO可用于制定生产计划,优化资源配置, 提高生产效率。
金融投资
LINGO可以用于金融投资组合优化,帮助投 资者实现风险和收益的平衡。
物流优化
LINGO可以帮助企业优化物流配送路线,降 低运输成本。
资源分配
LINGO可用于资源分配问题,如人员、设备、 资金的分配,以达到最优效果。
2023
PART 02
线性规划基本概念
REPORTING
线性规划定义
线性规划是数学优化技术的一种,它通过将问 题抽象为数学模型,利用数学方法来寻找最优 解。
线性规划的应用及计算机求解

等级
非常好 很好 一般 一般 非常好 很好
设投资于A,B,C,D,E,F六只债券上的投资额(万元)分别 为 x1 , x2 , x3 , x4 , x5 , x6 ,则可列出如下线性规划模型:
max P 0.085 x1 0.09 x2 0.1x3 0.095 x4 0.085 x5 0.09 x6 x1 x2 x3 x4 x5 x6 10000 x 2500 1 x2 2500 x3 2500 x 2500 4 x5 2500 x6 2500 x1 x2 x5 x6 5000 x x 3000 4 3 x1 , x2 , x3 , x4 , x5 , x6 0
ห้องสมุดไป่ตู้
s.t.
Excel求解汽车生产计划问题
用Excel求解线性规划问题,可以按照如下三个步骤 进行:
1
2 3
列出所求问题的标准表格
把标准表格转换为Excel电子表格。 利用Excel的“规划求解”进行求解。
其中:单元格J4(目标函数)的计算公式为: =SUMPRODUCT(B4:F4,$B$15:$F$15) 单元格Jk(约束条件k)的计算公式为: =SUMPRODUCT(Bk:Fk,$B$15:$F$15)
P59(a)
例题3:
max P 3 x1 2 x2 x1 2 x2 1 x x 2 2 1 2 x1 x2 6 x1 5 2 x1 x2 16 x x 12 2 1 x1 x2 21 x2 10 x1 , x2 0 P59(f)
线性规划模型及应用场景

线性规划模型及应用场景线性规划是一种运筹学中的数学方法,用于在有限的资源下寻找达到最佳目标的方案。
线性规划模型是通过建立线性关系式和目标函数以确定决策变量的最优值,来求解问题。
应用线性规划模型可以在诸多领域中找到合理的应用场景。
一、生产调度与物流管理生产调度是指以资源约束为条件,在规定时间内安排、组织和运用生产资源的管理活动。
而物流管理则是通过有效的供应链管理来实现流程和原料的优化配置。
线性规划可以通过建立生产资源约束条件和目标函数,来确定合理的生产进度和物流配送计划,从而提高生产效率、降低物流成本。
举个例子,某工厂生产两种产品A和B,生产线的时间和效率是有限的,同时每个产品有不同的售价和成本。
这时可以使用线性规划模型来确定每种产品的生产数量,使得总利润最大化。
二、金融投资与资产配置金融投资是指将资金投入到各种金融市场和资产中,以期获得回报。
而资产配置则是指在不同风险水平下,按照一定的比例配置资金到各种资产上。
线性规划可以通过建立风险约束条件和目标函数,来确定最佳的资产配置组合,以实现风险和回报间的平衡。
举个例子,某投资者有一笔固定资金,可以投资于股票、债券和货币市场基金等多个金融工具。
他可以将自己的投资目标、预期收益和风险偏好建立为线性规划模型,以确定最佳的资产配置比例,从而达到理想的投资回报。
三、运输与配送运输与配送是指将物品从生产地或仓库运往销售点或用户手中的过程。
针对运输与配送的问题,线性规划可以通过建立运输路径、运输容量和运输成本等约束条件,来确定合理的物流方案,从而达到最佳的运输效益。
例如,某物流公司需要将商品从N个供应商处运输到M个销售点,每个供应商的供货量和每个销售点的需求量是已知的,同时每个运输路径的距离和费用也是已知的。
利用线性规划模型,可以确定每个运输路径上的货物运输量和运输方式,从而降低运输成本,提高物流效率。
四、人力资源管理人力资源管理是指通过合理的组织、激励和管理,利用有限的人力资源实现组织目标。
求解线性规划问题的软件应用分析

司开发的一套专门用于求解最优化问题的 软件包。LINDO用 于 求 解 线 性 规 划 和 二 次 规划,LINGO除了具有LINDO的全部功能 外,还可用于求解非线性规划,以及一些线
性 和 非 线 性 方 程 组 的 求 解 、代 数 方 程 求 根 等。
件[M].北京:清华大学出版社,2005,7. [2] 丁以中.管理科学—— 运用Spreadsheet
建模和求解[M].北京:清华大学出版 社,2005,6. [3] 朱求长.运筹学及其应用[M].武汉大学 出版社,2004,7.
图6 第二次迭代
图7 EXCEL表格形式的问题及结果
36
科技创新导报 Science and Technology Innovation Herald
下面是一个典型的线性规划问题实例[3]:
min s.t. (P1)
z = 2x1 − x2 + 2x3 − x1 + x2 + x3 = 4 − x1 + x2 − x3 ≤ 6 x1 ≤ 0, x2 ≥ 0, x3无符号限制
(1) (2)
其中含有三个类型各异的变量以及两 个 线 性 约 束 。这 个 实 例 可 通 过 人 工 变 量 法 手工求解:将问题转换为标准形式后构造 辅助问题,通过求解辅助问题得到原问题 的 最 优 解 , 即 ( - 5 , 0 , - 1 ) T, 最 优 目 标 函 数 值 为 -12 。这 里 需 要 说 明 的 是 , 在 软 件 应 用 中 使用xi 表示带有下标的变量 xi 。
目前,多种软件都可以实现线性规划问 题的求解了,其中包括专业优化软件 LINDO/LINGO [1]、WINQSB,具备强大计算 功能的MATLAB、MATHEMATICA,具有规 划 求 解 功 能 的 E X C E L 软 件 [2], 以 及 主 要 求 解 全局优化的1stOpt软件。本文将通过一个典 型线性规划问题的求解过程,介绍各种软件 的使用方法,并分析它们的使用局限性。
LINDO软件求线性规划、整数规划和0-1规划

LINDO软件简介/求解线性规划问题LINDO是一种专门用于求解数学规划问题的软件包。
由于LINDO执行速度很快、易于方便输入、求解和分析数学规划问题。
因此在数学、科研和工业界得到广泛应用。
LINDO/GO主要用于解线性规划、非线性规划、二次规划和整数规划等问题。
也可以用于一些非线性和线性方程组的求解以及代数方程求根等。
LINDO/GO中包含了一种建模语言和许多常用的数学函数(包括大量概论函数),可供使用者建立规划问题时调用。
一般用LINDO(Linear Interactive and Discrete Optimizer)解决线性规划(LP—Linear Programming)。
整数规划(IP—Integer Programming)问题。
其中LINDO 6 .1 学生版至多可求解多达300个变量和150个约束的规划问题。
其正式版(标准版)则可求解的变量和约束在1量级以上。
LINGO则用于求解非线性规划(NLP—NON—LINEAR PROGRAMMING)和二次规则(QP—QUARATIC PROGRAMING)其中LINGO 6.0学生版最多可版最多达300个变量和150个约束的规则问题,其标准版的求解能力亦在10^4量级以上。
虽然LINDO和LINGO 不能直接求解目标规划问题,但用序贯式算法可分解成一个个LINDO和LINGO能解决的规划问题。
要学好用这两个软件最好的办法就是学习他们自带的HELP文件。
下面拟举数例以说明这两个软件的最基本用法。
(例子均选自张莹《运筹学基础》)例1.(选自《运筹学基础》P54.汽油混合问题,线性规划问题)一种汽油的特性可用两个指标描述:其点火性用“辛烷数”描述,其挥发性用“蒸汽压力”描述。
某炼油厂有四种标准汽油,设其标号分别为1,2,3,4,其特性及库存量列于下表1中,将上述标准汽油适量混合,可得两种飞机汽油,某标号为1,2,这两种飞机汽油的性能指标及产量需求列于表2中。
线性规划的计算机求解及应用举例

得:x天各时间段内所 需司机和乘务人员人数如下表所示:
班次 1 2 3 4 5 6 时间 6:00——10:00 10:00——14:00 14:00——18:00 18:00——22:00 22:00——2:00 2:00——6:00 所需人员 60 70 60 50 20 30
(1)建立Excel工作表。用
举例
在电子表格上建模(生产计划)
举例
使用Excel Solver求解模型求解生产计划 案例,求解的过程如下。
例1 A工厂计划生产甲、乙两种产品。每千克产品的销售价 格和能源消耗量、以及能源资源见表,怎样安排生产计划才 能使A工厂获益最大?
解:x1:产品甲的计划生产量;x2:产品乙的计划生产量,则有如下 线性规划问题: max z=7x1 + 12x2 (总销售收入) s.t. 9x1 + 4x2 360 (煤资源限制) 4x1 + 5x2 200 (电资源限制) 3x1 + 10x2 300 (油资源限制) x1 0,x2 0 (非负条件)
线性规划的计算机求解 及应用举例
计算机软件求解
关于线性规划问题的求解,有许多好的专业软件和 商务软件,通过计算机可十分方便地完成求解过程。 最简便易行的求解软件是Excel,下面介绍其使用方法。 一组单元格表示变量,作 为可变单元格(空);用几组单元格分别表示各约束 条件和目标函数的系数;用一些单元格输入公式表示 各组系数和变量的关系。 (2)打开工具栏中的“规划求解”对话框,指定存 有目标函数的单元格为目标单元格,指定表示变量的 单元格为可变单元格,建立约束条件。 (3)在规划求解对话框中按下“求解”按钮,即可 求出最优解和最优值。推出规划求解对话框。
设司机和乘务人员分别在各时间段开始时上班,并连续工作 8小时,问该公交线路应怎样安排司机和乘务人员,即能满 足工作需要,又使配备司机和乘务人员的人数减少?
线性规划算法的应用案例

线性规划算法的应用案例线性规划是应用最广泛的数学优化方法之一,也是一种非常有效的运筹学技术。
它的基本思想是将问题建模成一组线性方程和线性不等式的组合,通过寻找最优解来实现目标最大化或最小化。
线性规划算法广泛应用于制造业、金融、物流和交通等领域,以下将介绍几个重要的应用案例。
1. 生产计划和调度线性规划算法可以用于制造业的生产计划和调度。
例如,在一家造纸厂中,有若干个可用的生产线、仓库和运输车辆,需要考虑原材料的成本、工人的人工费用、工厂的能耗费用以及运输的成本等因素,制定出最佳的生产计划和调度方案。
对于这类问题,可以将目标函数设置为生产成本最小化或产出效率最大化,约束条件包括原材料的库存量、生产线的容量和物流的时间窗口等。
通过使用线性规划算法,可以得到最佳的生产计划和调度方案,使得企业的生产效率和盈利能力得到提升。
2. 市场营销和广告投放线性规划算法可以帮助企业制定最佳的市场营销和广告投放方案。
例如,在一家快递公司中,需要制定如何调整价格策略、开拓市场份额、投放广告等方案,以达到最大化利润或最小化成本的目标。
对于这类问题,可以将目标函数设置为销售额最大化或成本最小化,约束条件包括市场份额的限制、广告投放预算的限制等。
通过使用线性规划算法,可以得到最佳的市场营销和广告投放方案,提高企业的营销效率和市场竞争力。
3. 交通运输和物流配送线性规划算法可以用于交通运输和物流配送领域。
例如,在一个物流中心中,需要规划配送路线和运输车辆的分配,以最小化交通堵塞和物流成本的影响。
对于这类问题,可以将目标函数设置为运输成本最小化或配送效率最大化,约束条件包括车辆数量的限制、货物配送时间的限制等。
通过使用线性规划算法,可以得到最佳的路线规划和车辆分配方案,提高企业的配送效率和物流运转效率。
4. 金融投资和风险管理线性规划算法可以用于金融投资和风险管理领域。
例如,在一个投资银行中,需要制定最佳的投资组合和股票交易策略,以最大化收益和降低风险。
演示文稿应用和软件求解线性规划

第18页,共25页。
例1.4 用MATLAB求解线性规划问题
max z 2x1 3x2 5x3
s.t.
2
x1 x1
x2 x3 7 5x2 x3 10
xi 0,i 1, 2,3
解 首先转化为求最小值问题
min z S 2x1 3x2 5x3
为变量个数、约束条件个数、优化状态、耗费内存、所花时间
等信息, 点击Close关闭窗口, 屏幕上出现标题为 “Solution Report”(解的报告)的信息窗口, 显示优化计 算(线性规划中换基迭代)的步数、优化后的目标函数值、列出
各变量的计算结果。
第7页,共25页。
本例的具体内容如下:
Global optimal solution found at iteration: 5
(cgiterations)等。
(8)lambda表示解处的拉格朗日乘子,其中lower,upper,
ineqlin,eqlin分别对应于下界、上界、不等式约束与等 式约束。
第16页,共25页。
例1.3 用MATLAB解线性规划问题
min z 2x1 x2 x3
x1 x2 2x3 6
第4页,共25页。
LINGO的语法规定: (1)求目标函数的最大值或最小值分别用MAX=…或MIN=…来表示
; (2)每个语句必须以分号“;”结束,每行可以有许多语句,语
句可以跨行; (3)变量名称必须以字母(A~Z)开头,由字母、数字(0~9)和下划
线所组成,长度不超过32个字符,不区分大小写; (4)可以给语句加上标号,例如[OBJ]MAX=200*X1+300*X2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
石媛昌
例 1 max
s.t.
解 编写M文件如下:
z 0.4 x1 0.28 x2 0.32 x3 0.72 x 4 0.64 x5 0.6 x6 0.01x1 0.01x 2 0.01x3 0.03x 4 0.03x5 0.03x6 850 0.02 x1 0.05 x 4 700 0.02 x 2 0.05 x5 100 0.03x3 0.08 x6 900 xj 0 j 1,2, 6
原料费(元/件) 0.25 0.35 0.50 1.25 2.00 2.80
中国农业大学理学院
石媛昌
解:首先列出所有可能生产产品I、II、III的工序组合 形式,并假设按各种工序的组合形式进行生产的产量 具体如下: 按(A1,B1)组合方式生产产品I,其产量设为 x1 ; 按(A1,B2)组合方式生产产品I,其产量设为 x2; 按(A1,B3)组合方式生产产品I,其产量设为 x3; 按(A2,B1)组合方式生产产品I,其产量设为 x4; 按(A2,B2)组合方式生产产品I,其产量设为 x5; 按(A2,B3)组合方式生产产品I,其产量设为 x6; 按(A1,B1)组合方式生产产品II,其产量设为 x7 ; 按(A2,B1)组合方式生产产品II,其产量设为 x8 ; 按(A2,B2)组合方式生产产品III,其产量设为x9 ;
中国农业大学理学院
石媛昌
中国农业大学理学院
石媛昌
1
LinGo
输入模型 LinDo模式 LinGo模式 求解 点击求解按钮 结果
即可
LinGo 输 入 模 式
model: MAX=3*x1+5*x2+4*x3; 2*x1+3*x2<=1500; 2*x2+4*x3<=800; 3*x1+2*x2+5*x3<=2000; end
中国农业大学理学院
石媛昌
目标函数应为:
max Z (1.25 0.25)( x1 x2 x3 x4 x5 x6 ) (2.00 0.35)( x7 x8 ) (2.80 0.5) x9 300 [5( x1 x2 x3 ) 10 x7 ] A1设备实际 6000 使用的总台时 321 [7( x4 x5 x6 ) 9 x8 12 x9 ] 10000 250 [6( x1 x4 ) 8( x7 x8 )] 4000 783 [4( x2 x5 ) 11x9 ] 7000 200 [7( x3 x6 )] 4000
中国农业大学理学院
石媛昌
中国农业大学理学院
石媛昌
设按方案i(i=Ⅰ,Ⅱ,…,Ⅴ)下料的原材料根数为Xi, 则可以列出下面模型
由计算得到的最优下料方案为: 按方案I下料 30根, 按方案II下料 10根, 按方案IV下 料50根. 即需要 90根原料可以制造100套钢架 .
中国农业大学理学院
石媛昌
中国农业大学理学院
即可
!注释内容,可用中文 !目标函数:最大-max,最小-min,大小写不分 max 3 x1+5 x2+4 x3 !约束,以subject to开始 subject to 2 x1+3 x2<=1500 2 x2+4 x3<=800 3 x1+2 x2 +5 x3<=2000 end
中国农业大学理学院
A1每台时的设备费用
整理即可得出所求的线性规划数学模型为:
Max Z 0.37 x1 0.31x2 0.40 x3 0.34 x4 0.34 x5 0.43x6 0.65 x7 0.86 x8 0.68 x9 A1台时约束 5( x1 x2 x3 ) 10 x7 6000 A2台时约束 7( x4 x5 x6 ) 9 x8 12 x9 10000 B1台时约束 6( x1 x4 ) 8( x7 x8 ) 4000 B2台时约束 4( x2 x5 ) 11x9 7000 B3台时约束 7( x3 x6 ) 4000 决策变量的非负约束 x j 0
每天用料量 A B 8 6 5 3 9 8 产量 1号 2号 7 5 6 8
石媛昌
有配套约束的资源优化问题
某厂生产三种产品I、II、III,每种产品要经过A 、B 两道工序加工。设该厂有两种规格的设备能完成 A 工序,它们以 A1、A2 表示;有三种规格的设备能完 成 B 工序,它们以 B1、B2 、B3 表示。产品I可在A、B 任何一种规格设备上加工;产品II可在任何规格的 A 设备上加工,但在完成 B 工序时,只能在 B1 设备上加 工;产品III只能在 A2与 B2 设备上加工。已知在各种 机床设备的单件工时,原材料费,产品销售价格,各 种设备的有效台时以及满负荷操作时机床设备的费用 如下表所示,要求安排最优的生产计划,使该厂的利 润为最大。 石媛昌
中国.000000 B( 2) 800.0000 0.000000 B( 3) 2000.000 0.000000 A( 1, 1) 2.000000 0.000000 A( 1, 2) 3.000000 0.000000 A( 1, 3) 0.000000 0.000000 A( 2, 1) 0.000000 0.000000 A( 2, 2) 2.000000 0.000000 A( 2, 3) 4.000000 0.000000 A( 3, 1) 3.000000 0.000000 A( 3, 2) 2.000000 0.000000 A( 3, 3) 5.000000 0.000000 Row Slack or Surplus Dual Price 1 2675.000 1.000000 2 0.000000 1.050000 3 0.000000 0.6250000 4 0.000000 0.3000000
石媛昌
产品计划问题
m种资源可生产n种产品,问如何安排各种 产品数量,可获最大利润。 处理方法:以各种产品的数量为决策变量。
例 某工厂生产产品A,B,要经过两道工序。每 生产1吨B可得到2吨副产品C,如能销售出,每吨 获利300元,否则损失200元。据预测,每天最多 可卖出5吨C。问如何安排生产可获最大利润。
中国农业大学理学院
石媛昌
用MATLAB优化工具箱解线性规划
1、模型: min z=cX s.t. AX b 命令:x=linprog(c,A,b) 2、模型:min z=cX s.t. AX b Aeq X beq 命令:x=linprog(c,A,b,Aeq,beq)
AX b 存在,则令A=[ ],b=[ ]. 注意:若没有不等式:
中国农业大学理学院
石媛昌
中国农业大学理学院
石媛昌
注意与LinDo的区别
目标函数中加等号 变量与系数之间用“*” Model:-end可省略
LinGo 模 式
Model: Sets: !定义集合 Endsets Data: !定义数据 Enddata 调用函数与计算 end
中国农业大学理学院
石媛昌
c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6]; A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08]; b=[850;700;100;900]; Aeq=[]; beq=[]; vlb=[0;0;0;0;0;0]; vub=[]; [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub) 石媛昌 中国农业大学理学院
3
合理下料问题
棒料或板材按规格要求剪裁成一定毛坯, 已知所需毛坯的数量,问如何合理下料使 原材料最省? 处理方法:制定下料方案,根据方案决定 决策变量,列出规划模型,有时可删去明 显不合理的下料方案,简化模型。
例:某车间接到制作100套钢架的 订单,每套钢架用长为2.9米,2.1 米,1.5米的圆钢各一根。已知原 料长7.4米。问应如何下料,使原 材料最省。
石媛昌
中国农业大学理学院
石媛昌
注意事项
变量以字母开头,下标写在后面,系数与变 量之间加空格 不等号为:<= ( <),>=( >) , =, <=与 <等同 变量非负约束可省略 结束时以end标示
结 果
LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) 2675.000 VARIABLE VALUE REDUCED COST X1 375.000000 0.000000 X2 250.000000 0.000000 X3 75.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 1.050000 3) 0.000000 0.625000 4) 0.000000 0.300000
中国农业大学理学院
工厂1 工厂2 工厂3
9 4
中国农业大学理学院
产品 设备 A1 A2 B1 B2 B3 单价(元/件) I 5 7 6 4 7
产 II 10 9 8 — —
品 III — 12 — 11 —
设备有 满负荷时的 效台时 设备费用(元) 6000 10000 4000 7000 4000 300 321 250 783 200
工时 第1工序 第2工序 利润 (百元/吨) A 2 3 4 B 3 4 10
石媛昌
总工时 12 24
中国农业大学理学院
石媛昌
中国农业大学理学院
