数制转换与计算

二进制基本概念及常用数制之间的转换

二进制基本概念及常用数制之间的转换二进制是一种计数系统，它只使用两个数字0 和1。

二进制在计算机科学中被广泛使用，因为计算机中的所有数据都是由0 和1 组成的二进制数字表示的。

常用的数制包括：1. 十进制：使用0-9 十个数字，每次增加10 的幂次。

2. 二进制：使用0 和1 两个数字，每次增加2 的幂次。

3. 八进制：使用0-7 八个数字，每次增加8 的幂次。

4. 十六进制：使用0-9 和A-F 16个数字，每次增加16 的幂次。

常用数制之间的转换：1. 二进制转十进制：将二进制数按照权值相加的方式转换成十进制数。

例如，二进制数1011 转换成十进制数的计算方法为：1×2³+0×2²+1×2¹+1×2⁰=11。

2. 十进制转二进制：用除2 取余数的方式转换成二进制数。

例如，十进制数25 转换成二进制数的计算方法为：25÷2=12·1，12÷2=6·0，6÷2=3·0，3÷2=1·1，1÷2=0·1，所以25 的二进制表示为11001。

3. 二进制转八进制：将二进制数从右往左按每三位一组转换成八进制数。

例如，二进制数101101 转换成八进制数的计算方法为：1×2²+0×2¹+1×2⁰+1×2⁴+0×2³+1×2²=55，所以101101 的八进制表示为55。

4. 八进制转二进制：将八进制数每个数字转换成对应的三位二进制数。

例如，八进制数67 转换成二进制数的计算方法为：6 的二进制表示为110，7 的二进制表示为111，所以67 的二进制表示为110111。

5. 二进制转十六进制：将二进制数从右往左按每四位一组转换成十六进制数。

信息技术二进制十进制十六进制算法

信息技术二进制十进制十六进制算法信息技术中，二进制、十进制和十六进制是最常用的数制。

在计算机科学和计算机编程中，对于数据的存储、处理和表示而言，这三种数制起着重要的作用。

首先，二进制是一种由0和1组成的数制。

这是因为计算机中的信息通过电压的高低来表示，高电压为1，低电压为0。

二进制的每一位被称为一个比特（bit），8个比特组成一个字节（byte）。

二进制中的数字转换为十进制可以通过不断将二进制的每一位乘以相应的权值并求和得到。

例如，二进制数1101可以转换为十进制数的计算过程如下：1×2³+1×2²+0×2¹+1×2⁰=8+4+0+1=13其次，十进制是我们最为熟悉的数制，由0到9这10个数字组成。

十进制中的每一位权值为10的幂。

例如，十进制数253可以转换为二进制数的计算过程如下：2³×2+5×10²+3×10¹=8×2+5×100+3×10=16+500+30=546最后，十六进制是一种由0到9和字母A到F（代表10到15）这16个字符组成的数制。

十六进制中的每一位权值为16的幂。

它在计算机科学中被广泛应用，因为它可以简洁地表示二进制数。

十六进制中的A对应的十进制数为10，B对应的是11，C对应的是12，以此类推。

例如，十六进制数3A对应的十进制数的计算过程如下：3×16¹+10×16⁰=48+10=581.将二进制数按照4位分组：110110112.将每一组转换为十六进制数：DB3.得到十六进制数DB反过来，十六进制转换为二进制可以通过将每一位十六进制数转换为4位的二进制数。

例如，十六进制数7F可以通过如下的算法转换为二进制数的过程：1.将每一位十六进制数转换为4位的二进制数：01111111在信息技术中，二进制、十进制和十六进制算法是非常重要的基础知识。

数制与数制间的转换_大学计算机基础与计算思维_[共2页]

342.2 计算机中的数制与运算计算机内部采用二进制数表示信息，因为二进制在物理上实现容易；记忆和传输可靠；运算简单；方便使用逻辑代数工具。

2.2.1 数制与数制间的转换1．数制的概念数制是用一组固定的数字和一套统一的规则来表示数的方法。

在数值计算中，用数码表示数的大小时，仅仅用一位数往往不够用，因而常常采用多位数。

多位数码中每一位的构成和从低位向高位的进位规则称为进位计数制。

进位计数制的两个基本要素是基数和位权。

基数是指该进制中允许使用的基本数码的个数。

例如，十进制的基数为10，数码为0、1、2、……、9十个数。

二进制的基数为2，数码为0、1两个数。

位权是指数制每一位所具有的值。

例如，十进制数678.34按位权展开式为678.34=6×102+7×101+8×100+3×10-1+4×10-2，其中6、7、8、3、4是数码，10是基数，102是百位的位权，101是十位的位权，100是个位的位权，10-1是十分位的位权，10-2是百分位的位权。

2．计算机技术中常见的数制计算机中使用二进制数表示信息，但为了阅读和书写方便，在计算机技术中还常用八进制和十六进制数。

可以通过给数值加下标或在数值的末尾加标志符号的方式来区分不同数制的数。

（1）二进制二进制计数制中，数值用0、1表示，基数为2，是逢二进一的计数制，各数位的位权是以2为底的幂。

例如，二进制数10.01可表示为(10.01)2或10.01B，按位权展开多项式为(10.01)2=1×21+0×20+0×2-1+1×2-2。

（2）八进制八进制计数制中，数值用0、1、2、…、7表示，基数为8，是逢八进一的计数制，各数位的位权是以8为底的幂。

例如，八进制数3765.02可表示为(3765.02)8或3765.02O 或3765.02Q，按位权展开多项式为(3765.02)8 = 3×83+ 7×82+ 6×81+5×80+ 0×8-1+2×8-2。

十进制转换为十六进制方法

十进制转换为十六进制方法十进制和十六进制是计算机科学中常用的数制，其中十六进制是一种基数为16的进位制数，使用了数字0-9与字母A-F来代表16个数位。

在计算机编程中，经常需要将十进制转换为十六进制，下面介绍几种方法。

方法一：除以16取余法
这种方法是最常用的方法之一。

将十进制数不断除以16，每次取余数，直到商为0为止。

然后将余数按照相反顺序排列，即可得到十六进制数。

例如将十进制数57转换为十六进制，则按照以下方法计算：
57÷16=3 (9)
3÷16=0 (3)
因此57的十六进制为39。

方法二：商数依次减去16法
这种方法也比较常用，适合较小的十进制数。

将十进制数不断减去16的倍数，每次计算商数和余数，直到商数为0为止。

然后将余数按照相反顺序排列，即可得到十六进制数。

例如将十进制数21转换为十六进制，则按照以下方法计算：
21-16=5商1
5-16=-11商0
因此21的十六进制为15。

方法三：查表法
如果对于十六进制各位对应的十进制数比较熟悉，可以通过查表直接将十进制数转换为十六进制。

以下是常用的十六进制对应表：0123456789A B C D E F
012345678910111213 1415
例如将十进制数255转换为十六进制，则可以直接查表得到其十六进制为FF。

总的来说，将十进制数转换为十六进制需要掌握一些基础算法和数字对应关系。

掌握了这些知识后，计算起来就会更加容易和简便。

计算机中数的表示及运算

计算机中数的表示及运算张晓军编写引言人类在文字出现以前,就已经会用道具(如绳子打结)计数了.在日常生活中,我们每天都在与数字打交道,而数字与数制是密不可分的.比如:60秒为1分,60分为1小时,其特点是"逢60进1",可取的数字是0,1,2,...,59,共有60个,这就是"六十进制".再比如:24小时为1天,这是24进制;7天为1星期,这是7进制;12个为1打,这是12进制;10mm为1cm,10cm为1dm,10dm为1m,这是我们最为熟悉的10进制.不管是什么进制,其基数(如60进制的基数就是60,10进制的基数就是10)正好等于该数制中不同"数字符号"的个数(如60进制中采用0,1,2,...,59共60个不同的数字符号,10进制中采用0,1,2,...,9共10个不同的数字符号).一、常用数制及其相互转换在数制系统中,各位数字所表示的值不仅与该数字有关,而且与它所在的位置有关.例如,在10进制数123中,百位上的1表示1个100,十位上的2表示2个10,个位上的3表示3个1,因此,有:123=1*100+2*10+3*1,其中100,10,1被称为百位、十位、个位的权。

十进制中,个、十、百、千、万……等各数位的权分别是1，10，100，1000，10000，……，一般地，写成10的幂，就是100,101,102,103,104,……;10则被称为十进制的基数1.1 十进制数特点:采用0,1,2,3,4,5,6,7,8,9共10个不同的数字符号,并且是"逢十进一,借一当十".对于任意一个十进制数，都可以表示成按权展开的多项式。

例如：1999=1*103+9*102+9*101+9*1002003=2*103+0*102+0*101+3*10048.25=4*101+8*100+2*10-1+5*10-21.2 二进制数在电子计算机中采用的是二进制.二进制数只需2个不同的数字符号:0和1,并且是"逢二进一,借一当二",它的基数是2.对于二进制数,其整数部分各数位的权,从最低位开始依次是1,2,4,8,……写成2的幂，就是20,21,22,23,……；其小数部分各数位的权,从最高位开始依次是0.5,0.25,0.125,……，写成2的幂，就是2-1,2-2,2-3,…….对于任意一个二进制数，也都可以表示成按权展开的多项式。

二进制八进制十进制十六进制之间的转换方法

二进制八进制十进制十六进制之间的转换方法二进制、八进制、十进制和十六进制是计算机中常用的数制表示方法。

在进行转换时，可以利用其数制规则和特点来进行相互转换。

以下将详细介绍二进制、八进制、十进制和十六进制之间的转换方法。

1.二进制转八进制：二进制数是由0和1组成的数，八进制数是由0-7组成的数。

每3位二进制数可以转换为1位的八进制数，所以将二进制数从右到左以3位一组进行分组，并用八进制数表示每组即可。

2.二进制转十进制：二进制数转换为十进制数的方法是将二进制数分别乘以2的n次方，并将结果相加，其中n从0开始递增，对应于从右到左的二进制位数。

3.二进制转十六进制：二进制数转换为十六进制数的方法是将二进制数分组为4位一组，然后将每组转换为十六进制数。

4.八进制转二进制：八进制数转换为二进制数的方法是将八进制数的每位转换为对应的3位二进制数。

例如：将八进制数326转换为二进制数，可以将其每位转换为对应的3位二进制数，得到结果：011010110。

5.八进制转十进制：八进制数转换为十进制数的方法是将八进制数分别乘以8的n次方，并将结果相加，其中n从0开始递增，对应于从右到左的八进制位数。

例如：将八进制数326转换为十进制数，可以分别计算3*8^2+2*8^1+6*8^0，得到结果：2066.八进制转十六进制：将八进制数转换为十六进制数，首先将八进制数转换为二进制数，然后将二进制数转换为十六进制数。

例如：将八进制数326转换为十六进制数，可以先将其转换为二进制数011010110，然后将二进制数转换为十六进制数，得到结果：D67.十进制转二进制：将十进制数转换为二进制数的方法是将十进制数不断除以2，然后将余数逆序排列，最后将得到的余数连接在一起。

8.十进制转八进制：将十进制数转换为八进制数的方法是将十进制数不断除以8，然后将余数逆序排列，最后将得到的余数连接在一起。

例如：将十进制数214转换为八进制数，可以依次计算214/8=26余6，26/8=3余2，3/8=0余3、最后将得到的余数逆序排列，得到结果：3269.十进制转十六进制：将十进制数转换为十六进制数的方法是将十进制数不断除以16，然后将余数逆序排列，对于10~15的余数，分别用A~F表示，最后将得到的余数连接在一起。

一、二进制如何转十进制，十进制如何转二进制
1、十进制正整数转成二进制。

要点：除二取余，然后倒序排列，高位补零。

2、小数转换为二进制的方法：对小数点以后的数乘2取余，最后把取的整数部分按先后高位到低位次序记录即可。

3、二进制转换成十进制的方法比较简单，只要将被转换的数按式（2n）展开并计算出结果即可。

二、八进制的转换
1.（十进制转八进制）：整数部分，除8取余法，每次将整数部分除以8，余数为该位权上的数，商继续除以8，余数又为上一个位权上的数，然后以此类推一直下去，直到商为零，最后从最后一个余数向前排列就可以了
2. （十进制转八进制）：小数部分，与转二进制相同，这里是乘八取整法，最后从高位到低位去记录。

3.（八进制转二进制）：先将八进制转换成十进制，再转换成二进制。

4. （二进制转八进制）：将八进制的每一个数化解成“八进制的二进制表示形式”，最后合成即可。

例如：
三、十六进制的转换
1.
ASCII表的认识——（P 29）
认识一：只学习英文字母（大、小写）和数字。

认识二：表中的大小判断：小写＞大写＞数字
认识三：1. ASCII规定：大写字母A的十进制值为65；小写字母a的十进制值为97。

2. 大写字母转小写字母——直接+32即可；小写字母转大写字母直接减32即可。

例如：大写字母A为65，则e的值为？
65+32+4=101
a、b、c、d、e、f ……计算时应该从”b”开始记录位数，所以本算式中应该加4，而不是加5.
认识四：在ASCII表中，“A”的二进制值为：100 0001
“h”的二进制值为：110 1000。

进位计数制及数制转换_计算思维与算法设计_[共4页]

142.2 信息在计算机中的表示2.2.1 进位计数制及数制转换计算机可以处理各种形式的数据，例如数值、字符、汉字，而这些数据在计算机中都是以二进制形式表示的。

下面首先介绍数制的概念，再介绍二进制、八进制、十六进制以及它们之间的转换。

1．R进制数人类在生产实践和日常生活中，创造了很多表示数的方法，而这些数的表示规则被称为数制。

使用有限个数符采用进位方式记数的数制叫做进位计数制。

例如，人们常用的十进制，钟表计时中使用的60进制等。

从十进制计数制可以看出进位计数制的一些特点：任何一个十进制数均由0～9等10个数字符号组成，这些数字符号称为数码；数码的个数称为基数，十进制的基数为10，逢十进一；不同的位置具有不同的位权，整数部分第i位（从小数点开始从右至左数）的位权为10i-1，小数部分第i位（从小数点开始从左至右数）的位权为10-i；任何一个十进制数均可写为按位权展开的形式，例如123.45＝1×102＋2×101＋3×100＋4×10-1＋5×10-2。

任意R进制计数制同样有基数、位权和按位权展开式，其中R可以是任意正整数，比如，二进制的R为2，八进制的R为8，十六进制的R为16。

具体来讲，R进制计数制有如下特点。

（1）每一种数制所使用的数码的个数称为基数R。

（2）进位原则，逢R进位。

（3）不同的位置具有不同的位权，整数部分第i位（从小数点开始从右至左数）的位权为R i-1，小数部分第i位（从小数点开始从左至右数）的位权为R-i。

例如，十进制的基数为10（数码0～9），位权是10的n次幂，二进制的基数为2（数码0～1），位权是2的n次幂，八进制的基数为8（数码0～7），位权是8的n次幂，十六进制的基数为16（数码0～9、A-F），位权是16的n次幂。

（4）任何一个R进制数均可写为按位权展开的形式。

与十进制数值的表示类似，任一R进制数的值都可表示为数码本身的值与所在位置位权的乘积之和。

数制转换及其计算方式

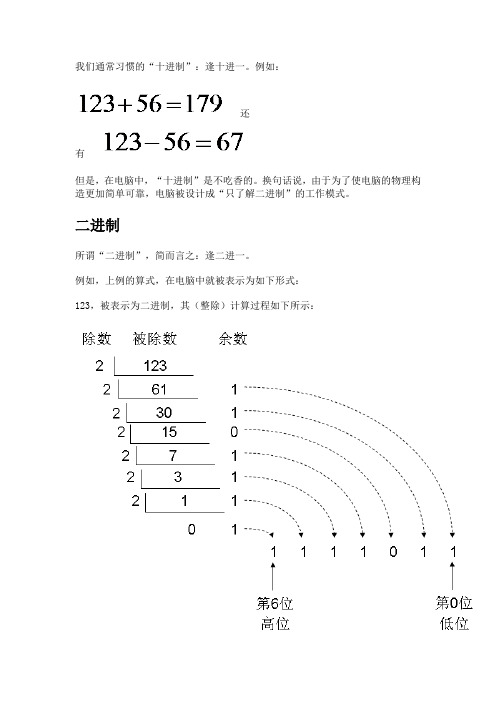
我们通常习惯的“十进制”：逢十进一。

例如：还有但是，在电脑中，“十进制”是不吃香的。

换句话说，由于为了使电脑的物理构造更加简单可靠，电脑被设计成“只了解二进制”的工作模式。

二进制所谓“二进制”，简而言之：逢二进一。

例如，上例的算式，在电脑中就被表示为如下形式：123，被表示为二进制，其（整除）计算过程如下所示：考虑到一个字节是8个二进制位，所以我们在“最高位”也就是“第7位”上补0，形成如下最终答案：同理，56的转换如下：56的二进制表示如下：再看加法的过程，注意：逢二进一！那么，二进制的10110011表示为十进制，应该是多少呢？计算过程如下：上述这个式子被称为“按权展开式”；按权展开式所得到的结果，一定是10进制的值。

自己算算看，答案是多少？根据按权展开式，我们总是可以得到“任何进制数所对应的十进制值”。

八进制和十六进制无论是八进制或是十六进制，都不是电脑所能“理解”的。

那为什么需要这两种进制呢？原因是，八进制和十六进制能够有效地提高二进制计算的效率。

换句话说，八进制或十六进制能够很方便地和二进制进行相互转换。

先来说说八进制：八进制“逢8进一”。

注意到：3个二进制位正好能表达1个八进制位的信息。

1个八进制位有共8种状态，对应的3个二进制位是所以，八进制和二进制的转换方式是十分简单的：3个二进制位转换成对应的1个八进制位。

举例来说，二进制到八进制的转换如下图所示：其中，每3位二进制数转换为1位八进制数。

注意到上图二进制数中，最左侧的0是我们手动补上去的，为的是凑足3个数进行转换。

同理，我们有下图：把上述转换得到的2个八进制数相加；按权展开，验算一下：这与十进制数计算的答案是相符的。

说明我们的八进制运算是正确的。

最后，我们也可以把八进制转为二进制，得到二进制的答案：（和先前的二进制形式的计算结果是相符的）由上运算过程可见，八进制的表示法，比二进制的表示法来得方便。

（尽管电脑不认识八进制，但是可以提高我们手工计算的速度。

二进制八进制十进制十六进制四种算法之间的互相转换

二进制八进制十进制十六进制四种算法之间的互相转换1.二进制转十进制：二进制数是基于2的数制系统，只包含0和1两个数字。

转换二进制数到十进制数非常简单，只需要将二进制数中的每个数字乘以2的幂次方，然后将结果相加即可。

例如，二进制数"1010"转换为十进制数的计算方法如下：1*2^3+0*2^2+1*2^1+0*2^0=8+0+2+0=102.八进制转十进制：八进制数是基于8的数制系统，只包含0到7的数字。

转换八进制数到十进制数也非常简单，只需要将八进制数中的每个数字乘以8的幂次方，然后将结果相加即可。

例如，八进制数"753"转换为十进制数的计算方法如下：7*8^2+5*8^1+3*8^0=7*64+5*8+3=448+40+3=4913.十六进制转十进制：十六进制数是基于16的数制系统，包含0到9的数字和A到F的字母。

转换十六进制数到十进制数也非常简单，只需要将每个十六进制数字乘以16的幂次方，然后将结果相加即可。

其中字母A到F分别表示10到15、例如，十六进制数"3AF"转换为十进制数的计算方法如下：3*16^2+10*16^1+15*16^0=3*256+10*16+15=768+160+15=9434.十进制转二进制：十进制数是我们日常生活中最常用的数制系统，包含数字0到9、转换十进制数到二进制数可以使用除2取余法。

具体步骤是：将十进制数除以2，直到商为0，然后将每次的余数倒序排列起来作为二进制数的结果。

例如，将十进制数10转换为二进制数的步骤如下：10/2=5余05/2=2余12/2=1余01/2=0余1倒序排列余数得到二进制数"1010"。

5.十进制转八进制：将十进制数转换为八进制数也可以使用除8取余法。

具体步骤与转换为二进制数相似，只需要将除数改为8即可。

例如，将十进制数25转换为八进制数的步骤如下：25/8=3余13/8=0余3倒序排列余数得到八进制数"31"。

数制及其转换

数制是指用一组固定的符号和统一的规则来表示数值的方法。

在数值计算中，一般采用进位计数制，即用进位的方法进行计数。

日常生活中人们习惯使用十进制，而在数字系统中常采用二进制、八进制、十进制和十六进制等。

数位是指数字符号在一个数中所处的位置，基数是指在某种进位计数制中，数位上所能使用的数字符号的个数，位权是指指在某种进位计数制中，数位所代表的大小，即处在某一位上的“1”所表示的数值大小。

数制转换是指将一种数制转换为另一种数制。

常见的数制转换包括二进制转换为十进制、八进制转换为十进制、十进制转换为二进制、十六进制转换为二进制等。

数制转换的方法包括按权展开法、逻辑运算法等。

计算机的数值通常采用二进制、八进制、十进制和十六进制表示。

其中，二进制是计算机中常用的数制，它具有运算简单、易于实现、易于进行逻辑运算等优点。

在计算机中，数值通常以二进制的形式存储和运算。

总之，数制及其转换是数值计算和计算机领域中非常重要的概念和方法。

通过了解不同数制的表示方法和转换规则，可以更好地理解计算机中数值的存储和运算原理，同时也可以为进行数值计算和研究计算机科学提供基础知识和技能。

二进制和十六进制都是计算机中常用的数制，它们的特点如下：1、二进制：二进制是计算机中最基本的数制，也是计算机内部数值表示的方式。

它只使用两个数字0和1来表示数值，是一种离散的数制。

在二进制中，每一位被称为一个“bit”（比特），它是计算机中最小的存储单位。

二进制的特点包括：➢简单易懂：只有两个数字0和1，容易理解和使用。

➢易于计算：二进制的计算规则与十进制相似，只需要掌握简单的加法和乘法规则即可。

➢适合电子电路实现：计算机内部的逻辑电路使用二进制信号进行控制和传输，二进制数制可以直接反映电路的状态。

此外，二进制也具有抗干扰能力强、可靠性高等优点，因为每位数据只有高低两个状态，当受到一定程度的干扰时，仍能可靠地分辨出它是高还是低。

2、十六进制：十六进制也是计算机中常用的数制，它使用16个数字（0-9和A-F）来表示数值。

数制转换及其计算方式

数制转换及其计算方式数制转换指的是将一个数从一种数制表示转换成另一种数制表示。

常见的数制包括十进制、二进制、八进制和十六进制。

在进行数制转换时，我们首先需要了解各种数制的计数规则和表示方式。

十进制是我们日常生活中最常使用的数制，它是一种基数为10的数制。

十进制中的每一位数字的权值分别为10的幂次方，从右向左依次为10^0、10^1、10^2、以此类推。

二进制是计算机系统中常用的数制，它是一种基数为2的数制。

二进制中的每一位数字的权值分别为2的幂次方，从右向左依次为2^0、2^1、2^2、以此类推。

八进制是一种基数为8的数制，它在计算机系统中使用较少。

八进制中的每一位数字的权值分别为8的幂次方，从右向左依次为8^0、8^1、8^2、以此类推。

十六进制是计算机系统中常用的数制之一，它是一种基数为16的数制。

十六进制中的每一位数字的权值分别为16的幂次方，从右向左依次为16^0、16^1、16^2、以此类推。

十六进制使用0-9和A-F表示数字10-15我们可以通过以下方法进行数制转换：1.二进制转换为十进制：首先将二进制数按权展开，然后将各位上的1与该位的权相乘，最后将所有乘积相加即可得到十进制数。

2.十进制转换为二进制：首先确定该十进制数在二进制中的最高位数，然后不断用该数除以2，记录余数，直到商为0为止，最后将所有余数倒序排列即得到二进制数。

3.八进制转换为十进制：八进制数的转换与二进制类似，只需要将权展开时使用的基数从2改为8即可。

4.十进制转换为八进制：十进制转八进制的方法与十进制转二进制类似，只需要将除法的除数从2改为8即可。

5.十六进制转换为十进制：十六进制数的各位数字和权相乘的方法与二进制和八进制相同，只需要将权展开时使用的基数从2或8改为16即可。

此外，十六进制数中的字母A-F分别表示10-15，需要进行对应替换。

6.十进制转换为十六进制：十进制转十六进制的方法与十进制转二进制类似，只需要将除法的除数从2改为16，同时将余数对应替换为字母A-F即可。

c语言二进制十进制十六进制转换计算

C语言是一种高级编程语言，它具有丰富的数学计算功能，其中包括二进制、十进制和十六进制之间的转换计算。

本文将重点介绍C语言中如何进行二进制、十进制和十六进制之间的转换计算，以及其相关的方法和注意事项。

一、二进制、十进制和十六进制的概念及表示方法1. 二进制二进制是一种基数为2的数制，它只包含0和1两个数字。

在C语言中，二进制数通常以0b或0B开头表示，例如0b1010表示十进制的10。

2. 十进制十进制是我们常用的数制，基数为10，包含了0到9这10个数字。

在C语言中，十进制数直接以数字形式表示，例如123表示十进制的123。

3. 十六进制十六进制是一种基数为16的数制，它包含0到9这10个数字以及A 到F这6个英文字母，分别对应10到15。

在C语言中，以0x或0X 开头表示十六进制数，例如0x1A表示十进制的26。

二、二进制与十进制的转换计算方法1. 二进制转十进制二进制转换为十进制可以使用加权法，即将二进制数从右向左依次乘以2的幂次方，然后将结果相加。

1010转换为十进制的计算过程为：1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 10。

2. 十进制转二进制十进制转换为二进制可以使用除2取余法，即将十进制数不断除以2，将每次的余数倒序排列即可得到二进制数。

26转换为二进制的计算过程为：26÷2=13……0，13÷2=6……1，6÷2=3……0，3÷2=1……1，1÷2=0……1，倒序排列得到xxx。

三、十六进制与十进制的转换计算方法1. 十六进制转十进制十六进制转换为十进制可以使用加权法，即将十六进制数从右向左依次乘以16的幂次方，然后将结果相加。

1A转换为十进制的计算过程为：1*16^1 + A*16^0 = 26。

2. 十进制转十六进制十进制转换为十六进制可以使用除16取余法，即将十进制数不断除以16，将每次的余数倒序排列，A对应10，B对应11，依次类推，直到商为0即可得到十六进制数。

十进制数的概念与转换

十进制数的概念与转换在日常生活中，我们经常会接触到数字，而这些数字大多采用了十进制数的表示方法。

十进制数是一种基数为10的数制体系，使用0~9这10个数字进行表示。

本文将介绍十进制数的概念以及它与其他进制数的转换方法。

一、十进制数的概念十进制数是最常见也是最为人熟知的数制体系，它在我们的现代计算中具有重要的地位。

以0~9这10个数字作为基本数字，每一位上的数字乘以10的幂次方，再进行求和，就可表示出一个十进制数。

例如，数字3578表示的就是一个十进制数。

其中，个位数8乘以10^0，十位数7乘以10^1，百位数5乘以10^2，千位数3乘以10^3，以此类推。

最终将各位上的结果相加，即可得到最终的十进制数3578。

二、其他进制数与十进制数的转换1. 二进制转十进制二进制是一种基数为2的数制体系，它只有0和1两个数字。

在二进制数中，每一位上的数字乘以2的幂次方，再进行求和，就可表示一个十进制数。

例如，二进制数1110表示的就是一个十进制数。

其中，个位数0乘以2^0，十位数1乘以2^1，百位数1乘以2^2，千位数1乘以2^3。

最终将各位上的结果相加，即可得到最终的十进制数14。

2. 八进制转十进制八进制是一种基数为8的数制体系，它使用数字0~7进行表示。

八进制数中，每一位上的数字乘以8的幂次方，再进行求和，就可表示一个十进制数。

例如，八进制数172表示的就是一个十进制数。

其中，个位数2乘以8^0，十位数7乘以8^1，百位数1乘以8^2。

最终将各位上的结果相加，即可得到最终的十进制数122。

3. 十六进制转十进制十六进制是一种基数为16的数制体系，它使用数字0~9和字母A~F进行表示。

十六进制数中，每一位上的数字或字母乘以16的幂次方，再进行求和，就可表示一个十进制数。

例如，十六进制数3A5表示的就是一个十进制数。

其中，个位数5乘以16^0，十位数A（对应10）乘以16^1，百位数3乘以16^2。

最终将各位上的结果相加，即可得到最终的十进制数933。

16进制转换10进制的方法

16进制转换10进制的方法十六进制（Hexadecimal）是一种基数为16的数制，使用数字0-9和字母A-F来表示。

而十进制（Decimal）是我们平时最常用的数制，基数为10，使用数字0-9来表示。

将十六进制转换为十进制，可以采用以下方法：方法一：逐位相乘法1.将十六进制数的每一位按权相加即可得到十进制数。

例如，十六进制数"2A"转换为十进制的计算过程如下：2A=(2×16^1)+(10×16^0)=32+10=42这个方法要求我们根据权重对每一位进行相乘再相加，十六进制数的每一位对应的权重是16的n次方，其中n是从右侧开始数的位数，从0开始递增的整数。

方法二：乘幂法1.将十六进制数从右往左依次排列，并为每一位标号（从0开始）。

例如，十六进制数"2A"的排列结果为"A2"，并为每一位进行标号(0号位为A，1号位为2)。

2.使用乘幂法，将每一位与16的幂相乘，并相加得到十进制的结果。

例如：A2=(10×16^1)+(2×16^0)=160+2=162这个方法是将每一位与16的幂相乘，并相加得到结果。

与逐位相乘法类似，十六进制数的每一位对应的幂是16的n次方，其中n是从右侧开始数的位数，从0开始递增的整数。

方法三：使用计算器或编程语言如果你需要进行大量的十六进制转换十进制操作，可以使用计算器或编程语言来进行转换。

大多数计算器和编程语言都提供了内置的函数或方法来实现这个转换，可以通过输入十六进制数作为参数，然后调用相应的函数或方法来得到转换结果。

例如，使用Python编程语言，可以使用int(函数来实现十六进制到十进制的转换。

示例代码如下：```hex_num = '2A'dec_num = int(hex_num, 16)print(dec_num)```运行结果为：```42```这个方法更简便，特别适用于需要进行大量转换的情况。

十进制二进制互转的计算方法

十进制二进制互转的计算方法在计算机科学中，我们经常需要在十进制和二进制之间进行转换。

十进制是我们日常生活中常用的数制体系，而二进制则是计算机中使用的数制体系。

了解如何进行这两个数制的转换对于理解计算机工作原理和算法非常重要。

一、十进制转二进制计算方法十进制转换为二进制的方法非常简单。

我们只需使用一个除以2的过程，直到结果为0为止。

具体的步骤如下：1.取需要转换的十进制数作为被除数。

2.将被除数除以2，得到商和余数。

3.将商作为新的被除数，重复步骤2，直到商为0。

4.将每次得到的余数按顺序排列，即为所求的二进制数。

以下是一个示例来说明该方法的计算过程：假设我们要将十进制数37转换为二进制数：37÷2=18...余118÷2=9...余09÷2=4...余14÷2=2...余02÷2=1...余01÷2=0...余1二、二进制转十进制计算方法二进制转换为十进制的方法也是非常简单的。

我们只需使用一个乘以2的过程，从最高位开始，依次累加每一位的值。

具体的步骤如下：1.将需要转换的二进制数从左向右依次编号，从0开始。

2.从最高位开始，依次累加每一位的值，该位的值是二进制位的数值乘以2的幂，幂的指数等于位的编号。

3.累加所有位得到的和即为所求的十进制数。

以下是一个示例来说明该方法的计算过程：1×2^4+0×2^3+1×2^2+1×2^1+0×2^0=16+0+4+2+0=22三、小数的二进制转换对于小数的二进制转换，我们可以使用以下的方法：1.将小数的整数部分转换为二进制，与之前的方法相同。

2.将小数的小数部分转换为二进制，使用一个乘以2的过程，从小数点后的第一位开始，依次乘以2的负幂，幂的指数等于位的编号。

3.将整数和小数部分的二进制数拼接在一起，以小数点分隔。

以下是一个示例来说明该方法的计算过程：假设我们要将小数0.625转换为二进制数：整数部分：0÷2=0...余0小数部分：0.625×2=1.25...将1记下0.25×2=0.50...将0记下0.50×2=1.00...将1记下因此，0.625的二进制表示为0.101四、二进制转换为其他进制除了十进制之外，我们还可以将二进制转换为其他进制，例如八进制和十六进制。

第二章进位计数制

第二章第一部分数制转换及运算1 进位计数制1.1现实生活中存在的进位计数制1.2分析十进制数1.3进位计数制三要素基数：逢N进一，N为基数数码：基数为N，共有N个数码，0—N-1位权：数位上固定大小的值。

对于基数为N的进位计数制，由小数点分割，分别是[…N4，N3，N2，N1，N0，N-1，N-2，N-3，N-4…]1.4分析二进制数、八进制数和十六进制数1.5数按位权展开任何一种数制表示的数，都可以写成按位权展开的多项式之和的形式。

此多项式之和是该数所对应的十进制数值大小（结果为十进制数，提供了由其它进制数向十进制数转换的方法）。

2不同进位计数制间的转换2.1 R进制数转换成十进制数按位权展开求和。

2.2 十进制数转换成R进制数对于整数部分采用“除R取余法”；对于小数部分采用“乘R取整法”。

下面以十进数转换为二进数为例进行分析。

1）十进制整数转换为二进制整数除2取余法：将十进制整数反复除以2，若余数为1则对应于二进制数相应位为1，余数为0则对应于二进制数相应位为0。

第一次相除得到的余数是二进制数的最低位，最后一次余数是二进制数的最高位。

从低位到高位逐次进行，直到商为0为止。

例：(215)10=( )22）十进位纯小数转换为二进制纯小数乘2取整法：将十进制纯小数反复乘以2，所得新数的整数部分为1，则二进制数相应位为1，整数部分为0，则二进制数相应位为0。

第一次得到的整数是二进制数的最高位，最后一次得到的整数是二进制数的最低位。

从高位到低位逐次进行，直到满足精度要求或小数部分为0为止。

例：(0.6531)10=( )2(0.125)10=( )23）十进制数转换为二进制数例：(215.6531)10=( )22.3二进制数与八进制数之间的转换1）二进制数转换成八进制数由于八进制数的最大数码为7，需要用三位二进制数来表示，因此：方法：由小数点作为分隔，对于整数部分，由低位到高位将二进制数每三位分为一组，不够三位时在高位左边用0被足(或不补)，对于小数部分，由高位到低位，每三位一组，不足三位时在低位右边填0补足。

二进制转换成十进制计算方法

二进制转换成十进制计算方法
宝子，今天咱来唠唠二进制转十进制的计算方法哈。

二进制呢，就是只有0和1这两个数字的数制。

那咋把它变成十进制呢？其实很简单啦。

比如说一个二进制数101。

咱从右往左看哈，最右边这个数字呢，它就代表2的0次方乘以这个数字本身。

在这里呢，最右边是1，那就是1乘以2的0次方，2的0次方等于1哦，所以就是1乘以1等于1。

再看中间这个数字0，它代表2的1次方乘以这个数字本身，也就是0乘以2的1次方，2的1次方是2，0乘以2就等于0啦。

最后看最左边这个1，它代表2的2次方乘以这个数字本身，2的2次方是4，那就是1乘以4等于4。

然后把这几个结果加起来，1+0+4 = 5，这个二进制数101就等于十进制的5啦。

再举个例子，二进制数1101。

从右往左开始算哈。

最右边的1，就是1乘以2的0次方等于1。

旁边这个0呢，0乘以2的1次方等于0。

再旁边这个1，1乘以2的2次方等于4。

最左边这个1，1乘以2的3次方等于8。

把这些结果加起来，1+0+4+8 = 13，所以二进制数1101就等于十进制的13。

宝子，你看，二进制转十进制是不是没有那么难呀？就按照这个从右往左，每个数字乘以2的相应次方然后再加起来的方法，就可以轻松搞定啦。

以后再遇到这种
转换就不怕啦。

八进制转二进制计算公式

八进制转二进制计算公式在计算机科学中，八进制和二进制都是常见的数制系统。

八进制是一种基数为8的数制系统，而二进制是一种基数为2的数制系统。

在实际应用中，我们经常需要将八进制数转换为二进制数。

本文将介绍八进制转二进制的计算公式，并给出一些示例来帮助读者更好地理解这个转换过程。

八进制转二进制的计算公式如下：1. 首先，将八进制数的每一位转换为对应的三位二进制数。

2. 然后，将所有的三位二进制数连接在一起，得到最终的二进制数。

下面我们来看一个具体的例子，以便更好地理解这个转换过程。

假设我们要将八进制数"345"转换为二进制数。

按照上面的计算公式，我们首先将八进制数的每一位转换为对应的三位二进制数。

具体的转换规则如下：数字3对应的三位二进制数为"011"数字4对应的三位二进制数为"100"数字5对应的三位二进制数为"101"然后，我们将所有的三位二进制数连接在一起，得到最终的二进制数为"011100101"。

通过这个例子，我们可以看到八进制转二进制的计算过程并不复杂，只需要按照规定的转换规则进行逐步计算即可。

下面我们再来看一个例子，加深对这个转换过程的理解。

假设我们要将八进制数"777"转换为二进制数。

按照上面的计算公式，我们首先将八进制数的每一位转换为对应的三位二进制数。

具体的转换规则如下：数字7对应的三位二进制数为"111"数字7对应的三位二进制数为"111"数字7对应的三位二进制数为"111"然后，我们将所有的三位二进制数连接在一起，得到最终的二进制数为"111111111"。

通过这个例子，我们可以看到无论八进制数是什么，转换为二进制数的过程都是一样的，只需要按照规定的转换规则进行逐步计算即可。

在实际应用中，八进制转二进制的计算过程可以通过编程语言来实现。