电磁场与电磁波理论(第二版)(徐立勤,曹伟)第4章习题解答
电磁场与电磁波课后习题及答案四章习题解答
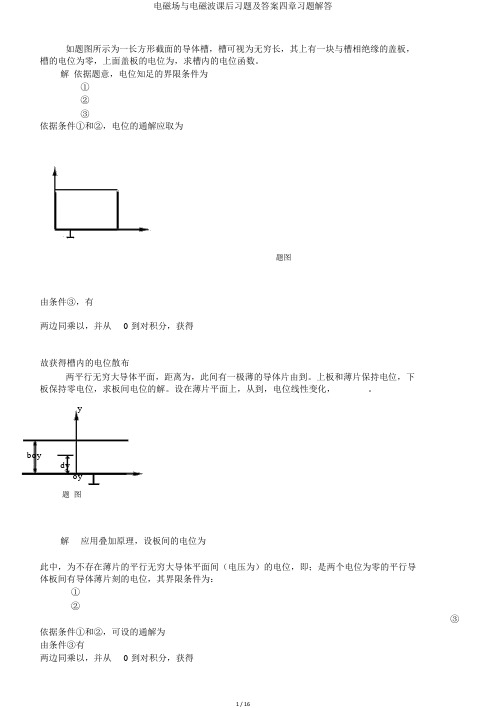
如题图所示为一长方形截面的导体槽,槽可视为无穷长,其上有一块与槽相绝缘的盖板,槽的电位为零,上面盖板的电位为,求槽内的电位函数。
解依据题意,电位知足的界限条件为①②③依据条件①和②,电位的通解应取为题图由条件③,有两边同乘以,并从0 到对积分,获得故获得槽内的电位散布两平行无穷大导体平面,距离为,此间有一极薄的导体片由到。
上板和薄片保持电位,下板保持零电位,求板间电位的解。
设在薄片平面上,从到,电位线性变化,。
yboydyoy题图解应用叠加原理,设板间的电位为此中,为不存在薄片的平行无穷大导体平面间(电压为)的电位,即;是两个电位为零的平行导体板间有导体薄片刻的电位,其界限条件为:①②③依据条件①和②,可设的通解为由条件③有两边同乘以,并从0 到对积分,获得故获得求在上题的解中,除开一项外,其余全部项对电场总储能的贡献。
并按定出边沿电容。
解在导体板()上,相应于的电荷面密度则导体板上(沿方向单位长)相应的总电荷相应的电场储能为其边沿电容为如题图所示的导体槽,底面保持电位,其余两面电位为零,求槽内的电位的解。
解依据题意,电位知足的界限条件为①题图②③依据条件①和②,电位的通解应取为由条件③,有两边同乘以,并从0 到对积分,获得故获得槽内的电位散布为一长、宽、高分别为、、的长方体表面保持零电位,体积内填补密度为的电荷。
求体积内的电位。
解在体积内,电位知足泊松方程( 1)长方体表面上,电位知足界限条件。
由此设电位的通解为代入泊松方程(1),可得由此可得或( 2)由式( 2),可得故如题图所示的一对无穷大接地平行导体板,板间有一与轴平行的线电荷,其地点为。
求板间的电位函数。
解因为在处有一与轴平行的线电荷,认为界将场空间切割为和两个地区,则这两个地区中的电位和都知足拉普拉斯方程。
而在的分界面上,可利用函数将线电荷表示成电荷面密度。
电位的界限条件为题图①②③由条件①和②,可设电位函数的通解为由条件③,有( 1)( 2)由式( 1),可得( 3)将式( 2)两边同乘以,并从到对积分,有(4)由式( 3)和( 4)解得故如题图所示的矩形导体槽的电位为零,槽中有一与槽平行的线电荷。
电磁场与电磁波理论第二版徐立勤,曹伟第2章习题解答

电磁场与电磁波理论第二版徐立勤,曹伟第2章习题解答第2章习题解答2.2已知半径为a 、长为l 的圆柱体内分布着轴对称的体电荷,已知其电荷密度()0Va ρρρρ=,()0a ρ≤≤。
试求总电量Q 。
解:2π200002d d d d π3laV VQ V z la aρρρρρ?ρ===?2.3 半径为0R 的球面上均匀分布着电荷,总电量为Q 。
当球以角速度ω绕某一直径(z 轴)旋转时,试求其表面上的面电流密度。
解:面电荷密度为 204πS QR ρ=面电流密度为 00200sin sin sin 4π4πS S S Q Q J v R R R R ωθρρωθωθ=?=== 2.4 均匀密绕的螺旋管可等效为圆柱形面电流0S S J e J ?=。
已知导线的直径为d ,导线中的电流为0I ,试求0S J 。
解:每根导线的体电流密度为 00224π(/2)πI I J d d== 由于导线是均匀密绕,则根据定义面电流密度为04πS IJ Jd d ==因此,等效面电流密度为04πS IJ e d=2.6 两个带电量分别为0q 和02q 的点电荷相距为d ,另有一带电量为0q 的点电荷位于其间。
为使中间的点电荷处于平衡状态,试求其位置。
当中间的点电荷带电量为-0q 时,结果又如何?解:设实验电荷0q 离02q 为x ,那么离0q 为x d -。
由库仑定律,实验电荷受02q 的排斥力为实验电荷受0q 的排斥力为要使实验电荷保持平衡,即21F F =,那么由00222114π4π()q q x d x εε=-,可以解得如果实验电荷为0q -,那么平衡位置仍然为d d x 585.0122=+=。
只是这时实验电荷与0q 和02q 不是排斥力,而是吸引力。
2.7 边长为a 的正方形的三个顶点上各放置带电量为0q 的点电荷,试求第四个顶点上的电场强度E 。
解:设点电荷的位置分别为()00,0,0q ,()0,0,0q a 和()00,,0q a ,由库仑定律可得点(),,0P a a 处的电场为2.9半径为0R 的半球面上均匀分布着面电荷,电荷密度为0S ρ,试求球心处的电场强度;若同样的电荷均匀分布在半径为0R 的半球内,再求球心处的电场强度。
电磁学第二版习题答案第四章

j
δ
=
ρ I 3.14 ×10−8 × 20 = = 0.2 V 2 −3 2 m πR 3.14 × (10 )
4.3.5 铜的电阻温度系数为 4.3 ×10−3 / 0C ,在 0 0C 时的电阻率为 1.6 ×10−8 Ω ⋅ m ,求直径为 5mm、长 为 160km 的铜制电话线在 25 0C 时的电阻。
b a
ρ dx ρ 1 1 ρ (b − a) = ( − )= 2 4π r 4π a b 4π ab
ρ dx 4π r 2
4.3.4 直径为 2mm 的导线由电阻率为 3.14 ×10−8 Ω ⋅ m 的材料制成,当 20A 的电流均匀地流过该导 体时,求导体内部的场强。
解:根据 j = δ E ,得 E =
lρ ⎡ 1 1 ⎤ lρ − = π (b − a) ⎢ ⎣a b⎥ ⎦ π ab lρ l =ρ 2 s πa
当 a = b 时: R =
4.3.3 球形电容器内外半径为 a 和 b,两极板间充满电阻率为 ρ 的均匀物质,试计算该电容器的漏 电电阻。 解:对漏电电阻,其内部电极电位差,电流沿径向从高电位向低电位流过,则有: dR = 积分得: R = ∫ dR = ∫
(a) Rab = 1K Ω , (b) Rab = 4.5Ω (c) Rab = 1.2Ω (d) Rab = 7.4Ω (e) Rab = 5Ω (f) Rab = 1.5Ω (g) Rab = 14Ω
4.2.3 当附图中的 R1 为何值时 A、B 间的总电阻恰等于 R0? 解:由 R总 = R1 +
U = 0.01× 103 = 10(V ) , U 额 = RW =
2 P 100 = 0.01 × 100 = 0.01(W )
电磁场理论 答案 习题4

( evr
2 cosθ
+
evθ
sin θ
)
4-5 接地无限大导体平板上有一个半径为 a 的半球形突起,在点 (0,0, d ) 处有一个
点电荷 q (如图 4-3),求导体上方的电
z
位。
d·q
解:计算导体上方的电位时,要保持导 体平板部分和半球部分的电位都为零。先找平
面导体的镜像电荷 q1 = −q ,位于 (0,0,−d )
k Q2
所以在整个过程中,外力作的总功为
8πε 0d
. 也可以用静电能计算,在移动以前,系统的静电能等于两个点电荷之间的相互 w 作用能:
wwW
=
1 2
q1ϕ1
+
1 2
q2ϕ
2
=
1 Q
2
4π
−Q ε0 (2d )
+
1 (−Q) 2 4π
−Q ε0 (2d )
=
− Q2 8π ε0d
移动点电荷到无穷远以后,系统的静电能为零。因此,在这个过程中,外力作
h 4-3 证明:一个点电荷 q 和一个带有电荷 Q 、半径为 R 的导体球之间的作用力为
.kF
=
q 4π ε 0
⎡ ⎢ ⎢ ⎢
Q
+ D
Rq
D
2
−
DRq (D2 − R2 )2
⎤ ⎥ ⎥ ⎥
w⎣
⎦
其中 D 是 q 到球心的距离 (D > R) 。
ww证明:使用镜像法分析。由于导体球不接地,本身又带电 Q ,必须在导体球内
om 处。再找球面镜像电荷 q2 = −aq / d ,位于
a b·q2 ·
-b·q3
电磁场与电磁波课后复习题与答案四章复习题解答
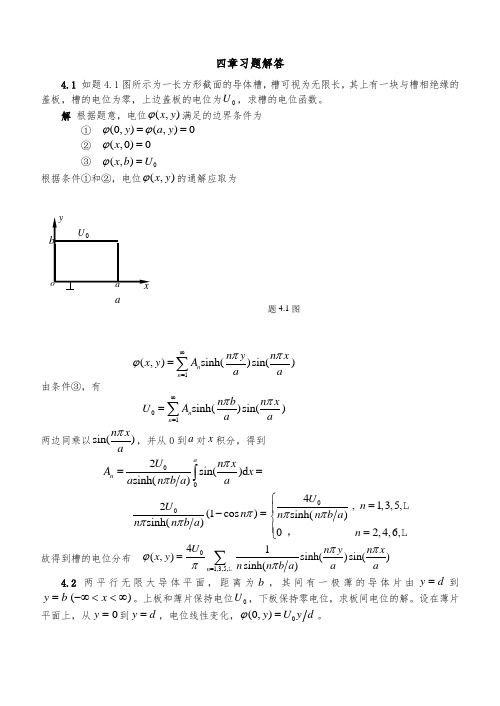
四章习题解答4.1 如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ=③ 0(,)x b U ϕ=根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a aππϕ∞==∑ 由条件③,有01sinh()sin()n n n b n x U A a aππ∞==∑ 两边同乘以sin()n xaπ,并从0到a 对x 积分,得到 002sin()d sinh()an U n xA x a n b a aππ==⎰ 02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩L L , 故得到槽的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑L 4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
a题4.1图解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:① 22(,0)(,)0x x b ϕϕ== ② 2(,)0()x y x ϕ=→∞③ 002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩根据条件①和②,可设2(,)x y ϕ的通解为 21(,)sin()e n x b n n n y x y A b ππϕ∞-==∑ 由条件③有 00100(0)sin()()n n U U y y d n y bA U U b y y d y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n yb π,并从0到b 对y 积分,得到 0002211(1)sin()d ()sin()d d bn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d bππ 故得到 (,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d n b b ππππ∞-=+∑ 4.3 求在上题的解中,除开0U y b 一项外,其他所有项对电场总储能的贡献。
电磁场与电磁波习题答案资料讲解

电磁场与电磁波习题答案第四章习题解答★【4.1】如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为0U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ==;② (,0)0x ϕ=; ③ 0(,)x b U ϕ= 根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a a ππϕ∞==∑ 由条件③,有 01sinh()sin()n n n b n xU A a a ππ∞==∑两边同乘以sin()n xa π,并从0到a 对x 积分,得到002sin()d sinh()an U n x A x a n b a a ππ==⎰ 02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩,故得到槽内的电位分布 01,3,5,41(,)sinh()sin()sinh()n U n y n xx y n n b a a aππϕππ==∑4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位0U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为0U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:22(,0)(,)0x x b ϕϕ==① 2(,)0()x y x ϕ=→∞②③ 002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b db ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩; 根据条件①和②,可设2(,)x y ϕ的通解为21(,)sin()en x bn n n yx y A b ππϕ∞-==∑;由条件③有 00100(0)sin()()n n U U y y d n y b A U U b y yd y b db π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n ybπ,并从0到b 对y 积分,得到 0002211(1)sin()d ()sin()d d bn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d bππ 故得到 (,)x y ϕ=0022121sin()sin()e n x b n U bU n d n y y b d nb b ππππ∞-=+∑ 4.4 如题4.4图所示的导体槽,底面保持电位0U ,其余两面电位为零,求槽内的电位的解。
电磁场与电磁波第二版课后答案

电磁场与电磁波第二版课后答案本文档为《电磁场与电磁波》第二版的课后答案,包含了所有章节的练习题的答案和解析。
《电磁场与电磁波》是电磁学领域的经典教材,它讲述了电磁场和电磁波的基本原理和应用。
通过学习本书,读者可以深入了解电磁学的基本概念和原理,并且能够解决一些相关问题。
第一章绪论练习题答案1.电磁场是由电荷和电流产生的一种物质性质,具有电场和磁场两种形式。
电磁波是电磁场的振动。
电磁辐射是指电磁波传播的过程。
2.对于一点电荷,其电场是以该点为中心的球对称分布,其强度与距离成反比。
对于无限长直导线产生的电场,其强度与距离呈线性关系,方向垂直于导线轴线。
3.电磁场的本质是相互作用力。
电场力是由于电荷之间的作用产生的,磁场力是由于电流之间的作用产生的。
解析1.电磁场是由电荷和电流产生的物质性质。
当电荷存在时,它会产生一个电场,该电荷周围的空间中存在电场强度。
同时,当电流存在时,它会产生一个磁场,该电流所在的区域存在磁场。
电磁波是电磁场的振动传播。
电磁波是由电磁场的变化引起的,相邻电磁场的振动会相互影响,从而形成了电磁波的传播。
电磁辐射是指电磁波在空间中的传播过程。
当电磁波从一个介质传播到另一个介质时,会发生折射和反射现象。
2.在一点电荷产生的电场中,电场强度与该点到电荷的距离成反比,即\(E = \frac{{k \cdot q}}{{r^2}}\),其中\(E\)为电场强度,\(k\)为电场常数,\(q\)为电荷量,\(r\)为距离。
对于无限长直导线产生的电场,其电场强度与离导线的距离呈线性关系。
当离无限长直导线的距离为\(r\)时,其电场强度可表示为\(E = \frac{{\mu_0 \cdot I}}{{2 \pi \cdot r}}\),其中\(E\)为电场强度,\(\mu_0\)为真空中的磁导率,\(I\)为电流强度。
3.电磁场的本质是相互作用力。
当两个电荷之间有作用力时,这个作用力是由于它们之间的电场力产生的。
电磁场与电磁波理论(第二版)(徐立勤-曹伟)第3章习题解答

第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇r r 和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+r r r0202εερA -=Φ∇-=(2) ()x y z E A e yz e xz e xy Φ=-∇=-++r r r r r020=Φ∇-=ερ(3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦r r r r20004sin sin 3sin Bz Bz A A A ρεΦεϕϕεϕρρ⎛⎫⎛⎫=-∇=-+-=-+ ⎪ ⎪⎝⎭⎝⎭(4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-r r r r r200cos 2cos cos 6sin cos sin sin A A A θϕϕρεΦεθϕθθ⎛⎫=-∇=-+- ⎪⎝⎭3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为22001111100()()22S S d R d R d ρρΦεε=+-=- 下顶面在球心产生的电位为22002222200()()22S S d R d R d ρρΦεε=+-=- 侧面在球心产生的电位为030014π4πS S SSRRρρΦεε==⎰式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为1230S R ρΦΦΦΦε=++=3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
电磁场与电磁波理论(第二版)(徐立勤,曹伟)第3章习题解答

第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+ 0202εερA -=Φ∇-= (2) ()x y z E A e yz e xz e xy Φ=-∇=-++ 020=Φ∇-=ερ (3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦20004sin sin 3sin BzBz A A A ρεΦεϕϕεϕρρ⎛⎫⎛⎫=-∇=-+-=-+ ⎪ ⎪⎝⎭⎝⎭ (4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-200cos 2cos cos 6sin cos sin sin A A A θϕϕρεΦεθϕθθ⎛⎫=-∇=-+- ⎪⎝⎭3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为22001111100()()22S S d R d R d ρρΦεε=+-=- 下顶面在球心产生的电位为22002222200()()22S S d R d R d ρρΦεε=+-=- 侧面在球心产生的电位为030014π4πS S SSRRρρΦεε==⎰式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为1230S R ρΦΦΦΦε=++=3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
电磁场与电磁波实际(第二版)(徐立勤-曹伟)第3章习题解答

第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+ 0202εερA -=Φ∇-= (2) ()x y z E A e yz e xz e xy Φ=-∇=-++ 020=Φ∇-=ερ (3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦20004sin sin 3sin BzBz A A A ρεΦεϕϕεϕρρ⎛⎫⎛⎫=-∇=-+-=-+ ⎪ ⎪⎝⎭⎝⎭ (4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-200cos 2cos cos 6sin cos sin sin A A A θϕϕρεΦεθϕθθ⎛⎫=-∇=-+- ⎪⎝⎭3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为0011100)()22S S d R d ρρΦεε==- 下顶面在球心产生的电位为0022200)()22S S d R d ρρΦεε==- 侧面在球心产生的电位为030014π4πS S SSRRρρΦεε==⎰式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为1230S R ρΦΦΦΦε=++=3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
电磁场与电磁波理论(第二版)(徐立勤,曹伟)第3章习题解答

For personal use only in study and research; not for commercial use第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+ 0202εερA -=Φ∇-= (2) ()x y z E A e yz e xz e xy Φ=-∇=-++ 020=Φ∇-=ερ (3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦ (4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为下顶面在球心产生的电位为 侧面在球心产生的电位为式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为 3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
已知0z >时,201050x y z E e e e =-+V /m 。
试求0z <时的D 。
解:由电场切向分量连续的边界条件可得代入电场法向方向分量满足的边界条件可得于是有3.9 如题 3.9图所示,有一厚度为2d 的无限大平面层,其中充满了密度为()0πcosxx dρρ=的体电荷。
电磁场与电磁波课后习题答案第四章

4.3若半径为a 、电流为I 的无线长圆柱导体置于空气中,已知导体的磁导率为0μ,求导体内、外的磁场强度H 和磁通密度B 。
解:(1)导体内:0≤ρ<a由安培环路定理,⎰•ll d H='I'I =22.I a πρπ=22I a ρ 所以,21.22I H a ρπρ=,122I H a ρπ=,122I H e a ϕρπ→→=,011022I B H e a ϕμρμπ→→→==(2)导体外:a ≤ρ<+∞⎰•l l d H =I, 所以2.2H I πρ=,22I H e ϕπρ→→=,022I B e ϕμπρ→→=4.5 在下面的矢量中,哪些可能是磁通密度B ?如果是,与它相应的电流密度J 为多少? (1)F a ρρ→→=解:1..()F F ρρρρ→∂∇=∂=1.2ρρ=2≠0所以F →不是磁通密度 (2)F →=-x a →y+y a →x 解:∇.F →=y x ∂-∂+xy ∂∂=0 所以F 是磁通密度 B →∇⨯=0μJ →=|x y ze e e x y zy x 0→→→∂∂∂∂∂∂-=2z e → 所以 J →=02μz e →(3)F →=x a →x —y a →y∇.F →=0F →是磁通密度B →∇⨯=0μJ →=|x y ze e e x y zx y→→→∂∂∂∂∂∂-=0所以J →=0 (4)F →=a ϕ→-r∇.F →=0所以F →是磁通密度B →∇⨯=r 2a a a r sin r sin rr 20r sin 0ϕθθθθϕθ→→→∂∂∂∂∂∂-=r a →-θcot +2a θ→=0μJ →所以J →=0cot θμ-r a →+02μa θ→ 4.6已知某电流在空间产生的磁矢位是A →=x a →2x y+y a →x 2y +z a →(2y —2z ) 求磁感应强度B →解:B →=A →∇⨯=|x y z2e e e x y z222x y xy y z →→→∂∂∂∂∂∂-=2y x e →+z e →(2y —2z )4.13已知钢在某种磁饱和情况下的磁导率为1μ=20000μ,当钢中的磁通密度为B 1=0.5×102T ,1θ= 75°时,试求此时的磁力线由钢进入自由空间一侧后,磁通密度2B 的大小与2B 与法线的夹角2θ。
电磁场与电磁波理论(第二版)(徐立勤,曹伟)第2章习题解答

第2章习题解答2.2已知半径为a 、长为l 的圆柱体内分布着轴对称的体电荷,已知其电荷密度()0V a ρρρρ=,()0a ρ≤≤。
试求总电量Q 。
解:2π200002d d d d π3laV VQ V z la aρρρρρϕρ===⎰⎰⎰⎰2.3 半径为0R 的球面上均匀分布着电荷,总电量为Q 。
当球以角速度ω绕某一直径(z 轴)旋转时,试求其表面上的面电流密度。
解:面电荷密度为 24πS QR ρ=面电流密度为 00200sin sin sin 4π4πS S S Q Q J v R R R R ωθρρωθωθ=⋅=== 2.4 均匀密绕的螺旋管可等效为圆柱形面电流0S S J e J ϕ=。
已知导线的直径为d ,导线中的电流为0I ,试求0S J 。
解:每根导线的体电流密度为 00224π(/2)πI I J d d ==由于导线是均匀密绕,则根据定义面电流密度为 04πS IJ Jd d ==因此,等效面电流密度为 04πS IJ e dϕ=2.6 两个带电量分别为0q 和02q 的点电荷相距为d ,另有一带电量为0q 的点电荷位于其间。
为使中间的点电荷处于平衡状态,试求其位置。
当中间的点电荷带电量为-0q 时,结果又如何? 解:设实验电荷0q 离02q 为x ,那么离0q 为x d -。
由库仑定律,实验电荷受02q 的排斥力为12214πq F x ε=实验电荷受0q 的排斥力为02214π()q F d x ε=-要使实验电荷保持平衡,即21F F =,那么由00222114π4π()q q x d x εε=-,可以解得d d x 585.0122=+=如果实验电荷为0q -,那么平衡位置仍然为d d x 585.0122=+=。
只是这时实验电荷与0q 和02q 不是排斥力,而是吸引力。
2.7 边长为a 的正方形的三个顶点上各放置带电量为0q 的点电荷,试求第四个顶点上的电场强度E 。
《电磁场与电磁波》习题参考答案

《电磁场与电磁波》常识点及参考答案第1章矢量剖析1.0,则矢量场是无散场,由旋涡源所产生,经由过程任何闭合曲面S的通量等于0.2.0,则矢量场是无旋场,由散度源所产生,的环流等于0.3.矢量剖析中的两个主要定理分离是散度定理(高斯定理)和斯托克斯定理, 它们的表达式分离是:4.在有限空间V中,矢量场的性质由其散度.旋度和V鸿沟上所知足的前提独一的肯定.(√)5.描写物理状况空间散布的标量函数和矢量函数,在时光为必定值的情形下,它们是独一的.(√)6.标量场的梯度运算和矢量场的旋度运算都是矢量.(√)7.梯度的偏向是等值面的切线偏向.(×)8.标量场梯度的旋度恒等于0.(√)9.习题1.12, 1.16.第2章电磁场的根本纪律(电场部分)1.静止电荷所产生的电场,称之为静电场;电场强度的偏向与正电荷在电场中受力的偏向雷同.2.在国际单位制中,电场强度的单位是V/m(伏特/米).3.静电体系在真空中的根本方程的积分情势是:V V sD dS dV Qρ⋅==⎰⎰和0lE dl ⋅=⎰.4.静电体系在真空中的根本方程的微分情势是:VD ρ∇⋅=和0E ∇⨯=.5.电荷之间的互相感化力是经由过程电场产生的,电流与电流之间的互相感化力是经由过程磁场产生的.6.在两种媒质分界面的两侧,电场→E 的切向分量E 1t -E 2t =0;而磁场→B 的法向分量 B 1n -B 2n =0.7.在介电常数为的平均各向同性介质中,电位函数为2211522x y zϕ=+-,则电场强度E =5x y z xe ye e --+.8.静电均衡状况下,导体内部电场强度.磁场强度等于零,导体概况为等位面;在导体概况只有电场的法向分量.9.电荷只能在分子或原子规模内作渺小位移的物资称为( D ).10.雷同的场源前提下,真空中的电场强度是电介质中的( C )倍. A.ε0εr B. 1/ε0εrC. εrD.1/εr11.导体电容的大小( C ).12.z >0半空间中为ε=2ε0的电介质,z <0半空间中为空气,在介质概况无自由电荷散布.则电介质中的静电场为( B ).13.,自由电荷的体密度为已知这些电荷产生的电场为E =E (x,y,z ),下面表达式中始终成立的是( C ).14.在静电场中电力线不是闭合的曲线,所以在交变场中电力线也长短闭合的曲线.(×)15.根据,Φ>0处,E<0; Φ<0处,E>0; Φ=0处,E=0.( × )16.恒定电场中,电源内部消失库仑场E 和非库仑场E ‘,两者的感化偏向老是相反.(√)17.电介质在静电场中产生极化后,在介质的概况肯定会消失约束电荷.( √ )18.在幻想导体与幻想介质的分界面上,不持续的.(× )19.,两种介质的电导率电容器极板的面积为S,如右图.求:⑴电容器的电场强度;⑵两种介质分界面上概况的自由电荷密度; ⑶电容器的漏电导;U 0问G/C=?(C 为电容器电容) 解:得⑵两介质分界面的法线由1指向2得知(磁场部分)1.位移电流与传导电流不合,它与电荷活动无关,只要电场随时光变更,就会有位移电流;并且频率越高,位移电流密度越大.2.当d ψ/dt>0时,其感应电流产生的磁场将阻拦原磁场增长; 磁场强度的单位是A/m(安培/米).3.在两种媒质分界面的两侧,E 1t -E 2t =0;而磁场B 1n -B 2n =0.4. A ).A.是自由电流密度B.是约束电流密度C.是自由电流和约束电流密度D.若在真空中则是自由电流密度;在介质中则为约束电流密度5.两个载流线圈之间消失互感,对互感没有影响的是( A ). A.线圈上的电流 B.两个线圈的相对地位C.线圈的尺寸 D.线圈地点空间的介质6.一导体回路位于与磁场力线垂直的平面内,欲使回路中产生感应电动势,应使(B).A.回路活动B.磁场随时光变更C.磁场散布不平均D.同时选择A和B7.在两种媒质的分界面上,若分界面上消失传导电流,则鸿沟前提为( B ).A. H t不持续,B n不持续B. H t不持续,B n持续C. H t持续,B n不持续D. H t持续,B n 持续8.磁感应强度在某磁媒质中比无界真空中小,称这种磁媒质是(B ).9.雷同尺寸和匝数的空心线圈的电感系数( C )铁心线圈的电感系数.10.恒定电流场是一个无散度场.(√)11.一般说来,电场和磁场是共存于统一空间的,但在静止和恒定的情形下,电场和磁场可以自力进行剖析.(√)12.静电场和恒定磁场都是矢量场,在本质上也是雷同的.(×)13.静电场是有源无旋场,恒定磁场是有旋无源场.(√)14.位移电流是一种假设,是以它不克不及象真实电流一样产生磁效应.(×)15.更的电场.(√)16.物资被磁化问题和磁化物资产生的宏不雅磁效应问题是不相干的两方面问题.(×)17.圆形载流线圈在远处一点的磁场相当于一个磁偶极子的磁场.(√)18.若半径为a.电流为I的无线长圆柱导体置于空气中,已知导体的磁导率为μ0,求导体内.外的磁场强度H和磁通密度B.解:(1)导体内:由安培环路定理所以(2)导体外:(麦克斯韦方程组部分)1.试解释其物理意义,并写出方程的微分情势.答:其物理意义:随时光变更的磁场可以产生电场.2.简述恒定磁场的性质,并写出其两个根本方程.答:恒定磁场是持续的场或无散场,即磁感应强度沿任一闭合曲面的积分等于零.产生恒定磁场的源是矢量源.3.写出麦克斯韦方程组,并简述其物理意义.答:麦克斯韦方程组的积分情势:麦克斯韦方程组的微分情势:每个方程的物理意义:(a) 安培环路定理,其物理意义为散布电流和时变电场均为磁场的源.(b) 法拉第电磁感应定律,暗示时变磁场产生时变电场,即动磁生电.(c) 磁场高斯定理,标明磁场的无散性和磁通持续性.(d)高斯定理,暗示电荷为激发电场的源.本章习题:P84—88 2.11.2.17.2.22.2.25.2.31.第3章静态电磁场及边值问题的解法1.镜象法的理论根据是静电场的独一性定理.根本办法是在所求场域的外部放置镜像电荷以等效的代替鸿沟概况的感应电荷或极化电荷.2.在鸿沟外形完整雷同的两个区域内的静电场,知足雷同的鸿沟前提,则两个区域中的场散布( C ).A .必定雷同B .必定不雷同C .不克不及断定雷同或不雷同 3.两订交并接地导体平板夹角为α,则两板之间区域的静电场(C ).A .总可用镜象法求出.B .不克不及用镜象法求出.C .当/n απ= 且n 为正整数时,可以用镜象法求出.D .当2/n απ= 且n 为正整数时,可以用镜象法求出.4.用镜像法求解电场边值问题时,断定镜像电荷的拔取是否准确的根据是(D ).A .镜像电荷是否对称B .电位所知足的方程是否未转变C .鸿沟前提是否保持不变D .同时选择B 和C5.静电场边值问题的求解,可归结为在给定鸿沟前提下,对拉普拉斯方程的求解,若鸿沟外形为圆柱体,则宜实用( B ).6.对于静电场问题,仅知足给定的泊松方程和鸿沟前提,而情势上不合的两个解是不等价的.( × )7.研讨物资空间内的电场时,仅用电场强度一个场变量不克不及完整反应物资内产生的静电现象.( √ )8.泊松方程和拉普拉斯方程都实用于有源区域.( × )9.静电场的边值问题,在每一类的鸿沟前提下,泊松方程或拉普拉斯方程的解都是独一的.( √ )10.将一无限大导体平板折成如图的90°角,一点电荷Q 位于图中(1, π/6)点处,图中标出解:在如图的极坐标系中,三个镜像 电荷的大小和地位分离为: Q 1 = -Q ,地位:(1, 5π/6) Q 2 = Q ,地位:(1, -5π/6) Q 3 = -Q ,地位:(1, -π/6)11.将一无限大导体平板折成90°角并接地,两点电荷Q 1=Q 2=5C 位于角等分线上距离极点1m 和2m 处,现欲应用镜像法求两点电荷地点区域内的场.(1)请在图中标出所有镜像电荷的地位; (2)请写出各镜像电荷的电量;(3)请写出各镜像电荷的坐标. 解:镜像电荷Q 3 .Q 4 .Q 5 .Q 6 .Q 7 .Q 8 的电量分离为: Q 3=Q 4=Q 5=Q 6=—5C, Q 7=Q 8=5C 各镜像电荷的坐标分离为:Q 34rQ 5: (22-,22), Q 6: (2-,2) Q 7: (22-,22-), Q 8: (2-,2-)12.设点电荷位于金属直角劈上方,如右下图所示,求:(1) 画出镜像电荷地点的地位(2)直角劈内随意率性一点),,(z y x 处的电位表达式解:(1)镜像电荷地点的地位如图1所示.(2)如图2所示任一点),,(z y x 处的电位为⎪⎪⎭⎫ ⎝⎛-+-=4321011114r r r r q πεφ 个中,()()()()()()()()222422232222222121212121z y x r z y x r z y x r z y x r +-++=++++=+++-=+-+-=本章习题:图1图2q-q+q-P167—168 3.7.3.19.第4章时变电磁场本章习题:P189—190 4.3.4. 9.4.15.。
电磁场与电磁波课后习题及答案四章习题解答

四章习题解答4.1如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的 盖板,槽的电位为零,上边盖板的电位为 U o ,求槽内的电位函数。
解根据题意,电位 (0, y) (x,0) (x,b)电位y b ( x )。
上板和薄片保持电位 U °,下板保持零电位,求板间电位的解。
设在薄片平面上,从y 0到y d ,电位线性变化,(0, y) U 0y d 。
解 应用叠加原理,设板间的电位为(x,y )1(x, y) 2(x, y)其中,1 (x, y)为不存在薄片的平行无限大导体平面间(电压为(x, y) n 1aa两边同乘以 题4.1图由条件③,有sin(nA nU oAsinh(— b)sin( n x)aa2U on sinh( n ba)(1 x―),并从 a cos n 0到a 对x 积分,得到an xsin( -- )dxasinh( n b a) 0 a4U 02U o ) n sinh(n ,n b a)1,3,5,L2,4,6,L sin h(^^)s135,L nsinh(n b a) aa4.2两平行无限大导体平面,距离为b ,其间有故得到槽内的电位分布(x,y)型 n y a 极薄的导体片由y d 到 (x, y)满足的边界条件为 (a, y) 0 0U 。
(x, y)的通解应取为 ① ② ③ 根据条件①和②, ②2(x,y) 0 (x )U°)的电位,即1(x,y) U0yb ;2(x,y)是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:①2(x,0) 2(x,b) 0根据条件①和②, 由条件③有 U o③ 2(0, y) (0,y) 可设 2(x, y )的通解为 2(x,y ) U o n y A sin(- 1 b U T yU E y(0 (d 1(o, y) Un y )e A V )eA n Sin( 1d) b) by(0 (dy d) y b)n y两边同乘以sin(- b 2U o d b o ),并从 o 到b 对y 积分,得到b )ysin( / 、U o 2bU o El L 厂求在上题的解中,除开 2W e 故得到 4.3 C f 厂定出边缘电容。
电磁场与电磁波理论(第二版)(徐立勤,曹伟)第4章习题解答

第4章习题解答4.1 电导率为σ的均匀、线性、各向同性的导体球,半径为R ,其表面的电位分布为0cos Φθ。
试确定表面上各点的电流密度。
解:由于导体球的外部是空气,所有在导体球的表面只有切向分量,即0t t t 11sin sin J E e e e R R R θϕθσΦΦΦσσΦσθθθϕ⎛⎫∂∂==-∇=-+= ⎪∂∂⎝⎭4.2 如题4.2图所示平板电容器。
板间填充两种不同的导电媒质,其厚度分别为1d 和2d ,两平板的面积均为S 。
若在两极板上加上恒定的电压0U 。
试求板间的电位Φ、电场强度E 、电流密度J 以及各分界面上的自由电荷和电容器的漏电导。
解:理想电容器021==σσ,满足的定解问题为210 Φ∇= 和 220 Φ∇=以及12111112120121200x x d d x d x dx d x d V xxΦΦΦΦΦΦεε==+====∂∂====∂∂由直接积分法可以得到电位的通解为1 Ax B Φ=+ 和 2Cx D Φ=+由100x Φ==和1220x d d V Φ=+=可以确定出0=B 及)(210d d C V D +-=,则上式电位的表达式为1 Ax Φ= 和 2012()Cx V C d d Φ=+-+利用电位在介质分界面的边界条件,则确定出211201211202d d V C d d V A εεεεεε+=+=因此电位分布为2012112V x d d εΦεε=+ 和 102110221122112()V d Vx d d d d εεεΦεεεε-=+++而对应的电场强度和电位移矢量为2101221xE e V d d εεε=-+ 和 1201221xE e V d d εεε=-+以及12101221xD e V d d εεεε=-+ 和 12201221x D e V d d εεεε=-+根据静电比拟法()E ED J εσΦΦ⇔⇔⇔⇔得到对平板电容器内恒定电场的电位为2012112V x d d σΦσσ=+ 和 102110221122112()V d V x d d d d σσσΦσσσσ-=+++ 电场强度为2101221xE e V d d σσσ=-+ 和 1201221x E e V d d σσσ=-+电流密度矢量为12101221xJ e V d d σσσσ=-+ 和 12201221xJ e V d d σσσσ=-+ 此时的电流称为电容器的漏电流,对应的电导称为电容器的漏电导G ,有121221d d d d SSCCJ S E SSIG Vd d E lE lσσσσσ⋅⋅====+⋅⋅⎰⎰⎰⎰S ——极板的面积4.3 如题4.3图所示矩形导体片的电导率为σ,试求导电片上的电位分布以及导电片中各处的电流密度。
(完整版)电磁场与电磁波理论(第二版)(徐立勤,曹伟)第4章习题解答

第4章习题解答4.1 电导率为σ的均匀、线性、各向同性的导体球,半径为R ,其表面的电位分布为0cos Φθ。
试确定表面上各点的电流密度。
解:由于导体球的外部是空气,所有在导体球的表面只有切向分量,即0t t t 11sin sin J E e e e R R R θϕθσΦΦΦσσΦσθθθϕ⎛⎫∂∂==-∇=-+= ⎪∂∂⎝⎭4.2 如题4.2图所示平板电容器。
板间填充两种不同的导电媒质,其厚度分别为1d 和2d ,两平板的面积均为S 。
若在两极板上加上恒定的电压0U 。
试求板间的电位Φ、电场强度E 、电流密度J 以及各分界面上的自由电荷和电容器的漏电导。
解:理想电容器021==σσ,满足的定解问题为210 Φ∇= 和 220 Φ∇=以及12111112120121200x x d d x d x dx d x d V xxΦΦΦΦΦΦεε==+====∂∂====∂∂由直接积分法可以得到电位的通解为1 Ax B Φ=+ 和 2Cx D Φ=+由100x Φ==和1220x d d V Φ=+=可以确定出0=B 及)(210d d C V D +-=,则上式电位的表达式为1 Ax Φ= 和 2012()Cx V C d d Φ=+-+利用电位在介质分界面的边界条件,则确定出211201211202d d V C d d V A εεεεεε+=+=因此电位分布为2012112V x d d εΦεε=+ 和 102110221122112()V d Vx d d d d εεεΦεεεε-=+++而对应的电场强度和电位移矢量为2101221xE e V d d εεε=-+ 和 1201221xE e V d d εεε=-+以及12101221xD e V d d εεεε=-+ 和 12201221x D e V d d εεεε=-+根据静电比拟法()E ED J εσΦΦ⇔⇔⇔⇔得到对平板电容器内恒定电场的电位为2012112V x d d σΦσσ=+ 和 102110221122112()V d V x d d d d σσσΦσσσσ-=+++ 电场强度为2101221xE e V d d σσσ=-+ 和 1201221x E e V d d σσσ=-+电流密度矢量为12101221xJ e V d d σσσσ=-+ 和 12201221xJ e V d d σσσσ=-+ 此时的电流称为电容器的漏电流,对应的电导称为电容器的漏电导G ,有121221d d d d SSCCJ S E SSIG Vd d E lE lσσσσσ⋅⋅====+⋅⋅⎰⎰⎰⎰S ——极板的面积4.3 如题4.3图所示矩形导体片的电导率为σ,试求导电片上的电位分布以及导电片中各处的电流密度。
电磁场与电磁波理论(第二版)(徐立勤-曹伟)第5章习题解答

第5章习题解答5.2 已知空气填充的矩形金属腔a b c ⨯⨯(,,a b c 分别为腔体在,,x y z 方向的长度)中的电场强度复矢量为0ππsinsin y x z E e E a c= 试求腔中的磁场强度复矢量H 及其各个内表面上的面电流密度S J 和面电荷密度S ρ(设金属为理想导体)。
解:腔中的磁场强度复矢量为00000001110j j j 0ππ11ππππsin cos cos sin j j xy z x y z yxy zy y x z x z e e e e e e H E xy z x z E E E E E E E E x z x z e e e e z x c a c a a c ωμωμωμωμωμ∂∂∂∂∂=-∇⨯=-=-∂∂∂∂∂⎛⎫∂∂⎛⎫=--+=- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭矩形金属腔内的下表面,0z =,n z e e =,00z E==,000ππsinj xz E xHe caωμ== 面电流密度 0n 00ππsinj S z yE x J e H e caωμ==⨯= 面电荷密度 ()n n 000S z z e De Eρε===⋅=⋅=5.3 已知某一理想介质()004,5,0εεμμσ===中的位移电流复矢量为j d 0πsine zx y J e J bβ-=。
求该媒质中的,,,E D H B 和ρ。
解:媒质中的电位移矢量为 j d 0πsin e j j z x J J yD e bβωω-== 媒质中的电场强度为 j 00πsin e j4z xJ DyE e bβεωε-== 媒质中的磁场强度为000j j 0020001110j5j5j500π11ππj sin e cos e j520xy z x yz xy z xz z x x y z x z e e e e e e H E xy z y z E E E E E E J y y e e e J e z y b b b ββωμωμωμβωμωμε--∂∂∂∂∂=-∇⨯=-=-∂∂∂∂∂⎛⎫∂∂⎛⎫=--=-- ⎪ ⎪∂∂⎝⎭⎝⎭媒质中的磁感应强度为 j j 00020π1ππ5j sin e cos e 4z z x z J y y B H H e J e b b b ββμμβωε--⎛⎫===-- ⎪⎝⎭媒质中的电荷密度为0y x z xy z D D D D e e e x y z ρ∂⎛⎫∂∂=∇⋅=++= ⎪∂∂∂⎝⎭5.4 已知空气填充的同轴线内外导体之间的磁场强度为 ()81cos 10ππH e t z ϕβρ=- (A /m ) 同轴线的内外导体半径分别为1a =mm ,4b =mm 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章习题解答4.1 电导率为的均匀、线性、各向同性的导体球,半径为,其表面的电位分布σR 为。
试确定表面上各点的电流密度。
0cos Φθ解:由于导体球的外部是空气,所有在导体球的表面只有切向分量,即0t t t 11sin sin J E e e e R R R θϕθσΦΦΦσσΦσθθθϕ⎛⎫∂∂==-∇=-+= ⎪∂∂⎝⎭4.2 如题4.2图所示平板电容器。
板间填充两种不同的导电媒质,其厚度分别为和,两平板的面积均为。
若在两极板上加上恒定的电压。
试求板间1d 2d S 0U 的电位、电场强度、电流密度以及各分界面上的自由电荷和电容器的漏ΦEJ 电导。
解:理想电容器,满足的定解问题为021==σσ 和 210 Φ∇=220Φ∇=以及12111112120121200x x d d x d x d x d x d V xxΦΦΦΦΦΦεε==+====∂∂====∂∂由直接积分法可以得到电位的通解为 和 1 Ax B Φ=+2Cx DΦ=+由和可以确定出及,则上式电位的表达式为10x Φ==1220x d d V Φ=+=0=B )(210d d C V D +-= 和 1 Ax Φ=2012()Cx V C d d Φ=+-+利用电位在介质分界面的边界条件,则确定出211201211202d d V C d d V A εεεεεε+=+=因此电位分布为和 2012112V x d d εΦεε=+102110221122112()V d Vx d d d d εεεΦεεεε-=+++而对应的电场强度和电位移矢量为和 2101221xE e V d d εεε=-+ 1201221xE e V d d εεε=-+以及和 12101221xD e d d εεεε=-+ 12201221x D e Vd d εεεε=-+ 根据静电比拟法得到对平板电容器内恒定电场的电位为()E ED J εσΦΦ⇔⇔⇔⇔和 2012112V x d d σΦσσ=+102110221122112()V d V x d d d d σσσΦσσσσ-=+++电场强度为和 2101221x E e d d σσσ=-+1201221x E e Vd d σσσ=-+电流密度矢量为和 12101221xJ e d d σσσσ=-+ 12201221x J e d d σσσσ=-+此时的电流称为电容器的漏电流,对应的电导称为电容器的漏电导,有G——极板的面积121221d d d d S SCCJ S E S S I G V d d E l E l σσσσσ⋅⋅====+⋅⋅⎰⎰⎰⎰ A A S 4.3 如题4.3图所示矩形导体片的电导率为,试求导电片上的电位分布σ以及导电片中各处的电流密度。
解:根据题意,定解问题为20Φ∇=以及 00π0 sin0 02nx x ay y byU bΦΦΦΦ====∂====∂于是可以将通解直接选为1212(,)(sinh||cosh||)(sin cos )y y y y x y C k x C k x D k y D k y Φ=++由得到,则0y Φ==02=D 12(,)(sinh ||cosh ||)sin y y y x y C k x C k x k yΦ=+由得到,即。
因此0y byΦ=∂=∂0cos =b k y (21)π,1,2,2y n k n b-== 1(21)π(21)π(21)π(,)sinhcosh sin 222n n n n x n x n yx y C D b b b Φ∞=---⎡⎤=+⎢⎥⎣⎦∑由得到,于是0y Φ==0=n D 1(21)π(21)π(,)sinhsin 22n n n x n yx y C b bΦ∞=--=∑再由可以得到0πsin2x ayU ybΦ=∂=∂01π(21)π(21)πsin sinh sin222n n y n a n yU C b b b ∞=--=∑比较系数法可以得到,而其余的系数均为零。
因此,导电片上电位分布为1πsinh2U C a b=0ππ(,)sinh sinπ22sinh 2U x yx y a b b bΦ=利用和可以计算出导电片上各处电流密度分布为E Φ=-∇ E Jσ=0ππππππcosh sin sinh cos π222222sh 2x y x y J E e e x y U x y x y e e a b b b b b b bΦΦσσΦσσ⎛⎫∂∂==-∇=-+ ⎪∂∂⎝⎭⎛⎫=-+ ⎪⎝⎭ 4.4 在电导率为的无限大导电媒质中流有电流密度的恒定电流。
今沿轴方向挖一半径为的无限σ0x J J e =z a 长圆孔。
试求空间各处的电位、电场强度和电流密度。
ΦEJ 解:在圆柱坐标系下,均匀电流密度产生的电位为,因此存在空腔的媒质中电位的定J ϕρσcos 0J-(,)Φρϕ解问题为20Φ∇=以及和 0aρΦρ=∂=∂0cos J ρΦρϕσ→∞=-根据分离变量法可以得到问题的通解为001(,)ln [(sin cos )(sin cos )]n n n n n n n A B A n B n C n D n Φρϕρρϕϕρϕϕ∞-==+++++∑代入边界条件可以得到,,即J A σ=-22a J B a A σ==-2(,)(cos J a Φρϕρϕσρ=-+而电流密度为220221(1cos (1)sin z J E e e e z a a J e e ρϕρϕΦΦΦσσΦσρρϕϕϕρρ⎛⎫∂∂∂==-∇=-++ ⎪∂∂∂⎝⎭⎡⎤=--+⎢⎥⎣⎦4.5 如题4.5图所示,厚度为的扇形弧片由两块大小相同但电导率不同的金属片构d 成。
弧片的内外半径分别为和。
当以和作为电极时,加上恒定的电1R 2R AB CD 压后,试求弧片上的电位分布、分界面上的面电荷密度以及极板间的电阻;若0U 以和作为电极,结果又如何?AAD A BC 解:弧片内电流只有分量,即,。
根据边界条件可以e ϕ 11J J e ϕ= 22J J e ϕ=1n 2n J J =得到,即。
而21JJ =2211E E σσ=π/4π/2021120π/4πd d d ()4CDAB U E e l E E E E ϕρϕρϕρ=-⋅=--=-+⎰⎰⎰ 可以解得 201012121244π()π()U U E e E e ϕϕσσσσρσσρ==++金属片1中的电位分布为10120124πd d 0π()4PABU E e l E ϕϕσΦρϕϕϕσσ=-⋅=-=≤≤+⎰⎰ 金属片2中电位分布为π/4201202210π/412124()ππd [d d ] π()()42PABU U E e l E E ϕϕσσσΦρϕρϕϕϕσσσσ-=-⋅=-+=+≤≤++⎰⎰⎰ 面电荷密度为 00021002121124()()()S U J E E εεεσσρεσσπσσρ⎛⎫-=-=-=⎪+⎝⎭电流为 21021021212144d d ln π()π()b S a U U RI J S d R σσσσρσσρσσ=⋅=⋅=++⎰⎰ 根据电阻的定义可得 1222101π()14ln U R R I U R σσσσ+==当电极改置于内圆弧和外圆弧,则,即,因此电位仅为的函数,21E E =12ΦΦ=Φr 1021d d 0() ()0d d R U R r ΦρΦΦρρ⎛⎫=== ⎪⎝⎭因此电位分布为 021221()ln(/) ln(/)U r R R R R R Φρρ=≤≤于是有 1020111122222121d()()ln(/)d ln(/)U U d J E r J E r d R R R R σσσσΦσσρρρρ==-===-=因此,总电流为12120121221π()ππd d 444ln(/)S S U d I J S J S J d J d R R σσρρ+=+=+=⎰⎰阻抗为211204ln(/)π()R R R U dσσ=+4.6 球形电容器的内球半径为,外球壳的内半径为。
将两种不同的 导电煤质分别填入两个半球,两种导电a b 煤质的 电导率分别为和。
求该电容器的漏电阻。
1σ2σ解:设在上电位为,上电位为零。
根据题意,电位仅为的函数,因此定解问题为a r =Ub r =Φr 221d d 0() ()0d d r a U b r r r ΦΦΦ⎛⎫=== ⎪⎝⎭因此,通解为C D rΦ=-+根据边界条件可以得到ba aU Db a abU C -=-=因此11abU b a r b Φ⎛⎫=- ⎪-⎝⎭在两种煤质中电流密度分别为2222221111r a b abU E J r a b abU E J σσσσ-==-==因此总电流为1212122πd d ()S S abUI J S J S b aσσ=+=+-⎰⎰于是电容器的漏电阻1212π()b a R ab σσ-=⋅+4.8 半径为的圆柱形导体内的磁场,试求导体中的总电流。
1a =cm 2424.77102210H e ϕρρ--⎛⎫=⨯- ⎪⨯⎝⎭A /m 解: J H =∇⨯ ()42134.77101210z z z ze e e H e e z H H H ρϕϕρϕρρρρρϕρρρ--∂∂∂∂⎛⎫===⨯- ⎪∂∂∂∂⨯⎝⎭2π0.0142003d 4.77101d 0210S I J S ρρρ--⎛⎫=⋅=⨯-= ⎪⨯⎝⎭⎰⎰⎰ 4.14 已知某一电流分布的矢量磁位为224x y z A e x y e y x e xyz=+-求该电流分布及其对应的。
B解:利用矢量磁位满足的泊松方程来求出电流分布为A222222222y x z x y z x y A A A J A e e e e y e xx y z ∂∂∂=-∇=---=--∂∂∂由可以求出磁感应强度为A B⨯∇=22244()y y x x z z x y z x y z A A A A A A B A e e y x e y z z x xy e xz e yz e y x ∂∂⎛⎫⎛⎫∂∂∂∂⎛⎫=∇⨯=-+-+- ⎪ ⎪⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭=--+-。
