清华大学2018年2月中学生标准学术能力诊断性测试数学(理)试卷
清华大学理科数学一卷答案THUSSAT2018年12月测试

S2
=
1 2
( y1
+
y2
) |
x1
−
x2
|=
1 2
2p k
a
=
ap k
,
所以 S1 = kb , S2 2 p
因为 0 kb p ,所以 0 S1 1 .
2
S2 4
ห้องสมุดไป่ตู้
21.12 分
……………………10 分 ……………………11 分 ……………………12 分
解 (Ⅰ)当 a 0 时, f (x) = a ex + (ax +1)ex = (ax + a +1)ex , ………………………1 分
2
2
GH 5
∴平面 CGE 与平面 ADEF 所成锐二面角的余弦值为 10 . …………………………12 分 5
19.12 分
解:(Ⅰ)抽取的螺帽质量指标值的样本平均数 x 和样本方差 s2 分别为:
x =170 0.05 +180 0.12 +190 0.18 + 200 0.30 + 210 0.19
20.12 分
解 (Ⅰ)由 A( p ,0) ,则 B( p + a,0) , D( p , p) ,则 C( p + a, p2 + 2 pa ) ,…………2 分
2
2
2
2
又a=
p ,所以 kCD
=
3p − p 3p − p
=
3 −1.
22
…………………4 分
(Ⅱ)设直线 CD 的方程为: y = kx + b (k 0) ,设 C(x1, y1) , D(x2 , y2 ) ,
清华大学中学生标准学术能力(TDA)诊断性测试2024-2025学年高二上学期数学试卷和答案

标准学术能力诊断性测试2024年9月测试数学试卷(A 卷)本试卷共150分,考试时间90分钟.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设,a b ∈R ,则“22log log a b >”是“1122b a ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.集合(){}{}22ln 23,23,A x y x x B y y x x x A ==--==-+∈∣∣,则A B ⋂=R ð()A.(),1∞-- B.()(],13,6∞--⋃C.()3,∞+ D.()[),16,∞∞--⋃+3.已知复数z 满足5z z ⋅=,则24i z -+的最大值为()C. D.4.已知非零向量,a b 满足3a b = ,向量a 在向量b 方向上的投影向量是9b - ,则a 与b 夹角的余弦值为() A.33 B.13 C.33- D.13-5.设函数()f x 的定义域为R ,且()()()()42,2f x f x f x f x -++=+=-,当[]1,2x ∈时,()()()2,303f x ax x b f f =+++=-,则b a -=()A.9-B.6-C.6D.96.班级里有50名学生,在一次考试中统计出平均分为80分,方差为70,后来发现有3名同学的分数登错了,甲实际得60分却记成了75分,乙实际得80分却记成了90分,丙实际得90分却记成了65分,则关于更正后的平均分和方差分别是()A.82,73 B.80,73 C.82,67D.80,677.已知()sin 404cos50cos40cos θθ-=⋅⋅ ,且ππ,22θ⎛⎫∈- ⎪⎝⎭,则θ=()A.π3- B.π6- C.π6 D.π38.已知函数()2221x f x x =-++,则不等式()()2232f t f t +->的解集为()A.()(),13,∞∞--⋃+ B.()1,3- C.()(),31,∞∞--⋃+ D.()3,1-二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得6分,部分选对但不全得3分,有错选的得0分.9.已知实数,,a b c 满足0a b c <<<,则下列结论正确的是()A.11a c b c>-- B.a a c b b c +<+C.b c a c a b --> D.2ac b bc ab+<+10.已知函数()sin3cos3f x a x x =-,且()3π4f x f ⎛⎫≤⎪⎝⎭对任意的x ∈R 恒成立,则下列结论正确的是()A.1a =±B.()f x 的图象关于点π,04⎛⎫ ⎪⎝⎭对称C.将()f x 的图象向左移π12个单位,得到的图象关于y 轴对称D.当π23π,1236x ⎡⎤∈-⎢⎥⎣⎦时,满足()2f x ≤-成立的x 的取值范围是π7π,3636⎡⎤-⎢⎥⎣⎦11.在长方体1111ABCD A B C D -中,已知4,2AB BC ==,13,AA M N =、分别为1111B C A B 、的中点,则下列结论正确的是()A.异面直线BM 与AC 所成角的余弦值为7210B.点T 为长方形ABCD 内一点,满足1D T ∥平面BMN 时,1D T的最小值为5C.三棱锥1B B MN -的外接球的体积为14πD.过点,,D M N 的平面截长方体1111ABCD A B C D -所得的截面周长为+三、填空题:本题共3小题,每小题5分,共15分.12.若实数,x y 满足1232,34x y x y ≤+≤≤-+≤,则x y +的取值范围是__________.13.如图所示,在梯形ABCD 中,1,3AE AB AD =∥,3,BC BC AD CE =与BD 交于点O ,若AO x AD y AB =+ ,则x y -=__________.14.在四面体ABCD 中,3,,CD AD CD BC CD =⊥⊥,且AD 与BC 所成的角为30 .若四面体ABCD 的体积为2,则它的外接球表面积的最小值为__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知复数12213i z =-+=--.(1)若12z z z =,求z ;(2)在复平面内,复数12,z z 对应的向量分别是,OA OB ,其中O 是原点,求AOB ∠的大小.16.(15分)在ABC 中,角,,A B C 的对边分别是,,a b c ,且cos cos 1a C b A c -+=.(1)求角A ;(2)已知b D =为BC 边上一点,且2,BD BAC ADC ∠∠==,求AD 的长.17.(15分)如图所示,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PA ⊥平面ABCD ,点Q 为PA 的三等分点,满足13PQ PA =.(1)设平面QCD 与直线PB 相交于点S ,求证:QS ∥CD ;(2)若3,2,60,AB AD DAB PA ∠==== ,求直线CQ 与平面PAD 所成角的大小.18.(17分)甲、乙两位同学进行投篮训练,每个人投3次,甲同学投篮的命中率为p ,乙同学投篮的命中率为()q p q >,且在投篮中每人每次是否命中的结果互不影响.已知每次投篮甲、乙同时命中的概率为15,恰有一人命中的概率为815.(1)求,p q 的值;(2)求甲、乙两人投篮总共命中两次的概率.19.(17分)已知函数()233x x f x a --=⋅+是偶函数,()246h x x x =-+.(1)求函数()e 2x y h a =-的零点;(2)当[],x m n ∈时,函数(()h f x 与()f x 的值域相同,求n m -的最大值.标准学术能力诊断性测试2024年9月测试数学(A卷)参考答案一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.12345678A B C C D B A C二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对但不全的得3分,有错选的得0分.91011AD BC BD三、填空题:本题共3小题,每小题5分,共15分.12.21,55⎡⎤-⎢⎥⎣⎦13.11114.73π-四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)解:(1)()() ()()12224i13i24i26i4i127i13i13i13i19i5 zzz-+---++-++ =====-+-+---5z∴==(2)依题意向量()()2,4,1,3OA OB=-=--于是有()()()214310OA OB⋅=-⨯-+⨯-=-OA OB====AOB∠为OA 与OB 的夹角,2cos2OA OBAOBOA OB∠⋅∴==-[]0,πAOB∠∈,3π4AOB∠∴=16.(15分)解:(1)由正弦定理可得:cos sin cos sin cos 1sin a C b A C B A c C--+==()cos 1sin sin cos sin A C A C B ∴+=-,由()sin sin B A C =+可得:()cos sin sin sin cos sin A C C A C A C ⋅+=-+,cos sin sin sin cos sin cos cos sin A C C A C A C A C ⋅+=--,cos sin sin cos sin A C C A C∴⋅+=-sin 0C ≠ 可得:cos 1cos A A +=-,1cos 2A ∴=-,()0,πA ∈ ,2π3A ∴=(2),BAC ADC BCA ACD ∠∠∠∠== ,BAC ∴ 与ADC 相似,满足:AC BC CD AC =,设CD x =,则有3x =解得:1,3x x ==-(舍去),即:1CD =2π3ADC BAC ∠∠== ,在ADC 中,由余弦定理可得:2222πcos 32AD CD AC AD CD+-=⋅⋅,即:211221AD AD +--=⨯⨯解得:1,2AD AD ==-(舍去),AD ∴的长为117.(15分)解:(1)证明:因为平面QCD 与直线PB 相交于点S ,所以平面QCD ⋂平面PAB QS=因为四边形ABCD 为平行四边形,AB ∴∥CD ,AB ⊄ 平面,QCD CD ⊂平面,QCD AB ∴∥平面QCDAB ⊂ 平面PAB ,平面QCD ⋂平面,PAB QS AB =∴∥QS ,AB ∥,CD QS ∴∥CD(2)过点C 作CH AD ⊥于点H ,PA ⊥ 平面,ABCD PA ⊂平面PAD ,所以平面PAD ⊥平面ABCD ,因为平面PAD ⋂平面ABCD AD =,且CH AD ⊥,CH ∴⊥平面PAD连接,QH CQH ∠∴是直线CQ 与平面PAD 所成的角因为点Q 为PA 的三等分点,232,223PA QA PA =∴==,在Rt DCH 中,333sin602CH =⋅= 在ACD 中,利用余弦定理可得:222223cos120,19223AC AC +-=∴=⨯⨯ ,在Rt QAC 中,222(22)1933QC QA AC =+=+=在Rt QCH 中,3312sin 233CH CQH CQ ∠===,可得π6CQH ∠=,即直线CQ 与平面PAD 所成的角等于π618.(17分)解:(1)设事件A :甲投篮命中,事件B :乙投篮命中,甲、乙投篮同时命中的事件为C ,则C AB =,恰有一人命中的事件为D ,则D AB AB =⋃,由于两人投篮互不影响,且在投篮中每人每次是否命中的结果互不影响,所以A 与B 相互独立,,AB AB 互斥,所以:()()()()P C P AB P A P B ==⋅()(()()(()()()P D P AB AB P AB P AB P A P B P A P B =⋃=+=⋅+⋅可得:()()1581115pq p q p q ⎧=⎪⎪⎨⎪-+-=⎪⎩解得:1335p q ⎧=⎪⎪⎨⎪=⎪⎩或3315,,,1533p p q p q q ⎧=⎪⎪>∴==⎨⎪=⎪⎩(2)设i A :甲投篮命中了i 次;j B :乙投篮命中了j 次,,0,1,2,3i j =,()30285125P A ⎛⎫== ⎪⎝⎭()2213223223365555555125P A ⎛⎫⎛⎫=⨯+⨯⨯+⨯= ⎪ ⎪⎝⎭⎝⎭()2223232323545555555125P A ⎛⎫⎛⎫=⨯+⨯⨯+⨯= ⎪ ⎪⎝⎭⎝⎭()3028327P B ⎛⎫== ⎪⎝⎭()2211221221433333339P B ⎛⎫⎛⎫=⨯+⨯⨯+⨯= ⎪ ⎪⎝⎭⎝⎭()2222112112233333339P B ⎛⎫⎛⎫=⨯+⨯⨯+⨯= ⎪ ⎪⎝⎭⎝⎭设E :甲、乙两人投篮总共命中两次,则021120E A B A B A B =++由于i A 与j B 相互独立,021120,,A B A B A B 互斥,()()()()()()()()021*********P E P A B A B A B P A P B P A P B P A P B ∴=++=⋅+⋅+⋅8236454830412591259125271125=⨯+⨯+⨯=19.(17分)解:(1)()233x x f x a --=⋅+ 是偶函数,则()()f x f x -=,即11333399x x x x a a --⋅+=⋅+,()113309x x a -⎛⎫∴--= ⎪⎝⎭,由x 的任意性得119a =,即9a =()246h x x x =-+ ,()()()()()22e 2e 4e 618e 4e 12e 6e 2x xx x x x x y h a ∴=-=-⋅+-=-⋅-=-+,令()()e 6e 20x x -+=,则e 6x =或e 2x =-(舍去),即ln6x =,()e 2x y h a ∴=-有一个零点,为ln6(2)设当[],x m n ∈时,函数()f x 的值域为[],s t ,则函数()()h f x 的值域也为[],s t ,由(1)知()2933332x x x x f x ---=⋅+=+≥=当且仅当33x x -=,即0x =时等号成立,令()p f x =,则2p ≥,()2246(2)2h x x x x =-+=-+ 在区间[)2,∞+上单调递增,所以当[],p s t ∈时,()2,s h p ≥的值域为()(),h s h t ⎡⎤⎣⎦,即()()h s s h t t ⎧=⎪⎨=⎪⎩,则224646s s s t t t ⎧-+=⎨-+=⎩,即,s t 为方程246x x x -+=的两个根,解得23s t =⎧⎨=⎩,所以当[],x m n ∈时,()f x 的值域为[]2,3令()30x x λ=>,则()133,1x x y f x λλλ-==+=+>,3x λ= 在()0,∞+上单调递增,对勾函数1y λλ=+在()1,∞+上单调递增,由复合函数的单调性知,()f x 在()0,∞+上单调递增,()f x 是偶函数,()f x ∴在(),0∞-上单调递减令()3f x =,即333x x -+=,解得332x +=或332x =,即33log 2x +=或33log 2x -=,故n m -的最大值为3333535735log log log 222-+-=答案解析1.A【解析】由22log log a b >可得0a b >>,由1122b a⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭可得a b >,由a b >得不到0a b >>,故必要性不成立;由0a b >>可以得到a b >,故充分性成立,则“22log log a b >”是“1122b a ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭”的充分不必要条件.2.B 【解析】集合(){}{}22ln 23230A x y x x x x x ==--=-->∣∣()(){}310{13},x x x x x x =-+>=<->∣∣或集合{}{}223,6B yy x x x A y y ==-+∈=>∣∣,{}()(]6,,13,6B y y A B ∞=≤∴⋂=--⋃R R ∣3.C【解析】复数z 满足5z z ⋅=,设22i,5z a b z z a b =+⋅=+=,()()2224i 24i (2)(4)z a b a b -+=-++=-++,则点()2,4-到圆225a b +=+=4.C【解析】设非零向量,a b 夹角为θ,向量a 在向量b 方向上的投影向量是39b - ,则cos ,39b a a b b θ⨯=-= ∣,解得3cos 3θ=-.5.D【解析】()()42f x f x -++= ,取()()1,312x f f =+=,()()()321211f f a b a b =-=-++=--,()()2f x f x +=- ,取()()0,2042x f f a b ===++,()()303,1423,2f f a b a b a +=---+++=-=- ,()()42f x f x -++= ,取2x =,则()21f =,则7b =,则729b a -=+=.6.B【解析】设更正前甲,乙,丙 的成绩依次为12350,,,,a a a a ,则12505080a a a +++=⨯ ,即507590655080a ++++=⨯ ,()222250(7580)(9080)(6580)807050a -+-+-++-=⨯ ,更正后平均分:()5016080908050x a =++++= ,()22222501(6080)(8080)(9080)807350s a ⎡⎤=-+-+-++-=⎣⎦ .7.A 【解析】()sin 40sin40cos cos40sin θθθ-=- 4cos50cos40cos 4sin40cos40cos θθ=⋅⋅=⋅⋅ 1cot40tan 4cos40θ⇒-=14cos40tan cot40θ-⇒=sin404sin40cos40cos40-=()sin 30102sin80cos40+-= 13cos102cos1022cos40+-=3313sin10cos10sin10cos102222cos40cos40--==()()sin 1060sin 50cos40cos40--===πππ,,223θθ⎛⎫∈-∴=- ⎪⎝⎭.8.C【解析】设()()21121x g x f x x =-=-++,()()2221112121x x x g x f x x x -⋅-=--=--+=--+++,()()2221102121x x x g x g x x x ⎛⎫⋅+-=-++--+= ⎪++⎝⎭,设()()1212121222,112121x x x x g x g x x x ⎛⎫⎛⎫>-=-+--+ ⎪ ⎪++⎝⎭⎝⎭()()()()()122121121222222021212121x x x x x x x x x x -⎛⎫=-+-=-+> ⎪++++⎝⎭,故()g x 为奇函数,且单调递增,()()()()()()22223212310230f t f t f t f t g t g t +->⇒-+-->⇒+->,()()()()()222302332g t g t g t g t g t +->⇒>--=-,故232t t >-,解得()(),31,t ∞∞∈--⋃+.9.AD【解析】A.0a b c <<<,可得a c b c -<-,故11a c b c>--,A 正确;B.设不等式成立,则()()a a c b c b b c b b b c++<++,可得ab ac ab bc +<+,即ac bc <,由0a b c <<<可得ac bc >,故假设不成立,B 错误;C.不妨假设211313210,,1332b c a c a b c a b --+--+=-<=-<=-<====--,故,C b c a c a b --<错误;D.设不等式成立,()()22,,,0ac b bc ab ac bc ab b a b c a b b a b c +<+-<--<-<<< ,()()a b c a b b -<-成立,故2ac b bc ab +<+成立,D 正确.10.BC【解析】A.()()sin3cos33sin 0,cos πf x a x x x ϕϕϕϕ⎛⎫=-=+=-=≤ ⎪⎝⎭()3π4f x f ⎛⎫≤ ⎪⎝⎭对任意x ∈R 恒成立,()f x ∴在3π4x =处取得极值,即3ππ3π42k ϕ⨯+=+,解得7π3ππ,sin 0,π,,sin 4422k ϕϕϕϕϕϕ=-+=-≤∴=-=-=- ,可求得1a =-,A 错误;B.()()3ππ3,0,44f x x f f x ⎛⎫⎛⎫=-=∴ ⎪ ⎪⎝⎭⎝⎭的图象关于点π,04⎛⎫ ⎪⎝⎭对称,B 正确;C.将()f x 的图象向左平移π12个单位,得到()π3ππ3331242g x x x x ⎛⎫⎛⎫=+⨯-=-=- ⎪ ⎪⎝⎭⎝⎭,函数图象关于y 轴对称,C 正确;D.()3π2342f x x ⎛⎫=-≤- ⎪⎝⎭,即3π1sin 342x ⎛⎫-≤- ⎪⎝⎭,7π3π11π2π32π646k x k ∴+≤-≤+,解得23π231π2ππ363363k x k +≤≤+,由题意知π23π,1236x ⎡⎤∈-⎢⎥⎣⎦,符合条件的k 的取值为1,0-,当1k =-时,π7π3636x -≤≤,均在定义域内,满足条件,当0k =时,23π31π3636x ≤≤,此时仅有23π36x =满足条件,所以满足()22f x ≤-成立的x 的取值范围为π7π23π,363636⎡⎤⎧⎫-⋃⎨⎬⎢⎣⎦⎩⎭,D 错误.11.BD【解析】A.MN ∥,AC BMN ∠∴为直线MN 与AC 所成角,在BMN 中,根据余弦定理可知222cos 2BM MN BN BMN BM MN∠+-=⋅,422BM MN BN ======,代入求得cos 10BMN A ∠=错误;B.取AD 的中点E ,取CD F ,取11A D 的中点S ,连接11,,,,EF D E D F AS SM ,SM ∥,AB AS ∥BM ,所以四边形ABMS 是平行四边形,AS ∥BM 且AS ∥11,D E D E ∴∥1BM D E ∴∥平面BMN ,同理可得1D F ∥平面BMN ,1DT ∥平面,BMN T ∈平面ABCD ,所以点T 的运动轨迹为线段EF ,在1ΔD EF 中,过点1D 作1D T EF ⊥,此时1D T 取得最小值,由题意可知,11D E D F EF ===,1111sin sin sin 105D EF BMN D T D E D EF ∠∠∠====,B 正确;C.取MN 的中点1O ,连接11B O ,则1111O N O M O B ==,过点1O 作1OO ∥1BB ,且111322OO BB ==,OM ∴为外接球的半径,在1Rt MB N 中,MN =,2R OM ∴==,34ππ,33V R C ∴==球错误;D.由平面11AA D D ∥平面11BB C C 得,过点,,D M N 的平面必与11,AA C C 有交点,设过点,,D M N 的平面与平面11AA D D 和平面11BB C C 分别交于,DO PM DO ∴∥,PM 同理可得DP ∥,ON 过点,,D M N 的平面截长方体1111ABCD A B C D -所得的截面图形为五边形DPMNO ,如图所示,以D 为坐标原点,以1,,DA DC DD 所在直线分别为,,x y z 轴建立空间直角坐标系,设,AO m CP n ==,则()()()()()0,0,0,2,0,,0,4,,1,4,3,2,2,3D O m P n M N ,()()()()0,2,3,1,0,3,2,0,,0,4,ON m PM n DO m DP n ∴=-=-== ,DP ∥,ON DO ∥PM ,()()2323m n n m ⎧=-⎪∴⎨=-⎪⎩,解得2m n ==,DO DP ∴==ON PM MN ====,所以五边形DPMNO 的周长为DO DP ON PM MN ++++==+,D 正确.12.21,55⎡⎤-⎢⎥⎣⎦【解析】令()()()()2323x y m x y n x y m n x m n y +=++-+=-++,2131m n m n -=⎧∴⎨+=⎩,解得()()2121,,235555m n x y x y x y ==-∴+=+--+,1232,34x y x y ≤+≤≤-+≤ ,则()()22441323,555555x y x y ≤+≤-≤--+≤-,24435555x y ∴-≤+≤-,即21,55x y ⎡⎤+∈-⎢⎣⎦.13.111【解析】建立如图所示的平面直角坐标系,设1AD =,则3BC =,()()()()220,0,3,0,,,1,,,33B C A m n D m n E m n ⎛⎫∴+ ⎪⎝⎭,所以直线BD 的方程为1n y x m =+,直线CE 的方程为()2329n y x m =--,联立两直线方程求得()()666655,,,,1,0,,11111111m n m n O AO AD AB m n +-⎛⎫⎛⎫∴=-==-- ⎪ ⎝⎭⎝⎭ ,6511,511m x my AO xAD y AB n ny -⎧=-⎪⎪=+∴⎨⎪-=-⎪⎩ ,解得651,,111111x y x y ==∴-=.14.73π-【解析】依题意,可将四面体ABCD 补形为如图所示的直三棱柱ADE FCB -,AD 与BC 所成的角为30 ,30BCF ∠∴= 或150,设,CB x CF y ==,外接球半径记为R ,外接球的球心如图点O ,11113sin 23324ABCD CBF V DC S xy BCF xy ∠⎛⎫∴=⋅⋅=⨯⨯== ⎪⎝⎭ ,解得8xy =,在2Rt OCO 中,2222222223922sin 4BF R OC OO CO BF BCF ∠⎛⎫⎛⎫==+=+=+ ⎪ ⎪⎝⎭⎝⎭,在BCF 中,由余弦定理可得2222cos BF BC CF BC CF BCF ∠=+-⋅⋅,要使外接球表面积最小,则R 要尽可能小,则BCF ∠应取30 ,(2222BF x y xy ∴=+≥-,当且仅当x y =时取等,(22min 99732444R BF xy ∴=+=+=-所以外接球表面积的最小值2min min 4π73πS R ==-.。
中学生标准学术能力诊断性测试(清华大学)2018年12月测试文科数学试卷(精编含解析)

6 a,
4
所以可以求得 S1 = 4´
3 a2 = 4
3a2 , S2
= 4p (
6 a)2 4
= 3 a2p , 2
所以 S1 =
3a2
=2
3
,
S2 3 a2p 3p
2
故选 C.
【点睛】该题考查的是有关正四面体的表面积与其外接球的表面积的比值问题,涉及到的知识点有正四面
体的外接球半径,球的表面积公式,正四面体的表面积公式,属于中档题目.
等,正确使用运算法则是解题的关键,属于简单题目.
7.已知 sin(p
+q )
=
2
p sin(
-
q ) ,则
3sinq
+4 cosq
=(
)
2
sinq - 2 cosq
1
1
A.
B. 2 C.
D. 3
2
3
【答案】A
【解析】
【分析】
首先利用三角函数的诱导公式,将式子进行化简,得到 tanq = - 2 ,之后将正余弦的齐次式的分式形式的
A. (2,1) B. (2, - 1) C. (- 1, 2) D. (- 1, - 2)
【答案】D 【解析】
【分析】
首先根据复数的运算法则,求得 z = - 1+2i ,进而求得其共轭复数,利用复数在复平面内对应点的坐标,
求得结果.
【详解】因为 (1- i)z =1+3i ,所以 z = 1+3i = (1+3i)(1+i) = - 2 +4i = - 1+2i ,
A. 人数最多的年级段是高二段 B. 初一段人数比高一段人数多
【清华大学】中学生标准学术能力诊断性2018年12月测试文科数学卷及解析

(清华大学)中学生标准学术能力诊断性测试2018年12月测试文科数学卷(本试卷共150分,考试时间120分钟.)一、选择题:本大题共12小题,每小题5分,共60分.1.已知复数z 满足(1)13i z i -=+,则复数z 在复平面内对应的点为()A.(2,1)B.(2,1)- C.(1,2)- D.(1,2)--2.某中学初中部共有500名学生,高中部共有600名学生,各年级段人数构成比例如图所示,则下列说法正确的是()A.人数最多的年级段是高二段B.初一段人数比高一段人数多C.高三段人数比初二段人数少D.高二段人数比初三段人数多一倍3.已知集合{|1,}2a P x x a Z ==+Î,1,2Q y m m Z 禳镲==+Î睚镲铪,则下列结论中正确的是()A.P Q Ç=ÆB.P Q QÇ= C.P Q QÈ= D.P Q RÈ=4.焦点在x 轴上,短轴长等于16,离心率等于35的椭圆的标准方程为()A.22110064x y += B.22164100x y += C.221400256x y += D.221256400x y +=5.设函数()x x f x ae e -=+.若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为()A.y x=- B.y x= C.2y x=- D.2y x=6.在ABC D 中,点D 是BC 的中点,点E 是AD 的中点,点M 在线段AC 上,且2AM MC = ,则ME =()A.11412AB AC +B.11412AB AC -C.11124AB AC +D.11124AB AC -7.已知sin()2sin()2p p q q +=-,则3sin 4cos sin 2cos q qq q+=-()A.12B.2C.13D.38.已知函数()cos 22sin f x x x =+,则A.()f x 的最小正周期为p ,最小值为1 B.()f x 的最小正周期为p ,最小值为-3C.()f x 的最小正周期为2p ,最小值为1D.()f x 的最小正周期为2p ,最小值为-39.若实数x ,y 满足不等式组(1)(23)013x y x y x ì--+-³ïí#ïî,则3z x y =-的取值范围是()A.[2,18]B.[2,12]C.[3,18]D.[3,12]10.某四棱锥的三视图如图所求,则该四棱锥的最长棱的长度为()A.B.3C.D.11.若一个正四面体的表面积为1S ,其外接球的表面积为2S ,则12S S =()A.pB.6pC.3pD.4p 12.已知函数33)2log (2),2()(2,2x x x f x x -ì-<ï=í-+³ïî ,则方程11f x a x骣琪+-=琪桫的实根个数不可能为()A.8B.7C.6D.5二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数2(log )1f x x =+,则(3)f =__________.14.已知四棱锥P ABCD -,底面ABCD 为正方形,PA ^面ABCD ,且满足PA AB =,点E 是PD 的中点,则异面直线AE 与PB 所成角的大小为__________.15.已知点A 在直线20x y a ++=上,过点A 引圆22:1O x y +=的切线,若切线长的最小值为5,则实数a 的值为__________.16.已知在ABC D 中,角,,A B C 分别对应边,,a b c ,且b =B A =,2c =+,则ABC D 的面积为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分17.已知数列{}n a 满足11a =,11232n n n a a -+=+´,设nn n a b =.(1)求1b ,2b ,3b ;(2)判断数列{}n b 是否为等差数列,并说明理由;(3)求数列{}n a 的通项公式.18.某集团公司计划从甲分公司中的3位员工1A 、2A 、3A 和乙分公司中的3位员工1B 、2B 、3B 选择2位员工去国外工作.(1)若从这6名员工中任选2名,求这2名员工都是甲分公司的概率;(2)若从甲分公司和乙分公司中各任选1名员工,求这2名员工包括1A 但不包括1B 的概率.19.如图,EA ^平面ABC ,AECD ,24AB AC CD AE ====,BC =M 为BD 的中点.(1)求证:平面AEM ^平面BCD ;(2)求三棱锥E ABM -的体积.20.已知O 为坐标原点,抛物线2:4C y x =,点()2,0A -,设直线l 与C 交于不同的两点P 、Q .(1)若直线l x ^轴,求直线PA 的斜率的取值范围;(2)若直线l 不垂直于x 轴,且PAO QAO Ð=Ð,证明:直线l 过定点.21.已知函数22()32x x f x e ae a x =--.(1)当1a =时,讨论()f x 的单调性;(2)若对于任意的12,x x R Î,12x x ¹,都有21212()()21f x f x a x x ->---恒成立,求实数a 的取值范围.(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.22.在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t y t a aì=+ïí=+ïî,(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 10r r q --=.(1)求曲线C 的直角坐标方程;(2)设曲线C 与直线l 交于点,A B ,求AB 的最小值.23.已知函数()21f x x x =-++,x R Î,其最小值为t .(1)求t 的值;(2)正实数,a b 满足a b t +=,求证:112+³++.(清华大学)中学生标准学术能力诊断性测试2018年12月测试文科数学卷二、选择题:本大题共12小题,每小题5分,共60分.1.已知复数z 满足(1)13i z i -=+,则复数z 在复平面内对应的点为()A.(2,1)B.(2,1)- C.(1,2)- D.(1,2)--【答案】D 【解析】【分析】首先根据复数的运算法则,求得12z i =-+,进而求得其共轭复数,利用复数在复平面内对应点的坐标,求得结果.【详解】因为(1)13i z i -=+,所以13(13)(1)2412122i i i iz i i +++-+====-+-,所以12zi =--,所以复数z 对应的点的坐标为(1,2)--,故选D.【点睛】该题考查的是有关复数的问题,涉及到的知识点有复数的除法运算,复数的共轭复数,复数在复平面内对应点点的坐标,属于简单题目.2.某中学初中部共有500名学生,高中部共有600名学生,各年级段人数构成比例如图所示,则下列说法正确的是()A.人数最多的年级段是高二段B.初一段人数比高一段人数多C.高三段人数比初二段人数少D.高二段人数比初三段人数多一倍【答案】A 【解析】首先根据题中所给的饼形图,根据各年级所占的比例,求得各年级的实有人数,从而可以比较大小,对选项逐一分析,得到结果.【详解】从题中所给的图可以求得初一学生有50035%175´=人,初二学生有50040%200´=人,初三学生有50025%125´=人;高一学生有60030%180´=人,高二学生有60036%216´=人,高三学生有60034%204´=人,根据所得的数据,对选项逐个分析,得到人数最多的年级是高二段,故选A.【点睛】该题考查的是有关统计的问题,涉及到的知识点有利用饼形图中各年级所占的比例,初、高中部的总人数,求得各年级的人数,需要对选项逐个分析,属于简单题目.3.已知集合{|1,}2a P x x a Z ==+Î,1,2Q y m m Z 禳镲==+Î睚镲铪,则下列结论中正确的是()A.P Q Ç=ÆB.P Q QÇ= C.P Q QÈ= D.P Q RÈ=【答案】B 【解析】【分析】首先对集合中对应的式子进行变形,结合题中所给的变量的取值情况,可以发现分母都是2,分子一个取整数,一个取奇数,得到两个集合的关系,结合其性质,得到结果.【详解】因为21211,2222a a m m +++=+=,当,a m Z Î时,2a Z +Î,而21m +是奇数,从而得到Q P Í,所以Q P Q Ç=,故选B.【点睛】该题考查的是有关集合的问题,涉及到的知识点有集合的关系,集合的交并运算性质,属于简单题目.4.焦点在x 轴上,短轴长等于16,离心率等于35的椭圆的标准方程为()A.22110064x y += B.22164100x y += C.221400256x y += D.221256400x y +=【答案】A【分析】由题意可得35c a =,又222,216a b c b -==,求解方程即可得到,a b 的值,则答案可求.【详解】依题意有:216b =,所以8b =,根据离心率35e =,结合222a b c =+,解得10a =,再结合焦点在x 轴上,所以椭圆的方程是22110064x y +=,故选A.【点睛】该题考查的是有关椭圆方程的求解问题,涉及到的知识点有椭圆的短轴长,椭圆的离心率,以及椭圆中,,a b c 三者之间的关系,属于简单题目.5.设函数()x x f x ae e -=+.若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为()A.y x =-B.y x= C.2y x=- D.2y x=【答案】C 【解析】【分析】首先根据奇函数的性质,利用(0)10f a =+=,求得1a =-,之后对函数求导,令0x =,求得其值,即为切线的斜率,之后应用直线方程的点斜式,求得结果.【详解】因为函数()f x 是奇函数,所以(0)10f a =+=,解得1a =-,所以()x x f x e e -=-+,'()x x f x e e -=--,所以(0)0,'(0)2f f ==-,所以曲线()y f x =在点()0,0处的切线方程为2y x =-,故选C.【点睛】该题考查的是有关曲线在某个点处的切线方程的问题,涉及到的知识点有奇函数的性质,导数的几何意义,正确理解基础知识是解题的关键.6.在ABC D 中,点D 是BC 的中点,点E 是AD 的中点,点M 在线段AC 上,且2AM MC = ,则ME =()A.11412AB AC +B.11412AB AC -C.11124AB AC +D.11124AB AC -【答案】B 【解析】【分析】首先根据题意,画出相应的图形,利用向量的运算法则,以及其关系,将向量ME 逐步转化为,AB AC的式子,得到结果.【详解】如图,根据向量的运算法则,可得1123ME AE AM AD AC =-=- 11111443412AB AC AC AB AC =+-=-,故选B.【点睛】该题考查的是有关向量用一组基底来表示的问题,涉及到的知识点有数乘向量,向量的加法运算等,正确使用运算法则是解题的关键,属于简单题目.7.已知sin()2sin()2p p q q +=-,则3sin 4cos sin 2cos q qq q+=-()A.12B.2C.13D.3【答案】A 【解析】【分析】首先利用三角函数的诱导公式,将式子进行化简,得到tan 2q =-,之后将正余弦的齐次式的分式形式的式子,化成关于切的式子,代入求得结果.【详解】根据诱导公式可得sin 2cos q q -=,根据同角三角函数关系可得tan 2q =-,将式子变形可得3sin 4cos 3tan 4641sin 2cos tan 2222q q q q q q ++-+===----,故选A.【点睛】该题考查的是有关三角函数化简求值问题,涉及到的知识点有三角函数诱导公式,同角三角函数的关系式,齐次式的分式的求值问题,属于中档题目.8.已知函数()cos 22sin f x x x =+,则A.()f x 的最小正周期为p ,最小值为1B.()f x 的最小正周期为p ,最小值为-3C.()f x 的最小正周期为2p ,最小值为1D.()f x 的最小正周期为2p ,最小值为-3【答案】D 【解析】【分析】首先利用余弦倍角公式,将式子进行化简,使得解析式中只有一个函数名,之后进行配方,结合正弦函数的周期和值域,求得函数的周期和最值,对选项逐一分析判断,得出结果.【详解】化简函数解析式可得2213()cos 22sin 12sin 2sin 2(sin f x x x x x x =+=-+=--+,可以求得其最小正周期为2T p =,其最大值为32,最小值为2132(1)322---+=-,故选D.【点睛】该题考查的是有关三角函数的性质的问题,涉及到的知识点有余弦倍角公式,利用配方法求函数的最值,三角函数的最小正周期的求解,属于中档题目.9.若实数x ,y 满足不等式组(1)(23)013x y x y x ì--+-³ïí#ïî,则3z x y =-的取值范围是()A.[2,18]B.[2,12]C.[3,18]D.[3,12]【答案】B 【解析】【分析】首先根据题中所给的约束条件画出相应的可行域,结合目标函数的特征,判断出最优解,解方程组,得到最优解对应点的坐标,代入求得最值,得到范围.【详解】根据约束条件,画出相应的可行域,如图所示,结合直线3y x z =-的走向,可以断定:当直线3y x z =-过点E 时,z 取得最大值,当直线3y x z =-过点A 时,z 取得最小值,解方程组1230x x y ì=ïí+-=ïî,得(1,1)A ,解方程组3230x x y ì=ïí+-=ïî,得(3,3)E -,代入求得min max 312,9(3)12z z =-==--=,所以z 的取值范围是[2,12],故选B.【点睛】该题考查的是有关线性规划问题,在解题的过程中,需要注意的是(1)(23)0x y x y --+-³所表示的平面区域的确定方法,对于目标函数的形式分三种情况,结合具体情况,求得结果.10.某四棱锥的三视图如图所求,则该四棱锥的最长棱的长度为()A.6B.3C.23D.33【答案】C 【解析】【分析】首先根据题中所给的几何体的三视图,还原几何体,得到其为底面是边长为3的正方形,且顶点在底面上的摄影是底面对角线的三等分点处,高为2的四棱锥,利用其关系,求得侧棱长,比较得出最长棱的长度.【详解】根据题中所给的三视图,可以想到该几何体是底面是边长为3的正方形的四棱锥,并且顶点在底面上的摄影是底面对角线的三等分点,且高为2,从而可以求得其四条侧棱分别等于426,45483+=+=+=,通过比较可得最长棱的长度是3故选C.【点睛】该题考查的是有关利用三视图还原几何体,求其最长的棱长的问题,涉及到的知识点为将棱放在相应的三角形中,利用公式求得其边长,比较大小得出结果,属于简单题目.11.若一个正四面体的表面积为1S ,其外接球的表面积为2S ,则12S S =()A.3pB.36pC.33pD.334p【答案】C 【解析】【分析】首先设出正四面体的棱长,利用结论得到其外接球的半径,之后应用相关的公式求得正四面体的表面积以及外接球的表面积,两者一比,得到结果.【详解】设正四面体的棱长为a,可知该四面体的外接球的半径是4R a =,所以可以求得221344S a =´=,222634()42S a a p p ==,所以2122332S S a p p ==,故选C.【点睛】该题考查的是有关正四面体的表面积与其外接球的表面积的比值问题,涉及到的知识点有正四面体的外接球半径,球的表面积公式,正四面体的表面积公式,属于中档题目.12.已知函数33)2log (2),2()(2,2x x x f x x -ì-<ï=í-+³ïî ,则方程11f x a x骣琪+-=琪桫的实根个数不可能为()A.8B.7C.6D.5【答案】D 【解析】【分析】首先根据题中所给的解析式,画出函数的图象,结合图象,对a 的范围进行讨论,解相应的关于x 的方程,从而判断出根的个数,从而选出正确的结果.【详解】画出函数图象,如图所示:当0x >时,111x x +-³,当0x <时,113x x+-£-,观察图像,当2a >时,11x m x+-=,m 有两个解,一个满足1729m <<,一个满足7m <-,此时对应的x 有四个解,即方程有四个根,当2a =时,11x m x +-=,m 有三个解,179m =或7m =-或3m =,对应的x 有6个解,即方程有6个根,同理可得当12a <<,1a =,01a <<,0a =,0a <分析,结合方程11x m x+-=的根的情况,可知方程的根不可能为5,故选D.【点睛】该题考查的是有关应用函数的图象完成方程解的个数的问题,涉及到的知识点为将方程根的个数问题转化为曲线与直线交点个数的问题,再者就是分类讨论思想的应用,属于较难的题目.二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数2(log )1f x x =+,则(3)f =__________.【答案】9【解析】【分析】首先令2log 3x =,求得8x =,代入题中所给的式子,得到结果.【详解】令2log 3x =,解得8x =,此时1819x +=+=,故答案是9.【点睛】该题考查的是有关复合函数求值问题,在解题的过程中,需要分清x 代表的是谁,哪个量等于3,注意内层函数的函数值充当外层函数的自变量.14.已知四棱锥P ABCD -,底面ABCD 为正方形,PA ^面ABCD ,且满足PA AB =,点E 是PD 的中点,则异面直线AE 与PB 所成角的大小为__________.【答案】60 【解析】【分析】首先根据题的条件,画出相应的图,利用异面直线所成角的定义,找出平行线,得到异面直线所成角的平面角,放在三角形当中,得到结果.【详解】连接AC 与BD 相交于O 点,连接EO ,则有OEPB ,所以AEO Ð即为所求,根据题中条件,可以求得AE EO AO ==,从而得到60AEO Ð= ,故答案是60 .【点睛】该题考查的是有关异面直线所成角的问题,在解题的过程中,涉及到的知识点就是异面直线所成角的概念,解决空间问题的思路就是将空间问题平面化,得出平面角,放到三角形当中来求解.15.已知点A 在直线20x y a ++=上,过点A 引圆22:1O x y +=的切线,若切线长的最小值为255,则实数a 的值为__________.【答案】3±【解析】【分析】根据题意,画出图形,结合图形求出点O 到直线20x y a ++=的距离d ,利用勾股定理求出a 的值,得到结果.【详解】设点O 到直线20x y a ++=的距离为d,则d =,又过垂足引圆221x y +=的切线,切线长的最小值为5,则有24155a +=,解得3a =±,故答案是3±.【点睛】该题考查的是有关圆的切线问题,涉及到的知识点有点到直线的距离公式,直线与圆的位置关系,特殊的三角形,正确转化题的条件是解题的关键.16.已知在ABC D 中,角,,A B C 分别对应边,,a b c ,且b =B A =,2c =+,则ABC D 的面积为__________.【答案】2+【解析】【分析】由已知b =,可得sin B A =B A =,可得cosB A =,利用平方关系,可得2211sin cos 32A A +=,利用22sin cos 1A A +=,解得cos ,cos 22A B ==,从而得到角A,B 的大小,之后应用三角形内角和,求得角C ,利用余弦定理,求得a =.【详解】因为b =,可得sin B A =,因为B A =,可得cosB A =,所以22))1A A +=,即2211sin cos 32A A +=,结合22sin cos 1A A +=,可得32cos ,cos A B ==,所以,64A B p p ==,可求得76412C p p pp =--=,所以由余弦定理2222cos c a b ab C =+-,可得2222))2)4a a -=++,解得a =,所以112sin 2)2222ABC S ac B D ==创+,故答案是2+.【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有正弦定理,同角三角函数关系,余弦定理,三角形面积公式,在解题的过程中,正确使用公式是解题的关键.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分17.已知数列{}n a 满足11a =,11232n n n a a -+=+´,设nn n a b =.(1)求1b ,2b ,3b ;(2)判断数列{}n b 是否为等差数列,并说明理由;(3)求数列{}n a 的通项公式.【答案】(1)112b =,254b =,32b =;(2)见解析;(3)2(31)2n n a n -=-×.【解析】【分析】(1)分别将1,2n n ==代入11232n n n a a -+=+´,求得23,a a 的值,再将123,,a a a 的值代入2nn n a b =,求得结果;(2)利用题中所给的式子,求得13n n b b +-=,利用等差数列的定义,得到其为等差数列;(3)先利用等差数列的通项公式求得n b ,利用2nn n a b =,进一步求得n a .【详解】(1)25a =,316a =,112b =,254b =,32b =;(2)∵113224n n n n a a ++=+,∴134n n b b +-=,∴{}n b 是等差数列;(3)由前面知,()()131131244n b n n =+-´=-,∴()2312n n a n -=-×【点睛】该题考查的是有关数列的问题,涉及到的知识点有利用递推公式求数列的项,判断一个数列是否是等差数列,数列通项公式的求法,正确应用公式是解题的关键,属于中档题目.18.某集团公司计划从甲分公司中的3位员工1A 、2A 、3A 和乙分公司中的3位员工1B 、2B 、3B 选择2位员工去国外工作.(1)若从这6名员工中任选2名,求这2名员工都是甲分公司的概率;(2)若从甲分公司和乙分公司中各任选1名员工,求这2名员工包括1A 但不包括1B 的概率.【答案】(1)15;(2)29.【解析】【分析】(1)从这6名员工中任选2个,基本事件一一列出,总共有15个,这两名员工都是甲分公司的基本事件为3,利用公式求得概率;(2)从甲分公司和乙分公司中各任选1名员工,用列举法找出其对应的基本事件,共2个,利用公式求得概率.【详解】(1)由题意得,从6名员工中任选2名,其一切可能的结果组成的基本事件有:{}{}{}121323,,,,,,A A A A A A {}{}{}111213,,,,,,A B A B A B {}{}{}212223,,,,,A B A B A B {}{}{}313233,,,,,A B A B A B {}{}{}121323,,,,,B B B B B B ,共15个所选两名员工都是甲分公司所包含的基本事件有:{}{}{}121323,,,,,A A A A A A ,共3个,所以所求事件的概率为31155p ==;(2)从甲分公司和乙分公司各任选1名员工,其一切可能的结果组成的基本事件有:{}{}{}111213,,,,,,A B A B A B {}{}{}212223,,,,,,A B A B A B {}{}{}313233,,,,A B A B A B 共9个,包含1A 但不包括1B 的事件所包含的基本事件有{}12,A B ,{}13,A B 共2个,所以所求事件的概率为29p =【点睛】该题考查的是有关古典概型及有关计算问题,解题的步骤是先写出实验所对应的基本事件,再找出满足条件的基本事件数,之后利用概率公式求得结果.19.如图,EA ^平面ABC ,AECD ,24AB AC CD AE ====,BC =M 为BD 的中点.(1)求证:平面AEM ^平面BCD ;(2)求三棱锥E ABM -的体积.【答案】(1)见解析;(2)39.【解析】【分析】(1)取BC 中点N ,连接MN ,AN ,结合题中的条件,利用线面垂直的判定定理,证得EM ^平面BCD ,再应用面面垂直的判定定理,证得结论;(2)将三棱锥的顶点和底面转换,E ABM M ABE E ABN V V V ---==,之后应用锥体的体积公式求解即可.【详解】(1)取BC 中点N ,连接MN ,AN ,∴MN AE =,MN AE ,∵EA ^平面ABC ,∴四边形AEMN 是矩形,∴EM MN ^,由题意知,ED EB ==,∵M 为BD 的中点,∴EM BD ^,又∵BD MN M Ç=,∴EM ^平面BCD ,∵EM Ì平面AEM ,∴平面AEM ^平面BCD(2)由题意知,E ABM M ABE V V --=,∵MN 平面ABE ,∴13M ABE N ABE E ABN ABN V V V S AE ---D ===鬃13AN =,13922ABN S BN AN D =鬃=,∴139392323E ABM V -=创=【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有面面垂直的判定,三棱锥体积的计算,在解题的过程中,应用了线面垂直的判定定理以及面面垂直的判定定理,以及应用等积法,将三棱锥的顶点和底面转换,再根据平行关系,将其进一步转化,使得其底面积和高比较明显好求,之后应用体积公式求得结果.20.已知O 为坐标原点,抛物线2:4C y x =,点()2,0A-,设直线l 与C 交于不同的两点P 、Q .(1)若直线l x ^轴,求直线PA 的斜率的取值范围;(2)若直线l 不垂直于x 轴,且PAO QAO Ð=Ð,证明:直线l 过定点.【答案】(1)22[,0)(0,]-È;(2)见解析.【解析】【分析】(1)先设点P 在第一象限时,设出点P 的坐标,利用斜率坐标公式,将PA 的斜率表示出来,之后对式子进行变形,利用基本不等式求得其范围,从而得到直线PA 的斜率的取值范围,同理可得点P 落在第四象限时,其斜率的取值范围,之后取并集得到结果.(2)设出直线的方程,将直线方程与抛物线方程联立,利用韦达定理求得两根的关系,利用两个角的关系,得到两条直线的斜率是互为相反数的,从而得到2b k =-,代入直线方程,求得直线过的定点.【详解】(1)当点P 在第一象限时,设(),P t t ,02222222PA t k t t t -==£+,∴0,2PA k 纟çÎçú棼,同理,当点P在第四象限时,∴,02PA k ÷êÎ-÷ê滕,综上所述∴,00,22PA k 轹纟麋犏Î-È麋犏滕棼(2)设直线l 的方程为()0y kx b k =+¹,联立方程24y kx b y x ì=+ïí=ïî,得2440ky y b -+=,16160kb D =->,设()11,P x y ,()22,Q x y ,124y y k +=,124b y y k×=,∵PAO QAO Ð=Ð∴121222AP AQ y y k k x x +=+=++()()()()1221122222y x y x x x +++=++()()()12211222221212432864y y y y y y y y y y ++++++22480448b k b k kb +==+-+,2b k =-,∴()22y kx k k x =-=-,∴直线l 恒过定点()2,0【点睛】该题考查的是有关解析几何的问题,涉及到的知识点有直线与抛物线的位置关系,直线过定点问题,在解题的过程中,注意对公式的正确应用,以及对直线与曲线相交的解题步骤的熟练应用.21.已知函数22()32x x f x e ae a x =--.(1)当1a =时,讨论()f x 的单调性;(2)若对于任意的12,x x R Î,12x x ¹,都有21212()()21f x f x a x x ->---恒成立,求实数a 的取值范围.【答案】(1)(,ln 2)x Î-¥时,()f x 单调递减;(ln 2,)x Î+¥时,()f x 单调递增;(2)3a £.【解析】【分析】(1)将1a =代入解析式,求出函数的导函数,求得导数等于零的点,从而可以判断出在相应区间上导数的符号,从而求得函数的单调区间;(2)先规定12x x >,对式子进行变形,再构造新函数,将问题转化为函数()()221f x a x ++在R 上单调递增,从而应用其导数大于等于零恒成立,之后向最值靠拢,求得结果.【详解】(1)()f x 定义域为R()22232x x f x e ae a =--¢,当1a =时,令()()()22322210x x x x f x e e e e ¢=--=-+=,解得0ln2x =,当(),2x ln Î-¥,()0f x ¢<,()f x 单调递减;当()ln2,x Î+¥,()0f x ¢>,()f x 单调递增;综上,(),ln2x Î-¥时,()f x 单调递减;()ln2,x Î+¥时,()f x 单调递增(2)∵()()1221221f x f x a x x ->---,∴不妨设12x x >,则()()()()2211222121f x a x f x a x ++>++,∴()()221f x a x ++在R 上单调递增;记()()()22213x x g x f x a x e ae x =++=-+,()22310x xg x e ae =-+³¢恒成立,∴22111233x x x x e a e e e 骣+琪£=+琪桫对x R Î恒成立,∴min 112x x a e e骣琪£+琪桫,∵12x x e e +³,当且仅当12x x e e =,即2x e =时等号取到,∴223a £【点睛】该题考查的是应用导数研究函数的问题,涉及到的知识点有利用导数研究函数的单调性,利用导数研究恒成立问题,属于中档题目.(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.22.在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t y t a aì=+ïí=+ïî,(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 10r r q --=.(1)求曲线C 的直角坐标方程;(2)设曲线C 与直线l 交于点,A B ,求AB 的最小值.【答案】(1)22410x y x +--=;(2).【解析】【分析】(1)根据极坐标与平面直角坐标之间的关系,将极坐标方程转化为平面直角坐标方程,即可得结果;(2)分情况讨论,随着角的变化,直线的斜率存在与不存在两种情况,再者就是要明确弦心距最大时,弦最短,利用勾股定理,求得结果.【详解】(1)根据极坐标与平面直角坐标的对应关系,可得222,cos x y x r r q =+=,代入求得:22410x y x +--=;(2)当()2n n Z p a p =+Î时,直线l :1x =,此时4AB =当()2n n Z p a p ¹+Î时,设直线l :()11y k x -=-,圆心()2,0到直线l 的距离最大值为max d =,此时AB ==,∵4>min ||AB =【点睛】该题考查的是有关坐标系与参数方程的问题,涉及到的知识点有极坐标方程与平面直角坐标方程的转化,动直线被圆截得最短弦问题,注意对公式的灵活应用.23.已知函数()21f x x x =-++,x R Î,其最小值为t .(1)求t 的值;(2)正实数,a b 满足a b t +=,求证:112123a b +³++.【答案】(1)3t=;(2)见解析.【解析】【分析】(1)结合绝对值的意义,去掉绝对值的符号,将函数解析式进行化简,结合其单调性,可以断定函数的最小值,从而求得t 的值;(2)根据3a b +=,得到126a b +++=,从而将式子进行转化,之后应用基本不等式证得结果.【详解】(1)()21,23,1221,1x x f x x x x ì->ïï=-#íï-+<-ïî,()min 3f x =,即3t =;(2)∵3a b +=,且0a >,0b >,∴1112a b +=++()11112612a b a b 骣琪++++琪++桫121226123b a a b 骣++琪=++³琪++桫.当且仅当213b a a b ì++=ïí++ï+=î,即21a b ì=ïí=ïî时,等号取到【点睛】该题考查的是有关不等式的问题,涉及到的知识点有绝对值不等式,函数的最值,基本不等式,在解题的过程中,注意对式子的拼凑.。
中学生标准学术能力诊断性测试 数学理科卷(2018年2月)

ln x2 ln x3 的值为 1 1 x2 x3
D. 1 a
1 f ( x) x 3 x 2 2 x 有极值点的概率是 3
A. 0.2 3.下列命题中: (1) “ x 1 ”是“ x 1 ”的充分不必要条件 (2) 命题“若 a, b 都是奇数, 则 a b 是偶数”的逆否命题是“若 a b 不是偶数, 则 a,b 都不是奇数” (3) 命题“ x 0 ,都有 x
B. 0.7
C. 0.3
D. 0.8
m , n 分别为 2016 , 612 ,则输出的 m
A. 0 C.36 B.72 D. 180
S OBC S ABC
.
9.函数 y
2 cos(
x) 3 3 2 (x [ , 0) (0, ]) 1 4 4 1 2 x
2
C. 8
D. 9 8. 如图所示, 程序框图的算法思路源于数学名著 《几 何原本》中的“辗转相除法”,执行该程序框图(图中 “ m MOD n ”表示 m 除以 n 的余数) ,若输入的
2.设随机变量 服从正态分布 N (1, ) ,若 P ( 1) 0.2 ,则函数
ln x1 x1 , x2 , x3 (其中 x1 x2 x3 ) ,则 1 x1
x y20 2y x 14 . 设 实 数 x , y 满 足 2 x y 2 0 , 则 m 的取值范围是 y 2x y 1 0
_____________. 15 . 已 知 双 曲 线
的图像大致是
(4) 已知 p,q 为简单命题,若 p 是假命题,则 p q 是真命题. 正确命题的个数为 A..1 个 B.2 个 C.3 个 D.4 个
中学生标准学术能力诊断性测试(清华大学)2018年12月测试文科数学试卷及解析

………○…………订_________班级:___________………○…………订中学生标准学术能力诊断性测试(清华大学)2018年12月测试文科数学试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题1.已知复数z 满足(1−i)z =1+3i ,则复数z 在复平面内对应的点为( )A. (2,1)B. (2,−1)C. (−1,2)D. (−1,−2)2.某中学初中部共有500名学生,高中部共有600名学生,各年级段人数构成比例如图所示,则下列说法正确的是( )A. 人数最多的年级段是高二段B. 初一段人数比高一段人数多C. 高三段人数比初二段人数少D. 高二段人数比初三段人数多一倍 3.已知集合P ={x|x =a 2+1,a ∈Z},Q ={y =m +12,m ∈Z},则下列结论中正确的是( )A. P∩Q =∅ B. P ∩Q =Q C. P ∪Q =Q D. P ∪Q =R4.焦点在x 轴上,短轴长等于16,离心率等于35的椭圆的标准方程为( ) A.x 2100+y 264=1 B. x 264+y 2100=1 C. x 2400+y 2256=1 D. x 2256+y2400=15.设函数f(x)=ae x +e −x .若f(x)为奇函数,则曲线y =f(x)在点(0,0)处的切线方程为( )A. y=−x B. y =x C. y =−2x D. y =2x6.在ΔABC 中,点D 是BC 的中点,点E 是AD 的中点,点M 在线段AC 上, 且2AM⃑⃑⃑⃑⃑⃑ =MC ⃑⃑⃑⃑⃑⃑ ,则ME⃑⃑⃑⃑⃑⃑⃑⃑ =( )答案第2页,总16页装…………○………※要※※在※※装※※订※※线※装…………○………A. 14AB ⃑⃑⃑⃑⃑⃑⃑ +112AC ⃑⃑⃑⃑⃑⃑ B. 14AB ⃑⃑⃑⃑⃑⃑⃑ −112AC ⃑⃑⃑⃑⃑⃑ C. 112AB ⃑⃑⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑⃑⃑ D. 112AB ⃑⃑⃑⃑⃑⃑⃑ −14AC ⃑⃑⃑⃑⃑⃑ 7.已知sin(π+θ)=2sin(π2−θ),则3sinθ+4cosθsinθ−2cosθ=( ) A. 12B. 2C. 13D. 3 8.已知函数f(x)=cos2x +2sinx ,则A. f(x)的最小正周期为π,最小值为1B. f(x)的最小正周期为π,最小值为-3C. f(x)的最小正周期为2π,最小值为1D. f(x)的最小正周期为2π,最小值为-3 9.若实数x ,y 满足不等式组{(x −y −1)(2x +y −3)≥01≤x ≤3,则z =3x −y 的取值范围是( )A. [2,18]B. [2,12]C. [3,18]D. [3,12]10.某四棱锥的三视图如图所求,则该四棱锥的最长棱的长度为( )A. √6B. 3C. 2√3D. 3√311.若一个正四面体的表面积为S 1,其外接球的表面积为S 2,则S1S 2=( )A. √3πB. √36πC. 2√33πD. 3√34π 12.已知函数f(x)={|log 3(2−x)|,x <2−(x −3)2+2,x ≥2,则方程f(x +1x −1)=a 的实根个数不可能为( )A. 8B. 7C. 6D. 5第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(题型注释)13.已知函数f(log 2x)=x +1,则f(3)=__________.14.已知四棱锥P−ABCD ,底面ABCD 为正方形,PA ⊥面ABCD ,且满足PA =AB ,点E 是PD 的…………装……校:___________姓名:___…………装……中点,则异面直线AE 与PB 所成角的大小为__________. 15.已知点A 在直线2x+y +a =0上,过点A 引圆O:x 2+y 2=1的切线,若切线长的最小值为2√55,则实数a 的值为__________.16.已知在ΔABC 中,角A,B,C 分别对应边a,b,c ,且b=√2a ,√3cosB =√2cosA ,c =2√3+2,则ΔABC 的面积为__________.三、解答题(题型注释)17.已知数列{a n }满足a 1=1,a n+1=2a n +3×2n−1,设b n =a n2n.(1)求b 1,b 2,b 3;(2)判断数列{b n }是否为等差数列,并说明理由; (3)求数列{a n }的通项公式.18.某集团公司计划从甲分公司中的3位员工A 1、A 2、A 3和乙分公司中的3位员工B 1、B 2、B 3选择2位员工去国外工作.(1)若从这6名员工中任选2名,求这2名员工都是甲分公司的概率;(2)若从甲分公司和乙分公司中各任选1名员工,求这2名员工包括A 1但不包括B 1的概率. 19.如图,EA ⊥平面ABC ,AE ∥CD ,AB =AC =CD =2AE =4,BC =2√3,M 为BD 的中点.(1)求证:平面AEM ⊥平面BCD ;(2)求三棱锥E−ABM 的体积.20.已知O 为坐标原点,抛物线C:y 2=4x ,点A(−2,0),设直线l 与C 交于不同的两点P 、Q .(1)若直线l⊥x 轴,求直线PA 的斜率的取值范围;(2)若直线l 不垂直于x 轴,且∠PAO =∠QAO ,证明:直线l 过定点.21.已知函数f(x)=e 2x −3ae x −2a 2x .(1)当a=1时,讨论f(x)的单调性;(2)若对于任意的x 1,x 2∈R ,x 1≠x 2,都有f(x 1)−f(x 2)x 1−x2>−2a 2−1恒成立,求实数a 的取值范围.答案第4页,总16页22.在直角坐标系xOy 中,直线l 的参数方程为{x =1+tcosαy =1+tsinα ,(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ2−4ρcosθ−1=0.(1)求曲线C 的直角坐标方程;(2)设曲线C 与直线l 交于点A,B ,求|AB|的最小值. 23.已知函数f(x)=|x −2|+|x +1|,x ∈R ,其最小值为t .(1)求t 的值; (2)正实数a,b 满足a+b =t ,求证:1a+1+1b+2≥23.参数答案1.D【解析】1.首先根据复数的运算法则,求得z =−1+2i ,进而求得其共轭复数,利用复数在复平面内对应点的坐标,求得结果. 因为(1−i)z=1+3i ,所以z =1+3i 1−i=(1+3i)(1+i)2=−2+4i 2=−1+2i ,所以z =−1−2i ,所以复数z 对应的点的坐标为(−1,−2),故选D. 2.A【解析】2.首先根据题中所给的饼形图,根据各年级所占的比例,求得各年级的实有人数,从而可以比较大小,对选项逐一分析,得到结果.从题中所给的图可以求得初一学生有500×35%=175人,初二学生有500×40%=200人,初三学生有500×25%=125人; 高一学生有600×30%=180人,高二学生有600×36%=216人, 高三学生有600×34%=204人,根据所得的数据,对选项逐个分析,得到人数最多的年级是高二段, 故选A. 3.B【解析】3.首先对集合中对应的式子进行变形,结合题中所给的变量的取值情况,可以发现分母都是2,分子一个取整数,一个取奇数,得到两个集合的关系,结合其性质,得到结果. 因为a2+1=a+22,m +12=2m+12,当a,m ∈Z 时,a +2∈Z ,而2m +1是奇数,从而得到Q ⊆P ,所以Q ∩P =Q ,故选B. 4.A答案第6页,总16页【解析】4.由题意可得ca =35,又a 2−b 2=c 2,2b =16,求解方程即可得到a,b 的值,则答案可求.依题意有:2b =16,所以b =8,根据离心率e=35,结合a 2=b 2+c 2,解得a =10,再结合焦点在x 轴上,所以椭圆的方程是x 2100+y 264=1, 故选A. 5.C【解析】5.首先根据奇函数的性质,利用f(0)=a +1=0,求得a =−1,之后对函数求导,令x =0,求得其值,即为切线的斜率,之后应用直线方程的点斜式,求得结果. 因为函数f(x)是奇函数,所以f(0)=a +1=0,解得a =−1,所以f(x)=−e x +e −x ,f′(x)=−e x −e −x , 所以f(0)=0,f′(0)=−2,所以曲线y =f(x)在点(0,0)处的切线方程为y =−2x ,故选C. 6.B【解析】6.首先根据题意,画出相应的图形,利用向量的运算法则,以及其关系,将向量ME ⃑⃑⃑⃑⃑⃑⃑⃑ 逐步转化为AB ⃑⃑⃑⃑⃑⃑⃑ ,AC ⃑⃑⃑⃑⃑⃑ 的式子,得到结果. 如图,……线…………○………线…………○…根据向量的运算法则,可得ME ⃑⃑⃑⃑⃑⃑⃑⃑ =AE ⃑⃑⃑⃑⃑⃑⃑ −AM ⃑⃑⃑⃑⃑⃑⃑⃑ =12AD ⃑⃑⃑⃑⃑⃑⃑ −13AC ⃑⃑⃑⃑⃑⃑ =14AB⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑⃑ −13AC ⃑⃑⃑⃑⃑ =14AB ⃑⃑⃑⃑⃑ −112AC⃑⃑⃑⃑⃑ , 故选B. 7.A【解析】7.首先利用三角函数的诱导公式,将式子进行化简,得到tanθ=−2,之后将正余弦的齐次式的分式形式的式子,化成关于切的式子,代入求得结果. 根据诱导公式可得−sinθ=2cosθ,根据同角三角函数关系可得tanθ=−2,将式子变形可得3sinθ+4cosθsinθ−2cosθ=3tanθ+4tanθ−2=−6+4−2−2=12, 故选A. 8.D【解析】8.首先利用余弦倍角公式,将式子进行化简,使得解析式中只有一个函数名,之后进行配方,结合正弦函数的周期和值域,求得函数的周期和最值,对选项逐一分析判断,得出结果. 化简函数解析式可得f(x)=cos2x +2sinx =1−2sin 2x +2sinx =−2(sinx −12)2+32,可以求得其最小正周期为T=2π,其最大值为32,最小值为−2(−1−12)2+32=−3,故选D. 9.B答案第8页,总16页…○…………订…………○…※装※※订※※线※※内※※答※※题※※…○…………订…………○…【解析】9.首先根据题中所给的约束条件画出相应的可行域,结合目标函数的特征,判断出最优解,解方程组,得到最优解对应点的坐标,代入求得最值,得到范围. 根据约束条件,画出相应的可行域,如图所示, 结合直线y =3x −z 的走向,可以断定:当直线y =3x −z 过点E 时,z 取得最大值, 当直线y=3x −z 过点A 时,z 取得最小值,解方程组{x =12x +y −3=0 ,得A(1,1),解方程组{x =32x +y −3=0,得E(3,−3), 代入求得z min=3−1=2,z max =9−(−3)=12,所以z 的取值范围是[2,12],故选B. 10.C【解析】10.首先根据题中所给的几何体的三视图,还原几何体,得到其为底面是边长为3的正方形,且顶点在底面上的摄影是底面对角线的三等分点处,高为2的四棱锥,利用其关系,求得侧棱长,比较得出最长棱的长度.根据题中所给的三视图,可以想到该几何体是底面是边长为3的正方形的四棱锥, 并且顶点在底面上的摄影是底面对角线的三等分点,且高为2,从而可以求得其四条侧棱分别等于√4+2=√6,√4+5=3,3,√4+8=2√3, 通过比较可得最长棱的长度是2√3,……○…………装………学校:___________姓名:______……○…………装………故选C. 11.C【解析】11.首先设出正四面体的棱长,利用结论得到其外接球的半径,之后应用相关的公式求得正四面体的表面积以及外接球的表面积,两者一比,得到结果.设正四面体的棱长为a ,可知该四面体的外接球的半径是R =√64a ,所以可以求得S 1=4×√34a 2=√3a 2,S 2=4π(√64a)2=32a 2π, 所以S 1S 2=√3a 232a 2π=2√33π,故选C. 12.D【解析】12.首先根据题中所给的解析式,画出函数的图象,结合图象,对a 的范围进行讨论,解相应的关于x 的方程,从而判断出根的个数,从而选出正确的结果. 画出函数图象,如图所示:当x>0时,x +1x−1≥1,当x <0时,x +1x−1≤−3,观察图像,当a >2时,x +1x−1=m ,m 有两个解,一个满足179<m <2,一个满足m <−7,此时对应的x 有四个解,即方程有四个根,当a=2时,x +1x−1=m ,m 有三个解,m =179或m =−7或m =3,对应的x 有6个解,即方程有6个根,答案第10页,总16页○…………装………※※请※※不※※要※※在※※○…………装………同理可得当1<a <2,a =1,0<a <1,a =0,a <0分析,结合方程x +1x−1=m 的根的情况,可知方程的根不可能为5,故选D. 13.9【解析】13.首先令log 2x =3,求得x =8,代入题中所给的式子,得到结果.令log 2x =3,解得x =8,此时x +1=8+1=9,故答案是9. 14.60∘【解析】14.首先根据题的条件,画出相应的图,利用异面直线所成角的定义,找出平行线,得到异面直线所成角的平面角,放在三角形当中,得到结果.连接AC 与BD 相交于O 点,连接EO ,则有OE∥PB ,所以∠AEO 即为所求,根据题中条件,可以求得AE =EO =AO ,从而得到∠AEO =60∘,故答案是60∘. 15.±3【解析】15.根据题意,画出图形,结合图形求出点O 到直线2x +y +a =0的距离d ,利用勾股定理求出a 的值,得到结果.…………线……………………线…………设点O 到直线2x +y +a =0的距离为d ,则d =√5,又过垂足引圆x 2+y 2=1的切线,切线长的最小值为2√55,则有1+45=a 25,解得a =±3,故答案是±3. 16.2√3+2【解析】16. 由已知b=√2a ,可得sinB =√2sinA ,由√3cosB =√2cosA ,可得cosB =√2√3,利用平方关系,可得sin2A +13cos 2A =12,利用sin 2A +cos 2A =1,解得cosA =√32,cosB =√22,从而得到角A,B 的大小,之后应用三角形内角和,求得角C ,利用余弦定理,求得a =2√2,之后应用三角形面积公式求得结果. 因为b=√2a ,可得sinB =√2sinA ,因为√3cosB =√2cosA ,可得cosB =√2√3,所以(√2sinA)2+(√232=1,即sin 2A +13cos 2A =12, 结合sin 2A +cos 2A =1,可得cosA =√32,cosB =√22,所以A=π6,B =π4,可求得C =π−π6−π4=7π12,所以由余弦定理c 2=a 2+b 2−2abcosC , 可得(2√3+2)2=a 2+(√2a)2+2a ×(√2a)×√6−√24,解得a =2√2,所以S ΔABC=12acsinB =12×2√2×(2√3+2)×√22=2√3+2,答案第12页,总16页故答案是2√3+2. 17.(1)b 1=12,b 2=54,b 3=2; (2)见解析; (3)a n =(3n −1)⋅2n−2.【解析】17. (1)分别将n=1,n =2代入a n+1=2a n +3×2n−1,求得a 2,a 3的值,再将a 1,a 2,a 3的值代入b n =a n2n,求得结果;(2)利用题中所给的式子,求得b n+1−b n=34,利用等差数列的定义,得到其为等差数列; (3)先利用等差数列的通项公式求得b n ,利用b n =a n 2n,进一步求得a n . (1)a 2=5,a 3=16,b 1=12,b 2=54,b 3=2; (2)∵a n+12n+1=a n2n +34,∴b n+1−b n =34,∴{b n }是等差数列; (3)由前面知,b n=12+(n −1)×34=14(3n −1),∴a n =(3n −1)⋅2n−2 18.(1)15; (2)29.【解析】18.(1)从这6名员工中任选2个,基本事件一一列出,总共有15个,这两名员工都是甲分公司的基本事件为3,利用公式求得概率;(2)从甲分公司和乙分公司中各任选1名员工,用列举法找出其对应的基本事件,共2个,利用公式求得概率.(1)由题意得,从6名员工中任选2名,其一切可能的结果组成的基本事件有:{A 1,A 2},{A 1,A 3},{A 2,A 3}, {A 1,B 1},{A 1,B 2},{A 1,B 3}, {A 2,B 1},{A 2,B 2}{A 2,B 3}, {A 3,B 1},{A 3,B 2}{A 3,B 3}, {B 1,B 2},{B 1,B 3},{B 2,B 3},共15个所选两名员工都是甲分公司所包含的基本事件有:{A 1,A 2},{A 1,A 3},{A 2,A 3},共3个, 所以所求事件的概率为p=315=15;(2)从甲分公司和乙分公司各任选1名员工,其一切可能的结果组成的基本事件有:{A 1,B 1},{A 1,B 2},{A 1,B 3}, {A 2,B 1},{A 2,B 2},{A 2,B 3}, {A 3,B 1},{A 3,B 2}{A 3,B 3}共9个,包含A1但不包括B1的事件所包含的基本事件有{A1,B2},{A1,B3}共2个,所以所求事件的概率为p=29 19.(1)见解析;(2)√393.【解析】19.(1)取BC中点N,连接MN,AN,结合题中的条件,利用线面垂直的判定定理,证得EM⊥平面BCD,再应用面面垂直的判定定理,证得结论;(2)将三棱锥的顶点和底面转换,V E−ABM=V M−ABE=V E−ABN,之后应用锥体的体积公式求解即可.(1)取BC中点N,连接MN,AN,∴MN=AE,MN∥AE,∵EA⊥平面ABC,∴四边形AEMN是矩形,∴EM⊥MN,由题意知,ED=EB=2√5,∵M为BD的中点,∴EM⊥BD,又∵BD∩MN=M,∴EM⊥平面BCD,∵EM⊂平面AEM,∴平面AEM⊥平面BCD(2)由题意知,V E−ABM=V M−ABE,∵MN∥平面ABE,∴V M−ABE=V N−ABE=V E−ABN=13⋅SΔABN⋅AEAN=√13,SΔABN=12⋅BN⋅AN=√392,∴V E−ABM=13×√392×2=√39320.(1)[−√22,0)∪(0,√22];(2)见解析.【解析】20.(1)先设点P在第一象限时,设出点P的坐标,利用斜率坐标公式,将PA的斜率表示出来,之后对式子进行变形,利用基本不等式求得其范围,从而得到直线PA的斜率的取值范围,同理可得点P落在第四象限时,其斜率的取值范围,之后取并集得到结果.(2)设出直线的方程,将直线方程与抛物线方程联立,利用韦达定理求得两根的关系,利用两个角的答案第14页,总16页关系,得到两条直线的斜率是互为相反数的,从而得到b=−2k ,代入直线方程,求得直线过的定点.(1)当点P 在第一象限时,设P(t,2√t),k PA =2√t−0t+2=2√t+2√t≤22=√22, ∴k PA ∈(0,√22],同理,当点P 在第四象限时,∴k PA ∈[−√22,0),综上所述∴k PA ∈[−√22,0)∪(0,√22](2)设直线l 的方程为y =kx +b(k ≠0),联立方程{y =kx +b y 2=4x,得ky 2−4y +4b =0, Δ=16−16kb >0,设P(x 1,y 1),Q(x 2,y 2),y 1+y 2=4k ,y 1⋅y 2=4bk, ∵∠PAO =∠QAO ∴k AP +k AQ =y 1x1+2+y 2x 2+2=y 1(x 2+2)+y 2(x 1+2)(x 1+2)(x 2+2)=4y 1y 2(y 2+y 1)+32(y 1+y 2)y 12y 22+8(y 12+y 22)+64 =4b+8k b 2+4k 2−4kb+8=0,b =−2k ,∴y =kx −2k =k(x −2),∴直线l 恒过定点(2,0)21.(1)x ∈(−∞,ln2)时,f(x)单调递减;x ∈(ln2,+∞)时,f(x)单调递增; (2)a ≤2√23.【解析】21. (1)将a=1代入解析式,求出函数的导函数,求得导数等于零的点,从而可以判断出在相应区间上导数的符号,从而求得函数的单调区间; (2)先规定x 1>x 2,对式子进行变形,再构造新函数,将问题转化为函数f(x)+(2a 2+1)x 在R上单调递增,从而应用其导数大于等于零恒成立,之后向最值靠拢,求得结果. (1)f(x)定义域为Rf ′(x)=2e 2x −3ae x −2a 2,当a =1时,令f ′(x)=2e 2x −3e x −2=(e x −2)(2e x +1)=0,解得x 0=ln2, 当x ∈(−∞,ln2),f ′(x)<0,f(x)单调递减; 当x ∈(ln2,+∞),f ′(x)>0,f(x)单调递增;综上,x ∈(−∞,ln2)时,f(x)单调递减;x ∈(ln2,+∞)时,f(x)单调递增(2)∵f(x1)−f(x2)x1−x2>−2a2−1,∴不妨设x1>x2,则f(x1)+(2a2+1)x1>f(x2)+(2a2+1)x2,∴f(x)+(2a2+1)x在R上单调递增;记g(x)=f(x)+(2a2+1)x=e2x−3ae x+x,g′(x)=2e2x−3ae x+1≥0恒成立,∴a≤2e2x+13e x =13(2e x+1e x)对x∈R恒成立,∴a≤13(2e x+1e x)min,∵2e x+1e x≥2√2,当且仅当2e x=1e x,即e x=√22时等号取到,∴a≤2√2322.(1)x2+y2−4x−1=0;(2)2√3.【解析】22.(1)根据极坐标与平面直角坐标之间的关系,将极坐标方程转化为平面直角坐标方程,即可得结果;(2)分情况讨论,随着角的变化,直线的斜率存在与不存在两种情况,再者就是要明确弦心距最大时,弦最短,利用勾股定理,求得结果.(1)根据极坐标与平面直角坐标的对应关系,可得ρ2=x2+y2,ρcosθ=x,代入求得:x2+y2−4x−1=0;(2)当α=nπ+π2(n∈Z)时,直线l:x=1,此时|AB|=4当α≠nπ+π2(n∈Z)时,设直线l:y−1=k(x−1),圆心(2,0)到直线l的距离最大值为d max=√2,此时|AB|=2√5−2=2√3,∵4>2√3,∴|AB|min=2√323.(1)t=3;(2)见解析.【解析】23.(1)结合绝对值的意义,去掉绝对值的符号,将函数解析式进行化简,结合其单调性,可以断定函数的最小值,从而求得t的值;(2)根据a+b=3,得到a+1+b+2=6,从而将式子进行转化,之后应用基本不等式证得结果.答案第16页,总16页(1)f(x)={2x −1,x >23,−1≤x ≤2−2x +1,x <−1,f(x)min =3,即t =3;(2)∵a+b =3,且a >0,b >0,∴1a+1+1b+2= 16(1a+1+1b+2)(a +1+b +2) =16(2+b+2a+1+a+1b+2)≥23.当且仅当{b+2a+1=a+1b+2a +b =3,即{a =2b =1 时,等号取到。
中学生标准学术能力诊断性测试(清华大学)2018年12月测试文科数学试卷(解析版)

中学生标准学术能力诊断性测试2018年12月测试文科数学试卷(一卷)本试卷共150分,考试时间120分钟.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z 满足(1)13i z i -=+,则复数z 在复平面内对应的点为( )A. (2,1)B. (2,1)-C. (1,2)-D. (1,2)--【答案】D【解析】【分析】首先根据复数的运算法则,求得12z i =-+,进而求得其共轭复数,利用复数在复平面内对应点的坐标,求得结果.【详解】因为(1)13i z i -=+,所以13(13)(1)2412122i i i i z i i +++-+====-+-, 所以12z i =--, 所以复数z 对应的点的坐标为(1,2)--,故选D.【点睛】该题考查的是有关复数的问题,涉及到的知识点有复数的除法运算,复数的共轭复数,复数在复平面内对应点点的坐标,属于简单题目.2.某中学初中部共有500名学生,高中部共有600名学生,各年级段人数构成比例如图所示,则下列说法正确的是( )A. 人数最多的年级段是高二段B. 初一段人数比高一段人数多C. 高三段人数比初二段人数少D. 高二段人数比初三段人数多一倍【答案】A【解析】【分析】首先根据题中所给的饼形图,根据各年级所占的比例,求得各年级的实有人数,从而可以比较大小,对选项逐一分析,得到结果.【详解】从题中所给的图可以求得初一学生有50035%175?人,初二学生有50040%200?人,初三学生有50025%125?人;高一学生有60030%180?人,高二学生有60036%216?人, 高三学生有60034%204?人,根据所得的数据,对选项逐个分析,得到人数最多的年级是高二段,故选A.【点睛】该题考查的是有关统计的问题,涉及到的知识点有利用饼形图中各年级所占的比例,初、高中部的总人数,求得各年级的人数,需要对选项逐个分析,属于简单题目.3.已知集合{|1,}2a P x x a Z ==+?,1,2Q y m m Z 禳镲==+?睚镲铪,则下列结论中正确的是( ) A. P Q?? B. P Q Q ? C. P Q Q ? D. P QR ? 【答案】B【解析】【分析】 首先对集合中对应的式子进行变形,结合题中所给的变量的取值情况,可以发现分母都是2,分子一个取整数,一个取奇数,得到两个集合的关系,结合其性质,得到结果. 【详解】因为21211,2222a a m m +++=+=,当,a m Z Î时,2a Z +?,而21m +是奇数, 从而得到Q P Í,所以Q PQ ?, 故选B.【点睛】该题考查的是有关集合的问题,涉及到的知识点有集合的关系,集合的交并运算性质,属于简单题目.4.焦点在x 轴上,短轴长等于16,离心率等于35的椭圆的标准方程为( ) A. 22110064x y += B. 22164100x y += C. 221400256x y += D. 221256400x y += 【答案】A【解析】【分析】 由题意可得35c a =,又222,216a b c b -==,求解方程即可得到,a b 的值,则答案可求. 【详解】依题意有:216b =,所以8b =, 根据离心率35e =,结合222a b c =+,解得10a =, 再结合焦点在x 轴上,所以椭圆的方程是22110064x y +=, 故选A.【点睛】该题考查的是有关椭圆方程的求解问题,涉及到的知识点有椭圆的短轴长,椭圆的离心率,以及椭圆中,,a b c 三者之间的关系,属于简单题目.5.设函数()x x f x ae e -=+.若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为( )A. y x =-B. y x =C. 2y x =-D. 2y x =【答案】C【解析】【分析】首先根据奇函数的性质,利用(0)10f a =+=,求得1a =-,之后对函数求导,令0x =,求得其值,即为切线的斜率,之后应用直线方程的点斜式,求得结果.【详解】因为函数()f x 是奇函数,所以(0)10f a =+=,解得1a =-,所以()x x f x e e -=-+,'()x x f x e e -=--,所以(0)0,'(0)2f f ==-,所以曲线()y f x =在点()0,0处的切线方程为2y x =-,【点睛】该题考查的是有关曲线在某个点处的切线方程的问题,涉及到的知识点有奇函数的性质,导数的几何意义,正确理解基础知识是解题的关键.6.在ABC D 中,点D 是BC 的中点,点E 是AD 的中点,点M 在线段AC 上, 且2AM MC =,则ME =( ) A. 11412AB AC + B. 11412AB AC - C. 11124AB AC + D. 11124AB AC - 【答案】B【解析】【分析】首先根据题意,画出相应的图形,利用向量的运算法则,以及其关系,将向量ME 逐步转化为,AB AC 的式子,得到结果.【详解】如图,根据向量的运算法则,可得1123ME AE AM AD AC =-=-11111443412AB AC AC AB AC =+-=-, 故选B. 【点睛】该题考查的是有关向量用一组基底来表示的问题,涉及到的知识点有数乘向量,向量的加法运算等,正确使用运算法则是解题的关键,属于简单题目.7.已知sin()2sin()2p p q q +=-,则3sin 4cos sin 2cos q q q q +=-( ) A. 12 B. 2 C. 13D. 3 【答案】A【解析】首先利用三角函数的诱导公式,将式子进行化简,得到tan 2q =-,之后将正余弦的齐次式的分式形式的式子,化成关于切的式子,代入求得结果.【详解】根据诱导公式可得sin 2cos q q -=,根据同角三角函数关系可得tan 2q =-, 将式子变形可得3sin 4cos 3tan 4641sin 2cos tan 2222q q q q q q ++-+===----, 故选A.【点睛】该题考查的是有关三角函数化简求值问题,涉及到的知识点有三角函数诱导公式,同角三角函数的关系式,齐次式的分式的求值问题,属于中档题目.8.已知函数()cos 22sin f x x x =+,则A. ()f x 的最小正周期为p ,最小值为1B. ()f x 的最小正周期为p ,最小值为-3C. ()f x 的最小正周期为2p ,最小值为1D. ()f x 的最小正周期为2p ,最小值为-3【答案】D【解析】【分析】首先利用余弦倍角公式,将式子进行化简,使得解析式中只有一个函数名,之后进行配方,结合正弦函数的周期和值域,求得函数的周期和最值,对选项逐一分析判断,得出结果.【详解】化简函数解析式可得 2213()cos 22sin 12sin 2sin 2(sin )22f x x x x x x =+=-+=--+, 可以求得其最小正周期为2T p =, 其最大值为32,最小值为2132(1)322---+=-, 故选D. 【点睛】该题考查的是有关三角函数的性质的问题,涉及到的知识点有余弦倍角公式,利用配方法求函数的最值,三角函数的最小正周期的求解,属于中档题目.9.若实数x ,y 满足不等式组(1)(23)013x y x y x ì--+-?ïí#ïî,则3z x y =-的取值范围是( ) A. [2,18] B. [2,12] C. [3,18] D. [3,12]【答案】B【解析】【分析】首先根据题中所给的约束条件画出相应的可行域,结合目标函数的特征,判断出最优解,解方程组,得到最优解对应点的坐标,代入求得最值,得到范围.【详解】根据约束条件,画出相应的可行域,如图所示,结合直线3y x z =-的走向,可以断定:当直线3y x z =-过点E 时,z 取得最大值,当直线3y x z =-过点A 时,z 取得最小值,解方程组1230x x y ì=ïí+-=ïî,得(1,1)A ,解方程组3230x x y ì=ïí+-=ïî,得(3,3)E -, 代入求得min max 312,9(3)12z z =-==--=,所以z 的取值范围是[2,12],故选B.【点睛】该题考查的是有关线性规划问题,在解题的过程中,需要注意的是(1)(23)0x y x y --+-?所表示的平面区域的确定方法,对于目标函数的形式分三种情况,结合具体情况,求得结果.10.某四棱锥的三视图如图所求,则该四棱锥的最长棱的长度为( )A. B. 3C.D. 【答案】C【解析】【分析】首先根据题中所给的几何体的三视图,还原几何体,得到其为底面是边长为3的正方形,且顶点在底面上的摄影是底面对角线的三等分点处,高为2的四棱锥,利用其关系,求得侧棱长,比较得出最长棱的长度.【详解】根据题中所给的三视图,可以想到该几何体是底面是边长为3的正方形的四棱锥,并且顶点在底面上的摄影是底面对角线的三等分点,且高为2,==通过比较可得最长棱的长度是故选C.【点睛】该题考查的是有关利用三视图还原几何体,求其最长的棱长的问题,涉及到的知识点为将棱放在相应的三角形中,利用公式求得其边长,比较大小得出结果,属于简单题目.11.若一个正四面体的表面积为1S ,其外接球的表面积为2S ,则12S S =( )A. pB. 6pC. 3pD. 4p【答案】C【解析】【分析】首先设出正四面体的棱长,利用结论得到其外接球的半径,之后应用相关的公式求得正四面体的表面积以及外接球的表面积,两者一比,得到结果.【详解】设正四面体的棱长为a,可知该四面体的外接球的半径是4R a =,所以可以求得2214S =?,22234)2S a p p ==,所以1222S S a p , 故选C.【点睛】该题考查的是有关正四面体的表面积与其外接球的表面积的比值问题,涉及到的知识点有正四面体的外接球半径,球的表面积公式,正四面体的表面积公式,属于中档题目.12.已知函数33)2log (2),2()(2,2x x x f x x -ì-<ï=í-+?ïî,则方程11f x a x骣琪+-=琪桫的实根个数不可能为( ) A. 8 B. 7 C. 6 D. 5【答案】D【解析】【分析】首先根据题中所给的解析式,画出函数的图象,结合图象,对a 的范围进行讨论,解相应的关于x 的方程,从而判断出根的个数,从而选出正确的结果.【详解】画出函数图象,如图所示:当0x >时,111x x +-?,当0x <时,113x x+-?, 观察图像,当2a >时,11x m x +-=,m 有两个解,一个满足1729m <<,一个满足7m <-,此时对应的x 有四个解,即方程有四个根, 当2a =时,11x m x +-=,m 有三个解,179m =或7m =-或3m =, 对应的x 有6个解,即方程有6个根,同理可得当12a <<,1a =,01a <<,0a =,0a <分析, 结合方程11x m x+-=的根的情况,可知方程的根不可能为5, 故选D.【点睛】该题考查的是有关应用函数的图象完成方程解的个数的问题,涉及到的知识点为将方程根的个数问题转化为曲线与直线交点个数的问题,再者就是分类讨论思想的应用,属于较难的题目. 二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数2(log )1f x x =+,则(3)f =__________.【答案】9【解析】【分析】首先令2log 3x =,求得8x =,代入题中所给的式子,得到结果.【详解】令2log 3x =,解得8x =,此时1819x +=+=,故答案是9.【点睛】该题考查的是有关复合函数求值问题,在解题的过程中,需要分清x 代表的是谁,哪个量等于3,注意内层函数的函数值充当外层函数的自变量.14.已知四棱锥P ABCD -,底面ABCD 为正方形,PA ^面ABCD ,且满足PA AB =,点E 是PD 的中点,则异面直线AE 与PB 所成角的大小为__________.【答案】60【解析】【分析】首先根据题的条件,画出相应的图,利用异面直线所成角的定义,找出平行线,得到异面直线所成角的平面角,放在三角形当中,得到结果.【详解】连接AC 与BD 相交于O 点,连接EO ,则有OE PB ,所以AEO Ð即为所求,根据题中条件,可以求得AE EO AO ==,从而得到60AEO ?, 故答案是60.【点睛】该题考查的是有关异面直线所成角的问题,在解题的过程中,涉及到的知识点就是异面直线所成角的概念,解决空间问题的思路就是将空间问题平面化,得出平面角,放到三角形当中来求解.15.已知点A 在直线20x y a ++=上,过点A 引圆22:1O x y +=的切线,则实数a 的值为__________.【答案】3±【解析】【分析】根据题意,画出图形,结合图形求出点O 到直线20x y a ++=的距离d ,利用勾股定理求出a 的值,得到结果.【详解】设点O 到直线20x y a ++=的距离为d ,则d ,又过垂足引圆221x y += 则有24155a +=,解得3a =?,故答案是3±.【点睛】该题考查的是有关圆的切线问题,涉及到的知识点有点到直线的距离公式,直线与圆的位置关系,特殊的三角形,正确转化题的条件是解题的关键.16.已知在ABC D 中,角,,A B C 分别对应边,,a b c ,且b B A ,2c =,则ABC D 的面积为__________.【答案】2 【解析】 【分析】由已知b ,可得sin B A B A ,可得cos B A =,利用平方关系,可得2211sin cos 32A A +=,利用22sin cos 1A A +=,解得cos A B =A,B 的大小,之后应用三角形内角和,求得角C ,利用余弦定理,求得a =结果.【详解】因为b ,可得sin B A ,B A ,可得cosB A =,所以22))1A A +=,即2211sin cos 32A A +=,结合22sin cos 1A A +=,可得cos A B , 所以,64A B p p ==,可求得76412C p p pp =--=, 所以由余弦定理2222cos c a b ab C =+-,可得2222))2)a a =++,解得a =所以11sin 2)2222ABC S ac B D ==创?,故答案是2.【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有正弦定理,同角三角函数关系,余弦定理,三角形面积公式,在解题的过程中,正确使用公式是解题的关键.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分17.已知数列{}n a 满足11a =,11232n n n a a -+=+?,设2nn na b =. (1)求1b ,2b ,3b ;(2)判断数列{}n b 是否为等差数列,并说明理由; (3)求数列{}n a 的通项公式. 【答案】(1)112b =,254b =,32b =; (2)见解析; (3)2(31)2n n a n -=-?. 【解析】 【分析】(1)分别将1,2n n ==代入11232n n n a a -+=+?,求得23,a a 的值,再将123,,a a a 的值代入2nn n a b =,求得结果;(2)利用题中所给的式子,求得134n n b b +-=,利用等差数列的定义,得到其为等差数列; (3)先利用等差数列的通项公式求得n b ,利用2n n nab =,进一步求得n a . 【详解】(1)25a =,316a =,112b =,254b =,32b =;(2)∵113224n n n n a a ++=+,∴134n nb b +-=,∴{}n b 是等差数列; (3)由前面知,()()131131244n b n n =+-?-,∴()2312n n a n -=-? 【点睛】该题考查的是有关数列的问题,涉及到的知识点有利用递推公式求数列的项,判断一个数列是否是等差数列,数列通项公式的求法,正确应用公式是解题的关键,属于中档题目.18.某集团公司计划从甲分公司中的3位员工1A 、2A 、3A 和乙分公司中的3位员工1B 、2B 、3B 选择2位员工去国外工作.(1)若从这6名员工中任选2名,求这2名员工都是甲分公司的概率;(2)若从甲分公司和乙分公司中各任选1名员工,求这2名员工包括1A 但不包括1B 的概率. 【答案】(1)15; (2)29. 【解析】 【分析】(1)从这6名员工中任选2个,基本事件一一列出,总共有15个,这两名员工都是甲分公司的基本事件为3,利用公式求得概率;(2)从甲分公司和乙分公司中各任选1名员工,用列举法找出其对应的基本事件,共2个,利用公式求得概率.【详解】(1)由题意得,从6名员工中任选2名,其一切可能的结果组成的基本事件有:{}{}{}121323,,,,,,A A A A A A {}{}{}111213,,,,,,A B A B A B {}{}{}212223,,,,,A B A B A B {}{}{}313233,,,,,A B A B A B {}{}{}121323,,,,,B B B B B B ,共15个所选两名员工都是甲分公司所包含的基本事件有:{}{}{}121323,,,,,A A A A A A ,共3个, 所以所求事件的概率为31155p ==; (2)从甲分公司和乙分公司各任选1名员工,其一切可能的结果组成的基本事件有:{}{}{}111213,,,,,,A B A B A B {}{}{}212223,,,,,,A B A B A B {}{}{}313233,,,,A B A B A B 共9个,包含1A 但不包括1B 的事件所包含的基本事件有{}12,A B ,{}13,A B 共2个,所以所求事件的概率为29p = 【点睛】该题考查的是有关古典概型及有关计算问题,解题的步骤是先写出实验所对应的基本事件,再找出满足条件的基本事件数,之后利用概率公式求得结果.19.如图,EA ^平面ABC ,AECD ,24AB AC CD AE ====,BC =M 为BD 的中点.(1)求证:平面AEM ^平面BCD ;(2)求三棱锥E ABM -的体积.【答案】(1)见解析; (2【解析】 【分析】(1)取BC 中点N ,连接MN ,AN ,结合题中的条件,利用线面垂直的判定定理,证得EM ^平面BCD ,再应用面面垂直的判定定理,证得结论;(2)将三棱锥的顶点和底面转换,E ABM M ABE E ABN V V V ---==,之后应用锥体的体积公式求解即可.【详解】(1)取BC 中点N ,连接MN ,AN ,∴MN AE =,MN AE ,∵EA ^平面ABC ,∴四边形AEMN 是矩形, ∴EM MN ^,由题意知,ED EB ==M 为BD 的中点, ∴EM BD ^, 又∵BD MNM ?,∴EM ^平面BCD ,∵EM Ì平面AEM ,∴平面AEM ^平面BCD (2)由题意知,E ABM M ABE V V --=,∵MN平面ABE ,∴13M ABE N ABE E ABN ABN V V V S AE ---D ===鬃AN 12ABN S BN AN D =鬃=,∴123E ABM V -==【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有面面垂直的判定,三棱锥体积的计算,在解题的过程中,应用了线面垂直的判定定理以及面面垂直的判定定理,以及应用等积法,将三棱锥的顶点和底面转换,再根据平行关系,将其进一步转化,使得其底面积和高比较明显好求,之后应用体积公式求得结果. 20.已知O 为坐标原点,抛物线2:4C y x =,点()2,0A -,设直线l 与C 交于不同的两点P 、Q . (1)若直线l x ^轴,求直线PA 的斜率的取值范围; (2)若直线l 不垂直于x 轴,且PAOQAO ??,证明:直线l 过定点.【答案】(1)[-?; (2)见解析. 【解析】 【分析】(1)先设点P 在第一象限时,设出点P 的坐标,利用斜率坐标公式,将PA 的斜率表示出来,之后对式子进行变形,利用基本不等式求得其范围,从而得到直线PA 的斜率的取值范围,同理可得点P 落在第四象限时,其斜率的取值范围,之后取并集得到结果.(2)设出直线的方程,将直线方程与抛物线方程联立,利用韦达定理求得两根的关系,利用两个角的关系,得到两条直线的斜率是互为相反数的,从而得到2b k =-,代入直线方程,求得直线过的定点.【详解】(1)当点P在第一象限时,设(,P t,2PA k ==?,∴PA k 纟çÎç棼,同理,当点P在第四象限时,∴PA k ÷ê?÷ê滕,综上所述∴PA k 纟麋??麋滕棼(2)设直线l 的方程为()0y kx b k =+?,联立方程24y kx by xì=+ïí=ïî,得2440ky y b -+=, 16160kb D=->,设()11,P x y ,()22,Q x y ,124y y k +=,124b y y k?, ∵PAO QAO ?? ∴121222AP AQ y yk k x x +=+=++ ()()()()1221122222y x y x x x +++=++ ()()()12211222221212432864y y y y y y y y y y ++++++22480448b kb k kb +==+-+,2b k =-, ∴()22y kx k k x =-=-,∴直线l 恒过定点()2,0【点睛】该题考查的是有关解析几何的问题,涉及到的知识点有直线与抛物线的位置关系,直线过定点问题,在解题的过程中,注意对公式的正确应用,以及对直线与曲线相交的解题步骤的熟练应用. 21.已知函数22()32x x f x e ae a x =--. (1)当1a =时,讨论()f x 的单调性; (2)若对于任意的12,x x R Î,12x x ¹,都有21212()()21f x f x a x x ->---恒成立,求实数a 的取值范围.【答案】(1)(,ln 2)x ??时,()f x 单调递减;(ln 2,)x ??时,()f x 单调递增; (2)a £【解析】 【分析】(1)将1a =代入解析式,求出函数的导函数,求得导数等于零的点,从而可以判断出在相应区间上导数的符号,从而求得函数的单调区间;(2)先规定12x x >,对式子进行变形,再构造新函数,将问题转化为函数()()221f x a x ++在R 上单调递增,从而应用其导数大于等于零恒成立,之后向最值靠拢,求得结果. 【详解】(1)()f x 定义域为R ()22232x x f x e ae a =--¢,当1a =时,令()()()22322210x x x x f x e e e e ¢=--=-+=,解得0ln2x =, 当(),2x ln ??,()0f x ¢<,()f x 单调递减;当()ln2,x ??,()0f x ¢>,()f x 单调递增;综上,(),ln2x ??时,()f x 单调递减;()ln2,x ??时,()f x 单调递增(2)∵()()1221221f x f x a x x ->---,∴不妨设12x x >,则()()()()2211222121f x a x f x a x ++>++,∴()()221f x a x ++在R 上单调递增;记()()()22213xx g x f x a x eae x =++=-+,()22310x xg x e ae =-+?¢恒成立,∴22111233x x xx e a e e e骣+琪?+琪桫对x R Î恒成立, ∴min1123x xa e e 骣琪?琪桫,∵12x x e e +?12x x e e =,即xe =时等号取到,∴a £【点睛】该题考查的是应用导数研究函数的问题,涉及到的知识点有利用导数研究函数的单调性,利用导数研究恒成立问题,属于中档题目.(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.22.在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t y t a aì=+ïí=+ïî,(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 10r r q --=. (1)求曲线C 的直角坐标方程;(2)设曲线C 与直线l 交于点,A B ,求AB 的最小值. 【答案】(1)22410x y x +--=; (2)【解析】 【分析】(1)根据极坐标与平面直角坐标之间的关系,将极坐标方程转化为平面直角坐标方程,即可得结果; (2)分情况讨论,随着角的变化,直线的斜率存在与不存在两种情况,再者就是要明确弦心距最大时,弦最短,利用勾股定理,求得结果.【详解】(1)根据极坐标与平面直角坐标的对应关系, 可得222,cos x y x r r q =+=,代入求得:22410x y x +--=;(2)当()2n n Z pa p =+?时, 直线l :1x =,此时4AB = 当()2n n Z pa p??时,设直线l :()11y k x -=-,圆心()2,0到直线l的距离最大值为max dAB ==4>min ||AB =【点睛】该题考查的是有关坐标系与参数方程的问题,涉及到的知识点有极坐标方程与平面直角坐标方程的转化,动直线被圆截得最短弦问题,注意对公式的灵活应用. 23.已知函数()21f x x x =-++,x R Î,其最小值为t . (1)求t 的值;(2)正实数,a b 满足a b t +=,求证:112123a b +?++. 【答案】(1)3t =; (2)见解析. 【解析】 【分析】(1)结合绝对值的意义,去掉绝对值的符号,将函数解析式进行化简,结合其单调性,可以断定函数的最小值,从而求得t 的值;(2)根据3a b +=,得到126a b +++=,从而将式子进行转化,之后应用基本不等式证得结果.【详解】(1)()21,23,1221,1x x f x x x x ì->ïï=-#íï-+<-ïî,()min3f x =,即3t =; (2)∵3a b +=,且0a >,0b >, ∴1112a b +=++ ()11112612a b a b 骣琪++++琪++桫 121226123b a a b 骣++琪=++?琪++桫. 当且仅当21123b a a b a b ì++=ïí++ï+=î,即21a b ì=ïí=ïî时,等号取到【点睛】该题考查的是有关不等式的问题,涉及到的知识点有绝对值不等式,函数的最值,基本不等式,在解题的过程中,注意对式子的拼凑.。
2018届清华大学中学生标准学术能力诊断性测试(11月)数学(理)试卷及答案

2018届清华大学中学生标准学术能力诊断性测试(11月试卷 )数学(理)第Ⅰ卷(选择题)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知集合(){}2|ln 32M x y x x==+-,集合{}2|4x N y y -==,则图中阴影部分表示的集合为A. (][)1,03,-+∞UB. [)0,3C. ()0,3D. (]()1,03,-+∞U 2.已知命题p :若8k <,则方程221358x y k k +=--表示焦点在x 轴上的双曲线;命题q :在ABC ∆中,若sin sin A B <,则A B <,则下列命题为真命题的是A. q ⌝B.()()p q ⌝∧⌝C. p q ∧D.()p q ∧⌝3.魏晋时期数学家刘徽首创割圆术,他在九章算术方田章圆填术中指出:“割之弥细,所失弥少。
割之又割,以至于不能割,则与圆周合体而无所失矣。
”这是一种无限与有限的转化过程,比如在正数121211++L 中的“…”代表无限次重复,设121211x =++L ,则可利用方程121x x=+求得x 555=L A. 3 B. 5 C. 7 D. 94.如图,在矩形OABC 中的曲线分别是()sin ,cos ,,0,0,12y x y x A C π⎛⎫== ⎪⎝⎭,在矩形OABC 内随机取一点,则此点取自阴影部分的概率为 A. )431π B. )421π C. )431π D. )421π5.下面的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。
若输入,a b 的分别为98和63,执行该程序框图后,输出a 的值6.某几何体的三视图如右图所示,则该几何体的最长棱为 1922 C.5 D. 277.数列{}n a 中,11a =且()1122n n n a a n ---=≥,则数列112n n n a a -+⎧⎫⎨⎬⎩⎭的前n 项和为 A. 1121n -- B. 11121n +-- C. 11122n⎛⎫- ⎪⎝⎭ D.1111221n +⎛⎫- ⎪-⎝⎭ 8.已知双曲线()2221054x y a a -=>的左、右顶点分别为12,A A ,虚轴的两个端点分别为12,B B ,若四边形1122A B A B 的内切圆的面积为18π,则双曲线的离心率为 2359.已知函数()313sin 6f x x x =+在0x =处的切线与直线60nx y --=平行,则12n x x ⎛⎫+- ⎪ ⎪⎝⎭的展开式中的常数项为A. -20B. 20C. -15D. 1510.将函数sin 221y x x =++的图象向左平移12π个单位,再将所有点的横坐标缩短为原来的12,纵坐标不变,得到函数()y g x =的图象,则下面关于函数()y g x =的叙述不正确的是A.函数()g x 的周期为2π B. 函数()g x 的一个对称中心为,08π⎛⎫-⎪⎝⎭ C.函数()g x 在区间,42ππ⎡⎤⎢⎥⎣⎦内单调递增 D.当()42k x k z ππ=+∈时,函数()g x 有最小值-1 11.已知定义在R 上的函数()f x 满足()()()()42,sin 2f x f x g x x π=--+=+,若函数()f x 的图象与函数()g x 图象的交点为()()()1122,,,,,,n n x y x y x y L ,则()1ni i i x y =+=∑A. nB. 2nC. 3nD.4n12.设点()()()()1122,,,M x f x N x g x 分别是函数()21ln 2f x x x =+和()26g x x =-图象上的点,121,1x x ≥≥,若直线//MN x 轴,则,M N 两点间距离的最小值为 A.54 B.94 C. 52 D.92二、填空题:本大题共4小题,每小题5分,共20分. 13.已知,a b r r 的夹角为4π,且b =r ,则2b a -r r 与a r 的夹角的正切值为 .14.已知变量,x y 满足431,1x y x y x y +≤⎧⎪+≥⎨⎪≥≥⎩,则225x xy y xy ++的取值范围为 . 15. 已知正四面体ABCD 的棱长为,四个顶点都在球心O 的球面上,点P 为棱BC 的中点,过P 作球O 的截面,则截面面积的最小值为 .16.过抛物线24x y =的焦点F 作直线l 与抛物线交于A,B 两点,记抛物线在A,B 两点处的切线12,l l 的交点为P,则ABP ∆面积的最小值为 .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.(本题满分12分)已知ABC ∆的面积为S,其外接圆半径为R,三个内角A,B,C 所对的边分别为())22,,,2sin sin 3sin .a b c R A C a b B -=-, (1)求角C; (2)若()222sin sin sin ,4S A B C a =--=⎝⎭,求c 及ABC ∆的面积18.(本题满分12分)如图,多面体A PCBE -中,四边形PCBE 是直角梯形,且,//PC BC PE BC ⊥,平面PCBE ⊥平面,,ABC AC BE M ⊥是AE 的中点,N 是PA 上的点.(1)若//MN 平面ABC ,求证:N 是PA 中点;(2)若13PE BC =,且AC BC PC ==,求二面角E AB C --的余弦值.19.(本题满分12分)某电视厂家准备在元旦期间举办促销活动,现根据近七年的广告费与销售量的数据确定此次广告费支出。
2018清华大学中学生学术能力标准测试理科数学试题及答案

1
27 7 1000 , 10
0
……………9 分
5
从而 的分布列为
E ( ) np 3
3 0.9 10 3 7 D( ) np(1 p) 3 0.63 10 10
, …………………12 分
20. (12 分) 解: (1)设 F (c,0) , P(t ,
3 P 0 C 10
0 3 1 3 0
3
343 7 1000 , 10
2
3
441 37 P 1 C 1000 , 10 10 189 3 7 P 2 C32 10 10 1000 , 3 P 3 C 10
中学生标准学术能力诊断性测试 理科数学科目参考答案 一、选择题 题号 答案 1 B 2 C 3 B 4 C 5 A 6 A 7 B 8 C 9 C 10 B 11 D 12 A
二、填空题(每题 5 分) 13.
1 5
14.
4 [3, ] 3
15. 4
16.
13 2
三、解答题 17. (12 分) 解: (1)因为������������������2 ������ = ������������������2
所以有 95% 以上的把握认为捐款数额是否多于或少于 500 元和自身经济 损失是否到 4000 元有关。…………………5 分 (Ⅱ)由频率分布直方图可知抽到自身经济损失超过 4000 元居民的频 率为 0.3,将频率视为概率. 由题意知 的取值可能有 0,1, 2,3 , ~ B(3,设点 P 到 AB 边的距离为 z ,则有:
1 SABC SPBC SPAC SPAB ( 3x y 2 z ) ; 2
中学生标准学术能力诊断性测试2018年12月理科数学试题(解析版)

中学生标准学术能力诊断性测试2018年12月测试理科数学试卷(一卷)本试卷共150分,考试时间120分钟.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知函数的定义域为,若,,则的取值范围是()A. B. C. D.【答案】C【解析】【分析】先根据函数的解析式求出定义域,再结合题意即可求出结果.【详解】由函数可得,因,,所以有且,解得,故选C.【点睛】本题主要考查元素与集合的关系,属于基础题型2.已知变量,满足约束条件,则的取值范围是()A. B. C. D.【答案】A【解析】【分析】先由不等式组作出平面区域,将目标函数转化为求斜率的问题即可求解.【详解】由不等式组作出如图所示的图像,因为令,则表示平面区域内的点与定点联系的斜率,由图像可知,,由点,所以,故.【点睛】本题主要考查简单的线性规范,属于基础题型.3.已知某几何体的俯视图是如图所示的边长为1的正方形,正视图与侧视图都是边长为1的正三角形,则此几何体的体积是()A. B. C. D.【答案】D【解析】【分析】根据几何体的三视图,得该几何体是正四棱锥,再由公式球体积即可.【详解】根据几何体的三视图,得该几何体是底面边长1,高为的正四棱锥,所以该几何体的体积为.【点睛】本题主要考查几何体的体积,属于基础题型.4.直线过抛物线的焦点,与该抛物线及其准线从上向下依次交于、、三点,若,,则()A. 2B.C. 3D. 4【答案】A【解析】【分析】分别过点、作准线的垂线,利用抛物线定义将、到焦点的距离转化为到准线的距离,结合已知比例关系,即可得p的值.【详解】如图,分别过点、作准线的垂线交准线于、,设,则,,所以,在直角三角形中,因为,所以,所以,即,因为,所以,,解得.【点睛】本题主要考查抛物线的简单性质,属于基础题型.5.定义,若展开式中一次项的系数为,则等于(为虚数单位)()A. B. C. 1 D. -1【答案】B【解析】【分析】先将按定义写出,进而求出m,再由复数的运算求出结果即可.【详解】由定义可得,因此其展开式中一次项是由每一个括号内的的一次项与其余括号内的常数项相乘再相加得到.括号内的一次项系数依次为,其余括号内的常数项都是1,所以展开式中一次项的系数为,所以.【点睛】本题主要考查复数的运算,属于基础题型.6.函数的大致图像是()A. B.C. D.【答案】A【解析】【分析】先由函数的零点排除B,D选项,再根据函数的单调性排除C选项,即可求出结果.【详解】令可得,,即函数仅有一个零点,所以排除B,D选项;又,所以由,可得,由得,即函数在上单调递增,在上单调递减,故排除C.【点睛】本题主要考查函数的图像,属于基础题型.7.已知正项等比数列的公比不为1,为其前项积,若,则()A. B. C. D.【答案】D【解析】【分析】由先得,从而用公比表示出,进而可求出结果.【详解】设等比数列的公比为q,因为为正项等比数列的前项积,,所以,所以,所以,因此,故,所以.【点睛】本题主要考查等比数列的性质和对数的运算,属于基础题型.8.在中,、、的对边分别是、、.若,,则的最大值为()A. 3B.C.D.【答案】B【解析】【分析】由正弦定理先将边化为角的正弦值,再由三角函数的性质,即可求出结果.【详解】因为,,设三角形外接圆半径为R,由正弦定理可得,所以,故其中.所以.【点睛】本题主要考查解三角形的问题,属于常考题型.9.已知,有下列命题:①若,则;②若,则;③若,则;④若,则;其中真命题的个数为()A. 1B. 2C. 3D. 4【答案】C【解析】【分析】借助平方差公式,立方差公式,结合题中条件,依次判断即可.【详解】①取,则,但,故①错;②因,所以,因此;即②正确;③因,所以,故③正确;④因,由,得,所以,故④正确.【点睛】本题主要考查不等式的基本性质,属于基础题型.10.已知圆锥的侧面展开图是一个半径为,圆心角为的扇形,圆锥内接圆柱的全面积与圆锥的侧面积相等,则圆柱的高为()A. B. C. D.【答案】C【解析】【分析】先设圆锥与圆柱的底面圆半径和高,由题意得到四者之间关系,用圆锥与圆柱的面积公式即可求解.【详解】设圆柱的底面圆半径为,高为h,设圆锥的底面圆半径为,高为H,则有,又圆锥的侧面展开图是一个半径为,圆心角为的扇形,所以圆锥的侧面积为,且,所以,所以,故圆柱的表面积为;又圆锥的侧面展开图是一个半径为,圆心角为的扇形,所以圆锥的侧面积为,由题意,即,解得.【点睛】本题主要考查几何体的表面积,属于基础题型.11.椭圆的右顶点为,下顶点为,左焦点为,若外接圆的圆心在直线的右下方,则此椭圆的离心率的取值范围是()A. B. C. D.【答案】B【解析】【分析】先由题意得的坐标,设出外接圆方程,将的坐标代入圆的方程,求出圆心,坐标,再根据圆心在直线的右下方,即可求出结果.【详解】由题意,,设外接圆方程为所以有,解之得,,所以圆心坐标为,又圆心在直线的右下方,所以有,整理得:即,所以,所以,因此椭圆的离心率的取值范围是.【点睛】本题主要考查椭圆的简单性质,属于中档试题.12.已知函数,若方程有且只有三个不同的实数根,则的取值范围是()A. B.C. D.【答案】D【解析】【分析】先将有且只有三个不同的实数根转化为两函数有三个交点的问题,结合函数图像,即可求出结果. 【详解】由得,即,设,,的顶点在直线上,而与的交点坐标为,,联立,可得,由,得,结合函数,的图像可得,要使有且只有三个不同的实数根,只需.【点睛】本题主要考查函数与方程的应用,难度较大.二、填空题:本大题共4小题,每小题5分,共20分.13.若函数图像的对称轴是,则非零实数的值为__________.【答案】【解析】【分析】利用含绝对值符号函数的对称性即可求解.【详解】因为,其对称轴为,由得.【点睛】本题主要考查函数的对称性,属于基础题型.14.已知,,,为线段上一点,且,若,则实数的取值范围是__________.【答案】【解析】【分析】根据可表示出,,的坐标,再由数量积的坐标表示即可求出结果.【详解】因为,所以,,,所以,所以,解得,因点M是线段BC上的一个动点,所以,即满足条件的实数的取值范围是.【点睛】本题主要考查向量的线性运算性质及几何意义,属于中档试题.15.设、是双曲线的左右焦点,是双曲线上任意一点,过作平分线的垂线,垂足为,则点的轨迹方程是__________.【答案】【解析】【分析】点关于的角平分线PQ的对称点P在直线的延长线上,由双曲线定义可得故,再由OQ是的中位线,可推出为定值,从而可求出结果.【详解】点关于的角平分线PQ的对称点P在直线的延长线上,故,又OQ是的中位线,故,点Q的轨迹是以原点为圆心,a为半径的圆,则点Q的轨迹方程为. 【点睛】本题主要考查双曲线的定义和简单几何性质,属于中档试题.16.若对任意的,均有成立,则称函数为函数和函数在区间上的“函数”.已知函数,,,且是和在区间上的“函数”,则实数的取值范围是__________.【答案】【解析】【分析】在区间上分及两种情况考虑即可.【详解】由题意可得,在区间上恒成立,即,当时,函数的图像为一条线段,于是,解得,另一方面,在上恒成立.令,则,因为,所以,于是函数为增函数,从而,所以,则函数为上的增函数,所以,即;综上所述,实数k的取值范围是.【点睛】本题主要考查函数的综合应用,难度较大.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.已知函数.(Ⅰ)求的最小正周期;(Ⅱ)在锐角中,,,分别为角,,的对边,且满足,求的取值范围. 【答案】(1);(2).【解析】【分析】(1)将函数解析式化简整理成正弦型复合函数的形式,即可求解;(2)由正弦定理和题中条件,先求出,结合三角函数的图像和性质即可求出结果.【详解】(Ⅰ)所以函数的最小正周期为.(Ⅱ)依题意,由正弦定理,.因为在三角形中,所以.即,当时,,;当时,两边平方得,故,,.由于锐角三角形,所以.则.又,,.所以.又,所以.由,则的取值范围.【点睛】本题主要考查三角函数的图像和性质,属于常考题型.18.如图,正方形与所在的平面互相垂直,且,,为的中点.(Ⅰ)求证:平面平面;(Ⅱ)求平面与平面所成锐二面角的余弦值.【答案】(1)见解析;(2).【解析】【分析】(1)由面面垂直的判定定理即可证明结论成立;(2)可用立体几何法以及空间向量法两种方法求二面角的余弦值.【详解】(Ⅰ)∵,,∴在中,,,∴,,又为正方形,∴,又,∴,,又面,面,,∴平面,又平面,∴平面平面.(Ⅱ)方法一:平面平面,,∴平面,,即、、两两垂直,以、、分别为,,轴,建立如图所示空间直角坐标系,则,,,,,取平面的法向量,设平面的法向量为,则,即,令,则,,故,设平面与平面所成锐二面角为,则.方法二:连接,,则、、共线,是平面与平面的交线,取的中点为,连接,,则由平面平面,平面平面,,且面,∴平面,即平面,又为正方形,为的中点,∴,∴.∴是平面与平面所成锐二面角的平面角,由(Ⅰ)可得,,,在中,.∴平面与平面所成锐二面角的余弦值为.【点睛】本题主要考查面面垂直的判定以及二面角的求法,属于常考题型. 19.为加强对企业产品质量的管理,市监局到区机械厂抽查机器零件的质量,共抽取了600件螺帽,将它们的直径和螺纹距之比作为一项质量指标,由测量结果得如下频率分布直方图:(Ⅰ)求这600件螺帽质量指标值的样本平均数,样本方差(在同一组数据中,用该区间的中点值作代表); (Ⅱ)由频率分布直方图可以近似的认为,这种螺帽的质量指标值服从正态分布,其中近似为样本平均数,近似为样本方差. (ⅰ)利用该正态分布,求;(ⅱ)现从该企业购买了100件这种螺帽,记表示这100件螺帽中质量指标值位于区间的件数,利用(ⅰ)的结果,求.附:. 若,则,.【答案】(1); (2)(ⅰ)(ⅱ).【解析】 【分析】(1)频率分布直方图中每一组的中间值可作为该组的平均数,再由公式即可求出平均数和方差; (2)根据正态分布的性质即可求出第一问,由二项分布即可求出第二小问. 【详解】(Ⅰ)抽取的螺帽质量指标值的样本平均数和样本方差分别为:. (Ⅱ)(ⅰ)由(Ⅰ)知,,从而,,,,,(ⅱ)由(ⅰ)知,一件螺帽的质量指标值位于区间的概率为,依题意知,所以.【点睛】本题主要考查频率分布直方图的特征,以及正态分布和二项分布,属于常考题型.20.已知,是轴正半轴上两点(在的左侧),且,过,作轴的垂线,与抛物线在第一象限分别交于,两点.(Ⅰ)若,点与抛物线的焦点重合,求直线的斜率;(Ⅱ)若为坐标原点,记的面积为,梯形的面积为,求的取值范围.【答案】(1);(2).【解析】【分析】(1)先由题意得出点坐标,进而可得,,点坐标,再由斜率公式即可求出结果;(2)先设直线的方程为:,,,再联立直线与抛物线方程吗,根据根与系数关系和弦长公式表示出,由点到直线距离公式表示出点到直线的距离,从而可表示出,,进而可求出结果.【详解】(Ⅰ)由,则,,则,又,所以.(Ⅱ)设直线的方程为:,设,,由,得,所以,得,又,,由,,可知,,由,点到直线的距离为,所以.又,所以,因为,所以.【点睛】本题主要考查抛物线的简单性质,以及直线与抛物线位置关系,属于中档试题.21.已知函数,.(Ⅰ)当时,证明:;(Ⅱ)当时,如果,且,证明:.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)求出函数的导数,用导数的方法判断出函数的单调性,进而可证明结论成立;(2)根据,判断出函数的单调性,再构造函数,根据单调性,再设,即可判断出结果.【详解】(Ⅰ)当时,,由,得,∴在上单调递减,在上单调递增.∴时,取得极小值,即最小值.当时,,,∵,∴,即.(Ⅱ)证明:当时,,则,∴时,,单调递减,时,,单调递增,令,则,∴,当时,,,,∴,单调递减,∴,即,∴当时,.又在内是增函数,在内是减函数.,且,∴,不再同一单调区间内,不妨设,由上可知:,∵,∴.∵,,又在内是增函数,∴,即.【点睛】本题主要考查导数的方法判断函数的单调性,难度较大.选考题:共10分.请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.22.已知曲线的参数方程为(为参数),以平面直角坐标系的原点为极点,的非负半轴为极轴建立极坐标系.(Ⅰ)求曲线的极坐标方程;(Ⅱ),为曲线上两点,若,求的值.【答案】(1);(2).【解析】【分析】(1)由曲线C的参数方程先求出曲线C的普通方程,再转化为极坐标方程即可.(2)先设点P和点Q的极坐标,结合题意即可求出结果.【详解】(Ⅰ)由,得到曲线的普通方程是:,又,,代入得,,即(也可得分).(Ⅱ)因为,所以,由,故,设点的极坐标为,则点的极坐标可设为,所以.【点睛】本题主要考查极坐标与参数方程的问题,属于基础题型.23.已知函数,.(Ⅰ)当时,求不等式的解集;(Ⅱ)若存在,使得不等式成立,求的取值范围.【答案】(1);(2).【解析】【分析】(1)由化简不等式,解化简后的不等式即可;(2)由题意可得:存在,使得不等式成立,只需成立即可,然后求最大值即可.【详解】(Ⅰ)当时,由,即,两边平方,得:,即,解得:,所以不等式的解集为:.(Ⅱ)若存在,使得不等式成立,即成立,所以存在,使得成立,令,只需即可.又函数,当时,单调递减,;当时,单调递增,;当时,单调递减,;可知函数,所以.【点睛】本题主要考查不等式的解法以及不等式成立问题,属于常考题型.。
中学生标准学术能力诊断性测试2018 年3 月测试理科数学试题及参考答案

1 e
x t ( t 为参数, y m t
,以原点 O 为极点, x 轴的非负半轴为极轴建立极坐标系,曲线 C2 m R )
理科数学试题 第 5 页 (共 6 页)
的极坐标方程为 2
3 0 . 3 2 cos 2
(1) 写出曲线 C1 的普通方程和曲线 C2 的直角坐标方程; (2) 已知点 P 是曲线 C2 上一点, 若点 P 到曲线 C1 的最小距离为 2 2 , 求m 的值. 23.[ 选修 4-5:不等式选讲](10 分) 已知函数 f x
.
2 x y 0 x 2 y 3y2 14 . 已 知 实 数 x, y 满 足 x y 6 0 , 则 的取值范围 x2 y 2 1 1 y x2 5 5
是 .
理科数学试题 第 3 页 (共 6 页)
11.设函数 f x min x ln x ,
中学生标准学术能力诊断性测试 数学(理科)科目参考答案 一.选择题
题号 答案 1 C 2 D 3 D 4 A 5 C 6 B 7 A 8 C 9 B 10 C 11 D 12 A
二.填空题:本大题共 4 小题,每小题 5 分,共 20 分。
13. 2 14.
69 ,3 29
15. 3 1
16.
2 3
三、解答题(共 70 分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题 12 分) u r r 2 解: f ( x) m n 1 2 cos x 2 3 sin x cos x 1 cos 2 x 3 sin 2 x .
2 sin(2 x
【清华大学】中学生标准学术能力诊断性2018年12月测试文科数学卷及解析

(清华大学)中学生标准学术能力诊断性测试2018年12月测试文科数学卷(本试卷共150分,考试时间120分钟.)一、选择题:本大题共12小题,每小题5分,共60分.1.已知复数满足(1)13i z i -=+,则复数z 在复平面内对应的点为( )A. (2,1)B. (2,1)-C. (1,2)-D. (1,2)--2.某中学初中部共有500名学生,高中部共有600名学生,各年级段人数构成比例如图所示,则下列说法正确的是( )A. 人数最多的年级段是高二段B. 初一段人数比高一段人数多C. 高三段人数比初二段人数少D. 高二段人数比初三段人数多一倍3.已知集合{|1,}2a P x x a Z ==+?,1,2Q y m m Z 禳镲==+?睚镲铪,则下列结论中正确的是( ) A. P Q ?? B. P Q Q ? C. P Q Q ? D. P QR ? 4.焦点在x 轴上,短轴长等于16,离心率等于35的椭圆的标准方程为( ) A. 22110064x y += B. 22164100x y += C. 221400256x y += D. 221256400x y += 5.设函数()x x f x ae e -=+.若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为( )A. y x =-B. y x =C. 2y x =-D. 2y x =z6.在ABC D 中,点D 是BC 的中点,点E 是AD 的中点,点M 在线段AC 上, 且2AM MC =,则ME =( ) A. 11412AB AC + B. 11412AB AC - C. 11124AB AC + D. 11124AB AC -7.已知sin()2sin()2pp q q +=-,则3sin 4cos sin 2cos q qq q +=-( ) A. 12 B. 2 C. 13 D. 38.已知函数()cos 22sin f x x x =+,则A. ()f x 的最小正周期为p ,最小值为1B. ()f x 的最小正周期为p ,最小值为-3C. ()f x 的最小正周期为2p ,最小值为1D. ()f x 的最小正周期为2p ,最小值为-39.若实数x ,y 满足不等式组(1)(23)013x y x y x ì--+-?ïí#ïî,则3z x y =-的取值范围是( )A. [2,18]B. [2,12]C. [3,18]D. [3,12]10.某四棱锥的三视图如图所求,则该四棱锥的最长棱的长度为( )A. B. 3C.D.11.若一个正四面体的表面积为1S ,其外接球的表面积为2S ,则12S S =( )A.B.C.D. 12.已知函数33)2log (2),2()(2,2x x x f x x -ì-<ï=í-+?ïî,则方程11f x a x骣琪+-=琪桫的实根个数不可能为( ) A. 8 B. 7 C. 6 D. 5二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数2(log )1f x x =+,则(3)f =__________.14.已知四棱锥P ABCD -,底面ABCD 为正方形,PA ^面ABCD ,且满足PA AB =,点E 是PD 的中点,则异面直线AE 与PB 所成角的大小为__________.15.已知点A 在直线20x y a ++=上,过点A 引圆22:1O x y +=的切线,若切线长的最小值为5,则实数a 的值为__________.16.已知在ABC D 中,角,,A B C 分别对应边,,a b c ,且b B A ,2c =,则ABC D 的面积为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分17.已知数列{}n a 满足11a =,11232n n n a a -+=+?,设2nn n a b =.(1)求1b ,2b ,3b ;(2)判断数列{}n b 是否为等差数列,并说明理由;(3)求数列{}n a 的通项公式.18.某集团公司计划从甲分公司中的3位员工1A 、2A 、3A 和乙分公司中的3位员工1B 、2B 、3B 选择2位员工去国外工作.(1)若从这6名员工中任选2名,求这2名员工都是甲分公司的概率;(2)若从甲分公司和乙分公司中各任选1名员工,求这2名员工包括1A 但不包括1B 的概率.19.如图,EA ^平面ABC ,AE CD ,24AB AC CD AE ====,BC =M 为BD 的中点.(1)求证:平面AEM ^平面BCD ;(2)求三棱锥E ABM -的体积.20.已知O 为坐标原点,抛物线2:4C y x =,点()2,0A -,设直线l 与C 交于不同的两点P 、Q .(1)若直线l x ^轴,求直线PA 的斜率的取值范围;(2)若直线l 不垂直于x 轴,且PAO QAO ??,证明:直线l 过定点.21.已知函数22()32x x f x e ae a x =--.(1)当1a =时,讨论()f x 的单调性;(2)若对于任意的12,x x R Î,12x x ¹,都有21212()()21f x f x a x x ->---恒成立,求实数a 的取值范围.(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.22.在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t y t a aì=+ïí=+ïî,(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 10r r q --=.(1)求曲线C 的直角坐标方程;(2)设曲线C 与直线l 交于点,A B ,求AB 的最小值.23.已知函数()21f x x x =-++,x R Î,其最小值为t .(1)求t 的值;(2)正实数,a b 满足a b t +=,求证:112123a b +?++.【解析卷】(清华大学)中学生标准学术能力诊断性测试2018年12月测试文科数学卷二、选择题:本大题共12小题,每小题5分,共60分.1.已知复数满足(1)13i z i -=+,则复数z 在复平面内对应的点为( )A. (2,1)B. (2,1)-C. (1,2)-D. (1,2)--【答案】D【解析】【分析】首先根据复数的运算法则,求得12z i =-+,进而求得其共轭复数,利用复数在复平面内对应点的坐标,求得结果.【详解】因为(1)13i z i -=+,所以13(13)(1)2412122i i i i z i i +++-+====-+-, 所以12z i =--, 所以复数z 对应的点的坐标为(1,2)--,故选D.【点睛】该题考查的是有关复数的问题,涉及到的知识点有复数的除法运算,复数的共轭复数,复数在复平面内对应点点的坐标,属于简单题目.2.某中学初中部共有500名学生,高中部共有600名学生,各年级段人数构成比例如图所示,则下列说法正确的是( )A. 人数最多的年级段是高二段B. 初一段人数比高一段人数多C. 高三段人数比初二段人数少D. 高二段人数比初三段人数多一倍【答案】A【解析】z首先根据题中所给的饼形图,根据各年级所占的比例,求得各年级的实有人数,从而可以比较大小,对选项逐一分析,得到结果.【详解】从题中所给的图可以求得初一学生有50035%175?人, 初二学生有50040%200?人,初三学生有50025%125?人; 高一学生有60030%180?人,高二学生有60036%216?人, 高三学生有60034%204?人,根据所得的数据,对选项逐个分析,得到人数最多的年级是高二段,故选A.【点睛】该题考查的是有关统计的问题,涉及到的知识点有利用饼形图中各年级所占的比例,初、高中部的总人数,求得各年级的人数,需要对选项逐个分析,属于简单题目.3.已知集合{|1,}2a P x x a Z ==+?,1,2Q y m m Z 禳镲==+?睚镲铪,则下列结论中正确的是( ) A. P Q?? B. P Q Q ? C. P Q Q ? D. P QR ? 【答案】B【解析】【分析】 首先对集合中对应的式子进行变形,结合题中所给的变量的取值情况,可以发现分母都是2,分子一个取整数,一个取奇数,得到两个集合的关系,结合其性质,得到结果. 【详解】因为21211,2222a a m m +++=+=,当,a m Z Î时,2a Z +?,而21m +是奇数, 从而得到Q P Í,所以Q PQ ?, 故选B.【点睛】该题考查的是有关集合的问题,涉及到的知识点有集合的关系,集合的交并运算性质,属于简单题目. 4.焦点在x 轴上,短轴长等于16,离心率等于35的椭圆的标准方程为( ) A. 22110064x y += B. 22164100x y += C. 221400256x y += D. 221256400x y += 【答案】A【分析】 由题意可得35c a =,又222,216a b c b -==,求解方程即可得到,a b 的值,则答案可求. 【详解】依题意有:216b =,所以8b =, 根据离心率35e =,结合222a b c =+,解得10a =, 再结合焦点在x 轴上,所以椭圆的方程是22110064x y +=, 故选A.【点睛】该题考查的是有关椭圆方程的求解问题,涉及到的知识点有椭圆的短轴长,椭圆的离心率,以及椭圆中,,a b c 三者之间的关系,属于简单题目.5.设函数()x x f x ae e -=+.若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为( )A. y x =-B. y x =C. 2y x =-D. 2y x =【答案】C【解析】【分析】首先根据奇函数的性质,利用(0)10f a =+=,求得1a =-,之后对函数求导,令0x =,求得其值,即为切线的斜率,之后应用直线方程的点斜式,求得结果.【详解】因为函数()f x 是奇函数,所以(0)10f a =+=,解得1a =-,所以()x x f x e e -=-+,'()x x f x e e -=--,所以(0)0,'(0)2f f ==-,所以曲线()y f x =在点()0,0处的切线方程为2y x =-,故选C. 【点睛】该题考查的是有关曲线在某个点处的切线方程的问题,涉及到的知识点有奇函数的性质,导数的几何意义,正确理解基础知识是解题的关键.6.在ABC D 中,点D 是BC 的中点,点E 是AD 的中点,点M 在线段AC 上, 且2AM MC =,则ME =( ) A. 11412AB AC + B. 11412AB AC - C. 11124AB AC + D. 11124AB AC - 【答案】B【解析】【分析】首先根据题意,画出相应的图形,利用向量的运算法则,以及其关系,将向量ME 逐步转化为,AB AC 的式子,得到结果.【详解】如图,根据向量的运算法则,可得1123ME AE AM AD AC =-=-11111443412AB AC AC AB AC =+-=-, 故选B. 【点睛】该题考查的是有关向量用一组基底来表示的问题,涉及到的知识点有数乘向量,向量的加法运算等,正确使用运算法则是解题的关键,属于简单题目.7.已知sin()2sin()2p p q q +=-,则3sin 4cos sin 2cos q q q q+=-( ) A. 12 B. 2 C. 13D. 3 【答案】A【解析】【分析】首先利用三角函数的诱导公式,将式子进行化简,得到tan 2q =-,之后将正余弦的齐次式的分式形式的式子,化成关于切的式子,代入求得结果.【详解】根据诱导公式可得sin 2cos q q -=,根据同角三角函数关系可得tan 2q =-, 将式子变形可得3sin 4cos 3tan 4641sin 2cos tan 2222q q q q q q ++-+===----,故选A.【点睛】该题考查的是有关三角函数化简求值问题,涉及到的知识点有三角函数诱导公式,同角三角函数的关系式,齐次式的分式的求值问题,属于中档题目. 8.已知函数()cos 22sin f x x x =+,则A. ()f x 的最小正周期为p ,最小值为1B. ()f x 的最小正周期为p ,最小值为-3C. ()f x 的最小正周期为2p ,最小值为1D. ()f x 的最小正周期为2p ,最小值为-3 【答案】D 【解析】 【分析】首先利用余弦倍角公式,将式子进行化简,使得解析式中只有一个函数名,之后进行配方,结合正弦函数的周期和值域,求得函数的周期和最值,对选项逐一分析判断,得出结果. 【详解】化简函数解析式可得2213()cos 22sin 12sin 2sin 2(sin )22f x x x x x x =+=-+=--+, 可以求得其最小正周期为2T p =, 其最大值为32,最小值为2132(1)322---+=-, 故选D.【点睛】该题考查的是有关三角函数的性质的问题,涉及到的知识点有余弦倍角公式,利用配方法求函数的最值,三角函数的最小正周期的求解,属于中档题目.9.若实数x ,y 满足不等式组(1)(23)013x y x y x ì--+-?ïí#ïî,则3z x y =-的取值范围是( )A. [2,18]B. [2,12]C. [3,18]D. [3,12] 【答案】B 【解析】 【分析】首先根据题中所给的约束条件画出相应的可行域,结合目标函数的特征,判断出最优解,解方程组,得到最优解对应点的坐标,代入求得最值,得到范围.【详解】根据约束条件,画出相应的可行域,如图所示, 结合直线3y x z =-的走向,可以断定:当直线3y x z =-过点E 时,z 取得最大值,当直线3y x z =-过点A 时,z 取得最小值,解方程组1230x x y ì=ïí+-=ïî,得(1,1)A ,解方程组3230x x y ì=ïí+-=ïî,得(3,3)E -, 代入求得minmax 312,9(3)12z z =-==--=,所以z 的取值范围是[2,12],故选B.【点睛】该题考查的是有关线性规划问题,在解题的过程中,需要注意的是(1)(23)0x y x y --+-?所表示的平面区域的确定方法,对于目标函数的形式分三种情况,结合具体情况,求得结果. 10.某四棱锥的三视图如图所求,则该四棱锥的最长棱的长度为( )A.B. 3C.D.【答案】C 【解析】 【分析】首先根据题中所给的几何体的三视图,还原几何体,得到其为底面是边长为3的正方形,且顶点在底面上的摄影是底面对角线的三等分点处,高为2的四棱锥,利用其关系,求得侧棱长,比较得出最长棱的长度. 【详解】根据题中所给的三视图,可以想到该几何体是底面是边长为3的正方形的四棱锥, 并且顶点在底面上的摄影是底面对角线的三等分点,且高为2,从而可以求得其四条侧棱分别等于==通过比较可得最长棱的长度是故选C.【点睛】该题考查的是有关利用三视图还原几何体,求其最长的棱长的问题,涉及到的知识点为将棱放在相应的三角形中,利用公式求得其边长,比较大小得出结果,属于简单题目.11.若一个正四面体的表面积为1S ,其外接球的表面积为2S ,则12S S =( )A.B.C.D. 【答案】C 【解析】 【分析】首先设出正四面体的棱长,利用结论得到其外接球的半径,之后应用相关的公式求得正四面体的表面积以及外接球的表面积,两者一比,得到结果.【详解】设正四面体的棱长为a,可知该四面体的外接球的半径是R ,所以可以求得2214S =?,22234)2S a p p ==,所以1222S S a p =, 故选C.【点睛】该题考查的是有关正四面体的表面积与其外接球的表面积的比值问题,涉及到的知识点有正四面体的外接球半径,球的表面积公式,正四面体的表面积公式,属于中档题目.12.已知函数33)2log (2),2()(2,2x x x f x x -ì-<ï=í-+?ïî,则方程11f x a x骣琪+-=琪桫的实根个数不可能为( ) A. 8 B. 7 C. 6 D. 5 【答案】D 【解析】 【分析】首先根据题中所给的解析式,画出函数的图象,结合图象,对a 的范围进行讨论,解相应的关于x 的方程,从而判断出根的个数,从而选出正确的结果. 【详解】画出函数图象,如图所示:当0x >时,111x x +-?,当0x <时,113x x+-?, 观察图像,当2a >时,11x m x+-=,m 有两个解, 一个满足1729m <<,一个满足7m <-,此时对应的x 有四个解,即方程有四个根, 当2a =时,11x m x +-=,m 有三个解,179m =或7m =-或3m =, 对应的x 有6个解,即方程有6个根,同理可得当12a <<,1a =,01a <<,0a =,0a <分析, 结合方程11x m x+-=的根的情况,可知方程的根不可能为5, 故选D.【点睛】该题考查的是有关应用函数的图象完成方程解的个数的问题,涉及到的知识点为将方程根的个数问题转化为曲线与直线交点个数的问题,再者就是分类讨论思想的应用,属于较难的题目.二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数2(log )1f x x =+,则(3)f =__________.【答案】9 【解析】 【分析】 首先令2log 3x =,求得8x =,代入题中所给的式子,得到结果.【详解】令2log 3x =,解得8x =,此时1819x +=+=,故答案是9.【点睛】该题考查的是有关复合函数求值问题,在解题的过程中,需要分清x 代表的是谁,哪个量等于3,注意内层函数的函数值充当外层函数的自变量.14.已知四棱锥P ABCD -,底面ABCD 为正方形,PA ^面ABCD ,且满足PA AB =,点E 是PD 的中点,则异面直线AE 与PB 所成角的大小为__________. 【答案】60【解析】 【分析】首先根据题的条件,画出相应的图,利用异面直线所成角的定义,找出平行线,得到异面直线所成角的平面角,放在三角形当中,得到结果.【详解】连接AC 与BD 相交于O 点,连接EO ,则有OEPB ,所以AEO Ð即为所求,根据题中条件,可以求得AE EO AO ==,从而得到60AEO ?,故答案是60.【点睛】该题考查的是有关异面直线所成角的问题,在解题的过程中,涉及到的知识点就是异面直线所成角的概念,解决空间问题的思路就是将空间问题平面化,得出平面角,放到三角形当中来求解.15.已知点A 在直线20x y a ++=上,过点A 引圆22:1O x y +=的切线,若切线长的最小值为则实数a 的值为__________. 【答案】3± 【解析】 【分析】根据题意,画出图形,结合图形求出点O 到直线20x y a ++=的距离d ,利用勾股定理求出a 的值,得到结果.【详解】设点O 到直线20x y a ++=的距离为d ,则d ,又过垂足引圆221x y += 则有24155a +=,解得3a =?,故答案是3±.【点睛】该题考查的是有关圆的切线问题,涉及到的知识点有点到直线的距离公式,直线与圆的位置关系,特殊的三角形,正确转化题的条件是解题的关键.16.已知在ABC D 中,角,,A B C 分别对应边,,a b c ,且b B A ,2c =,则ABC D 的面积为__________.【答案】2【解析】 【分析】由已知b ,可得sin B A B A ,可得cos B A =,利用平方关系,可得2211sin cos 32A A +=,利用22sin cos 1A A +=,解得cos 2A B ==,从而得到角A,B 的大小,之后应用三角形内角和,求得角C ,利用余弦定理,求得a =.【详解】因为b ,可得sin B A ,因为B A ,可得cos B A ,所以22))1A A +=,即2211sin cos 32A A +=,结合22sin cos 1A A +=,可得cos 22A B ==, 所以,64A B p p ==,可求得76412C p p pp =--=,所以由余弦定理2222cos c a b ab C =+-,可得2222))2)a a =++,解得a =所以11sin 2)222ABC S ac B D ==创?,故答案是2.【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有正弦定理,同角三角函数关系,余弦定理,三角形面积公式,在解题的过程中,正确使用公式是解题的关键.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分17.已知数列{}n a 满足11a =,11232n n n a a -+=+?,设2n n nab =.(1)求1b ,2b ,3b ;(2)判断数列{}n b 是否为等差数列,并说明理由;(3)求数列{}n a 的通项公式.【答案】(1)112b =,254b =,32b =; (2)见解析; (3)2(31)2n n a n -=-?. 【解析】 【分析】(1)分别将1,2n n ==代入11232n n n a a -+=+?,求得23,a a 的值,再将123,,a a a 的值代入2nn n a b =,求得结果;(2)利用题中所给的式子,求得134n n b b +-=,利用等差数列的定义,得到其为等差数列; (3)先利用等差数列的通项公式求得n b ,利用2nn n a b =,进一步求得n a . 【详解】(1)25a =,316a =,112b =,254b =,32b =;(2)∵113224n n n na a ++=+,∴134n n b b +-=,∴{}n b 是等差数列; (3)由前面知,()()131131244n b n n =+-?-,∴()2312n n a n -=-? 【点睛】该题考查的是有关数列的问题,涉及到的知识点有利用递推公式求数列的项,判断一个数列是否是等差数列,数列通项公式的求法,正确应用公式是解题的关键,属于中档题目.18.某集团公司计划从甲分公司中的3位员工1A 、2A 、3A 和乙分公司中的3位员工1B 、2B 、3B 选择2位员工去国外工作.(1)若从这6名员工中任选2名,求这2名员工都是甲分公司的概率;(2)若从甲分公司和乙分公司中各任选1名员工,求这2名员工包括1A 但不包括1B 的概率. 【答案】(1)15; (2)29. 【解析】 【分析】(1)从这6名员工中任选2个,基本事件一一列出,总共有15个,这两名员工都是甲分公司的基本事件为3,利用公式求得概率;(2)从甲分公司和乙分公司中各任选1名员工,用列举法找出其对应的基本事件,共2个,利用公式求得概率. 【详解】(1)由题意得,从6名员工中任选2名,其一切可能的结果组成的基本事件有:{}{}{}121323,,,,,,A A A A A A {}{}{}111213,,,,,,A B A B A B{}{}{}212223,,,,,A B A B A B {}{}{}313233,,,,,A B A B A B {}{}{}121323,,,,,B B B B B B ,共15个所选两名员工都是甲分公司所包含的基本事件有:{}{}{}121323,,,,,A A A A A A ,共3个,所以所求事件的概率为31155p ==; (2)从甲分公司和乙分公司各任选1名员工,其一切可能的结果组成的基本事件有:{}{}{}111213,,,,,,A B A B A B{}{}{}212223,,,,,,A B A B A B {}{}{}313233,,,,A B A B A B 共9个,包含1A 但不包括1B 的事件所包含的基本事件有{}12,A B ,{}13,A B 共2个,所以所求事件的概率为29p =【点睛】该题考查的是有关古典概型及有关计算问题,解题的步骤是先写出实验所对应的基本事件,再找出满足条件的基本事件数,之后利用概率公式求得结果.19.如图,EA ^平面ABC ,AECD ,24AB AC CD AE ====,BC =M 为BD 的中点.(1)求证:平面AEM ^平面BCD ; (2)求三棱锥E ABM -的体积.【答案】(1)见解析; (2)3. 【解析】 【分析】(1)取BC 中点N ,连接MN ,AN ,结合题中的条件,利用线面垂直的判定定理,证得EM ^平面BCD ,再应用面面垂直的判定定理,证得结论;(2)将三棱锥的顶点和底面转换,E ABMM ABE E ABN V V V ---==,之后应用锥体的体积公式求解即可.【详解】(1)取BC 中点N ,连接MN ,AN ,∴MN AE =,MN AE ,∵EA ^平面ABC ,∴四边形AEMN 是矩形, ∴EM MN ^,由题意知,ED EB ==M 为BD 的中点, ∴EM BD ^, 又∵BD MNM ?,∴EM ^平面BCD ,∵EM Ì平面AEM ,∴平面AEM ^平面BCD (2)由题意知,E ABM M ABE V V --=,∵MN平面ABE ,∴13M ABE N ABE E ABN ABN V V V S AE ---D ===鬃AN12ABN S BN AN D =鬃=123E ABM V -==【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有面面垂直的判定,三棱锥体积的计算,在解题的过程中,应用了线面垂直的判定定理以及面面垂直的判定定理,以及应用等积法,将三棱锥的顶点和底面转换,再根据平行关系,将其进一步转化,使得其底面积和高比较明显好求,之后应用体积公式求得结果.20.已知O 为坐标原点,抛物线2:4C y x =,点()2,0A -,设直线l 与C 交于不同的两点P 、Q .(1)若直线l x ^轴,求直线PA 的斜率的取值范围;(2)若直线l 不垂直于x 轴,且PAO QAO ??,证明:直线l 过定点.【答案】(1)[,0)(0,]22-?; (2)见解析. 【解析】【分析】(1)先设点P 在第一象限时,设出点P 的坐标,利用斜率坐标公式,将PA 的斜率表示出来,之后对式子进行变形,利用基本不等式求得其范围,从而得到直线PA 的斜率的取值范围,同理可得点P 落在第四象限时,其斜率的取值范围,之后取并集得到结果.(2)设出直线的方程,将直线方程与抛物线方程联立,利用韦达定理求得两根的关系,利用两个角的关系,得到两条直线的斜率是互为相反数的,从而得到2b k =-,代入直线方程,求得直线过的定点.【详解】(1)当点P在第一象限时,设(,P t,222PA k =?,∴PA k 纟çÎç棼,同理,当点P在第四象限时,∴PA k ÷ê?÷ê滕,综上所述∴0,22PA k 纟麋犏??麋犏滕棼 (2)设直线l 的方程为()0y kx b k =+?,联立方程24y kx b y xì=+ïí=ïî,得2440ky y b -+=, 16160kb D=->,设()11,P x y ,()22,Q x y ,124y y k +=,124b y y k?, ∵PAO QAO ?? ∴121222AP AQ y y k k x x +=+=++ ()()()()1221122222y x y x x x +++=++ ()()()12211222221212432864y y y y y y y y y y ++++++ 22480448b k b k kb +==+-+,2b k =-, ∴()22y kx k k x =-=-,∴直线l 恒过定点()2,0【点睛】该题考查的是有关解析几何的问题,涉及到的知识点有直线与抛物线的位置关系,直线过定点问题,在解题的过程中,注意对公式的正确应用,以及对直线与曲线相交的解题步骤的熟练应用.21.已知函数22()32x x f x e ae a x =--.(1)当1a =时,讨论()f x 的单调性;(2)若对于任意的12,x x R Î,12x x ¹,都有21212()()21f x f x a x x ->---恒成立,求实数a 的取值范围. 【答案】(1)(,ln 2)x ??时,()f x 单调递减;(ln 2,)x ??时,()f x 单调递增; (2)3a £【解析】【分析】(1)将1a =代入解析式,求出函数的导函数,求得导数等于零的点,从而可以判断出在相应区间上导数的符号,从而求得函数的单调区间;(2)先规定12x x >,对式子进行变形,再构造新函数,将问题转化为函数()()221f x a x ++在R 上单调递增,从而应用其导数大于等于零恒成立,之后向最值靠拢,求得结果.【详解】(1)()f x 定义域为R()22232x x f x e ae a =--¢, 当1a =时,令()()()22322210x x x x f x e e e e ¢=--=-+=,解得0ln2x =, 当(),2x ln ??,()0f x ¢<,()f x 单调递减; 当()ln2,x ??,()0f x ¢>,()f x 单调递增; 综上,(),ln2x ??时,()f x 单调递减;()ln2,x ??时,()f x 单调递增 (2)∵()()1221221f x f x a x x ->---,∴不妨设12x x >, 则()()()()2211222121f x a x f x a x ++>++,∴()()221f x a x ++在R 上单调递增;记()()()22213x x g x f x a x e ae x =++=-+,()22310x xg x e ae =-+?¢恒成立,∴22111233x x x x e a e e e 骣+琪?+琪桫对x R Î恒成立, ∴min 1123x xa e e 骣琪?琪桫,∵12x x e e +?12x x e e =,即2x e =时等号取到,∴a £【点睛】该题考查的是应用导数研究函数的问题,涉及到的知识点有利用导数研究函数的单调性,利用导数研究恒成立问题,属于中档题目.(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.22.在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t y t a aì=+ïí=+ïî,(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 10rr q --=. (1)求曲线C 的直角坐标方程;(2)设曲线C 与直线l 交于点,A B ,求AB 的最小值.【答案】(1)22410x y x +--=; (2)【解析】【分析】 (1)根据极坐标与平面直角坐标之间的关系,将极坐标方程转化为平面直角坐标方程,即可得结果;(2)分情况讨论,随着角的变化,直线的斜率存在与不存在两种情况,再者就是要明确弦心距最大时,弦最短,利用勾股定理,求得结果.【详解】(1)根据极坐标与平面直角坐标的对应关系, 可得222,cos x y x r r q =+=,代入求得:22410x y x +--=;(2)当()2n n Z p a p =+?时, 直线l :1x =,此时4AB =当()2n n Z p a p ??时,设直线l :()11y k x -=-,圆心()2,0到直线l 的距离最大值为max d此时AB ==4>min ||AB =【点睛】该题考查的是有关坐标系与参数方程的问题,涉及到的知识点有极坐标方程与平面直角坐标方程的转化,动直线被圆截得最短弦问题,注意对公式的灵活应用.23.已知函数()21f x x x =-++,x R Î,其最小值为t .(1)求t 的值;(2)正实数,a b 满足a b t +=,求证:112123a b +?++. 【答案】(1)3t =; (2)见解析.【解析】【分析】(1)结合绝对值的意义,去掉绝对值的符号,将函数解析式进行化简,结合其单调性,可以断定函数的最小值,从而求得t 的值;(2)根据3a b +=,得到126a b +++=,从而将式子进行转化,之后应用基本不等式证得结果. 【详解】(1)()21,23,1221,1x x f x x x x ì->ïï=-#íï-+<-ïî,()min 3f x =,即3t =; (2)∵3a b +=,且0a >,0b >, ∴1112a b +=++ ()11112612a b a b 骣琪++++琪++桫 121226123b a a b 骣++琪=++?琪++桫. 当且仅当21123b a a b a b ì++=ïí++ï+=î,即21a b ì=ïí=ïî时,等号取到 【点睛】该题考查的是有关不等式的问题,涉及到的知识点有绝对值不等式,函数的最值,基本不等式,在解题的过程中,注意对式子的拼凑.。
2018年3月17日清华大学中学生标准学术能力诊断性测试理科综合科目参考答案
化的硝酸银溶液,如有白色浑浊现象产生,则未洗涤干净,反之则洗涤干净。 (2 分)
29.【答案】(除标注外,其余每空 1 分,共 10 分)
(1) 有 细胞呼吸过程中能产生 ATP 和[H] 无 夜间室内无光, 光反
应无法进行,不能为暗反应提供所需的 ATP 和[H],所以暗反应无法进行(2 分,答出夜间 光反应无法进行得 1 分,不能产生暗反应所需 ATP 和[H]得另 1 分) (2)CO2 农家肥被微生物分解后为植物提供 CO2;提供矿质元素;促进土壤小动物
27.(1)△ H1/2 + △ H2/2 + 2△ H3(2 分); (2)<(2 分) AC(2 分); 1:3(2 分);
(3)4NH3+O2+SO2+2NO2+2H2O=(NH4)2SO4+2NH4NO3(2 分) (4)①左室、右室(2 分) ② 2(2 分)
28.(1)7:4(2 分) (2)过滤(2 分),MgO、Fe2O3。 (3 分) (3)称取一定质量的样品,加入过量的氢氧化钠溶液溶解、过滤、再向滤液中 通入足量的二氧化碳气体,过滤、洗涤、干燥、灼烧、冷却、称量,再称量所得 干燥固体的质量并计算。(4 分) (4) 2CrO42-+ 2H+ 铬酸根离子 (2 分) (5)取最后的洗涤液少许加入到一支洁净的试管中,向其中滴入 2-3 滴硝酸酸 Cr2O72-+ H2O,酸性增强,有利于将铬酸根离子转化为重
tan
kd 2 (1 分) 2 g cos
偏大 (1 分)
23.考查:电路的设计,电表的选取 答案:(1)
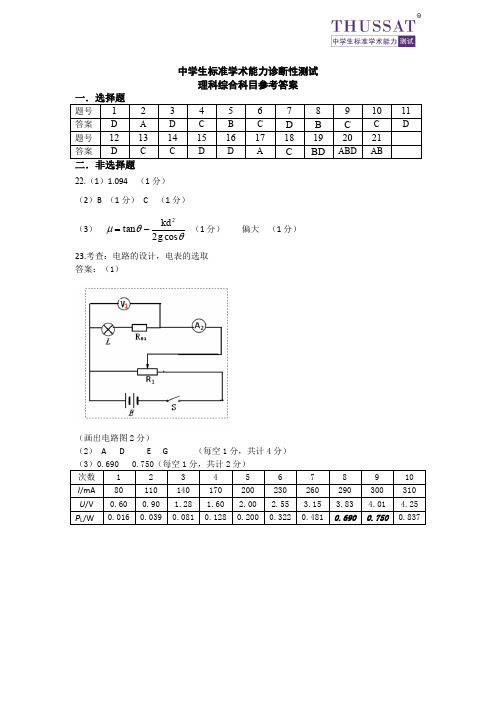
(画出电路图 2 分) (2) A D E G (每空 1 分,共计 4 分) (3)0.690 0.750(每空 1 分,共计 2 分) 次数 I/mA U/V 1 80 0.60 0.016 2 110 0.90 0.039 3 140 1.28 0.081 4 170 1.60 0.128 5 200 2.00 0.200 6 230 2.55 0.322 7 260 3.15 0.481 8 290 3.83 9 300 4.01 10 310 4.25 0.837
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学理科试卷
本试卷共150分,考试时间120分钟。
一、选择题:本题共.12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合A={33<811|
1≤∈-x Z x },B=={0<3
2|-+∈x x N x },则集合 {B y A x xy z z ∈∈=,,|}的元素个数为 A. 6
B. 7
C.
8 D. 9
2.设随机变量ξ服从正态分布),1(2
σN , 若2.0)1-<(=ξP ,则函数x x x x f 223
3
1)(ξ++=有极值点的概率是
A. 0.2
B.0.7
C.0.3
D.0.8 3.下列命题中:
(1)“>1x ”是“>12x ”的充分不必要条件
(2)命题“若a, b 都是奇数,则a + b 是偶数”的逆否命题是“若a+ b 不是偶数,则a ,b 都不是奇数”
(3)命题“>0x ∀,都有21
≥+
x
x ”的否定是“>00x ∃,使得<210o x x +”
(4)已知p ,q 为简单命题,若p ⌝是假命题,则q p ∧是真命题。
正确命题的个数为 A.1个 B.2个
C.3个
D.4个
4.设{a n }是公差为2的等差数列,b n =a 2n ,若{b n }为等比数列,其前n 顼 和为S n ,则S n 为 A. )12(2-n
B. )12
(21
-+n C. )12(4-n D. )12(41-+n
5.若函数a e x f x
-=)(,(e 为自然数的底数),对任意实数x ,)()(x f x f --≥恒成立,则实数a 的取值范围是
A.(-∞,1]
B.(1.+∞)
C.(e,-∞)
D.[1.+∞) 6. 设101022105
2
......)23(x a x a x a x a x x ++++==-, 则1a 等于
A.-240
B.-120
C.240
D.120
7. —个四面体的顶点在空间直角坐标系xyz O -中的坐标分别是(0,0,0),(1,0,1),(0,1,1),(2
1
,1,0),绘制该四面体三视图时,按照如下图所示的方向画正视图,则得到左视图可以为
8.如图所示,程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中 “mMODn 表示m 所除以n 的余数),若输入的 m ,n 分别为2016,612,则输出的m = A. 0
B. 72
C. 36
D. 180
9.函数 ])33,0()0,43[(11)
2cos(22πππ
Y -∈+-=x x
x y 的图像大致是
10.已知抛物线C: )0>(22
p px y =,过焦点F
且斜率为3的直线与C 相交于P,Q 两点,且P,Q 两点在准线上的投影分别为M ,N 两点,则S △MFN =
A.
2
3
8p B. 2332p C. 2334p D. 2338p 11.已知函数mx x x f -=2
)(的图象在点1=x 处的切线l 与直线
023=-+y x 垂直,记数列{
)
(1
n f }的前n 项和为n S ,则2018S 的值为 A.
20152016 B. 20162017 C. 20172018 D. 2018
2019
12,已知函数a x
x
a x x x f -+-+=1ln )1()ln ()(2有三个不同的零点1x ,2x ,3x (其中1x <2x <3x )
,则)ln 1)(ln 1)(ln 1(3
322
11x x x x x x ---的值为 A. 1
B.a-1
C.-1
D. 1-a
二、填空题:本题共4小题,每小题5分,共20分。
13. O 为△ABC 内一点,且02=++OC OB OA ,△ABC 和△OBC 的面积分别是
ABC
OBC
S S ∆∆= 。
14.设实数y x ,满足⎪⎩
⎪
⎨⎧≤-≤--≥-+0
10220
2y y x y x ,则x y x y m 22-+=的取值范围是 。
15.已知双曲线)0>,0>(12222b a b
y a x =-的两条渐近线与抛物线)0>(22
p px y =
的准线分别交于A ,B 两点,O 为坐标原点,若 双曲线的一条渐近线的倾斜角为
3
π
,△AOB 的面积为34,则P= 。
16.如图,三棱锥P-ABC 是边长为3的等边三角形,D 是线段AB 中点,DE∩PB =E ,且DE 丄AB ,若∠EDC=0120,PA=2
3
,PB=233,则三棱锥P
一 ABC 的外接球的半径为 .
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤,第17〜21 题为必考题,每个试题考生都必须作答,第22、23题为选考題,考生根据要求作答。
(―)必考题:共60分。
17.(12分)在△ABC 中,角A ,B,C 对应的边分别为a ,b ,c ,己知c = 2.b = 1,且 2
sin sin 22C
B A +=. (1)求角A 的大小和B
C 边的长;
(2)若点P在△ABC内运动(包括边界),且点P到三边的距离之和为d, 设点P到BC的距离分别为x,y,试用x,y表示d,并求d的最大值和最小值。
18.( 12分)如图,四棱锥P - ABCD中,底面ABCD中,BC∥AD,CD丄AD,P
在底面的射影0在AD上,PA = PD,O,E 分别为AD,PC的中点,且P0=AD = 2BC
= 2CD.
(1)求证:AB⊥DE;;
(2) 求二面角A-PE-O的余弦值。
19. (12分)今年某台风在沿海登陆,适逢暑假,小张调査了当地某小区100户居民由于台风造成的经济损失,将收集的数据分成(0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(图1):
(1)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表格,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
(1)将上述调查所得到的频率视为概率*现在从该地区大量受灾居民中,釆用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为ξ。
若每次抽取的结
ξ
ξ
果是相互独立的,求ξ的分布列,期望E()和方差D().
20. (12分)已知椭圆M: )0>,0>(122
22b a b
y a x =+,右焦点为F ,与直线773=y 相交于P 、Q 两点,
若椭圆从经过点(0,3)且PF 丄QF. (1)求椭圆M 的方程;
(2) 0为坐标原点,A 、B 、C 是椭圆M 上不同的三点,并且O 为△ABC 的重心,试求△ABC 的面积。
21. (12分)已知函数R a ne x
a x f x ∈+=-,_1
ln
)(1. (1)若a=1,求)(x f 的单调区间;
(2)若)()(>0,m f x f x ≥∀恒成立,且0)(≥x f ,求证: )1(2)(2
m m m f -≥.
(二)选考题:共10分。
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.[选修4-4:坐标系与参数方程](10分)
在直角坐标系xoy 中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系。
半圆C (圆心为点C )的参数方程为ϕϕϕ
⎩
⎨
⎧+==sin 1cos y x 为参数,{),0(πϕ∈.
(l)求半圆C 的极坐标方程;
(2)若一直线与量坐标轴的交点分别为A,B,其中A(0,-2),点D 在半圆C 上,且真线CD 的倾斜角是直线AB 倾斜角的2倍,若△ABD 的面积为4,点D 的直角坐标。
23.[选修 4-5 不等式选讲] (10分) 已知函数.|1||2|)(--+=x m x x f ⑴若 m = -2 时,解不等式5)(≥x f ; (2)若)5()(+≤x m x f ,求m 的最小值。
