一线三等角模型
一线三等角模型结论及证明

一线三等角模型结论及证明
摘要
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
本文将详细阐述一线三等角模型的结论及证明,以及如何使用它来解决实际问题。
一、定义
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,它们的夹角均为120度。
二、结论
一线三等角模型的结论如下:
1、如果在一条直线上有三个等角,则它们的夹角均为120度。
2、如果三条直线的夹角均为120度,则它们共线。
三、证明
1、证明一:假设在一条直线上有三个等角,设它们的夹角为α,β,γ,则有
α+β+γ=360°,由等角性质可知α=β=γ=120°,得证。
2、证明二:假设三条直线的夹角均为120°,设它们的夹角分别为α,β,γ,则有α+β+γ=360°,此时α=β=γ=120°,由此可知,三条直线共线,得证。
四、实际应用
一线三等角模型可以用来解决实际问题,比如,在建筑设计中,可以根据一线三等角模型设计出美观的建筑结构,如三角形的屋顶,具有特殊的视觉效果。
结论
一线三等角模型是几何学中的重要概念,它指的是在一个给定的直线上,存在三个等角,
它们的夹角均为120度。
本文详细阐述了一线三等角模型的结论及证明,并且给出了如何使用它来解决实际问题的实例。
专题 相似三角形一线三等角模型(老师版)

专题04相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·浙江·九年级专题练习)如图①,在等边三角形ABC中,点D是边BC上一动点(不与点B,C重合),以AD为边向右作等边△ADE,边DE与AC相交于点F,设BD=x,CF=y,若y与x的函数关系的大致图象如图②所示,则等边三角形ABC的面积为()A.3B.5C.2【答案】C,设90DFN DNF ∠+∠=︒MFH ∠90D MHD ∠=∠=︒在MFH MF MH FH 【答案】(1)见解析;(2)成立;理由见解析;(3)5【分析】(1)由90DPC A B ∠=∠=∠=︒可得ADP BPC ∠=∠,即可证到ADP BPC ∽即可解决问题;(2)由DPC A B α∠=∠=∠=可得ADP BPC ∠=∠,即可证到ADP 性质即可解决问题;(3)证明ABD DFE ∽△△,求出4DF =,再证EFC DEC ∽△△(1)如图2,在53⨯个方格的纸上,小正方形的顶点为格点、边长均为1,AB 为端点在格点的已知线段.请用三种不同连接格点.....的方法,作出以线段AB 为等联线、某格点P 为等联点的等联角,并标出等联角,保留作图痕迹;图3,在Rt APC △中,90A ∠=,AC AP >,延长AP 至点B ,使AB AC =,作A ∠的等联角,⊥(2)①PCF是等腰直角三角形.理由为:如图,过点C作CN BE由折叠得AC CM =,90CMP CME A ︒∠==∠=,12∠=∠AC AB =,A PBD N ∠︒=∠=∠,∴四边形ABNC 为正方形CN AC CM∴=又CE CE =,()Rt HL CME CNE ∴≌△34∴∠=∠,而12390∠+∠+∠+︒,90CPF ∠=︒例5.(2022·浙江·嘉兴一中一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC 中,∠ACB =90°,AC =BC ,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:△ADC ≌△CEB .(1)探究问题:如果AC ≠BC ,其他条件不变,如图②,可得到结论;△ADC ∽△CEB .请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y =12x 与直线CD 交于点M (2,1),且两直线夹角为α,且tanα=32,请你求出直线CD 的解析式.(3)拓展应用:如图④,在矩形ABCD 中,AB =4,BC =5,点E 为BC 边上一个动点,连接AE ,将线段AE 绕点E 顺时针旋转90°,点A 落在点P 处,当点P 在矩形ABCD 外部时,连接PC ,PD .若△DPC 为直角三角形时,请你探究并直接写出BE 的长.【答案】(1)见解析(2)41577y x =-+(3)4或372+【分析】(1)由同角的余角相等可得∠BCE =∠DAC ,且∠ADC =∠BEC =90°,可得结论;(2)过点O 作ON ⊥OM 交直线CD 于点N ,分别过M 、N 作ME ⊥x 轴NF ⊥x 轴,由(1)的结论可得:△NFO ∽△OEM ,可得NF OF NO OE ME MO==,可求点N 坐标,利用待定系数法可求解析式;(3)分两种情况讨论,由全等三角形的性质和相似三角形的性质可求解.(1)解:理由如下,∵∠ACB =90°,∴∠ACD +∠BCE =90°,又∵∠ADC =90°,∴∠ACD +∠DAC =90°,∴∠BCE =∠DAC ,且∠ADC =∠BEC =90°,∴△ADC ∽△CEB ;(2)解:如图,过点O 作ON ⊥OM 交直线CD 于点N ,分别过M 、N 作ME ⊥x 轴,NF ⊥x 轴,由(1)可得:△NFO ∽△OEM ,∴NF OF NO OE ME MO==,∵点M (2,1),∴OE =2,ME =1,∵tanα=ON OM =32,∴3212NF OF ==,∴NF =3,OF =32,∴点N (32-,3),∵设直线CD 表达式:y =kx +b ,∴12332k b k b =+⎧⎪⎨=-+⎪⎩∴47157k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线CD 的解析式为:y =-47x +157;(3)若点D在BC的反向延长线上运动,是否存在点D,使∵D 和B 不重合,∴45AED ∠<︒,又45ADE ∠=︒,90DAE ∠>︒,∴AD AE ≠≠DE .FE ;(2)若3,4AB AD ==16∵3,4AB AD ==,∴BD AB =∵DF AE ⊥,∴12ABD S AB =△∴341255AB AD AF BD ⋅⨯===,∴1695BF BD DF =-=-=,∵A .()9,3B .(9,2【答案】D 【分析】过C 作CE ⊥x 轴于E ,根据矩形的性质得到而得出△BCE ∽△ABO ,根据相似三角形的性质得到结论.【详解】解:过C 作CE ⊥x 轴于∵四边形ABCD 是矩形,∴CD=AB ∴∠ABO+∠CBE=∠CBE+∠BCE=90°∵90AOB BEC ∠=∠=︒,∴△∴CE CB BE BO AB AO==,∵4OB =∵AB=2BC ,∴BC=1AB=4,∵=4.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=_____.【答案】54【分析】先证明ABF GAE ∽,得到AB BF GA AE =,进而即可求解.【详解】∵在正方形ABCD 中,AF ⊥EG ,∴∠AGE +∠GAM =90°,∠FAB +∠GAM =90°,∴∠FAB =∠AGE ,又∵∠ABF =∠GAE =90°,∴ABF GAE ∽,∴AB BF GA AE =,即:5511BF =-,∴BF =54.故答案是:54.【点睛】本题主要考查正方形的性质,相似三角形的判定和性质,证明ABF GAE ∽,是解题的关键.5.(2023·浙江九年级专题练习)如图,ABC 为等边三角形,点D ,E 分别在边AB ,AC 上,3BD =,将ADE V 沿直线DE 翻折得到FDE V ,当点F 落在边BC 上,且4BF CF =时,DE AF ⋅的值为.【答案】9833【分析】根据△ABC 为等边三角形,△ADE 与△FDE 关于DE 成轴对称,可证△BDF ∽△CFE ,根据BF =4CF ,可得CF =4,根据AF 为轴对称图形对应点的连线,DE 为对称轴,可得DE ⊥AF ,根据S 四边形ADFE =12DE AF ⋅=S △CEF =-S △ABC -S △CEF ,进而可求9833DE AF ⋅=.【详解】解:如图,作△ABC 的高AL ,作△BDF 的高DH ,DAE的函数关系式△∽△(1)求证:ABF FCE【答案】(1)见解析(2)CE长为【分析】(1)根据矩形的性质得到用角之间的互余关系推出(1)求证:BEG CDE△∽△;(2)求AFG 【答案】(1)证明见解析(2)9【分析】(1)先根据正方形的性质可得证;90 NAF CAD∠+∠= ANE DCE∠=∠,D D∠=∠,EDC∴∴343DE=,DE∴【解决问题]若点D是BC边上任意一点时,上述结论是否成立,请说明理由.(3)【拓展探究】在整个运动过程中,请直接写出N点运动的路径长,及CN的最小值.,(1)若正方形ABCD的边长为2,E是AD的中点.①如图1,当FEC∠=②如图2,当2tan3FCE∠=时,求AF的长;(2)如图3,延长CF,DA交于点证:AE AF=.【答案】(1)①详见解析;②6AF=(2)详见解析①90ADC BAD FEC∠=∠=︒,∴AEF CED∠+∠AEF ECD∴∠=∠,AEF DCE∽△,②如图,延长DA交于点G,作GH CE⊥,垂足为且CED GEH∠=∠,CED∴△2,1CD DE==,5CE∴=,5290EDC EHG ∠=∠=︒设,AD CD a GE DE ===x y t t a n ∴==,2,t x n ∴=在Rt CHG △中,sin FCE ∠①请按要求画图:将ABC 绕点A 顺时针方向旋转90︒,点B 的对应点为点B ',点C 的对应点为点②在①中所画图形中,AB B '∠=______︒.【问题解决】如图2,在Rt ABC △中,190BC C =∠=︒,,延长CA 到D ,使1CD =,将斜边90︒到AE ,连接DE ,求ADE ∠的度数.②由作图可知,AB AB '=,90BAB '∠=︒∴'ABB 是等腰直角三角形,∴45AB B '∠=︒,故答案为:45;【问题解决】如图2中,过点E 作EH CD ⊥交CD 的延长线于H .∵90C BAE H ∠=∠=∠=︒,∴90B CAB ∠+∠=︒,90CAB EAH ∠+∠=︒,∴B EAH ∠=∠,∵AB AE =,∴()AAS ABC EAH ≌,∴BC AH EH AC ==,,∵BC CD =,∴CD AH =,∴DH AC EH ==,∴45EDH ∠=︒,∴135ADE ∠=︒.【拓展延伸】如图3中,连接AC ,∵AE BC BE EC ⊥=,,即AE 垂直平分BC ,∴AB AC =,将ABD △绕点A 逆时针旋转得到ACG ,连接DG .则BD CG =,∵BAD CAG ∠=∠,∴BAC DAG ∠=∠,∵AB AC AD AG ==,,∴ABC ACB ADG ∠∠∠===∴ABC ADG ∽△△,∵2=AD AB ,∴24DG BC ==,(1)如图1,求直线AB 的解析式.(2)如图2,线段OA 上有一点C ,直线BC 为2(0)y kx k k =-<,AD y ⊥轴,将BC 绕点B 顺时针旋转∵DA y ⊥轴,∴90DAO AOB DHO ∠=∠=∠=∴四边形DAOH 为矩形,∴2DH AO OB ===,由题可得,90CBD ∠=︒,∴90CBO DBH ∠+∠=︒,又∵90DBH BDH ∠+∠=︒,∴CBO BDH ∠=∠,在CBO 与BDH △中,90COB BHD OB HD CBO BDH ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,∴(ASA)CBO BDH ≌,∴CO BH =,令0x =,则22y kx k k =-=-,∴(0,2)C k -,∴2BH CO k ==-,∴22OH OB BH k =+=-,∴(22,2)D k -;(3)如图2,连接CD ,取CD 中点N ,连接AN ,BN ,则在Rt ACD △中,AN CN DN ==,同理,BN CN DN ==,∴AN CN DN BN ===,∴A ,C ,B ,D 四点共圆,∴,ABC ADC CDB OAB ∠=∠∠=∠,∵,90OA OB AOB =∠=︒,∴45OAB OBA ∠=∠=︒,∵345ABC BDO ∠-∠=︒,∴()345ADC BDC CDO ∠-∠-∠=︒,∴2AOD ADC ∠=∠,在AD 上取一点M ,使MD MC =则MCD ADC ∠=∠,∴2AMC ADC AOD ∠=∠=∠,∴tan tan AMC AOD ∠=∠,∴AC AD AM AO=,AM x =,22,MC MD k x AC ==--∵222MC AM AC =+,∴222(22)(22)k x x k --=++,∴41k x k =-,∴2222421k k k +-=-,解得,13k =-,∴直线BC 解析式为:13y x =-+设直线OD 解析式为:y mx =,把8(,2)3D 代入得823m =,∴34m =,则直线OD 解析式为:34y x =,第一步,以点A为圆心,任意长为半径画弧,分别交BA的延长线和AC于点E,F,如图21EF的长为半径画弧,两弧相交于点D,作射线AD 第二步,分别以点E,F为圆心,大于GAD ∠=∠=∠由(1)(2)可得NAM CAM B18.(2022·湖南郴州·中考真题)如图1,在矩形ABCD 中,4AB =,6BC =.点E 是线段AD 上的动点(点E 不与点A ,D 重合),连接CE ,过点E 作EF CE ⊥,交AB 于点F .(1)求证:AEF DCE ∽;(2)如图2,连接CF ,过点B 作BG CF ⊥,垂足为G ,连接AG .点M 是线段BC 的中点,连接GM .①求AG GM +的最小值;②当AG GM +取最小值时,求线段DE 的长.【答案】(1)见解析(2)①5;②3DE =或3DE =【分析】(1)证明出DCE AEF ∠=∠即可求解;(2)①连接AM .先证明132BM CM GM BC ====.确定出点G 在以点M 为圆心,3为半径的圆上.当A ,G ,M 三点共线时,AG GM AM +=.此时,AG GM +取最小值.在Rt ABM 中利用勾股定理即可求出AM ,则问题得解.②先求出AF ,求AF 的第一种方法:过点M 作∥MN AB 交FC 于点N ,即有CMN CBF ∽△△,进而有12MN CM BF CB ==.设AF x =,则4BF x =-,()142MN x =-.再根据∥MN AB ,得到AFG MNG ∽△△,得到AF AG MN GM =,则有()21342x x =-,解方程即可求出AF ;求AF 的第二种方法:过点G 作GH AB ∥交BC 于点H .即有MHG MBA ∽△△.则有GM GH MH AM AB MB ==,根据5AM =,可得3543GH MH ==,进而求出125GH =,95MH =.由GH AB ∥得CHG CBF ∽△△,即可求出AF .求出AF 之后,由(1)的结论可得AF AE DE DC =.设DE y =,则6AE y =-,即有164y y -=,解得解方程即可求出DE .(1)证明:如图1,∵四边形ABCD 是矩形,∴90A D ∠=∠=︒,∴90CED DCE ∠+∠=︒.∵EF CE ⊥,∴90CED AEF ∠+∠=︒,∴DCE AEF ∠=∠,∴AEF DCE ∽;(2)①解:如图2-1,连接AM .∵BG CF ⊥,∴BGC 是直角二角形.∴132BM CM GM BC ====.∴点G 在以点M 为圆心,3为半径的圆上.当A ,G ,M 三点不共线时,由三角形两边之和大于箒三边得:AG GM AM +>,当A ,G ,M 三点共线时,AG GM AM +=.此时,AG GM +取最小值.在Rt ABM 中,5AM ==.∴AG GM +的最小值为5.②(求AF 的方法一)如图2-2,过点M 作∥MN AB 交FC 于点N ,∴CMN CBF ∽△△.∴12MN CM BF CB ==.设AF x =,则4BF x =-,∴()11422MN BF x ==-.∵∥MN AB ,∴AFG MNG ∽△△,∴AF AG MN GM =,由①知AG GM +的最小值为5、即5AM =,又∵3GM =,∴2AG =.∴()21342x x =-,解得1x =,即1AF =.(求AF 的方法二)如图2-3,过点G 作GH AB ∥交BC 于点H .∴MHG MBA ∽△△.∴GM GH MH AM AB MB==,由①知AG GM +的最小值为5,即5AM =,又∵3GM =,∴3543GH MH ==.∴125GH =,95MH =.由GH AB ∥得CHG CBF ∽△△,∴GH CH FB CB =,即1293556FB +=,解得3FB =.∴1AF AB FB =-=.由(1)的结论可得AF AE DE DC =.设DE y =,则6AE y =-,∴164y y -=,解得3y =或3∵036<+<,036<-<,∴3DE =或3DE =.【点睛】本题主要考查了相似三角形的判定与性质、平行的性质、勾股定理以及一元二次方程的应用等知识,掌握相似三角形的判定与性质是解答本题的关键.。
几何模型:一线三等角模型知识讲解

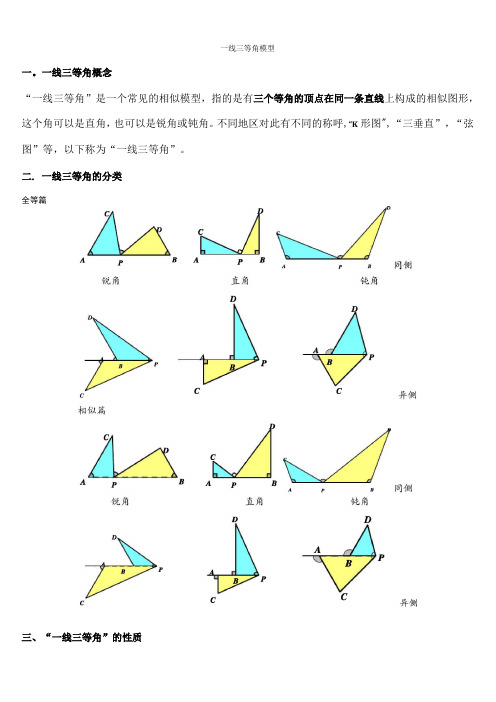
几何模型:一线三等角模型一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇同侧锐角直角钝角P异侧相似篇A同侧锐角直角钝角异侧三、“一线三等角”的性质1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC ∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED ,则△AEC ≌△BDE.3.中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(了解) 如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关,1902BOC BAC ∠=︒+∠这是内心的性质,反之未必是内心.在图 3-4(右图)中,如果延长 BE 与 CF ,交于点 P ,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明 )图 3-5其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。
几何模型:一线三等角模型 (最终版)

初中几何模型之“一线三等角模型”一.【一线三等角概念】“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.【一线三等角的分类】2.1 全等篇_同侧A PA P锐角直角钝角2.2 全等篇_异侧PDPP锐角直角钝角2.3 相似篇_同侧DCA BPP锐角直角钝角2.4 相似篇_异侧PDPP锐角直角钝角三、【性质】1.相似,如图 3-1,由∠1=∠2=∠3,或者α=α2=α3易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如下图,若 CE=ED,则△AEC≌△BDE.异侧结果同样。
3.中点型“一线三等角”——相似中多了一位兄弟如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE. 4.“中点型一线三等角“的变式(了解)如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明)图 3-5四、【“一线三等角”的应用】1.应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,构造“一等角”模型解题;c.图形中只有直线上一个角,构造“二等角”模型解题.注意:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.适应场景:在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造步骤:找角、定线、构相似【引例】例 1如图,l1、l2、l3是同一平面内的三条平行线,l1、l2之间的距离是21/5,l2、l3之间的距离是21/10,等边△ABC 的三个顶点分别在l1、l2、l3上,求△ABC 的边长.思路引导:【脑洞大开-三角构造】例 1 如图,四边形 ABCD 中,∠ABC=∠BAD=90°,∠ACD=45°,AB=3,AD=5.求 BC 的长.横向构造纵向构造斜向构造斜A相似构造:例 2 如图,△ABC 中,∠BAC=45°,AD⊥BC,BD=2,CD=3,求 AD 的长.纵向横向斜向一线三垂直的补形:角含半角补形练一练:1.如图,在△ABC 中,∠BAC=135°, AC= 2AB, AD⊥AC 交 BC 于点 D,若 AD = 2,求△ABC的面积思路提示:【中点型一线三等角】例1、如图,在Rt⊿ABC 中,AB = AC =2,∠A = 90°,现取一块等腰直角三角板,将45° 角的顶点放在BC 中点O 处,三角板的直角边与线段AB、AC 分别交于点E、F,设BE =x,CF = y,∠BOE = α( 45° ≤ α ≤ 90°) .( 1) 试求y 与x 的函数关系式,并写出x 的取值范围;( 2) 试判断∠BEO 与∠OEF 的大小关系?并说明理由;( 3) 在三角板绕O 点旋转的过程中,⊿OEF 能否成为等腰三角形? 若能,求出对应x 的值; 若不能,请说明理由.例2.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90∘,△DEF的顶点E与△ABC的斜边BC的中点重合。
一线三等角模型

几何模型04——一线三等角一、一线三等角(45度)基本图形:例1.如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).设点P为线段OB的中点,连接PA,PC,若∠CPA =∠ABO,求m的值.解:作OD=OC=2,连接CD.则∠PDC=45°,如图,由y=﹣x+m可得A(m,0),B(0,m).所以OA=OB,则∠OBA=∠OAB=45°.当m<0时,∠APC>∠OBA=45°,所以,此时∠CP A>45°,故不合题意.所以m>0.因为∠CP A=∠ABO=45°,所以∠BP A+∠OPC=∠BAP+∠BP A=135°,即∠OPC=∠BAP,则∠PCD∠∠APB,所以=,即=,解得m=12.例2.如图,∠ABC中,AB=3,∠B=45°,以点A为直角顶点作等腰Rt∠ADE,点D在BC上,点E在AC上,若CE=2,求CD的长解:过点E作EF与CD交于点F,使∠EFD=45°,过点E作EG∠CD,∠∠B=∠ADE=45°,∠∠BAD=∠EDF,∠∠ABD∠∠DFE,∠,∠∠ADE是等腰直角三角形,∠DE=AD,∠AB=3,∠DF=3,∠∠EFD=45°,∠AED=45°,∠∠EFC=∠DEC=135°,∠∠EFC∠∠DEC,∠,∠EC=2,∠EC2=FC•CD=FC•(3+FC),∠(2)2=FC(3+FC),∠FC2+3FC﹣20=0,解得:FC=﹣5(舍)或2.∠CD=DF+FC=2+3=5练习1.已知:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB =45°,求OC提示:练习2.如图,一次函数y=x+4与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC=45°,PC=PO,求点P的坐标.二、一线三等角(60度)基本图形:例3.如图,正∠ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,2D3C ,则∠ABC的边长为.解:设∠ABC的边长为x,∠∠ABC是等边三角形,∠∠DCP=∠PBA=60°.∠∠APC=∠APD+∠DPC=∠BAP+∠ABP,∠APD=60°,∠∠BAP=∠CPD.∠∠ABP∠∠CPD.∠,∠=.∠x=3.即∠ABC的边长为3.练习3.如图,∠ABC为等边三角形,D是BC边上一点,在AC边上取一点F,使CF=BD,在AB上取一点E,使BE=DC,则∠EDF=.三、一线三垂直基本图形:例4.(1)如图1,∠ABC为等腰直角三角形,AC=BC,AC∠BC,点A(0,3),C(1,0),求点B的坐标;(2)如图2,∠ABC为等腰直角三角形,AC=BC,AC∠BC,点A(﹣1,0),C(1,3),求点B的坐标;(3)如图3,∠ABC为等腰直角三角形,AC=AB,AC∠AB,点B(2,2),C (4,﹣2),求点A的坐标.解:(1)如图,作BD∠x轴于D点,∠BD∠x轴于D点,∠∠AOC=∠CDB=90°,∠∠ACB=90°,∠∠ACO+∠BCD=90°,∠∠ACO+∠OAC=90°,∠∠OAC=∠BCD,在∠AOC和∠CDB中,,∠∠AOC∠∠CDB(AAS),∠CD=AO,OC=BD,∠点C(1,0),A(0,3),∠OC=1,BD=1,CD=3,∠OD=4,∠点B的坐标为(4,1);(2)如图2,过点C作直线l∠x轴,作AE∠l于E,BF∠l于F,∠∠ACB是等腰直角三角形,∠AC=BC,∠AEC=∠ACB=∠BFC=90°,∠∠ACE+∠EAC=90°,∠ACE+∠BCF=90°,∠∠EAC=∠BCF,在∠AEC和∠CFB中,,∠∠AEC∠∠CFB(AAS),∠AE=CF=3,BF=EC=2,∠EF=5,∠点B的坐标为(4,1);(3)如图3,过点A作直线l∠y轴,过点B作BE∠l于点E,过点C作CF∠l 于点F∠BE∠l,CF∠l,∠∠BEA=∠CF A=90°=∠BAC,∠∠BAE+∠CAF=90°=∠BAE+∠ABE,∠∠ABE=∠CAF,在∠ABE和∠CAF中,,∠∠ABE∠∠CAF(AAS),∠BE=AF,CF=BE,设点A(m,n),∠点B(2,2),C(4,﹣2),∠2﹣n=4﹣m,n+2=2﹣m,∠m=1,n=﹣1,∠点A的坐标为(1,﹣1)练习4.如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若∠AOC=90°,点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为()A.4米B.4.5米C.5米D.5.5米例5.已知直线l1:y=﹣x+4与x、y轴分别交于点A、B,直线l2过点B,且与l1的夹角等于45°,如图2,求直线l2的函数表达式.解:由y=﹣x+4得,OB=4,OA=3,作∠BAC=90°,交l2于C,作CD∠OA于D,∠∠ABC=45°,∠可得∠BAC是等腰直角三角形,由上知:∠AOB∠∠CDA,∠AD=OB=4,CD=OA=3,∠OD=OA+AD=7,∠C(7,3),设l2的解析式是:y=kx+b,∠,∠,∠y=﹣x+4,练习5.如图,将边长为5的正方形OACD放在平面直角坐标系中,O是坐标原点,点D的横坐标为3,求A的坐标.练习6.如图,在∠ABC中,∠BAC=60°,∠ABC=90°,直线l1∠l2∠l3,l1与l2之间的距离为1,l2与l3之间的距离等于2,且l1、l2、l3分别经过点A、B、C,则边AC的长为.练习7.如图,正方形ABCD中,AB=12,AE=AB,点P在BC上运动(不与B、C重合),过点P作PQ∠EP,交CD于点Q,则CQ的最大值为()A.6 B.2C.3 D.4例6.如图,直角梯形ABCD中,AD∠BC,AB∠BC,AD=3,BC=5,将腰DC 绕点D逆时针方向旋转90°至DE,连接AE,求∠ADE的面积解:过点D作DG垂直于BC于G,过E作EF垂直于AD交AD的延长线于F,∠∠EDF+∠CDF=90°,∠CDF+∠CDG=90°,∠∠EDF=∠CDG,又∠∠EFD=∠CGD=90°,DE=DC,∠∠EDF∠∠CDG(AAS),∠EF=CG,∠CG=BC﹣BG=5﹣3=2,∠EF=2,∠S∠ADE=×AD×EF=×3×2=3.练习8.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B 三点共线,AB=4,则阴影部分的面积是.练习8.已知,如图,Rt∠ABC中,∠ACB=90°,AC=BC,D为BC上一点,CE∠AD 于E,若CE=2,则S∠BEC=.例6.如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,求点C的坐标解:如图,过B作BF∠AC于F,过F作FD∠y轴于D,过A作AE∠DF于E,则∠ABF为等腰直角三角形,易得∠AEF∠∠FDB,设BD=a,则EF=a,∠点A(2,3)和点B(0,2),∠DF=2﹣a=AE,OD=OB﹣BD=2﹣a,∠AE+OD=3,∠2﹣a+2﹣a=3,解得a=,∠F(,),设直线AF的解析式为y=k'x+b,则,解得,∠y=3x﹣3,解方程组,可得或,∠C(﹣1,﹣6),练习9.如图,已知点A(3,3),点B(0,2),点A在二次函数y=x2+bx﹣9的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交二次函数图象于点C,则点C的坐标为.练习10.如图,已知抛物线y=x2+2x﹣3过点A(1,0),B(0,﹣3),与x轴交于另一点C.若在第三象限的抛物线上存在点P,使∠PBC为以点B为直角顶点的直角三角形,求点P的坐标;解:过点P作PD∠y轴,垂足为D,令y=0,得x2+2x﹣3=0,解得x1=﹣3,x2=1,∠点C(﹣3,0),∠B(0,﹣3),∠∠BOC为等腰直角三角形,∠∠CBO=45°,∠PB∠BC,∠∠PBD=45°,∠PD=BD.∠可设点P(x,﹣3+x),则有﹣3+x=x2+2x﹣3,∠x=﹣1,∠P点坐标为(﹣1,﹣4);四、一线三等角(普通角度)例7.如图,在平面直角坐标系中,点O为坐标原点,直线y=,点P在第三象限的直线AB上,点C在点A上方的y轴上,连接PC、BC,PC交x轴于点N,且tan∠APC=,设点P的横坐标为t,∠ABC的面积为S,求S与t的函数关系;解:过点A作EA∠AB交PC于点E,过E点作EG∠y轴,垂足为G,过点P作PF∠y轴,垂足为F,∠∠P AE=90°,∠∠P AF+∠EAG=90°,∠∠P AF+∠APF=90°,∠∠APF=∠EAG,∠∠EGA=∠AFP=90°,∠∠AEG∠∠P AF,∠tan∠APC=,∠==,设P(t,),则PF=﹣t,AF=﹣,∠AG==﹣,EG==﹣,∠点A的坐标为:(0,2),∠E(),设PE的解析式为:y=ax+b,由P(t,),E()可得:,解得:,∠C(0,2﹣),∠AC=2﹣﹣2=﹣,∠BO=4,∠S==﹣t,练习11.如图,在∠ABC中,AB=AC,点E在边BC上移动(点E不与点B,C 重合),点D,F分别在边AB,AC上,且满足∠DEF=∠B.(1)求证:∠BDE∠∠CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.五、课后练习1.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF.已知AG∠GF,AC=,则AB的长为()A.B.2B.C.D.2.如图,正方形ABCD中,M为BC上一点,ME∠AM,ME交AD的延长线于点E,若AB=12,BM=5,则DE的长为()A.B.18B.C.D.3.如图所示,已知∠ABC中,∠BAC=45°,AD∠BC于D,BD=2,CD=3,试求AD的长.4.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC 与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是.5.在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O 作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.如图,当点A 的横坐标为﹣时,则点B的坐标为.6.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.7.如图,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD,求∠AOD的度数;。
专题02 全等模型-一线三等角(K字)模型(解析版)

专题02全等模型--一线三等角(K 字)模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K 字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K 型图)模型(同侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角(常见):锐角一线三等角直角一线三等角(“K 型图”)钝角一线三等角条件:A CED B ∠=∠=∠+CE=DE证明思路:,A B C BED ∠=∠∠=∠+任一边相等BED ACE⇒≅ 例1.(2023·江苏·八年级假期作业)探究:如图①,在ABC 中,90BAC ∠=︒,AB AC =,直线m 经过点A ,BD m ⊥于点D ,CE m ⊥于点E ,求证:ABD CAE ≌ .应用:如图②,在ABC 中,AB AC =,,,D A E 三点都在直线m 上,并且有BDA AEC BAC ∠=∠=∠.求出,DE BD 和CE 的关系.拓展:如图①中,若10DE =,梯形BCED 的面积______.【答案】探究:证明过程见详解;应用:DE BD CE =+,理由见详解;拓展:50【分析】探究:90BAC ∠=︒,AB AC =,可知ABC 是等腰直角三角形,BD m ⊥,CE m ⊥,可知90BDA AEC ∠=∠=︒,可求出BAD ACE ∠=∠,根据角角边即可求证;应用:AB AC =,,,D A E 三点都在(1)如图①,若AB AC ⊥,则BD 与AE 的数量关系为___________,CE 与AD 的数量关系为(2)如图②,判断并说明线段BD ,CE 与DE 的数量关系;(3)如图③,若只保持7BDA AEC BD EF cm ∠=∠==,,点A 在线段DE 上以2cm/s 的速度由点例3.(2022·陕西七年级期末)(1)【问题发现】如图1,△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=3,ED=4,则BE=_____.(2)【问题提出】如图2,在Rt△ABC 中,∠ABC=90°,BC=4,过点C作CD⊥AC,且CD=AC,求△BCD的面积.(3)【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为12且CD的长为6,求△BCD的面积.【答案】(1)7;(2)S△BCD=8;(3)S△BCD=6.【分析】(1)∠B=∠E=∠ACD=90°,据同角的余角相等,可得∠ACB=∠D,由已知条件可证△ABC≌△CED,运动(D 不与B 、C 重合),连接AD ,作40ADE ∠=︒,DE 交线段AC 于E .(1)当115BDA ∠=︒时,EDC ∠=_____︒,BAD ∠=_____︒,AED =∠_____︒;点D 从B 向C 运动时,BDA ∠逐渐变_____(填“大”或“小”);(2)当DC 等于多少时,ABD DCE ≌△△,请说明理由;(3)在点D 的运动过程中,ADE V 的形状可以是等腰三角形吗?若可以,请直接写出BDA ∠的度数,若不可以,请说明理由.【答案】(1)25,25,65,小(2)当2DC =时,ABD DCE ≌△△,理由见解析;(3)当BDA ∠的度数为110︒或80︒时,ADE V 的形状是等腰三角形.【分析】(1)先求出ADC ∠的度数,即可求出EDC ∠的度数,再利用三角形的外角性质即可求出AED ∠的度数,根据点D 从B 向C 运动时,BAD ∠逐渐增大,而B ∠不变化,180B BAD BDA ∠+∠+∠=︒,即可得到答案;(2)根据全等三角形的判定条件求解即可;(3)先证明当ADE V 时等腰三角形,只存在AD ED =或AE DE =两种情况,然后分这两种情况讨论求解即可;【详解】(1)解:∵115BDA ∠=︒,∴18011565ADC ∠=︒-︒=︒,∵40ADE ∠=︒,∴25EDC ADC ADE ∠︒=∠-∠=,∵ADC ADE EDC B BAD ∠=∠+∠=∠+∠,∴25BAD EDC ∠=∠=︒,∴65AED EDC C ︒∠=∠+∠=;∵点D 从B 向C 运动时,BAD ∠逐渐增大,而B ∠不变化,180B BAD BDA ∠+∠+∠=︒,∴点D 从B 向C 运动时,BDA ∠逐渐变小,故答案为:25,25,65,小;(2)解:当2DC =时,ABD DCE ≌△△,理由:∵40B C ∠=∠=︒,∴140DEC EDC ∠+∠=︒,又∵40ADE ∠=︒,∴140ADB EDC ∠+∠=︒,∴ADB DEC ∠=∠,又∵2AB AC ==,∴()AAS ABD DCE ≌△△;(3)解:当BDA ∠的度数为110°或80°时,ADE V 的形状是等腰三角形,理由:∵40C ADE ∠=∠=︒,AED C EDC ∠=∠+∠,∴AED ADE ∠>∠,∴当ADE V 时等腰三角形,只存在AD ED =或AE DE =两种情况,模型2.一线三等角(K 型图)模型(异侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
2024河南中考数学二轮复习微专题 “一线三等角”模型探究系列 课件

模型说明
“一线三等角”模型指的是三个等角的顶点在同一条直线上的模型,也称为“ K
型”相似模型,如图, ∠ = ∠ = ∠ .
特别地,当 ∠ = ∠ = ∠ = 90∘ 时,该模型是“一线三直角”模型.
模型类别及相关结论
型:三等角在直线同侧
△ 是等腰三角形时, 的长为____________.源自 7.图(1)图(2)
图(3)
(1)探索发现
如图(1),在 △ 中,点 在边 上, △ 与 △ 的面积分别记
1
为 1 与 2 ,试判断 与 的数量关系,并说明理由.
2
[答案]
______,
= + ③____.
重要结论:
1. △ ∼△ ;
2.若 = ,则 △ ≌△ .
强化训练
1.[2023山东东营] 如图, △ 为等边三角形,点 ,
分别在边 , 上, ∠ = 60∘ .若 = 4 ,
论:①等边三角形 的边长为4; ② =
1
−
2
①③
③ = 1 .其中正确的是______(填序号).
(第4题)
− 4 ,其中 0 < < 4 ;
5.如图,正方形 的边长为4,点 为 边上一点,且
= 1.5 ,点 为 边上一动点,连接 ,以 为边向右
∠ = ∠ = 90∘ ,试判断 , , 三条线段之间的数量关系.
小东利用一对全等三角形,经过推理使问题得以解决.
填空:
△ ≌△
①图(2)中的一对全等三角形为________________;
全等之一线三等角模型(含答案)

全等之一线三等角模型1. 一线三垂直【核心考点】:只要出现等腰直角三角形,可以过直角点作一条直线,然后过°顶点作该直线的垂线,构造三垂直模型.必有如下全等三角形:【经典图形】:【变式图形】:由得由得≌≌(1)(2)1.如图,正方形的顶点在直线上,,于点,于点.求证:≌.若,求点到直线的距离.2.如图,直线经过正方形的顶点,分别过正方形的顶点、作于点,于点,若,,则的长为 .(1)(2)3.如图,在中,,,于点,于点,,.求证:.求线段的长度.4.如图,点在线段上,,,,且,,,,求的度数.5.如图,是等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则 .6.如图,为等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则点坐标为 .(1)(2)7.如图,,,,,垂足分别为,.证明:≌.若,,求的长.(1)(2)(3)8.在中,,,直线经过点,且于,于.当直线绕点旋转到图①的位置时,求证:.图当直线绕点旋转到图②的位置时.求证:.图当直线绕点旋转到图③的位置时,试问:、、有怎样的等量关系?请写出这个等量关系,并加以证明.图9.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知,.则两条凳子的高度之和为 .A. B. C. D.10.如图,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积是( ).(1)(2)11.如图,中,,,是过点的一条直线,且点,在的同侧时,于,于.求证:.变成如图,,在的异侧时,,,关系如何?并加以证明.(1)(2)(3)12.如图所示,已知、为直线上两点,点为直线上方一动点,连接、,另以、为边向外作正方形和正方形,过点作于点,过点作于点.如图,当点恰好在直线上时,(此时与重合),试说明.如图,当、两点都在直线的上方时,试探求三条线段、、之间数量关系,并说明理由.如图,当点在直线的下方时,线段,、之间的数量关系又如何?请写出你的结论,并说明理由.2. 一线三等角【核心考点】:只要在一条直线上出现三个角相等,一般都可以构造全等三角形解决问题.【经典图形】:A. B. C. D.13.如图,在等边中,,点在上,且,点是上一动点,连结,将线段绕点逆时针旋转得到线段,要使点恰好落在上,则的长是( ).14.如图,已知中,点为上一点,,两点分别在边,上,若,,,,则.ACBFDE 15.如图,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .16.感知:如图①,点在正方形的边上,于点,于点,可知≌.(不要求证明)拓展:如图②,点,分别在的边,上.点,在内部的射线上,,分别是,的外角.已知,,求证:≌.应用:如图③,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .图图图图图图(1)(2)(3)17.某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图,已知:在中,,,直线经过点,直线,直线,垂足分别为点、.求证:.组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图,将()中的条件改为:在中,,、、三点都在直线上,并且有(其中为任意锐角或钝角),请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图,是角平分线上的一点,且和均为等边三角形,、分别是直线上点左右两侧的动点(、、互不重合),在运动过程中线段的长度始终为,连接、.若,则周长是 .(请直接写出答案)(1)(2)18.如图,是经过顶点的一条直线,,、分别是直线上两点,且.若直线经过的内部,且、在直线上,请解决下面两个问题:①如图①,若,,则;(填“”、“”、“”);图②如图②,若,请添加一个关于与关系的条件 ,使①中的两个结论仍然成立,并证明这两个结论.图如图③,若直线经过的外部,,请提出、、三条线段数量关系的合理猜想(不要求证明).图全等之一线三等角模型1. 一线三垂直【核心考点】:只要出现等腰直角三角形,可以过直角点作一条直线,然后过°顶点作该直线的垂线,构造三垂直模型.必有如下全等三角形:【经典图形】:【变式图形】:由得由得≌≌【备注】【教法指导】通过例1.1可以详细给学生示范一下三垂直模型的书写过程,其中倒角用的是“同角的余角相等”,提醒书生注意1.如图,正方形的顶点在直线上,,于点,于点.(1)(2)(1)(2)【解析】【标注】求证:≌.若,求点到直线的距离.【答案】(1)(2)证明见解析..∵四边形是正方形,,,∴,,,∴,,∴,∴在与中,,∴≌.过作,∵四边形是正方形,,∴,,,,∴,,,∴在与中,,∴≌,∴,∴在中,,,,∴点到直线的距离.【知识点】正方形与全等综合2.【解析】【标注】如图,直线经过正方形的顶点,分别过正方形的顶点、作于点,于点,若,,则的长为 .【答案】∵四边形是正方形,∴,,∵则是直角三角形,∴,,又∵,∴,在和中,,∴≌,∴,∴.【知识点】三垂直模型3.如图,在中,,,于点,于点,,.(1)(2)(1)(2)【解析】【标注】求证:.求线段的长度.【答案】(1)(2)证明见解析..∵,,,∴,,∴,在和中,,∴≌,∴.∵≌,∴,,∴.【知识点】三垂直模型4.【解析】如图,点在线段上,,,,且,,,,求的度数.【答案】.连接、.∵,,.∴.【标注】在和中,∴≌∴,,∴.∴为等腰三角形.同理可得为等腰三角形.∴..【能力】分析和解决问题能力【知识点】SAS【知识点】全等三角形的性质5.【解析】【标注】如图,是等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则.【答案】由三垂直模型易证≌,∴.【知识点】坐标与距离;三垂直模型6.如图,为等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则点坐标为 .【解析】【标注】【答案】由三垂直模型易证≌,∴,,∴点坐标为,故答案为:.【知识点】根据坐标描点、根据点写坐标;三垂直模型(1)(2)7.(1)【解析】如图,,,,,垂足分别为,.证明:≌.若,,求的长.【答案】(1)(2)证明见解析..∵,,,∴,∴,,∴,在和中,(2)【标注】,∴≌.∵≌,∴,,∴().【知识点】一线三等角模型(1)(2)(3)8.在中,,,直线经过点,且于,于.当直线绕点旋转到图①的位置时,求证:.图当直线绕点旋转到图②的位置时.求证:.图当直线绕点旋转到图③的位置时,试问:、、有怎样的等量关系?请写出这个等量关系,并加以证明.图【答案】(1)(2)(3)证明见解析.证明见解析..(1)(2)(3)【解析】【标注】∵中,,∴,又直线经过点,且于,于,∴,∴,∴,在和中,,∴≌(),∴,,∴.∵中,,直线经过点,且于,于,∴,,而,∴≌,∴,,∴.∵中,,直线经过点,且于,于,∴,,∴,∵,∴≌,∴,,∴;、、之间的关系为.【能力】推理论证能力【能力】运算能力【知识点】AAS【知识点】全等三角形的对应边与角9.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知,.则两条凳子的高度之和为 .【解析】【标注】【答案】由题意可得:,,,在和中,,∴(),故,,则两条凳子的高度之和为:.故答案为:.【知识点】全等三角形实际生活中的应用A. B. C. D.10.方法一:【解析】如图,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积是( ).【答案】A ∵,,∴,∵在和中,,方法二:【标注】∴≌(),同理 ≌(),∴,,,,∵梯形的面积,,,∴图中实线所围成的图形的面积.∵且,,,,,∴,,≌,∴,.同理证得≌得,.故,故.故选:.【知识点】三垂直模型(1)(2)11.如图,中,,,是过点的一条直线,且点,在的同侧时,于,于.求证:.变成如图,,在的异侧时,,,关系如何?并加以证明.(1)(2)【解析】【标注】【答案】(1)(2)证明见解析...∵,,,∴,∴,∴.∵,在和中,,∴≌,∴,,∴.∵,∴.成立.∵,,,∴.∵,,∴.∵,在和中,,∴≌,∴,.∵,∴.【能力】推理论证能力【能力】分析和解决问题能力【知识点】全等三角形的性质【知识点】AAS(1)(2)(3)12.(1)【解析】如图所示,已知、为直线上两点,点为直线上方一动点,连接、,另以、为边向外作正方形和正方形,过点作于点,过点作于点.如图,当点恰好在直线上时,(此时与重合),试说明.如图,当、两点都在直线的上方时,试探求三条线段、、之间数量关系,并说明理由.如图,当点在直线的下方时,线段,、之间的数量关系又如何?请写出你的结论,并说明理由.【答案】(1)(2)(3)证明见解析...∵四边形和为正方形,(2)(3)∴,,,∴,∵,∴,∴,∵,∴≌(),∴.,理由如下:过点作于,∵,∴,∴,∵四边形为正方形,∴,,∴,∴,∴≌(),∴,同理得:,∵,∴.,理由如下:过点作于,【标注】∵,∴,∴,∵四边形为正方形,∴,,∴,∴,∴≌(),∴,同理得:,∵,∴.【知识点】正方形与全等综合2. 一线三等角【核心考点】:只要在一条直线上出现三个角相等,一般都可以构造全等三角形解决问题.【经典图形】:【备注】【教法指导】注意三个相等的角度可以在直线同侧,也可以在直线异侧.A. B. C. D.13.【解析】如图,在等边中,,点在上,且,点是上一动点,连结,将线段绕点逆时针旋转得到线段,要使点恰好落在上,则的长是( ).【答案】B如图所示∵,,∴,∵为等边三角形,∴,∵线段绕点逆时针旋转得到线段,【标注】要使点恰好落在上,∴,,∵,,∴,在和中,∵,∴≌,∴.故选.【知识点】等边三角形的性质14.【解析】【标注】如图,已知中,点为上一点,,两点分别在边,上,若,,,,则.ACBFDE 【答案】∵,,∴,在和中,,∴≌,∴,∵,,∴.【知识点】一线三等角模型15.【解析】【标注】如图,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .【答案】∵,∴与等高,底边比值为,∴与面积比为,又的面积为,∴与面积分别为和.∵,∴.∵,,∴.在和中,,∴≌.∴,∴.【知识点】三角形的周长与面积问题16.感知:如图①,点在正方形的边上,于点,于点,可知≌.(不要求证明)拓展:如图②,点,分别在的边,上.点,在内部的射线上,,分别是,的外角.已知,,求证:≌.【解析】【标注】应用:如图③,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .图图图【答案】见解析拓展:证明:∵,∴.∵,,又,∴.在和中,,∴≌.应用:解:∵,∴.∵,,,∴.在和中,,∴≌.∴.∵在中,,∴.∵,∴.∴.【知识点】全等三角形实际生活中的应用17.某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.图图图(1)(2)(3)图(1)【解析】如图,已知:在中,,,直线经过点,直线,直线,垂足分别为点、.求证:.组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图,将()中的条件改为:在中,,、、三点都在直线上,并且有(其中为任意锐角或钝角),请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图,是角平分线上的一点,且和均为等边三角形,、分别是直线上点左右两侧的动点(、、互不重合),在运动过程中线段的长度始终为,连接、.若,则周长是 .(请直接写出答案)【答案】(1)(2)(3)证明见解析.证明见解析.如图,∵直线,直线,∴,∵,∴,∵,∴,在与中,,∴≌,∴,,∴,∴.图(2)图(3)【标注】.如图,证明如下:∵,∴,∴,在和中,,∴≌,∴,,∴,∴.∵≌,∴,,∵和均为等边三角形,∴,,∴,即,在和中,,∴≌,∴且,∵,∴,∴,∴是等边三角形,∴.【知识点】多解或多种判定混合(1)18.如图,是经过顶点的一条直线,,、分别是直线上两点,且.若直线经过的内部,且、在直线上,请解决下面两个问题:21(2)【标注】①如图①,若,,则 ; (填“”、“”、“”);图②如图②,若,请添加一个关于与关系的条件 ,使①中的两个结论仍然成立,并证明这两个结论.图如图③,若直线经过的外部,,请提出、、三条线段数量关系的合理猜想(不要求证明).图【答案】(1)(2)();.,先证明,再证明≌..【知识点】全等三角形的性质。
初中数学几何模型(五)一线三等角模型

初中数学几何模型(五)一线三等角模型一线三等角模型:指有三个相等角的顶点在同一直线上构成的相似或全等(相等角所对的边相等)图形,相等的角可以是锐角,也可以是直角或钝角。
(一)全等1、相等的三个角和全等三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD≌△BEC。
证明:∵∠BCD=∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,CD=CE,∴△ACD≌△BEC(AAS)。
2、相等的三个角和全等三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD ≌△BEC。
证明:∵∠2=∠D+∠ACD,∠3=∠BCE+∠ACD,∠2=∠3,∴∠D=∠BCE,∵∠2=∠1,∴∠DAC=∠CBE,∵CD=CE,∴△ACD≌△BEC(AAS)。
一线三等角结论1:当等角所对边相等时,则两个三角形全等。
(二)相似1、相等的三个角和相似三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠BCD+∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴△ACD∽△BEC。
2、相等的三个角和相似三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠1=∠D+∠ACD,∠3=∠BCE+∠ACD,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴∠DAC=∠CBE,∴△ACD∽△BEC。
一线三等角结论2:一线三等角两个三角形相似。
(三)一线三等角变式:中点型如图,点C在相等AB上,且AC=BC,∠1=∠2=∠3。
求证:△ACD∽△BEC∽△CED证明:∵∠1=∠2=∠3,∴△ACD ∽△BEC ,∴AD BC =CD CE , ∵AC=BC ,∴AD AC =CD CE ,∵∠1=∠3,∴△ACD ∽△CED ,∴△ACD ∽△BEC ∽△CED ,∴∠4=∠5=∠8,∠9=∠6=∠7。
一线三等角相似模型

在物理学中,可以利用一线三等角 相似模型来研究物理现象和规律, 如光的反射和折射、波的传播等。
04 一线三等角相似模型的证 明方法
直接证明法
定义
直接证明法是通过直接使用已知条件和定理来证明结论的 方法。
步骤
首先,根据已知条件,明确一线三等角的定义和性质;然后, 通过比较两个三角形中的角度和边长,利用相似三角形的性质
03
注意事项
反证法需要熟练掌握反证法的原理和 推理技巧,以及能够灵活运用已知条 件。
综合法与分析法
定义
综合法是从已知条件出发,逐步推导出结论的方法;分析法是从结论出发,逐步推导出已知条件的方法。
步骤
在综合法中,首先明确已知条件和目标结论;然后,根据已知条件逐步推导所需结论;最后,总结推导过程。在分析 法中,首先明确目标结论和已知条件;然后,根据结论逐步推导所需条件;最后,总结推导过程。
,逐步推导出所需的结论。
注意事项
直接证明法需要熟练掌握相似三角形的性质和定理,以及 灵活运用已知条件。
反证法
01
定义
反证法是通过假设结论不成立,然后 推导出矛盾,从而证明结论成立的方 法。
02
步骤
首先,假设结论不成立;然后,根据 已知条件和反证法的原理,推导出与 已知条件相矛盾的结论;最后,根据 矛盾的结论,得出结论成立。
相似变换的性质
相似变换具有一些重要的性质,如保持角度不变、线 段长度比例不变等。
相似变换的应用
相似变换在几何学、物理学、工程学等领域有着广泛 的应用,如建筑设计、机械制造、航天技术等。
相似多边形的性质与应用
1 2
相似多边形的定义
相似多边形是指各对应角相等、各对应边成比例 的多边形。
几何模型:一线三等角模型 (最终版)

初中几何模型之“一线三等角模型”一.【一线三等角概念】“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.【一线三等角的分类】2.1 全等篇_同侧A PA P锐角直角钝角2.2 全等篇_异侧PDPP锐角直角钝角2.3 相似篇_同侧DCA BPP锐角直角钝角2.4 相似篇_异侧PDPP锐角直角钝角三、【性质】1.相似,如图 3-1,由∠1=∠2=∠3,或者α=α2=α3易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如下图,若 CE=ED,则△AEC≌△BDE.异侧结果同样。
3.中点型“一线三等角”——相似中多了一位兄弟如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE. 4.“中点型一线三等角“的变式(了解)如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明)图 3-5四、【“一线三等角”的应用】1.应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,构造“一等角”模型解题;c.图形中只有直线上一个角,构造“二等角”模型解题.注意:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.适应场景:在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造步骤:找角、定线、构相似【引例】例 1如图,l1、l2、l3是同一平面内的三条平行线,l1、l2之间的距离是21/5,l2、l3之间的距离是21/10,等边△ABC 的三个顶点分别在l1、l2、l3上,求△ABC 的边长.思路引导:【脑洞大开-三角构造】例 1 如图,四边形 ABCD 中,∠ABC=∠BAD=90°,∠ACD=45°,AB=3,AD=5.求 BC 的长.横向构造纵向构造斜向构造斜A相似构造:例 2 如图,△ABC 中,∠BAC=45°,AD⊥BC,BD=2,CD=3,求 AD 的长.纵向横向斜向一线三垂直的补形:角含半角补形练一练:1.如图,在△ABC 中,∠BAC=135°, AC= 2AB, AD⊥AC 交 BC 于点 D,若 AD = 2,求△ABC的面积思路提示:【中点型一线三等角】例1、如图,在Rt⊿ABC 中,AB = AC =2,∠A = 90°,现取一块等腰直角三角板,将45° 角的顶点放在BC 中点O 处,三角板的直角边与线段AB、AC 分别交于点E、F,设BE =x,CF = y,∠BOE = α( 45° ≤ α ≤ 90°) .( 1) 试求y 与x 的函数关系式,并写出x 的取值范围;( 2) 试判断∠BEO 与∠OEF 的大小关系?并说明理由;( 3) 在三角板绕O 点旋转的过程中,⊿OEF 能否成为等腰三角形? 若能,求出对应x 的值; 若不能,请说明理由.例2.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90∘,△DEF的顶点E与△ABC的斜边BC的中点重合。
非学科数学学培训-一线三等角-模型

自学资料一、相似三角形判定与性质综合【知识探索】1.一线三直角型:2.一线三等角型(非直角):三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景第1页共10页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训【错题精练】例1.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C1处,点D落在点D1处,C1D1交线段AE 于点G.(1)求证:△BC1F∽△AGC1;(2)若C1是AB的中点,AB=6,BC=9,求AG的长.例2.如图,四边形ABCD中,∠A=∠B=90∘,P是线段AB上的一个动点.(1)若AD=2,BC=6,AB=8,且以A,D,P为顶点的三角形与以B,C,P为顶点的三角形相似,求AP的长;(2)若AD=a,BC=b,AB=m,则当a,b,m满足什么关系时,一定存在点P使△ADP∽△BPC?并说明理由.例3.如图,在△ABC中,∠BAC=90∘,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC 上取E点,使∠ADE=45∘,(1)求证:△ABD∽△DCE;(2)设BD=x,AE=y,求y关于x的函数关系式.第2页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训例4.如图,在RtΔABC中,∠ABC=90∘,AB=BC,点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①AGAB =AFFC;②若点D是AB的中点,则AF=√32AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若DBAD =12,则SΔABC=9SΔBDF,其中正确的结论序号是()A. ①②;B. ③④;C. ①②③;D. ①②③④.例5.【提出问题】(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.【类比探究】(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.第3页共10页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训例6.在△ABC中,AB=AC=5,BC=6,点D在边AB上,DE⊥AB,点E在边BC,点F在边AC上,且∠DEF=∠B.(1)求证:△FCE∽△EBD;(2)当点D在线段AB上运动时,是否有可能使S△FCE=4S△EBD?如果有可能,那么求出BD的长;如果不可能,请说明理由.例7.如图,A的坐标是(0,4),点C是x轴上的一个动点,点B与点O在直线AC两侧,∠BAC=∠OAC,BC⊥AC,点B的坐标为(x,y),y与x的函数关系式为()A. y=8xB. y=C. y=D. y=例8.如图,O为矩形ABCD的中心,将直角△OPQ的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若AB=4,AD=6,BM=x,AN=y,则y与x之间的函数图象是()第4页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训A.B.C.D.例9.在平面直角坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第2个正方形A1B1C1C;延长C1B1交x轴于点A2,作第3个正方形A2B2C2C1…按这样的规律进行下去,第2011个正方形的面积为()A. 5B.C.D.【举一反三】1.如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q 在边AD上,将△CBP和△QAP分别沿PC、PQ折叠,使B点与E点重合,A点与F点重合,且P、E、F三点共线.第5页共10页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训(1)若点E平分线段PF,则此时AQ的长为多少?(2)若线段CE与线段QF所在的平行直线之间的距离为2,则此时AP的长为多少?(3)在“线段CE”、“线段QF”、“点A”这三者中,是否存在两个在同一条直线上的情况?若存在,求出此时AP的长;若不存在,请说明理由.2.如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.(1)求证:△EBF∽△FCD(2)如果BC=12,BF=3,求BE的值.3.如图,梯形ABCD中,AB∥DC,∠ABC=90∘,AB=4,CD=1,BC=4.在腰BC上取一点P,使得以A、B、P为顶点的三角形与以C、D、P为顶点的三角形相似,这样的点P有()A. 1个B. 2个C. 3个D. 4个4.如图,直角梯形ABCD中,AB⊥BC,AD∥BC,点E是AB的中点,且AD+BC=DC、下列结论中:①△ADE∽△BEC;②DE2=DA•DC;③若设AD=a,CD=b,BC=c,则关于x的方程ax2+bx+c=0有两个不相等的实数根;④若设AD=a,AB=b,BC=c,则关于x的方程ax2+bx+c=0有两个相等的实数根.其中正确的结论有()个.第6页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训A. 1个B. 2个C. 3个D. 4个5.点E为正方形ABCD的对角线上一点,连接DE,BE并延长交AD于点F,EG⊥DE交BC于G,下列结论:①△BEC≌△DEC;②∠BED=120°时,EF平分∠AED;③BG=AE;④当点G为BC的中点时,DF=2AF.其中正确的是()A. ①②B. ①③④C. ②③④D. ①②③④6.如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C 在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.(1)直接写出D,E 两点的坐标,D(),E()(2)求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?(3)当t为何值时,DP平分∠EDA?(4)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.第7页共10页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训7.如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D 与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.(1)当点E与点A重合时,折痕EF的长为;(2)写出使四边形EPFD为菱形的x的取值范围,并求出当x=2时菱形的边长;(3)令EF2=y,当点E在AD、点F在BC上时,写出y与x的函数关系式(写出x的取8.(2009•武汉)如图1,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.(1)求证:△ABF∽△COE;(2)当O为AC的中点,时,如图2,求的值;(3)当O为AC边中点,时,请直接写出的值.1.如图,在正方形ABCD中,E为AB边的中点,G、F分别为AD、BC边上的点.若AG=1,BF=2,∠GEF=90°,则GF的长为__________.第8页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训2.如图,已知AM∥BN,∠A=∠B=90°,AB=4,点D是射线AM上的一个动点(点D与点A不重合),点E是线段AB上的一个动点(点E与点A、B不重合),连接DE,过点E作DE的垂线,交射线BN 于点C,连接DC.设AE=x,BC=y.(1)当AD=1时,求y关于x的函数关系式,并写出它的定义域;(2)在(1)的条件下,取线段DC的中点F,连接EF,若EF=2.5,求AE的长;(3)如果动点D、E在运动时,始终满足条件AD+DE=AB,那么请探究:△BCE的周长是否随着动点D、E的运动而发生变化?请说明理由.3.把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ______.(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由.(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)4.△ABC中,AB=AC=2,∠BAC=90°,O是BC的中点,小敏拿着含45°角的透明三角板,使45°角的顶点落在点O,三角板绕O点旋转.(1)如图(a),当三角板的两边分别交AB、AC于点E、F时,求证:△BOE∽△CFO;(2)操作:将三角板绕点O旋转到图(b)情形时,三角板的两边分别交BA的延长线、边AC于E、F.①探索:△BOE与△CFO还相似吗?(只需写结论):连接EF,△BOE与△OFE是否相似?请说明理由.②设EF=x,△EOF的面积是S,写出S与x的函数关系式.第9页共10页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训第10页共10页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训。
(完整版)几何模型:一线三等角模型
一线三等角模型一。
一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K形图",“三垂直”,“弦图”等,以下称为“一线三等角”。
二. 一线三等角的分类全等篇三、“一线三等角”的性质1。
一般情况下,如图3—1,由N 仁Z2=Z3,易得△AECs^BDEo2. 当等角所对的边相等时,则两个三角形全等.如图3.中点型“一线三等角 如图3—2,当Z1=Z2=Z3,且D 是BC 中点时,△BDEs^CFDs^DFE 。
4。
“中点型一线三等角“的1如图3—4“中点型一线三等角”通常与三角形的内心或旁心相关,ZBOC 二90。
+A BAC 这是内心的^2 性质,反之未必是内心.在图3-4(右图)中,如果延长BE 与CF ,交于点P,则点D 是APEF 的旁心.图3—5其实这个第4图,延长DC 反而好理解•相当于两侧型的,不延长理解,以为是一种新型的,同 侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1•“一线三等角”应用的三种情况.图3-1图3-3图3-4+Ja。
图形中已经存在“一线三等角”,直接应用模型解题;b。
图形中存在“一线二等角”,不上“一等角”构造模型解题;c・图形中只有直线上一个角,不上“二等角”构造模型解题。
体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2。
在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造一线三等角解决问题更是重要的手段。
在DC的延檢銭上截眼匚E二J3•构造一线三等角的步骤:找角、定线、构相似1IJttnZAEP=aaZPFB=啦-工上则以’唾二ZPFB=a二ZAPE』所I^APAEwABPF.在CP±WCE=则曲厶斗EOunZBFD=⑶“则ZAEC-ZBFD=ZAPB•所I^APAE«ABPF・坐标系中,要讲究“线"的特殊性如图3—6,线上有一特殊角,就考虑构造同侧型一线三等角(完整版)几何模型:一线三等角模型当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过C、D两点作直线I的垂线是必不可少的。
全等模型 —“一线三等角”

全等模型—“一线三等角”一线三等角模型,顾名思议,一线三等角是指三个相等的角的顶点在同一条直线上,这个模型贯穿初中几何的始终,在相似三角形这个章节中是很重要的知识点,下面来具体分析一下。
1,等腰直角三角形一线三等角模型口诀:多个垂直先倒角相等,互余角少不了分析1:已知△OAB是等腰直角三角形,过点O作直线CD且AD⊥CD,BC⊥CD,由题意得,∵△OAB是等腰直角三角形∴∠BOA=90°OB=OA即∠COB+∠AOD=90°又因为AD⊥CD,BC⊥CD所以∠COB+∠CBO=90°(互余角)∠DAO+∠AOD=90°(互余角)因此∠CBO+∠DAO=90°(互余角)则有∠COB=∠DAO∠CBO=∠AOD综上结论,则有在△BCO和△ODA中∠COB=∠DAOOB=OA(角边角)∠CBO=∠AOD因此△BCO≌△ODA分析2,已知△OAB是等腰直角三角形,做一条直线穿过∠BOA,AD⊥CD,BC⊥CD,如下图所示:由题意得,∵△OAB是等腰直角三角形∴∠BOA=90°OB=OA即∠COB+∠AOD=90°又因为AD⊥CD,BC⊥CD所以∠COB+∠CBO=90°(互余角)∠DAO+∠AOD=90°(互余角)因此∠CBO+∠DAO=90°(互余角)则有∠COB=∠DAO,∠CBO=∠AOD综上结论,则有在△BCO和△ODA中,∠COB=∠DAO,OB=OA,∠CBO=∠AOD因此△BCO≌△ODA“一线三等角”全等模型——适用于直角的情况条件:∠BAC=∠BFA=∠AEC=90°,AC=BA,结论:△ACE≌△BAF.由题意得,∵∠BAC=∠BFA=∠AEC=90°∴∠EAC+∠BAF=90°(互余角),∠EAC+∠ECA=90°,∠ABF+∠BAF=90°,即∠ABF=∠EAC,在△ACE和△BAF中,∠ABF=∠EAC∠BFA=∠AEC(角角边)AC=BA因此:△ACE≌△BAF(AAS)则有:CE=AF,AE=BF,EF=CE+BF.条件:∠BAC=∠BFA=∠AEC=90°,AC=BA,结论:△ACE≌△BAF由题意得,∵∠BAC=∠BFA=∠AEC=90°∴∠EAC+∠BAF=90°(互余角)∠EAC+∠ECA=90°∠ABF+∠BAF=90°即∠ABF=∠EAC在△ACE和△BAF中∠ABF=∠EAC∠BFA=∠AEC(角角边)AC=BA因此:△ACE≌△BAF(AAS)则有:CE=AF AE=BFEF=BF-EC【典例1】:已知,如图所示,B,C,E三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A,∠A与∠D互为余角B,∠A=∠DCEC,△ABC≌△CED D,∠ACB=∠DCE【答案】D【精准解析】由题意得因为AC⊥CD,所以∠ACD=90°,所以∠ACB+∠DCE=90°故选择D 又因为∠B=∠E=90°所以∠A+∠ACB=90°∠D+∠DCE=90°∠A=∠DCE∠ACB=∠D故B正确所以∠A+∠D=90°故A正确再根据全等三角形判定定理得:AC=CD∠B=∠E∠A=∠DCE因此最终答案是D2,“一线三等角”全等模型的拓展——同时也适用于锐角和钝角的情况条件:∠CAE=∠B=∠D,AC=AE结论:△ABC≌△EDA由题意得,∠CAB+∠CAE+∠EAD=180°∠CAB+∠B+∠C=180°∵∠CAE=∠B∴∠C=∠EAD在△CAB和△EAD中,∠B=∠D,∠C=∠EAD,AC=AE,因此△CAB≌△EAD(AAS)所以BC=AD,AB=DE,BD=BC+DE由题意得,∠CAB+∠CAE+∠EAD=180°∠CAB+∠B+∠C=180°∵∠CAE=∠B∴∠C=∠EAD在△CAB和△EAD中,∠B=∠D,∠C=∠EAD,AC=AE,因此△CAB≌△EAD(AAS),锐角和钝角的结论:BC=AD,AB=DE,BD=BC+DE.【典例2】:在三角形ABC中,∠A=40°,∠B=∠C,BE=CD,BD=CF,求∠EDF的度数?【答案】由题意得在△BDE和△CFD中BE=CD∠B=∠C(边角边)BD=CF所以△BDE≌△CFD∵∠BDE+∠EDF+∠FDC=180°∠BDE+∠B+∠BED=180°∵∠EDF=∠B又因为∠A=40°∠B=∠C根据三角形内角和得∠B=∠EDF=∠B=70°=70°因此∠EDF=∠B=70°【精准解析】根据已知条件证明△BDE≌△CFD,即ED=DF,∠EDF=∠B=∠C,因此属于一线三等角模型,已知∠A=40°,即先求∠B=∠C=70°,即可得出答案【典例3】如图,在三角形ABC中,依然有AB=AC,若点B,C位于直线l的两侧,若果∠BDA+∠BAC=180°,∠BDA=∠AEC,求证BD=CE+DE【答案】由题意得∵∠BDA+∠BAC=180°∠BDA+∠BDE=90°∴∠BAC=∠BDE又∵∠ABD+∠BAD=∠BDE∠CAE+∠BAD=∠BAC∴∠ABD=∠CAE在△BDA和△CEA中∠ABD=∠CAE∠BDA=∠AEC(角角边)AB=AC所以△BDA≌△CEA即AD=CE BD=AE因此BD=CE+DE【精准答案】首先证明△BDA≌△CEA,由此得到AD=CE BD=AE,即可得出答案。
专题06 全等三角形之一线三等角模型全攻略(解析版)

专题06全等三角形之一线三等角模型全攻略目录【知识点归纳】 (1)【例题精讲】 (2)【课后练习】 (13)【知识点归纳】“一线三垂直”模型,是初中几何图形中的最重要模型,一般只要图形中出现一线三垂直或二垂或一垂图形,不管它是出现在全等图形中,还是在以后学习的相似图形中,函数图形中,它的辅助线、解题思路过程基本固定,一定要熟悉它的变化及用法。
“三垂直模型”是一个应用非常广泛的模型,它可以应用在三角形,矩形,平面直角坐标系,网格,一次函数,反比例函数,三角函数,二次函数以及圆等诸多的中考重要考点之中,所以掌握好这一模型会使你在中考中技高一筹。
基本图形如下:同侧型一线三等角(常见):锐角一线三等角直角一线三等角钝角一线三等角条件:A CED B ∠=∠=∠,CE=DE证明思路:,A B C BED ∠=∠∠=∠,任一边相等BED ACE⇒ ≌异侧型一线三等角:锐角一线三等角直角一线三等角钝角一线三等角条件:FAC ABD CED ∠=∠=∠,任意一边相等证明思路:,A B C BED ∠=∠∠=∠,任一边相等BED ACE ⇒ ≌【例题精讲】例1.(同侧一线三直角)(1)如图1,已知:在ABC ∆中,90BAC ∠=︒,AB AC =,直线l经过点A ,BD l ⊥,CE l ⊥垂足分别为点D 、E .证明:①CAE ABD ∠=∠;②DE BD CE =+.(2)如图2,将(1)中的条件改为:在ABC ∆中,AB AC =,D 、A 、E 三点都在l 上,并且有BDA AEC BAC α∠=∠=∠=,其中α为任意锐角或钝角.请问结论DE BD CE =+是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)如图3,过ABC ∆的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.【答案】(1)①见解析;②见解析;(2)成立:DE=BD+CE ;证明见解析;(3)见解析【分析】(1)①根据平行线的判定与性质即可求解;②由条件可证明△ABD ≌△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知∠BAD +∠CAE =180°−α,且∠DBA +∠BAD =180°−α,可得∠DBA =∠CAE ,结合条件可证明△ABD ≌△CAE ,同(1)可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI ≌△GNI ,可得出结论I 是EG 的中点.【详解】(1)①∵BD ⊥直线l ,CE ⊥直线l∴∠BDA=∠CEA=90°∵∠BAC=90°∴∠BAD+∠CAE=90°∵∠BAD+∠ABD=90°∴∠CAE=∠ABD②在△ADB 和△CEA 中ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△CEA (AAS )∴AE=BD ,AD=CE∴DE=AE+AD=BD+CE ;(2)成立:DE=BD+CE 证明如下:∵∠BDA=∠BAC=α∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α∴∠DBA=∠CAE在△ADB 和△CEA 中ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△CEA (AAS )∴AE=BD 、AD=CE∴DE=AE+AD=BD+CE ;(3)如图过E 作EM ⊥HI 于M ,GN ⊥HI 的延长线于N∴∠EMI=GNI=90°由(1)和(2)的结论可知EM=AH=GN∴EM=GN在△EMI 和△GNI 中GIH EIM EM GN GHI EMI ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△EMI ≌△GNI (AAS )∴EI=GI∴I 是EG 的中点.【点睛】本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD =AE 、CE =AD 是解题的关键.例2.(异侧一线三直角)如图1,OA OB ⊥,OC OD ⊥,OA OB =,OC OD =,连接AD 、BC ,交于点H .(1)写出AD 和BC 的数量关系及位置关系,并说明理由;(2)如图2,连接BD ,若DO 、BO 分别平分ADB ∠和CBD ∠,求BOD ∠的度数;(3)如图3,连接AC 、BD ,设AOC 的面积为1S ,BOD 的面积为2S ,探究1S 与2S 的数量关系,并说明理由.OA OB ⊥,OC OD ⊥90AOB COD ∴∠=∠=︒,AOB AOC AOC ∠+∠=∠ AOD BOC ∴∠=∠,又 OA OB =,OC OD =AOD BOC ∴ ≌()SAS ,(3)如图,过点,C D ,分别作90CFO OGD ∴∠=∠=︒,90COD ∠=︒ ,90COF GOD ∴∠=︒-∠=∠又CO DO = ,()AAS CFO OGD ∴ ≌,FO GD ∴=,AOC 的面积为1S ,BOD 在MAN ∠的边AM 、AN 上,且AB AC =,CF AE ⊥于点F ,BD AE ⊥于点D ,求证:ABD CAF V V ≌;(2)如图2,点B 、C 分别在MAN ∠的边AM 、AN 上,点E 、F 都在MAN ∠内部的射线AD 上,已知AB AC =,且12BAC ∠=∠=∠,求证:ABE CAF V V ≌;(3)如图3,已知ABC 的面积为15,且AB AC =,AB BC >,点D 在边BC 上,点E 、F 在线段AD 上,12BAC ∠=∠=∠,若ACF △与BDE △的面积之和是6,求:CD BC 的值.∵12∠=∠,∴AFC BEA ∠=∠,∵34BAC ∠+∠=∠,1∠∴4ABE ∠=∠,∵AB AC =,∴()AAS ABE CAF △≌△∵12BAC ∠=∠=∠,∴3ACF ∠=∠,BEA ∠∵AB AC =,∴(AAS ABE CAF △≌△∴ABE CAF S S = ,∵ACF △与BDE △的面积之和是∴ABD ABE BDE S S S =+ △△∵ACD 与ABC 等高,∴底边之比3:5,∴:3:5CD BC =.【点睛】本题主要考查了三角形全等的判定和性质,等的判定方法,是解题的关键.例4.(坐标系中的K 字模型)A B y 轴上.(1)如图①,若点C 的横坐标为5,求点B 的坐标;(2)如图②,若x 轴恰好平分BAC ∠,BC 交x 轴于点M ,过点C 作CD x ⊥轴于点D ,求CD AM的值;(3)如图③,若点A 的坐标为()4,0-,点B 在y 轴的正半轴上运动时,分别以OB 、AB 为边在第一、第二象限中作等腰Rt OBF ,等腰Rt ABE ,连接EF 交y 轴于点P ,当点B 在y 轴上移动时,PB 的长度是否发生改变?若不变求PB 的值;若变化,求PB 的取值范围.例.()已知等腰ABE 和,连接,若直线BD CE 、交于点O ,则BOC ∠=;(2)如图所示,90,,BAE DAC AB AE AD AC ∠=∠=︒==,连接BC 和DE ,过点A 作AF D E ⊥交BC 于点G ,垂足为F ,若11,10AG GF ==,求ABC 的面积.如图:∵100,,BAE DAC AB AE AD ∠=∠=︒==∴BAD EAC ∠=∠,(2)作BM AF ⊥于M ,CN AF ⊥于N ,∵AF D E ⊥,∴90BMA AFE ∠=∠=︒,∵90,BAE AB AE ∠=︒=,∴90BAM FAE ∠+∠=︒,E FAE ∠+∠=∴BAF E ∠=∠,∴BAM AEF ≌,【点睛】本题考查了全等三角形的判定与性质,解题关键是恰当作辅助线,构建全等三角形,利用全等三角形的性质解决问题.【课后练习】1.通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图1,90BAD ∠=︒,AB AD =,过点B 作BC AC ⊥于点C ,过点D 作DE AC ⊥于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90ACB AED ∠=∠=︒,可以推理得到ABC DAE △≌△.进而得到AC =___________,BC =___________.我们把这个数学模型称为“K 字”模型或“一线三等角”模型;【模型应用】(2)①如图2,90BAD CAE ∠=∠=︒,AB AD =,AC AE =,连接BC ,DE ,且BC AF ⊥于点F ,DE 与直线AF 交于点G .求证:点G 是DE 的中点;②如图3,在平面直角坐标系xOy 中,点A 的坐标为()2,6,点B 为平面内任一点.若AOB 是以OA 为斜边的等腰直角三角形,请直接写出点B 的坐标.【答案】(1)DE ;AE(2)①证明见解析;②()4,2或()2,4-【分析】(1)根据全等三角形的对应边相等解答;(2)①作DM AF ⊥于M ,EN AF ⊥于N ,证明ABF DAM △≌△,ACF EAN △≌△,根据全等三角形的性质得到EN DM =,再证明DMG ENG △≌△,根据全等三角形的性质证明结论;②过点B 作DC x ⊥轴于点C ,过点A 作DE y ⊥轴于点E ,两直线交于点D ,过点B '作B H x '⊥轴于点H ,B H '交DE 于点G ,利用(1)的结论即可解答.【详解】(1)解:∵12290D ∠+∠=∠+∠=︒,∴1D ∠=∠,在ABC 和DAE 中,1D ACB DEA AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABC DAE △≌△,∴AC DE =,BC AE =.故答案为:DE ;AE .(2)①证明:如图2,作DM AF ⊥于M ,EN AF ⊥于N ,∵BC AF ⊥,90BAD ∠=︒,∴90BFA AMD ∠=∠=︒,12190B ∠+∠=∠+∠=︒∴2B ∠=∠,在ABF △和DAM △中,2BFA AMD B AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABF DAM △≌△,∴AF DM =,∵BC AF ⊥,90CAE ∠=︒,∴90CFA ANE ∠=∠=︒,90FAC NAE FAC C ∠+∠=∠+∠=︒∴C NAE =∠∠,在ACF △和EAN 中,CFA ANE C NAE AC EA ∠=∠⎧⎪∠=∠⎨⎪=⎩,一副三角板(在ABC 中,90ABC ∠=︒,AB BC =;DEF 中,90DEF ∠=︒,30EDF ∠=︒),并提出了相应的问题(1)【发现】如图1,将两个三角板互不重叠地摆放在一起,当顶点B 摆放在线段DF 上时,过点A 作AM DF ⊥,垂足为点M ,过点C 作CN DF ⊥,垂足为点N ,易证ABM BCN ≌△△,若2AM =,7CN =,则MN =______;(2)【类比】如图2,将两个三角板叠放在一起,当顶点B 在线段DE 上且顶点A 在线段EF 上时,过点C 作CP DE ⊥,垂足为点P ,猜想AE ,PE ,CP 的数量关系,并说明理由;(3)【拓展】如图3,将两个三角板叠放在一起,当顶点A 在线段DE 上且顶点B 在线段EF 上时,若5AE =,1BE =,连接CE ,则ACE △的面积为______.【答案】(1)9(2)=-PE CP AE ;理由见解析(3)10【分析】本题综合考查了全等三角形的判定与性质,熟记相关定理内容进行几何推理是解题关键.(1)由ABM BCN ≌△△,利用两个三角形全等的性质,得到2AM BN ==,7BM CN ==,即可得到MN ;(2)根据两个三角形全等的判定定理,得到ABE BCP ≌△△,利用两个三角形全等的性质,得到AE BP =,BE CP =,由BE BP PE =+中,即可得到三者的数量关系;(3)延长FE ,过点C 作CP FE ⊥于P ,由两个三角形全等的判定定理得到ABE BCP ≌△△,从而1PC BE ==,5PB AE ==,则可求得PE ,延长AE ,过点C 作CF AE ⊥于F ,由平行线间的平行线段相等可得4CF PE ==,代入面积公式得ACE S ,即可得到答案.【详解】(1)解:ABM BCN ≌,2AM =,7CN =,2AM BN ∴==,7BM CN ==,9MN BM BN ∴=+=;故答案为:9.(2)解:=-PE CP AE理由:90ABC ∠=︒ ,90ABE CBE ∴∠+∠=︒,CP BE ⊥ ,90CPB ∴∠=︒,90BCP CBP ∴∠+∠=︒ABE BCP ∴∠=∠,90AEB ∠=︒ ,90AEB CPB ∴∠=∠=︒,AB BC = ,ABE BCP ∴V V ≌,AE BP ∴=,BE CP=BE BP PE =+ ,PE BE BP PC AE ∴=-=-;90ABE EBC ∠+∠=︒ ,ABE ∠EBC BAE ∴∠=∠,90AEB CPB ∠=∠=︒Q ,AB ABE BCP ∴V V ≌,1PC BE ∴==,5PB AE ==514PE PB BE ∴=-=-=,延长AE ,过点C 作CF AE ⊥AF PE ⊥Q ,CP PE ⊥,AF CP ∴∥,AF PE ⊥Q ,CF AF ⊥,PE CF ∴∥,由平行线间的平行线段相等可得115422ACE S AE CF =⨯⨯=⨯⨯V 故答案为:10.3.通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图,90ACE ∠=︒,AC CE =,过点A 作AB BC ⊥于点B ,过点E 作ED BC ⊥交BC 的延长线于点D .由90ACB DCE DCE E ∠+∠=∠+∠=︒,得CAB E ∠=∠.又90ABC CDE ∠=∠=︒,AC CE =,可以推理得到ABC CDE △△≌,进而得到AB =______,BC =______.(请完成填空)我们把这个数学模型称为“K 字”模型或“一线三等角”模型.【模型应用】(2)①如图,90ACE BCD ∠=∠=︒,AC CE =,BC CD =,连接AB 、DE ,且DE CG ⊥于点G ,AB 与直线CG 交于点F ,求证:点F 是AB 的中点;②如图,若点M 为x 轴上一动点,点N 为y 轴上一动点,点P 的坐标为()51,,是否存在以M 、N 、P 为顶点且以PM 为斜边的三角形为等腰直角三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.【答案】(1)CD ,DE ;(2)见解析;(3)存在,()4,0-或()6,0-【分析】本题是三角形综合题目,考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、坐标与图形性质、直角三角形的性质等知识;(1)由全等三角形的性质可得出答案;(2)过点A 作AM FG ⊥交FG 于点M ,过点B 作BN FG ⊥交FG 于点N ,证明(AAS)ACM CEG ≌,得出AM CG =;同理可得:BCN CDG ≌.得出BN CG =,证明ED CG ⊥ ,90ACE ∠=︒,ACF ECG ECG ∴∠+∠=∠+∠ACF E ∴∠=∠,在ACM △和CEG 中,ACM E AMC CGE AC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)ACM CEG ∴ ≌514DP ∴=-=,4EN ∴=,(4,0)M ∴-;当点N 在x 轴负半轴上时,同理可得(6,0)M -.综上所述,点M 的坐标为(4,0)-或(6,0)-.4.综合与实践:在ABC 中,90ACB ∠=︒,AC BC =,点C 在直线l 上,点A 、B 在直线l 的同侧,过点A 作AD l ⊥于点D .(1)问题情境:如图1,在直线l 上取点E ,使BE l ⊥.则BE 与CD 的数量关系是_________________,此时AD BE DE 、、之间的数量关系是_________________.(2)探究证明:如图2,在直线l 上取点F ,使BF BC =,猜想CF 与AD 的数量关系,并说明理由.(3)拓展延伸:在直线l 上任取一点P ,连接BP ,以点P 为直角顶点作等腰直角三角形BPM ,作MN l ⊥于点N ,请直接写出在图3、图4中MN AD CP 、、之间的数量关系.【答案】(1),BE CD AD BE DE =+=;(2)2CF AD =,理由见解析(3),MN AD CP MN AD CP+=-=【分析】本题考查了全等三角形的判定与性质,熟练掌握“一线三垂直”模型是解答本题的关键.(1)根据AAS 证明ACD CBE ≌,得BE CD =,CE AD =,进而可证AD BE DE +=;(2)过点B 作BH l ⊥于点H ,根据AAS 证明DAC HCB ≌,得AD CH =,由三线合一得2CF CH =,进而可得;2CF AD=(3)如图3,作BH l ⊥于点H ,作PF l ⊥,作BF PF ⊥于点F ,作ME PF ⊥于点E ,可证四边形MEPN 和四边形PFBH 都是矩形,从而BF BH =,MN PE =.结合ACD CBH △≌△,可证MN AD CP +=;如图4,作BH l ⊥于点H ,由ACD CBH △≌△,MNP PHB ≌,得MN PH =,AD CH =,进而可证MN AD CP -=.【详解】(1)解:∵AD l ⊥,BE l ⊥,∴90ADC CEB ∠=∠=︒.∵90ACB ∠=︒,∴90ACD BCE ∠+∠=︒,∵90CAD ACD ∠+∠=︒,∴CAD BCE ∠=∠.∵AC BC =,∴()AAS ACD CBE ≌,∴BE CD =,CE AD =,∵CE CD DE +=,∴AD BE DE +=.故答案为:BE CD =,AD BE DE +=;(2)2CF AD=理由如下:过点B 作BH l ⊥于点H ,如图,则90BHC ∠=︒,∴四边形MEPN 和四边形PFBH 都是长方形,∴BF BH =,MN PE =.由(1)知,ACD CBH △≌△, ∴AD CH PE BF ==,,∴PH MN =,∵CH PH CP +=,∴MN AD CP +=;由(1)知,ACD CBH △≌△,MNP PHB ≌,∴MN PH AD CH ==,,∵PH CH CP -=,∴MN AD CP -=.5.如图1所示,已知AB 为直线a 上两点,点C 为直线a 上方一动点,连接AC 、BC ,分别以AC 、BC 为边向△ABC 外作△ACD 和△BCE ,且90DAC CBE ∠=∠=︒,AD AC =,BC BE =,过点D 作1DD a ⊥于点1D ,过点E 作1EE a ⊥于点1E .(1)【问题探究】小华同学想探究图1中线段1DD 、1EE 、AB 之间的数量关系.他的方法是:作直线CH AB ⊥于点H ,可以先证明1ADD CAH ≌△△和1BEE ≌△________,于是可得:________和________,所以得到线段1DD 、1EE 、AB 之间的数量关系是________;(2)【方法应用】在图2中,当D 、E 两点分别在直线a 的上方和下方时,试探究三条线段1DD 、1EE 、AB 之间的数量关系,并说明理由;(3)【拓展延伸】在图2中,当D 、E 两点分别在直线a 的上方和下方时,小华同学测得线段11D E m =,AB n =,请用含有m 、n 的代数式表示△ABC 的面积为________.三角形面积公式求出答案.【详解】解:(1)∵1DD a ⊥,CH AB ⊥,∴∠1DD A =∠CHA=90DAC ∠=︒,∴∠1D DA+∠1D AD=90°,∠1D AD+∠CAH=90°,∴∠1D DA=∠CAH ,∵AD=AC ,∴△1D DA ≌△HAC ,同理1BEE ≌△△CBH ,∴D 1D =AH ,1EE =BH ,∴11AB DD EE =+故答案为:△CBH ,1DD AH =,1EE BH =,11AB DD EE =+;(2)11AB DD EE =-.理由:如图,过点C 作CG a ⊥于点G ,∵1DD a ⊥,CG a ⊥,1EE a ⊥,∴1DD A AGC ∠=∠,1CGB BE E ∠=∠,∴1190DAD ADD ︒∠+∠=,90∠+∠=︒CBG BCG ,∵90DAC CBE ∠=∠=︒,∴190DAD CAG ︒∠+∠=,190CBG E BE ︒∠+∠=,∴1ADD CAG ∠=∠,1BCG EBE ∠=∠,在1ADD 和CAG 中,11,,,ADD CAG DD A AGC AD CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴1ADD ≌CAG ,∴1DD AG =,同理可得:1BCG EBE ≅△△,∴1BG EE =,由图可得:AB AG BG =-,∴11AB DD EE =-;侧作AE AD ⊥,且AE AD =.(1)如图1,当点D 在线段BC 上时,过点E 作EF AC ⊥于F ,求证:ACD EFA △≌△;(2)如图2,当点D 在线段BC 的延长线上时,连接BE 交直线AC 于点M .试探究BM 与EM 的数量关系,并说明理由.(3)当点D 在射线CB 上时,连接BE 交直线AC 于点M ,若4AC CM =,求ADB AEMS S △△的值.=90DAE ∠︒,F ACD MCB ∴∠=∠=∠,90FAE CDA ∠=∠=在FAE 和CDA 中,F ACD FAE CDA AE DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS FAE CDA ∴ ≌,EF AC BC ∴==,MCB F ∠=∠⎧90FAE D DAC ∴∠=∠=︒-∠,在AFE △和DCA △中,F ACD FAE D AE DA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS AFE DCA ∴ ≌,AF DC ∴=,EF AC BC ==,AF AC DC BC ∴-=-,CF DB ∴=,18090BCM ACB ∠=︒-∠=︒ ,4AC n ∴=,3AM n ∴=,11222ADB S DB AC n AC n AC ∴=⋅=⨯⋅=⋅ ,12AEM S AM EF =⋅ ∴2332ADB AEM S n AC S n AC ⋅==⋅ ,综上所述,ADB AEM S S △△的值为25或23.。
2023年中考数学微专题复习课件4 一线三等角模型

;
【类比探究】如图2,在(1)的条件下,若90°<α<180°,则线段DE、BD、CE之间的
数量关系是
DE=BD+CE
;
【拓展探究】如图3,若点A是DE的中点,∠BAC=∠BDA=∠AEC=α,请问线段AD、
BD、CE之间满足什么数量关系?并说明理由.
7
思路点拨
= ∠,
ቃ
(1)∠ = ∠ = ∠➝∠ = ∠
൨→△BDA≌△AEC➝ =
∠ = ∠, =
→DE=BD+CE
(2)同(1)易得DE=BD+CE
(3)∠ = ∠ = ∠➝∠ = ∠
൨
∠ = ∠,
BD·CE
8
→△ ≌△
➝
=
→AD2=
点是的中点➝ =
注:三个相等的角可以是锐角、直角或钝角.
2
3.构造一线三等角的基本步骤
做题过程中,若出现一角的顶点在一条直线上的形式,就可以构造两侧的两个相等
的角,利用全等三角形或相似三角形解决相关问题,本质就是找角、定线、构相似.
3
类型
条件
图示
结论
点P在线段AB上,∠1
一线三
等角
(不包
含直
角)
同侧型(三
=∠2=∠3,三个角在
又∵∠PAD+∠PDA=90°,
∠PAD+∠QAM=90°,
∴∠PDA=∠QAM.
26
∠ = ∠,
ቐ∠ = ∠,
在△APD和△MQA中, = ,
∴△APD≌△MQA(AAS).
∴AQ=PD=2,
∴可设M(5,n),将M(5,n)代入y=,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)设BP=x,CM=y.求y与x的函数解析式,并写出函数的定义域.
(3)当△APM为等腰三角形时,求PB的长.
3.如图,在△ABC中,AB=AC=5,BC=6,P是BC上一点,且BP=2,将一个大小与∠B相等的角的顶点放在P点,然后将这个角绕P点转动,使角的两边始终分别与AB、AC相交,交点为D、E。
5.已知:如图,在△ABC中, , ,点D在边AB上, ,点E在边BC上.又点F在边AC上,且 .
(1)求证:△FCE∽△EBD;
(2)当点D在线段AB上运动时,是否有可能使 .如果有可能,求出BD的长.如果不可能请说明理由.
6.等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.
(1)求证△BPD∽△CEP
(2)是否存在这样的位置,△PDE为直角三角形?
若存在,求出BD的长;若不存在,说明理由。
4、已知在等腰三角形 中, , 是 的中点, 是 上的动点(不与 、 重合),连结 ,过点 作射线 ,使 ,射线 交射线 于点 ,交射线 于点 .
(1)求证: ∽ ;
(2)设 .①用含 的代数式表示 ; ②求 关于 的函数解析式,并写出 的定义域.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE~△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
1探究1:△BPE与△CFP还相似吗?
2探究2:连结EF,△BPE与△PFE是否相似?请说明理由;
3设EF=m,△EPF的面积为S,试用m的代数式表示S.
1.如图,已知在△ABC中,AB=AC=6,BC=5,D是AB上一点,BD=2,E是BC上一动点,联结DE,并作 ,
射线EF交线段AC于F.
(1)求证:△DBE∽△ECF;
(2)当F是线段AC中点时,求线段BE的长;
(3)联结DF,如果△DEFFra bibliotek△DBE相似,求FC的长.
2如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
