一线三等角模型
几何模型:一线三等角模型

一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.一线三等角的分类全等篇同侧锐角直角钝角P异侧相似篇A同侧锐角直角钝角P异侧三、“一线三等角”的性质1.一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如图 3-1,若 CE=ED,则△AEC≌△BDE.3.中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(了解) 如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的心.可以考虑构造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的心或旁心相关,1902BOC BAC ∠=︒+∠这是心的性质,反之未必是心.在图 3-4(右图)中,如果延长 BE 与 CF ,交于点 P ,则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明 )图 3-5其实这个第 4 图,延长 DC 反而好理解.相当于两侧型的,不延长理解,以为是一种新型的,同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c.图形中只有直线上一个角,不上“二等角”构造模型解题.体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特殊性如图 3-6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过 C、D 两点作直线 l 的垂线是必不可少的。
中考数学相似三角形重要模型一线三等角模型
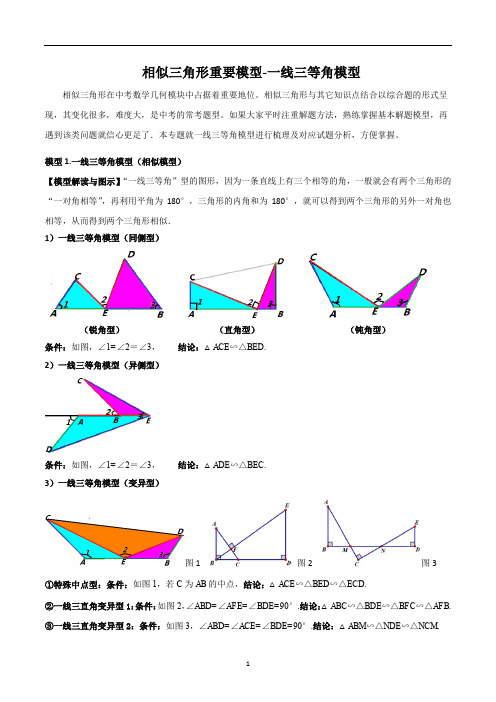
相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1 图2 图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·山东东营·统考中考真题)如图,A B C为等边三角形,点D,E分别在边B C,A B上,60A D E∠=︒,若4B D D C=, 2.4D E=,则A D的长为()A.1.8B.2.4C.3D.3.2例2.(2023·湖南·统考中考真题)如图,,C A ADE D A D⊥⊥,点B是线段A D上的一点,且C B B E⊥.已知8,6,4A B A C D E===.(1)证明:A B C D E B∽△△.(2)求线段B D的长.例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在ABC中,∠BAC=90°,A BA C=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:B DA E=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在ABC中,A BA C=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在ABC中,沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG,A BA E =A CA G=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.例4.(2022·四川·一模)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:(1)如图1,已知:在△ABC 中,A B A C=,D 、A 、E 三点都在直线m 上,并且有B D AA E CB AC α∠=∠=∠=.试猜想DE 、BD 、CE 有怎样的数量关系,请证明你的结论;(2)老师鼓励学习小组继续探索相似的情形.于是,学习小组又研究以下问题:如图2,△ABC 中,(060)B C αα∠=∠=<<︒.将一把三角尺中30°角顶点P 放在BC 边上,当P 在BC 边上移动时,三角尺中30°角的一条边始终过点A ,另一条边交AC 边于点Q ,P 、Q 不与三角形顶点重合.设C P Qβ∠=.当β在许可范围内变化时,α取何值总有△ABP ∽△PCQ ?当α在许可范围内变化时,β取何值总有△ABP ∽△QCP ?(3)试探索有无可能使△ABP 、△QPC 、△ABC 两两相似?若可能,写出所有α、β的值(不写过程);若不可能,请说明理由.例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在A B C中,90A C B ∠=︒,A C B C=,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:A D C C E B△≌△.(1)探究问题:如果A CB C≠,其他条件不变,如图②,可得到结论;A D CC E B△∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x=与直线C D 交于点()2,1M ,且两直线夹角为α,且3ta n 2α=,请你求出直线C D 的解析式.(3)拓展应用:如图④,在矩形A B C D 中,3A B=,5B C=,点E为B C 边上—个动点,连接A E ,将线段A E 绕点E 顺时针旋转90︒,点A 落在点P 处,当点P 在矩形A B C D外部时,连接P C ,P D .若D P C △为直角三角形时,请你探究并直接写出B E 的长.Rt ABD中,上一动点,连接折叠得H E F,延长②B E M H E M≅;③当M2B,则正确的有(九年级校考阶段练习)已知A B C是等边三角形,E F和B D F∠,将B C E沿B则A F=P C D△;九年级校考阶段练习)如图,在A B C中,12.(2022·山东济宁·二模)情境观察:将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别为P,Q,(1)如图1.观察图1可知:与NQ相等的线段是______________,与N R Q∠相等的角是_____(2)问题探究直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作正方形ACEF 和正方形CDGH,如图2,过E,H分别作BC所在直线的垂线,垂足分别为K,L.试探究EK与HL之间的数量关系,并证明你的结论.(3)拓展延伸:直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作矩形ACEF和矩形CDGH,连接EH交BC所在的直线于点T,如图3.如果A C kC E=,试探究TE与TH=,C D kC H之间的数量关系,并证明你的结论.将.A B P沿着这样的点P,使得点问题解决(3)15.(2023春·四川广安·九年级校考阶段练习)如图1和图2,在平面直角坐标系中,点C的坐标为(0,4),A是x轴上的一个动点,M是线段AC的中点.把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB.过B作x轴的垂线、过点C作y轴的垂线,两直线交于点D,直线DB交x轴于点E.设A点的横坐标为m.(1)求证:△AOC∽△BEA;(2)若m=3,则点B的坐标为;若m=﹣3,则点B的坐标为;(3)若m>0,△BCD的面积为S,则m为何值时,S=6?(4)是否存在m,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时m的值;若不存在,请说明理由.16.(2020·四川雅安·中考真题)如图,已知边长为10的正方形A B C D E、不重,是B C边上一动点(与B C 合),连结A E G,是B C延长线上的点,过点E作A E的垂线交D C G∠的角平分线于点F,若F G B G⊥.(1)求证:A B E E G FE C=,求C E F△△;(2)若2∽△的△的面积;(3)请直接写出E C为何值时,C E F面积最大.的何位置时有B E H B A E∽?B C。
2024年中考数学几何模型归纳(全国通用):全等与相似模型-一线三等角(K字)模型(学生版)

专题14全等与相似模型-一线三等角(K 字)模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K 型图)模型【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角:锐角一线三等角直角一线三等角(“K 型图”)钝角一线三等角条件:A CED B +CE=DE证明思路:,A B C BED +任一边相等BED ACE异侧型一线三等角:锐角一线三等角直角一线三等角钝角一线三等角条件:FAC ABD CED +任意一边相等证明思路:,A B C BED +任一边相等BED ACE例1.(2021·山东日照·中考真题)如图,在矩形ABCD 中,8cm AB ,12cm AD ,点P 从点B 出发,以2cm/s 的速度沿BC 边向点C 运动,到达点C 停止,同时,点Q 从点C 出发,以cm/s v 的速度沿CD 边向点D 运动,到达点D 停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v 为_____时,ABP △与PCQ △全等.例2.(2022·黑龙江·九年级期末)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明∶DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.例3.(2022·广东·汕头市潮阳区一模)(1)模型建立,如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;,OB=4,将线段AB绕(2)模型应用:①已知直线AB与y轴交于A点,与x轴交于B点,sin∠ABO=35点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x 5上的一点,若△APD是以D为直角顶点的等腰直角三角形,请求出所有符合条件的点D的坐标.例4.(2023·湖南岳阳·统考一模)如图,在ABC 中,AB =AC =2,∠B =40°,点D 在线段BC 上运动(点D 不与点B 、C 重合),连接AD ,作∠ADE =40°,DE 交线段AC 于点E .(1)当∠BDA =115°时,∠EDC =______°,∠AED =______°;(2)线段DC 的长度为何值时,△ABD ≌△DCE ,请说明理由;(3)在点D 的运动过程中,△ADE 的形状可以是等腰三角形吗?若可以,求∠BDA 的度数;若不可以,请说明理由.例5.(2022·浙江杭州·一模)老师在上课时,在黑板上写了一道题:“如图,ABCD 是正方形,点E 在BC 上,DF ⊥AE 于F ,请问图中是否存在一组全等三角形?”小杰同学经过思考发现:△ADF ≌△EAB .理由如下:因为ABCD 是正方形(已知)所以∠B =90°且AD =AB 和AD ∥BC又因为DF ⊥AE (已知)即∠DFA =90°(垂直的意义)所以∠DFA =∠B (等量代换)又AD ∥BC 所以∠1=∠2(两直线平行,内错角相等)在△ADF 和△EAB 中12DFA B AD AB所以△ADF ≌△EAB (AAS )小胖却说这题是错误的,这两个三角形根本不全等.你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF 全等的三角形,请能说出此线段的做法吗?并说明理由.例6.(2022·山东·九年级课时练习)(1)课本习题回放:“如图①,90ACB ,AC BC ,AD CE ,BE CE ,垂足分别为D ,E , 2.5cm AD , 1.7cm DE .求BE 的长”,请直接写出此题答案:BE 的长为________.(2)探索证明:如图②,点B ,C 在MAN 的边AM 、AN 上,AB AC ,点E ,F 在MAN 内部的射线AD 上,且BED CFD BAC .求证:ABE CAF ≌.(3)拓展应用:如图③,在ABC 中,AB AC ,AB BC .点D 在边BC 上,2CD BD ,点E 、F 在线段AD 上,BED CFD BAC .若ABC 的面积为15,则ACF 与BDE 的面积之和为________.(直接填写结果,不需要写解答过程)例7.(2023·贵州遵义·八年级统考期末)过正方形ABCD (四边都相等,四个角都是直角)的顶点A 作一条直线MN .(1)当MN 不与正方形任何一边相交时,过点B 作BE MN 于点E ,过点D 作DF MN 于点F 如图(1),请写出EF ,BE ,DF 之间的数量关系,并证明你的结论.(2)若改变直线MN 的位置,使MN 与CD 边相交如图(2),其它条件不变,EF ,BE ,DF 的关系会发生变化,请直接写出EF ,BE ,DF 的数量关系,不必证明;(3)若继续改变直线MN 的位置,使MN 与BC 边相交如图(3),其它条件不变,EF ,BE ,DF 的关系又会发生变化,请直接写出EF ,BE ,DF 的数量关系,不必证明.模型2.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·山东东营·统考中考真题)如图,ABC,为等边三角形,点D,E分别在边BC,AB上,60ADE若4DE ,则AD的长为()BD DC, 2.4A.3B.5C.2例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在 ABC中,∠BAC=90°,ABAC=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:BDAE=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在 ABC中,ABAC=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在 ABC中,沿 ABC的边AB、AC向外作矩形ABDE和矩形ACFG,ABAE=ACAG=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.问题探究:(1)先将问题特殊化,如图(2),当90 时,直接写出GCF 的大小;(2)再探究一般情形,如图(1),求GCF 与 的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120 时,若12DG CG ,求BE CE 的值.例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在ABC中,90ACB,AC BC,分别过A、B向经过点C直线作垂线,垂足分别为D、E,我们很容易发现结论:ADC CEB△≌△.(1)探究问题:如果AC BC,其他条件不变,如图②,可得到结论;ADC CEB△∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x与直线CD交于点 2,1M,且两直线夹角为 ,且3tan2,请你求出直线CD的解析式.(3)拓展应用:如图④,在矩形ABCD中,3AB ,5BC ,点E为BC边上—个动点,连接AE,将线段AE绕点E顺时针旋转90 ,点A落在点P处,当点P在矩形ABCD 外部时,连接PC,PD.若DPC△为直角三角形时,请你探究并直接写出BE的长.【观察与猜想】(1)如图1,在正方形ABCD中,E,F分别是AB,AD则DECF的值为___________;(2)如图2,在矩形ABCD中,7AD ,BD,若CE BD,则CEBD的值为___________;【类比探究】(3)如图3,在四边形ABCD中,90A B,E为线交ED的延长线于G,交AD的延长线于F,求证:DE AB CF课后专项训练1.(2022·湖南·长沙市二模)如图,等腰直角三角形ABC 的直角顶点C 与坐标原点重合,分别过点A 、B 作x 轴的垂线,垂足为D 、E ,点A 的坐标为(-2,5),则线段DE 的长为()A .4B .6C .6.5D .72.(2022·贵州·凯里一模)如图,在平面直角坐标系中 0,4A 、 6,0C ,BC x 轴,存在第一象限的一点 ,25P a a 使得PAB △是以AB 为斜边的等腰直角三角形,则点P 的坐标().A . 3,1或 3,3B . 5,5C . 3,1或 5,5D .3,3A . 9,3B . 9,24.(2023·湖南长沙·九年级专题练习)如图,在矩形CD 或延长线上运动,且∠BEF5.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=_____.7.(2022·安徽·九年级专题练习)如图,矩形取BE的中点G,点G绕点E运动路径=,△CEF10.(2023·浙江·九年级期末)如图,已知ABC 和CDE 均是直角三角形,Rt ACB CED ,AC CE ,AB CD 于点F .(1)求证:ABC ≌CDE ;(2)若点B 是EC 的中点,10cm DE ,求AE 的长.11.(2022·江苏·九年级专题练习)【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:①如图1,ABC 是等腰直角三角形,90C ,AE =BD ,则AED ≌_______;②如图2,ABC 为正三角形,,60BD CF EDF ,则BDE ≌________;③如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l 于E ,CF l 于F .若1AE ,2CF ,则EF 的长为________.【模型应用】(2)如图4,将正方形OABC 放在平面直角坐标系中,点O 为原点,点A 的坐标为 ,则点C 的坐标为________.【模型变式】(3)如图5所示,在ABC 中,90ACB ,AC BC ,BE CE 于E ,AD ⊥CE 于D ,4cm DE ,6cm AD ,求BE 的长.12.(2022·江苏镇江·二模)模型构建:如图1,AM MN 于点M ,BN MN 于点N ,AB 的垂直平分线交MN 于点P ,连接AP 、BP .若90APB ,求证:AM BN MN .数学应用:如图2,在ABC 中,D 是BC 上一点,AC AD BD ,90CAD ,8AB ,求ABC 的面积.实际运用:建设“交通强国”是满足人民日益增长的美好生活需要的必然要求.建设“美丽公路”是落实美丽中国建设、回应人民日益增长的美好生活对优美生态环境的需要.如图3是某地一省道与国道相交处的示意图,点Q 处是一座古亭,鹅卵石路QA 、QB 以及 AB 两旁栽有常青树,其它区域种植不同的花卉;设计要求QA QB ,QA QB , AB 是以Q 为圆心、QA 为半径的圆弧(不计路宽,下同).请在图4中画出符合条件的设计图,要求尺规作图,保留作图痕迹,标注必要的字母,写出详细的作法,不要求说明理由;13.(2022·黑龙江·桦南县九年级期中)如图1,在ABC 中,90ACB ,AC BC ,直线MN 经过点C ,且AD MN 于D ,BE MN 于E .(1)由图1,证明:DE AD BE ;(2)当直线MN 绕点C 旋转到图2的位置时,请猜想出DE ,AD ,BE 的等量关系并说明理由;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).14.(2022·黑龙江佳木斯·三模)在ABC 中,90ABC ,AB BC ,D 为直线AB 上一点,连接CD ,过点B 作BE CD 交CD 于点E ,交AC 于点F ,在直线AB 上截取AM BD ,连接FM .(1)当点D ,M 都在线段AB 上时,如图①,求证:BF MF CD ;(2)当点D 在线段AB 的延长线上,点M 在线段BA 的延长线上时,如图②;当点D 在线段BA 的延长线上,点M 在线段AB 的延长线上时,如图③,直接写出线段BF ,MF ,CD 之间的数量关系,不需要证明.15.(2022·安徽·合肥二模)(1)如图1,等腰直角ABC 中,90ACB ,CB CA ,线段ED 经过点C ,过A 作AD ED 于点D ,过B 作BE ED 于.E 求证:BEC △≌CDA .(2)如图2,已知在平面直角坐标系xOy 中,O 为坐标原点,点A 的坐标为 0,4,点C 的坐标为 3,0 ,点B 是平面直角坐标系中的一点,若ABC 是以AC 为直角边的等腰直角三角形,求点B 的坐标;(3)如图3,已知在平面直角坐标系xOy 中,O 为坐标原点,在等腰直角OAB 中,90OAB ,4OA AB ,点M 在线段OB 上从O 向B 运动(运动到点B 停止),以点M 为直角顶点向右上方做等腰直角AMN ,求点N 移动的距离.(3)【拓展探究】在整个运动过程中,请直接写出N 点运动的路径长,及CN 的最小值.(1)若正方形ABCD 的边长为2,E 是AD 的中点.①如图1,当FEC ②如图2,当2tan 3FCE 时,求AF 的长;(2)如图3,延长CF ,DA 交于点时,求证:AE AF .18.(2023·广东深圳·九年级校考阶段练习)如图,在ABC 中6cm AB AC ,8cm BC ,点E 是线段BC 边上的一动点(不含B 、C 两端点),连接AE ,作AED B ,交线段AB 于点D .(1)求证:BDE CEA △∽△(2)设BE x ,AD y ,请求y 与x 之间的函数关系式.(3)E 点在运动的过程中,ADE V 能否构成等腰三角形?若能,求出BE 的长;若不能,请说明理由.19.(2023·浙江·九年级专题练习)在平面直角坐标系中,O 为坐标原点,直线AB 与y 轴交于点A ,与x 轴交于点B ,2OA ,AOB 的面积为2.(1)如图1,求直线AB 的解析式.(2)如图2,线段OA 上有一点C ,直线BC 为2(0)y kx k k ,AD y 轴,将BC 绕点B 顺时针旋转90 ,交AD 于点D ,求点D 的坐标.(用含k 的式子表示)(3)如图3,在(2)的条件下,连接OD ,交直线BC 于点E ,若345ABC BDO ,求点E 的坐标.20.(2022·湖南郴州·中考真题)如图1,在矩形ABCD 中,4AB ,6BC .点E 是线段AD 上的动点(点E 不与点A ,D 重合),连接CE ,过点E 作EF CE ,交AB 于点F .(1)求证:AEF DCE ∽;(2)如图2,连接CF ,过点B 作BG CF ⊥,垂足为G ,连接AG .点M 是线段BC 的中点,连接GM .①求AG GM 的最小值;②当AG GM 取最小值时,求线段DE 的长.。
一线三等角模型特征及结论

一线三等角模型特征及结论好嘞,咱们来聊聊“一线三等角模型”,这个听起来高大上的名词其实也没那么复杂。
就像一碗热腾腾的面条,虽然看起来简单,但其中却藏着不少讲究。
咱们先说说这“一线三等角”是个啥。
简单来说,就是在某些情况下,我们可以把事情简化成一条线和三个角。
这听起来是不是有点像数学课上学的那些东西?但实际上,它在很多领域里都能派上用场,比如说设计、分析,甚至日常生活中也能找到它的身影。
想象一下,你和朋友们一起去泡温泉,那个水雾缭绕的地方,大家围坐在一起,谈笑风生。
这时候,气氛就像那一条线,大家都聚在这条线上,享受着温暖。
而那些欢声笑语,正是那三个角,分别代表着不同的情感、不同的观点。
你看,一个简单的场景,运用这个模型,就能让我们更好地理解和分析这个过程。
这就是“一线三等角”的魅力所在,能把复杂的事情,变得简单又生动。
再说说这个模型的特征。
这条线就代表着一个核心主题或者主线,围绕着这个主题,大家可以展开不同的讨论。
就像我们在聊天的时候,始终围绕着一个话题,有时候跑偏了,但大家又会很自然地拉回来。
这种核心的连结,让人觉得踏实,也让讨论有了方向。
这三个角嘛,分别代表着不同的视角。
比如说,一个角可能是乐观的,一个是现实的,还有一个可能是有点悲观的。
每个角都有它的价值,咱们不能只看一个角度,这样就会错过很多精彩的细节。
可能有人会想,这种模型有什么用呢?嘿嘿,别急,接下来咱们就来看看它的实际应用。
想想看,在工作中,我们常常需要开会讨论项目。
这个时候,一条主线就是项目的目标,而三个角可以代表不同团队的反馈和建议。
大家围绕着这个目标,分享各自的想法,碰撞出火花,真是热闹得很。
经过这样的讨论,最后能形成一个更完善的方案,让大家都心服口服,简直就像是团队合作的缩影。
在学习上,咱们也能用这个模型。
想象你在复习一门课程,主线就是你要掌握的知识点,而那些角度则可以是不同的例题、应用和理论。
换个角度看问题,会让你豁然开朗,原来原本的难题竟然也能迎刃而解。
几何模型:一线三等角模型 (最终版)

初中几何模型之“一线三等角模型”一.【一线三等角概念】“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二.【一线三等角的分类】2.1 全等篇_同侧A PA P锐角直角钝角2.2 全等篇_异侧PDPP锐角直角钝角2.3 相似篇_同侧DCA BPP锐角直角钝角2.4 相似篇_异侧PDPP锐角直角钝角三、【性质】1.相似,如图 3-1,由∠1=∠2=∠3,或者α=α2=α3易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等.如下图,若 CE=ED,则△AEC≌△BDE.异侧结果同样。
3.中点型“一线三等角”——相似中多了一位兄弟如图 3-2,当∠1=∠2=∠3,且 D 是 BC 中点时,△BDE∽△CFD∽△DFE. 4.“中点型一线三等角“的变式(了解)如图 3-3,当∠1=∠2 且1902BOC BAC ∠=︒+∠时,点 O 是△ABC 的内心.可以考虑构造“一线三等角”.5.“一线三等角”的各种变式(图 3-5,以等腰三角形为例进行说明)图 3-5四、【“一线三等角”的应用】1.应用的三种情况.a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,构造“一等角”模型解题;c.图形中只有直线上一个角,构造“二等角”模型解题.注意:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.适应场景:在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在 x 轴或 y 轴(也可以是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段.3.构造步骤:找角、定线、构相似【引例】例 1如图,l1、l2、l3是同一平面内的三条平行线,l1、l2之间的距离是21/5,l2、l3之间的距离是21/10,等边△ABC 的三个顶点分别在l1、l2、l3上,求△ABC 的边长.思路引导:【脑洞大开-三角构造】例 1 如图,四边形 ABCD 中,∠ABC=∠BAD=90°,∠ACD=45°,AB=3,AD=5.求 BC 的长.横向构造纵向构造斜向构造斜A相似构造:例 2 如图,△ABC 中,∠BAC=45°,AD⊥BC,BD=2,CD=3,求 AD 的长.纵向横向斜向一线三垂直的补形:角含半角补形练一练:1.如图,在△ABC 中,∠BAC=135°, AC= 2AB, AD⊥AC 交 BC 于点 D,若 AD = 2,求△ABC的面积思路提示:【中点型一线三等角】例1、如图,在Rt⊿ABC 中,AB = AC =2,∠A = 90°,现取一块等腰直角三角板,将45° 角的顶点放在BC 中点O 处,三角板的直角边与线段AB、AC 分别交于点E、F,设BE =x,CF = y,∠BOE = α( 45° ≤ α ≤ 90°) .( 1) 试求y 与x 的函数关系式,并写出x 的取值范围;( 2) 试判断∠BEO 与∠OEF 的大小关系?并说明理由;( 3) 在三角板绕O 点旋转的过程中,⊿OEF 能否成为等腰三角形? 若能,求出对应x 的值; 若不能,请说明理由.例2.如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90∘,△DEF的顶点E与△ABC的斜边BC的中点重合。
一线三等角模型

几何模型04——一线三等角一、一线三等角(45度)基本图形:例1.如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).设点P为线段OB的中点,连接PA,PC,若∠CPA =∠ABO,求m的值.解:作OD=OC=2,连接CD.则∠PDC=45°,如图,由y=﹣x+m可得A(m,0),B(0,m).所以OA=OB,则∠OBA=∠OAB=45°.当m<0时,∠APC>∠OBA=45°,所以,此时∠CP A>45°,故不合题意.所以m>0.因为∠CP A=∠ABO=45°,所以∠BP A+∠OPC=∠BAP+∠BP A=135°,即∠OPC=∠BAP,则∠PCD∠∠APB,所以=,即=,解得m=12.例2.如图,∠ABC中,AB=3,∠B=45°,以点A为直角顶点作等腰Rt∠ADE,点D在BC上,点E在AC上,若CE=2,求CD的长解:过点E作EF与CD交于点F,使∠EFD=45°,过点E作EG∠CD,∠∠B=∠ADE=45°,∠∠BAD=∠EDF,∠∠ABD∠∠DFE,∠,∠∠ADE是等腰直角三角形,∠DE=AD,∠AB=3,∠DF=3,∠∠EFD=45°,∠AED=45°,∠∠EFC=∠DEC=135°,∠∠EFC∠∠DEC,∠,∠EC=2,∠EC2=FC•CD=FC•(3+FC),∠(2)2=FC(3+FC),∠FC2+3FC﹣20=0,解得:FC=﹣5(舍)或2.∠CD=DF+FC=2+3=5练习1.已知:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB =45°,求OC提示:练习2.如图,一次函数y=x+4与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB上的点,且∠OPC=45°,PC=PO,求点P的坐标.二、一线三等角(60度)基本图形:例3.如图,正∠ABC中,P为BC上一点,D为AC上一点,∠APD=60°,BP=1,2D3C ,则∠ABC的边长为.解:设∠ABC的边长为x,∠∠ABC是等边三角形,∠∠DCP=∠PBA=60°.∠∠APC=∠APD+∠DPC=∠BAP+∠ABP,∠APD=60°,∠∠BAP=∠CPD.∠∠ABP∠∠CPD.∠,∠=.∠x=3.即∠ABC的边长为3.练习3.如图,∠ABC为等边三角形,D是BC边上一点,在AC边上取一点F,使CF=BD,在AB上取一点E,使BE=DC,则∠EDF=.三、一线三垂直基本图形:例4.(1)如图1,∠ABC为等腰直角三角形,AC=BC,AC∠BC,点A(0,3),C(1,0),求点B的坐标;(2)如图2,∠ABC为等腰直角三角形,AC=BC,AC∠BC,点A(﹣1,0),C(1,3),求点B的坐标;(3)如图3,∠ABC为等腰直角三角形,AC=AB,AC∠AB,点B(2,2),C (4,﹣2),求点A的坐标.解:(1)如图,作BD∠x轴于D点,∠BD∠x轴于D点,∠∠AOC=∠CDB=90°,∠∠ACB=90°,∠∠ACO+∠BCD=90°,∠∠ACO+∠OAC=90°,∠∠OAC=∠BCD,在∠AOC和∠CDB中,,∠∠AOC∠∠CDB(AAS),∠CD=AO,OC=BD,∠点C(1,0),A(0,3),∠OC=1,BD=1,CD=3,∠OD=4,∠点B的坐标为(4,1);(2)如图2,过点C作直线l∠x轴,作AE∠l于E,BF∠l于F,∠∠ACB是等腰直角三角形,∠AC=BC,∠AEC=∠ACB=∠BFC=90°,∠∠ACE+∠EAC=90°,∠ACE+∠BCF=90°,∠∠EAC=∠BCF,在∠AEC和∠CFB中,,∠∠AEC∠∠CFB(AAS),∠AE=CF=3,BF=EC=2,∠EF=5,∠点B的坐标为(4,1);(3)如图3,过点A作直线l∠y轴,过点B作BE∠l于点E,过点C作CF∠l 于点F∠BE∠l,CF∠l,∠∠BEA=∠CF A=90°=∠BAC,∠∠BAE+∠CAF=90°=∠BAE+∠ABE,∠∠ABE=∠CAF,在∠ABE和∠CAF中,,∠∠ABE∠∠CAF(AAS),∠BE=AF,CF=BE,设点A(m,n),∠点B(2,2),C(4,﹣2),∠2﹣n=4﹣m,n+2=2﹣m,∠m=1,n=﹣1,∠点A的坐标为(1,﹣1)练习4.如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若∠AOC=90°,点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为()A.4米B.4.5米C.5米D.5.5米例5.已知直线l1:y=﹣x+4与x、y轴分别交于点A、B,直线l2过点B,且与l1的夹角等于45°,如图2,求直线l2的函数表达式.解:由y=﹣x+4得,OB=4,OA=3,作∠BAC=90°,交l2于C,作CD∠OA于D,∠∠ABC=45°,∠可得∠BAC是等腰直角三角形,由上知:∠AOB∠∠CDA,∠AD=OB=4,CD=OA=3,∠OD=OA+AD=7,∠C(7,3),设l2的解析式是:y=kx+b,∠,∠,∠y=﹣x+4,练习5.如图,将边长为5的正方形OACD放在平面直角坐标系中,O是坐标原点,点D的横坐标为3,求A的坐标.练习6.如图,在∠ABC中,∠BAC=60°,∠ABC=90°,直线l1∠l2∠l3,l1与l2之间的距离为1,l2与l3之间的距离等于2,且l1、l2、l3分别经过点A、B、C,则边AC的长为.练习7.如图,正方形ABCD中,AB=12,AE=AB,点P在BC上运动(不与B、C重合),过点P作PQ∠EP,交CD于点Q,则CQ的最大值为()A.6 B.2C.3 D.4例6.如图,直角梯形ABCD中,AD∠BC,AB∠BC,AD=3,BC=5,将腰DC 绕点D逆时针方向旋转90°至DE,连接AE,求∠ADE的面积解:过点D作DG垂直于BC于G,过E作EF垂直于AD交AD的延长线于F,∠∠EDF+∠CDF=90°,∠CDF+∠CDG=90°,∠∠EDF=∠CDG,又∠∠EFD=∠CGD=90°,DE=DC,∠∠EDF∠∠CDG(AAS),∠EF=CG,∠CG=BC﹣BG=5﹣3=2,∠EF=2,∠S∠ADE=×AD×EF=×3×2=3.练习8.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角且点E,A,B 三点共线,AB=4,则阴影部分的面积是.练习8.已知,如图,Rt∠ABC中,∠ACB=90°,AC=BC,D为BC上一点,CE∠AD 于E,若CE=2,则S∠BEC=.例6.如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,求点C的坐标解:如图,过B作BF∠AC于F,过F作FD∠y轴于D,过A作AE∠DF于E,则∠ABF为等腰直角三角形,易得∠AEF∠∠FDB,设BD=a,则EF=a,∠点A(2,3)和点B(0,2),∠DF=2﹣a=AE,OD=OB﹣BD=2﹣a,∠AE+OD=3,∠2﹣a+2﹣a=3,解得a=,∠F(,),设直线AF的解析式为y=k'x+b,则,解得,∠y=3x﹣3,解方程组,可得或,∠C(﹣1,﹣6),练习9.如图,已知点A(3,3),点B(0,2),点A在二次函数y=x2+bx﹣9的图象上,作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交二次函数图象于点C,则点C的坐标为.练习10.如图,已知抛物线y=x2+2x﹣3过点A(1,0),B(0,﹣3),与x轴交于另一点C.若在第三象限的抛物线上存在点P,使∠PBC为以点B为直角顶点的直角三角形,求点P的坐标;解:过点P作PD∠y轴,垂足为D,令y=0,得x2+2x﹣3=0,解得x1=﹣3,x2=1,∠点C(﹣3,0),∠B(0,﹣3),∠∠BOC为等腰直角三角形,∠∠CBO=45°,∠PB∠BC,∠∠PBD=45°,∠PD=BD.∠可设点P(x,﹣3+x),则有﹣3+x=x2+2x﹣3,∠x=﹣1,∠P点坐标为(﹣1,﹣4);四、一线三等角(普通角度)例7.如图,在平面直角坐标系中,点O为坐标原点,直线y=,点P在第三象限的直线AB上,点C在点A上方的y轴上,连接PC、BC,PC交x轴于点N,且tan∠APC=,设点P的横坐标为t,∠ABC的面积为S,求S与t的函数关系;解:过点A作EA∠AB交PC于点E,过E点作EG∠y轴,垂足为G,过点P作PF∠y轴,垂足为F,∠∠P AE=90°,∠∠P AF+∠EAG=90°,∠∠P AF+∠APF=90°,∠∠APF=∠EAG,∠∠EGA=∠AFP=90°,∠∠AEG∠∠P AF,∠tan∠APC=,∠==,设P(t,),则PF=﹣t,AF=﹣,∠AG==﹣,EG==﹣,∠点A的坐标为:(0,2),∠E(),设PE的解析式为:y=ax+b,由P(t,),E()可得:,解得:,∠C(0,2﹣),∠AC=2﹣﹣2=﹣,∠BO=4,∠S==﹣t,练习11.如图,在∠ABC中,AB=AC,点E在边BC上移动(点E不与点B,C 重合),点D,F分别在边AB,AC上,且满足∠DEF=∠B.(1)求证:∠BDE∠∠CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.五、课后练习1.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF.已知AG∠GF,AC=,则AB的长为()A.B.2B.C.D.2.如图,正方形ABCD中,M为BC上一点,ME∠AM,ME交AD的延长线于点E,若AB=12,BM=5,则DE的长为()A.B.18B.C.D.3.如图所示,已知∠ABC中,∠BAC=45°,AD∠BC于D,BD=2,CD=3,试求AD的长.4.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC 与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是.5.在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O 作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.如图,当点A 的横坐标为﹣时,则点B的坐标为.6.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.7.如图,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)若C为x轴正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连OD,求∠AOD的度数;。
2024中考数学总复习冲刺专题:《一线三等角模型》通用版

《一线三等角模型》一、教材分析“一线三等角”是指三个相等角的顶点在同一直线上,其中两个角的一边与该直线重合,第三个角的两边均不与直线重合,这样会形成一组全等或相似三角形.根据等角的度数,此模型可分为锐角一线三等角、直角一线三等角和钝角一线三等角.“一线三等角”模型本质上是一个重要的基本几何模型,数学模型是对客观事物的空间形式和数量关系的表现形式,初中阶段的“一线三等角”模型是利用方程或函数等来表示数量之间的关系或变化规律.它一般不单独出现,通常与其他特殊图形结合,如等腰三角形、等边三角形、矩形、正方形,以及与翻折、坐标系结合等,从而考查这些图形的性质.因此“一线三等角”模型可以出现在选择题、填空题的最后一题,也可以出现在解答题的几何证明、综合题中,是一个使用频率高、综合性较强的模型.平时的训练中,需要提升自己的模型思想,提炼问题的基本图形,利用基本图形的性质特点来突破考题,在具体分析过程中,也要结合数形结合思想,如根据题干信息提炼图形的结构特点,然后结合图形,采用代数运算的方式探求深层信息,促进信息的融合、转化.二、核心素养分析2022年版义务教育数学课程标准希望学生在初中阶段形成模型观念、数据观念;数学学科核心素养也提到数学抽象和直观想象,逻辑推理和运算能力,数学模型和数据分析.因此在数学学习中,我们有必要及时归纳一些数学模型.“一线三等角”问题的核心思想就是模型思想,关键的解题途径是能从复杂图形中分离出此模型,把握基本图形并建立方程或函数,帮助我们塑造模型观念,增强数学能力,提高解题技巧,提升数学核心素养.三、学情分析本次教学设计的授课对象为九年级学生,学生已有与本课时内容相关的知识基础如下:①全等三角形的性质与判定;②相似三角形的性质与相似;③三角函数;④二元一次方程(组).本课程适用于对中考几何题有一定解决能力并有待提升综合能力的学生,弥补和改善学生漏听或未听懂这部分知识的不足,旨在促进学生深入理解方法和思想,从复杂图形中分离出基本数学模型,对解决问题有化繁为简的效果.四、教学任务分析1.课堂教学目标(1)知识与技能:探索“一线三等角”的基本特征,并且能够在不同背景中认识和把握基本图形,能利用“一线三等角”模型解决相关计算和证明问题;能够构造“一线三等角”模型,解决较为复杂的几何问题.(2)过程与方法:通过观察分析,大胆猜想,探索“一线三等角”基本图形,培养学生合作交流、逻辑推理的能力;让学生在解决相关问题时感受几何基本模型对几何学习的重要性.(3)情感态度与价值观:在学习活动中积累对数学的兴趣,培养与同学的交往、合作意识,在动手动脑的过程中发展想象力,体会模型思想、转化思想、分类讨论思想和数形结合思想;提高解题技巧,提升数学核心素养.2.教学重点和难点(1)教学重点①识别“一线三等角”模型的基本特征,并应用“一线三等角”模型解决相关问题;②构造“一线三等角”模型,解决复杂的几何问题.(2)教学难点构造“一线三等角”模型,并解决较为复杂的几何问题.五、具体教学过程设计1、概述:引导学生回顾一线三等角模型的基本分类:1)全等篇:条件:∠1=∠CPD=∠2,结论:△ACP ≅△BPD 1)全等篇:条件:∠1=∠CPD=∠2,结论:△ACP ≅△BPD同侧锐角直角钝角异侧2)相似篇:条件:∠1=∠CPD=∠2,结论:△ACP∽△BPD同侧锐角直角钝角222111122222211111异侧3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,当∠1=∠2=∠3,且D是BC中点时.结论:△BDE∽△CFD∽△DFE.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.2、模块一三角齐见,模型自现——图形中已经存在“一线三等角”,直接应用模型解题.(一)典例精讲例1.如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为________.222111例1图例2图2.如图,△ABC中,∠B=∠C=30°,∠DEF=30°,且点E为边BC的中点.将∠DEF绕点E旋转,在旋转过程中,射线DE与线段AB相交于点P,射线EF与射线CA相交于点Q,连结PQ.(1)如图1,当点Q 在线段CA 上时,①求证:△BPE ∽△CEQ ;②线段BE ,BP ,CQ 之间存在怎样的数量关系?请说明理由;(2)当△APQ 为等腰三角形时,求BPCQ的值.3、模块二模型隐藏,及时添补——模型隐藏,及时添补,图形中存在“一线二等角”,补上“一等角”构造模型解题;图形中只有直线上一个角,补上“二等角”构造模型解题.(一)知识铺垫找角、定线、构相似如果直线上只有1个角,该角通常是特殊角(30°、45°、60°),就考虑构造同侧型一线三等角,当然只加这两条线通常是不够的,为了利用这个特殊角与线段的关系,过C、D 两点作直线l 的垂线是必不可少的.两条垂线通常情况下是为了“量化”的需要。
专题02 全等模型-一线三等角(K字)模型(解析版)

专题02全等模型--一线三等角(K 字)模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K 字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K 型图)模型(同侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角(常见):锐角一线三等角直角一线三等角(“K 型图”)钝角一线三等角条件:A CED B ∠=∠=∠+CE=DE证明思路:,A B C BED ∠=∠∠=∠+任一边相等BED ACE⇒≅ 例1.(2023·江苏·八年级假期作业)探究:如图①,在ABC 中,90BAC ∠=︒,AB AC =,直线m 经过点A ,BD m ⊥于点D ,CE m ⊥于点E ,求证:ABD CAE ≌ .应用:如图②,在ABC 中,AB AC =,,,D A E 三点都在直线m 上,并且有BDA AEC BAC ∠=∠=∠.求出,DE BD 和CE 的关系.拓展:如图①中,若10DE =,梯形BCED 的面积______.【答案】探究:证明过程见详解;应用:DE BD CE =+,理由见详解;拓展:50【分析】探究:90BAC ∠=︒,AB AC =,可知ABC 是等腰直角三角形,BD m ⊥,CE m ⊥,可知90BDA AEC ∠=∠=︒,可求出BAD ACE ∠=∠,根据角角边即可求证;应用:AB AC =,,,D A E 三点都在(1)如图①,若AB AC ⊥,则BD 与AE 的数量关系为___________,CE 与AD 的数量关系为(2)如图②,判断并说明线段BD ,CE 与DE 的数量关系;(3)如图③,若只保持7BDA AEC BD EF cm ∠=∠==,,点A 在线段DE 上以2cm/s 的速度由点例3.(2022·陕西七年级期末)(1)【问题发现】如图1,△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=3,ED=4,则BE=_____.(2)【问题提出】如图2,在Rt△ABC 中,∠ABC=90°,BC=4,过点C作CD⊥AC,且CD=AC,求△BCD的面积.(3)【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为12且CD的长为6,求△BCD的面积.【答案】(1)7;(2)S△BCD=8;(3)S△BCD=6.【分析】(1)∠B=∠E=∠ACD=90°,据同角的余角相等,可得∠ACB=∠D,由已知条件可证△ABC≌△CED,运动(D 不与B 、C 重合),连接AD ,作40ADE ∠=︒,DE 交线段AC 于E .(1)当115BDA ∠=︒时,EDC ∠=_____︒,BAD ∠=_____︒,AED =∠_____︒;点D 从B 向C 运动时,BDA ∠逐渐变_____(填“大”或“小”);(2)当DC 等于多少时,ABD DCE ≌△△,请说明理由;(3)在点D 的运动过程中,ADE V 的形状可以是等腰三角形吗?若可以,请直接写出BDA ∠的度数,若不可以,请说明理由.【答案】(1)25,25,65,小(2)当2DC =时,ABD DCE ≌△△,理由见解析;(3)当BDA ∠的度数为110︒或80︒时,ADE V 的形状是等腰三角形.【分析】(1)先求出ADC ∠的度数,即可求出EDC ∠的度数,再利用三角形的外角性质即可求出AED ∠的度数,根据点D 从B 向C 运动时,BAD ∠逐渐增大,而B ∠不变化,180B BAD BDA ∠+∠+∠=︒,即可得到答案;(2)根据全等三角形的判定条件求解即可;(3)先证明当ADE V 时等腰三角形,只存在AD ED =或AE DE =两种情况,然后分这两种情况讨论求解即可;【详解】(1)解:∵115BDA ∠=︒,∴18011565ADC ∠=︒-︒=︒,∵40ADE ∠=︒,∴25EDC ADC ADE ∠︒=∠-∠=,∵ADC ADE EDC B BAD ∠=∠+∠=∠+∠,∴25BAD EDC ∠=∠=︒,∴65AED EDC C ︒∠=∠+∠=;∵点D 从B 向C 运动时,BAD ∠逐渐增大,而B ∠不变化,180B BAD BDA ∠+∠+∠=︒,∴点D 从B 向C 运动时,BDA ∠逐渐变小,故答案为:25,25,65,小;(2)解:当2DC =时,ABD DCE ≌△△,理由:∵40B C ∠=∠=︒,∴140DEC EDC ∠+∠=︒,又∵40ADE ∠=︒,∴140ADB EDC ∠+∠=︒,∴ADB DEC ∠=∠,又∵2AB AC ==,∴()AAS ABD DCE ≌△△;(3)解:当BDA ∠的度数为110°或80°时,ADE V 的形状是等腰三角形,理由:∵40C ADE ∠=∠=︒,AED C EDC ∠=∠+∠,∴AED ADE ∠>∠,∴当ADE V 时等腰三角形,只存在AD ED =或AE DE =两种情况,模型2.一线三等角(K 型图)模型(异侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
全等之一线三等角模型(含答案)

全等之一线三等角模型1. 一线三垂直【核心考点】:只要出现等腰直角三角形,可以过直角点作一条直线,然后过°顶点作该直线的垂线,构造三垂直模型.必有如下全等三角形:【经典图形】:【变式图形】:由得由得≌≌(1)(2)1.如图,正方形的顶点在直线上,,于点,于点.求证:≌.若,求点到直线的距离.2.如图,直线经过正方形的顶点,分别过正方形的顶点、作于点,于点,若,,则的长为 .(1)(2)3.如图,在中,,,于点,于点,,.求证:.求线段的长度.4.如图,点在线段上,,,,且,,,,求的度数.5.如图,是等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则 .6.如图,为等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则点坐标为 .(1)(2)7.如图,,,,,垂足分别为,.证明:≌.若,,求的长.(1)(2)(3)8.在中,,,直线经过点,且于,于.当直线绕点旋转到图①的位置时,求证:.图当直线绕点旋转到图②的位置时.求证:.图当直线绕点旋转到图③的位置时,试问:、、有怎样的等量关系?请写出这个等量关系,并加以证明.图9.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知,.则两条凳子的高度之和为 .A. B. C. D.10.如图,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积是( ).(1)(2)11.如图,中,,,是过点的一条直线,且点,在的同侧时,于,于.求证:.变成如图,,在的异侧时,,,关系如何?并加以证明.(1)(2)(3)12.如图所示,已知、为直线上两点,点为直线上方一动点,连接、,另以、为边向外作正方形和正方形,过点作于点,过点作于点.如图,当点恰好在直线上时,(此时与重合),试说明.如图,当、两点都在直线的上方时,试探求三条线段、、之间数量关系,并说明理由.如图,当点在直线的下方时,线段,、之间的数量关系又如何?请写出你的结论,并说明理由.2. 一线三等角【核心考点】:只要在一条直线上出现三个角相等,一般都可以构造全等三角形解决问题.【经典图形】:A. B. C. D.13.如图,在等边中,,点在上,且,点是上一动点,连结,将线段绕点逆时针旋转得到线段,要使点恰好落在上,则的长是( ).14.如图,已知中,点为上一点,,两点分别在边,上,若,,,,则.ACBFDE 15.如图,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .16.感知:如图①,点在正方形的边上,于点,于点,可知≌.(不要求证明)拓展:如图②,点,分别在的边,上.点,在内部的射线上,,分别是,的外角.已知,,求证:≌.应用:如图③,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .图图图图图图(1)(2)(3)17.某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图,已知:在中,,,直线经过点,直线,直线,垂足分别为点、.求证:.组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图,将()中的条件改为:在中,,、、三点都在直线上,并且有(其中为任意锐角或钝角),请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图,是角平分线上的一点,且和均为等边三角形,、分别是直线上点左右两侧的动点(、、互不重合),在运动过程中线段的长度始终为,连接、.若,则周长是 .(请直接写出答案)(1)(2)18.如图,是经过顶点的一条直线,,、分别是直线上两点,且.若直线经过的内部,且、在直线上,请解决下面两个问题:①如图①,若,,则;(填“”、“”、“”);图②如图②,若,请添加一个关于与关系的条件 ,使①中的两个结论仍然成立,并证明这两个结论.图如图③,若直线经过的外部,,请提出、、三条线段数量关系的合理猜想(不要求证明).图全等之一线三等角模型1. 一线三垂直【核心考点】:只要出现等腰直角三角形,可以过直角点作一条直线,然后过°顶点作该直线的垂线,构造三垂直模型.必有如下全等三角形:【经典图形】:【变式图形】:由得由得≌≌【备注】【教法指导】通过例1.1可以详细给学生示范一下三垂直模型的书写过程,其中倒角用的是“同角的余角相等”,提醒书生注意1.如图,正方形的顶点在直线上,,于点,于点.(1)(2)(1)(2)【解析】【标注】求证:≌.若,求点到直线的距离.【答案】(1)(2)证明见解析..∵四边形是正方形,,,∴,,,∴,,∴,∴在与中,,∴≌.过作,∵四边形是正方形,,∴,,,,∴,,,∴在与中,,∴≌,∴,∴在中,,,,∴点到直线的距离.【知识点】正方形与全等综合2.【解析】【标注】如图,直线经过正方形的顶点,分别过正方形的顶点、作于点,于点,若,,则的长为 .【答案】∵四边形是正方形,∴,,∵则是直角三角形,∴,,又∵,∴,在和中,,∴≌,∴,∴.【知识点】三垂直模型3.如图,在中,,,于点,于点,,.(1)(2)(1)(2)【解析】【标注】求证:.求线段的长度.【答案】(1)(2)证明见解析..∵,,,∴,,∴,在和中,,∴≌,∴.∵≌,∴,,∴.【知识点】三垂直模型4.【解析】如图,点在线段上,,,,且,,,,求的度数.【答案】.连接、.∵,,.∴.【标注】在和中,∴≌∴,,∴.∴为等腰三角形.同理可得为等腰三角形.∴..【能力】分析和解决问题能力【知识点】SAS【知识点】全等三角形的性质5.【解析】【标注】如图,是等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则.【答案】由三垂直模型易证≌,∴.【知识点】坐标与距离;三垂直模型6.如图,为等腰直角三角形,点坐标为,点坐标为,过作轴的垂线,垂足为点,则点坐标为 .【解析】【标注】【答案】由三垂直模型易证≌,∴,,∴点坐标为,故答案为:.【知识点】根据坐标描点、根据点写坐标;三垂直模型(1)(2)7.(1)【解析】如图,,,,,垂足分别为,.证明:≌.若,,求的长.【答案】(1)(2)证明见解析..∵,,,∴,∴,,∴,在和中,(2)【标注】,∴≌.∵≌,∴,,∴().【知识点】一线三等角模型(1)(2)(3)8.在中,,,直线经过点,且于,于.当直线绕点旋转到图①的位置时,求证:.图当直线绕点旋转到图②的位置时.求证:.图当直线绕点旋转到图③的位置时,试问:、、有怎样的等量关系?请写出这个等量关系,并加以证明.图【答案】(1)(2)(3)证明见解析.证明见解析..(1)(2)(3)【解析】【标注】∵中,,∴,又直线经过点,且于,于,∴,∴,∴,在和中,,∴≌(),∴,,∴.∵中,,直线经过点,且于,于,∴,,而,∴≌,∴,,∴.∵中,,直线经过点,且于,于,∴,,∴,∵,∴≌,∴,,∴;、、之间的关系为.【能力】推理论证能力【能力】运算能力【知识点】AAS【知识点】全等三角形的对应边与角9.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两条凳子之间(凳子与地面垂直).已知,.则两条凳子的高度之和为 .【解析】【标注】【答案】由题意可得:,,,在和中,,∴(),故,,则两条凳子的高度之和为:.故答案为:.【知识点】全等三角形实际生活中的应用A. B. C. D.10.方法一:【解析】如图,且,且,请按照图中所标注的数据,计算图中实线所围成的图形的面积是( ).【答案】A ∵,,∴,∵在和中,,方法二:【标注】∴≌(),同理 ≌(),∴,,,,∵梯形的面积,,,∴图中实线所围成的图形的面积.∵且,,,,,∴,,≌,∴,.同理证得≌得,.故,故.故选:.【知识点】三垂直模型(1)(2)11.如图,中,,,是过点的一条直线,且点,在的同侧时,于,于.求证:.变成如图,,在的异侧时,,,关系如何?并加以证明.(1)(2)【解析】【标注】【答案】(1)(2)证明见解析...∵,,,∴,∴,∴.∵,在和中,,∴≌,∴,,∴.∵,∴.成立.∵,,,∴.∵,,∴.∵,在和中,,∴≌,∴,.∵,∴.【能力】推理论证能力【能力】分析和解决问题能力【知识点】全等三角形的性质【知识点】AAS(1)(2)(3)12.(1)【解析】如图所示,已知、为直线上两点,点为直线上方一动点,连接、,另以、为边向外作正方形和正方形,过点作于点,过点作于点.如图,当点恰好在直线上时,(此时与重合),试说明.如图,当、两点都在直线的上方时,试探求三条线段、、之间数量关系,并说明理由.如图,当点在直线的下方时,线段,、之间的数量关系又如何?请写出你的结论,并说明理由.【答案】(1)(2)(3)证明见解析...∵四边形和为正方形,(2)(3)∴,,,∴,∵,∴,∴,∵,∴≌(),∴.,理由如下:过点作于,∵,∴,∴,∵四边形为正方形,∴,,∴,∴,∴≌(),∴,同理得:,∵,∴.,理由如下:过点作于,【标注】∵,∴,∴,∵四边形为正方形,∴,,∴,∴,∴≌(),∴,同理得:,∵,∴.【知识点】正方形与全等综合2. 一线三等角【核心考点】:只要在一条直线上出现三个角相等,一般都可以构造全等三角形解决问题.【经典图形】:【备注】【教法指导】注意三个相等的角度可以在直线同侧,也可以在直线异侧.A. B. C. D.13.【解析】如图,在等边中,,点在上,且,点是上一动点,连结,将线段绕点逆时针旋转得到线段,要使点恰好落在上,则的长是( ).【答案】B如图所示∵,,∴,∵为等边三角形,∴,∵线段绕点逆时针旋转得到线段,【标注】要使点恰好落在上,∴,,∵,,∴,在和中,∵,∴≌,∴.故选.【知识点】等边三角形的性质14.【解析】【标注】如图,已知中,点为上一点,,两点分别在边,上,若,,,,则.ACBFDE 【答案】∵,,∴,在和中,,∴≌,∴,∵,,∴.【知识点】一线三等角模型15.【解析】【标注】如图,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .【答案】∵,∴与等高,底边比值为,∴与面积比为,又的面积为,∴与面积分别为和.∵,∴.∵,,∴.在和中,,∴≌.∴,∴.【知识点】三角形的周长与面积问题16.感知:如图①,点在正方形的边上,于点,于点,可知≌.(不要求证明)拓展:如图②,点,分别在的边,上.点,在内部的射线上,,分别是,的外角.已知,,求证:≌.【解析】【标注】应用:如图③,在等腰三角形中,,.点在边上,,点,在线段上,.若的面积为,则与的面积之和为 .图图图【答案】见解析拓展:证明:∵,∴.∵,,又,∴.在和中,,∴≌.应用:解:∵,∴.∵,,,∴.在和中,,∴≌.∴.∵在中,,∴.∵,∴.∴.【知识点】全等三角形实际生活中的应用17.某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.图图图(1)(2)(3)图(1)【解析】如图,已知:在中,,,直线经过点,直线,直线,垂足分别为点、.求证:.组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图,将()中的条件改为:在中,,、、三点都在直线上,并且有(其中为任意锐角或钝角),请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图,是角平分线上的一点,且和均为等边三角形,、分别是直线上点左右两侧的动点(、、互不重合),在运动过程中线段的长度始终为,连接、.若,则周长是 .(请直接写出答案)【答案】(1)(2)(3)证明见解析.证明见解析.如图,∵直线,直线,∴,∵,∴,∵,∴,在与中,,∴≌,∴,,∴,∴.图(2)图(3)【标注】.如图,证明如下:∵,∴,∴,在和中,,∴≌,∴,,∴,∴.∵≌,∴,,∵和均为等边三角形,∴,,∴,即,在和中,,∴≌,∴且,∵,∴,∴,∴是等边三角形,∴.【知识点】多解或多种判定混合(1)18.如图,是经过顶点的一条直线,,、分别是直线上两点,且.若直线经过的内部,且、在直线上,请解决下面两个问题:21(2)【标注】①如图①,若,,则 ; (填“”、“”、“”);图②如图②,若,请添加一个关于与关系的条件 ,使①中的两个结论仍然成立,并证明这两个结论.图如图③,若直线经过的外部,,请提出、、三条线段数量关系的合理猜想(不要求证明).图【答案】(1)(2)();.,先证明,再证明≌..【知识点】全等三角形的性质。
几何模型:一线三等角模型

一线三等角模型—.一线三等角概念“一线三等角”就是一个常见得相似模型,指得就是有三个等角得顶点在同一条 直线上构成得相似图形,这个角可以就是直角,也可以就是锐角或钝角。
不同地区 对此有不同得称呼, 角” 二、一线三等角得分类全等篇三、“一线三等角”得性质K …般情况下,如图3-1,由Z1=Z2=Z3,易得△ AEC^ABDE.2、当等角所对得边相等时,则两个三角形全等、如图37若CE=ED,则△AEC 丝△BDE.“K 形图”,“三垂直”,"弦图”等,以下称为“一线三等 同侧异侧B钝角锐角rPPA相似篇异侧钝角宜角 D锐角 PAPBP图3・2 3、 中点型“一线三等角”如图 3・2,当Z 1=Z2=Z3,且 D 就是 BC 中点ABDE^ACFD^ADFE. 4、 “中点型一线三等角"得变式(了解) 如图37,当ZrZ2且眄点0就是ZkABC 得内心.可以考虎构造“一线三等角鮮、 N C C tfZ 图3斗如图3-4 “中点型一线三等角"通常与三角形得内心或旁心相关, 这就是内心得性质,反之未必就是内心、 在图3-4佑图)中,如果延长BE 与CF,交于点P,则点D 就是△PEF 得旁心、5. “一线三等角”得各种变式(图3-5,以等腰三角形为例进行说明)图3~5 其实这个第4图,延长DC 反而好理解、相当于两侧型得,不延长理解,以为就 是一种新型得,同侧穿越型?不管怎么变,都就是由三等角确定相似三角形来进 行解题 四、“一线三等角”得应用 1. “F 三等角”应用得三 a 、 况、!角”,直接应用 代,不上“一等 ,木上“二等角7构造模型解题.轴题中\经常会 特殊角 题. C 申己经存在“_绻 b/图畤存在“一线二《 只有直线上 一种情况出现比较多眈其就角函"・一 * 造“r:一线三等角就是基本手段,尤其就是直角坐标系中 体? 2、 忑鷄对需角问题中, 得张角问题,在X 轴或y 轴(也可以就是平行于X 轴或y 轴得直线)上构造 一线三等角解决问题更就是重要得手段. 3. 构造一线三等角得步骤:找角、定线、构相似A "c c cD/ / /在DC 的延长銭上截职CE= — , S CD 的延长线上截取DF=— > tana tana 贝I 」tanZAEPt tanZPFB= tans MljZAEP= ZPFB= a= ZAPB ,所以厶吨® ABPF •在CP 上截取CE 二竺,在DP 截^DF= —>tana tana则 tanZAEC= tanZBFD= tans 则Z.AEC= Z.BFD= a= Z.APB ,所以△ PAE^ ABPF •C g TXM V O F*A 尸得特殊性如图3・6,线上有一特殊角,就考虑构造同侧型一线三等角当然只加这两条线通常就是不够得,为了利用这个特殊角导线段得关系,过C> D 两点作直线1得垂线就是必不可少得。
初中数学几何模型(五)一线三等角模型

初中数学几何模型(五)一线三等角模型一线三等角模型:指有三个相等角的顶点在同一直线上构成的相似或全等(相等角所对的边相等)图形,相等的角可以是锐角,也可以是直角或钝角。
(一)全等1、相等的三个角和全等三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD≌△BEC。
证明:∵∠BCD=∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,CD=CE,∴△ACD≌△BEC(AAS)。
2、相等的三个角和全等三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,且CD=CE,则△ACD ≌△BEC。
证明:∵∠2=∠D+∠ACD,∠3=∠BCE+∠ACD,∠2=∠3,∴∠D=∠BCE,∵∠2=∠1,∴∠DAC=∠CBE,∵CD=CE,∴△ACD≌△BEC(AAS)。
一线三等角结论1:当等角所对边相等时,则两个三角形全等。
(二)相似1、相等的三个角和相似三角形在直线同侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠BCD+∠1+∠D,∠BCD=∠3+∠BCE,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴△ACD∽△BEC。
2、相等的三个角和相似三角形在直线异侧。
已知:如图,点A、B、C在同一直线上,∠1=∠2=∠3,则△ACD∽△BEC。
证明:∵∠1=∠D+∠ACD,∠3=∠BCE+∠ACD,∠1=∠3,∴∠D=∠BCE,∵∠1=∠2,∴∠DAC=∠CBE,∴△ACD∽△BEC。
一线三等角结论2:一线三等角两个三角形相似。
(三)一线三等角变式:中点型如图,点C在相等AB上,且AC=BC,∠1=∠2=∠3。
求证:△ACD∽△BEC∽△CED证明:∵∠1=∠2=∠3,∴△ACD ∽△BEC ,∴AD BC =CD CE , ∵AC=BC ,∴AD AC =CD CE ,∵∠1=∠3,∴△ACD ∽△CED ,∴△ACD ∽△BEC ∽△CED ,∴∠4=∠5=∠8,∠9=∠6=∠7。
一线三等角相似模型

在物理学中,可以利用一线三等角 相似模型来研究物理现象和规律, 如光的反射和折射、波的传播等。
04 一线三等角相似模型的证 明方法
直接证明法
定义
直接证明法是通过直接使用已知条件和定理来证明结论的 方法。
步骤
首先,根据已知条件,明确一线三等角的定义和性质;然后, 通过比较两个三角形中的角度和边长,利用相似三角形的性质
03
注意事项
反证法需要熟练掌握反证法的原理和 推理技巧,以及能够灵活运用已知条 件。
综合法与分析法
定义
综合法是从已知条件出发,逐步推导出结论的方法;分析法是从结论出发,逐步推导出已知条件的方法。
步骤
在综合法中,首先明确已知条件和目标结论;然后,根据已知条件逐步推导所需结论;最后,总结推导过程。在分析 法中,首先明确目标结论和已知条件;然后,根据结论逐步推导所需条件;最后,总结推导过程。
,逐步推导出所需的结论。
注意事项
直接证明法需要熟练掌握相似三角形的性质和定理,以及 灵活运用已知条件。
反证法
01
定义
反证法是通过假设结论不成立,然后 推导出矛盾,从而证明结论成立的方 法。
02
步骤
首先,假设结论不成立;然后,根据 已知条件和反证法的原理,推导出与 已知条件相矛盾的结论;最后,根据 矛盾的结论,得出结论成立。
相似变换的性质
相似变换具有一些重要的性质,如保持角度不变、线 段长度比例不变等。
相似变换的应用
相似变换在几何学、物理学、工程学等领域有着广泛 的应用,如建筑设计、机械制造、航天技术等。
相似多边形的性质与应用
1 2
相似多边形的定义
相似多边形是指各对应角相等、各对应边成比例 的多边形。
全等三角形单元复习: 一线三等角模型课件(16张PPT)2024-2025学年人教版八年级上学期

(1)试说明: = ;
(2)当∠ = 40°时,求∠的度数;
(3)请你猜想:当∠为多少度时,∠ + ∠ = 120°,并说明理由.
(2)∵∠ = 40°
1
2
∴∠ = ∠ = (180° − 40°) = 70°
∴ ∠ + ∠ = 110°
又∵△ ≌△
∴∠ = ∠
∴∠ + ∠ = 110°
∴∠ = 70°.
2. 如图,在 △ 中,∠ = ∠,点、、分别在、、上,且
= , + = .
(1)试说明: = ;
(2)当∠ = 40°时,求∠的度数;
∴∠ + ∠ = 90°
∵∠ + ∠ + ∠ = 180°
∴∠ = 90°.
2. 如图,在 △ 中,∠ = ∠,点、、分别在、、上,且
= , + = .
(1)试说明: = ;
(2)当∠ = 40°时,求∠的度数;
∴∠ = ∠ = 90°
在 △ 和 △ 中,
=
ቊ
=
∴ △ ≌ △ (HL)
∴ = , =
∴ = + = + .
(2)∵ △ ≌ △
∴∠ = ∠
∵∠ + ∠ = 90°
∴ = + .
模型2:“一线三等角”(两个三角形在直线同侧)
利用“一线三等角”可以证明三角形全等,反过来,由三角形全等可以反推,这也
是常考点,具体模型如下:
拓展模型:若、、三点在一条直线上,∠ = ∠ = , △ ≌△ ,则有
∠ = .
证明:∵△ ACP ≌△ BPD
相似专题:一线三等角相似模型

注意事项:需要熟练掌握代数公式和定理以及灵活运用代数方法进行证明
三角函数证明法
利用三角函数的性质通过角度相等来证明三角形相似 利用三角函数的诱导公式将角度相等转化为边长比例相等 利用三角函数的和差公式将角度相等转化为边长比例相等 利用三角函数的倍角公式将角度相等转化为边长比例相等
一线三等角相似的判定条件
两个三角形中如果一个角分别与另两个角相等则这两个三角形相似。
在两个三角形中如果一个角的对边与另一个角的对边成比例则这两个三角形相似。 在两个三角形中如果一个角的对边与另一个角的邻边成比例则这两个三角形相似。
在两个三角形中如果一个角的对边与另一个角相等则这两个三角形相似。
一线三等角相似模型的 应用
单击添加标题
题目:在三角形BC中D是B上一点E是C上一点DE平行于BC且E:EC=1:2 则S△DE:S△BC=?
代数表达式简化:利用一线三等角 相似模型可以将复杂的代数表达式 进行简化。
代数应用实例
代数不等式证明:利用一线三等角 相似模型可以证明一些代数不等式。
添加标题
添加标题
添加标题
添加标题
代数方程求解:通过一线三等角相 似模型可以求解一些代数方程。
一线三等角相似模型的 应用实例
几何证明实例
单击添加标题
题目:已知三角形BC中D是B上一点E是C上一点DE平行于BC且D:DB=2: 1则S△DE:S△BC=?
单击添加标题
题目:在三角形BC中D是B上一点E是C上一点DE平行于BC且E:EC=2:1 则S△DE:S△BC=?
单击添加标题
题目:在三角形BC中D是B上一点E是C上一点DE平行于BC且BD:B=1:3 则S△DE:S△BC=?
(完整版)几何模型:一线三等角模型
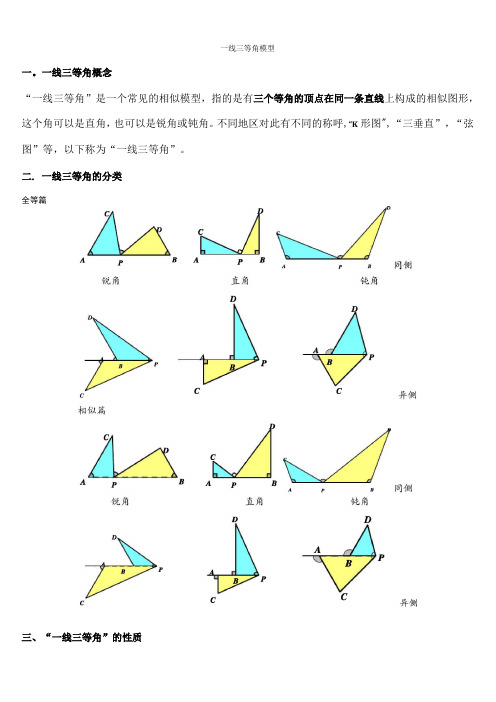
一线三等角模型一。
一线三等角概念“一线三等角”是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,“K形图",“三垂直”,“弦图”等,以下称为“一线三等角”。
二. 一线三等角的分类全等篇三、“一线三等角”的性质1。
一般情况下,如图3—1,由N 仁Z2=Z3,易得△AECs^BDEo2. 当等角所对的边相等时,则两个三角形全等.如图3.中点型“一线三等角 如图3—2,当Z1=Z2=Z3,且D 是BC 中点时,△BDEs^CFDs^DFE 。
4。
“中点型一线三等角“的1如图3—4“中点型一线三等角”通常与三角形的内心或旁心相关,ZBOC 二90。
+A BAC 这是内心的^2 性质,反之未必是内心.在图3-4(右图)中,如果延长BE 与CF ,交于点P,则点D 是APEF 的旁心.图3—5其实这个第4图,延长DC 反而好理解•相当于两侧型的,不延长理解,以为是一种新型的,同 侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1•“一线三等角”应用的三种情况.图3-1图3-3图3-4+Ja。
图形中已经存在“一线三等角”,直接应用模型解题;b。
图形中存在“一线二等角”,不上“一等角”构造模型解题;c・图形中只有直线上一个角,不上“二等角”构造模型解题。
体会:感觉最后一种情况出现比较多,尤其是压轴题中,经常会有一个特殊角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2。
在定边对定角问题中,构造一线三等角是基本手段,尤其是直角坐标系中的张角问题,在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造一线三等角解决问题更是重要的手段。
在DC的延檢銭上截眼匚E二J3•构造一线三等角的步骤:找角、定线、构相似1IJttnZAEP=aaZPFB=啦-工上则以’唾二ZPFB=a二ZAPE』所I^APAEwABPF.在CP±WCE=则曲厶斗EOunZBFD=⑶“则ZAEC-ZBFD=ZAPB•所I^APAE«ABPF・坐标系中,要讲究“线"的特殊性如图3—6,线上有一特殊角,就考虑构造同侧型一线三等角(完整版)几何模型:一线三等角模型当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过C、D两点作直线I的垂线是必不可少的。
一线三等角模型的定义

一线三等角模型的定义1. 什么是一线三等角模型一线三等角模型,听起来是不是有点高大上?其实它的原理挺简单的,就像我们平时聊天时,想要把一件事说得明明白白,搞得清清楚楚。
简单来说,这个模型主要用来描述事物之间的关系。
它的核心思想是把复杂的问题拆分成三个部分,就像我们吃西瓜,一刀切开,既能看见里面的红瓤,又能轻松分享。
通过这种方式,我们能更好地理解事物的本质,避免那种“说了半天,还是不明白”的窘境。
2. 三等角的构成2.1 第一等角:要素这个第一等角就像是一个基础,让我们理解整个模型。
想象一下,你在做一道菜,首先得有食材。
这里的“要素”就是构成事物的基本成分。
比如说,一个团队要成功,首先得有人才,有资源,有目标。
如果没有这些基本要素,那就跟没米下锅一样,做不出美味的饭菜。
2.2 第二等角:关系接下来,第二等角就是这些要素之间的关系了。
就像是朋友之间的交情,有的人深交,有的人泛泛之交。
在模型里,这个关系决定了要素之间的互动。
比如,一个团队里,有的成员擅长沟通,有的则技术过硬。
他们之间的合作关系,就像是一支乐队,各司其职,才能演奏出和谐的乐曲。
如果每个人都只顾自己,那就成了“众星捧月”,乱得不成样子。
2.3 第三等角:环境最后,我们得提提第三等角,就是环境。
环境就像是天气,晴天的时候大家心情都不错,工作效率高;而下雨天可能就会有点阴沉,士气也跟着低落。
这一角强调的是外部因素对要素和关系的影响。
比如,在经济不景气的时候,一个好团队可能也会受到影响,资源变得紧张,目标实现的难度就加大了。
3. 应用场景3.1 工作场所那么,这一线三等角模型在现实生活中有什么用呢?首先,在工作场所,领导可以用这个模型来分析团队的表现。
比如,发现团队里有人才流失,领导就可以先看看团队的基本要素是不是齐全,再分析成员之间的关系是否良好,最后再看外部环境对团队的影响。
这样一来,问题就能迎刃而解,领导也能做出更加精准的决策。
3.2 教育领域在教育领域,这个模型同样大显身手。
全等模型 —“一线三等角”

全等模型—“一线三等角”一线三等角模型,顾名思议,一线三等角是指三个相等的角的顶点在同一条直线上,这个模型贯穿初中几何的始终,在相似三角形这个章节中是很重要的知识点,下面来具体分析一下。
1,等腰直角三角形一线三等角模型口诀:多个垂直先倒角相等,互余角少不了分析1:已知△OAB是等腰直角三角形,过点O作直线CD且AD⊥CD,BC⊥CD,由题意得,∵△OAB是等腰直角三角形∴∠BOA=90°OB=OA即∠COB+∠AOD=90°又因为AD⊥CD,BC⊥CD所以∠COB+∠CBO=90°(互余角)∠DAO+∠AOD=90°(互余角)因此∠CBO+∠DAO=90°(互余角)则有∠COB=∠DAO∠CBO=∠AOD综上结论,则有在△BCO和△ODA中∠COB=∠DAOOB=OA(角边角)∠CBO=∠AOD因此△BCO≌△ODA分析2,已知△OAB是等腰直角三角形,做一条直线穿过∠BOA,AD⊥CD,BC⊥CD,如下图所示:由题意得,∵△OAB是等腰直角三角形∴∠BOA=90°OB=OA即∠COB+∠AOD=90°又因为AD⊥CD,BC⊥CD所以∠COB+∠CBO=90°(互余角)∠DAO+∠AOD=90°(互余角)因此∠CBO+∠DAO=90°(互余角)则有∠COB=∠DAO,∠CBO=∠AOD综上结论,则有在△BCO和△ODA中,∠COB=∠DAO,OB=OA,∠CBO=∠AOD因此△BCO≌△ODA“一线三等角”全等模型——适用于直角的情况条件:∠BAC=∠BFA=∠AEC=90°,AC=BA,结论:△ACE≌△BAF.由题意得,∵∠BAC=∠BFA=∠AEC=90°∴∠EAC+∠BAF=90°(互余角),∠EAC+∠ECA=90°,∠ABF+∠BAF=90°,即∠ABF=∠EAC,在△ACE和△BAF中,∠ABF=∠EAC∠BFA=∠AEC(角角边)AC=BA因此:△ACE≌△BAF(AAS)则有:CE=AF,AE=BF,EF=CE+BF.条件:∠BAC=∠BFA=∠AEC=90°,AC=BA,结论:△ACE≌△BAF由题意得,∵∠BAC=∠BFA=∠AEC=90°∴∠EAC+∠BAF=90°(互余角)∠EAC+∠ECA=90°∠ABF+∠BAF=90°即∠ABF=∠EAC在△ACE和△BAF中∠ABF=∠EAC∠BFA=∠AEC(角角边)AC=BA因此:△ACE≌△BAF(AAS)则有:CE=AF AE=BFEF=BF-EC【典例1】:已知,如图所示,B,C,E三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A,∠A与∠D互为余角B,∠A=∠DCEC,△ABC≌△CED D,∠ACB=∠DCE【答案】D【精准解析】由题意得因为AC⊥CD,所以∠ACD=90°,所以∠ACB+∠DCE=90°故选择D 又因为∠B=∠E=90°所以∠A+∠ACB=90°∠D+∠DCE=90°∠A=∠DCE∠ACB=∠D故B正确所以∠A+∠D=90°故A正确再根据全等三角形判定定理得:AC=CD∠B=∠E∠A=∠DCE因此最终答案是D2,“一线三等角”全等模型的拓展——同时也适用于锐角和钝角的情况条件:∠CAE=∠B=∠D,AC=AE结论:△ABC≌△EDA由题意得,∠CAB+∠CAE+∠EAD=180°∠CAB+∠B+∠C=180°∵∠CAE=∠B∴∠C=∠EAD在△CAB和△EAD中,∠B=∠D,∠C=∠EAD,AC=AE,因此△CAB≌△EAD(AAS)所以BC=AD,AB=DE,BD=BC+DE由题意得,∠CAB+∠CAE+∠EAD=180°∠CAB+∠B+∠C=180°∵∠CAE=∠B∴∠C=∠EAD在△CAB和△EAD中,∠B=∠D,∠C=∠EAD,AC=AE,因此△CAB≌△EAD(AAS),锐角和钝角的结论:BC=AD,AB=DE,BD=BC+DE.【典例2】:在三角形ABC中,∠A=40°,∠B=∠C,BE=CD,BD=CF,求∠EDF的度数?【答案】由题意得在△BDE和△CFD中BE=CD∠B=∠C(边角边)BD=CF所以△BDE≌△CFD∵∠BDE+∠EDF+∠FDC=180°∠BDE+∠B+∠BED=180°∵∠EDF=∠B又因为∠A=40°∠B=∠C根据三角形内角和得∠B=∠EDF=∠B=70°=70°因此∠EDF=∠B=70°【精准解析】根据已知条件证明△BDE≌△CFD,即ED=DF,∠EDF=∠B=∠C,因此属于一线三等角模型,已知∠A=40°,即先求∠B=∠C=70°,即可得出答案【典例3】如图,在三角形ABC中,依然有AB=AC,若点B,C位于直线l的两侧,若果∠BDA+∠BAC=180°,∠BDA=∠AEC,求证BD=CE+DE【答案】由题意得∵∠BDA+∠BAC=180°∠BDA+∠BDE=90°∴∠BAC=∠BDE又∵∠ABD+∠BAD=∠BDE∠CAE+∠BAD=∠BAC∴∠ABD=∠CAE在△BDA和△CEA中∠ABD=∠CAE∠BDA=∠AEC(角角边)AB=AC所以△BDA≌△CEA即AD=CE BD=AE因此BD=CE+DE【精准答案】首先证明△BDA≌△CEA,由此得到AD=CE BD=AE,即可得出答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题九:“一线三角型”模型的应用1如图,在△ ABC中,AB=AC P、M分别在BC AC边上,
且.APM ,AP=MP,求证:△ APB^A PMC
分析:证明两个三角形全等,找边、角的等量关系,根据已有的知识经验,学生很快能够解决。
2、如果把第1题中的等腰三角形改为等边三角形,如图,
△ ABC为等边三角形,.APM =60 , BP=1,CM =?,求△ ABC的边长
3
AD//BC, AD 二3cm, BC 二7cm, 一B 二
3、如图,等腰梯形ABCD中,
60 ,
P为BC上一点(不与B C重合),连结AP,过P点作PM交DC于M,使得
APM "B。
(1)求证:△ ABP^A PCM
(2)求AB的长;
(3)在底边BC上是否存在一点P,使得DM:MC=5:3若存在, 求出BP的长;若不存在,请说明理由
4、如图,AB I BD,CD _ BD ,且 AB = 6cm,CD = 4cm, BD = 14cm , 问:在
BD 上是否存在P 点,使以P 、B 、A 为顶点的三角形与以P 、DC 为顶点的三角形相似?如果存在,求 BP 的长;如果不存在,请说明理由。
5、已知在梯形 ABCD 中, AD//BC, AD :: BC ,且 AD=5,AB=DC=2
(1) 如图a ,P 是AD 上的一点,满足.BPC- A
①求证:△ ABP^A DPC ②求AP 的长。
(2) 如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满
足.BPE W^A ,PE
交直线BC 于点E ,同时交直线DC 于点Q,那么:
①当点Q 在线段DC 的延长线上时,设AP 二x,CQ 二y ,求y 关于x
的函数解析式, 并写出函数自变量的取值范围;
②当CE=1时,求出AP 的长 6、正方形ABCD 边长为4, M N 分别是BC CD 上的两个动点, 当M
点在BC 上运动时,保持AM 和 MN 垂直,如图。
(1) 证明 Rt △ ABMh Rt △ MCN
(2) 设BM =x ,梯形ABCN 勺面积为y ,求y 与x 之间的函数 关系
式;当M 点运动到什么位置时,四边形 ABCNS 积最大,并求出
占 ~~
最大面积;
(3) 当M点运动到什么位置时Rt△ ABMT Rt△ AMN求x的值
7、如图,正方形ABCD勺边长为4cm点P是BC边上不与点B、C重合的任意一点,连结AP,过点P作PQ _ AP交DC于点Q, 设BP的长为xcm ,
CQ的长为ycm。
(1)求点P在BC上运动的过程中y的最大值;
1
(2)当y = — cm时,求x的值。
4
8如图,边长为1的正方形OABC勺顶点为坐标原点,点A在
x轴的正半轴上,点C在y轴的正半轴上。
动点D在线段BC上移动
(不与B、C重合),连结0D过点D作DE丄0D,交边AB于点E,连
结0E设CD=t。
(1)当时,求直线DE的函数表达式;
3
(2)当OD2• DE2的算术平方根取最小值时,求点E的坐标。
9、如图,在矩形ABCD中, AB二m (m是大于0的常数),
BC=8 E为线段BC上的动点(不与B C重合),连结DE
作EF — DE,EF与射线BA交于点F,设CE二x, BF二y
(1) 求y关于x的函数关系式;
(2) 若m=8,求x为何值时,y的值最大,最大值是多少?
12
(3) 若y二一,要使△ DEF为等腰三角形,m的值应为多少?
m
D
10、如图,已知在矩形ABCD中, AB=2,BC=3 P是线段AD边上
的任意一点(不含端点A、D),连结PC,过点P作PE_ PC交AB于E。
(1)在线段AD上是否存在不同于P的点Q,使得QC _QE ?若存在,
求线段AP 与AQ之间的数量关系;若不存在,请说明理由;
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围
11、在四边形ABCD中AB _ BC,DC _ BC, AB 二a,DC 二b, BC 二a b,且a ^b,取
AD的中点P,连结PB PG
(1)试判断三角形PBC的形状;
(2)在线段BC上,是否存在点M使AM丄MD。
若存在,:/
眉-------- 厂
请求出BM的长;若不存在,请说明理由。
