《传热学》第8章热辐射基本定律和辐射特性
合集下载
传热学-热辐射基本定律和辐射特性
所以，不同方向上辐射能量的强弱，还要 在相同的看得见的辐射面积的基础上才能 作合理的比较
C1 (λT
eC2 /(λT )
)−5
d −1
(
λT
)
=
f
(λT )
f(λT)称为黑体辐射函数，表示温度为T 的黑体所发射的辐射能 中在波段0～λ内的辐射能所占的百分数。
利用黑体辐射函数数值表（360页表8－1）可以很容易地用 下式计算黑体在某一温度下发射的任意波段的辐射能量：
Eb(λ1−λ2 ) = ⎡⎣ Fb(0−λ2 ) − Fb(0−λ1) ⎤⎦ Eb
∫ 显然有
Eb =
∞ 0
Ebλ
d
λ
普朗克定律解释了黑体辐射能按波长分布的规律：
Ebλ
=
c1λ−5
ec 2
(λT )
−1
式中，Ebλ—黑体光谱辐射力，W/m3
λ— 波长，m ； T — 黑体温度，K ； c1 — 第一辐射常数，3.7419×10-16 W⋅m2； c2 — 第二辐射常数，1.4388×10-2 W⋅K；
8.1.2 从电磁波角度描述热辐射的特性
8.1.2 从电磁波角度描述热辐射的特性
c 电磁波的数学描述： = λν
c — 电磁波传播速度, m/s ν — 频率, 单位 1/s λ — 波长, 常用μm为单位
从理论上说，物体热辐射的电磁波波长范围可以包括整个波谱，即波长从零到无穷大 然而，在工业上所遇到的温度范围内，即2000K以下，有实际意义的热辐射波长位于 0.38—100μm之间，且大部分能量位于红外线区段的0.76—20μm范围内，而在可见 光区段、即波长为0.38—0.76μm 的区段，热辐射能量的比重不大
τ =0, α + ρ =1
C1 (λT
eC2 /(λT )
)−5
d −1
(
λT
)
=
f
(λT )
f(λT)称为黑体辐射函数，表示温度为T 的黑体所发射的辐射能 中在波段0～λ内的辐射能所占的百分数。
利用黑体辐射函数数值表（360页表8－1）可以很容易地用 下式计算黑体在某一温度下发射的任意波段的辐射能量：
Eb(λ1−λ2 ) = ⎡⎣ Fb(0−λ2 ) − Fb(0−λ1) ⎤⎦ Eb
∫ 显然有
Eb =
∞ 0
Ebλ
d
λ
普朗克定律解释了黑体辐射能按波长分布的规律：
Ebλ
=
c1λ−5
ec 2
(λT )
−1
式中，Ebλ—黑体光谱辐射力，W/m3
λ— 波长，m ； T — 黑体温度，K ； c1 — 第一辐射常数，3.7419×10-16 W⋅m2； c2 — 第二辐射常数，1.4388×10-2 W⋅K；
8.1.2 从电磁波角度描述热辐射的特性
8.1.2 从电磁波角度描述热辐射的特性
c 电磁波的数学描述： = λν
c — 电磁波传播速度, m/s ν — 频率, 单位 1/s λ — 波长, 常用μm为单位
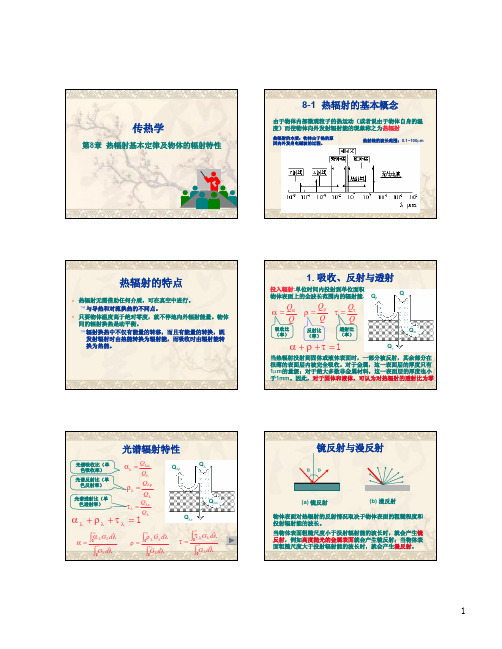
从理论上说，物体热辐射的电磁波波长范围可以包括整个波谱，即波长从零到无穷大 然而，在工业上所遇到的温度范围内，即2000K以下，有实际意义的热辐射波长位于 0.38—100μm之间，且大部分能量位于红外线区段的0.76—20μm范围内，而在可见 光区段、即波长为0.38—0.76μm 的区段，热辐射能量的比重不大
τ =0, α + ρ =1
新大《传热学》习题及解答第8章 热辐射基本定律和辐射特性
第8章 热辐射基本定律和辐射特性（题解）【习题8-3】 把太阳表面近似地看成是K 5800=T 的黑体，试确定太阳发出的辐射能中可见光所占的百分数。
解：K μm 220458003801⋅=⨯=.T λ，K μm 440858007602⋅=⨯=.T λ ()%.F b 191010=-λ，()%.F b 045520=-λ()()()%.%.%.F F F b b b 854419100455122100=-=-=---λλλλ【习题8-4】 一炉膛内火焰的平均温度为500K 1，炉墙上有一看火孔。
试计算当看火孔打开时从孔（单位面积）向外辐射的功率。
该辐射能中波长为μm 2的光谱辐射力是多少？哪一种波长下的能量最多？ 解：小孔辐射看成黑体辐射：25484m W 10872150010675⨯=⨯⨯==-..T E b σ对μm 2=λ的辐射：()()()31015001021043881561651m W 107449110210741931622⨯=-⨯⨯⨯=-=⨯⨯⨯------.e .e c E .T c b λλλ最大辐射能对应波长m λ：31092-⨯=.T m λ，m 109331150010921092633---⨯=⨯=⨯=..T .m λ【习题8-6】 一人工黑体腔上的辐射小孔是一个直径为0mm 2的圆。
辐射力25m W 1072.3⨯=b E 。
一个辐射热流计置于该黑体小孔的正前方m 5.0=l 处，该热流计吸收热量的面积为25m 106.1-⨯。
问该热流计所得到的黑体投入辐射是多少？解：2422m 10141634020141634d -⨯=⨯==...d A π sr 1046501061d d 5252--⨯=⨯==...l S Ω ()()545104610141631416310723d d d d d --⨯⨯⨯⨯⨯=⎪⎭⎫⎝⎛==....A E A I b ΩπΩθθΦW 103823-⨯=.【习题8-17】 一漫射表面在某一温度下的光谱辐射强度与波长的关系可以近似地用附图表示，试：（1）计算此时的辐射力；（2）计算此时法线方向的定向辐射强度，及与法向成o 60角处的定向辐射强度。
传热学第8章热辐射基本定律和辐射特性
1. 立体角
A r2
sr 球面度
对整个半球：
A 2r 2 2 sr
对微元立体角：
d
dA r2
s in dd
sr
n θ
dΩ r dA1
立体角定义
dθ dA2
φ dφ
r sind
rd
dA2
2. 定向辐射强度（辐射强度） 物体单位时间单位可见辐射面积单位立体角
内发出的辐射能量。
L( ,) d
n
W /(m2 sr)
引入辐射比 Fb(1 2 )
0
1
2
黑体波段内的辐射力
F b(12 )
E d 2
1
b
0 Eb d
1
0T 4
E d 2
1
b
F F b(02 )
b(01 )
其中： Fb(0) 为黑体辐射函数（表8-1）
则波段内黑体辐射力：
Eb(1 2 ) [Fb(02 ) Fb(01 ) ]Eb
8.2.3 兰贝特定律
dф
dAcosd
θ
dA2
对各向同性物体表面：
dΩ
L( ,) L( )
dA1
dA1cosθ
3. 定向辐射力 单位时间单位面积物体表面向某个方向发射
单位立体角内的辐射能, 称为该物体表面在该 方向上的定向辐射力。Eθ，W/(m2.sr)
4. 兰贝特定律 黑体的定向辐射强度与方向无关， 即半球空间各方向上的辐射强度都相等。
热辐射投射到固体，液体表面上：
1 0
表面性
热辐射投射到气体表面上：
1 0 容积性
（3）固体表面的两种反射现象 ✓镜反射 (Specular reflection) ✓漫反射 (Diffuse reflection) 主要取决于固体表面不平整尺寸 的大小（表面粗糙度）。
《传热学》第8章热辐射基本定律和辐射特性
Eb
光辐射能力随着波长的 c15 c 2 / T 增加，先是增加，然后 e 1 又减少
λ— 波长，m ； T — 黑体温度，K ； c1 — 第一辐射常数，3.74.4388×10-2 WK；
8
第8章 热辐射基本定律和辐射特性
射能力和吸收能力都是最大的。
6
第8章 热辐射基本定律和辐射特性
8.2 黑体热辐射的基本定律
三个定律分别从不同角度揭示在一定的温度下，单位表面黑体辐射能的
多少及其随空间方向与随波长分布的规律。
8.2.1 斯忒藩-波尔兹曼定律
为了定量分析热辐射能量大小，引入辐射力的概念 辐射力：单位时间内单位表面积向其上的半球空间的所有方向辐射出去
d 45o IdA b cos 2 d 2 7000 W / m 2 sr 2 103 m 2 1 4.00103 sr 1.9810 2 W 2 16
7000 W / m 2 sr 103 m 2 3.46103 sr 2.8010 2 W
光谱辐射力最大处的波长λm亦随温度不同而 变化： mT 2.8976103 m K 2.9 103 m K 随着温度的增高，最大光辐射力的波长会减 小，曲线峰值向左移动。 波长与温度成反比的规律称为维恩位移定律 3. 普朗克定律与斯忒藩-玻耳兹曼定律的关系 光辐射力曲线下的面积就是该温度下黑 体的辐射力
反射能量—Qρ—反射率—ρ
穿透能量—Qτ—穿透率—τ
1
Q Q Q Q Q Q Q 1 Q Q Q
4
第8章 热辐射基本定律和辐射特性
固体和液体：α+ρ=1
传热学热辐射基本定律和辐射特性课件
工业辐射加热与冷却
工业辐射加热
利用辐射方式将热量传递给物料 ，实现高效、均匀的加热效果。
工业辐射冷却
利用辐射方式将热量传递给冷却 介质，实现高效、快速的冷却效
果。
工业辐射干燥
利用辐射方式将热量传递给物料 ，实现快速、均匀的干燥效果。
05
热辐射研究展望
新型热辐射材料研究
总结词
随着科技的发展，新型热辐射材料的研究成为传热学领域的重要方向。
详细描述
通过研究热辐射与大气、水体和地表 的相互作用，可以深入了解地球系统 的能量平衡和蔼候变化机制。同时， 这种研究也为可再生能源的利用和环 境保护提供了理论支持。
热辐射在新能源领域的应用研究
总结词
热辐射在新能源领域的应用研究具有广阔的前景。
详细描述
利用热辐射进行光热转换，可以实现太阳能的利用和转化。此外，热辐射在高温核聚变、磁流体发电和地热能利 用等领域也有着重要的应用价值。通过深入研究热辐射在这些新能源领域的应用，有望为解决能源危机和环境污 染问题提供新的解决方案。
意义。
吸取率
总结词
详细描述
吸取率是物体吸取热辐射能量的能力，它 决定了物体对热辐射的吸取程度。
吸取率表示物体在特定温度下吸取的热量 与入射到物体上的总热量之比。物体的吸 取率与其发射率和反射率有关。
总结词
详细描述
吸取率的值介于0和1之间，完全吸取的物 体吸取率为1，完全不吸取的物体吸取率为 0。
了解物体的吸取率对于设计热辐射系统、 控制热能传递和优化热能利用具有重要意 义。
普朗克辐射定律
总结词
普朗克辐射定律描述了黑体光谱辐射的能量散布。
详细描述
普朗克辐射定律指出，黑体的光谱辐射强度与波长、温度有关。在任意波长下 ，黑体的光谱辐射强度与温度成正比。该定律是量子力学的基础之一，适用于 所有温度下的黑体辐射。
第八章-热辐射基本定律和辐射基本特性分解
8-3 灰体和基尔霍夫定律
一、实际物体的辐射特性和发射率
▲光谱辐射力随波长呈现不规则的变化；
实际物体 辐射特性：
▲辐射力并不严格地同热力学温度四次方成正比；
▲定向辐射强度在不同方向上有变化谱发射率( )
—修正光谱辐射力Eb
定向发射率( )
—修正定向辐射强度I
★发射率（黑度）ε—— 实际物体的辐射力与同温度下黑体的辐射力的比值。
固体和液体对辐射能的吸收和反射基本上属于表面效应： 金属的表面层厚度小于1m；绝大多数非金属的表面层厚度小 于1mm。
二、黑体模型
能吸收投入到其表面上的所有热辐射能的物体，是 一种科学假想的物体，现实中并不存在。
黑体： 白体或镜体：
1
1
透明体：
1
煤烟、炭黑、粗糙的钢板 0.9以上
黑体吸收和发射辐射能的能力最强
热辐射是热量传递的 基本方式之一，以热辐 射方式进行的热量交换 称为辐射换热。
传热学
第八章 热辐射基本定律和辐射特性
§8-1 热辐射现象的基本概念
1. 热辐射特点
(1) 定义：由热运动产生的，以电磁波形式传递的能量；
(2) 特点：a 任何物体，只要温度高于0K，就会不停地向周
围空间发出热辐射；b 可以在真空中传播；c 伴随能量形
可见光波段的辐射能量比例为 0.545 8－0.099 32 = 0.446 5
0.76 m ~ 40 m红外波段的辐射能量比例
1.0－0.545 8 = 0.454 2
计算表明： (1) 大气层外太阳辐射中可见光的能量比例接近45％，而
40 m以内的红外辐射也占大约45％。 (2) 太阳辐射温度下，40m以上的红外辐射能量几乎为零。
第八章热辐射的基本定律_传热学
发射的一切波长的能量
d () I () dA cos d
单位：W/m2· sr
2) Lambert定律：
黑体表面具有漫辐射性质，在半球空间各个方向辐射强度相等
I 1 I 2 ...... I n
E I cos I n cos En cos
如果已知黑体温度，则可以求得最大单色辐射力 Eb， max 所对应的波长 max
25
讨论：黑体温度在3800K以下时，其峰值波长处在红外线区域。 因此，在一般工程中所遇到的辐射换热，基本上属于红外辐射。
思考：金属在加热过程中，随 着温度的升高，金属颜色呈暗 红、红、黄、白，请解释这一 现象。
Fb 0－T
T E c1 b d T d T f T 5 0 T C2 5 b b T exp 1 T
30
根据黑体辐射函数，可以计算出给定温度下λ1－λ2波段内的 黑体辐射力为：
Eb 1－ 2 Eb Fb 0－ 2T Fb 0－1T
f (T )
23
三、维恩位移定律
黑体的峰值波长 max 与热力学温度T之间的函数关系
Eb
c15 ec
2
( T )
1
根据普朗克定律，将Eb 对 波长求极值，可得： maxT 2897.6m.K
随着温度T的升高，最大单色辐射 力 Eb， 所对应的峰值波长 max max 逐渐向短波方向移动
• 实际物体的辐射力并不严格遵从四次方定律,怎么办？ 认为E∝T4 由此引起的误差修正归入用实验方法确定的中 因此除了与物性有关，还与物体本身的温度有关
39
2 实际物体的光谱辐射力E
E Eb
d () I () dA cos d
单位：W/m2· sr
2) Lambert定律：
黑体表面具有漫辐射性质，在半球空间各个方向辐射强度相等
I 1 I 2 ...... I n
E I cos I n cos En cos
如果已知黑体温度，则可以求得最大单色辐射力 Eb， max 所对应的波长 max
25
讨论：黑体温度在3800K以下时，其峰值波长处在红外线区域。 因此，在一般工程中所遇到的辐射换热，基本上属于红外辐射。
思考：金属在加热过程中，随 着温度的升高，金属颜色呈暗 红、红、黄、白，请解释这一 现象。
Fb 0－T
T E c1 b d T d T f T 5 0 T C2 5 b b T exp 1 T
30
根据黑体辐射函数，可以计算出给定温度下λ1－λ2波段内的 黑体辐射力为：
Eb 1－ 2 Eb Fb 0－ 2T Fb 0－1T
f (T )
23
三、维恩位移定律
黑体的峰值波长 max 与热力学温度T之间的函数关系
Eb
c15 ec
2
( T )
1
根据普朗克定律，将Eb 对 波长求极值，可得： maxT 2897.6m.K
随着温度T的升高，最大单色辐射 力 Eb， 所对应的峰值波长 max max 逐渐向短波方向移动
• 实际物体的辐射力并不严格遵从四次方定律,怎么办？ 认为E∝T4 由此引起的误差修正归入用实验方法确定的中 因此除了与物性有关，还与物体本身的温度有关
39
2 实际物体的光谱辐射力E
E Eb
新大《传热学》复习题及解答第8章 热辐射基本定律和辐射特性
第8章热辐射基本定律和辐射特性（复习题解答）【复习题8-1】什么叫黑体？在热辐射理论中为什么要引入这一概念？答：吸收比α=l的物体叫做黑体。
黑体完全吸收投入辐射，从黑体表面发出的辐射都为自身辐射，没有反射，因而黑体辐射的特性反映了物体辐射的规律，这为研究实际物体的辐射提供了理论依据和简化分析的基础。
【复习题8-2］温度均匀的空腔壁面上的小孔具有黑体辐射的特性，那么空腔内部壁面的辐射是否也是黑体辐射？答：空腔内部壁面不一定是黑体辐射。
小孔之所以呈现黑体特性，是因为辐射在空腔内经历了多次的吸收和反射，辐射能基本基本都被内壁面吸收，从小孔射出的辐射能基本为零。
【复习题8-3］试说明，为什么在定义物体的辐射力时要加上“半球空间”及“全部波长”的说明？答：因为辐射表面会向半球空间各个方向辐射能量，且辐射能中包含各种波长的电磁波，而辐射力必须包括辐射面辐射出去的所有能量，所以要加上“半球空间”和“全部波长”的说明。
【复习题8-4】黑体的辐射能按波长是怎样分布的？光谱辐射力E根的单位中分母的“n?”代表什么意义？答：黑体辐射能按波长的分布服从普朗克定律。
光谱辐射力单位中的分母“n?”代表了单位辐射面积“n?”和辐射的电磁波单位波长范围“m”的意思。
【复习题8-5］黑体的辐射能按空间方向是怎样分布的？定向辐射强度与空间方向无关是否意味着黑体的辐射能在半球空间各方向上是均匀分布的？答：黑体辐射能按空间方向分布服从拦贝特定律。
定向辐射强度与空间方向无关并不意味着黑体的辐射能在半球空间是均匀分布的。
因为定向辐射强度是指单位可见辐射面积，而在空间不同方向可见辐射面积是不同的，辐射能在各个方向也不同。
【复习题8-6】什么叫光谱吸收比？在不同光源的照耀下，物体常呈现不同的颜色，如何解释？答：光谱吸收比是指物体对某一特定波长的投入辐射所吸收的百分比。
在光源照射下，物体会吸收一部分辐射，并反射一部分辐射，物体呈现的是反射光的颜色,因而光源不同，反射光也会不同，物体也会呈现不同的颜色。
热辐射基本定律及物体的辐射特性
本章的主要内容 （1）从电磁辐射的观点来认识热辐射的本质及辐射能传递过程 中的一些特性。 （2）讨论热辐射的三个基本定律。 （3）介绍实际物体（固体与液体）的辐射特性。 以便为下一章讨论辐射换热量的计算打下基础。
第八章 热辐射基本定律及物体的
1
辐射特性
§8-1 热辐射的基本概念
1热辐射的本质与特征
第八章 热辐射基本定律及
物体的辐射特性
热量传递的另一种方式——热辐射在过程的机理上与导热、对 流换热是根本不同的。导热与对流换热是由于物体的宏观运动和微 观粒子的热运动所造成的能量转移，而热辐射是由于物体的电磁运 动所引起的热量的传递。因而其研究方法与思路都与导热和对流换 热部分的讨论有很大的区别。
②黑体辐射函数:
第八章 热辐射基本定律及物体的
15
辐射特性
在许多实际问题中，往往需要确定某一特定波长区段内的辐射能量。 黑体在[λ 1,λ 2]区段所发出的辐射能为（见图7-7）
Eb
E d 2
1 b
通常把这一波段的辐射能表示成同温下黑体辐射力（0-∞）的
百分数，记为Fb(λ 1-λ 2)。于是
第八章 热辐射基本定律及物体的
18
辐射特性
图7-8 立体角定义图
第八章 热辐射基本定律及物体的
19
辐射特性
图7-9 计算微元立体角的几何关系
第八章 热辐射基本定律及物体的
20
辐射特性
②定向辐射强度的概念
任意微元表面在空间指定方向上 发射出的辐射能量的强弱，首先必 须在相同的立体角的基础上比较才 有意义。但还不够，因为在不同方 向上所能看到的辐射面积是不一样 的。见图（7-10）。微元辐射面dA 在任意方向p 看到的辐射面积不是 dA，而是dAcosθ 。所以，不同方向 上辐射能量的强弱，还要在相同的 可见辐射面积的基础上才能作出合 理的比较。
第八章 热辐射基本定律及物体的
1
辐射特性
§8-1 热辐射的基本概念
1热辐射的本质与特征
第八章 热辐射基本定律及
物体的辐射特性
热量传递的另一种方式——热辐射在过程的机理上与导热、对 流换热是根本不同的。导热与对流换热是由于物体的宏观运动和微 观粒子的热运动所造成的能量转移，而热辐射是由于物体的电磁运 动所引起的热量的传递。因而其研究方法与思路都与导热和对流换 热部分的讨论有很大的区别。
②黑体辐射函数:
第八章 热辐射基本定律及物体的
15
辐射特性
在许多实际问题中，往往需要确定某一特定波长区段内的辐射能量。 黑体在[λ 1,λ 2]区段所发出的辐射能为（见图7-7）
Eb
E d 2
1 b
通常把这一波段的辐射能表示成同温下黑体辐射力（0-∞）的
百分数，记为Fb(λ 1-λ 2)。于是
第八章 热辐射基本定律及物体的
18
辐射特性
图7-8 立体角定义图
第八章 热辐射基本定律及物体的
19
辐射特性
图7-9 计算微元立体角的几何关系
第八章 热辐射基本定律及物体的
20
辐射特性
②定向辐射强度的概念
任意微元表面在空间指定方向上 发射出的辐射能量的强弱，首先必 须在相同的立体角的基础上比较才 有意义。但还不够，因为在不同方 向上所能看到的辐射面积是不一样 的。见图（7-10）。微元辐射面dA 在任意方向p 看到的辐射面积不是 dA，而是dAcosθ 。所以，不同方向 上辐射能量的强弱，还要在相同的 可见辐射面积的基础上才能作出合 理的比较。
《传热学》第8章-热辐射基本定律及物体的辐射特性
2. 斯忒藩—玻耳兹曼定律
v 斯忒藩（J. Stefan）—玻耳兹曼（D. Boltzmann）定律确 定了黑体的辐射力Eb与热力学温度T之间的关系
v 斯忒藩在1879年从实验中得出，后来玻耳兹曼于1884年运
用热力学理论进行了证明。
斯忒藩—玻耳兹曼 常数，又称为黑体
辐射常数
Eb = σT 4
σ= 5.67×10-8
光谱辐射力: 只对某一波长辐射能的辐射力, Eλ ,单位为W/m3。
∞
∫ E =
E
0
λ
dλ
定向辐射力: 单位时间内，单位面积物体表面向某个方向发射 的单位立体角内的辐射能 , Eθ,单位是W/(m2⋅Sr)。
∫ E = Ω=2π Eθ dΩ
∫ E = L(θ) cosθdΩ Ω =2π
2
8-2 黑体辐射的基本定律
∫ ∫ Fb(λ1−λ2 ) =
Eb(λ1 −λ2 ) Eb
=
λ2 0
Ebλ dλ
−
Eb
λ1 0
Ebλ dλ
Eb
=
Fb (0−λ2 ) −
Fb (0−λ1 )
[ ] E = b(λ1 −λ2 ) Fb(0−λ2T ) − Fb (0−λ1T ) Eb
例题
v 试计算太阳辐射中可见光所占的比例。
解：太阳可认为是表面温度为T = 5762 K的黑体，可见光的 波长范围是0.38～0.76µm ，即λ1 = 0.38 µm , λ2 = 0.76 µm , 于是
∞
2 Ebλ dλ Eb
Fb(0−2) =0.02 .6341
= 0.45Fb(0−2) + 0.1(1− Fb(0−2) )
0.1
第8章 热辐射的基本定律PPT课件
47
结束语
当你尽了自己的最大努力时，失败也是伟大的， 所以不要放弃，坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人：XXXXXX 时 间：XX年XX月XX日
25
2－2 斯蒂芬－玻尔兹曼定律
传热学
斯蒂芬－玻尔兹曼定律表达式：
Eb Ebd
C1 5 C2
d
bT4
0
0eT1
W2 /m
Eb Cb(1T00)4 W/2m 黑体辐射常数
黑体辐射系数
26
传热学
工程上常计算某一波段范围内黑体的辐射能及其在 辐射力中所占的百分数。
2
E b(12) Ebd E E b(02) b(01) 1
辐射力与定向辐射力的关系
E Ed 2
辐射力与定向辐射强度的关系 辐射力与单色辐射强度的关系
E I cosd 2
E Icosdd 2 0
15
传热学
光谱辐射力（单色辐射力）：单位时间内，物体的每单 位面积，在波长λ附近的单位波长间隔内，向半球空间所 发射全波长的能量。
E
单位：W/(m2.μm)
Fb(0T)
Eb(0) Eb
0EbbTd40Tb(T)c51(ecT2
d(T)f(T)
1)
黑体辐射函数 f (T) 见表8-1
27
传热学
表8-1 ，黑体辐射函数表
F
b(0T ) 表示波长从0~ 的辐射能
占到了百分之多少！
28
传热学
例题8-3
已知某太阳能集热器的透光玻璃在波长 1
=0.35微米到 2 =2.7微米范围内的穿透比为
结束语
当你尽了自己的最大努力时，失败也是伟大的， 所以不要放弃，坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人：XXXXXX 时 间：XX年XX月XX日
25
2－2 斯蒂芬－玻尔兹曼定律
传热学
斯蒂芬－玻尔兹曼定律表达式：
Eb Ebd
C1 5 C2
d
bT4
0
0eT1
W2 /m
Eb Cb(1T00)4 W/2m 黑体辐射常数
黑体辐射系数
26
传热学
工程上常计算某一波段范围内黑体的辐射能及其在 辐射力中所占的百分数。
2
E b(12) Ebd E E b(02) b(01) 1
辐射力与定向辐射力的关系
E Ed 2
辐射力与定向辐射强度的关系 辐射力与单色辐射强度的关系
E I cosd 2
E Icosdd 2 0
15
传热学
光谱辐射力（单色辐射力）：单位时间内，物体的每单 位面积，在波长λ附近的单位波长间隔内，向半球空间所 发射全波长的能量。
E
单位：W/(m2.μm)
Fb(0T)
Eb(0) Eb
0EbbTd40Tb(T)c51(ecT2
d(T)f(T)
1)
黑体辐射函数 f (T) 见表8-1
27
传热学
表8-1 ，黑体辐射函数表
F
b(0T ) 表示波长从0~ 的辐射能
占到了百分之多少！
28
传热学
例题8-3
已知某太阳能集热器的透光玻璃在波长 1
=0.35微米到 2 =2.7微米范围内的穿透比为
传热学8-10章总结问答题及答案
第八章 热辐射基本定律和辐射特性一、名词解释黑体：指能吸收投入到其表面上的所有热辐射能量的物体。
其吸收比1=α灰体：在热辐射分析中，把光谱吸收比与波长无关的物体称为灰体漫射体：辐射能按空间分布满足兰贝特定律的物体投入辐射：单位时间内投入到单位表面积上的总辐射能吸收比：投入辐射中被吸收能量的百分比。
穿透比：投入辐射中穿透过物体能量的百分比。
反射比：投入辐射中被反射能量的百分比。
发射率： 物体的辐射力与同温度下黑体辐射力之比，为ε辐射力：单位辐射面积向半球空间辐射出去的各种波长能量的总和，E ，单位是2/m W 。
光谱辐射力：单位辐射面积向半球空间辐射出去的包括波长λ在内的单位波长间隔内的辐射能λE 定向辐射强度：单位可见辐射面积向半球空间θ方向的单位立体角中辐射出去的各种波长能量的总和。
二、解答题和分析题1、四次方定律、普朗克定律、兰贝特定律及维恩位移定律和基尔霍夫定律分别描述了什么内容？ 答案： 看书362页公式8-16下面有详细的总结。
2、影响实际物体吸收比和发射率的因素各有哪些？答：实际物体的吸收比取决于两方面的因素：1）吸收物体本身的情况。
系指物质的种类、物体的温度以及表面状况。
2）投入辐射的特性。
实际物体表面的发射率取决于物质的种类、表面温度和表面状况。
只与发射辐射的物体本身有关，而不涉及外界条件第九章 辐射传热的计算一、名词解释角系数：表面1发出的辐射能中落到表面2的百分数称为表面1对表面2 的角系数，记为2,1X 。
有效辐射：是指单位时间内离开表面单位面积的总辐射能。
二、解答题和分析题1、简述角系数的定义及其性质。
答：表面1发出的辐射能中落到表面2的百分数称为表面1对表面2 的角系数，记为X。
2,11）角系数的相对性 2）角系数的完整性 3）角系数的可加性2、分析气体辐射的基本特点？(1) 气体辐射对波长具有选择性。
它只在某些波长区段内具有发射和吸收辐射的本领，而对于其他光带则呈现透明状态。
传热学-第八章 热辐射特性
§ 8-3 固体和液体的辐射特性
发射率 前面定义了黑体的发射特性：同温度下，黑体发射热辐 射的能力最强，包括所有方向和所有波长；
真实物体表面的发射能力低于同温度下的黑体；
因此，定义了发射率 (也称为黑度) ：相同温度下，实际 物体的半球总辐射力与黑体半球总辐射力之比:
E E 4 Eb T
c2 T
5
0
1
d T
0
内所发射的辐射力：
Eb 1 2 Fb 0 2 Fb 0 1 Eb
图8-7 特定波长区段内的黑体辐射力
11
立体角
定义：球面面积除以球半径的平方称为立体角，单位：sr(球面度)
dAc rd r sin d d 2 sin d d 2 r r
0.76 0.38
Eb dλ=0.45Fb0.380.76 Eb
E 0.380.76 E
§8-4
实际物体对辐射能的吸收与辐射的关系
上一节简单介绍了实际物体的发射情况，那么当外界 的辐射投入到物体表面上时，该物体对投入辐射吸收 的情况又是如何呢？
Semi-transparent medium
吸收比为
吸收的总能量 1 投入的总能量
0
( , T1 ) ( , T2 ) Eb (T2 )d
0
( , T2 ) Eb (T2 )d
f (T1 , T2 , 表面1的性质， 表面2的性质)
32
如果投入辐射来自黑体，由于 b ( , T2 ) 1 ，则上式可为
第八章 热辐射基本定律 和辐射特性
1
§8-1 热辐射的基本概念
传热学第八章 热辐射基本定律和辐射特性资料
（服从兰贝特定律的辐射，E 与 I 存在倍数关系）
河海大学常州校区热能与动力工程系—传热学
2020年9月14日9时1分 杨祥花
注意：
• 黑体表面为漫辐射表面 • 漫辐射表面：辐射强度在空间各个方向上都相等
• 只有漫辐射表面：Ι是常数
河海大学常州校区热能与动力工程系—传热学
2020年9月14日9时1分 杨祥花
2020年9月14日9时1分 杨祥花
• 关于物体的颜色
我们所看到的物体颜色是由于从该表面发出的单 色光线（辐射）投入到了我们的眼睛。
•
而从表面发出的辐射可能是自身发射的，也可能是反射投入
其表面上的可见光。
• 如果物体全部吸收各种可见光，它就呈黑色；
• 如果物体全部反射各种可见光，它就呈白色；
• 如果物体只反射了一种波长的可见光，则它就呈现该反射的辐射 线的颜色。
在可见光部分呈白色）不一定是白体；黑颜色物体 不一定是黑体
• 例如：雪对可见光是良好的反射体，所以肉眼看到 是白色的，但对红外线几乎能全部吸收α= 0.985 ， ε= 0.8
• 白布和黑布对可见光吸收率不同，但对红外线的吸 收率基本相同
• 玻璃只透过可见光，对λ> 3 µ m的红外线不透明
河海大学常州校区热能与动力工程系—传热学
（8-19）
则
E 1 Eb T 4
0
E d
1
T
4
0 Eb d
E
Eb
T
4
C0
(T 100
)4
W
m2
（8-18）
河海大学常州校区热能与动力工程系—传热学
2020年9月14日9时1分 杨祥花
2、定义定向发射率（定向黑度）
传热学第八章-热辐射基本定律和辐射特性
( )
I ( ) I ( ) I b ( ) Ib
Emission from Real Surface vs. Blackbody Directional distribution Spectral distribution Total, hemisphere
光谱发射率：实际物体光谱辐射力与同温度黑体光谱辐射力的比值。
E
0
E d
辐射力是光谱辐射力曲线下的总面积 黑体一般采用下标 b 表示，如黑体的辐射力为Eb，黑体的光谱辐射力为Ebλ 黑体辐射三大定律：普朗克定律、斯忒潘-玻耳兹曼定律、兰贝特定律
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong Unive热辐射的吸收、反射与穿透： 可见光、声波、热射线
Q Q Q Q
能量守恒
Q Q Q 1 Q Q Q 1
式中α、ρ和τ 分别为吸收比、反射比和穿透比 黑体：α＝1 镜体（白体）： ρ＝ 1 透明体： τ ＝1 辐射表面的状况影响大
( )
E Eb
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
8-3 实际固体和液体的辐射特性
发射率：实际物体辐射力与同温度黑体辐射力的比值。 Emission from Real Surface vs. Blackbody Directional distribution Spectral distribution Total, hemisphere
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d 45o IdA b cos 2 d 2 7000 W / m 2 sr 2 103 m 2 1 4.00103 sr 1.9810 2 W 2 16
7000 W / m 2 sr 103 m 2 3.46103 sr 2.8010 2 W
c=fλ
c=3*108m/s为电磁波传播速度，f为频率，λ为波长。
2. 电磁波的波谱 2000k以下热辐射: 0.8~100μm 可见光波长：0.38~0.76 μm 太阳辐射能量：0.2~2 μm 热辐射研究的波长区段为：
0.1~100μm
3
第8章 热辐射基本定律和辐射特性
不同波长热辐射的用途： 1) 以25μm为界分为近红外线和远红外线，对物体进行远红外线加热。 2) 1mm~1m的电磁波为微波，能穿透塑料玻璃和陶瓷，会被水吸收产生 内热源，对物体均匀加热。(转，蚂蚁) 3) 大于1m的电磁波广泛用于无线电技术。 3. 物体表面对电磁波的作用 (1) 吸收比、反射比与穿透比之间的一般关系 热辐射投射到物体表面时，分为三部分 吸收能量—Qα—吸收率—α
第8章 热辐射基本定律和辐射特性
8.3 固体和液体的辐射特性(实际物体)
黑体是研究热辐射的标准物体，对于实际物体的辐射特性，将在与黑体 的辐射特性进行对比的基础上进行研究。
8.3.1 实际物体的辐射力
实际物体的辐射力E总是小于同温度下的黑体的辐射力Eb，两者的比值 称为实际物体的发射率，记为ε： E Eb 实际物体的辐射力E可以表示为：
光谱辐射力最大处的波长λm亦随温度不同而 变化： mT 2.8976103 m K 2.9 103 m K 随着温度的增高，最大光辐射力的波长会减 小，曲线峰值向左移动。 波长与温度成反比的规律称为维恩位移定律 3. 普朗克定律与斯忒藩-玻耳兹曼定律的关系 光辐射力曲线下的面积就是该温度下黑 体的辐射力
黑体模型：
自然界不存在黑体，但是可以通过人工方法制造出类似黑体的模型。 选择吸收比较大的材料制造一个空腔，并在壁面上开一个小孔，并使空
腔壁面保持均匀的温度，这种带有小孔的温度均匀的空腔就是黑体模型 特点： 1) 在一定的小孔面积和腔体总面积之比下，材料本身的吸收比越大，黑
体模型的有效吸收比越大；反之亦然。 2) 等温空腔内部的辐射是均匀且各向同性的，在相同物体中，黑体的辐
Eb
光辐射能力随着波长的 c15 c 2 / T 增加，先是增加，然后 e 1 又减少
λ— 波长，m ； T — 黑体温度，K ； c1 — 第一辐射常数，3.742×10-16 Wm2；
c2 — 第二辐射常数，1.4388×10-2 WK；
8
第8章 热辐射基本定律和辐射特性
10
第8章 热辐射基本定律和辐射特性
8.2.3 兰贝特定律
兰贝特定律是黑体辐射能按空间方向的分布规律； 1. 立体角 二维空间中利用平面角表示某一方向空间所占的大小； 三维空间中利用立体角及微元立体角表示某一方向的空间所占的大小 Ac dAc Ω 2 dΩ 2 r r 在球坐标中， 为经度角， 为纬度角 空间的方向可以用该方向的纬度角和
d d I I为常数，与θ方向无关 I cos 或者 dAd cos dAd dA cos 可以视为从θ方向看过来的面积，称为可见面积 右边公式中左端物理量时从黑体单位可见面积发射出去的落到空间任意 方向的单位立体角中的能量，称为定性辐射强度。
12
同方向分布是不均匀的，按空间纬度角θ的余
弦规律变化：在垂直于该表面的方向最大，而 在于表面平行的方向为零，称为余弦定律
Lambert定律图示
13
第8章 热辐射基本定律和辐射特性
4. 兰贝特定律与斯忒藩-玻耳兹曼定律间的关系 在公式(8-15a)两端各乘以dΩ，然后对整个半球空间进行积分，得到从 单位黑体表面发射出去落到整个半球空间的能量，即黑体的辐射力。 d Eb I b cos d 总结： 2 2 dA 1. 黑体的辐射力由斯忒藩-玻耳兹曼 将公式(8-14)代入上式得 定律确定，辐射力正比于热力学温度 的四次方 ； 2. 黑体辐射能量按波长的分布服从普 2 2 I b d cos sin d 朗克定律，而按照空间方向的分布服 0 0 I b 从兰贝特定律 遵守兰贝特定律的辐射，数值上其 3. 黑体的光辐射能力有个峰值，与此 辐射力等于定向辐射强度的π倍。 峰值相对应的波长由维恩位移定律确 定，随着温度的升高，λm向波长短 的方向移动。
的全部波长范围内的能量,记为E,其单位为W/m2。
黑体辐射力与热力学温度的关系由斯忒藩-波耳兹曼定律确定： σ=5.67*10-8W/(m2K4)为黑体辐射常数， 4 T Eb T 4 C0 C0=5.67W/(m2K4)称为黑体辐射系数，
100
下角码b表示黑体
以上公式称为辐射四次方定律，是辐射传热计算基础； 该公式表明：随着温度上升，辐射力急剧增大。
Fb 0
0
Eb d
T
4
0
c1 T 1 d T f T c 2 / T e 1
5
黑体辐射函数
任意两个波长λ2、λ1之间黑体的辐射能为
Eb1 2 Fb1 2 Eb Fb02 Fb01 Eb
面积dA1，dA2和dA3所吸收的来
自黑体微元面积的能量，后者 还与三个微元面积本身的辐射
特性有关。
d 60o IdA b cos1d1 1 7000 W / m 2 sr 103 m 2 3.46103 sr 1.2110 2 W 2 d 0o IdA b cos1d 2
对辐射能没有反射能力，只能吸收或穿透。 (2) 固体表面的两种反射 镜面反射：物体表面的不平整尺寸小于投入辐射的波长时 辐射能的 反射方式 漫反射：物体表面的不平整尺寸大于投入辐射的波长时
5
第8章 热辐射基本定律和辐射特性
8.1.3 黑体模型及其重要性
绝对黑体：吸收比为1的物体 镜体：反射比为1的物体 绝对透明体：穿透比为1的物体 由理想情况到 复杂情况分析
E Eb d
0
0
c15 d c 2 / T e 1
9
第8章 热辐射基本定律和辐射特性
4. 黑体辐射能按波段的分布 为了确定在某个特定的波段范围内黑体的辐射能，需要对Ebλ进行积分 Eb 0 Eb d
0
这份能量在黑体辐射力中所占的百分数为：
经度角表示。
立体角的单位称为空间度，记为sr 从图中可以看出，单位面积可以表示为：dA c rd r sin d
从而得到微元立体角为： d sin dd
11
第8章 热辐射基本定律和辐射特性
2. 定向辐射强度 相同纬度角、不同经度角下，从微元黑体面 积dA单位立体角中辐射出去的能量是相等的， 因此，只要查明辐射能按不同纬度角分布的 规律就可以了。 设面积为dA的黑体微元面积向围绕空间纬度 角θ方向的微元立体角dΩ内辐射出去的能量 为dΦ(θ)，则实验测定表明：
可得到所求解的能量。
15
第8章 热辐射基本定律和辐射特性
计算：根据公式(8-12)可以得到
d1
3 2 o
dA 10 m cos30 3 1 3 . 46 10 sr 体角中的能量，但未必是微元 2 2 r 0.5m
注意：本题得出的是落到该立
dA2 103 m 2 cos0o 3 d 2 2 4 . 00 10 sr 2 r 0.5m dA3 103 m 2 cos0o d3 2 4.00103 sr 2 r 0.5m
第8章 热辐射基本定律和辐射特性
8.1 热辐射现象的基本概念
8.2 黑体热辐射的基本定律
8.3 固体和液体的辐射特性 8.4 实际物体对辐射能的吸收与辐射的关系 8.5 太阳与环境辐射
1
第8章 热辐射基本定律和辐射特性
8.1 热辐射现象的基本概念 8.1.1 热辐射的定义及区别导热对流的特点
定义：由热运动产生的，以电磁波的形式传递能量的一种现象。它是物 体内部微观粒子的热运动状态发生改变时激发出来的。 特点：1) 任何物体，只要温度高于绝对温度0 K，就会不停地向周围空 间发出热辐射；2) 热辐射的能量传递不需要任何介质，且在真空 中传递效率最高；3) 伴随电磁能和热能之间的能量形式的转变； 4) 热辐射具有强烈的方向性；5) 辐射能与温度和波长均有关； 6) 热辐射的热量取决于绝对温度的4次方。
射能力和吸收能力都是最大的。
6
第8章 热辐射基本定律和辐射特性
8.2 黑体热辐射的基本定律
三个定律分别从不同角度揭示在一定的温度下，单位表面黑体辐射能的
多少及其随空间方向与随波长分布的规律。
8.2.1 斯忒藩-波尔兹曼定律
为了定量分析热辐射能量大小，引入辐射力的概念 辐射力：单位时间内单位表面积向其上的半球空间的所有方向辐射出去
14
Eb I b cos sin dd
ห้องสมุดไป่ตู้
第8章 热辐射基本定律和辐射特性
例题8-4 有一个微元黑体面积dAb 103 m2 ，与该黑体表面相距0.5m处另 有三个微元面积dA1，dA2，dA3,面积均 为 103 m 2 ，该三个微元面积的空 间方位如图中所示。使计算从dAb发出分别落在dA1，dA2，dA3对dAb所 张的立体角中的辐射能量。 分析：现根据dA1，dA2 和dA3的大小与方向确定 它们对dAb所张的立体角， 然后根据公式(8-15a)即
7
第8章 热辐射基本定律和辐射特性
8.2.2 普朗克定律
普朗克定律揭示了黑体辐射能按波长分布的规律 1. 光谱辐射力 定义：单位时间内单位表面积向其上的半球空间的所有方向辐射出去的 在包含波长λ在内的单位波长内的能量，Ebλ，单位W/(m2· μm) 2. 普朗克定律 黑体的光辐射力随波长的变化关系为：