八年级数学立方根同步练习
青岛版(五四)数学八年级下7.7用计算器求平方根和立方根(同步练习)

7.7 用计算器求平方根和立方根一、选择题1.被开方的小数点向右移动两位查得的平方根的小数点相应地()A.向左移两位 B.向右移两位C.向左移一位 D.向右移一位2.已知:250.2062.5=,115.762.50=,则=±2.506()A.22.50 B.71.15C.50.22± D.15.71±3.已知858.46.23=,536.136.2=,则00236.0的值等于()A.485.8 B.15360 C.0.01536 D.0.048584.已知208.146.1=,则下列值为08.12±的是()A.146B.0146.0±C.146±D.6.14±5.由140.542.26=,下列各式的值可求得的是()A.642.2 B.0146.0±C.146±D.6.14±6.已知2250.0,115.762.50,250.2062.5===x,则x等于()A.5.062 B.0.5062 C.0.005062 D.0.050627.若58.674567,137.2567.4==,则0.4567的平方根是()A.02137.0± B.06758.0±C.2137.0D.6758.0±二、填空题1.710.153=,则=35000,=3005.0.2.若684.3503=,则=-305.0.3.若7937.05.03=,则=⨯--35105 . 4.709.288.193=,则=319880 . 5.若68.28,868.26.2333==x ,则x=__.6.若107.330,442.1333==,则=303.0 ,=3003.0 . 7.比较大小:36.15 38.17. 8.94.66,6694.03.033-==x 则x=__.三、解答题1.求下列各数的近似值(保留四个有效数字):.7473,516,36218,09.14,9.25,86-2.求下列各数的平方根(保留三个有效数字):42,53.4,7629.3,0.00256,.197128,9417,325 3.求出下列各组数的算术平方根,保留四个有效数字,并研究一下这些数的算术平方根有什么规律,你自己再按这个规律列出一些数,求出它们的算术平方根,看一看是否符合你找出的规律:(1)46000,460,4.6,0.046,0.00046.(2)460000,4600,46,0.46,0.0046.4.求下列各数的近似值(保留四个有效数字):,3142,536,33.21,691.5,8.412,693333335.求下列各数的立方根,保留四个有效数字,并研究一下这些数的立方根有什么规律,你自己再按这个规律列出一些数,求出它们的立方根,看一看是否符合你找出的规律:(1)36000,36,0.036;(2)360000,360,0.36;(3)3600,3.6,0.0036.6.求下列各数的算术平方根(保留四个有效数字):438000,25.964,0.000512,3.28×104,7.85×106,2.22×10-4.7.求下列各数的立方根(保留四个有效数字):927000,-42.369,0.000193,2.81×105,-1.32×106,3.56×10-5.8.一个面积为60cm2的正方形纸片的边长是多少?用四张这样的纸片拼成一个正方形,拼成的正方形的边长是多少?用一百张这样的纸片拼成一个大正方形,这个大正方形的边长是多少?(精确到0.1cm)9.如图,一个小正方体的体积为100cm3,这个正方体的棱长是多少cm,要拼成一个如图那样的大正方体,需要多少块体积为100cm3的小正方体?拼成的大正方体的棱长是多少cm?(精确到0.1cm)10.用六块面积为80cm2的正方形组成一个立方体的六个面,这个立方体的体积是多少立方厘米?11.在一个长5.80m,宽2.90m,高3.3m的集装箱里,装进体积为0.064m3的正方体的纸箱,最多可装入多少只这样的纸箱?参考答案一、选择题1. C 2.C 3.D 4.C 5.B 6. D 7.D二、填空题1.17.10,0.1710 2.-0.3684 3.79.37 4. 27.09 5.236006.0.3107 0.1442 7. < 8.-300000三、解答题1.9.274,5.089,3.754,190.3,-2.490,8.5772.±6.48,±7.31,±87.3,±0.0515,±2.38,±4.18,±11.32·1·c·n·j·y3.(1)214.5,21.45,2.145,0.2145,0.02145(2)678.2,67.82,6.782,0.6782,0.06782被开方数的小数点向左或向右移动两位,平方根的小数点向左或向右移动一位.4.4.102,7.446,1.785,2.773,1.876,6.506,5.(1)33.02,3.302,0.3302;(2)71.14,7.114,0.7114;(3)15.33,1.533,0.1533.被开方数的小数点向左或向右移动三位,立方根的小数点向左或向右移动一位.6.66.18,5.095,0.02263,181.1,2802,0.014907.97.50,-3.486,0.05779,65.50,-109.7,0.032908.7.7cm,15.5cm,77.5cm9.4.6cm,27块,13.9cm.10.正方形边长为8.94cm,立方体的体积为714.5cm3.11.784只.初中数学试卷。
2022-2023学年北师大版八年级数学上册《2-3立方根》填空题专项练习题(附答案)
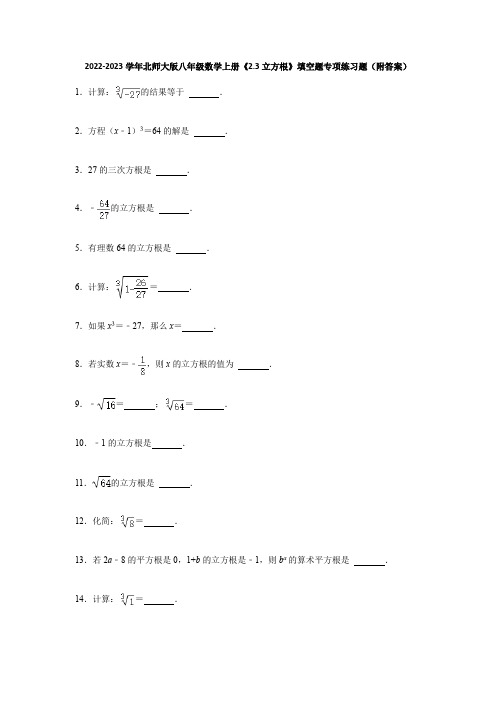
2022-2023学年北师大版八年级数学上册《2.3立方根》填空题专项练习题(附答案)1.计算:的结果等于.2.方程(x﹣1)3=64的解是.3.27的三次方根是.4.﹣的立方根是.5.有理数64的立方根是.6.计算:=.7.如果x3=﹣27,那么x=.8.若实数x=﹣,则x的立方根的值为.9.﹣=;=.10.﹣1的立方根是.11.的立方根是.12.化简:=.13.若2a﹣8的平方根是0,1+b的立方根是﹣1,则b a的算术平方根是.14.计算:=.15.计算的结果等于.16.计算:=.17.的立方根是.18.﹣=.19.计算:=.20.有理数﹣8的立方根是.21.一个正数a的两个平方根是2b﹣1和b+4,则a+b的立方根为.22.若实数x,y满足(2x+3)2+|9﹣4y|=0,则xy的立方根为.23.已知m﹣7和2m+4是某正数的两个平方根,n﹣7的立方根是1,m+n的平方根.24.有一个数值转换器,原理如图所示,当输入的x为512时,输出的y是.25.观察下列各式,并用所得出的规律解决问题:(1)≈1.414,≈14.14,≈141.4…≈0.1732,≈1.732,≈17.32…由此可见,被开方数的小数点每向右移动位,其算术平方根的小数点向移动位;(2)已知≈2.236,≈7.071,则≈,≈;(3)=1,=10,=100…小数点变化的规律是:;(4)已知=2.154,=4.642,则=,﹣=.参考答案1.解:=﹣3,故答案为:﹣3.2.解:∵(x﹣1)3=64,∴x﹣1==4.解得x=5.故答案为:5.3.解:∵33=27,∴,故答案为:3.4.解:因为(﹣)3=﹣,所以﹣的立方根是﹣,故答案为:﹣.5.解:有理数64的立方根是4,故答案为:4.6.解:原式==.故答案为:.7.解:∵(﹣3)3=﹣27,而x3=﹣27,∴x=﹣3,故答案为:﹣3.8.解:∵实数x=﹣,∴x的立方根的值为:﹣.故答案为:﹣.9.解:﹣=﹣4,=4.故答案为:﹣4、4.10.解:∵(﹣1)3=﹣1∴﹣1的立方根是﹣1.11.解:∵=8,23=8,∴的立方根是2,.故答案为:2.12.解:∵23=8∴=2.故填2.13.解:由题意可知:2a﹣8=0,1+b=﹣1,∴a=4,b=﹣2,∴原式=(﹣2)4=16,∴16的算术平方根是4,故答案为:4.14.解:∵13=1,∴1的立方根是1,即=1,故答案为:1.15.解:∵(﹣)3=﹣,∴=﹣.故答案为:﹣.16.解:=﹣2.故答案为:﹣2.17.解:∵3的立方等于=27,∴的立方根等于3,故答案为:3.18.解:∵,∴,∴,故答案为:﹣.19.解:原式=﹣.故答案为:﹣.20.解:∵(﹣2)3=﹣8,∴有理数﹣8的立方根是﹣2.故答案为:﹣2.21.解:∵一个正数a的两个平方根是2b﹣1和b+4,∴2b﹣1+b+4=0,∴b=﹣1.∴b+4=﹣1+4=3,∴a=9.∴a+b=9+(﹣1)=8,∵8的立方根为2,∴a+b的立方根为2.故答案为:2.22.解:∵(2x+3)2+|9﹣4y|=0,∴2x+3=0,解得x=﹣,9﹣4y=0,解得y=,xy=﹣×=﹣,∴xy的立方根为﹣.故答案为:﹣.23.解:∵m﹣7和2m+4是某正数的两个平方根,∴m﹣7+2m+4=0,解得m=1;∵n﹣7的立方根是1,∴n﹣7=1,解得n=8,∴m+n=1+8=9,∴m+n的平方根为±3.故答案为:±3.24.解:由题中所给的程序可知:把512取立方根,结果为8,因为8是有理数,所以再取立方根为2,2是有理数,所以再取立方根为,因为是无理数,输出,故答案为:.25.解:(1)由被开方数的小数点、其算术平方根的小数点的移动规律可知,被开方数的小数点每向右移动2位,其算术平方根的小数点向右移动1位,故答案为:2,右,1;(2)由(1)的规律可得,≈0.7071,≈23.26,故答案为:0.7071,23.26;(3)由(1)的结论类推可得,一个数的小数点向右移动3位,其立方根的小数点向右移动1位,故答案为:一个数的小数点向右移动3位,其立方根的小数点向右移动1位;(4)由(3)的结论得,==×10=21.54,﹣=﹣=﹣=﹣0.4642,故答案为:21.54,﹣0.4642.。
新人教数学 8年级上:同步测控优化训练(10.2立方根)

立方根5分钟训练(预习类训练 ,可用于课前)1.以下说法不正确的选项是( )A. -1的立方根是 -1B. -1的平方是1C. -1的平方根是 -1D.1的平方根是±1解析:求某些数的平方根或立方根,常利用其定义来解.答案:C2.以下说法中正确的有( )①±2都是8的立方根 ②x x =33 ③81的立方根是3 ④38-- =2A.1个B.2个C.3个D.4个解析:根据立方根的意义判断.因为8的立方根是2,81的立方根是39,所以说法①③错误,说法②④正确.答案:B3.(1)23 =8,所以_____________是_____________的立方根.(2) ( -5)3 = -125,所以_____________是_____________的立方根.(3) ( )3 = -27,所以 -27的立方根是_____________.(4) ( )3 =4,所以4的立方根是_____________.解析:根据立方根的意义答复.答案: (1)2 8 (2) -5 -125 (3) -3 -3 (4)3434 4.求以下各数的立方根:(1) -27; (2 )1258; (3 ); (4 ) -5. 分析:根据立方根意义可求解.解: (1 )因为 ( -3 )3 = -27,所以 -27的立方根是 -3,即327- = -3;(2 )因为1258)52(3=,所以1258的立方根是52; (3 )因为3 =0.216,所以的立方根是0.6,即3216.0 =0.6;(4 ) -5的立方根是35-.10分钟训练(强化类训练 ,可用于课中)1.立方根等于本身的数是( )A. -1B.0C.±1D.±1或0解析:在实数范围内,一个数的立方根只有一个,并且它们同号.[来源:学科网ZXXK] 答案:D2.以下说法错误的个数是( )①负数没有立方根 ②1的立方根与平方根都是1 ③38的平方根是±2 ④361的立方根是61A.1B.2C.3D.4解析:根据立方根与平方根的意义可知,负数有立方根,1的平方根是±1,38的平方根是±2,361的立方根是3361,所以说法①③④不正确,说法③正确. 答案:C 3.33)6(- =____________,3027.0- = ____________.解析:根据33a =a, 33a a -=-答复.答案:4.估算以下数的大小.(1 )3261 (误差小于1 ); (2 )5.25(误差小于0.1).解析:估算一个根号表示的无理数一般是采用夹逼方法.解: (1 )因为6<3261<7,所以3261≈6或7.(2 )因为5.0<5.25<5.1,所以5.25或5.0.5.用计算器求:(1 )的平方根 (精确到 );(2 )36 -35228 (结果保存四个有效数字 );(3 )39578.0 (精确到 );[来源:学,科,网Z,X,X,K](4 )315786- (精确到 ).解析:用计算器可求得.如果求一个负数的立方根,可以先求它的相反数的立方根,再在结果前加上负号即可.[来源:学科网ZXXK]解:(1)±18.23 =±4.815.[来源:学科网ZXXK](2)3635228-≈541.3. (3)39578.0≈0.986. (4)315786-≈ -25.086.6.某化工厂使用一种球形储气罐储藏气体.现在要造一个新的球形储气罐,如果它的体积是原来的8倍,那么它的半径是原储气罐半径的多少倍?提示:利用球体的体积公式得出变化前后半径的关系式,化简后开立方.解:设原来的球形储气罐的半径为r 1,后来的储气罐的半径为r 2,由球体积公式V =334r π得8×32313434r r ππ=, 所以8r 13 =r 23.[来源:Z +xx +] 所以r 2 =3318r .所以r 2 =2r 1,答:新储气罐的半径是旧储气罐半径的2倍.30分钟训练(稳固类训练 ,可用于课后)1.(甘肃兰州模拟,1)函数y =42113-+-x x 的自变量x 的取值范围是( ) A.x≥1且x≠2 B.x≠2C.x >1且x≠2解析:开立方时被开方数可取任意实数,分母不能为零,所以x≠2.答案:B是 (9- )2的平方根,y 是64的立方根,那么x +y 的值为( )A.3B.7C.3,7D.1,7解析:因为(9-)2 =9,x 是 (9- )2的平方根,所以x =±3.因为y 是64的立方根,所以y =4.当x =3时,x +y =7.当x = -3时,x +y = -3 +4 =1.答案:D3.(1)比拟大小:325_____________25.(2)利用计算器,比拟大小:138____________216-. 解析:(1)因为25 =5,而53 =125>25,所以325<5,即325<25;(2)求出近似值再作比拟.答案:(1)< (2)<4.求以下各式的值: (1)38-;(2)3064.0;(3)31258-;(4)33)9(. 分析:根据立方根性质可求解.解: (1 )333)2(8-=- = -2; (2)333)4.0(064.0= =0.4; (3)52)52(1258333-=--;(4)(39)3 =9.5.求以下各式中的x.(1)8x 3 +125 =0;(2)(x +5)3 = -27.解析:此题实质上是解关于x 的三次方程,两边开立方是解此类题的最|根本方法.第 (1 )小题变形可得x 3 =8125-,所以x 是8125-的立方根;第 (2 )小题中,x +5是 -27的立方根,两边开立方求出x +5后再求x. 解: (1 )∵8x 3 +125 =0,∴x 3 =8125-. ∴x =38125-,即x =25-. (2 )∵(x +5)3 = -27,∴x +5 =327-,即x +5 = -3.∴x = -8.[来源:Z .xx ]6.求满足31-x +1 =x 的x 的值.分析:移项后得31-x =x -1,从而由 "0,1, -1的立方根等于它本身〞可求得x 的值. 解:因为31-x =x -1,[来源:学#科#网Z#X#X#K]所以x -1 = -1或x -1 =0或x -1 =1.所以x =0或x =1或x =2.7.一个正方体木块的体积是125 cm 3,现将它锯成8块同样大小的正方体小木块,求每个小正方体木块的外表积.提示:先根据正方体体积求得正方体木块的边长,再求外表积.解析:设小正方体木块的边长为a,那么a 3 =8125,a =25cm, 所以外表积 =6a 2 =6×(25)2 =275 cm 2.[来源:学|科|网Z|X|X|K] 8.实数x 、y 满足32--y x +(2x -3y -5)2 =0,求x -8y 的平方根和立方根.提示:利用 "如果几个非负数的和等于0,那么这几个非负数都为0”.解析:由题意可知32--y x =0且(2x -3y -5)2 =0,即⎩⎨⎧=--=--,0532,032y x y x 解这个方程组得⎩⎨⎧-==,1,1y x ∴9)1(818±=-⨯-±=-±y x =±3. ∴3398=-y x .9.一个正方体的棱长是5 cm,再做一个正方体,使它的体积是原正方体的体积的2倍,求所做的正方体的棱长(精确到0.1 cm ).解析:正方体的棱长等于体积的立方根.设所做的正方体的棱长为a (a>0 ),那么a3 =2×53,所以a =5×32≈6.3(cm).答:所做的正方体的棱长为6.3 cm.10.任意找一个小于1的正数,利用计算器对它不断进行开立方的运算,其结果如何?根据这个规律,比拟3a和a(0<a<1)的大小.[来源:学#科#网Z#X#X#K]提示:这是一道蕴含极限思想的数学问题,主要是利用计算器去探索规律,并要记住这一规律. 解析:任意找一个小于1的正数,利用计算器对它不断进行开立方的运算,其结果是随着开方次数的增加,运算结果越来越接近于1.[来源:Z,xx,]当0<a<1时,3a>a.。
初中数学冀教版八年级上册第十四章 实数14.2 立方根-章节测试习题(2)

章节测试题1.【答题】立方根是-8的数是______,的立方根是______.【答案】-512,2【分析】根据平方根以及立方根的定义即可求解.【解答】根据立方根的意义,由(-8)3=-512,所以立方根是-8的数是-512;根据算术平方根的意义可知=8,然后由23=8,可知8的立方根为2,即求得的立方根为2.故答案为:-512;2.方法总结:此题主要考查了求一个数的立方根,根据立方根的意义,一个数的立方等于a,那么这个数就是a的立方根,关键是判断a是谁的立方.2.【答题】9的平方根是______;的立方根是______.【答案】3,-3;-2【分析】根据平方根以及立方根的定义即可求解.【解答】因为3的平方是9,-3的平方是9,所以9的平方根是,因为-2的立方是-8,所以-8的立方根是-2,故答案为: ,-2.3.【答题】已知,则a和b的关系是______.【答案】互为相反数【分析】已知等式利用立方根定义化简,得出a与b关系即可.【解答】因为,所以与互为相反数,则a与b互为相反数,故答案为互为相反数.4.【答题】的算术平方根是______,-8的立方根是______.【答案】2,-2【分析】根据算术平方根以及立方根的定义即可求解.【解答】=4,4算术平方根是2;-8的立方根是-2.故答案为2,-25.【答题】如果一个数的平方根等于这个数的立方根,那么这个数是______.【答案】0【分析】根据平方根与立方根的定义求解.【解答】根据平方根与立方根的定义,可知0的平方根等于0的立方根.故答案为:0方法总结:本题考查了立方根:如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果x3=a,那么x叫做a的立方根.记作:,也考查了平方根.6.【答题】若=-7,则a=______.【答案】-343【分析】根据立方根的定义直接计算.【解答】解:∵,∴a=-343故答案为:-3437.【答题】已知2x+1的平方根是±5,则5x+4的立方根是______.【答案】4【分析】根据平方根的定义即可得到一个关于x的方程求得x的值,进而得到5x+4的值,然后根据立方根的定义即可求解.【解答】解:根据题意得:即2x+1=25,解得:x=12.则5x+4=5×12+4=64,64的立方根是4.故答案为:4.8.【题文】求下列各式中的的值:(1);(2);(3);(4);【答案】(1)或;(2)3或-2;(3)-1;(4)-【分析】(1)两边同时除以4后开平方,然后解一元一次方程可得;(2)直接开平方得2x﹣1=±5,然后解该一元一次方程可得;(3)两边同时除以3后,开立方即可;(4)移项后,再开立方后解方程即可.【解答】解:(1)(2-x)2=,∴x-2=或x-2=﹣,解得:x=或x=;(2)2x﹣1=±5,∴2x﹣1=5或2x﹣1=-5,解得:x=3或-2;(3)由得:(x﹣4)3=-125,∴x﹣4=﹣5,解得:x=﹣1;(4)由得:(2x﹣1)3=-8,∴2x﹣1=-2,解得:.9.【题文】(1)已知2a-1的平方根是±3,3a+b-1的立方根是2,求2a-b的平方根.(2)我们知道时,也成立,若将a看成的立方根,b看成的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.①试举一个例子来判断上述猜测结论是否成立;②若与互为相反数,求的值.【答案】(1) ±4;(2) 结论成立;-1【分析】(1)先根据平方根、立方根的定义得到关于a、b的二元一次方程组,解方程组即可求出a、b的值;将a、b的值代入2a-b,进而得到2a-b的平方根.(2)①结合立方根的概念,可用2与-2来验证;②根据题目中的结论可将与互为相反数转化为1-2x与3x-5互为相反数,由此求出x的值后代入计算.【解答】解(1) ∵2a-1的平方根是±3,∴2a-1=9,a=5, ∵3a+b-1的立方根是2,∴3a+b-1=8,∴b=-6, ∴2a-b=16, ∴2a-b的平方根是±4.(2) ①∵2+(-2)=0,而且,有8+(-8)=0,∴若两个数的立方根互为相反数,则这两个数也互为相反数结论成立;②由(1)验证的结果知, 若两个数的立方根互为相反数,则这两个数也互为相反数,∴(1-2x)+(3x-5)=0,∴x=4, ∴1- =1-2= -1.方法总结:本题主要考查了平方根和立方根的定义, ,根据题中的信息:“若两个数的立方根互为相反数,则这两个数也互为相反数.”答题.解答本题的关键是掌握平方根和立方根的定义.10.【题文】求下列各式中的x:(1) (2)【答案】(1) ;(2) x=【分析】(1)由可得,然后根据立方根的定义求解;(2)由可得,然后根据立方根的定义求解.【解答】解:(1)(2)11.【题文】先判断下列等式是否成立:(1)()(2)()(3)()(4)()……….经判断:(1)请你写出用含的等式表示上述各式规律的一般公式.(2)证明你的结论.【答案】四个结论均成立,(1);(2)见解析.【分析】(1)根据立方根的意义,化简判断,然后根据特点列出规律的式子即可;(2)利用立方根的意义,化简变形,得到证明过程.【解答】解:经判断四个结论均成立.(1) .(2).12.【题文】已知A=是n-m+3的算术平方根,B=是m+2n的立方根,求B-A的立方根.【答案】1【分析】根据算术平方根的意义和立方根的意义,得到方程组,然后求解出m、n 的值,代入求出A、B的值,从而求出B-A的立方根.【解答】解:由题意,得,解得∴A∴∴13.【题文】若2x+19的立方根是3,求3x+4的平方根.【答案】【分析】根据题意,由立方根的意义求出x的值,然后再代入求平方根即可. 【解答】解:∴x=4∴14.【题文】求下列各式的值或x.(1);(2);(3);(4)【答案】(1) ;(2) ;(3) ;(4)x=-6【分析】(1)根据题意,先把带分数化为假分数,然后再根据立方根的意义求解即可;(2)先计算被开方数,然后根据立方根的意义求解;(3)通过移项,系数化为1,再利用立方根求解即可;(4)把x+3看做一个整体,然后移项后利用立方根求解.【解答】解:(1)(2)(3)(4)15.【题文】求下列各式中的x .(1) (2)【答案】(1)x=(2)x=0.4【分析】(1)先移项,再系数化为1,最后再求平方根,(2)先求立方根,再移项. 【解答】(1) ,,,所以x=(2) ,,.16.【题文】小明买了一箱苹果,装苹果的纸箱的尺寸为50×40×30(长度单位为厘米),现小明要将这箱苹果分装在两个大小一样的正方体纸箱内,问这两个正方体纸箱的棱长为多少厘米?(结果精确到1cm)【答案】这两个正方体纸箱的棱长为31厘米.【分析】根据题意列出方程,再借助于开立方计算方程的解.【解答】设这两个正方体纸箱的棱长为x厘米,根据题意得,所以,所以≈31(cm ).因此,这两个正方体纸箱的棱长为31厘米.方法总结:本题主要考查立方根和近似数和有效数字等知识点,解题关键是根据正方体的体积公式列出方程求出棱长.17.【题文】求下列各式中x的值(1)(2x﹣1)2=9(2)2x3﹣6=.【答案】(1)x1=2,x2=﹣1,(2)x=【分析】(1)根据平方根的意义,把方程转化为一元一次方程可求解;(2)先移项,系数化为1,再根据立方根的意义,把方程转化为一元一次方程可求解.【解答】解:(1)(2x﹣1)2=92x-1=±3即2x-1=3或2x-1=-3解得x1=2,x2=﹣1(2)移项2x3=6+即2x3=x3=解得x=18.【题文】求下列x的值:(1)(3x+2)2=16(2)(2x﹣1)3=﹣27.【答案】(1)x=,2)x=﹣1【分析】(1)根据平方根的意义,把方程转化为一元一次方程可求解;(2)根据立方根的意义,把方程转化为一元一次方程可求解.【解答】解:(1)(3x+2)2=16,3x+2=±4,∴x=或x=2;(2)(2x﹣1)3=﹣27,2x﹣1=﹣3,∴x=﹣1.19.【题文】已知2a﹣1的平方根是±3,3a+b﹣1的立方根是4,求a+b的平方根.【答案】±【分析】根据平方根可求出2a-1=9,根据立方根可求出3a+b-1=64,然后解方程求出a、b的值即可.【解答】解:∵2a﹣1的平方根是±3,∴2a﹣1=9,∴a=5,∵3a+b﹣1的立方根是4,∴3a+b﹣1=64,∴b=50,∴a+b=55,∴a+b的平方根是.方法总结:此题主要考查了立方根和平方根的意义的应用,关键是根据平方根,求出2a-1=9,根据立方根求出3a+b-1=64,转化为解方程得问题解决.20.【题文】某居民生活小区需要建一个大型的球形储水罐,需储水13.5立方米,那么这个球罐的半径r为多少米(球的体积V=πr3,π取3.14,结果精确到0.1米)?【答案】这个球罐的半径r约为1.5米.【分析】利用球体的体积公式和立方根的定义计算即可.【解答】解:根据球的体积公式,得:=13.5,解得:r≈1.5.答:这个球罐的半径r为1.5米.方法总结:本题主要考查了立方根在实际生活中的应用,要求学生掌握球的体积公式,熟练进行开立方.。
青岛版初中数学八年级下册《用计算器求平方根和立方根》同步测试练习题卷练习题2

B. 0.06758
C. 0.2137
D. 0.6758
TB:小初高题库
青岛版初中数学
二、填空题
1. 3 5 1.710 ,则 3 5000 ___, 3 0.005 ________.
3
2.若
50
3.684 ,则 3
0.05
____.
3
3.若
0.5
0.7937 ,则 3
5105
4.求下列各数的近似值(保留四个有效数字):
3
69, 3
412.8, 3
5.691,,
5
3
TB:小初高题库
青岛版初中数学
5.求下列各数的立方根,保留四个有效数字,并研究一下这些数的立方根有什 么规律,你自己再按这个规律列出一些数,求出它们的立方根,看一看是否符 合你找出的规律:(1)36000,36,0.036;(2)360000,360,0.36;(3) 3600,3.6,0.0036. 6. 求 下 列 各 数 的 算 术 平 方 根 ( 保 留 四 个 有 效 数 字 ) : 438000, 25.964, 0.000512,3.28×104,7.85×106,2.22×10-4. 7. 求 下 列 各 数 的 立 方 根 ( 保 留 四 个 有 效 数 字 ) : 927000, - 42.369, 0.000193,2.81×105,-1.32×106,3.56×10-5. 8.一个面积为 60cm2 的正方形纸片的边长是多少?用四张这样的纸片拼成一个 正方形,拼成的正方形的边长是多少?用一百张这样的纸片拼成一个大正方 形,这个大正方形的边长是多少?(精确到 0.1cm) 9.如图,一个小正方体的体积为 100cm3,这个正方体的棱长是多少 cm,要拼 成一个如图那样的大正方体,需要多少块体积为 100cm3 的小正方体?拼成的大 正方体的棱长是多少 cm?(精确到 0.1cm)
湘教版数学八年级上册_《立方根》习题课件2

会用计算器求立方根. 【例 2】已知3 518≈8.031,3 5180≈17.303,3 51800≈37.277. 试求:(1)下列各式的值:3 5.18,3 0.0518,3 518000,3 -0.00518. (2)你能得出什么规律? 【思路分析】根据“移动规律”解答. 【 规 范 解 答 】 (1) 3 5.18 ≈1.7303 , 3 0.0518 ≈0.37277 , 3 518000 ≈80.31 ,
解:∵x-2 的平方根是±2,∴x-2=4,∴x=6,∵2x+y+7 的立方根是 3, ∴2x+y+7=27,将 x=6 代入得 y=8.∴x2+y2=100,即 x2+y2 的算术平方 根是 10.
19.将棱长分别为 3 cm 和 4 cm 的两个正方体铝块熔化,制成一个大正方体 铝块.求这个大正方体铝块的棱长.(不计损耗,精确到 0.01)
15.求下列各式的值: (1)-3 -64;
3 (3)
-0.729;
3 (2)
-122156;
3 (3)-
6634-1.
解:(1)4
(2)-65
(3)-0.9
1 (4)4
16.求下列各式中的 x. (1)x3+729=0; (2)(x-3)3-64=0. 解:(1)x=-9 (2)x=7
17.若3 2x+3和3 x-12互为相反数,求 4x-4 的立方根. 解:由题意得:2x+3+x-12=0,∴x=3,∴3 4x-4=3 8=2. 18.x-2 的平方根是±2,2x+y+7 的立方根是 3,求 x2+y2 的算术立方根.
解:3 33+43=3 91≈4.50 cm
1.实数-8 的立方根是 -2 .
_11.1平方根与立方根同步练习-2021-2022学年华东师大版八年级上册

初中数学华师大版八年级上学期第11章11.1平方根与立方根同步练习一、单选题1.3的算术平方根是( )A. √3B. -√3C.D. 92.若√x=3,则x的值是()A. 3B.C. 9D.3.一个正方形的面积扩大为原来9倍,它的周长变为原来的()倍A. 2B. 3C. 9D. 124.如果,则x,y的关系是()A. x=yB.C.D. 无法确定5.一个正数x的两个不相等平方根分别是和,则x的值是()A. 4B. 9C. 25D. 496.下列说法错误的是()A. 1的平方根是±1B. –1的立方根是–1C. √2是2的算术平方根D. -3是的平方根7.若a是的平方根,则=()A. ﹣3B.C. 或D. 3或﹣38.下列命题中正确的是()①0.027的立方根是0.3;② 不可能是负数;③如果a是b的立方根,那么ab≥0;④一个数的平方根与其立方根相同,则这个数是1.A. ①③B. ②④C. ①④D. ③④9.求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如.但可以利用计算器求得,还可以通过一组数的内在联系,运用规律求得.请同学们观察下表:n 0.09 9 900 90000 …0.3 3 30 300 …运用你发现的规律解决问题,已知≈1.435,则≈()A. 14.35B. 1.435C. 0.1435D. 143.5二、填空题10.√81的算术平方根是________.1611.的立方根是________.12.已知√3+a=3,那么a=________.13.已知某数的平方根是3a-1和a+5,那么这个数是________.三、解答题14.求式中x的值:(1)(2).15.喜欢探索数学知识的小明遇到一个新的定义:对于三个互不相等的正整数,若其中任意两个数乘积的算术平方根都是整数,则称这三个数为“老根数”,其结果中最小的整数称为“最小算术平方根”,最大的整数称为“最大算术平方根”.例如:1,4,9这三个数,=2,=3,=6,其结果分别为2,3,6都是整数,所以1,4,9这三个数称为“老根数”,其中“最小算术平方根”是2,“最大算术平方根”是6.(1)请证明:2,8,50这三个数是“老根数”,并求出任意两个数乘积的最小算术平方根与最大算术平方根;(2)已知16,a,36这三个数是“老根数”,且任意两个数乘积的算术平方根中,最大算术平方根是最小算术平方根的2倍,求a的值.16.某地气象资料表明此地雷雨持续的时间t(h)可以用公式t2=d2来估计,其中d(km)是雷雨区域的直径.900(1)如果雷雨区域的直径为8 km,那么这场雷雨大约能持续多长时间?(2)如果一场雷雨持续了2 h,那么这场雷雨区域的直径大约是多少?17. (1)已知a、b是有理数,且满足:a的立方根是-2,b的平方是25,求a2+2b的值;(2)已知当时,代数式值为18,求代数式的值.18.已知一个正数的两个不同的平方根是和a+2,b+11的立方根为(1)求a,b的值(2)求的平方根19.观察发现:a … 0.0 001 0.01 1 100 10 000 …√a… 0.01 x 1 y 100 …(1)表格中x=________,y=________.(2)应用:利用a与√a数位的规律解决下面两个问题:①已知√10≈ 3.16,则≈________,√0.1≈________;②已知= k,√20.21=________,=________(用含k的式子表示).3=________,=________(用含m的式子表示)(3)拓展:= m,√2.0220.数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:① ,又,,∴能确定59319的立方根是个两位数.②∵59319的个位数是9,又,∴能确定59319的立方根的个位数是9.③如果划去59319后面的三位319得到数59,而,则,可得,由此能确定59319的立方根的十位数是3因此59319的立方根是39.(1)现在换一个数195112,按这种方法求立方根,请完成下列填空.①它的立方根是________位数.②它的立方根的个位数是________.③它的立方根的十位数是________.④195112的立方根是________.(2)请直接填写....结果:① ________.② ________.答案解析部分一、单选题1.【答案】A2.【答案】C3.【答案】B4.【答案】C5.【答案】D6.【答案】D7.【答案】C8.【答案】A9.【答案】A二、填空题10.【答案】3211.【答案】-0.112.【答案】613.【答案】16三、解答题14.【答案】(1)解:x2−36=0 ;∴x2=36,∴x=±6;(2)解:(x-2)3+29=2,(x-2)3=-27,∴x-2=-3,∴x=-1.15.【答案】(1)解:,且4,10,20都是整数,这三个数是“老根数”,,最小算术平方根为4,最大算术平方根为20;(2)解:这三个数是“老根数”,为正整数,√16a=4√a,√36a=6√a,且4√a,6√a都是整数,因为,所以分以下两种情况:①当6√a<24,即a<16时,则最大算术平方根是24,最小算术平方根是4√a,因此有,解得a=9<16,符合题设,且符合“老根数”的定义;②当4√a>24,即a>36时,则最大算术平方根是6√a,最小算术平方根是24,因此有,解得a=64>36,符合题设,且符合“老根数”的定义,综上,a的值为9或64.16.【答案】(1)t2=d2900,t=√d2900,将d=8代入得:t=√82900=√64900=830=415.答:这场雷雨大约能持续415h.(2)t2=d2900,d2=900t2,,将t=2代入可得. 答:这场雷雨区域的直径大约是60 km.17.【答案】(1)解:∵a的立方根是-2,b的平方是25,∴a=(-2)3=-8,b=±5,∴a2+2b=(-8)2+2×5=74或a2+2b=(-8)2+2×(-5)=54,即:a2+2b=74或54;(2)解:∵当时,代数式值为18,∴,即:,∴= =3×10+2=32,答:代数式的值是32.18.【答案】(1)由题意得,,解得:a=3,,解得:;(2),的平方根是.19.【答案】(1)0.1;10k;10k(2)31.6;0.316;110m;10 m(3)11020.【答案】(1)两;8;5;58(2)24;56。
八年级数学13.2 立方根练习题及答案

13.2 立方根练习题及答案一、填空题:1、a 的立方根是 :-a 的立方根是 :若x3=a : 则x= 33a = :33)(a -= :-33a = :)(33a =2、每一个数a 都只有 个立方根:即正数只有 个立方根:负数只有 个立方根:零只有 个立方根:就是 本身。
3、2的立方等于 :8的立方根是 :(-3)3= :-27的立方根是 .。
: 的立方根是-4: 的立方根是32。
5、计算:3125.0= :335= :)13(33 = :)13(33-= 33)3(-= :-3641= :-38-= :31-= 327= :3278= :-3001.0= :33)2(-=二、选择题(1)下列说法正确的是( ).(A )-64的立方根是-4 (B )-64的立方根是-8(C )8的立方根是2± (D )()33--的立方根是-3(2)下列各式正确的是( ).(A )1=± (B 2=± (C 6=- (D 3=(3)下列说法错误的是( ).(A )任何一个有理数都有立方根:而且只有一个立方根(B )开立方与立方互为逆运算(C )不一定是负数(D(4)下列说法正确的是( ).(A )一个数的立方根一定比这个数小(B )一个数的算术平方根一定是正数(C )一个正数的立方根有两个(D )一个负数的立方根只有一个:且为负数(5 ).(A )4±(B )2±: (C )2(D )2±(6)如果-b 是a 的立方根:则下列结论正确的是( ).(A )3b a -= (B )3b a -= (C )3b a = (D )3b a =(7)()3a b -的立方根是( ).(A )b a - (B )a b - (C )()a b ±- (D )()3a b -(84a =-成立:则a 的取值范围是( ).(A )a 4≤ (B )-a 4≤ (C )a 4≥ (D )一切实数(9)平方根和立方根相同的数为a :立方根和算术平方根相同的数为b :则a+b 的立方根为(). (A )0 (B )1 (C )0或1 (D )1±(100.6694 1.442==,那么下列各式中正确的是( ).(A 14.42= (B 6.694=(C 144.2= (D 66.94=三、判断下列说法是否正确:1、5是125的立方根 。
立方根 同步达标测评 2021-2022学年苏科版八年级数学上册

苏科版八年级数学上册 4.2立方根同步达标测评注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5 毫米黑色墨水签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B 铅笔画出,确定后必须用0.5 毫米黑色墨水签字笔描黑.一.选择题(共8小题,满分40分)1.4的平方根是x,27的立方根是y,则x+y的值为()A.2B.3C.5或1D.5或﹣1 2.下列计算正确的是()A.B.C.=3D.﹣=2 3.已知x为实数,且﹣=0,则x2+x﹣3的算术平方根为()A.3B.2C.3和﹣3D.2和﹣2 4.实数x满足x3=81,则下列整数中与x最接近的是()A.3B.4C.5D.65.的平方根是()A.B.±C.2D.±26.下列说法错误的是()A.中的a可以取正数、负数、零B.是的一个平方根C.的立方根为±2D.表示2的算术平方根7.已知≈6.882,若≈68.82,则x的值约为()A.326000B.32600C.3.26D.0.326 8.如果x2=64,那么等于()A.2B.±2C.4D.±4二.填空题(共8小题,满分40分)9.求值:=.10.若一个正数的平方根是m+3和2m﹣15,n的立方根是﹣2,则﹣n+2m的算术平方根是.11.若一个数的立方根与它的算术平方根相同,则这个数是.12.计算=.13.若5x+19的立方根是4,则2x+7的平方根是.14.若a、b为实数,且满足,则c﹣a﹣b的立方根为.15.1的立方根是;﹣1的立方根是;=.16.一个正方体木块的体积为1000cm3,现要把它锯成8块同样大小的正方体小木块,小木块的棱长是cm.三.解答题(共5小题,满分40分)17.解方程:(1)(x+2)2=9.(2).18.李师傅打算把一个长、宽、高分别为50cm,8cm,20cm的长方体铁块锻造成一个立方体铁块,问锻造成的立方体铁块的棱长是多少cm?19.如果一个正数a的两个平方根是x+2和3﹣2x.求(1)x和这个正数a的值;(2)22﹣3a的立方根.20.已知实数x、y满足y=,求的值.21.如图,这是由8个同样大小的立方体组成的魔方,体积为64cm3.(1)求出这个魔方的棱长.(2)图中阴影部分是一个正方形,求出阴影部分的面积及其边长.参考答案一.选择题(共8小题,满分40分)1.解:∵4的平方根是x,∴x=±2,∵27的立方根是y,∴y=3,∴x+y=2+3=5,或x+y=﹣2+1=﹣1.故选:C.2.解:A、=3,原计算错误,故此选项不符合题意;B、=6,原计算错误,故此选项不符合题意;C、,原计算错误,故此选项不符合题意;D、﹣=2,原计算正确,故此选项符合题意.故选:D.3.解:∵﹣=0,∴.∴x﹣3=2x+1.∴x=﹣4.∴x2+x﹣3=16﹣4﹣3=9.∴x2+x﹣3的算术平方根为.故选:A.4.解:∵33=27,43=64,53=125,63=216,x3=81,∴与x最接近的是4,故选:B.5.解:=2,2的平方根为:,故的平方根为:,故选:B.6.解:A选项,正数的立方根是正数,负数的立方根是负数,0的立方根是0,故该选项不符合题意;B选项,的平方根有2个,﹣是的一个平方根,故该选项不符合题意;C选项,=8,8的立方根是2,故该选项符合题意;D选项,表示2的算术平方根,故该选项不符合题意;故选:C.7.解:∵68.82=6.882×10,∴x=326×103=326000,故选:A.8.解:∵x2=64,∴x=±8,∴==±2.故选:B.二.填空题(共8小题,满分40分)9.解:∵.∴.故答案为:.10.解:∵一个正数的两个平方根分别是m+3和2m﹣15,∴(m+3)+(2m﹣15)=0,解得:m=4,∵n的立方根是﹣2,∴n=﹣8,把m=4,n=﹣8代入﹣n+2m=8+8=16,∵42=16,∴16的算术平方根是4,即﹣n+2m的算术平方根是4.故答案为:4.11.解:若一个数的立方根与它的算术平方根相同,则这个数是0或1,故答案为:0或112.解:,故答案为:.13.解:∵5x+19的立方根是4,∴5x+19=64,解得x=9则2x+7=2×9+7=25,∴25的平方根是±5故答案±5.14.解:∵|a﹣2|≥0,≥0,(c﹣4)4≥0,又∵,∴|a﹣2|=0,=0,(c﹣4)4=0解得a=2,b=3,c=4.∴c﹣a﹣b=4﹣2﹣3=﹣1.所以=﹣1.故答案为:﹣1.15.解:1的立方根是1;﹣1的立方根是﹣1;=﹣.故答案为:1,﹣1,.16.解:根据题意得:==5,则小木块的棱长是5cm,故答案为:5三.解答题(共5小题,满分40分)17.解:(1)(x+2)2=9,开方得:x+2=±3,解得:x1=1,x2=﹣5;(2)(x+3)3=27x+3=3x=0.18.解:=20(cm),答:锻造成的立方体铁块的棱长是20cm19.解:(1)根据题意,x+2+3﹣2x=0,解得x=5,即a=49(2)由(1)得a=49,故22﹣3a=22﹣3×49=﹣125故=﹣5;20.解:∵4 x﹣1≥0,1﹣4 x≥0∴x≥,x≤,∴x=,∴y=,∴=.21.解:(1)(cm).(2)∵魔方的棱长为4cm,∴小立方体的棱长为2cm,∴阴影部分面积为:×2×2×4=8(cm2),边长为:=(cm).。
全国通用版八年级数学上册 立方根练习

课时作业(二十八)[4.2 立方根]一、选择题1.2017·聊城64的立方根是( )A .4B .8C .±4D .±82.下列说法中,错误的是( )A .27的立方根是3 B.13是127的立方根 C.64的立方根是2 D .125的立方根是±53.2016·襄阳-8的立方根是( )A .2B .-2C .±2D .-324.2016·毕节38的算术平方根是( )A .2B .±2 C. 2 D .±25.立方根等于本身的数是( )A .±1B .1,0C .±1,0D .以上都不对6.(-5)2的平方根与(-5)3的立方根的和是( )A .0B .-10C .0或-10D .0或10二、填空题7.计算:(1)(38)3=________;(2)(35)3=________; (3)3(-4)3=________.8.2016·昆山市期末已知一个球体的体积为288π cm 3,则该球体的半径为________cm.(注:球体的体积计算公式为V 球体=43πr 3,r 为球体的半径) 三、解答题9.求下列各数的立方根:(1)-0.001; (2)21027; (3)(-4)3.10.求下列各式中的x :(1)x 3-216=0; (2)(x +5)3=64;(3)⎝⎛⎭⎫12x +13=8.11.若5x +19的立方根是4,求2x +7的平方根.材料阅读题阅读下列短文,然后解答问题.一般地,如果一个数的n (n 为大于1的整数)次方等于a ,这个数就叫做a 的n 次方根.换句话说,如果x n =a (n 为大于1的整数),那么x 叫做a 的n 次方根.求a 的n 次方根的运算,叫做把a 开n 次方,a 叫做被开方数,n 叫做根指数.例如:由于24=16和(-2)4=16,故我们把2,-2叫做16的4次方根,这个运算叫做把16开4次方,4叫做根指数.与平方根一样,正数的偶次方根有两个,它们互为相反数.当n 为偶数时,正数a 的正的n 次方根用符号n a 表示,负的n 次方根用符号-n a 表示,也可以合起来写作±n a .例如:416=2,-416=-2,合起来写作±416=±2.(1)根据短文提供的知识,结合平方根与立方根的概念,用类比的方法填空:①负数有偶次方根吗?答:________.②32的5次方根是________,-128的7次方根是________.③正数的奇次方根是一个________,负数的奇次方根是一个________;当n 为奇数时,a 的n 次方根表示为________.④__________________________叫做a 的n 次算术根;零的n 次方根也叫做零的n 次算术根,它是________.(2)求下列各式的值. ①5243;②±664;③7(-3)7;④8(-3)8.详解详析[课堂达标]1.[解析] A ∵4的立方是64,∴64的立方根是4.故选A .2.D3.[解析] B ∵(-2)3=-8,∴-8的立方根是-2.故选B .4.[解析] C38=2,2的算术平方根是 2.故选C . 5.C6.[导学号:00282293][解析] C ∵(-5)2=25,∴(-5)2的平方根是±5.∵(-5)3的立方根是-5,∴(-5)2的平方根与(-5)3的立方根的和为0或-10.故选C .7.(1)8 (2)5 (3)-48.[答案] 6[解析] ∵一个球体的体积为288π cm 3,∴V 球体=43πr 3=288π, 则r 3=288×34=216, 故r =6.9.解:(1)因为(-0.1)3=-0.001,所以-0.001的立方根为-0.1,即3-0.001=-0.1.(2)因为21027=6427,(43)3=6427, 所以21027的立方根为43,即321027=43. (3)3(-4)3=-4.10.解:(1)两边同时加上216,得x 3=216.因为63=216,所以x =6.(2)因为43=64,所以x +5=4,所以x =-1.(3)因为23=8,所以12x +1=2,所以12x =1,x =2. 11.解:因为5x +19的立方根是4,所以5x +19=64,所以x =9,所以2x +7=25,所以2x +7的平方根是±5.[素养提升][导学号:00282295]解:(1)①没有 ②2 -2 ③正数 负数n a ④正数a 的正的n 次方根 零(2)①5243表示243的5次算术根.因为243=35,所以5243=535=3.②±664表示64的6次方根.因为(±2)6=64,所以±664=±2. ③7(-3)7表示(-3)7的7次方根,7(-3)7=-3. ④8(-3)8表示(-3)8的8次算术根.因为(-3)8=38,所以8(-3)8=838=3.。
初中数学八年级数学同步练习题及答案:立方根

xx学校xx学年xx 学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:下列说法不正确的是()A.-1的立方根是-1B.-1的平方是1C.-1的平方根是-1D.1的平方根是±1试题2:下列说法中正确的是()A.-4没有立方根B.1的立方根是±1C.的立方根是D.-5的立方根是试题3:在下列各式中:=,=0.1,=0.1,-=-27,其中正确的个数是()A.1B.2C.3D.4试题4:若m<0,则m的立方根是()A. B.- C.± D. 试题5:评卷人得分如果是x-6的三次算术根,那么x的值为()A.0B. 3C.5D.6试题6:已知x是5的算术平方根,则x2-13的立方根是()A.-13B.--13C.2D.-2试题7:在无理数,,,中,其中在与之间的有()A.1个 B.2个 C.3个 D.4个试题8:一个正方体的体积为28360立方厘米,正方体的棱长估计为()A.22厘米B.27厘米C.30.5厘米D.40厘米试题9:已知,,则的值等于( ) A.485.8 B.15360 C.0.01536 D.0.04858试题10:若+有意义,则的值是( )A.0B.C.D.试题11:-的立方根是,125的立方根是。
的立方根是 .试题13:=_____.试题14:-3是的平方根,-3是的立方根.试题15:若,则试题16:将数,,,,1按从小到大的顺序排列为。
试题17:若x<0,则=______,=______.试题18:若x=()3,则=______.试题19:125x3=8试题20:(-2+x)3=-216试题21:已知第一个正方体纸盒的棱长为6 cm,第二个正方体纸盒的体积比第一个纸盒的体积大127 cm3,求第二个纸盒的棱长.如图,公路MN和公路PQ在点P处交会,点A处有一所中学,且A点到MN的距离是米.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由;如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?试题1答案:C 【思路分析】负数没有平方根,所以本题答案是C.试题2答案:D【思路分析】任何数都有立方根,且一个数的立方根只有一个,据此可以排除A,B两个选项;由于的算术平方根是,故C选项也是错误的.试题3答案:C 【思路分析】由于=,=0.1, -=-27,故本题答案是C.试题4答案:A 【思路分析】负数的立方根是负数,任意一个数a的立方根都表示成,故本题答案是A.试题5答案:D【思路分析】立方根的性质:正数的立方根是正数,负数的立方根是负数。
八年级上册平方根立方根天天练1

平方根立方根练习题一、填空题 1.如果9=x ,那么x =________;如果92=x ,那么=x ________2.如果x 的一个平方根是7.12,那么另一个平方根是________.3.2-的相反数是 , 13-的相反数是 ;4.一个正数的两个平方根的和是________.一个正数的两个平方根的商是________. 5.若一个实数的算术平方根等于它的立方根,则这个数是_________;6.算术平方根等于它本身的数有________,立方根等于本身的数有________. 7.81的平方根是_______,4的算术平方根是_________,210-的算术平方根是 ;8.若一个数的平方根是8±,则这个数的立方根是 ;9.当______m 时,m -3有意义;当______m 时,33-m 有意义;10.若一个正数的平方根是12-a 和2+-a ,则____=a,这个正数是 ;11.已知0)3(122=++-b a ,则=332ab ;12.21++a 的最小值是________,此时a 的取值是________.13.12+x 的算术平方根是2,则x =________. 二、选择题14.下列说法错误的是( )A 、1)1(2=-B 、()1133-=-C 、2的平方根是2±D 、81-的平方根是9± 15.2)3(-的值是( ).A .3-B .3C .9-D .9 16.设x 、y 为实数,且554-+-+=x x y ,则yx -的值是( )A 、1B 、9C 、4D 、517.下列各数没有平方根的是( ). A .-﹙-2﹚ B .3)3(-C .2)1(- D .11.118.计算3825-的结果是( ). A.3 B.7 C.-3 D.-719.若a=23-,b=-∣-2∣,c=33)2(--,则a 、b 、c 的大小关系是( ).A.a >b >cB.c >a >bC.b >a >cD.c >b >a 20.如果53-x 有意义,则x 可以取的最小整数为( ). A .0 B .1 C .2 D .321.一个等腰三角形的两边长分别为25和32,则这个三角形的周长是( )A、32210+ B、3425+ C 、32210+或3425+D 、无法确定 三、解方程22.0252=-x23. 8)12(3-=-x24.4(x+1)2=8四、计算 25.914414449⋅26.49427.41613+-平方根、立方根、实数练习题一、选择题 1、化简(-3)2的结果是( )A.3B.-3C.±3 D .92.已知正方形的边长为a ,面积为S ,则( ) A .S = B .±a =C .a =.a S =±3、算术平方根等于它本身的数( ) A 、不存在;B 、只有1个;C 、有2个;D 、有无数多个;4、下列说法正确的是( )A .a 的平方根是±a ;B .a的算术平方根是a ;C .a 的算术立方根3a ;D .-a 的立方根是-3a .5、满足-2<x <3的整数x 共有()a . -1. 0b .. 1.A .4个;B .3个;C .2个;D .1个. 6、如果a 、b 两数在数轴上的位置如图所示,则()2b a +的算术平方根是( );A 、a+b ;B 、a-b ;C 、b-a ;D 、-a-b ; 7、如果-()21x -有平方根,则x 的值是( )A 、x ≥1;B 、x ≤1;C 、x=1;D 、x ≥0; 8a是正数,如果a 的值扩大100)A 、扩大100倍;B 、缩小100倍;C 、扩大10倍;D 、缩小10倍;9、2008年是北京奥运年,下列各整数中,与)A .43;B 、44;C 、45;D 、46;10.如果一个自然数的算术平方根是n ,则下一个自然数的算术平方根是( ) A 、n+1;B 、2n +1;CD。
立方根 同步达标训练 2021-2022学年苏科版八年级数学上册

苏科版八年级数学上册4.2立方根同步达标训练注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.非选择题答案用0.5 毫米黑色墨水签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.作图可先使用2B 铅笔画出,确定后必须用0.5 毫米黑色墨水签字笔描黑.一.选择题(共8小题)1.下列说法中,正确的是()①﹣64的立方根是﹣4;②49的算术平方根是7;③的平方根为±;④的平方根是.A.①②B.②③C.③④D.②④2.已知M=是9的算术平方根,7a+3b﹣1的平方根为±4,N=,则M+2N 的立方根为()A.﹣1B.1C.﹣2D.23.已知≈0.5981,≈1.289,≈2.776,则≈()A.27.76B.12.89C.59.81D.5.9814.已知=﹣1,=1,=0,则abc的值为()A.0B.﹣1C.﹣D.5.已知x为实数,且﹣=0,则x2+x﹣3的算术平方根为()A.3B.2C.3和﹣3D.2和﹣26.4的平方根是x,27的立方根是y,则x+y的值为()A.2B.3C.5或1D.5或﹣17.已知=2x+1,则x的值为()A.0B.﹣1C.﹣D.0,﹣1或﹣8.﹣8的立方根与的平方根的和为()A.2B.0C.2或﹣4D.0或﹣4二.填空题(共8小题)9.比27的立方根小5的数是.10.若+=0,则x的值为.11.已知一个体积为24dm3的正方体,则这个正方体的棱长为.12.方程的实数根是.13.已知实数a,b满足,则(a+b)2021的立方根为.14.已知x+1的平方根是±2,2x+y+7的立方根是3,则x2+y的立方根为.15.若x+3是4的算术平方根,则x=;若﹣27的立方根是y﹣1,则y=.16.我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案39,邻座的乘客忙问计算的奥妙.(1)下面是探究59319的过程,请补充完整:①由103=1000,1003=1000000,可以确定是两位数;②由59319的个位上的数是9,可以确定59319的个位上的数是9;③如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定的十位上的数是,由此求得=39.(11)已知103823也是一个整数的立方,请你用类似的方法求=.三.解答题(共5小题)17.已知3a﹣6和a﹣10是某正数的两个不同的平方根,b+9的算术平方根是4,求4b+9a 的立方根.18.解方程:(3x+1)3+=﹣1.19.解答下列问题:(1)已知2a﹣2和a﹣4是一个正数的两个平方根,求这个正数的立方根.(2)若实数a,b满足|a+2|+=0,求a+b的算术平方根.20.已知(x+1)3=8,=3,求x+y的平方根与立方根.21.观察下列各式,并用所得出的规律解决问题:(1)≈1.414,≈14.14,≈141.4,…,≈0.1732,≈1.732,≈17.32,….由此可见,被开方数的小数点每向右移动位,其算术平方根的小数点向移动位.(2)已知≈3.873,≈1.225,则≈;≈.(3)=1,=10,=100,…,小数点的变化规律是.(4)已知≈2.154,≈﹣0.2154,则y=.参考答案1.解:①﹣64的立方根是﹣4,原说法正确;②49的算术平方根是7,原说法正确;③﹣没有平方根,原说法错误;④的平方根是±,原说法错误;正确的有①②;故选:A.2.解:∵9的算术平方根是3,∴M==3,∴5a+2b=9,又∵7a+3b﹣1的平方根为±4,∴7a+3b﹣1=16,∴,解得a=﹣7,b=22,∴N====﹣2,∴M+2N=3+2×(﹣2)=3﹣4=﹣1,而﹣1的立方根为﹣1,∴M+2N的立方根为﹣1,故选:A.3.解:==×=10≈2.776×10=27.76.故选:A.4.解:∵=﹣1,=1,=0,∴a=(﹣1)3=﹣1,b=12=1,c=.∴abc=﹣1×1×=﹣.故选:C.5.解:∵﹣=0,∴.∴x﹣3=2x+1.∴x=﹣4.∴x2+x﹣3=16﹣4﹣3=9.∴x2+x﹣3的算术平方根为.故选:A.6.解:∵4的平方根是x,∴x=±2,∵27的立方根是y,∴y=3,∴x+y=2+3=5,或x+y=﹣2+1=﹣1.故选:C.7.解:∵=2x+1,∴2x+1=0或±1,∴x=0,﹣1或﹣.故选:D.8.解:﹣8的立方根是=﹣2,的平方根,即4的平方根,也就是±=±2,所以﹣8的立方根与的平方根的和为﹣2+2=0或﹣2﹣2=﹣4,故选:D.9.解:﹣5=3﹣5=﹣2,故答案为:﹣2.10.解:∵+=0,∴.∴2x﹣1=﹣(5x+8).∴x=﹣1.故答案为:﹣1.11.解:设正方体的棱长为xdm,由题意得,x3=24,∴x==2(dm),故答案为:2dm.12.解:∵,∴.∴.∴x=.∴x=.故答案为:.13.解:由题意得:a﹣1=0,b+2=0,解得:a=1,b=﹣2,则(a+b)2021=(1﹣2)2021=﹣1,所以(a+b)2021的立方根为﹣1.故答案为:﹣1.14.解:由x+1的平方根是±2,可得x+1=4,即x=3,由2x+y+7的立方根是3,可得2x+y+7=27,而x=3,所以y=14,因此x2+y=23,所以23的立方根为,故答案为:.15.解:根据题意得:x+3=,解得x=﹣1;根据题意得(y﹣1)3=﹣27,解得y=﹣2.故答案为:﹣1,﹣2.16.解:(1)如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定的十位上的数是3,由此求得=39.故答案为:3;(2)∵103=1000,1003=1 000 000,而1000<103823<1000000,∴10<<100,因此结果为两位数;只有7的立方的个位数字是3,因此结果的个位数字是7;如果划去103823后面的三位823得到数103,而43=64,53=125,可以确定的十位数字为4,于是可得=47;故答案为:47.17.解:∵3a﹣6和a﹣10是某正数的两个不同的平方根,∴3a﹣6+a﹣10=0,∴a=4;∵b+9的算术平方根是4,∴b+9=42,∴b=7;∴4b+9a=4×7+9×4=64,∴4b+9a的立方根为4.18.解:(3x+1)3+=﹣1,(3x+1)3=﹣1﹣,(3x+1)3=﹣,3x+1=﹣,3x=﹣,x=﹣.19.解:(1)根据题意得:2a﹣2+a﹣4=0,解得:a=2,∴2a﹣2=2×2﹣2=2,∴这个正数为22=4,∴这个正数的立方根为;(2)根据题意得:a+2=0,b﹣3=0,∴a=﹣2,b=3,∴a+b=﹣2+3=1,∴1的算术平方根为1.20.解:因为(x+1)3=8,所以x+1=2,解得x=1,因为=3,所以y=9,所以x+y=10,所以x+y的平方根是±,立方根是.21.解:(1)由题意知被开方数的小数点每向右移动两位,其算术平方根的小数点向右移动1位,故答案为:两,右,1;(2)∵≈3.873,≈1.225,∴≈12.25;≈0.3873,故答案为:12.25,0.3873;(3)=1,=10,=100,…,小数点的变化规律是被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位;故答案为:被开方数的小数点向右(左)移三位,其立方根的小数点向右(左)移动一位.(4)∵≈2.154,≈﹣0.2154,∴y=﹣0.01,故答案为:﹣0.01.。
苏科版八年级数学上册《4.2 立方根》同步练习题-附答案

苏科版八年级数学上册《4.2 立方根》同步练习题-附答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.下列说法不正确的是( )A .0.3±是0.09的平方根,即0.090.3=±B 644C .正数的两个平方根的积为负数D .存在立方根和平方根相等的数2.下列各数:3.14159 38- 0.131131113(⋯每相邻两个3之间依次多一个1) 2π-17 8() A .1个B .2个C .3个D .4个3.下列说法正确的是( )A .8的立方根是±2B .12-是16-的立方根C .立方根等于它本身的数是0和1D .64和-64的立方根互为相反数4.下列说法正确的是( )A 327B 3272C 27D .面积为27的正方形边长是275.下列命题是真命题的是( )A .过一点有且只有一条直线和已知直线平行B 22a b =a b =C .a 与b 3b 3aD 36426.下列判断正确的是( )A .若x y =,则x y =B .若x y <x yC .若)2x y =,则x y =D .若x y =33x y 7.下列各式中,正确的是( )A 164=±B .93=C 3273-=-D ()244--8.下列说法正确的是( )A .平方根是本身的数只有0;B .立方根是本身的数只有0和1;C .绝对值是本身的数只有0和1;D .相反数是本身的数只有0和1.9.在实数13- 8 38 0.518- 3π 37- 2,无理数的个数为( ) A .1 B .2 C .3D .4 10.2的立方根是( )A 2B .2C 32D .32±二、填空题11.12527-的立方根是 . 1216的算术平方根是 ;-64的立方根是 .13.若x +1是125的立方根,则x 的平方根是 .14.已知:一个正数的两个平方根分别是2a -2和a -4,则这个正数的立方根是 .15.9的算术平方根是 ,2-的绝对值是 ,8-的立方根是 .16.据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥秘.华罗庚给出了如下方法:(1)由3101000=,31001000000=359319(2)由59319个位上的数是93593199;(3)划去59319后面的三位319得到59,而3327=,3464=由此确定3593193.请你类比上述过程,确定21952的立方根是 .17.若28a -的平方根是0,1b +的立方根是-1,则a b 的算术平方根是 .18.25的绝对值是 ,116的算术平方根是 ,364的倒数是 . 19.已知x 满足(x +3)3=64,则x 等于 .20.81的平方根是 ,64 .三、解答题21.把一个长、宽、高分别为25cm 8cm 20cm ,,的长方体铁块锻造成4个同样的立方体铁块,问锻造成的每个立方体铁块的棱长是多少厘米?22.为了制作某城市雕塑,需要把一根截面面积为256cm,高为32cm的长方体钢体熔铸成两个正方体,其中大正方体的棱长是小正方体的棱长的3倍,求这两个正方体的棱长.23.已知第一个正方体木箱的棱长是60cm,第二个正方体木箱的体积比第一个木箱的体积的3倍还多381000cm,求第二个正方体木箱的表面积是多少平方厘米?24.如图,由8个同样大小的正方体组成一个“2阶魔方”,整个魔方的体积为8.(1)求这个魔方的棱长;(2)图①中阴影部分是一个正方形ABCD,它的面积是魔方侧面EFGH面积的一半,求正方形ABCD的边长a.(3)把正方形ABCD放到数轴上,如图①,使得点A与1 重合,那么点D在数轴上表示的数为.25.已知第一个正方体纸盒的棱长为6cm,第二个正方体纸盒的体积比第一个正方体纸盒的体积大3184cm,求第二个正方体纸盒的棱长.(结果精确到0.001cm)参考答案1.B2.C3.D4.B5.C6.D7.C8.A9.D10.C11.5 3 -12. 2 -413.±2143415. 3 2-2 16.2817.418.52121 419.1.20.±9 221.10cm22.这两个正方体的棱长分别为4cm和12cm 23.48600平方厘米24.(1)22(3)12-25.7.368cm。
2022-2023学年华东师大版八年级数学上册《11-1-2立方根》同步达标测试题(附答案)

2022-2023学年华东师大版八年级数学上册《11.1.2立方根》同步达标测试题(附答案)一.选择题(共10小题,满分40分)1.的立方根是()A.B.C.D.2.下列运算正确的是()A.=±2B.(﹣3)3=27C.=3D.=23.﹣27的立方根为()A.±3B.±9C.﹣3D.﹣94.下列说法正确的是()A.4的算术平方根是2B.0.16的平方根是0.4C.0没有立方根D.1的立方根是±15.面积为9的正方形的边长是()A.9的算术平方根B.9的平方根C.9的立方根D.9开平方的结果6.下列说法错误的是()A.﹣1的立方根是﹣1B.3的平方根是C.0.1是0.01的一个平方根D.算术平方根是本身的数只有0和17.下列说法:①±3都是27的立方根;②的算术平方根是±;③﹣=2;④的平方根是±4;⑤﹣9是81的算术平方根,其中正确的有()A.1个B.2个C.3个D.4个8.若≈0.6694,≈1.442,则下列各式中正确的是()A.≈14.42B.≈6.694C.≈144.2D.≈66.94 9.()2的平方根是x,64的立方根是y,则x+y的值为()A.3B.7C.3或7D.1或710.有一个数值转换器,原理如图所示,当输入x为64时,输出y的值是()A.4B.C.D.二.填空题(共8小题,满分40分)11.64的立方根是.12.16的平方根是;16的立方根是.13.一个球形容器的容积为36π立方米,则它的半径R=米.(球的体积:V球=πR3,其中R为球的半径)14.的平方根是,﹣的立方根是.15.已知≈0.6993,≈1.507,则≈.16.如果与(2x﹣4)2互为相反数,那么2x﹣y的立方根是.17.若取1.817,则计算的结果是.18.已知x﹣2的平方根是±4,2x+y﹣1的算术平方根是5,则x﹣y﹣1的立方根是.三.解答题(共6小题,满分40分)19.求下列各式中x的值:(1)(x﹣5)2﹣9=0;(2)64(x﹣1)3=27.20.解方程:(1)(x﹣1)2﹣64=0;(2).21.已知2a﹣1的平方根是±3,3a+b+1的立方根是3.(1)求a,b的值;(2)求a+b的算术平方根.22.已知某正数的两个不同的平方根是3a﹣14和a﹣2;b﹣15的立方根为﹣3.(1)求a、b的值;(2)求4a+b的平方根.23.已知x﹣1的算术平方根是2,y﹣1的立方根是﹣1,求代数式x+y的平方根.24.观察求算术平方根的规律,并利用这个规律解决下列问题:=0.01,=0.1,=1,=10,=100,……(1)已知≈4.47,求的值;(2)已知≈1.918,≈191.8,求a的值;(3)根据上述探究方法,尝试解决问题:已知≈1.26,≈12.6,用含n的代数式表示m.参考答案一.选择题(共10小题,满分40分)1.解:∵=,∴的立方根是.故选:C.2.解:A.根据算术平方根的定义,,那么A错误,故A不符合题意.B.根据有理数的乘方,(﹣3)3=﹣27,那么B错误,故B不符合题意.C.根据立方根的定义,,那么C错误,故C不符合题意.D.根据算术平方根的定义,,那么D正确,故D符合题意.故选:D.3.解:=﹣3.故选:C.4.解:A:4的算术平方根是2,∴符合题意;B:0.16的平方根是±0.4,∴不符合题意;C:0有立方根,∴不符合题意;D:1的立方根是1,∴不符合题意;故选:A.5.解:设正方形边长为x,根据面积公式得:x2=9,解得x=±3,﹣3不合题意,舍去,故选:A.6.解:A、﹣1的立方根是﹣1,原说法正确,故此选项不符合题意;B、3的平方根是±,原说法错误,故此选项符合题意;C、0.1是0.01的一个平方根,原说法正确,故此选项不符合题意;D、算术平方根是本身的数只有0和1,原说法正确,故此选项不符合题意.故选:B.7.解:①3是27的立方根,原来的说法错误;②的算术平方根是,原来的说法错误;③﹣=2是正确的;④=4,4的平方根是±2,原来的说法错误;⑤9是81的算术平方根,原来的说法错误.故其中正确的有1个.故选:A.8.解:∵被开立方数的小数点向右移动3位,则其立方根的小数点向右移动1位,∴≈0.6694×10=6.694,故选:B.9.解:∵(﹣)2=9,∴()2的平方根是±3,即x=±3,∵64的立方根是y,∴y=4,当x=3时,x+y=7,当x=﹣3时,x+y=1.故选:D.10.解:64的立方根是4,4的立方根是:.故选:B.二.填空题(共8小题,满分40分)11.解:∵43=64,∴64的立方根为4,即=4,故答案为:4.12.解:16的平方根是±4,16的立方根是.故答案为:±4,.13.解:∵V球=πR3,∴πR3=36π,解得R=3;故答案为:3.14.解:∵=4,∴的平方根是±2;∵=8,∴﹣的立方根是﹣2.故答案为:±2;﹣2.15.解:∵≈0.6993,∴≈0.06993,故答案为:0.06993.16.解:∵与(2x﹣4)2互为相反数,∴+(2x﹣4)2=0,∴y﹣7=0,2x﹣4=0,解得:y=7,x=2,∴2x﹣y=4﹣7=﹣3,∴2x﹣y的立方根是﹣.故答案为:﹣.17.解:原式=﹣100,∵=1.817,∴原式=﹣100×1.817=﹣181.7.故答案为:﹣181.7.18.解:∵x﹣2的平方根是±4,2x+y﹣1的算术平方根是5,∴x﹣2=16,2x+y﹣1=25,解得:x=18,y=﹣10,∴x﹣y﹣1=18﹣(﹣10)﹣1=18+10﹣1=27,∴x﹣y﹣1的立方根是3,故答案为:3.三.解答题(共6小题,满分40分)19.解:(1)(x﹣5)2=9,x﹣5==±3,x﹣5=3,x﹣5=﹣3,x=8或x=2;(2)(x﹣1)3=,x﹣1=,x﹣1=,x=.20.解:(1)(x﹣1)2﹣64=0,x﹣1=±8,x=1±8,∴x1=9,x2=﹣7;(2),(2x+3)3=125,2x+3=5,∴x=1.21.解:(1)由题意得,∴;(2)由(1)可得a+b=16,所以,a+b的算术平方根为4.22.解:(1)∵正数的两个不同的平方根是3a﹣14和a﹣2,∴3a﹣14+a﹣2=0,解得a=4,∵b﹣15的立方根为﹣3,∴b﹣15=﹣27,解得b=﹣12∴a=4、b=﹣12;(2)a=4、b=﹣12代入4a+b得4×4+(﹣12)=4,∴4a+b的平方根是±2.23.解:∵x﹣1的算术平方根是2,y﹣1的立方根是﹣1,∴x﹣1=4,y﹣1=﹣1,∴x=5,y=0,∴x+y=5,∴x+y的平方根为±.答:x+y的平方根为±.24.解:(1)∵≈4.47,∴=≈4.47×10=44.7.(2)∵191.8=1.918×100,∴===.∴a=36800.(3)∵1.26×10=12.6,∴.∴.∴1000n=m,即m=1000n.。
立方根

(3)下列说法中正确的是( )
A.-4没有立方根
B.1的立方根是±1
C.361的立方根是61
D.-5的立方根是35-
(4)如果a<0,那么a 的立方根是( )
A.3a
B.3 3a -
C.-3a
D.±3a
(5)下列运算正确的是( )
A.-丨-3丨 =3
B.(31
)-1
C.9=±3
D.327-=-3
(6)在下列各式
389=23
,3001.0=0.1,301.0=0.1, =-27中,正确的个数是( )
A.1
B.2
C.3
D.4
3.求下列各数的立方根:
(1)64125; (2)-0.216;(3)1258; (4)-343
27(5)26
4.求下列各式的值:
(2)-3512.0;
5.求下列各式中x 的值:
(1)x 3-216=0;
(2)125x 3=-1;
(3)(x+5)3=64;
(4)(x+1)3+1000=0.
数学思考
6.已知x-2的平方根是±2,2x+y+7的立方根是3,求xy 的值.
解决问题 7.小明买了一箱苹果,装苹果的纸箱的尺寸为80×60×40(单位:cm).现小明要将这箱苹果分装在三个大小一样的正方体纸箱内,问这三个正方体纸箱的棱长为多少厘米? 开阔视野
8.若=k-4,求k 的值.
参考答案
开阔视野8.4。
2023学年北师大版数学八年级上学期同步考点解读训练2-2 立方根(专项训练)

专题2.2 立方根(专项训练)1.(2021秋•雁江区期末)下列运算正确的是()A.﹣12=1B.(﹣1)3=1C.D.2.(2021秋•沂源县期末)2是8的()A.平方根B.立方根C.算术平方根D.立方数3.(2022•碑林区校级二模)﹣27的立方根为()A.±3B.±9C.﹣3D.﹣94.(2021秋•龙华区校级期末)下列各式中正确的是()A.﹣|﹣2|=2B.C.=4D.5.(2021秋•任丘市期末)求下列各式的值.(1);(2);6.(2021秋•东台市期末)解方程:(1﹣x)3=8.7.(2019秋•东台市期末)解方程:8.(2021春•大同期末)已知≈6.882,若≈68.82,则x的值约为()A.326000B.32600C.3.26D.0.326 9.(2021春•清河县期末)若一个数的平方根和立方根都是它的本身,则这个数是()A.0B.1C.0或1D.0或±1 10.(2021春•雨花区期末)下列结论正确的是()A.64的立方根是±4B.﹣没有立方根C.立方根等于本身的数是0D.=﹣311.(2021秋•阜新县校级期末)若+|b+4|=0,则﹣ab的立方根为.12.(2021秋•于洪区期末)一个正方体的体积是5m3,则这个正方体的棱长是()A.m B.m C.25m D.125m13.(2021春•福州期末)如图,有一块正方形铁皮,从四个顶点处分别剪掉一个面积为25cm2的正方形后,所剩部分正好围成一个无盖的长方体容器,量得该容器的体积是180cm3,求原正方形铁皮的边长.14.(2019秋•邢台期末)如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.(1)这个魔方的棱长为.(2)图中阴影部分是一个正方形,求出阴影部分的周长.15.(2021秋•平昌县期末)9的算术平方根是;的立方根是;=.16.(2021秋•蓬莱市期末)﹣27的立方根与的平方根的和是.17.(2021秋•盱眙县期末)已知某正数的两个不同的平方根是3a﹣14和a﹣2;b﹣15的立方根为﹣3.(1)求a、b的值;(2)求4a+b的平方根.18.(2021秋•东台市期末)解方程:(1﹣x)3=8.19.(2021秋•衡阳期末)已知5a﹣1的算术平方根是3,3a+b﹣1的立方根为2(1)求a与b的值;(2)求2a+4b的平方根.20.(2021春•前郭县期末)已知2a+1的平方根是±3,3a+2b﹣4的立方根是﹣2,求的立方根.21.(2020春•潮南区期末)已知a+b﹣5的平方根是±3,a﹣b+4的立方根是2.求3a﹣b+2的值.专题2.2 立方根(专项训练)1.(2021秋•雁江区期末)下列运算正确的是()A.﹣12=1B.(﹣1)3=1C.D.【答案】C【解答】解:A.由于﹣12=﹣1,因此选项A不符合题意;B.由于(﹣1)3=﹣1,因此选项B不符合题意;C.由于22=4,所以=2,因此选项C符合题意;D.由于(﹣2)3=﹣8,所以=﹣2,因此选项D不符合题意;故选:C.2.(2021秋•沂源县期末)2是8的()A.平方根B.立方根C.算术平方根D.立方数【答案】B【解答】解:∵23=8,∴2是8的立方根.故选:B.3.(2022•碑林区校级二模)﹣27的立方根为()A.±3B.±9C.﹣3D.﹣9【答案】C【解答】解:=﹣3.故选:C.4.(2021秋•龙华区校级期末)下列各式中正确的是()A.﹣|﹣2|=2B.C.=4D.【答案】C【解答】解:∵﹣|﹣2|=﹣2,∴选项A不符合题意;∵=2,∴选项B不符合题意;∵=4,∴选项C符合题意;∵无意义,∴选项D不符合题意.故选:C.5.(2021秋•任丘市期末)求下列各式的值.(1);(2);【解答】解:(1);(2);6.(2021秋•东台市期末)解方程:(1﹣x)3=8.【解答】解:(1﹣x)3=8,∴1﹣x=2,解得x=﹣1.7.(2019秋•东台市期末)解方程:(x+1)3﹣27=0【解答】解:(x+1)3﹣27=0,(x+1)3=27,x+1=3,x=28.(2021春•大同期末)已知≈6.882,若≈68.82,则x的值约为()A.326000B.32600C.3.26D.0.326【答案】A【解答】解:∵68.82=6.882×10,∴x=326×103=326000,故选:A.9.(2021春•清河县期末)若一个数的平方根和立方根都是它的本身,则这个数是()A.0B.1C.0或1D.0或±1【答案】A【解答】解:∵02=0,∴一个数的平方根是它的本身的数是0,∵03=0,(﹣1)3=﹣1,13=1,∴一个数的立方根是它本身的数是﹣1或0或1,∴一个数的平方根和立方根都是它本身的数为0,故选:A.10.(2021春•雨花区期末)下列结论正确的是()A.64的立方根是±4B.﹣没有立方根C.立方根等于本身的数是0D.=﹣3【答案】D【解答】解:A、64的立方根是4,原说法错误,故这个选项不符合题意;B、﹣的立方根为﹣,原说法错误,故这个选项不符合题意;C、立方根等于本身的数是0和±1,原说法错误,故这个选项不符合题意;D、=﹣3,原说法正确,故这个选项符合题意;故选:D.11.(2021秋•阜新县校级期末)若+|b+4|=0,则﹣ab的立方根为.【答案】2【解答】解:由题意得,a﹣2=0,b+4=0,解得a=2,b=﹣4,∴﹣ab=﹣2×(﹣4)=8,∵23=8,∴﹣ab的立方根为2.故答案为:212.(2021秋•于洪区期末)一个正方体的体积是5m3,则这个正方体的棱长是()A.m B.m C.25m D.125m【答案】B【解答】解:设这个正方体的棱长为am,由题意得,a3=5,∴a=(m),故选:B.13.(2021春•福州期末)如图,有一块正方形铁皮,从四个顶点处分别剪掉一个面积为25cm2的正方形后,所剩部分正好围成一个无盖的长方体容器,量得该容器的体积是180cm3,求原正方形铁皮的边长.【解答】解:∵从四个顶点处分别剪掉一个面积为25 cm2的正方形,∴剪掉的正方形边长为5 cm,设原来正方形的边长为xcm,由题意可得:5(x﹣10)2=180,∴(x﹣10)2=36,x﹣10=±6,解得:x=16或x=4(不合题意,舍去),∴原来正方形的边长为16 cm.14.(2019秋•邢台期末)如图,这是由8个同样大小的立方体组成的魔方,体积为8cm3.(1)这个魔方的棱长为.(2)图中阴影部分是一个正方形,求出阴影部分的周长.【答案】【解答】解:(1)=2(cm).故这个魔方的棱长是2cm.故答案为:2cm.(2)∵魔方的棱长为2cm,∴小立方体的棱长为1cm,∴阴影部分是正方形,其边长为:=(cm),∴出阴影部分的周长4cm.15.(2021秋•平昌县期末)9的算术平方根是;的立方根是;=.【答案】3、2、.【解答】解:9的算术平方根是3,∵=8,∴的立方根是2,=﹣,故答案为:3、2、.16.(2021秋•蓬莱市期末)﹣27的立方根与的平方根的和是.【答案】0或﹣6【解答】解:∵﹣27的立方根是﹣3,的平方根是±3,所以它们的和为0或﹣6.故答案为:0或﹣6.17.(2021秋•盱眙县期末)已知某正数的两个不同的平方根是3a﹣14和a﹣2;b﹣15的立方根为﹣3.(1)求a、b的值;(2)求4a+b的平方根.【解答】解:(1)∵正数的两个不同的平方根是3a﹣14和a﹣2,∴3a﹣14+a﹣2=0,解得a=4,∵b﹣15的立方根为﹣3,∴b﹣15=﹣27,解得b=﹣12∴a=4、b=﹣12;(2)a=4、b=﹣12代入4a+b得4×4+(﹣12)=4,∴4a+b的平方根是±2.18.(2021秋•东台市期末)解方程:(1﹣x)3=8.【解答】解:(1﹣x)3=8,∴1﹣x=2,解得x=﹣1.19.(2021秋•衡阳期末)已知5a﹣1的算术平方根是3,3a+b﹣1的立方根为2(1)求a与b的值;(2)求2a+4b的平方根.【解答】解:(1)由题意,得5a﹣1=32,3a+b﹣1=23,解得a=2,b=3.(2)∵2a+4b=2×2+4×3=16,∴2a+4b的平方根=±4.20.(2021春•前郭县期末)已知2a+1的平方根是±3,3a+2b﹣4的立方根是﹣2,求的立方根.【解答】解:∵2a+1的平方根是±3,3a+2b﹣4的立方根是﹣2,∴2a+1=9,3a+2b﹣4=﹣8,解得a=4,b=﹣8,∴4a﹣5b+8=4×4﹣5×(﹣8)+8=64,∴==8,∴的立方根为=221.(2020春•潮南区期末)已知a+b﹣5的平方根是±3,a﹣b+4的立方根是2.求3a﹣b+2的值.【解答】解:∵a+b﹣5的平方根是±3,a﹣b+4的立方根是2,∴a+b﹣5=9,a﹣b+4=8,解得:a=9,b=5.∴3a﹣b+2=27﹣5+2=24.。
青岛版数学八年级下册7.7《用计算器求平方根和立方根》同步练习1

用计算器求平方根和立方根一、选择题〕A.15B.±15489.3结果为〔保存四个有效数字〕〔 〕A.12.17B.±1.8682,33,55用不等号连接起来为〔 〕 A. 2<33<55 B. 55< 33< 2C. 33<2<55D. 55< 2< 334.以下各组数,能作为三角形三条边的是〔 〕A.23.0,37.0,54.1B.34.11,16.20,36.97C.101,352,800D.48.4,4.70,1.945.一个正方形的草坪,面积为658平方米,问这个草坪的周长是〔〕 A.6.42 B.2.565二、填空题53.568的按键顺序为__________.7.〔7.14132.25+〕÷31.65=______.8.0.0288的平方根为______.3317331⨯〔保存四个有效数字〕=______.10.填“<〞“>〞或“=〞号〔1〕14 ____356 〔2〕3100 ____21〔3〕-2.0 ____307.0-〔4〕-26 ____3128-三、解答题11.用计算器求以下各式的值〔结果保存四个有效数字〕〔1〕-3247.39 〔2〕483.41 〔3〕4.12 〔4〕371800x 的近似值〔结果准确到0.01)〔1〕3x 2-142=29〔2〕2(x +5)2=1713.当人造地球卫星的运行速度大于第一宇宙速度而小于第二宇宙速度时,它能环绕地球运行,第一宇宙速度的公式是v 1=gR (米/秒〕,第二宇宙速度的公式是v 2=gR 2 (米/秒),其中g =9.8米/秒,R =6.4×106米.试求第一、第二宇宙速度〔结果保存两个有效数字〕.V =61πd 3(d 为圆柱的底面直径) 〔1〕用V 表示d .〔2〕当V =110 cm 3时,求d 的值.(结果保存两个有效数字)15.用计算求以下各数的算术平方根〔保存四个有效数字〕,并观察这些数的算术平方根有什么规律.〔1〕78000,780,7.8,0.078,0.00078.〔2〕0.00065,0.065,6.5,650,65000.参考答案二、6.略7.2.10 8.±0.1697 9.1.86510.〔1〕< 〔2〕> 〔3〕< 〔4〕< 12.略×103米/秒 1.1×104米/秒14.〔1〕36V〔2〕15.被开方数的小数点向左〔右〕移动两位,那么其平方根的小数点就向左〔右〕移动一位。
