常用参数检验方法
参数检验方法

参数检验方法一、概述参数检验是指对某个或一组参数进行检验,以确定其是否符合特定的要求或标准。
在科学研究、工程设计、质量控制等领域中,参数检验是一个非常重要的工具。
本文将介绍参数检验的方法及步骤。
二、参数检验方法1. 正态性检验正态性检验是指对数据进行正态分布的验证。
正态分布是指数据呈现出钟形曲线分布,符合高斯分布规律。
在进行许多统计分析时,都需要先判断数据是否符合正态分布。
常用的正态性检验方法有:(1)直方图法:通过绘制数据的频率直方图来判断数据是否呈现出正态分布。
(2)Q-Q图法:通过绘制样本与理论正态分布之间的散点图来判断数据是否呈现出正态分布。
(3)K-S检验法:通过计算样本与理论正态分布之间的最大差异来判断数据是否呈现出正态分布。
2. 方差齐性检验方差齐性检验是指对不同样本之间方差是否相等进行验证。
当不同样本之间方差不相等时,可能会影响到后续统计推断结果的准确性。
常用的方差齐性检验方法有:(1)Levene检验法:通过计算不同样本之间方差的平均值来判断是否方差齐性。
(2)Bartlett检验法:通过计算不同样本之间方差的总和来判断是否方差齐性。
3. 独立性检验独立性检验是指对两个或多个变量是否独立进行验证。
当两个或多个变量存在相关关系时,可能会影响到后续统计推断结果的准确性。
常用的独立性检验方法有:(1)卡方检验法:通过计算实际观测值与理论期望值之间的差异来判断两个变量是否独立。
(2)Fisher精确概率法:对于小样本数据,可以采用Fisher精确概率法进行独立性检验。
4. 均值比较均值比较是指对不同样本之间均值是否相等进行验证。
当不同样本之间均值不相等时,可能会影响到后续统计推断结果的准确性。
常用的均值比较方法有:(1)t检验法:通过计算不同样本之间均值之差与标准误差之比来判断是否存在显著差异。
(2)方差分析法:对于多个样本之间的均值比较,可以采用方差分析法进行检验。
三、参数检验步骤1. 数据收集:收集所需的数据,并对数据进行整理和清洗。
工艺参数和检验方法(陶瓷砖)

工艺参数和检验方法一、工艺参数1、泥浆水分:32-35%流速:35-70S比重:1.740-1.668g/ml细度(250目筛余):地砖3-5g/100ml、外墙2-3g/100ml2、釉浆(1)地砖面釉比重:水晶釉1.80-1.86/100ml、哑光釉1.91-1.94/100ml细度(325目筛余):水晶釉2-3g/100ml、哑光釉<0.2g/100ml(2)外墙面釉比重:1.65-1.70g/100ml细度(325目筛余):0.1-0.2g/100ml(3)地砖底釉比重:1.78-1.82g/100ml细度(325目筛余):0.3-0.5g/100ml(4)外墙底釉比重:1.35-1.845g/100ml细度:(325目筛余):0.1-0.2g/100ml3、粉制水分:地砖6.5-7.5%(微波炉)、外墙4-5%(微波炉)级配:20目以上<5%、80目以下<8%4、成型水分:地砖5.5-6.5%、外墙3-4%级配:20目以上<5%、80目以下<8%压力:地砖2200-2500T、外墙920-980T5、施釉线(1)面釉比重:依工艺通知单为准。
允许偏差±0.01g/cm2质量:依工艺通知单为准,地砖允许偏差±0.5g、中间与两侧偏差<2g、外墙允许偏差±0.1g(2)底釉要求同面釉6、其他地砖干燥窑出炉水分<2%(烘箱)外墙干燥窑出炉水分<0.5%(烘箱)地砖素坯尺寸603-606mm(600*600)、翘曲<±1mm地砖釉坯尺寸601-603mm(600*600)、内翘<1.5mm外墙釉坯尺寸98-99mm(100*100)、72-73mm(73*73)地砖磨边尺寸598±0.5mm、对角线845.5±1mm(600*600)地砖釉坯吸水率12-15%外墙釉坯吸水率3-6%二、检验方法1、比重用100ml标准比重瓶取100ml泥浆或釉浆称重,减去比重瓶重量,即为泥浆或釉浆比重。
参数检验和非参数检验

参数检验和非参数检验参数检验和非参数检验是统计学中两种常用的假设检验方法。
参数检验假设总体服从其中一种特定的概率分布,而非参数检验则不对总体的概率分布进行特定的假设。
本文将分析和比较这两种假设检验方法,并讨论它们的优缺点和适用范围。
参数检验的基本思想是假设总体的概率分布属于一些已知的参数化分布族,例如正态分布或泊松分布。
然后根据样本数据计算出统计量的观察值,并基于它们进行假设检验。
常见的参数检验方法有t检验、F检验和卡方检验等。
以t检验为例,它适用于研究两个样本均值之间是否存在显著差异的情况。
假设我们有两组样本数据,分别服从正态分布。
可以使用t检验来计算两组样本均值的差异是否显著。
t检验基于样本均值和标准差来估计总体均值的差异,并通过计算t值和查表或计算p值来判断差异是否显著。
参数检验的优点是它们对总体概率分布的假设比较明确,计算方法相对简单,适用于数据符合特定分布的情况。
此外,参数检验通常具有较好的效率和统计性质。
然而,参数检验也有一些限制和缺点。
首先,参数检验通常对数据的分布假设要求较高,如果数据不符合指定的分布假设,则结果可能不可靠。
另外,参数检验对样本大小的要求较高,需要较大的样本才能获得可靠的检验结果。
此外,参数检验对异常值和离群值比较敏感,这可能会导致统计结论的错误。
与参数检验相比,非参数检验更加灵活,不需要对总体的概率分布做出特定的假设。
它适用于更广泛的数据类型和样本分布。
常见的非参数检验方法有Wilcoxon符号秩检验、Mann-Whitney U检验和Kruskal-Wallis检验等。
以Wilcoxon符号秩检验为例,它适用于比较两个相关样本的差异。
这个检验不要求样本数据满足正态分布的假设,它基于样本差值的秩次来判断差异是否显著。
非参数检验的优点在于其适用范围广泛,不需要对总体分布做出特定假设,对数据平均性和对称性的要求较低,对异常值和离群值的鲁棒性较好。
此外,非参数检验对样本大小的要求较低,可以在较小的样本情况下获得可靠的结果。
实验室常用统计方法

实验室常用统计方法1.描述统计方法:描述统计方法是通过汇总和整理实验数据的相关特征来进行分析的方法。
包括计算数据的均值、标准差、中位数等,以对数据的集中趋势、离散程度、分布情况等进行描述。
2.参数检验方法:参数检验方法用于比较两个或多个样本之间的差异,并判断这些差异是否显著。
常见的参数检验方法包括t检验、方差分析等。
t检验用于比较两个样本均值之间的差异,方差分析则用于比较多个样本均值之间的差异。
3. 非参数检验方法:非参数检验方法是针对无法满足参数检验假设的实验数据而设计的。
常见的非参数检验方法包括Wilcoxon秩和检验、Kruskal-Wallis检验等。
Wilcoxon秩和检验用于比较两个相关样本之间的差异,Kruskal-Wallis检验则用于比较多个独立样本之间的差异。
4.回归分析:回归分析用于研究自变量和因变量之间的关系,并建立预测模型。
在实验室中,回归分析常用于研究因变量与多个自变量之间的线性关系。
通过回归分析可以确定自变量对因变量的贡献程度,以及预测因变量的可能取值。
5. 生存分析:生存分析是用于研究事件发生的时间和相关因素之间的关系的统计方法。
在实验室中,生存分析常用于研究生物学实验中事件发生的概率和时间。
生存分析的常见方法包括Kaplan-Meier生存曲线分析和Cox比例风险模型分析。
6.方差分析:方差分析是用于比较多个样本均值差异的统计方法。
在实验室中,方差分析常用于比较多个处理组之间的差异,并确定是否存在显著差异。
方差分析可分为单因素方差分析和多因素方差分析,用于比较不同因素对实验结果的影响。
7.聚类分析:聚类分析是将样本按照相似性分为不同的组别的统计方法。
在实验室中,聚类分析常用于将实验数据按照其特征进行分类,以寻找样本之间的相似性和差异性。
综上所述,实验室常用的统计方法涵盖了描述统计、参数检验、非参数检验、回归分析、生存分析、方差分析和聚类分析。
通过运用这些统计方法,实验室可以更好地处理和分析实验数据,为科研工作提供有力的支持。
参数方法 非参数方法

参数方法非参数方法参数方法和非参数方法是统计学中两种常用的数据分析方法。
参数方法是指在数据分析过程中,需要预先对数据的分布做出假设,并基于假设建立参数模型。
参数模型可以用来估计总体参数,并使用统计推断方法进行假设检验。
常见的参数方法包括t检验、方差分析、回归分析等。
t检验是一种用于比较两个样本均值是否有显著差异的参数方法。
在t检验中,我们需要预先假设样本数据服从正态分布,并且方差齐性成立。
通过计算样本均值的差异与预期均值差异之间的差异大小,得出结论是否拒绝原假设。
方差分析是一种用于比较两个或多个样本组均值差异是否显著的参数方法。
它假设样本数据服从正态分布,且不同样本组的方差相等。
通过计算组间均方与组内均方之间的比值,得出结论是否拒绝原假设。
回归分析是一种用于探究变量之间关系的参数方法。
它假设因变量与自变量之间存在线性关系,并且误差项服从正态分布。
通过最小化误差平方和,估计出回归系数,从而得到模型的偏回归系数。
参数方法的优点是可以对总体参数进行估计和推断,结果具有精确性。
然而,参数方法对数据的分布假设要求较高,如果数据偏离了假设的分布,会导致统计推断结果的失真。
与之相反,非参数方法则不依赖于总体的分布假设,基于样本数据进行推断和分析。
非参数方法主要通过排序和秩次转换的方法,来对比样本之间的差异。
常用的非参数方法包括Wilcoxon符号秩检验、Kruskal-Wallis检验、Spearman相关分析等。
Wilcoxon符号秩检验是一种用于比较两个相关样本均值差异是否显著的非参数方法。
它将样本数据转换为秩次,通过对比秩次差异的大小,得出结论是否拒绝原假设。
Kruskal-Wallis检验是一种用于比较多个无关样本组均值差异是否显著的非参数方法。
它将样本数据转换为秩次,通过对比不同样本组秩次和的大小,得出结论是否拒绝原假设。
Spearman相关分析是一种用于探究变量之间关系的非参数方法。
它基于秩次转换的数据,计算出秩次之间的相关系数,从而推断变量之间的相关性。
统计学方法常用的检验指标

统计学方法常用的检验指标1. t检验是常用的参数检验方法,用于比较两组样本的平均值是否有显著差异。
2. 卡方检验适用于分析分类变量之间的相关性和独立性。
3. 方差分析(ANOVA)用于比较三个或三个以上组别的均值是否有显著差异。
4. Pearson相关系数衡量两个变量之间的线性相关程度。
5. 线性回归中的回归系数用于衡量自变量对因变量的影响程度。
6. 均方误差是衡量回归模型拟合程度的指标,值越小表示拟合效果越好。
7. F统计量用于判断回归模型整体拟合程度是否显著。
8. 残差分析是检验线性回归模型的适用性和拟合效果的重要方法。
9. 二项分布的成功概率 p 常用于评估二分类变量或Bernoulli试验的结果。
10. 置信区间用于估计参数的不确定性范围。
11. 同质性检验用于判定样本方差是否相等。
12. 生存分析中的生存率和生存函数是评估不同组别之间生存情况的重要指标。
13. 多重比较方法如Bonferroni校正可以降低在多组比较中出现假阳性的风险。
14. 效应量用于衡量实验结果或样本差异的大小。
15. Kappa系数常用于评估观察者之间的一致性程度。
16. ROC曲线和AUC值用于评估二分类模型的分类性能。
17. Chow检验适用于时间序列数据中分割点的检验。
18. 多元方差分析用于同时比较多个因素对因变量的影响。
19. 独立性检验用于检验两个变量之间是否存在独立关系。
20. 组间差异的效应大小可通过η^2或ω^2等指标来衡量。
21. 对数几率是二分类变量中常用的效应量指标之一。
22. Friedman检验适用于重复测量设计或配对设计的非参数检验。
23. 各种协方差结构的估计常用于线性模型中对数据相关性的考虑。
24. 饱和模型的拟合优度指标常使用最大似然估计。
25. 多重共线性可通过方差膨胀因子(VIF)等指标检验。
26. 滞后效应检验用于时间序列数据中探究滞后期的影响。
27. 非参数回归中的局部加权回归(Loess)常用于处理非线性关系的拟合。
参数检验与非参数检验的区别与应用

参数检验与非参数检验的区别与应用统计学中的参数检验和非参数检验是两种常用的假设检验方法。
本文将详细介绍参数检验和非参数检验的区别以及它们在实际应用中的具体场景。
一、参数检验参数检验是建立在对总体分布形态有所假定的基础上,通过对样本数据进行统计推断,来对总体参数进行假设检验。
它通常要求总体分布服从特定的概率分布,如正态分布。
参数检验的常见方法有:1. 单样本t检验:用于检验样本均值是否与已知总体均值有显著差异。
2. 独立样本t检验:用于比较两个独立样本的均值是否存在显著差异。
3. 配对样本t检验:用于比较同一组样本在不同条件下的均值是否存在显著差异。
4. 方差分析:用于比较多个样本组之间的均值是否存在显著差异。
参数检验的优势在于其具有较高的效率和灵敏度,适用于对总体分布形态有所了解的情况。
但它也有一些限制,如对分布形态的假设可能不成立,以及对样本量和数据类型的要求较高。
二、非参数检验非参数检验是对总体分布形态没有具体假设的情况下,通过对样本数据进行统计推断,来对总体参数进行假设检验。
非参数检验不少于参数检验的分析方法,常见的包括:1. Wilcoxon符号秩检验:用于比较两个相关样本的差异是否存在显著差异。
2. Mann-Whitney U检验:用于比较两个独立样本的中位数是否存在显著差异。
3. Kruskal-Wallis检验:用于比较多个样本组的中位数是否存在显著差异。
非参数检验的优势在于对总体分布形态没有具体要求,适用于对总体分布了解较少或不了解的情况。
它相对于参数检验来说更具广泛的适用性,但由于其推断效果较差,需要更大的样本量才能达到相同的检验效果。
三、参数检验与非参数检验的区别1. 假设要求:参数检验对总体分布形态有假设要求,如正态分布假设,而非参数检验对总体分布形态没有具体要求。
2. 统计量选择:参数检验基于已知概率分布,可以选择特定的统计量如t值、F值等;而非参数检验使用秩次统计量,如秩和、秩和秩二样序差等。
常用参数检验方法

常用参数检验方法参数检验是在统计学中常用的一种方法,用于评估统计模型中的参数的显著性。
常见的参数检验方法包括假设检验、置信区间和P值。
假设检验是参数检验的一种方法,它基于一个假设,即原假设(null hypothesis)和备择假设(alternative hypothesis)。
原假设是我们要证伪的假设,而备择假设是我们要支持的假设。
常见的假设检验方法有:t检验、F检验、卡方检验等。
t检验是用于比较两个样本均值是否有显著差异的方法。
它可以用于两个独立样本的比较(独立样本t检验)或同一样本的比较(配对样本t 检验)。
F检验用于比较两个或多个样本方差是否有显著差异的方法。
它通常用于方差分析(ANOVA)中,比较不同组之间的平均差异是否显著。
卡方检验是用于比较两个或多个分类变量之间的关联性是否显著的方法。
它可以用于两个分类变量的比较(卡方独立性检验)或多个分类变量的比较(卡方拟合度检验)。
置信区间是参数估计的一种方法,它给出了参数的一个估计范围,通常以一定的置信水平表示。
常见的置信区间包括均值的置信区间、比例的置信区间等。
均值的置信区间给出了总体均值的一个估计范围。
它可以用于比较两个样本均值的差异是否显著。
比例的置信区间给出了总体比例的一个估计范围。
它可以用于比较两个样本比例的差异是否显著。
P值是参数检验结果的一个度量,它表示在原假设成立的情况下,观察到比实际观测结果更极端的结果出现的概率。
如果P值小于一些显著性水平(通常是0.05),则可以拒绝原假设。
P值的计算通常依赖于具体的参数检验方法。
在假设检验中,P值可以用于判断观测结果是否具有统计显著性。
总之,参数检验是统计学中一种常用的方法,用于评估统计模型中参数的显著性。
常见的参数检验方法包括假设检验、置信区间和P值。
这些方法可以帮助我们判断观测结果是否具有统计显著性,并进行合适的推断和决策。
工艺参数和检验方法

工艺参数和检验方法一、工艺参数1. 外观尺寸:陶瓷砖的外观尺寸是指瓷砖的长度、宽度和厚度。
外观尺寸的合格范围根据所用途不同,一般为±0.5mm。
测量方法可以使用高精度的测量工具,如游标卡尺。
2. 平整度:平整度是指陶瓷砖表面的平整程度,用来衡量瓷砖的平整程度。
平整度的合格范围根据地面用途和瓷砖尺寸而异,一般为正对角线落差不超过0.5mm。
测量方法可以使用平整度测试仪。
3.直角度:直角度是指陶瓷砖四个相邻边之间的直角度数,用来衡量瓷砖的直角度。
直角度的合格范围一般为±0.5°。
测量方法可以使用角度测量仪。
4.水平度:水平度是指陶瓷砖表面的水平程度,用来衡量瓷砖的水平程度。
测量方法可以使用水平度测试仪。
5.抗折强度:抗折强度是指陶瓷砖在弯曲作用下的抵抗能力,用来衡量瓷砖的抗弯强度。
抗折强度的合格范围根据瓷砖类型和用途而异。
测量方法可以使用弯曲试验机。
6.吸水率:吸水率是指陶瓷砖吸水的能力,用来衡量瓷砖的耐水性能。
吸水率的合格范围根据瓷砖类型而异,一般为3%以下。
测量方法可以使用水浸法或称重法。
二、检验方法1.外观检验:通过目视观察和外观尺寸测量,检查陶瓷砖的外观是否完好,尺寸是否合格。
外观检验包括检查瓷砖表面是否有裂纹、斑点、色差等缺陷。
2.平整度检验:通过平整度测试仪测量瓷砖表面的平整度,检查瓷砖是否满足平整度要求。
测量时需要将测试仪沿表面移动,记录测量值。
3.直角度检验:通过角度测量仪测量瓷砖相邻边的直角度,检查瓷砖是否满足直角度要求。
测量时需要将角度测量仪夹在相邻边之间,记录测量值。
4.水平度检验:通过水平度测试仪测量瓷砖表面的水平度,检查瓷砖是否满足水平度要求。
测量时需要将测试仪放置在瓷砖表面,记录测量值。
5.抗折强度检验:通过弯曲试验机进行抗折强度测试,检查瓷砖的抗弯强度是否满足要求。
测量时需要将瓷砖放置在试验机上,进行弯曲试验,记录断裂负载值。
6.吸水率检验:通过水浸法或称重法测量瓷砖的吸水率,检查瓷砖的耐水性能是否满足要求。
一元线性回归模型的参数检验

模型拟合的质量检验
1
残差分析
通过分析模型的残差,可以评估模型对数据的拟合程度。较小的残差表示模型拟合较好。
2
参数的显著性检验
通过t检验或F检验,判断模型参数是否显著。显著的参数表示自变量对因变量的影响是真实 存在的解释程度。取值范围为0到1,越接近1表示模型拟合的越 好。
残差分析
残差分析是评估一元线性回归模型拟合质量的重要方法。通过分析残差的分 布、模式和异常值,可以判断模型是否可靠。
参数的显著性检验
在一元线性回归模型中,参数的显著性检验是判断自变量对因变量的影响是否显著的方法。常用的方法有t检 验和F检验。
t检验的基本原理
t检验是一种用于检验样本均值与总体均值之间差异的统计方法。在一元线性 回归模型中,用于检验参数估计值与真实值之间的差异。
一元线性回归模型的参数 检验
在统计学中,一元线性回归模型是一种用于描述两个变量之间线性关系的模 型。本节将介绍一元线性回归模型的参数检验方法。
什么是一元线性回归模型?
一元线性回归模型用于分析一个自变量与一个因变量之间的线性关系。它通 过拟合一个直线来描述这种关系,并根据模型参数进行推断和解释。
数据预处理
在进行一元线性回归之前,需要对数据进行预处理,包括数据清洗、缺失值 处理和异常值检测。通过这些步骤,可以确保模型建立在可靠的数据基础上。
拟合一元线性回归模型
通过最小化残差平方和来拟合一元线性回归模型。这可以通过最小二乘法来 实现,求解模型参数使得预测值与观测值的差异最小。
模型参数的估计
一元线性回归模型的参数估计使用普通最小二乘法。通过计算样本数据的协 方差和方差,可以得到模型参数的估计值。
几种常见的显著性检验方法

几种常见的显著性检验方法显著性检验是统计学中常用的一种方法,用于判断样本数据是否由一个总体生成,或者判断两个或多个样本数据是否来自同一个总体。
它的主要目的是通过计算样本数据之间的差异,并基于概率理论判断这些差异是否由随机因素引起,从而得出结论。
下面将介绍几种常见的显著性检验方法:1.t检验:t检验是一种常用的参数检验方法,用于判断两个样本均值是否有显著差异。
当总体的方差未知时,可以使用独立样本t检验;当总体的方差已知时,可以使用配对样本t检验。
2.方差分析:方差分析是一种用于比较两个或多个样本均值是否有显著差异的方法。
它通过比较组间变异与组内变异来判断均值的差异是否有统计学意义。
常用的方差分析方法包括单因素方差分析和多因素方差分析。
3.卡方检验:卡方检验是一种用于比较观察值与期望值之间的差异是否有显著性的非参数检验方法。
它适用于分类数据的分析,常用于分析两个或多个分类变量之间的关联性。
4.相关分析:相关分析是一种用于衡量两个变量之间相关关系的方法,常用于测量变量之间的线性相关性。
通过计算相关系数来判断两个变量是否存在显著的相关关系。
5.回归分析:回归分析是一种用于研究自变量与因变量之间关系的方法。
通过拟合回归模型并进行参数估计,可以判断自变量对因变量的影响是否显著。
除了上述几种常见的显著性检验方法外,还有其他一些方法,如非参数检验方法(如Wilcoxon秩和检验和Mann-Whitney U检验)、生存分析中的log-rank检验等。
在实际应用中,应根据具体问题选择适当的检验方法,并进行合理的假设设置和数据分析,以得出准确的结论。
临床研究中的统计分析方法

临床研究中的统计分析方法临床研究中的统计分析方法在医学领域扮演着至关重要的角色。
通过运用统计学原理和方法,研究者能够对临床实验数据进行客观、科学的分析,从而帮助医学界做出准确的结论和决策。
本文将介绍一些常见的临床研究中使用的统计分析方法。
1. 描述性统计分析描述性统计分析是临床研究中最基础的统计方法之一。
它帮助研究者对研究对象的特征进行整体描述,如平均数、中位数、标准差等。
通过描述性统计分析,研究者可以对研究样本的分布情况有一个直观的认识。
2. 参数检验参数检验是用来对两个或多个样本进行比较的一种统计方法。
通过参数检验,我们可以判断不同样本之间的差异是否具有统计学意义。
常见的参数检验方法包括t检验、方差分析(ANOVA)等。
根据实际情况,研究者可以选择不同的参数检验方法来分析他们的临床实验数据。
3. 非参数检验与参数检验不同,非参数检验方法不依赖于数据的分布情况,因此在一些情况下更为适用。
例如,当样本数据不满足正态分布假设时,非参数检验就能够提供可靠的结果。
常见的非参数检验方法有Mann-Whitney U检验、Wilcoxon符号秩检验等。
4. 相关分析相关分析用于研究两个或多个变量之间的关系。
它能够帮助研究者确定这些变量之间的相关性强度以及相关性的方向。
最常见的相关分析方法是皮尔逊相关系数。
通过皮尔逊相关系数,我们可以得到两个变量之间的相关系数,从而判断它们之间的相关性。
5. 回归分析回归分析是研究自变量与因变量之间关系的一种统计方法。
通过回归分析,研究者可以确定自变量对因变量的影响程度,并得到一个数学模型来预测因变量的取值。
常见的回归分析方法包括线性回归、逻辑回归等,在临床研究中得到广泛应用。
6. 生存分析生存分析用于研究人群中个体的生存时间以及相关因素对生存时间的影响。
通过生存分析,研究者可以估计疾病患者的存活率,并确定各种风险因素对于患者生存的影响。
生存分析方法包括卡普兰-米尔法曲线、生存率比较等。
设置参数的检验及调节方法

设置参数的检验及调节方法参数的检验及调节方法是在进行实验或工程设计时非常重要的一个步骤,它能够保证系统的稳定性和性能符合要求。
本文将详细介绍设置参数的检验及调节方法,帮助读者更好地实施参数设置。
首先,参数的检验是指确保所设定的参数符合系统要求和设计规范的过程。
在进行参数检验时,需要考虑以下几个方面:1. 参数的范围:首先需要明确参数的允许范围,确保所设定的参数在允许范围内。
如果参数超出范围,可能会导致系统性能不稳定甚至发生故障。
2. 参数的精度:参数的检验需要考虑参数的精度,确保参数设置的准确性和可靠性。
如果参数精度不高,可能会影响系统的性能和稳定性。
3. 参数的一致性:在进行参数检验时,需要确保各个参数之间的一致性,即参数设置的逻辑性和合理性。
如果参数之间存在矛盾或不一致,可能会导致系统无法正常工作。
其次,参数的调节是指根据系统实际情况和要求,对参数进行调整和优化的过程。
在进行参数调节时,需要考虑以下几个方面:1. 参数的优化:根据系统的实际需求和性能要求,对参数进行优化和调整,以提高系统的性能和稳定性。
优化参数可以使系统运行更加高效和可靠。
2. 参数的实时性:参数的调节需要考虑系统的实时性和灵活性,及时根据实际情况进行参数调整,以保证系统在不同情况下能够稳定运行。
3. 参数的反馈:在进行参数调节时,需要考虑参数的反馈机制,及时获取系统的反馈信息,并根据反馈信息进行参数调整,以保证系统的稳定性和可靠性。
综上所述,参数的检验及调节方法是确保系统性能和稳定性的关键步骤。
通过合理设置参数的检验和调节方法,可以帮助我们更好地实施参数设置,提高系统的性能和稳定性,确保系统能够正常运行和达到设计要求。
参数检验方法

参数检验方法引言在软件开发过程中,参数检验是一项非常重要的工作。
通过对输入参数的检查和验证,可以保证程序的稳定性,避免潜在的错误和安全漏洞。
本文将介绍参数检验的方法和技巧,帮助开发者有效地进行参数检验。
为什么进行参数检验在程序中,参数的使用非常常见。
参数的合法性和正确性直接影响程序的健壮性和安全性。
因此,对参数进行检验是非常有必要的。
以下是进行参数检验的主要原因:1.防止程序出现异常:通过对参数进行检验,可以在程序运行之前就捕获到错误,避免程序因为参数问题而异常终止。
2.提高程序的容错性:合理的参数检验可以减少程序的错误率,提高程序的容错能力,增强用户体验。
3.防范安全风险:恶意用户可能会通过输入非法参数来攻击程序,通过参数检验可以有效地避免安全隐患。
常用的参数检验方法1. 类型检验类型检验是最基本的参数检验方法之一。
根据参数的类型,可以进行必要的转换和验证。
常见的类型检验方法有以下几种:•检查参数的数据类型是否符合要求,例如检查是否为整数、浮点数、字符串等。
•检查参数的取值范围是否合法,例如检查整数是否在某个范围内。
•检查字符串长度是否符合要求,例如检查字符串的最大长度和最小长度。
2. 格式检验在某些情况下,参数的格式需要满足一定的要求。
对于这类参数,可以通过格式检验方法来验证其正确性。
常见的格式检验方法有以下几种:•正则表达式验证:使用正则表达式匹配参数的格式,例如验证邮箱格式是否正确。
•字符串格式化验证:通过字符串的格式化方法,验证参数是否满足规定的格式要求,例如验证日期格式是否正确。
3. 值域检验有些参数需要满足特定的值域要求。
对于这类参数,需要进行值域检验。
常见的值域检验包括以下几种:•枚举值检验:检查参数是否属于一组预定义的枚举值之一。
•数值范围检验:检查参数是否在指定的数值范围内,例如检查年龄是否在0到100之间。
•集合成员检验:检查参数是否在某个集合成员之中,例如检查某个用户ID 是否在指定的用户列表中。
常用建筑材料检测参数取样方法及报告时间
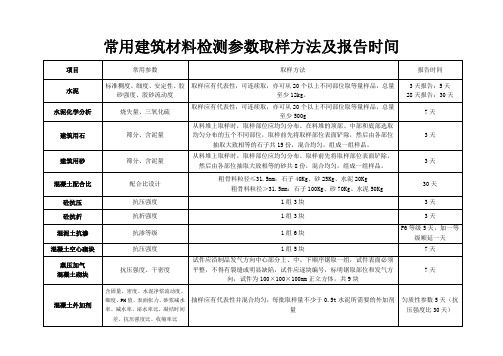
12天
土工击实
最佳含水率、最大干密度
土:30Kg
二灰土:15Kg
砂、石:各50Kg
二灰碎石:100Kg
砂:3Kg
8天
无侧限抗压强度
抗压强度
二灰土 4kg
二灰碎石 250kg
11天
12天
玻璃
中空玻璃露点、
可见光透射比
露点:510×360mm×20块
可见光:100×100mm×3块
拉伸粘结强度、浸水拉伸粘结强度
3kg
35天
界面砂浆
拉伸粘结强度、浸水拉伸粘结强度
3kg
35天
胶粘剂
拉伸粘结强度、浸水拉伸粘结强度
2kg
30天
耐碱玻纤网格布
单位质量面积、断裂强力、耐碱保留率
1卷(≥4m
≥5平方)
32天
热镀锌电焊钢丝网
网孔中心距、丝径、焊点抗拉力、镀锌层厚度
1卷(≥3m
≥4平方)
3天
EPS板
混凝土防冻剂
减水率、泌水率比、凝结时间差、抗压强度比、28d收缩率比、渗透高度比
抽样应有代表性并混合均匀,每批取样量不少于0.15t所需要的防冻剂量
负温抗压强度比约68天
砂浆配合比
配合比设计
砂40Kg、水泥10Kg
30天
砂浆
抗压强度
1组3块
3天
钢材
拉伸、冷弯
所有钢筋均送4根,2拉2弯。直径25mm以下钢筋送两根30mm,两根40mm
浸渍胶膜纸饰面人造板):取样数量150×150mm,4块
5天
水质分析
具有代表性的水样5L,放置于聚乙烯或硬质玻璃瓶中,密封保存,最好现取现做
参 数 检 验
解:第一,设立假设。假设该样本取自一个X 500 的总体 。原假设H0 : X 500 ;备择假设:H1 : X 500 。
第统计量。显著性水平 0.05,自
由度 n 9,查 t 分布表得对应的临界值:t /2 (9) 2.262
二、假设检验的步骤
1.建立原假设和备择假设。 2.确定显著性水平。 3.寻找检验统计量 4.根据样本观测值检验统计量的值。 5.根据检验统计量的值和临界值做出判断,是 拒绝还是接受原假设。
三、常用的参数检验方法
1.总体期望的假设检验
(1)总体为正态分布且方差已知。
【例10.10】设总体服从标准差为50的正态分布,从该总体抽
x1和
x
,
2
如果这两个样本来自同一总体,它们就有相同的均值,
即 1 2,有同一的方差 2。要检验的假设是:H0 : 1 2;
H1 : 1 2 ,和一个样本均值的情况一样,对于取自正态
总体的任意大小样本,(x1 x2 )的抽样分布是正态的。对 于取自非正态总体的样本,只要 n1和 n2充分的大(大于
解:第一,设立假设。原假设 H 0: P 0.85 ;
备择假设 H1: P 0.85。
第二,根据显著性水平确定临界值。显著性水平 0.05时,
查《正态分布表》得对应的临界值: z0.025 1.96, z0.025 1.96
第三,构造检验统计量。t p P 0.82 0.85 1.19 P(1 P) 0.85 0.15
30),则其抽样的分布近似于正态分布。
因此,若有两个样本均值 x1和 x2,我们建立它们是 来自具有标准差为 的同一总体的原假设,然后就可以
检验两均值之差是否显著地不等于0。
z (x1 x2 ) 0 x1 x2
样本数据的分布检验方法

样本数据的分布检验方法1.参数检验参数检验是基于对总体参数的假设进行检验的方法。
它假定总体数据服从特定的分布,并且以该分布的参数进行统计推断。
常见的参数检验方法有正态分布检验和t检验。
正态分布检验:用于检验样本数据是否来自正态分布。
常用的正态分布检验方法有Kolmogorov-Smirnov检验、Shapiro-Wilk检验和Anderson-Darling检验等。
t检验:用于比较两个样本均值是否有显著差异。
常用的t检验包括单样本t检验、独立样本t检验和配对样本t检验等。
2.非参数检验非参数检验是不依赖总体分布形式的统计检验方法,适用于总体分布未知或不满足正态分布的情况。
这些方法使用的是样本数据的排序信息,而不是直接使用数据的具体值。
常见的非参数检验方法有Wilcoxon秩和检验、Kruskal-Wallis单因素方差分析、Mann-Whitney U检验和卡方检验等。
Wilcoxon秩和检验:用于比较两个相关样本的差异,通过对样本差值的秩和进行统计推断。
Kruskal-Wallis单因素方差分析:用于比较多个独立样本的差异,通过对各个样本的秩和进行统计推断。
Mann-Whitney U检验:用于比较两个独立样本的差异,通过对样本秩和进行统计推断。
卡方检验:用于比较观察值与理论值之间的偏离程度,适用于分类变量的比较。
除了参数检验和非参数检验,还有其他的分布检验方法,如拟合优度检验和残差分析等。
拟合优度检验:用于比较样本数据的分布是否与理论分布相吻合。
常用的拟合优度检验有卡方拟合优度检验和Kolmogorov-Smirnov拟合优度检验等。
在实际应用中,我们需要根据数据的特点和问题的需求来选择合适的分布检验方法。
需要注意的是,分布检验方法只能提供样本数据是否可能来自其中一特定分布或分布类型的判断,不能肯定地证明分布的真实性。
因此,在进行分布检验时,还需要综合考虑多个指标和实际情况,并结合领域知识来进行判断和分析。
医学研究中常用的数据统计方法

医学研究中常用的数据统计方法1.描述性统计分析:描述性统计分析是对数据进行描述和总结的方法。
包括计算平均数、中位数、标准差、频数和百分比等,以提供对数据集的基本了解。
2.参数检验:参数检验是用于比较两个或多个群体之间差异的统计方法。
在医学研究中,例如比较新治疗方法与常规治疗方法的有效性,或比较不同年龄组的患者的生存率等。
常用的参数检验方法包括t检验、方差分析(ANOVA)等。
3. 非参数检验:非参数检验方法适用于数据不具备正态分布的情况,或者样本量较小无法满足参数检验的要求。
例如,当样本数据不服从正态分布或采样尺寸较小时,可以使用Wilcoxon秩和检验、Mann-Whitney U检验等进行假设检验。
4.相关分析:相关分析用于研究两个或多个变量之间的关系,可以确定它们之间的线性关系程度及方向。
例如,相关性分析可以分析流行病学数据中的因果关系,评估一些疾病与风险因素之间的相关性。
常用的相关分析方法包括皮尔逊相关系数和斯皮尔曼等级相关系数。
5.回归分析:回归分析用于建立预测模型,可以通过依赖变量与自变量之间的关系来预测未来的结果。
医学研究中,可以用回归分析找出与其中一种疾病相关的危险因素,并预测其中一种疾病的患病率。
常用的回归分析方法包括线性回归、逻辑回归等。
6. 生存分析:生存分析是用于评估一些事件(如患病、死亡等)发生的时间以及对该事件发生的影响因素的统计方法。
生存分析可以在医学研究中用于评估药物的治疗效果、预测患者的生存时间等。
常用的生存分析方法包括Kaplan-Meier方法、Cox比例风险回归等。
7.因子分析:因子分析是一种统计方法,用于分析多个变量中的共同因素,将它们简化为一组主要因素。
在医学研究中,因子分析可用于确定一些症状或体征与其中一种疾病的相关性。
常用的因子分析方法有主成分分析、因子旋转等。
此外,还有很多其他的统计方法在医学研究中得到应用,例如区域增长分析、随机模型、混合效应模型等,这些方法可以帮助研究人员更好地理解复杂的医学数据。
多元回归模型参数的各种检验及相关关系总结

多元回归模型参数的各种检验及相关关系总结常用的参数检验方法包括:回归系数的t检验、回归系数的显著性检验、决定系数(R-square)和方差分析(ANOVA)。
1.回归系数的t检验:回归系数的t检验用于检验回归系数是否显著。
在这里,我们假设零假设为回归系数等于0,备择假设为回归系数不等于0。
如果t值的绝对值大于临界值(通常取2),则拒绝零假设,即认为回归系数显著。
2.回归系数的显著性检验:回归系数的显著性检验用于检验回归系数是否显著不等于0。
一般情况下,我们使用p值来进行显著性检验。
如果p值小于显著性水平(通常取0.05),则拒绝零假设,即认为回归系数显著。
3. 决定系数(R-square):决定系数用于衡量模型的拟合程度,表示因变量中能被自变量解释的比例。
决定系数的取值范围为0到1,越接近1表示模型的拟合程度越好。
但是,决定系数本身不能代表模型的好坏,因为它不考虑模型中所使用的自变量的数量和质量等因素。
4.方差分析(ANOVA):方差分析用于检验模型整体的显著性。
方差分析的原假设为自变量对因变量没有影响,备择假设为自变量对因变量有影响。
通过计算方差分析中的F值来进行检验,如果F值大于临界值(通常取4),则拒绝原假设,认为模型整体显著。
在多元回归模型中,参数之间也存在一些相关关系。
1.多重共线性:多重共线性是指自变量之间存在高度相关性。
在多重共线性存在的情况下,模型的参数估计可能不准确,标准误差会增大。
可以通过计算自变量之间的相关系数矩阵来判断是否存在多重共线性,如果相关系数的绝对值大于0.7,则存在多重共线性。
2.自变量之间的相关性:自变量之间的相关性可以影响模型的解释和预测能力。
如果自变量之间存在高度相关性,可能需要对自变量进行筛选或变换,以减少相关性。
3.变量的重要性:通过参数的t检验或显著性检验可以确定回归系数的显著性,从而判断变量的重要性。
如果一些变量的回归系数显著,说明该变量对因变量有显著影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判断两总体平均数相等
两总体平均数相等
1、总体服从正态分布
2、两总体方差不相等
从两个总体中各抽取一个样本
配对样本T—检验
判断指标实验前后平均值相等
指标实验前后平均数相等
1、总体服从正态分布
2、两组数据是同一试验对象在试验前后的测试值
抽取一组试验对象,在试验前测得试验对象某指标的值,进行试验后再测得试验对象该指标的取值
从总体中抽取一个样本
P110
F—检验
判断两总体方差相等
两总体方差相等
总体服从正态分布
从两个总体中各抽取T—检验
(T—检验)
判断两总体平均数相等
两总体平均数相等
1、总体服从正态分布
2、两总体方差相等
从两个总体中各抽取一个样本
P111
注意数据输入格式
独立样本T—检验
P114
非参数检验方法
检验方法名称
问题类型
假设
概率计算方法
卡方检验
用于检验实际观测频数与理论频数之间是否有差异
观测频数与理论频数无差异
P119
游程检验
检验一组观测值是否有明显变化趋势
无明显变化趋势
P121
K-S检验
检验变量取值是否为正态分布
服从正态分布
P123
常用参数检验方法
检验方法名称
问题类型
假设
适用条件
抽样方法
概率计算方法
单样本T—检验
F—检验
独立样本T—检验
(T—检验)
独立样本T—检验
(校正T—检验)
配对样本T—检验
常用参数检验方法
检验方法名称
问题类型
假设
适用条件
抽样方法
概率计算方法
单样本T—检验
判断一个总体平均数等于已知数
总体平均数等于A
总体服从正态分布
