第五章(修改)准静态电磁场
合集下载
第五章准静态电磁场

电容器两极板间电压
U BA
q 1 idt C C
B B
A
第 五 章
准静态电磁场
有
di 1 (t ) L idt i( Ri r R) uL uC uR dt c 即集总电路的基尔霍夫电压定律 u 0
表明电路理论是特殊情况下得麦克斯韦电磁理论的近似。 当满足MQS的似稳条件时,研究场的问题时可以采用路 的方法。
(0) J 当 x , Jy 有限,故 C2 0 , C1 J y 0
则
x jx J y ( x) J 0 e e
E 由 J
1 x jx E y ( x) J 0 e e
jH H ( x) j 由 E z
解: 极板间是EQS场
aE1 bE2 U S
分界面衔接条件 ( 2 E2 1E1 ) ( 2 E2 1E1 ) 0 t 解方程,得面电荷密度为
图5.3.2 双层有损介质的平板 电容器
t τ
结论 电荷的驰豫过程导致分界面有累积的面电荷。
返 回 上 页 下 页
MQS场的磁场与恒定磁场满足相同的基本方程,
在任一时刻 t ,两种磁场分布一致,解题方法相同。
B 而MQS场的电场按 计算。 E t
以下两种情况可看作磁准静态场来计算:
1 1,对于导体中的时变电磁场,满足: 则位移电流可以忽略,可按磁准静态场来处理。把
满足上述条件的导体称为良导体。
为电导率很大,驰豫时间远小于1,e指数约为0,
一般认为良导体内无自由电荷的积累。电荷分布在
导体表面。
返 回
上 页
下 页
U BA
q 1 idt C C
B B
A
第 五 章
准静态电磁场
有
di 1 (t ) L idt i( Ri r R) uL uC uR dt c 即集总电路的基尔霍夫电压定律 u 0
表明电路理论是特殊情况下得麦克斯韦电磁理论的近似。 当满足MQS的似稳条件时,研究场的问题时可以采用路 的方法。
(0) J 当 x , Jy 有限,故 C2 0 , C1 J y 0
则
x jx J y ( x) J 0 e e
E 由 J
1 x jx E y ( x) J 0 e e
jH H ( x) j 由 E z
解: 极板间是EQS场
aE1 bE2 U S
分界面衔接条件 ( 2 E2 1E1 ) ( 2 E2 1E1 ) 0 t 解方程,得面电荷密度为
图5.3.2 双层有损介质的平板 电容器
t τ
结论 电荷的驰豫过程导致分界面有累积的面电荷。
返 回 上 页 下 页
MQS场的磁场与恒定磁场满足相同的基本方程,
在任一时刻 t ,两种磁场分布一致,解题方法相同。
B 而MQS场的电场按 计算。 E t
以下两种情况可看作磁准静态场来计算:
1 1,对于导体中的时变电磁场,满足: 则位移电流可以忽略,可按磁准静态场来处理。把
满足上述条件的导体称为良导体。
为电导率很大,驰豫时间远小于1,e指数约为0,
一般认为良导体内无自由电荷的积累。电荷分布在
导体表面。
返 回
上 页
下 页
五、准静态电磁场

第五章
准静态电磁场
§5-1 电准静态场和磁准静态场
基 本 内 容
§5-2 磁准静态场与电路 §5-3 电准静态场与电荷驰豫 §5-4 集肤效应 §5-5 涡流及其损耗 §5-6 导体的交流内阻抗 §5-7 邻近效应和电磁屏蔽
基本要求
掌握电准静态场和磁准静态场的基本定义 电准静态场和磁准静态场的基本定义、 1.掌握电准静态场和磁准静态场的基本定义、 判别条件及基本方程。 判别条件及基本方程。 2.了解导体中的驰豫过程、分界面上的积累过 了解导体中的驰豫过程、 程。 3.了解导体中电流流动、涡流和磁扩散过程。 了解导体中电流流动、涡流和磁扩散过程。 4.定性说明集肤效应、邻近效应、电磁屏蔽。 定性说明集肤效应、邻近效应、电磁屏蔽。 5.了解交流内阻抗的概念。 了解交流内阻抗的概念。
J = γ (E + Ee ) ∂A Ee = − E = + + ∇ϕ γ γ ∂t J J
B B
Ee C A B
L
ε
B i ∂ B ∫AEe ⋅ dl = ∫A γS ⋅ dl + ∂t ∫A A⋅ dl + ∫Adϕ di 1 + ∫ idt (t) = i(R + r + R) + L i dt C 或 (t) =UR +UL +UC • 说明:路是场的近似, 说明:路是场的近似,
ε
• 基尔霍夫第二定律
实际问题中采用场或 路的方法进行计算, 路的方法进行计算, 需要根据具体条件。 需要根据具体条件。
§5-4 集肤效应
导体内通过交变 交变电流时,周围、内部产生交变的磁场, 交变 而交变的磁场产生感应电场,使导体内部的电流分布不均, 在靠近导体表面处电流密度增加,而内部电密减小,高频时 更趋于只有表面有电流通过,这种现象称为集肤效应。
准静态电磁场
§5-1 电准静态场和磁准静态场
基 本 内 容
§5-2 磁准静态场与电路 §5-3 电准静态场与电荷驰豫 §5-4 集肤效应 §5-5 涡流及其损耗 §5-6 导体的交流内阻抗 §5-7 邻近效应和电磁屏蔽
基本要求
掌握电准静态场和磁准静态场的基本定义 电准静态场和磁准静态场的基本定义、 1.掌握电准静态场和磁准静态场的基本定义、 判别条件及基本方程。 判别条件及基本方程。 2.了解导体中的驰豫过程、分界面上的积累过 了解导体中的驰豫过程、 程。 3.了解导体中电流流动、涡流和磁扩散过程。 了解导体中电流流动、涡流和磁扩散过程。 4.定性说明集肤效应、邻近效应、电磁屏蔽。 定性说明集肤效应、邻近效应、电磁屏蔽。 5.了解交流内阻抗的概念。 了解交流内阻抗的概念。
J = γ (E + Ee ) ∂A Ee = − E = + + ∇ϕ γ γ ∂t J J
B B
Ee C A B
L
ε
B i ∂ B ∫AEe ⋅ dl = ∫A γS ⋅ dl + ∂t ∫A A⋅ dl + ∫Adϕ di 1 + ∫ idt (t) = i(R + r + R) + L i dt C 或 (t) =UR +UL +UC • 说明:路是场的近似, 说明:路是场的近似,
ε
• 基尔霍夫第二定律
实际问题中采用场或 路的方法进行计算, 路的方法进行计算, 需要根据具体条件。 需要根据具体条件。
§5-4 集肤效应
导体内通过交变 交变电流时,周围、内部产生交变的磁场, 交变 而交变的磁场产生感应电场,使导体内部的电流分布不均, 在靠近导体表面处电流密度增加,而内部电密减小,高频时 更趋于只有表面有电流通过,这种现象称为集肤效应。
电磁场课件12准静态电磁场涡流平面电磁波资料教学文案

HJDJ t
H J
J E
B H
E B t
B0
2H H 0
t
2E E 0
t
J E
2J j J 正弦稳态情况 2J J 0
t
在正弦稳态下,电流密度满足扩散方程。
2J k 2J
式中 k j / 2 (1 j)
1 (1 j) j
d
设半无限大导体中,电流
沿 y 轴流动,则有
定义: d
1
2 称为透入深度(skin depth)或集肤深度
其大小反映电磁场衰减的快慢。
当 x = x0 时, J y (x0 ) J0e x0
当 x=x0+d 时,
J y (x0 d ) J0e (x 0d)
J0ex0 e1
J
y
透入深度
(x0 ) 36.8%
d 表示电磁场衰减到原来值的36.8% 所经过的距离。
用洛仑兹规范 A t ,化简得到泊松方程
2 A J , 2 /
一般低频交流电情况下,平板电容器中的电磁场属于电准静态场。
5.1.2 磁准静态场MQS
若位移电流远小于传导电流,忽略感应项 D 的
作用,即
JD
D t
0
t
条件:场与源近似具有瞬时 对应关系,忽略推迟效应。
麦氏方程: H J , B 0 ,
在 MQS 场中,磁场满足涡流场方程(扩散方程)
2H k 2H
d 2 Hz dx2
jHz
k 2Hz
解方程得到
HZ B0ch(kx) /
Bz B0ch(kx)
利用 (kx)
Bz和 Jy 的幅值分别为
1
Bz
B0
《电磁场与电磁波》准静态电磁场

导电媒质的典型特征是电导率 ≠ 0
电磁波在导电媒质中传播时,有传导电流J=E
存在,同时伴随着电磁能量的损耗
1 导电媒质的复介电常数
D
H E
t
H = E +j E j ( j ) E
c j
H j c E
复介电常数
电磁波的相位速度仅与媒质相关
z 增大,相位滞后变
大,故k 称相位常数
dz
1
vp
dt k
真空中电磁波的相位速度: v0
1
0 0
5)电磁场关系—波阻抗
Ex Ex0 cos t kz
Hy
k
Ex 0 cos t kz
Z
Hy
理想介质
Z
(实数,纯电阻性质)
Ɛ替换为Ɛc
导电媒质 Z c
c
Zc
Z c e j
j
1
1
tan
2
π
0~
4
(呈电阻电感性)
6)相位速度(波速)
1
理想媒质中:v k
损耗媒质中:
媒质损耗使波的传播速度变慢,波长变短
波长 λ:相位差2π的两个相邻空间点的间隔
k 2π
k
2π
=
波数 k:2π距离内的波长数
k :相移常数
单位距离内相位的变化量
相位变化的快慢: 随时间--频率
随空间--波数
电磁波在导电媒质中传播时,有传导电流J=E
存在,同时伴随着电磁能量的损耗
1 导电媒质的复介电常数
D
H E
t
H = E +j E j ( j ) E
c j
H j c E
复介电常数
电磁波的相位速度仅与媒质相关
z 增大,相位滞后变
大,故k 称相位常数
dz
1
vp
dt k
真空中电磁波的相位速度: v0
1
0 0
5)电磁场关系—波阻抗
Ex Ex0 cos t kz
Hy
k
Ex 0 cos t kz
Z
Hy
理想介质
Z
(实数,纯电阻性质)
Ɛ替换为Ɛc
导电媒质 Z c
c
Zc
Z c e j
j
1
1
tan
2
π
0~
4
(呈电阻电感性)
6)相位速度(波速)
1
理想媒质中:v k
损耗媒质中:
媒质损耗使波的传播速度变慢,波长变短
波长 λ:相位差2π的两个相邻空间点的间隔
k 2π
k
2π
=
波数 k:2π距离内的波长数
k :相移常数
单位距离内相位的变化量
相位变化的快慢: 随时间--频率
随空间--波数
准静态电磁场优秀课件

基本方程组(微分形式):
E 0 , H J D , D , B 0 t
特点: 与静电场相比,磁场方程发生变化,电场方程无变化。
11.10.2020
2
求解方法:分两步 1)电场的求解采用静电场的公式 2)磁场的求解通过电准静态场的基本方程求解
电荷 静电场公式
分布
E、D
HJD,B0 t
5.2 磁准静态场与电路 MQS Filed and Circuit
1 证明基尔霍夫电流定律
在 MQS 场中, H J J 0J dS 0 S
S J dS S 1 J 1 d S S 2J 2d S S 3J 3 d S
i1i2i30
即集总电路的基尔霍夫电流定律
i 0
结点电流
设电源到负载的距离远小于六分之一波长。
解:
E
U
ln(b/
a)
e
H
I
2
e
a
I
b H
S E
SE H *22U lIn*b/(a)ez
P RS 2 e2 U [ l I * b n /a )d (] S Ra be lU I b n [ * /a )d (] R U I * e ] [
荷决定。
11.10.2020
15
例3 一无限大金属平板,其上方的半无限空间内充满了
均匀的不良导体。在t=0瞬时,在该导体中已形成了一球
形自由电荷云,球内电荷密度为ρ0。问电荷驰豫过程中
电位如何分布?
z
解:
'
3a2 r2
5
求解方法:分两步 1)磁场的求解静态场的公式 2)电场的求解通过磁准静态场的基本方程求解
BA, EA
准静态电磁场PPT讲稿

H、B
3/48
例1 内外导体半径分别为a和b的同轴圆柱形电容器,其长度为l (>>a,b),充填有电介质(μ,ε)。若内外导体间加一正弦电压 u=U0sinωt,且假定频率不高,则可认为电容器内的电场分布与恒定情 况相同。试求(1)电容器中的电场强度E;(2)证明通过半径为ρ的
圆柱面的位移电流总值等于电容器引线中的传导电流。
E
U ln(b /
a)
e
a
H
H 2I e b P
Re[
S
2
UI* 2 ln(b /
a)
dS ]
Re[
b a
UI* ln(b /
a)
d ]
Re[UI* ]
I
S E
S
E
H*
2
UI* 2 ln(b
/
a)
ez
5.3 电准静态场与电荷驰豫 EQS Field and Charge Relaxation
a. 磁准静态场方程是交流电路的场理论基础。 b. 电路理论是在特殊条件下的麦克斯韦电磁理论
的近似。 c. 当系统尺寸远小于波长时,推迟效应可以忽略,
此时采用磁准静态场定律来研究。
2020/6/30
11/48
例2 用磁准静态场的方法处理同轴电缆内的电磁问题。
设电源到负载的距离远小于六分之一波长。
解:
解:由于频率不高,故电场为电准静态场
E
U0 sint ln(b / a)
e
ρ
JD
D t
E t
U0 cost ln(b / a)
e
iD
sJ D
dS
2l
U0 cost ln(b / a)
3/48
例1 内外导体半径分别为a和b的同轴圆柱形电容器,其长度为l (>>a,b),充填有电介质(μ,ε)。若内外导体间加一正弦电压 u=U0sinωt,且假定频率不高,则可认为电容器内的电场分布与恒定情 况相同。试求(1)电容器中的电场强度E;(2)证明通过半径为ρ的
圆柱面的位移电流总值等于电容器引线中的传导电流。
E
U ln(b /
a)
e
a
H
H 2I e b P
Re[
S
2
UI* 2 ln(b /
a)
dS ]
Re[
b a
UI* ln(b /
a)
d ]
Re[UI* ]
I
S E
S
E
H*
2
UI* 2 ln(b
/
a)
ez
5.3 电准静态场与电荷驰豫 EQS Field and Charge Relaxation
a. 磁准静态场方程是交流电路的场理论基础。 b. 电路理论是在特殊条件下的麦克斯韦电磁理论
的近似。 c. 当系统尺寸远小于波长时,推迟效应可以忽略,
此时采用磁准静态场定律来研究。
2020/6/30
11/48
例2 用磁准静态场的方法处理同轴电缆内的电磁问题。
设电源到负载的距离远小于六分之一波长。
解:
解:由于频率不高,故电场为电准静态场
E
U0 sint ln(b / a)
e
ρ
JD
D t
E t
U0 cost ln(b / a)
e
iD
sJ D
dS
2l
U0 cost ln(b / a)
电磁场理论优秀课件

第五章 准静态电磁场
麦克斯韦方程组描述了时变电磁场中时变电场与时变磁场相 互依存又相互制约,并以有限速度在空间传播,形成电磁波旳普 遍规律。此时,电磁场量旳鼓励与响应不是同步发生旳,场量旳 时间变量t与空间变量r有关。但在许多工程问题中,尤其在电气 设备、电力传播、生命科学等领域,时变电磁场旳频率教低,因 而在某些特定旳情况下,能够忽视二次源 B 或 D 旳作用,
例5-3 研究具有双层有损介质旳平板电容器接至直流电压 源旳过分过程,如图5-3所示。[书p.195例5-4]
解:设电容器在t≤0-时
处于零状态,极板上没有电
S
荷,即E1(0-)=E2(0-)=0,u(0-)
=0;t≥0+时,电容器旳端电 压被强制跃变,即u(0+)=U。
U
o
根据电容旳伏安关系
ε2 γ2 ε1 γ1
内外导体之间旳坡印亭矢量是
S E H •
•
•
••
U I
2 2 ln
b a
ez
同轴线传播旳平均功率应是坡印亭矢量在内外导体之间旳横截面
S上旳面积分,即
P
Re
S
••
U I
2 2 ln
b
a
dS
• ReUln
•
I
b a
b a
d
•
Re[U
•
I
]
P Re
••
U I
dS
• ReU
•
I
t
旳库仑电场Ec和感应电场Ei。在低频电磁场中,假如感应电场Ei
远不大于旳库仑电场Ec,则能够忽视Bt 现无旋性
旳作用,这时旳电场呈
E (E c E i) E c 0 (5-1)
麦克斯韦方程组描述了时变电磁场中时变电场与时变磁场相 互依存又相互制约,并以有限速度在空间传播,形成电磁波旳普 遍规律。此时,电磁场量旳鼓励与响应不是同步发生旳,场量旳 时间变量t与空间变量r有关。但在许多工程问题中,尤其在电气 设备、电力传播、生命科学等领域,时变电磁场旳频率教低,因 而在某些特定旳情况下,能够忽视二次源 B 或 D 旳作用,
例5-3 研究具有双层有损介质旳平板电容器接至直流电压 源旳过分过程,如图5-3所示。[书p.195例5-4]
解:设电容器在t≤0-时
处于零状态,极板上没有电
S
荷,即E1(0-)=E2(0-)=0,u(0-)
=0;t≥0+时,电容器旳端电 压被强制跃变,即u(0+)=U。
U
o
根据电容旳伏安关系
ε2 γ2 ε1 γ1
内外导体之间旳坡印亭矢量是
S E H •
•
•
••
U I
2 2 ln
b a
ez
同轴线传播旳平均功率应是坡印亭矢量在内外导体之间旳横截面
S上旳面积分,即
P
Re
S
••
U I
2 2 ln
b
a
dS
• ReUln
•
I
b a
b a
d
•
Re[U
•
I
]
P Re
••
U I
dS
• ReU
•
I
t
旳库仑电场Ec和感应电场Ei。在低频电磁场中,假如感应电场Ei
远不大于旳库仑电场Ec,则能够忽视Bt 现无旋性
旳作用,这时旳电场呈
E (E c E i) E c 0 (5-1)
第5章 准静态静电场

/ 2 (1 j )
1 d
(1 j ) j
半无限大导体,电流沿 y 轴流动:
2 2 J y( x ) k J y( x )
通解形式:
kx kx J y ( x ) C 1e C 2e
x , J y 有限
x j x J y ( x ) J0e e
x0
( x 当 x=x0+d时,幅值 J y ( x 0 d ) J 0 e
0
d )
J y ( x 0 ) 36 . 8 %
d 表示电磁场衰减 到原来值的36.8% 所经过的距离 。
考虑:透入深度与哪些因素有关?
5.4 邻近效应
相互靠近的导体通有交变电流时,会受到邻近导体的影响,
这种现象称为邻近效应(Proximity effect)。 频率越高,导体靠得越近,邻近效应愈显著。邻近效应与
集肤效应共存,它会使导体的电流分布更不均匀。
两根交流汇流排的邻近效应
5.5 电磁屏蔽(Shielding)
电磁屏蔽 屏蔽 磁屏蔽 电屏蔽 在高频电磁场中,利用电磁波在良导体中很快衰减的原理。选择屏 蔽层厚度h=(3-6)d。 在低频或恒定磁场中,利用磁通总是走磁阻小的路径的原理,采用 有一定厚度的铁磁材料。 在任何频率下,利用金属感应电荷,且通过接地线流入大地的原理,
H J D t E B t
(4) MQS的电场计算:
参考资料:
[1] 晁立东,仵杰,王仲奕. 工程电磁场基础[M]. 西北工业大学出版社,2002.1.
[2] 倪光正. 工程电磁场原理[M]. 高等教育出版社,2002.6
5.2 涡流(Eddy Current)
第5章 准静态电磁场

设电容内部为EQS场,且
dl ( ex e y ez ) (dxex dye y dzez ) x y z
( dx dy dz ) d x y z b b dl d b a uc
的表达式。
解: 极板间是EQS场
aE1 bE2 U S
分界面衔接条件
( 2 E2 1E1 ) ( 2 E2 1E1 ) 0 t
解方程,得面电荷密度为
双层有损介质的平板电容器
t 2 1 1 2 σ U s (1 e τ ) a 2 b 1
1 J y J 0 (ch 2 Kx cos 2 Kx) 2
1 2
1 2
Bz , J y 模值分布曲线
式中 K / 2 结论:
k j K (1 j)
去磁效应,薄板中心处磁场最小; 集肤效应,电流密度奇对称于y 轴,表面密度
大,中心处 J y 。 0
似稳场
电磁波
磁准静态场
电准静态场
(忽略推迟效应)
D ( 0) t
具有静态电磁场的特点
B ( 0) t
第5章 准静态电磁场
5.1 电准静态场和磁准静态场
电准静态场
B 库仑电场远大于感应电场,忽略二次源 的作用,即 Ei 0 t
E 0 D H J t B 0 D
第5章 准静态电磁场
第5章
准静态电磁场
第5章 准静态电磁场
5.0 序
低频时,时变电磁场可以简化为准静态场。 电准静态场(Electroquasistatic) 简写 EQS
dl ( ex e y ez ) (dxex dye y dzez ) x y z
( dx dy dz ) d x y z b b dl d b a uc
的表达式。
解: 极板间是EQS场
aE1 bE2 U S
分界面衔接条件
( 2 E2 1E1 ) ( 2 E2 1E1 ) 0 t
解方程,得面电荷密度为
双层有损介质的平板电容器
t 2 1 1 2 σ U s (1 e τ ) a 2 b 1
1 J y J 0 (ch 2 Kx cos 2 Kx) 2
1 2
1 2
Bz , J y 模值分布曲线
式中 K / 2 结论:
k j K (1 j)
去磁效应,薄板中心处磁场最小; 集肤效应,电流密度奇对称于y 轴,表面密度
大,中心处 J y 。 0
似稳场
电磁波
磁准静态场
电准静态场
(忽略推迟效应)
D ( 0) t
具有静态电磁场的特点
B ( 0) t
第5章 准静态电磁场
5.1 电准静态场和磁准静态场
电准静态场
B 库仑电场远大于感应电场,忽略二次源 的作用,即 Ei 0 t
E 0 D H J t B 0 D
第5章 准静态电磁场
第5章
准静态电磁场
第5章 准静态电磁场
5.0 序
低频时,时变电磁场可以简化为准静态场。 电准静态场(Electroquasistatic) 简写 EQS
西安交大工程电磁场导论第五章

2
V
dV
B
(J C
D
V
t 4 r
) er
dV
结论
① EQS中忽略感应电场,场量是时间的函数,电 场是无旋场,可以引入电位概念。 ② 电场分布同静电场,利用静电场的方法求解出电 场后,再用Maxwell方程求解与之共存的磁场。 ③ 工程中如两线间的电磁场和电容器中的电磁场可 以看作EQS。
其解为
oe
t
e
e
初始电荷密度
驰豫时间
上 页 下 页
说明良导体中电荷的弛豫过程非常短暂,除有局外电 源作用,一般认为良导体内部无积累的自由电荷,电荷分 布在导体表面。
对于电准静态场
2
t τe
1
0e
τ
t
e
(r , t ) V
0
4r
当 l 0
J 2 n J 1n
t
0
上 页
下 页
根据 J E 及 D2 n D1n
J 2 n J 1n
t t 研究双层有损介质平板电容器接至直流电压源的过
极板间是EQS场
0
( 2 E2 n 1E1n )
( 2 E2 n 1E1n ) 0
J C ( E Ee )
Ee A t t
E
JC
A t
A
B
) dl
B
E
l
e
dl (
l
A
B
JC
US
A dl υ dl γ S dl t
V
dV
B
(J C
D
V
t 4 r
) er
dV
结论
① EQS中忽略感应电场,场量是时间的函数,电 场是无旋场,可以引入电位概念。 ② 电场分布同静电场,利用静电场的方法求解出电 场后,再用Maxwell方程求解与之共存的磁场。 ③ 工程中如两线间的电磁场和电容器中的电磁场可 以看作EQS。
其解为
oe
t
e
e
初始电荷密度
驰豫时间
上 页 下 页
说明良导体中电荷的弛豫过程非常短暂,除有局外电 源作用,一般认为良导体内部无积累的自由电荷,电荷分 布在导体表面。
对于电准静态场
2
t τe
1
0e
τ
t
e
(r , t ) V
0
4r
当 l 0
J 2 n J 1n
t
0
上 页
下 页
根据 J E 及 D2 n D1n
J 2 n J 1n
t t 研究双层有损介质平板电容器接至直流电压源的过
极板间是EQS场
0
( 2 E2 n 1E1n )
( 2 E2 n 1E1n ) 0
J C ( E Ee )
Ee A t t
E
JC
A t
A
B
) dl
B
E
l
e
dl (
l
A
B
JC
US
A dl υ dl γ S dl t
准静态静电场
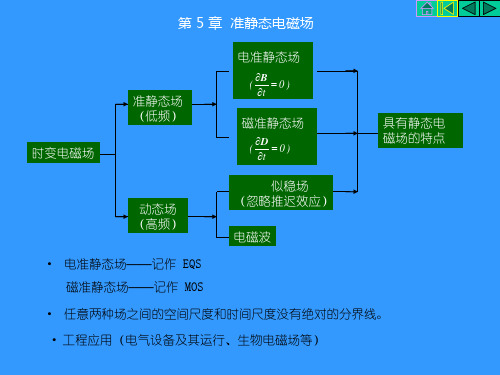
图5.5.1 涡流
工程应用:叠片铁芯(电机、变压器、电抗器等)、电磁屏蔽、电磁炉等。 5 .5 .2 涡流场分布
以变压器铁芯叠片为例,研究涡流场分布。
图5.5.2 变压器铁芯叠片
图5.5.3 薄导电平板
假设:· l , h a ,场量仅是 x的函数; · B Bz ez ,故 E, J 分布在 xoy 平面,且仅有 y分量;
a 讨论当频率较低的特殊情况时,即当 较小时,则 d
P
1 2 2 a 2 BzavV 12
可以看出,为了减小涡流损耗,薄板应尽量薄,电导率应尽量小。因此, 交流电器的铁心都是由彼此绝缘的硅钢片叠装而成的。
5.1
电 准 静 态 场
电准静态场和磁准静态场
的作用,即 Ei 0, 电磁场基本方程为 D H J , B 0 , t E 0 , D
B ( 0) 低频时,忽略二次源 t
特点: 电场的有源无旋性与静电场相同,称为电准静态场(EQS)。 用洛仑兹规范 A t ,得到动态位满足的微分方程
· 磁场呈 y 轴对称,且 x 0 时, Bz B0。
在MQS场中,磁场满足涡流场方程(扩散方程)
图5.5.4 薄导电平板的磁场
. 2 H k H 2
d 2H z jH z k 2 H z 2 dx
解方程,代入假设条件,可以得到
H Z B0 ch( kx ) /
A J , 2 /
5.2
磁准静态场与集总电路
在MQS场中, J 0 即 J dS 0 ,故有 s J1 dS J 2dS J3dS i1 i2 i3 0 J dS S S S
工程应用:叠片铁芯(电机、变压器、电抗器等)、电磁屏蔽、电磁炉等。 5 .5 .2 涡流场分布
以变压器铁芯叠片为例,研究涡流场分布。
图5.5.2 变压器铁芯叠片
图5.5.3 薄导电平板
假设:· l , h a ,场量仅是 x的函数; · B Bz ez ,故 E, J 分布在 xoy 平面,且仅有 y分量;
a 讨论当频率较低的特殊情况时,即当 较小时,则 d
P
1 2 2 a 2 BzavV 12
可以看出,为了减小涡流损耗,薄板应尽量薄,电导率应尽量小。因此, 交流电器的铁心都是由彼此绝缘的硅钢片叠装而成的。
5.1
电 准 静 态 场
电准静态场和磁准静态场
的作用,即 Ei 0, 电磁场基本方程为 D H J , B 0 , t E 0 , D
B ( 0) 低频时,忽略二次源 t
特点: 电场的有源无旋性与静电场相同,称为电准静态场(EQS)。 用洛仑兹规范 A t ,得到动态位满足的微分方程
· 磁场呈 y 轴对称,且 x 0 时, Bz B0。
在MQS场中,磁场满足涡流场方程(扩散方程)
图5.5.4 薄导电平板的磁场
. 2 H k H 2
d 2H z jH z k 2 H z 2 dx
解方程,代入假设条件,可以得到
H Z B0 ch( kx ) /
A J , 2 /
5.2
磁准静态场与集总电路
在MQS场中, J 0 即 J dS 0 ,故有 s J1 dS J 2dS J3dS i1 i2 i3 0 J dS S S S
第五章准静态场

路的电流无关。
自感又分为内自感 Li 和外自感 L0 。L Li L0
Li
i I
——内自感是导体内部仅与部分电流交链的磁链与回路电流比值。
L0
0 I
—— 外自感是导体外部闭合的磁链与回路电流的比值。
自感计算的一般步骤:
设 I H B L( Li , L0 )
A
图5.5.1 内磁链与外磁链
• 回路不变,磁场随时间变化
d dt
S
B dS t
称为感生电动势,这是变压器 工作的原理,又称为变压器电势。
图5.1.1感生电动势的参考方向 图5.1.2 感生电动势
d dt
S
B t
dS
CE
dl
S
E
dS
S
B t
dS
E
B
B0 B A
E
(
A)
t
t
E
A t
Jdv
J
V
0
J
t
dv
0
t
在恒定电流的情况下,电流连续性方程的积分、微分形式为:
SJ dS 0 J 0
5.3 准静态场
电
低频时,忽略二次源
B ( 0 ) t
的作用,即 Ei 0, 电磁场基本方程为
准 静
H J D , B 0 , J
t
t
态
E 0 , D
导线 B 的作用
mB
mB
0 I 2
l
ln
BC BD
由于这两个部分磁通方向相同
m
mA
mB
0I 2
l
ln
AD BC AC BD
M m 0l ln AD BC (H) I 2 AC BD
090525第五章准静态电磁场
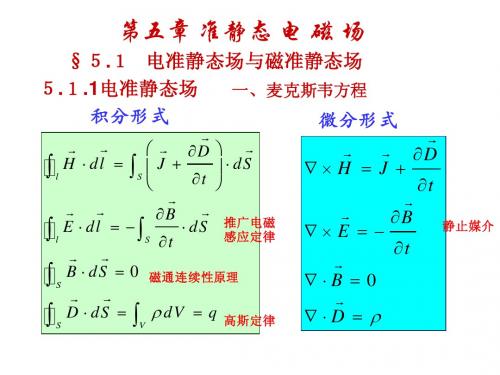
s
教材P335 教材
∫ J ⋅ dS = 0
流出任意闭合曲面的总传导电流是0。 流出任意闭合曲面的总传导电流是 。
5. 2磁准静态场和电路
∫ J ⋅ dS = 0
s
i1 i1 +i2 +i3 =0 i3 基尔霍夫电压定律(自学) 二、基尔霍夫电压定律(自学)
i2
5. 4 集肤效应
交流电流流过线圈, 交流电流流过线圈,导线周围变化的磁场在导线中感应电 流,从而使导线截面的电流分布步均匀。尤其频率较高时 从而使导线截面的电流分布步均匀。 电流几乎在导线表面附近的一薄层中流动, 集肤效应。 电流几乎在导线表面附近的一薄层中流动,即集肤效应。 (讨论导线自身有电流,其内部电流流动及电磁场分布) 讨论导线自身有电流,其内部电流流动及电磁场分布) 导线自身有电流 磁准静态场(MQS):位移电流密度忽略不计。 磁准静态场(MQS):位移电流密度忽略不计。 (MQS):位移电流密度忽略不计
二、磁准静态场E、B与动态位A和φ关系 磁准静态场E、B与动态位A E、B 关系
同恒定磁场
(1)矢量动态位
: A
B = ∇× A
∂A ∴∇ × E + =0 ∂t
(2)标量动态位 ϕ :Φ标量函数 标量函数
∂B ∂ ∵ ∇× E = − = − (∇ × A) ∂t ∂t
令
∂A E+ = −∇ϕ ∂t
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ H
2
得
∇ × J = ∇(∇ ⋅ H ) − ∇ H
2
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ 2 H ∇ × J = ∇(∇ ⋅ H ) − ∇ 2 H
教材P335 教材
∫ J ⋅ dS = 0
流出任意闭合曲面的总传导电流是0。 流出任意闭合曲面的总传导电流是 。
5. 2磁准静态场和电路
∫ J ⋅ dS = 0
s
i1 i1 +i2 +i3 =0 i3 基尔霍夫电压定律(自学) 二、基尔霍夫电压定律(自学)
i2
5. 4 集肤效应
交流电流流过线圈, 交流电流流过线圈,导线周围变化的磁场在导线中感应电 流,从而使导线截面的电流分布步均匀。尤其频率较高时 从而使导线截面的电流分布步均匀。 电流几乎在导线表面附近的一薄层中流动, 集肤效应。 电流几乎在导线表面附近的一薄层中流动,即集肤效应。 (讨论导线自身有电流,其内部电流流动及电磁场分布) 讨论导线自身有电流,其内部电流流动及电磁场分布) 导线自身有电流 磁准静态场(MQS):位移电流密度忽略不计。 磁准静态场(MQS):位移电流密度忽略不计。 (MQS):位移电流密度忽略不计
二、磁准静态场E、B与动态位A和φ关系 磁准静态场E、B与动态位A E、B 关系
同恒定磁场
(1)矢量动态位
: A
B = ∇× A
∂A ∴∇ × E + =0 ∂t
(2)标量动态位 ϕ :Φ标量函数 标量函数
∂B ∂ ∵ ∇× E = − = − (∇ × A) ∂t ∂t
令
∂A E+ = −∇ϕ ∂t
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ H
2
得
∇ × J = ∇(∇ ⋅ H ) − ∇ H
2
∇ × (∇ × H ) = ∇(∇ ⋅ H ) − ∇ 2 H ∇ × J = ∇(∇ ⋅ H ) − ∇ 2 H
第五章准静态电磁场
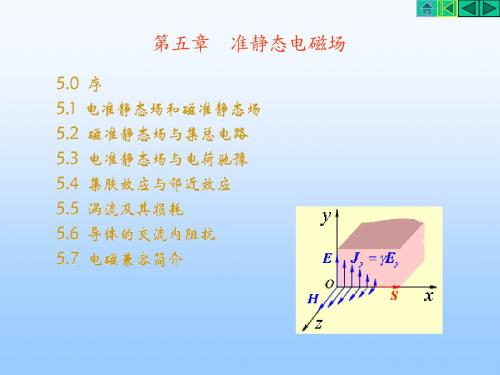
在MQS场中,磁场满足涡流场方程(扩散方程)
图5.5.4 薄导电平板的磁场
& ∇ H =k H
2 2
→
& d 2H z & & = j ωµγ H z = k 2 H z 2 dx
解方程,代入假设条件,可以得到
& & HZ = B0ch( kx ) / µ
& & Bz = B0ch( kx )
1 2
−
t
时的电荷分布τ ,= ε e
/γ
( 驰豫时间),
说明导电媒质在充电瞬间,以体密度分布的电荷随时间迅速衰减。 t − ρ 1 EQS场中,导体媒质内的电位满足 2ϕ = − = − ρ 0 e τ e ∇ 特解之一为
ϕ ( r ,t ) = ∫ V
− − ρ0 τ e dV = ϕ 0 ( r ) e τ 4 πε r
以电工钢片为例设kxcoskx50500图556电工钢片的集肤效应56导体的交流内阻抗561计算圆柱导体的交流参数设透入深度直流或低频交流电流均匀分布高频交流集肤去磁效应电流不均匀分布电流不均匀分布图561圆柱导体57电磁兼容简介电磁兼容是在有限空间时间频谱资源条件下各种用电设备生物可以共存不致于引起降级的一门科学
例5.3.1 研究双层有损介质平板电容器接至直流电压源的过渡过程,写出分界面 上面电荷密度σ 的表达式。 解 EQS: aE1 + bE2 = US
∂ (ε 2 E2 − ε1E1 ) = 0 ∂t
分界面衔接条件
(γ 2 E2 − γ 1E1 ) +
图5.3.2 双层有损介质的平板电容器
解方程,得面电荷密度为
5.3
电准静态场与电荷驰豫
时变电磁场和准静态电磁场

两项结论相加得到最后结论.
4.麦克斯韦假设:
除了电荷产生电场外,变化的磁场也要 产生电场--感应电场. 例如 , 法拉第所述闭合回路中感应电流 就是在感应电场的作用下引起的 . 然而这 里不仅仅局限于回路中.
d m d l Ei dl S B dS dt dt
式中的 D / t 是有限量, 所以最后一项趋向于零 得
H1t H2t J s n (H1 H2 ) J s 若分界面上Js=0, 则 n ( H1 H 2 ) 0
例题 4-3 比较传导电流和位移电流的大小. 设导体 中存在电场,电场强度为 Em sin t , 导体的电导率: r 107 S / m 介电常数为 0 D (E ) 解: 传导电流密度为 J E , J d 0 Em cost t t J d 0 | | 1017 f J 这里 2f 该题说明, 在良导体中位移电流很小. 例题4-4 两块导电平板z=0和z=d之间的空气中传播 的电磁波的电流强度为 E E0 sin d z cos(t x)ey , 其中 为常数,试求:(1) 磁场强度; (2) 两块导电平板表 面上的电流线密度.
A A A (E ) 0 E 或者 E t t t
3.达朗贝尔方程-确定动态位与场源关系 根据 B H 和 D E , 以及 D 得到下列方程:
2
A 2 2 A 2 J ( A ) 和 ( A) t t t
S D dS q
对比几种特例:
S B dS 0
D H J t B E t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S
20lg
H0 H1
单位:dB
屏蔽的谐振现象 :当电磁波频率与屏蔽体固
有频率相等时,发生谐振,使屏蔽效能急剧下降,
甚至于加强原电磁场。
5.6 导体的交流内阻抗
直流或低频交流
电流均匀分布 R l / s
高频交流
集肤、去磁效应,电流不均匀分布
Z
1 I2
( E H * )dS
S
例 5.6.1 计算圆柱导体的交流参数(设透入深度 d a )
解 在MQS场中,设 H dl I H E S~ Z L
d a ,无反射,电流不均匀分布I' I0 ek( ar )
身着化纤衣物、脚穿与地绝缘的鞋子的人运动时,会积
扰
源
累一定静电荷,当人接触金属后会放电;
通信系统 核电脉冲
各种无线电广播、电视台、雷达站、通信设备等工作时, 都要辐射强能量的电磁波。 继电器接触开断、核磁共振检测……
抗电磁干扰的两个主要措施:接地、电磁屏蔽。
保护接地 在金属体(含设备外壳)与大地之间建立
5.4.2 邻近效应 相互靠近的导体通有交变电流时,会受到邻近导体的
影响,这种现象称为邻近效应(Proximate effect)。 频率越高,导体靠得越近,邻近效应愈显著。邻近效
应与集肤效应共存,它会使导体的电流分布更不均匀。
单根交流汇流排的电流集肤效应
两根交流汇流排的邻近效应
5.5.1 涡流
微分方程
2 A J , 2 /
磁准静态场
低频时,忽略二次源 磁场基本方程为
D t
的作用,即 H D
0,电
H J , B 0,
E B / t , D
特点:磁场的有旋无源性与恒定磁场相同,称为磁 准静态场(MQS)。
用库仑规范 A 0 ,得到动态位满足的微分方程
2 A J , 2 /
· MQS的磁场与恒定磁场满足相同的基本方程,在
任一时刻 t ,两种磁场的分布一致,解题方法相同,
MQS的电场按 E B t计算。
,A
·
在两种场中满足相同的微分方程,描述不相
同的场,为什么?
a)A的散度不同,A 必不相同, B A 也不相同; b) E (EQS)和 E A t (MQS),
idt i(Ri r R) uL uC uR
即集总电路的基尔霍夫电压定律
u0
5.3 电准静态场与电荷驰豫
导体中,自由电荷体密度随时间衰减的过 程称为电荷驰豫。
5.3.1 电荷在均匀导体中的驰豫过程
设导电媒质 , 均匀,且各向同性,在EQS场中
式中o
J
t
J D / D
5.4 集肤效应与邻近效应
5.4.1 集肤效应 在正弦电磁场中,J JC JD E j E ,
满足 的材料称为良导体,良导体中可
以忽略位移电流,场为MQS:
H JC 和 E j H
在导体中,MQS场中同时存在自由电流和感应电流。 靠近轴线处,场量减小;靠近表面处,场量增加,称为 集肤效应(skin effect )。
EQS 与 MQS 的共性与个性
·
满足泊松方程,说明 EQS 和 MQS 忽略了滞
,A
后效应和波动性,属于似稳场。
· EQS和MQS 场中,同时存在着电场与磁场,两者 相互依存。
· EQS场的电场与静电场满足相同的基本方程,
在任一时刻t ,两种电场的分布一致,解题方法相同。
EQS的磁场按 H J D t 计算。
接
低阻抗电路,使雷电、过电流、漏电流等
地
直接引入大地。
工作接地 系统内部带电体接参考点(不一定与大地
相连),以保证设备、系统内部的电磁兼
容。
电磁屏蔽 在高频电磁场中,利用电磁波在良导体中
很快衰减的原理,选择 d 小且具有一定厚
度(h 2d)的屏蔽材料。
屏 蔽
磁屏蔽 在低频或恒定磁场中,利用磁通总是走磁阻
表明 E 不相同。
5.2 磁准静态场与集总电路
图5.2.1 结点电流
在MQS场中, J 0
即
J
s
dS
0
故有
J
s
dS
S1 J1 dS S2 J2dS S3 J3dS
i1 i2 i3 0
即集总电路的基尔霍夫电流定律
i0
i
+R
uS
L
_s C
AB 环路电压
us
L
di dt
1 c
电力传输系统 高压传输线绝缘子的电晕放电;
高压传输线中电流与电压的谐波分量;
高压传输线之间的邻近效应; 电
磁
电牵引系统 电气化铁道、有轨无轨电车上的受电弓与电网线间的放电和电
干 扰
力电子器件整流后的电流谐波分量(0.1~150kHz) ;
源
人 气体放电灯
荧光灯、高压汞灯、放电管等产生的放电噪音;
为
干 静电放电
安培环路定律H
I 2r
e
I0 2r
ek( ar )e
根据 H Ezez 有
图5.6.1 圆柱导体
交流参数
E z
1
1 r
r
(
rH
)
k
H
I0k ek( ar ) 2 r
2
(1
j
)H
1
Z R jX I02
( E H
S
) dS
1 I02
S
(
2
(1
j
)H
H
dS
l ( 1 j ) 2 2a
5.5 涡流及其损耗
当导体置于交变的磁场中,与磁
场正交的曲面上将产生闭合的感应电
流,即涡流 (eddy current)。其特
涡流
点:
· 热效应 涡流是自由电子的定向运动,有与传导
电流相同的热效应。
· 去磁效应,涡流产生的磁场反对原磁场的变化。
工程应用:叠片铁芯(电机、变压器、电抗器等)、 电磁屏蔽、电磁炉等。
l 2 d a ,故
,且随 的增加而减小,去磁效应的结果。
L直 L
5.7 电磁兼容简介
电磁兼容是在有限空间、时间、频谱资源条件下, 各种用电设备(生物)可以共存,不致于引起降级的一 门科学。即电磁干扰与抗电磁干扰问题。
自然干扰源 雷电、太阳黑子、磁暴、沙暴、地球磁场等
第五章 准静态电磁场
第 5 章 准静态电磁场
时变电磁场
准静态场 (低频)
动态场 (高频)
电准静态场
( B 0 ) t
磁准静态场
( D 0 ) t
似稳场(忽略推 迟效应)
电磁波
具有静态电 磁场的特点
• 电准静态场——Electroquasistatic 简写 EQS
磁准静态场—— Magnetoquasistatic 简写 MQS
以半无限大导体为例,电流沿 y 轴流动,求得:
式中 k j /2 (1 j)
1 d
(1
j)
j
·
令
d
1
2
称为
透入深度,d 的大小反
半无限大导体中的电流 Jy的分布
透入深度
映电磁场衰减的快慢。
d 表示电磁场衰减到原来值的36.8% 所经过的距离
当材料确定后, d 衰减快 电流不均匀分布。
• 任意两种场之间的空间尺度和时间尺度没有绝对的 分界线。
5.1 电准静态场和磁准静态场
电准静态场
低频时,忽略二次源
B t
(
0)
的作用,即
Ei
0,
电磁场基本方程为
H J D , B 0 , t
E 0 , D
特点: 电场的有源无旋性与静电场相同,称为电准 静态场(EQS)。
用洛仑兹规范 A t ,得到动态位满足的
0 通解为 t
为t 0 时的电荷分布,e /
( 驰豫时间),
t
oe e
说明导电媒质在充电瞬间,以体密度分布的电荷随时间迅速衰减。
EQS场中,导体媒质内的电位满足 2
1
t
0e e
特解之一为
( r ,t
)
V
0 4 r
t
e e dV
0( r
t
)e e
说明在EQS场中,导电媒质中自由电荷体密度 产生的电位很快衰减至零。
其中
RX l
2a
2
, L l
2a 2
R l 2a 2
L l 2a 2
·交流电阻 R 随 的增加而增大
R l a 1 a a 2
2
l a2
a 2
2
R直
a 2d
由于 d a ,故 R R直 ,且随 的增加而增大,集肤效应的结果。 · 自感 L 随 的增加而减小
L l 8 1 8 2 2a
小的路径的原理,采用有一定厚度的铁磁材
料。
电屏蔽 在任何频率下,利用金属感应电荷,且通过
接地线流入大地的原理,采用金属屏蔽材料,
且接地。若是静电场,可实现全屏蔽;若允
许磁场存在,金属选非磁性的。
屏蔽效能用分贝表示(E0 ,H0 表示无屏蔽时的场量)
静电屏蔽效能
S
20lg
E0 E1
,
单位:dB
静磁屏蔽效能
