激光光束发散角的测量
刀口法测量He-Ne激光束发散角实验的再认识

对 功率为 0 . 2 5和 0 . 7 5的点位 于高斯分布 曲线极大值两侧 , 距离为 e p=0 . 6 7 4 5 :0 . 3 3 7 3 W, 对测量
实验数据进行 曲线拟合 , 求得 其激 光光束发散角 。
关 键 词: 刀 口法 ; 曲线拟合 ; 发散角
文献 标 志码 : A D OI : 1 0 . 1 4 1 3 9 / j . c n k i . c n 2 2 — 1 2 2 8 . 2 0 1 5 . 0 0 4 . 0 2 5 中图分类号 : T N 2 0 6
所示)
3 1×7
1 1
c + 南 ×
×(
) +…… 当激光束发散角在其
为0 . 2 5时 ( 4 ) 可式写 为
P — 2~ √ f p [ 一 : ] : 丢, 所以 √ 』 眦 ~ …
:
一
~
o
√ 口
— —
图l a 归 一化 高 斯分 布
( 4 ) 可 式 写 为
2 测 量 装 置及 实验 数 据处 理
2 . 1 测量 装置
测量 装置 如 图 2所 示 , 激 光 器 是 工作 波 长 为 一 2一 √ f 。 p [ 一 : ] : 丢 , 所 63 √ 』 腿 一 以 2 . 8 n m 的基 横模 H e - N e 激光器 , 将 刀 口装 在 螺
刀 口法 测 量 H e — N e激 光 束 发 散 角 实 验 的 再 认 识
魏奶 萍 , 张相武
( 西安文理学院 , 陕西 西安 7 1 0 0 6 5 )
摘
要: 对 刀 口法 测 量 H e — N e激 光束 发 散 角 的 测 量 原 理 从 理 论 上 进 行 了 证 明 , 然 后 根 据 激 光 束 相
vcsel远场发散角测量原理

vcsel远场发散角测量原理
VCSEL(垂直腔面发射激光器)是一种特殊类型的激光器,其发散角度是指激光束从激光器中发射出来后,横向扩散的角度。
VCSEL 远场发散角测量的原理涉及到光学和电子学的知识。
首先,VCSEL的远场发散角测量通常使用的是光电探测器和角度测量设备。
在测量过程中,激光器会被放置在一个特定的位置,然后激光束被照射到光电探测器上。
光电探测器会测量激光束的强度分布,并将其转换为电信号。
通过测量激光束在不同角度上的强度分布,可以确定其远场发散角度。
其次,测量原理涉及到光束的传播特性。
根据光学理论,激光束在远场会形成一个特定的光斑,其尺寸和形状取决于激光器的发散角度。
通过测量这个光斑的大小和形状,可以推导出激光束的远场发散角度。
此外,测量原理还涉及到数据处理和分析。
通过收集光电探测器输出的信号,并进行数据处理和分析,可以得出准确的远场发散角度。
这通常涉及到使用数学算法和模型来处理实际测量得到的数据,以获得最终的结果。
总的来说,VCSEL远场发散角测量的原理涉及光学、电子学和数据处理等多个方面的知识,通过光电探测器的测量和数据处理分析,可以准确地确定VCSEL激光器的远场发散角度。
实验一光斑半径和发散角的测量讲义

实验十三 氦氖激光束光斑大小和发散角测量一、激光原理概述1.普通光源的发光——受激吸收和自发辐射普通常见光源的发光(如电灯、火焰、太阳等的发光)是由于物质在受到外来能量(如光能、电能、热能等)作用时,原子中的电子就会吸收外来能量而从低能级跃迁到高能级,即原子被激发。
激发的过程是一个“受激吸收”过程。
处在高能级(E2)的电子寿命很短(一般为10-8~10-9秒),在没有外界作用时会自发地向低能级(E1)跃迁,跃迁时将产生光(电磁波)辐射。
辐射光子能量为12E E h −=ν这种辐射称为自发辐射。
原子的自发辐射过程完全是一种随机过程,各发光原子的发光过程各自独立,互不关联,即所辐射的光在发射方向上是无规则的射向四面八方,另外位相、偏振状态也各不相同。
由于激发能级有一个宽度,所以发射光的频率也不是单一的,而有一个范围。
在通常热平衡条件下,处于高能级E 2上的原子数密度N 2,远比处于低能级的原子数密度低,这是因为处于能级E 的原子数密度N 的大小随能级E 的增加而指数减小,即N∝exp(-E/kT),这是著名的波耳兹曼分布规律。
于是在上、下两个能级上的原子数密度比为]/)(exp[/1212kT E E N N −−∝式中k 为波耳兹曼常量,T 为绝对温度。
因为E 2>E 1,所以N 2<N 1。
例如,已知氢原子基态能量为E 1=-13.6eV,第一激发态能量为E 2=-3.4eV,在20℃时,kT≈0.025eV,则0)400exp(/12≈−∝N N可见,在20℃时,全部氢原子几乎都处于基态,要使原子发光,必须外界提供能量使原子到达激发态,所以普通广义的发光是包含了受激吸收和自发辐射两个过程。
一般说来,这种光源所辐射光的能量是不强的,加上向四面八方发射,更使能量分散了。
2.受激辐射和光的放大由量子理论知识了解,一个能级对应电子的一个能量状态。
电子能量由主量子数n(n=1,2,…)决定。
实验8HeNe激光器光束强度分布及其发散角的测量

实验 8 He —Ne 激光器光束强度分布及其发散角的测量一、实验目的1.熟悉基横模光束特性2.掌握TEM 00模高斯光束强度分布的测量方法和鉴别 3.测量He-Ne 激光器的远场发射角二、实验原理He -Ne 激光器的模式(指横模)和远场发散角是激光器的基本参数之一。
在激光准直、导航等许多应用中使用的He -Ne 激光器,既要求是TEM ,有要求激光束具有很好的方向性和准直性。
而激光器的远场发散角越小,输出光束准直距离越长,即准直性越好。
我们能够把共焦腔基模光束的空间分布情况,用如下的空间曲线方程表示:222221(0)()x y z L Zω+−= (1)式中, (0)是Z =0处基模光斑半径,也就是高斯光束的束腰半径。
TEM 模光束沿X 轴是按双曲线规律变化的,包含Z 轴的任何一小平面,如XZ 平面内,光束传播轨迹是两条双曲线包围部分,如图l 所示。
在垂直于Z 轴的平面内是一个圆,在横截面内,其光强分布是高斯型的。
圆的大小就是基模光斑半径 (z ):ω(z=ω (2) ω(z )代表在Z 处光斑半径,即光强度下降到中心强度的l /e 2时,对应的半径r =221/2()()x y z ω+=。
由此可见,光斑半径ω(z )随|z|增大而增大。
图1 共焦腔基模光束空间分布1 .TEM 00模式的鉴别鉴别He -Ne 激光器输出光束是否是TEM 模,最简单的方法是让激光束垂直射到距离激光器输出端1米处的白屏上,观察光斑的亮度分布。
若是基模光斑,它是一个圆,中心光强最大,则He -Ne 激光器工作在TEM 模。
精确的方法是用扫描干涉仪,在示波器上观察激光器的输出频谱,如果激光器输出光束是基横模,那么,在示波器上就能观察到同一荧光谱线内各个振荡纵模 C /2L 的频率间隔的均匀分布。
本实验采用计算机和CCD 摄象机与A/D 采集卡结合,记录下光斑的强度分布,以鉴别它是否是高斯分布,从而确定激光器是否工作在TEM 模。
He-Ne laser 激光发散角测量说明

1、激光束发散角说明
2、测量方式
a 、接收屏用来观测激光光斑尺寸,可以为纸板,墙壁等平面,接收屏到激光器距离为x ,通过测量确定,建议距离x 大于4米;点亮激光器后,在接收屏上测量光斑直径2ω。
b 、图中束腰位置为激光束光斑尺寸最小的轴向位置 (即激光器出射光束自然会聚的位置,可沿轴向移动白纸,观察光点尺寸变化找到),束腰一般与HeNe 激光器的出射窗口重合或在其附近,测量束腰到激光器出射窗口的距离x 0
c 、发散角可按下式计算
2θ=2ω/(x −x 0)
如光束尺寸2ω以毫米(mm)为单位,距离x 以米(m)为单位,则上式所得发散角单位为mrad 。
根据激光器标称参数(发散角<1.5mrad ),4米处光斑直径应小于6mm 。
d 、补充:
1、如激光自窗口出射后能观察到明显的汇聚效果,则说明激光器准直性较差。
2、如激光自窗口出射后未观察到明显的汇聚,则光束束腰位置可能与窗口重合或在激光管内部,此时可认为x 0=0。
3、当接收屏离激光器较远时(此处取x >4m ),则直接测量屏上光斑尺寸即可作为判断准直性优劣的标准。
2ω0 HeNe 激光器 2ω
x 0
x
接收屏 束腰位置 激光出
射窗口。
2016新编激光光束发散角的测量

2016新编激光光束发散角的测量激光光束发散角的测量一、高斯光束由激光器产生的激光束既不是平面光波,也不是均匀的球面光波。
虽然在特定位置,看似一个球面波,但它的振幅和等相位面都在变化。
从理论上来讲,光在稳定的激光谐振腔中进行无限次的反射后,激光器所发出的激光将以高斯光束的形式在空间传输。
而且反射(衍射)次数越多,其光束传输形状越接近高斯光束。
从另一方面讲,形状越接近高斯光束的激光束,在传播、偶合及光束变换过程中,其形状越不易改变,在高斯光束时,不论怎样变换,其形状依然是高斯光束。
在激光器产生的各种模式的激光中,最基本、应用最多的是基模高斯光束。
在以光束传播方向z轴为对称轴的柱面坐标系中,基模高斯光束的电矢量振动可以表示为22rrz,[()arctan,,ikz2E,,it()2()wzRzf0 (1) (,,),,,Erzteee00()wz式中,E为常数,其余各符号意义表示如下: 0222 rxy,,2,, k,z2 wzw()1(),,0f2fRzz(),, z2,w0,f,其中,wwz,,(0)为基模高斯光束的束腰半径,f称为高斯光束的共焦参数或瑞利长度,0R(z)为与传播轴线交于z点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径,w(z) 是与传播轴线相交于z点高斯光束等相位面上的光斑半径。
图1 高斯光束的横截面图2 高斯光束的纵剖面,按双曲线的规律扩展基模高斯光束具有以下基本特点:1)基模高斯光束在横截面内的电矢量振幅分布按照高斯函数规律从中心向外平滑下降,如图1所示。
由中心振幅值下降到1/e点所对应的宽度,定义为光斑半径,光斑半径是传播位置z的函数z2 (1) wzw()1(),,0f由(1)式可见,光斑半径随着传播位置坐标z按双曲线的规律展开,即22wzz() (2) ,,122wf0如图2所示,在z=0处,,光斑达到极小值,称为束腰半径。
由(2)式可wzw(),0知,知道束腰半径和瑞利长度,即可确定任何位置处的光斑半径。
氦氖激光束光斑大小和发散角的测量-5页

氦氖激光束光斑大小和发散角的测量实验目的1、 掌握测量激光束光斑大小和发散角的方法。
2、 深入理解基模激光束横向光场高斯分布的特性及激光束发散角的意义。
实验仪器氦氖激光器、光功率指示仪、硅光电池接收器、狭缝、微动位移台等。
实验原理1、激光原理概述普通光源的发光是由于物质在受到外界能量作用,物质的原子吸收能量跃迁到某高能级(2E ),原子处于此高能级的寿命约为891010s -- ,即处于高能级的原子很快自发地向低能级(1E )跃迁,产生光电磁辐射,辐射光子能量为21h E E ν=-这种辐射为自发辐射,此辐射过程是随机的,即各发光原子的发光过程各自独立,互不关联。
各原子发出的光子位相、偏振态和传播方向也各不相同。
另一方面由于原子能级有一定宽度,所发出的光的频率也不是单一的。
根据波耳兹曼分布规律,在通常热平衡条件下,处于高能级的原子数密度远低于处于低能级的原子数密度。
因此普通光源所辐射出的光的能量是不强的。
由量子理论可知,物质原子的一个能级对应其电子的一个能量状态。
描写原子中电子运动状态,除能量外,还有轨道角动量L 和自旋角动量s ,它们都是量子化的。
电子从高能级态向低能级态跃迁只能发生在1L =±的两个状态之间,这是选择原则。
若选择原则不满足,则跃迁的几率很小,甚至接近零。
在原子中可能存在这样一些能级,一旦电子被激发到这一能级上,由于不满足跃迁的选择规则,可使它在这种能级上的寿命很长,不易发生自发跃迁,这种能级称为亚稳态能级。
但在外加光的诱发下可以迅速跃迁到低能级,并发出光子。
此过程称为受激辐射,是激光的基础。
受激辐射过程大致如下:原子开始处于高能级(2E ),当一个外来光子所带的能量h ν正好为某一对能级之差(21E E -),则这原子在此外来光子的诱发下由2E 跃迁至1E ,发生受激辐射,并辐射一个光子。
受激辐射的光子有显著的特点,就是受激辐射发出的光子与诱发光子为同态,即两光子的频率(能量)、发射方向、偏振态以及光波的相位都完全一样。
激光光束远场发散角测量方法

激光光束远场发散角测量方法丁罕;王海娟;樊翔【摘要】Divergence angle of laser beams which used in laser measurement is an important signifcance. Divergence angle of laser beams is an important parameter of Medical laser. This article introduces three measurement ways of far-field divergence angle of laser beams. Far-feld divergence angle of the laser beams is calculated by CCD camera technique measuring spot size. These measurement ways are variously and simply used, they can help to check compliances of diverse clauses from different laser standards and make the tests convenient for test institution and company.% 激光光束发散角的测量对于激光测量有着重要的意义。
激光光束发散角是医用激光质量的一个重要参数。
本文介绍了三种激光光束远场发散角的测量方法。
利用CCD相机数据采集,通过测量光斑大小来计算激光光束的远场发散角。
测试方法适用范围广泛,操作简单,可以满足医用激光类产品相关标准的测试要求,为相关企业和检测机构对激光光束发散角的测试提供便利。
【期刊名称】《中国医疗器械信息》【年(卷),期】2013(000)006【总页数】4页(P42-44,69)【关键词】激光;远场发散角;测量方法【作者】丁罕;王海娟;樊翔【作者单位】国家食品药品监督管理局广州医疗器械质量监督检验中心广州510663;国家食品药品监督管理局广州医疗器械质量监督检验中心广州 510663;国家食品药品监督管理局广州医疗器械质量监督检验中心广州 510663【正文语种】中文【中图分类】R454.20.引言光束发散角是指光束宽度或光束直径随着离束腰位置距离的增加而增大的程度。
氦氖激光束光斑大小和发散角的测量

实验六 氦氖激光束光斑大小和发散角的测量【实验目的】1、 加深对高斯光束物理图像的理解;2、 掌握外腔式氦氖激光器的使用和调整方法;3、 掌握测量激光束光斑大小和发散角的方法;4、 深入理解基模激光束横向光场高斯分布的特性及激光束发散角的意义。
【实验仪器】氦氖激光器、光功率指示仪、硅光电池接收器、狭缝、微动位移台【实验原理】激光束的发散角和横向光斑大小是激光应用中的两个重要参数,激光束虽有方向性好的特点,但它也不是理想的平行光,而是具有一定大小的发散角。
在激光准直和激光干涉测长仪中都需要设置扩束望远镜来减小激光束的发散角。
1、 激光束的发散角θ激光器发出的激光束在空间的传播如图1所示,光束截面最细处为束腰,z 是光束传播方向。
若束腰截面半径为0ω,距束腰为z 处的光斑半径为()z ω,则有()z ωω=其中λ是激光波长,上式可改写成双曲线方程22222()1()z zωπωωλ-= 双曲线的形状如图1所示。
定义双曲线渐近线的夹角θ为激光束的发散角,则有22()z zλωθπω==(z 很大) (1)由(1)式可知,只要我们测得离束腰很远的z 处的光斑大小2()z ω,便可算出激光束发散角。
图1 高斯光束的发散角2、 激光束横向光场分布如图1,激光束沿z 轴传播,其基模的横向光场振幅00E 随柱坐标值r 的分布为高斯分布的形式22[()]0000()()rz E r E z eω-= (2)式中00()E z 是离束腰z 处横截面内中心轴线上的光场振幅,()z ω是离束腰z 处横截面的光束半径,00()E r 则是该横截面内离中心r 处的光场振幅。
由于横向光场振幅分布是高斯分布,故这样的激光束称为高斯光。
当量值()r z ω=时,则00()E r 为00()E z 的1e 倍。
光束半径()z ω定义为振幅下降到中心振幅1e 的点离中心的距离。
实际测量中,我们测得的是光束横向光强分布,光强正比于振幅的平方,故将(2)式两边平方,得222222[2()]000000[2()]00()()()()rz rz I r Er Ez eI z eωω--=== (3)式中I 表示所对应的光强,光束半径()z ω也可定义为光强下降为中心光强21e倍的点离中心点的距离。
光信息专业实验报告:氦氖激光模式实验 (2)
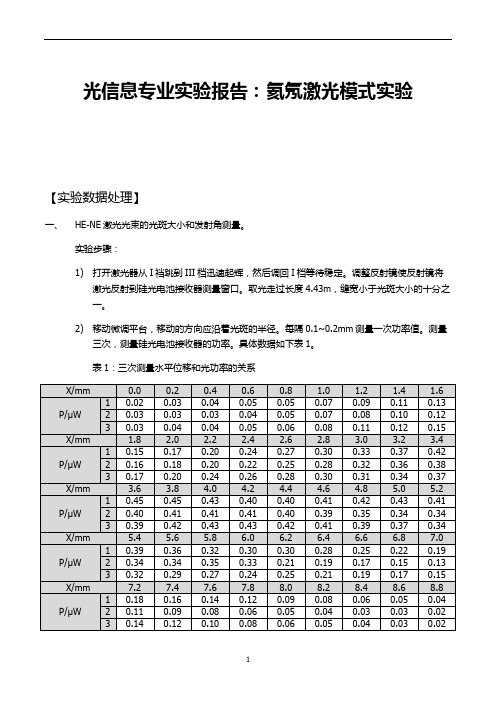
光信息专业实验报告:氦氖激光模式实验【实验数据处理】一、HE-NE激光光束的光斑大小和发射角测量。
实验步骤:1)打开激光器从I裆跳到III档迅速起辉,然后调回I档等待稳定。
调整反射镜使反射镜将激光反射到硅光电池接收器测量窗口。
取光走过长度4.43m,缝宽小于光斑大小的十分之一。
2)移动微调平台,移动的方向应沿着光斑的半径。
每隔0.1~0.2mm测量一次功率值。
测量三次,测量硅光电池接收器的功率。
具体数据如下表1。
表1:三次测量水平位移和光功率的关系分别做出三条曲线,如下图1、2、3光功率P /μW图1m m光功率P /μW图2mm光功率P /μW图3m m我们知道,HE-NE 激光光束的光强是高斯分布,所以从以上三图对比可以看出,曲线的分布基本成高斯分布。
同时图3比较平滑,误差点较少,所以一下的分析我们均在第三组数据中讨论。
对第三组数据进行高斯拟合,如图4。
2468100.00.10.20.30.40.5光功率P /μW图4:第三组数据进行高斯拟合的图拟合曲线的表达式为:从拟合的结果可以看出,相关系数为0.9907。
可见相关程度较高,数据基本符合事实。
光斑半径的值为 3.6680w mm =发散角公式为:2()0.0949w z zθ== 实验室中光斑束腰半径为:1/21/4010.2864L R w mm L λπ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭光束发散角理论值为:0020.0806w λθπ== 光斑半径为:01 3.11532w z mm θ== 所以综上,实验测量相对误差为:3.6680 3.1153100%17.74%3.1153w E -=⨯=0.09490.0806100%17.74%0.0806E θ-=⨯=总结:从上面的分析可以看出,测量得出的误差较大,主要是有以下几个方面: 1, 由于光功率测量的数值较小,所以功率变化不明显,所以拟合曲线并不完全一致。
2, 测量的时候,环境光影响到了功率计的数值。
光束发散角测试

光束发散角测试光束发散角测试是一种用于测量光束发散程度的实验方法。
它可以帮助我们了解光线传播的规律,对于光学器件的设计和优化具有重要意义。
在进行光束发散角测试时,我们通常会利用一台激光器和一套光束展宽系统。
首先,我们将激光器的输出光束通过透镜或准直器进行整形,使其成为一个平行光束。
然后,我们将这个平行光束通过一个测量装置,如光束展宽系统,来测量其发散角。
光束展宽系统通常由一组透镜和狭缝组成。
当光束通过透镜组时,透镜会将光束聚焦或展宽。
而当光束通过狭缝时,只有符合一定条件的光线才能通过,其他光线则被屏蔽。
通过调节透镜和狭缝的位置和参数,我们可以控制光束的展宽程度,从而测量其发散角。
在实验中,我们可以通过观察光束经过一定距离后的扩散情况来确定光束的发散角。
通常情况下,光束的展宽程度与传播距离成正比。
我们可以通过测量光束的展宽情况,并结合理论模型,计算出光束的发散角。
在光束发散角测试中,有几个关键的参数需要注意。
首先是透镜的焦距,它决定了透镜对光束的聚焦或展宽效果。
其次是狭缝的宽度和位置,它们决定了光束通过的条件。
最后是测量距离,它决定了光束的展宽程度。
光束发散角测试可以应用于各种光学器件的设计和评估中。
例如,在激光器的设计中,我们需要确定激光器输出光束的发散角,以便选择合适的透镜和光学元件来控制光束的传播。
在光通信系统中,我们也需要了解光纤对光束发散的影响,以确保信号的传输质量。
光束发散角测试还可以用于研究光束在大气中的传播特性。
在大气光学研究中,我们需要了解大气湍流对光束的扩散影响,以评估光通信和激光雷达等系统的性能。
光束发散角测试是一种重要的实验方法,它可以帮助我们了解光束的传播规律,对光学器件的设计和优化具有重要意义。
通过合理选择透镜和狭缝的参数,并结合测量距离,我们可以准确地测量光束的发散角。
这对于光学领域的研究和应用具有重要的指导意义。
实验3 氦氖激光器的偏振与发散特性测试数据处理与分析

He-Ne激光器偏振光数据处理与分析1、He-Ne激光器偏振光测量表1 He-Ne激光器偏振光测量数据表偏振角度(°)输出功率(mW)偏振角度(°)输出功率(mW)偏振角度(°)输出功率(mW)0 1.1361250.8032500.0905 1.0731300.8592550.096100.9951350.9342600.119150.835140 1.0022650.169200.743145 1.0662700.204250.665150 1.1172750.252300.556155 1.1452800.315350.464160 1.1872850.412400.378165 1.2012900.495450.291170 1.1722950.618500.225175 1.1473000.710550.170180 1.1043050.801600.130185 1.0343100.867650.0981900.9483150.966700.0881950.841320 1.027750.0922000.755325 1.102800.1132050.659330 1.145850.1532100.574335 1.174900.1982150.473340 1.192950.2812200.386345 1.1831000.3622250.285350 1.1681050.4592300.223355 1.1471100.5252350.172360 1.0981150.6082400.1271200.6992450.099图1 He-Ne激光器偏振特性曲线图分析:由图1 He-Ne 激光器偏振特性曲线图可知,He-Ne 激光器输出的光为线偏振光;而且从图中曲线可知,曲线并非完全的平滑,有一定的凹凸瑕疵,这说明实验存在误差,这主要是受实验环境光变化的影响所致。
激光光束发散角的测量

激光光束发散角的测量一、高斯光束由激光器产生的激光束既不是平面光波,也不是均匀的球面光波。
虽然在特定位置,看似一个球面波,但它的振幅和等相位面都在变化。
从理论上来讲,光在稳定的激光谐振腔中进行无限次的反射后,激光器所发出的激光将以高斯光束的形式在空间传输。
而且反射(衍射)次数越多,其光束传输形状越接近高斯光束。
从另一方面讲,形状越接近高斯光束的激光束,在传播、偶合及光束变换过程中,其形状越不易改变,在高斯光束时,不论怎样变换,其形状依然是高斯光束。
在激光器产生的各种模式的激光中,最基本、应用最多的是基模高斯光束。
在以光束传播方向z 轴为对称轴的柱面坐标系中,基模高斯光束的电矢量振动可以表示为222[()arctan ()2()000(,,)()r r z i k z i t w z R z f E E r z t e e e w z ω-+--=⋅⋅ (1)式中,E 0为常数,其余各符号意义表示如下:222r x y =+2k πλ=()w z w =2()f R z z z=+ 20w f πλ= 其中,0(0)w w z ==为基模高斯光束的束腰半径,f 称为高斯光束的共焦参数或瑞利长度,R (z )为与传播轴线交于z 点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径,w (z ) 是与传播轴线相交于z 点高斯光束等相位面上的光斑半径。
图1 高斯光束的横截面图2 高斯光束的纵剖面,按双曲线的规律扩展基模高斯光束具有以下基本特点:1)基模高斯光束在横截面内的电矢量振幅分布按照高斯函数规律从中心向外平滑下降,如图1所示。
由中心振幅值下降到1/e 点所对应的宽度,定义为光斑半径,光斑半径是传播位置z 的函数()w z w =(1) 由(1)式可见,光斑半径随着传播位置坐标z 按双曲线的规律展开,即22220()1w z z w f-= (2) 如图2所示,在z =0处,0()w z w =,光斑达到极小值,称为束腰半径。
半导体激光器发散角

数据记录
40o
30o
30 o
40 o
实验内容与步骤
2.2. 半导体激光器的偏振度测量
1)旋转偏振片,读出偏振片处于不同角度 2)记录对应的半导体激光器输出值 3)将实验值列表,并计算出其偏振度。
图 3 测量半导体激光器的偏振度
注意事项
1、用光功率获取输出功率时,每选择一个量程都需要重新调零。 2、半导体激光器输出或反射光应避免直接照射人眼。
T10 1l
2)焦距为f的薄透镜的透射矩阵:为 T 11/ f 10
r0 f
f0
(1
g f
) 0
由于半导体激光器快轴方向发散角非常大,不能用上述方法测量,用单点 扫描法。
快轴是单横模输出,其光强基本上按正弦(余弦)函数形式分布。
远场分布是近场分布的Fourier变换。 半导体激光器的模式分为空间模和纵模(轴模)。
半导体激光器的空间模和纵模(轴模)
空间模描述围绕输出光束轴线某处光强分布,
或者是空间几何位置上的光强(或者光功率)的分布,也称为远场分布
纵模表示是一种频谱,它反映所发射的激光其功率
在不同频率分量上的分布。
两者都可能是单模或者出现多个模式(多模)。 边发射半导体激光器具有非圆对称的波导结构,而且在垂直于结平面方向(称横向) 和平行于结平面方向(称侧向)有不同的波导结构和光场限制。
假定一条光线在输出面 的位置 (r0 ,0 );
离输出面 g的地方放一薄透镜 F,薄透镜的焦距 f ,
传输到透镜的后焦平面 时为(rf , f ),则
rff
1 0
f 1
束散角标准

束散角标准
束散角是一个物理量,用于描述光束从其中心向外发散的程度。
目前,国际标准组织(ISO)已经发布了一系列关于激光光束发散角的测试方法以及横模的鉴别方法的标准,其中最常用的是GB/T 13739-2011 标准。
该标准规定了激光光束宽度、发散角的测试方法以及横模的鉴别方法。
该标准适用于在均匀介质自由传播并在传播中功率密度分布取向相同或正交的激光光束进行测试。
该标准适用于高斯光束的横模的鉴别,但不适用于列阵类半导体激光器。
除了GB/T 13739-2011 标准外,美国国家标准学会(ANSI)也发布了一系列关于激光光束发散角的测试方法的标准。
其中最常用的是ANSI Z136.1-2014 标准,该标准规定了激光光束发散角的测试方法以及横模的鉴别方法。
该标准适用于高斯光束的横模的鉴别,并且适用于所有类型的激光器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
激光光束发散角的测量
一、高斯光束
由激光器产生的激光束既不是平面光波,也不是均匀的球面光波。
虽然在特定位置,看似一个球面波,但它的振幅和等相位面都在变化。
从理论上来讲,光在稳定的激光谐振腔中进行无限次的反射后,激光器所发出的激光将以高斯光束的形式在空间传输。
而且反射(衍射)次数越多,其光束传输形状越接近高斯光束。
从另一方面讲,形状越接近高斯光束的激光束,在传播、偶合及光束变换过程中,其形状越不易改变,在高斯光束时,不论怎样变换,其形状依然是高斯光束。
在激光器产生的各种模式的激光中,最基本、应用最多的是基模高斯光束。
在以光束传播方向z 轴为对称轴的柱面坐标系中,基模高斯光束的电矢量振动可以表示为
222[()arctan ()2()000(,,)()r r z i k z i t w z R z f E E r z t e e e w z ω-+--=⋅⋅ (1)
式中,E 0为常数,其余各符号意义表示如下:
222r x y =+
2k πλ
=
()w z w =2
()f R z z z
=+ 20w f πλ
= 其中,0(0)w w z ==为基模高斯光束的束腰半径,f 称为高斯光束的共焦参数或瑞利长度,R (z )为与传播轴线交于z 点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径,w (z ) 是与传播轴线相交于z 点高斯光束等相位面上的光斑半径。
图1 高斯光束的横截面
图2 高斯光束的纵剖面,按双曲线的规律扩展
基模高斯光束具有以下基本特点:
1)基模高斯光束在横截面内的电矢量振幅分布按照高斯函数规律从中心向外平滑下降,如图1所示。
由中心振幅值下降到1/e 点所对应的宽度,定义为光斑半径,光斑半径是传播位置z 的函数
()w z w =(1) 由(1)式可见,光斑半径随着传播位置坐标z 按双曲线的规律展开,即
22
220()1w z z w f
-= (2) 如图2所示,在z =0处,0()w z w =,光斑达到极小值,称为束腰半径。
由(2)式可知,知道束腰半径和瑞利长度,即可确定任何位置处的光斑半径。
束腰半径w 0是由激光器谐振腔决定的,改变激光器谐振腔的结构设计,即可改变w 0值。
2)由(1)式,基模高斯光束的相位因子为
200(,)()arctan 2()r z r z k z R z f
ϕ=+- (3) 其中2()2()r k z R z +描述了高斯光束的几何相移,arctan z f
描述了高斯光束在空间z 处,相对于几何相移的附加相移。
因子2
2()
r k R z 表明高斯光束的相移还与横向位置有关,只考虑几何相移时的高斯光束的等相位面是以R (z )为半径的球面。
R (z )随z 的变化规律为
2
()f R z z z
=+ (4) 对(4)式分析可知
(1)当z =0时,()R z →∞,表明束腰处的等相位面为平面。
(2)当z →±∞时,()R z z →,表明离束腰很远处的等相位面是球面,曲率中心在
束腰处。
(3)当z f →±时,()2R z f =,曲率半径达到最小值。
3)如图2所示,基模高斯光束的远场发散角定义为在远场时(z →∞),光强度为中
心的1/e 2点所夹角的全宽度
21/0
2()2lim e z w z z w λθπ→∞== (5) 综上所述所述,基模高斯光束在其传播轴线附近,可以近似地看作一种非均匀的球面波,其等相位面是曲率中心不断变化的球面,振幅和强度在横截面内保持高斯分布。
二、激光光束远场发散角的测量
根据对发散角的理解方法不同,其测量方法有很多,在此我们例举几个典型的发散角测量方法,同学们可以收集整理更多的测量方法。
1.透镜变换方法
对高斯光束,设理想薄透镜(所谓理想薄透镜,是指在光路中引入的理想薄透镜不影响光束的强度分布,不截断光束,紧靠透镜两边的光斑大小和光强分布完全一样)的焦距为f ,光腰半径为0ω的高斯光束在透镜焦平面上的光斑半径F ω为
f F 0
πωλω=
(6) 高斯光束的远场发散角θ为 f
F ωπωλθ==0 (7) 由测量实际光束在透镜后焦平面处的光斑半径实际F ω,计算得到实际高斯光束远场发散角
f F 实际实际ωθ= (8)
在会聚透镜的后焦面内测量光斑尺寸,光斑直径与聚焦透镜焦距之比即为出远场发散角。
对基模高斯光束,ω为半径的环围内含有总功率的86.5%。
相应的实际光束远场发散角实际θ即为其焦平面光斑中含86.5%总能量的环围的角半径。
需要注意,这里测量的是透镜焦平面处的光斑,而不是透镜后的光腰尺度,光腰位置并不与焦平面重合,只有透镜焦平面处光斑才是入射光的远场。
也有采用峰值光强的1/e 处的光束半径计算远场发散角的,其中含有约63.2%的总能量,这表明应用者更关心焦斑中心部分的光强。
2.光强度分布测量法
激光光束束腰的位置根据谐振腔腔型的不同而定,通常可以认为束腰在光束输出窗口附近。
在远场时我们用光电测量装置测得光强的横向分布,确定强度为中心强度1/e2处的直径d,测得测量点到束腰的距离L,则远场发散角可以认为是
d
θ=(9)
L
在此种方法的测量中,如果是小发散角的激光光束,需要一个长的测量距离,通常可以采用平面镜多次反射的办法增加测量距离,但因为平面镜面形引起激光光束形貌改变将增加光强横向分布测量的误差。
3.双孔法
利用两个大小一致的圆孔(光阑)相隔一定距离放在激光光路中,要求光阑与激光束腰处的直径相当,保证通过的光束能量为全部能量的86%左右。
由第一个光阑发出光被第二个光阑遮挡了一部分,在第二个光阑圆孔的外围形成亮斑。
如果实验条件简陋,可以直接测量这个亮斑的直径;如果有激光功率测量仪,可以分别测量两个圆孔出射的光强度,由光衍射的爱里斑换算出激光光束发散角(具体公式留给同学们自己导出)。
由于该方法简单易行,采用此种方法测量激光光束发散角的人较多。
三、实验内容
1.氦氖激光器激光光束横向强度分布测量。
2.半导体激光器激光光束发散角的测量。
四、讨论题
1.除了实验中使用的测量方法外,再设计一种激光光束发散角的测量方法,论述该方法的可行性。
2.在测量两个圆孔出射的光强度这种测量方法中,推导出激光光束发散角的实验公式。
Welcome !!! 欢迎您的下载,资料仅供参考!。
