比较器失调的仿真方法
运算放大器及电压比较器失调电压测试方法的研究

运算放大器及电压比较器失调电压测试方法的研究运算放大器和电压比较器是电子领域中最常用的两种模拟集成电路。
在电路设计和实际应用中,失调电压是衡量这两种器件性能的重要参数。
本文将对运算放大器和电压比较器的失调电压测试方法进行研究,以期为电子工程师提供参考。
一、运算放大器失调电压测试方法1.直流偏置测试法直流偏置测试法是最常见的失调电压测试方法。
该方法通过在运算放大器的同相输入端和反相输入端分别加入相同的直流电压,测量输出端的电压差,从而得到失调电压。
测试步骤如下:(1)将运算放大器配置为同相放大器。
(2)在运算放大器的同相输入端和反相输入端加入相同的直流电压。
(3)测量输出端的电压差,即为失调电压。
2.交流测试法交流测试法主要用于测量运算放大器的动态失调电压。
该方法通过在输入端加入交流信号,测量输出端的电压差,从而得到失调电压。
测试步骤如下:(1)将运算放大器配置为同相放大器。
(2)在运算放大器的同相输入端和反相输入端加入相同的交流信号。
(3)测量输出端的电压差,通过计算得到失调电压。
二、电压比较器失调电压测试方法1.直流偏置测试法电压比较器的失调电压测试方法与运算放大器类似,同样采用直流偏置测试法。
测试步骤如下:(1)将电压比较器的同相输入端和反相输入端分别加入相同的直流电压。
(2)测量输出端的电压差,即为失调电压。
2.交流测试法电压比较器的交流测试法与运算放大器也有所不同。
测试步骤如下:(1)在电压比较器的同相输入端和反相输入端加入相同的交流信号。
(2)测量输出端的电压差,通过计算得到失调电压。
三、总结运算放大器和电压比较器的失调电压测试方法有多种,本文主要介绍了直流偏置测试法和交流测试法。
在实际应用中,工程师需要根据具体需求选择合适的测试方法,以确保电路的性能和稳定性。
同时,了解各种测试方法的优缺点,有助于提高测试的准确性和效率。
需要注意的是,测试过程中应严格控制测试条件,如温度、电源电压等,以确保测试结果的准确性。
PWM比较器电路仿真设计

论文题目:PWM比较器电路仿真设计本科生毕业论文,绝对原创, 2011年06月01日摘要脉冲宽度调制(PWM)是利用微处理器的数字输出来对模拟电路进行控制的一种非常有效的技术,广泛应用在从测量、通信到功率控制与变换的许多领域中。
脉冲宽度调制是一种模拟控制方式,其根据相应载荷的变化来调制晶体管栅极或基极的偏置,来实现开关稳压电源输出晶体管或晶体管导通时间的改变,这种方式能使电源的输出电压在工作条件变化时保持恒定,是利用微处理器的数字输出来对模拟电路进行控制的一种非常有效的技术。
本文通过对PWM发展现状的了解,在掌握PWM反相器原理的基础上,比较分析了几种常见的比较器电路结构,根据PWM中对比较器的性能要求,设计了一种具有高增益和适当带宽、小的失调电压、在低功耗情况下具有较短响应时间的比较器;利用集成电路EDA设计软件,对各子模块电路进行了参数设计及仿真分析,同时进行了PWM比较器整体电路的仿真,并绘制了整体的电路版图。
本文所设计PWM比较器的增益达80dB以上,总版图面积为5674um2。
关键词PWM;比较器;增益;时延AbstractPWM is in English "Pulse Width Modulation" abbreviation ,It is used digital output ofmicroprocessor to control of the analog circuit this is a very effective technology,Used for everything from measuring, communications to power control and conversion of many areas.PWM is an analog control method,The changes under the appropriate load modulation transistor gate or base bias,To achieve the switching power supply output transistors or transistor conduction time change,This approach enables make the power supply output voltage changes in working conditions, constant,It is used digital output to microprocessor to control of the analog circuit a very effective technique.This paper is based on the PWM comparator Development of understanding.In the control based on PWM principle,Comparative analysis of several common comparator circuit structure,PWM comparator based on performance requirements,Design a suitable bandwidth, high gain and small offset voltage, low power consumption in case of a short response time comparator; Using integrated circuit design EDA software, each of sub-module circuit design and simulation parameters,PWM comparator and the overall simulationof the whole circuit.PWM comparator design in this paper gain of up to 100dB.For the overall layout of the drawing, the total layout areas 5674um2.KeywordsPWM; comparator; gain; delay目录第一章引言1.1 PWM介绍脉冲宽度调制(PWM),是英文“Pulse Width Modulation”的缩写,简称脉宽调制,是利用微处理器的数字输出来对模拟电路进行控制的一种非常有效的技术,广泛应用在从测量、通信到功率控制与变换的许多领域中。
9-比较器仿真实验
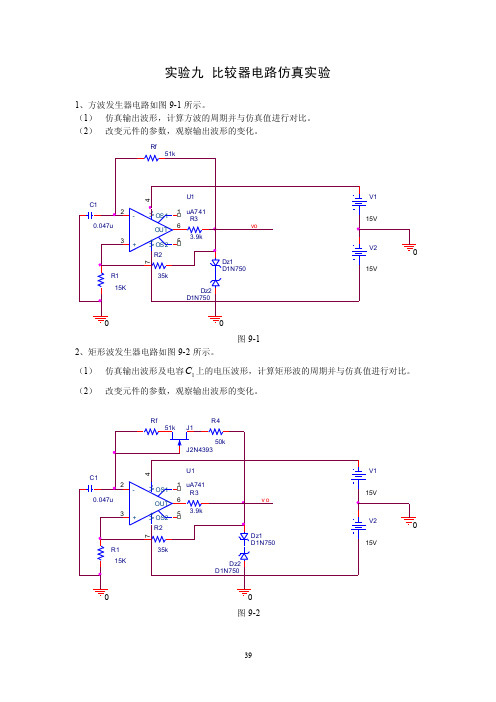
实验九比较器电路仿真实验1、方波发生器电路如图9-1所示。
(1)仿真输出波形,计算方波的周期并与仿真值进行对比。
(2)改变元件的参数,观察输出波形的变化。
Rf图9-12、矩形波发生器电路如图9-2所示。
C上的电压波形,计算矩形波的周期并与仿真值进行对比。
(1)仿真输出波形及电容1(2)改变元件的参数,观察输出波形的变化。
Rf R43、双极点Butterworth 低通滤波器电路如图9-3所示,仿真滤波器特性曲线及截止频率,并与计算值进行比较。
图9-34、阶梯波发生器电路如图9-4所示,场效应管参数已知,仿真场效应管的转移特性曲线及输出波形,分别改变场效应管模型参数Vto 和积分电容C 3 的值,观察输出阶梯波的变化。
场效应管参数: .model J2N4393 NJF(Beta=9.109m Betatce=-.5 Rd=1 Rs=1 Lambda=6m Vto=-0.5+ Vtotc=-2.5m Is=10f Isr=33f N=1 Nr=2 Xti=3 Alpha=20.98u+ Vk=123.7 Cgd=4.57p M=.4069 Pb=1 Fc=.5 Cgs=4.06p Kf=123E-18 + Af=1)* National pid=51case=TO18*88-07-13 bam BVmin=40D4图9-45、反相比例运算放大电路如图9-5所示,设集成运放型号为μA741,且运放的电源电压12+=CC V V ,12-=EE V V 。
若输入信号幅度为1±V ,周期为100μs 的方波脉冲。
试求输出电压1o v 、o v 的波形。
图9-56、 电路如图9-6所示,运放μA741的电源电压15+=CC V V ,15-=EE V V,电容器的初始电压0)0(=C v 。
(1) 若输入500=f Hz ,幅度为4±V 的方波信号时,试观察输出电压o v 的波形。
(2) 改变方波频率,观察波形变化,若波形失真应如何调整电路参数?验证分析。
3.1.2 比较器电路的仿真分析_实例讲解Multisim 10电路仿真_[共5页]
![3.1.2 比较器电路的仿真分析_实例讲解Multisim 10电路仿真_[共5页]](https://img.taocdn.com/s3/m/ed5e96d7bed5b9f3f80f1c1e.png)
3.1.1.5 案例应用 案例 8421 码转换成余 3 码。
由余 3 码的定义可知为了实现这种转换,用一
个 4 位加法器即可。只要在 4 位加法器的输入端 A3、A2、A1、A0 输入 8421 码,在输入端
B3、B2、B1、B0 输入常数 0011,进位输入端 Ci 置 0,则在输出端 S3、S2、S1、S0 得到余
码后为 1010。其他的仿真结果读者可自行分析。
图 3-12 8421 码转换成余 3 码仿真电路
3.1.2 比较器电路的仿真分析
在各种数字系统尤其是在数字电子计算机中,经常需要对两个二进制数进行大小判别, 然后根据判别结果转向执行某种操作。用来完成两个二进制数的大小比较的逻辑电路称为数
147
3 码,如图 3-11 所示。
数 字 电 路 案 例第 分3 析章
图 3-11 8421 码转换成余 3 码示意图
仿真电路如图 3-12 所示,要选取指示灯,单击元器件栏的 Place Indicator 按钮,出现如
图 3-7 所示元器件库,然后选择 PROBE 中的一种。图 3-12 中,8421 码的 0111 转换成余 3
一种动态比较器及其失调校准的方法[发明专利]
![一种动态比较器及其失调校准的方法[发明专利]](https://img.taocdn.com/s3/m/50787df7b7360b4c2f3f6470.png)
专利名称:一种动态比较器及其失调校准的方法专利类型:发明专利
发明人:李福乐,裴蕊寒
申请号:CN201610933177.6
申请日:20161031
公开号:CN108011635A
公开日:
20180508
专利内容由知识产权出版社提供
摘要:本发明公开了一种动态比较器及其失调校准的方法,该动态比较器包括:锁存器和包括预放大电路和校准辅助电路的预放大器;所述校准辅助电路包括存储失调电压的电荷存储电容、充放电开关、共模开关、第一校准控制开关和第二校准控制开关;通过在动态比较器的输入端串联电荷存储电容,并通过充放电开关、共模开关、第一校准控制开关和第二校准控制开关的控制进行失调校准。
申请人:深圳市中兴微电子技术有限公司
地址:518055 广东省深圳市南山区西丽街道留仙大道中兴工业园
国籍:CN
代理机构:北京派特恩知识产权代理有限公司
更多信息请下载全文后查看。
一种比较器失调电压和漂移的测试方法

负反馈机制自动收敛到比较器的亚稳 态。在长时间的漂移测试中,这种自 动跟随的能力大大简化了寻找亚稳态 的过程,使得测试简便而又可靠。影
本方案测试方法 因此,本文中提出一种测试比较
器失调电压漂移的闭环方法。该方法 利用负反馈特性得到比较器的输入失 调电压,并能够自动跟随电源、温度
比较器的主要技术指标是速度 和精度。比较器的速度决定了其能够 正确解析模拟信号的最短时间间隔; 精度则决定了比较器能够做出正确解 析的最小电压差。随着现代集成电路 生产工艺由深亚微米级转到纳米级, M O S器件的尺寸不断减小,器件的速 度得以大幅提高;但与此同时,M O S 器件的失配误差变得更大(C M O S工 艺中M O S管的失配程度和器件面积 平方根成反比)。由于比较器一般采 用对称性设计,M O S器件的失配会 对比较器产生解析误差,对比较器的 精度要求提出了更大的挑战。如图2
· 2018年9月 · 今日电子
48 应用设计
Applications
图3 比较器开环测试方法示意图
图4 比较器闭环测试方法示意图 压并观察比较器的输出状态:当输入 电压差值较大时,比较器会输出稳定 的“0”或“1”,当输入电压差接近 失调电压时,比较器输出结果变得有 “0”有“1”,然后微调输入电压使 得输出“0”和“1”的概率相等时, 比较器处于亚稳态,这时输入端的 电压差值就是比较器的失调电压。如 果长时间观测失调电压随温度、电源 电压等外界因素影响导致的漂移,就 需要不断地去主动寻找比较器的亚稳 态,对整个测试系统控制的复杂度提 出了较高的要求。
图1 高速链路系统示意图
图2 失调电压及漂移的定义
随着电压、温度等环境因素的变化, 产生失调电压的漂移(d r i f t),从而 影响比较器的工作精度。因此,精确 测量比较器的失调电压及其漂移变得 尤为关键。
运算放大器及电压比较器失调电压测试方法的研究

运算放大器及电压比较器失调电压测试方法的研究全文共四篇示例,供读者参考第一篇示例:运算放大器和电压比较器是电子电路中常用的集成电路之一,它们在许多应用中发挥着重要作用。
在实际应用过程中,由于器件制造工艺和温度等因素的影响,这两种器件的失调电压是难以避免的。
失调电压是指在理想情况下应该为零的输入信号为零时放大器输出仍有输出的电压,这会对电路的性能产生不利影响。
了解并测试失调电压是必不可少的。
失调电压主要包括输入失调电压、输出失调电压和共模失调电压。
输入失调电压是指在理想情况下,两个输入端的电压应该完全相等,但是实际上存在微小偏差。
输出失调电压是指在理想情况下,输出应该为零,但是实际上输出有一个微小的偏移值。
共模失调电压是指在理想情况下,放大器对共模信号的增益应该为零,即共模信号不会被放大,但是实际上由于失调电压的存在,共模信号也会被放大。
测试失调电压是非常重要的。
对运算放大器和电压比较器的失调电压进行测试有许多种方法,其中一种常用的方法是零漂移方法。
零漂移方法是一种通过比较两个电路的输出来准确测量失调电压的方法。
将一个信号源输入到被测试的运算放大器或电压比较器中,然后将另一个信号源输入到另外一个电路中,通过测量两个电路的输出,可以准确地测量出失调电压。
除了零漂移方法外,还有一些其他方法可以用来测试失调电压,例如差动输入电压法、差分输入电压法和传递函数法等。
不同的方法适用于不同的电路和应用场景。
对运算放大器和电压比较器的失调电压进行测试是非常必要的。
了解失调电压可以帮助我们评估电路的性能,并且可以采取相应的措施来减小失调电压的影响,提高电路的性能表现。
希望以上内容能对大家有所帮助。
第二篇示例:运算放大器和电压比较器是电子电路中常用的器件,它们在各种应用中起着至关重要的作用。
由于制造工艺和环境因素的影响,这些器件会存在一定程度的失调。
失调电压是指在理想情况下应为零的输入信号为零时,实际输出信号与理想输出信号之间的误差,它会影响到电路的性能和稳定性。
零漂移放大器失调电压仿真

零漂移放大器失调电压仿真摘要:1.零漂移放大器简介2.失调电压的概念及其在放大器中的影响3.零漂移放大器失调电压的仿真方法4.仿真结果及分析5.结论正文:一、零漂移放大器简介零漂移放大器是一种具有输入失调电压为零、输入偏置电流为零的特殊运算放大器。
它在模拟电路设计中有着广泛应用,如用于电压跟随器、放大器、滤波器等。
零漂移放大器之所以重要,是因为在许多应用中,输入信号的直流分量需要被放大,这就要求放大器必须具有很低的输入失调电压。
二、失调电压的概念及其在放大器中的影响失调电压(Offset Voltage)是指运算放大器在输入端加入直流信号时,输出端产生的直流电压。
在理想的情况下,运算放大器的失调电压应该为零。
然而,由于制造工艺等原因,实际运算放大器的失调电压往往不为零,这就会对电路的性能产生影响。
对于零漂移放大器而言,由于其具有输入失调电压为零的特点,因此在电路设计中可以大大降低由于输入信号直流分量引起的误差。
同时,零漂移放大器还具有较低的输入偏置电流和输入失调电流,这使得它在模拟电路设计中具有更高的性能。
三、零漂移放大器失调电压的仿真方法在设计零漂移放大器时,需要对其失调电压进行仿真以验证其性能。
常见的仿真方法有以下两种:1.基于电路模型的仿真:通过建立运算放大器的电路模型,然后使用仿真软件(如SPICE)进行模拟,从而得到失调电压的数值。
2.基于器件参数的仿真:通过查阅运算放大器的数据手册,获取其输入失调电压参数,然后根据实际电路设计进行计算,从而得到失调电压的数值。
四、仿真结果及分析在仿真过程中,我们可以得到零漂移放大器的失调电压数值。
通过对比不同放大器的仿真结果,我们可以发现,零漂移放大器的失调电压确实为零,而其他类型的运算放大器的失调电压则不为零。
这说明零漂移放大器在输入失调电压方面具有明显优势。
五、结论零漂移放大器具有输入失调电压为零的特点,使其在模拟电路设计中具有更高的性能。
蒙特卡洛分析比较器的输入误差

原理:From《A Methodology for the Offset-Simulation of Comparators》上图是测量用蒙特卡洛测offset的原理,由于器件的失配,可以到如图,在本该输出0的地方输出了1.经过多次仿真可以得到其中N是蒙特卡洛次数,ni为在xi输入下输出为1的次数由概率的知识可以看出,这个函数其实就是xoff的概率分布函数pdf,所以我们可以由这个函数来估计offset的一系列特性(详见下文matlab程序的注释)步骤:用mento carlo分析对比较器的失调(offset)进行仿真的步骤如下:搭建testbench如下:其中使用到sah_ideal这是抽样保持电路,一般将其中的vtrans_clk设为你的vdd的一半,这个vtrans_clk在ahdllib库中的verilog A语言描述是当以上升的方式越过vtrans_clk的时候进行采样并保持xfmr进行单双端转换,连接方式如图所示,vcm一般设置为你想要的值,vcm也会对offset产生一些影响,一般都设vdd/2我的comparator是动态的,后面接了两个inv缓冲,这里有一个小问题大家注意一下,刚开始我做的时候,因为估计误差只需要用到outp的值不用到outn,所以我只在outp后面加了缓冲,outn后面什么都没有加,后来怎么测怎么不对,原因是comparator输出端的电容负载将一定程度上影响比较器的offset,所以要都加上buffer激励的话我们采用斜坡信号,这样可以更全面的估计offset的范围,vpwl的设置如下:这里我的时钟周期为1us,由于我是12bit的adc,所以步长选的比较小(0.25mv),大家根据自己情况考虑。
下面就可以进行蒙特卡洛分析啦,mc的设置如下在仿真之前要在model library导入mc模型,有的可能还需要导入失配的模型,我用的工艺mc section 里面已经有失配的模型了还有就是要用有失配模型的管子之后仿真就好了,我结果如下(仅取其中几次的)下面需要导出仿真的数据到matlab分析Ocean脚本如下:openResult(“....../psf”)%...../psf为你的psf文件路径selectResult(‘tran)Ocn(?output“..../mc.txt”?precision4NumberNotation‘none?from0.7r-6?to 40.7e-6?step1e-6v(“/outp”))%...../mc.txt为输出文件路径具体函数参见cadence的oceanref运行ocean程序只需在terminal下键入ocean回车就可以了导出后还需要对这个txt修改,去掉时间以及名称只保留输出电压信息,然后导入matlab matlab部分程序如下Xdata=-5:0.25:5;%这个因人而异,取决于你的ramp的范围和步长X=load(‘d:\mc.txt’);Ydata=[];For i=1:41Y=sum(x1(i,:))/(1.8*100)Ydata=[ydata y];EndPlot(xdata,ydata);V=sqrt(2)*erfinv(ydata(1:41)*2-1)%估计在ydata概率出的标准正态分布的x取值I=find(v>-3&v<3);%3sigma准则[p,s]=polyfit(xdata(i),v(i),1);%用一阶xdata去拟合v从而得出xdata的方差和均值Sigma=1/p(1);Mu=-p(2)/p(1);%%%%%%%%%%%%%%%%原文后面还有一段程序,但很多人不需要那一段,那一段是描述拟合程度的,这里不再写了,有兴趣的朋友去参考原文即可。
一种比较器电路的自动失调补偿方法

一种比较器电路的自动失调补偿方法
杨士华;李文渊
【期刊名称】《电子与封装》
【年(卷),期】2009(9)7
【摘要】文章提出了一种适用于高精度传感器和高精度模数转换器的比较器电路.该电路利用失调自动补偿技术提高了比较器的精度,该补偿技术不需要增加前置放大器的增益,也不需要增加静态电流,从而获得低噪声和低功耗.电路设计和Hspice 仿真基于CSMC 0.5μm CMOS工艺,电源电压3.3V.仿真结果表明,在时钟为100kHz、电源电压为3.3V下补偿之后的比较器的失调较补偿前由原来的
9.75mV降低为0.31mV.
【总页数】3页(P31-33)
【作者】杨士华;李文渊
【作者单位】东南大学射频与光电集成电路研究所,南京,210096;东南大学射频与光电集成电路研究所,南京,210096
【正文语种】中文
【中图分类】TN402
【相关文献】
1.自动温度补偿电路的一种实现电路 [J], 吾布力
2.一种对失调和电容失配误差进行补偿的流水线ADC子级电路 [J], 戴强;薛颜;杨霄垒;周启才;吴俊;郭良权
3.一种采用CMOS工艺实现LDD自动温度补偿电路的方法 [J], 乔庐峰;聂辰;徐勇;王欢;王志功
4.一种比较器失调电压和漂移的测试方法 [J], 吴佩
5.一种基于运放失调补偿的CMOS传感读出电路 [J], 钱莹莹
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比较器失调的仿真用到了蒙特卡罗分析:
首先是蒙特卡罗分析窗口的一些设置,如下图所示,在此不再赘述。
其中Analysis Variation:Process是指device mismatch on two different dies(die to die)。
Mismatch是指device mismatch on the same die。
记得要把“Save Data Between Runs to Allow Family Plots”勾选,通过Calculator可以获取output的表达式。
比较器失调仿真的整体仿真图如图1所示:(其中包含有①单端到差分的转换(xfmr),输入的共模电平值由VCM确定,②理想的采保电路sah_ideal,其属性设置如图2所示。
③比较器)
本实例中的比较器是由预放大器与锁存器组成,锁存器由时钟控制,当时钟的上升沿到来后,比较器产生比较结果,当时钟变为低电平后,比较器的输出复位到Vdd。
图1
图2
输入源vpwl的设置如图3所示:
图3
仿真后得到Comp的VP和VN的输入分别如图4所示。
对于每一个输入值Xi,在时钟的上升沿到来后,比较器都有一个确定的输出值。
由于对称性,我们只选取16.4ns之前的41组Xdata数据:
图4
在理想的情况下,当Xi>Xth时,比较器输出为高电平;当Xi<Xth时,比较器输出为低
电平(如图5所示)。
实际情况下,当Xi>Xth时,比较器输出可能为低电平;同时Xi<Xth 时,比较器输出可能为高电平,将实际的比较器模型等效为图6所示。
图5
图6
仿真可以得到P(y i=1)=P((X i-X th)>X off)=n i/N=z i,其中N是蒙特卡罗分析的总次数,n i是某个X i下输出为1的次数。
这个函数是X off的概率密度函数的积分,从而得到比较
器失调的统计特性。
拟合出Z i和X i的关系曲线,z=p1*X+p2。
代码部分
导出cadence仿真数据到matlab处理的ocean脚本程序:
openResults("/home/music/simulation/SIM_pre_amp1/spectre/schematic/psf")
selectResult('tran)
ocnPrint(?output
"/home/music/simulation/SIM_pre_amp1/spectre/schematic/psf/comp.txt" ?precision
2 ?numberNotation `none ?from 0.1e-6 ?to 16.1e-6 ?step 0.4e-6 v("/OUTP"))
offset仿真的第一段matlab代码:
xdata=-20:1:20;
x=load('J:\comp.txt');
ydata=[]; %ydata原来为空
x(:,1)=[]; %删除x中的第一列,为时间
x1=x; %将新的x记作x1
for i=1:41
y=sum(x1(i,:))/(1.8*50); %输出为1的概率(本实例进行了50次蒙特卡罗仿真)
ydata=[ydata y]; %每次存入新的y
end
plot (xdata,ydata);
axis([-20 20 0 1.05]);
offset仿真的第二段matlab代码:
v=sqrt(2)*erfinv(ydata(1:41)*2-1);
i=find(v>-3&v<3); %3sigma原则
[p,s]=polyfit(xdata(i), v(i),1); %对离散点进行拟合,1表示直线拟合
sigma=1/p(1); %标准差
mu=-p(2)/p(1); %平均值
figure(2);
plot(xdata(i),v(i),'.k',xdata(i),polyval(p,xdata(i)),'r');
axis([-15 15 -3 3]);
text(-4,2,sprintf('sigma=%2.2f mV \n mu=%3.2f uV',sigma,mu*1000));
更详细的情况请参见文档《A Methodology for the offset Simulation of Comparators》。
---西安电子科技大学。
