第5章 区间估计与假设检验
计量经济学第5章假设检验

假设检验中的小概率原理
假设检验中的小概率原理
什么小概率? 1. 在一次试验中,一个几乎不可能发生的事
件发生的概率 2. 在一次试验中小概率事件一旦发生,我们
就有理由拒绝原假设 3. 小概率由研究者事先确定
5-17
假设检验中的小概率原理
由以往的资料可知,某地新生儿的平均体重为3190克,从今年的新生儿中随机 抽取100个,测得其平均体重为3210克,问今年新生儿的平均体重是否为 3190克(即与以往的体重是否有显著差异)?
决策:
在 = 0.05的水平上拒绝H0
结论:
有证据表明新机床加工的零件 的椭圆度与以前有显著差异
5-56
2 已知均值的检验
(P 值的计算与应用)
第1步:进入Excel表格界面,选择“插入”下拉菜单 第2步:选择“函数”点击 第3步:在函数分类中点击“统计”,在函数名的菜单下选
与原假设对立的假设 表示为 H1
5-12
确定适当的检验统计量
什么检验统计量?
1.用于假设检验决策的统计量 2.选择统计量的方法与参数估计相同,需考虑
是大样本还是小样本 总体方差已知还是未知
检验统计量的基本形式为 Z X 0 n
5-13
规定显著性水平(significant level)
(P-value)
1. 是一个概率值
2. 如果原假设为真,P-值是抽样分布中大
于或小于样本统计量的概率
左侧检验时,P-值为曲线上方小于等于检
验统计量部分的面积
右侧检验时,P-值为曲线上方大于等于检
验统计量部分的面积
3. 被称为观察到的(或实测的)显著性水平
5-44
双侧检验的P 值
区间估计和假设检验

在回归分析中,区间估计可以用来估计未知参数的取值范围,从 而更好地理解参数对结果的影响。
假设检验的应用场景
检验假设是否成立
在科学研究或实际应用中,我们经常需要通过假设检验来检验某个 假设是否成立,以做出决策或得出结论。
诊断准确性评估
在医学诊断中,假设检验常用于评估诊断方法的准确性,例如比较 新方法与金标准之间的差异。
非参数检验的优点是不受总体分布限制,适用于更广泛的情况。常见的非参数检验包括秩和检验、符 号检验等。
假设检验的步骤
选择合适的统计方法
根据假设和数据类型选择合适 的统计方法进行检验。
确定临界值
根据统计量的分布情况,确定 临界值。
提出假设
根据研究问题和数据情况,提 出一个或多个假设。
计算统计量
根据选择的统计方法计算相应 的统计量。
区间估计和假设检验
目录
• 区间估计 • 假设检验 • 区间估计与假设检验的联系 • 应用场景 • 案例分析
01
区间估计
定义
区间估计
基于样本数据,对未知参数或总体分布特征 给出可能的取值范围。
参数估计
基于样本数据,对总体参数进行估计,如均 值、方差等。
非参数估计
基于样本数据,对总体分布特征进行估计, 如分位数、中位数等。
结果具有互补性
03
区间估计和假设检验的结果可以相互补充,帮助我们更全面地
了解总体的情况。
区别
1 2 3
目的不同
区间估计的目的是估计一个参数的取值范围,而 假设检验的目的是检验一个关于总体参数的假设 是否成立。
侧重点不同
区间估计更侧重于估计总体参数的可能取值范围 ,而假设检验更侧重于对总体参数的假设进行接 受或拒绝的决策。
生物医学研究统计方法 第5章 假设检验思考与练习参考答案

第5章 假设检验思考与练习参考答案一、最佳选择题1. 样本均数比较作t 检验时,分别取以下检验水准,以( E )所取Ⅱ类错误最小。
A.0.01α=B. 0.05α=C. 0.10α=D. 0.20α=E. 0.30α=2. 在单组样本均数与一个已知的总体均数比较的假设检验中,结果t =3.24,t 0.05,v =2.086, t 0.01,v =2.845。
正确的结论是( E )。
A. 此样本均数与该已知总体均数不同B. 此样本均数与该已知总体均数差异很大C. 此样本均数所对应的总体均数与该已知总体均数差异很大D. 此样本均数所对应的总体均数与该已知总体均数相同E. 此样本均数所对应的总体均数与该已知总体均数不同3. 假设检验的步骤是( A )。
A. 建立假设,选择和计算统计量,确定P 值和判断结果B. 建立无效假设,建立备择假设,确定检验水准C. 确定单侧检验或双侧检验,选择t 检验或Z 检验,估计Ⅰ类错误和Ⅱ类错误D. 计算统计量,确定P 值,作出推断结论E. 以上都不对4. 作单组样本均数与一个已知的总体均数比较的t 检验时,正确的理解是( C )。
A. 统计量t 越大,说明两总体均数差别越大B. 统计量t 越大,说明两总体均数差别越小C. 统计量t 越大,越有理由认为两总体均数不相等D. P 值就是αE. P 值不是α,且总是比α小5. 下列( E )不是检验功效的影响因素的是:A. 总体标准差σB. 容许误差δC. 样本含量nD. Ⅰ类错误αE. Ⅱ类错误β二、思考题1.试述假设检验中α与P 的联系与区别。
答:α值是决策者事先确定的一个小的概率值。
P 值是在0H 成立的条件下,出现当前检验统计量以及更极端状况的概率。
P ≤α时,拒绝0H 假设。
2. 试述假设检验与置信区间的联系与区别。
答:区间估计与假设检验是由样本数据对总体参数作出统计学推断的两种主要方法。
置信区间用于说明量的大小,即推断总体参数的置信范围;而假设检验用于推断质的不同,即判断两总体参数是否不等。
计量经济学----.区间估计和假设检验

即
P[ 2 t se( 2 ) 2 2 t se( 2 )] 1
2 2
8
^
^
^
^
假设检验
检验某一给定的观测是否与虚拟假设(原假设)相符, 若相符,则接受假设,反之拒绝。 当我们拒绝虚拟假设时,我们说该统计量是统计上显 著的,反之则不是统计上显著的。
的临界值 t 2 (n 2) ,则有
ˆ ˆ P{[YF t 2 SE (eF )] YF [YF t 2 SE (eF )]} 1
1 因此,一元回归时 Y 的个别值的置信度为 的 预测区间上下限为 1 ( X F X )2 ˆ ˆ YF YF t 2 1 n xi2
给定,查t分布表得t (n 2) 2 ( )若t -t 2 (n 2), 或t t 2 (n 2),则拒绝原假设 1 H 0: 2 0,接受备择假设H1: 2 0; (2)若 - t 2 (n 2) t t 2 (n 2), 则接受原假设。
30
^
^
应变量Y 区间预测的特点
1、Y 平均值的预测值与真实平均值有误差,主要是 受抽样波动影响
YF Y F t 2
^ ^
1 ( X F X )2 n xi2
Y 个别值的预测值与真实个别值的差异,不仅受抽
样波动影响,而且还受随机扰动项的影响
1 ( X F X )2 ˆ ˆ YF YF t 2 1 n xi2
^
1 ( X F X )2 ˆ SE (YF ) n xi2
Y F 服从正态分布,将其标准化,
^
当
2
2 ei2 (n 2) 代替,这时有 未知时,只得用 ˆ ˆ YF E (YF X F ) t ~ t (n 2) 1 ( X F X )2 ˆ n xi2
假设检验与方差分析

三、假设检验的步骤
1、提出原假设(null hypothesis)和备择假设 (alternative hypothesis)
原假设为正待检验的假设:H0; 备择假设为可供选择的假设:H1 一般地,假设有三种形式:
(1)双侧检验:
H0 : 0; H1 :0 (2)左侧检验:
这两个例子中都是要对某种“陈述”做出判
断:
例1要判明工艺改革后零件平均 长度是否仍为4cm;
进行这种判断 的信息来自
例2要判明该批产品的次品率是 所抽取的样本
否低于3%。
所谓假设检验,就是事先对总体参数或总体分 布形式作出一个假设,然后利用样本信息来判断 原假设是否合理,即判断样本信息与原假设是否 有显著差异,从而决定是否接受或否定原假设
对比来构造检验统计量。
可以证明,若H0为真,则
2
(n 1)S 2
2 0
~
2 (n 1)
因此,可构造2 统计量进行总体方差
的假设检验。
当H0成立时,S2/02 接近于1,2的 值在一个适当的范围内,
当H0不成立时,S2/02远离1,2的值 相当大或相当小。
在例2中,由于所抽样本只为10,为小样本,因 此无法构造Z统 计量进行总体比例的假设检验。
如果总体X~N(,2),在方差已知的情况下,对总体均 值进行假设检验。
由于
因此,可通过构造Z统计量来进行假设检验:
注意: 如果总体方差未知,且总体分布未知,但如果是大样
本(n>=30),仍可通过 Z 统计量进行检验,只不过总体 方差需用样本方差 s 替代。
例3:根据以往的资料,某厂生产的产品的使用寿命服从正 态分布N(1020, 1002)。现从最近生产的一批产品中随机抽取16 件,测得样本平均寿命为1080小时。问这批产品的使用寿命 是否有显著提高(显著性水平:5%)?
第5章 区间估计与假设检验

分布(如t分布,F分布,正态分布, χ 2 分布等)。构造出统计
量以后,就可以利用样本数据计算出这个统计量的样本值,再 把这个样本值与给定某一显著水平的临界值进行比较,看它与 临界值是否有显著差别,从而作出判断,决定拒绝还是接受所 作的假设。
, βˆ2
+
δ
)
包含 β2 的概率
Pr(βˆ2 − δ ≤ β 2 ≤ βˆ2 + δ ) = 1−α (5.2.1)
这样的区间称为置信区间(confidence interval);1−α 称为置
信系数(confidence coefficient);而α 称为显著性水平(level of
significance)。置信区间的端点称置信限(confidence limits)也 称临界值(critical values)。
βˆ2 − δ 为置信下限(lower confidence limit)
βˆ2 + δ 为置信上限(upper confidence limit)
(5.2.1)式表示的是:随机区间包含真实 β2的概率为 1−α。
点估计与区间估计:
单一的点估计量可能不同于总体真值,即存在估计误差。点 估计既不能给出误差范围的大小,也没有给出估计的可靠程度。
进行统计假设检验,就是要制定一套步骤和规则,以使决定 接受或拒绝一个虚拟假设(原假设)。一般来说,有两种相互 联系、相互补充的方式:置信区间(confidence interval)和显 著性检验(test of significance)。
§5.6假设检验:置信区间的方法
区间估计与假设检验

"### 参数的区间估计与假设检验之间的区别
参数的区间估计和假设检验从不同的角度回答同一问 题, 它们的统计处理是相通的。 但是它们之间又有区别, 体现 以下三点: 第一, 参数估计解决的是多少 (或 范 围 ) 问题, 假设检验 则判断结论是否成立。前者解决的是定量问题, 后者解决的 是定性问题。 第二, 两者的要求各不相同。区间估计确定在一定概率 保证程度下给出未知参数的范围。 而假设检验确定在一定的 置信水平下, 未知参数能否接受已给定的值。 第三, 两者对问题的了解程度各不相同。进行区间估计 之前不了解未知参数的有关信息。 而假设检验对未知参数的 信息有所了解, 但作出某种判断无确切把握。 因而在实际应用中,究竟选择哪种方法进行统计推断, 需要根据实际问题的情况确定相应的处理方法。 否则将会产
" 拒 绝 域 为 +)J.)0!+#)(-- , 查表 %’#$#"4" 统计量 0’ ,)"" ’ & , %
得 0"$":’!$"(: , 计 算 得 0’)($A::A. 由 此 可 见 统 计 量 的 值 未 落 入 拒绝域中, 因而接受原假设, 认为符合设计要求。
(9!
统计与决策 !""# 年 # 月 (下)
上述关系虽就一特例而言, 但也有普遍意义。由区间估 计可以很容易构造检验函数。 下面来说明怎样由检验函数构 造区间估计。 设 # 是问题
生不同的结论, 做出错误的统计推断。 例 ! 测试某个品牌的汽车的百公里耗油量,假设在正 常的情况下汽车百公里耗油量服从正态分布, 路况以及驾驶 员的技术符合正常要求。现对该批汽车进行测试, 随机选取
+&".!-。
简述假设检验与区间估计之间的关系 统计学原理

简述假设检验与区间估计之间的关系统计学原理一、简介假设检验与区间估计是统计学中两个重要的概念,它们都是基于样本数据对总体参数进行推断的方法。
假设检验主要用于判断总体参数是否符合某种特定假设,而区间估计则用于对总体参数进行范围性的估计。
本文将从统计学原理角度出发,详细介绍假设检验与区间估计之间的关系。
二、假设检验1. 假设检验的基本思想在进行假设检验时,我们首先要提出一个关于总体参数的假设(称为原假设),然后根据样本数据来判断这个假设是否成立。
具体来说,我们会根据样本数据计算出一个统计量(如t值、F值等),然后通过比较这个统计量与某个临界值(也称为拒绝域)来决定是否拒绝原假设。
2. 假设检验中的错误类型在进行假设检验时,有可能会犯两种错误:一种是将一个正确的原假设错误地拒绝了(称为第一类错误),另一种是将一个错误的原假设错误地接受了(称为第二类错误)。
通常情况下,我们会将第一类错误的概率控制在一个较小的水平(如0.05或0.01),这个水平被称为显著性水平。
3. 假设检验的步骤进行假设检验时,通常需要按照以下步骤进行:(1)提出原假设和备择假设;(2)选择适当的检验统计量,并计算出样本数据所对应的值;(3)确定显著性水平,并找到相应的拒绝域;(4)比较样本统计量与拒绝域,得出结论。
三、区间估计1. 区间估计的基本思想在进行区间估计时,我们会根据样本数据来构建一个区间,这个区间包含了总体参数真值的可能范围。
具体来说,我们会根据样本数据计算出一个点估计量(如样本均值、比例等),然后根据中心极限定理和大数定律等原理来构建置信区间。
2. 区间估计中的置信度在进行区间估计时,我们通常会给出一个置信度,表示该区间包含总体参数真值的概率。
例如,如果我们给出了一个95%置信度,则意味着在大量重复实验中,有95%的置信区间都会包含总体参数真值。
3. 区间估计的步骤进行区间估计时,通常需要按照以下步骤进行:(1)选择适当的点估计量,并计算出样本数据所对应的值;(2)确定置信度,并找到相应的置信区间;(3)解释置信区间的含义,得出结论。
统计学导论 科学出版社 第五章 假设检验

右侧检验
或
H1 : µ > µ0
H1 : µ > µ0
确定适当的检验统计量
什么检验统计量? 什么检验统计量?
用于假设检验问题的统计量 选择统计量的方法与参数估计相同, 选择统计量的方法与参数估计相同,需考虑
是大样本还是小样本 总体方差已知还是未知
检验统计量的基本形式为
z= x − µ0
σ
n
选择显著性水平α,确定临界值
☺
☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺
抽取随机样本
均值 ☺ ☺ X = 20
假设检验的基本思想
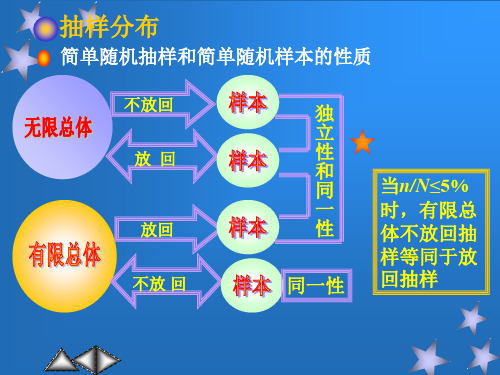
抽样分布
这个值不像我 们应该得到的 样本均值 ... ... 因此我们拒 绝假设 µ = 50
... 如果这是总 体的真实均值 20
µ = 50 H0
样本均值
假设检验应用举例
例1:抽样检验食品包装机工作是否正常 : 例2:由样本推断产品次品率是否超标 : 例3:研究黑人儿童是否有民族意识 : 例4:检验电池寿命波动性是否有显著变化 : 5: 例5:判断男女职工看电视时间是否有显著差异 例6:检验新工艺是否比旧工艺更好 : 例7:研究生活习惯是否影响血压 : 例8:检验两次地震间的天数是否服从指数分布 : 例9:比较两公司进货次品率,作出进货决策 :比较两公司进货次品率,
3、特点 、
采用逻辑上的反证法 依据统计上的小概率原理
第一节 假设检验的基本原理
一. 假设检验的一般思想 二. 假设检验的步骤 三. 假设检验的两类错误
假设检验的过程
(提出假设→抽取样本→作出决策) 提出假设→抽取样本→作出决策)
提出假设 作出决策
拒绝假设! 拒绝假设 别无选择. 别无选择
总体
区间估计与假设检验的联系与区别讲义资料

区间估计与假设检验的联系与区别讲义资料
区间估计与假设检验是统计推断的两种常见方法。
它们虽然都属于推断统计,但也有明显的不同之处。
区间估计的主要目的是估计总体参数的值,也可以称作参数估计。
根据样本信息,我们可以得出一个可能的参数值范围,也就是置信区间,从而得到一个可靠的估计区间。
估计是不断变化的,每一次统计分析给出的参数估计值都可能有所变化,从而慢慢趋近真实值。
假设检验即“判断”,是统计学中比较常用的检验方法,目的是确定两个总体之间的差异是由随机因素造成的,还是由特定的因素(如环境因素)造成的。
假设检验涉及两个立场:备择假设和原假设。
假设检验的结果由抽样分布决定,不同的抽样分布对应不同的结论,比如有抽样分布下假设检验结果可能是拒绝备择假设,也可能是接受备择假设。
从概念上讲,区间估计技术计算的是一个参数的值的估计,而假设检验是用于检查参数的方法,它只检验两个总体是否具有显著的性质差异,而不会真正测量它们的差异。
总的来说,区间估计通过单组数据范围尽可能准确地估计参数的取值范围,而假设检验则是针对任何特定统计主题,利用数据样本来检验其是否与假设相符。
两者都具有自己的优点和不足,可以结合使用来为抽样荟萃而得出结论,从而更准确地了解样本的真实情况。
区间估计与假设检验的联系与区别

区间估计与假设检验 的联系与区别
11406
a
1
区间估计
参数估计:指的是用样本中的数据估计总体分布 的某个或某几个参数
参数估计的方法:点估计和区间估计。
点估计:用估计量的某个取值直接作为总体参数 的估计值。点估计的缺陷是没法给出估计的可靠 性,也没法说出点估计值与总体参数真实值接近 的程度。
区间估计:在点估计的基础上给出总体参数估计 的一个估计区间,该区间通常是由样本统计量加 减估计误差得到的。在区间估计中,由样本估计 量构造出的总体参数在一定置信水平下的估计区 间称为置信区间。
主要区别: a、参数估计是以样本资料估计总体参数的真 值,假设检验是以样本资料检验对总体参数 的先前假设是否成立; b、区间估计求得的是求以样本估计值为中心 的双侧置信区间,假设检验既有双侧检验, 也有单侧检验; c、区间估计立足于大概率,假设检验立足于 小概率。
a
6
拒绝域。 4.比较并作出统计推断。
a
4
区间估计与假设检验的联系
主要联系: a、都是根据样本信息推断总体参数; b、都以抽样分布为理论依据,建立在概率 论基础之上的推断,都具有一定的可信程 度和风险; c、二者可相互转换,区间估计问题可以转 换成假设问题,假设问的区别
a
2
区间估计
总体均值的区间估计 (1)大样本的估计方法:总体方差已知,用z
分布。 (2)小样本(样本数小于30)的估计方法:总
体方差未知 , t分布。 总体比率的区间估计 z分布 总体方差的区间估计 χ^2分布
简述假设检验与区间估计之间的关系 统计学原理

假设检验与区间估计的关系假设检验和区间估计是统计学中两个重要的概念和方法。
它们在数据分析和推断中经常被使用,并且有密切的关联。
假设检验假设检验是统计学中一种通过样本数据对总体参数进行推断的方法。
它的基本思想是,我们根据样本数据得到的统计量,与我们对总体参数的假设进行比较,从而判断这个假设是否合理。
在假设检验中,我们通常会提出一个原假设(null hypothesis)和一个备择假设(alternative hypothesis)。
原假设是我们要进行推断的对象,备择假设则是原假设不成立时所代表的情况。
然后,我们根据样本数据计算得到一个统计量,并且利用该统计量对原假设进行检验。
这个统计量通常会服从某种已知或近似已知的概率分布。
最后,根据统计量在概率分布中所处位置的概率来决定是否拒绝原假设。
如果这个概率非常小(小于显著性水平),则我们有充分的证据拒绝原假设;反之,如果这个概率较大,则我们没有充分的证据拒绝原假设。
总结一下,假设检验的步骤如下:1.提出原假设和备择假设;2.根据样本数据计算得到一个统计量;3.假设这个统计量服从某种概率分布;4.利用概率分布来计算统计量在概率分布中所处位置的概率;5.根据这个概率来决定是否拒绝原假设。
区间估计区间估计是统计学中一种通过样本数据对总体参数进行估计的方法。
它的基本思想是,我们根据样本数据得到的统计量,以及该统计量的抽样分布特性,构建一个区间,这个区间可以包含真实总体参数的真值。
在区间估计中,我们通常会选择一个置信水平(confidence level),表示我们对该区间包含真实总体参数的程度的置信程度。
常用的置信水平有95%和99%。
然后,我们根据样本数据计算得到一个统计量,并且利用该统计量和抽样分布特性来构建一个置信区间。
这个置信区间具有以下特点:如果我们重复使用相同方法对不同样本进行估计,那么约有95%(或99%)的置信区间会包含真实总体参数的真值。
最后,我们根据置信区间来进行参数估计。
简述假设检验与区间估计之间的关系统计学原理

简述假设检验与区间估计之间的关系统计学原理假设检验与区间估计是统计学中两个重要的概念和方法,它们都是用于推断总体参数的。
假设检验是一种通过利用样本信息来判断总体参数的一个或一组特定值是否有效或可接受的方法。
在假设检验中,我们首先设立一个虚无假设(null hypothesis)H0,表示总体参数的一些值或总体参数之间的关系成立;然后通过收集样本数据,计算样本的统计量,然后与建立在虚无假设下的分布进行比较,从而得出对虚无假设的结论。
假设检验的结果可以分为接受虚无假设,拒绝虚无假设两种情况。
区间估计是一种通过利用样本信息来估计总体参数的取值范围的方法。
在区间估计中,我们使用样本数据计算样本的统计量,并根据统计量的抽样分布来构建一个置信区间。
置信区间表示总体参数在一些置信水平下的估计范围,置信水平通常取95%或90%等。
在这个范围内,我们可以合理地认为总体参数落在其中。
区间估计进一步提供了总体参数的不确定性程度。
此外,假设检验与区间估计之间还存在一种互补关系。
在假设检验中,我们可以根据检验的结果拒绝或接受虚无假设,从而判断总体参数是否落在一些给定的取值范围内,这可以视为一种特殊的区间估计。
而在区间估计中,我们利用样本数据估计总体参数的取值范围,这可以视为一种特殊的假设检验,即总体参数的真值是否落在估计的区间内。
综上所述,假设检验与区间估计是统计学中两个重要的概念和方法,它们都是推断总体参数的方法。
假设检验通过对总体参数的一个或一组特定值进行判断来推断,而区间估计通过构建置信区间来估计总体参数的取值范围。
两者在原理和方法上有相似之处,可以互相补充和解释。
在实际应用中,我们可以根据具体的问题选择使用假设检验还是区间估计,或者两者结合应用,从而得出更准确和可靠的推断结果。
第五章参数估计和假设检验PPT课件
抽样
X ~ N(, 2)
n,S2
则 (n 1)S 2 / 2 ~ 2 (n 1)
当 n 30, 2分布趋近于正态分布
若X ~ x2 (n 1) 则 Z 2 2 2(n 1)
两个样本方差之比的抽样分布
从两个正态总体中分别独立抽样所得到的两个样本方 差之比的抽样分布。
抽样
X1
~
N
(
1
,
2 1
极大似然估计是根据样本的似然函数对总体参数进行 估计的一种方法 。
其实质就是根据样本观测值发生的可能性达到最大这 一原则来选取未知参数的估计量θ,其理论依据就是 概率最大的事件最可能出现。
区间估计
估计未知参数所在的可能的区间。 P(ˆL<<ˆU ) 1
评价准则
一般形式
置信度 精确度
(ˆ △)<<(ˆ △) 或 ˆ △
2
2
2
n
Z
2
2
Pq
△
2 pˆ
Z
2
PqN
n
2
N
△
2 pˆ
Z
2
Pq
2
假设检验
基本思想 检验规则 检验步骤 常见的假设检验 方差分析
基本思想
•小概率原理:如果对总体的某种假设是真实的,那么不利于 或不能支持这一假设的事件A(小概率事件) 在一次试验中几乎不可能发生的;要是在一次 试验中A竟然发生了,就有理由怀疑该假设的 真实性,拒绝这一假设。
参数的区间估计
待估计参数
已知条件
置信区间 ˆ △
总体均值 (μ)
正态总体,σ2已知 正态总体,σ2未知
非正态总体,n≥30
X Z / n
2
统计中的区间估计与假设检验

统计中的区间估计与假设检验统计学是一门应用广泛的学科,其中的区间估计与假设检验是统计学中常用的两种方法。
这两种方法在研究和实践中被广泛应用,用于推断总体参数、比较样本之间的差异以及验证科学假设的有效性。
本文将介绍统计中的区间估计与假设检验的概念、原理以及应用。
一、区间估计区间估计是基于样本数据推断总体参数的取值范围。
在统计学中,常常无法获得整个总体的完整数据,而只能通过抽取部分样本数据,利用样本数据来推断总体的特征。
区间估计给出了参数估计的下限和上限,以一定的置信水平表示。
一般而言,置信水平常用的有95%和99%。
在区间估计中,经常使用的方法有点估计法和区间估计法。
点估计法基于样本数据对总体参数进行点估计,即使用样本数据作为总体参数的估计值。
而区间估计法则给出一个区间范围,以包含总体参数真实值的可能性,而不仅仅是一个点估计的值。
区间估计的步骤可以总结为以下几个:1. 选择合适的抽样方法,获取样本数据;2. 根据样本数据计算参数的点估计值;3. 根据样本数据计算置信水平和抽样误差等;4. 根据置信水平和抽样误差计算置信区间。
二、假设检验假设检验是一种用于验证科学假设的统计方法。
在假设检验中,我们根据样本数据对总体参数或者总体分布是否满足某种假设进行判断。
假设检验通常包括原假设(H0)和备择假设(H1)两个假设。
原假设通常是关于总体参数的一个陈述,而备择假设则是关于总体参数的一个替代陈述。
我们根据样本数据的表现来判断原假设是否应该被拒绝,从而接受备择假设。
通常使用统计量和p值来进行假设检验。
假设检验的步骤可以总结为以下几个:1. 建立原假设和备择假设;2. 选择适当的假设检验方法;3. 设置显著性水平,通常为0.05或0.01;4. 根据样本数据计算统计量的值;5. 根据统计量的值和显著性水平,判断原假设是否应该被拒绝。
三、区间估计与假设检验的应用区间估计与假设检验在实际应用中有着广泛的领域。
比如,在医学研究中,我们可以利用区间估计来估计某种治疗方法的疗效范围;在市场调研中,我们可以利用假设检验来判断广告的效果是否显著。
假设检验和区间估计

第7章假设检验和区间估计7.1 内容框图7.2 基本要求(1)理解假设检验的基本思想及两类错误的含义.(2)掌握有关正态总体参数的假设检验的基本步骤和方法.(3)理解单侧检验与双侧检验的异同.(4)理解并掌握正态总体参数区间估计的的基本方法.(5)了解总体分布的检验和独立性检验的基本方法.7.3 内容概要1)假设检验α值为显著水平。
然后,根据显著水平α来确定临界值,用临界值来划分接受域W和拒绝域 1W 。
这样的检验,称为显著性检验。
假设检验的一般步骤是: (1)提出原假设 0H ;(2)选取合适的检验统计量 U ,从样本求出 U 的值;(3)对于给定的显著水平α,查 U 的分布表,求出临界值,用它划分接受域 0W 和拒绝域 1W ,使得当 0H 为真时,有 α=∈}{1W U P ;(4)若 U 的值落在拒绝域 1W 中,就拒绝 0H ,若 U 的值落在接受域 0W 中,就接受 0H 。
假设检验的理论依据是所谓的小概率事件原理,即一个概率很小的事件在一次试验中几乎是不可能发生的.要检验一个根据实际问题提出的原假设0H 是否成立,如果已知在0H 成立时,某个事件发生的可能性很小,而试验的结果却是这个事件发生了,那么根据小概率事件原理,我们就可以认为所提出的这个假设0H 是不成立的,即拒绝0H ;反之,则接受0H .这里的原假设0H 可以根据实际问题提出,事件是否发生可根据试验观测值判断,因此假设检验的关键问题就是要确定在0H 成立时,发生可能性很小的某个事件.我们知道,正态分布有个3σ原则,即ξ若服从正态分布,那么ξ的取值会大多集中在其均值附近,落入两侧的可能性很小.事实上,当ξ服从t 分布,2x 分布,F 分布时,其取值落入两侧的可能性也都相对很小.因此,我们要确定0H 成立时一个发生可能性很小的事件,只需根据样本构造出服从正态分布,t 分布,2x 分布或F 分布的随机变量(统计量)就可以了. 根据上述分析,正态总体参数的假设检验可概括为如下步骤。
区间估计与假设检验的分类总结

区间估计与假设检验的分类总结区间估计和假设检验是统计推断的两个主要方法。
它们都是根据样本数据对总体参数进行推断,但是它们的目的和原理不同。
下面我将对区间估计和假设检验进行分类总结。
一、区间估计分类总结:区间估计是根据样本数据对总体参数进行估计,并给出估计结果的一个范围。
根据不同的参数和样本情况,区间估计可以分为以下几种类型:1.均值的区间估计:a.单个总体均值的区间估计:当总体标准差已知时,使用正态分布进行估计;当总体标准差未知时,使用t分布进行估计。
b.两个总体均值之差的区间估计:根据两个总体样本的样本均值和样本方差的差异,使用正态分布或t分布进行估计。
c.大样本均值的区间估计:对于大样本,总体均值的估计可以使用正态分布进行估计。
2.方差的区间估计:a.单个总体方差的区间估计:对于正态总体,使用卡方分布进行估计。
b.两个总体方差之比的区间估计:根据两个总体样本方差的比值,使用F分布进行估计。
c.大样本方差的区间估计:对于大样本,总体方差的估计可以使用卡方分布进行估计。
3.比例的区间估计:b.两个总体比例之差的区间估计:根据两个总体样本比例的差异,使用正态分布进行估计。
二、假设检验分类总结:假设检验是根据样本数据对总体参数的一些假设进行检验,并得出是否拒绝假设的结论。
根据不同的参数和样本情况,假设检验可以分为以下几种类型:1.均值的假设检验:a.单个总体均值的假设检验:当总体标准差已知时,使用正态分布进行检验;当总体标准差未知时,使用t分布进行检验。
b.两个总体均值之差的假设检验:根据两个总体样本的样本均值和样本方差的差异,使用正态分布或t分布进行检验。
c.大样本均值的假设检验:对于大样本,总体均值的检验可以使用正态分布进行检验。
2.方差的假设检验:a.单个总体方差的假设检验:对于正态总体,使用卡方分布进行检验。
b.两个总体方差之比的假设检验:根据两个总体样本方差的比值,使用F分布进行检验。
c.大样本方差的假设检验:对于大样本,总体方差的检验可以使用卡方分布进行检验。
区间估计与假设检验

区间估计与假设检验在统计学中,区间估计和假设检验是两个常用的推断方法,用于对总体参数进行估计和推断。
本文将对区间估计和假设检验进行介绍,并讨论它们的应用和差异。
一、区间估计区间估计是用样本数据来推断总体参数的取值范围。
它通过计算估计值以及与之相关的置信水平,给出一个参数的范围估计。
这个范围被称为置信区间。
置信区间常用于描述一个参数的不确定性。
例如,我们要估计某种药物的平均效果。
通过对随机抽取的样本进行实验,我们可以得到样本均值和标准差。
然后,结合样本容量和置信水平,可以计算出药物平均效果的置信区间。
例如,我们可以得出一个95%置信区间为(0.2, 0.6),表示我们有95%的置信水平相信真实的平均效果在这个区间内。
二、假设检验假设检验是用于判断总体参数是否符合某种假设的统计方法。
假设检验通常分为两类:单样本假设检验和双样本假设检验。
1. 单样本假设检验单样本假设检验用于推断一个总体参数与某个特定值之间是否存在显著差异。
它包括以下步骤:(1)建立原假设(H0)和备择假设(H1),其中原假设是要进行检验的假设,备择假设是对原假设的补充或对立的假设。
(2)选择合适的显著性水平(α),表示我们接受原假设的程度。
(3)计算样本数据的检验统计量,例如t值或z值。
(4)根据显著性水平和检验统计量,判断是否拒绝原假设。
2. 双样本假设检验双样本假设检验用于比较两个总体参数之间是否存在显著差异。
常见的双样本假设检验包括独立样本t检验和配对样本t检验。
独立样本t检验用于比较两个独立样本的均值是否有差异,而配对样本t检验用于比较同一样本的两个相关变量的均值是否有差异。
三、区间估计与假设检验的差异区间估计和假设检验都是推断总体参数的方法,但它们的应用和目的略有不同。
区间估计主要关注参数的范围估计,给出了参数估计值的不确定性范围。
它强调了估计的稳定性和精确度,但不直接涉及参数的显著性判断。
因此,区间估计对于参数的精确度提供了一个相对准确的度量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5.6假设检验:置信区间的方法 双侧或双尾检验 (Two-sided or Two-Tail Test)
ˆ 利用P88页Table 3.2的数据,估计出MPC(边际消费倾向 2 ) 是0.5091。可以造构如下的检验假设:
H 0: 2 0.3
H 1: 2 0.3
在虚拟假设下,MPC是0.3,在对立假设下MPC大于或小于 0.3。虚拟假设是一个简单假设,而对立假设则是一个复合假设; 实际上就是我们所说的双侧假设(two-sided hypothesis)。
对于这种单尾检验,最好的方法是显著性检验方法。
§5.7 假设检验:显著性检验法 检验回归系数的显著性:t检验
显著性检验法(test-of-significance approach)是由R.A.Fisher (费希尔),Negman(尼曼)和Pearson(皮尔逊)合作发明的, 它是利用样本结果,来证实一个虚拟假设的真伪的一种检验程 序。 t分布的来历: student
决策规则:构造一个 2 的 100 (1 )% 置信区间。如果 2 在 假设H0下落入此区间,就不要拒绝H0。但如果它落在此区间之外, 就要拒绝H0。 在上例中, H 0 : 2 0.3,很明显地落在(0.4268,0.5914)这 个置信区间之外,因此我们能以95%的置信度拒绝MPC的真值是 0.3的假设。
即 2 的100 (1 )% 水平的置信区间为:
ˆ ˆ 2 t / 2 se( 2 )
例子:P123
两个游戏: 掷硬币 套圈
请问: 区间估计更象哪一个?
置信区间的两个特点: 位置的随机性 长度的随机性
二、 的置信区间: 1 2 ˆ 利用 E ( 1 ) 1 和 ˆ
在区间估计中,置信区间的宽度与估计量的标准误
100 (1 )% ˆ ˆ 1 t / 2 se( 1 )
水平的置信区间为:
(5.3.8)
或
§5.4 2 的置信区间 在正态性假定下,变量:
ˆ 2 2 (n 2) 2 (5.4.1) 服从自由度为n-2的 2 分布。因此,可以用 2 分布构造
1
n xi
Xi
2
2 2
进行类似的推导,可得:
ˆ ˆ ˆ ˆ Pr[ 1 t / 2 se( 1 ) 1 1 t / 2 se( 1 )] 1 (5.3.7e( 1 ) 成正比例。这说明,标准误越大,置信区间越宽,对总 ˆ se( 2 ) 体真值进行估计的接近程度越差。因此,估计量的标准误被看 作是估计量的精度(precision),它反映了估计量的精确程度。
在正态性假设下的变量:
ˆ ˆ ( 2 2 ) 2 2 t ˆ ˆ se( )
2
xi
2
(5.3.2)
服从自由度为n-2的t分布。 在虚拟假设下 2 的真值被设定,就可以利用样本数据算 出(5.3.2)式,即这个t统计量是可以算出来的,从而可以作出 如下的置信区间:
第5章 区间估计与假设检验 (Interval Estimation and Hypothesis Testing)
§5.1 统计学的预备知识 自己复习 §5.2 区间估计:一些基本概念
第三章给出了边际消费倾向(MPC)的估计值为0.5091。 ˆ E( 2 ) 2 我们也知道, ,但是,由于抽样的波动性,单个估计 值可能并不等于真值。因此,我们不能完全依赖一个点估计值, 而是要围绕点估计量构造出一个区间,使这一区间在一定的概 率保证之下包含真实的参数值(真值),这就是区间估计。
这里定义的t变量服从自由度为n-2的t分布
证明:令
ˆ ˆ 2 2 ( 2 2 ) Z1 ˆ se( )
2
xi
2
(1)
ˆ 2 Z 2 (n 2) 2 (2) ˆ 如果 已知,(1)式就是对 2 进行标准化,所以Z1服从 标准正态分布, Z1 ~ N (0,1) 。 2 分布(证明参见有关的数理统 Z2服从(n-2)个自由度的 计教程),而且,可以证明Z2的分布独立于Z1。运用P160定理5.5 (附录),
备择假设可以是简单的(simple)或复合的(composite)。例 如, H1 : 2 1.5 是一个简单假设,而 H1 : 2 1.5 则是一个复 合假设。 进行统计假设检验,就是要制定一套步骤和规则,以使决定 接受或拒绝一个虚拟假设(原假设)。一般来说,有两种相互 联系、相互补充的方式:置信区间(confidence interval)和显 著性检验(test of significance)。
它是统计上高度显著(highly statistically significant)。
单侧或单尾检验 One-Sided or One-Tail Test
当我们有着很强的理论支撑或者先验性预期时,可以把备择假 设H1取为单侧的或单向的。如:H 0 : 2 0.3 和 H1 : 2 0.3
用统计上的话说,这个指定的(声称的)假设叫做虚拟假设 (null hypothesis),或维持假设(maintained hypothesis),用 H0来表示。 通俗地说,是一个靶子。
另 外 , 还 需 要 一 个 备 择 假 设 ( 对 立 假 设 ) ( alternative hypothesis),用H1表示。H0和H1构成一个完备事件。
在统计上,当虚拟假设被我们拒绝时,就称我们的发现是统计 上显著的(statistically significant)。反之,当我们不拒绝虚拟假 设时,我们说,我们的发现不是统计上显著的。 当选择的显著性水平又比较低,比如 1% ,从而置信系数
1 比较高,如99%时,仍然达到了统计上是显著的,我们就称
xi
2
(5.3.1)
则,Z为一个标准化正态变量,Z ~ N (0,1) 。
如果总体方差 2 已知,就可以用正态分布对 2
作出概率上的表述。在正态曲线下,
1 之间的面积为68.26%
1.96 之间的面积为95%
2 之间的面积为95.45%
3
之间的面积为99.73%
显著性检验的关键在于构造出一个检验统计量(test statistic) (作为估计量),在虚拟假设下这个统计量会服从一定的抽样 2 分布(如t分布,F分布,正态分布, 分布等)。构造出统计 量以后,就可以利用样本数据计算出这个统计量的样本值,再 把这个样本值与给定某一显著水平的临界值进行比较,看它与 临界值是否有显著差别,从而作出判断,决定拒绝还是接受所 作的假设。
从而 2 的区间估计就容易了。选定1 为95%,则
ˆ 2 2 Pr[ 1.96 1.96 ] 0.95 ˆ ) se( 2
但是,在许多实际问题中,总体方差 2 都是未知的,只能 用其无偏估计量 2 来替代。(5.3.1)式便为: ˆ
ˆ ˆ ( 2 2 ) xi 2 2 2 t (5.3.2) ˆ ˆ se( 2 ) ˆ ˆ se( 2 ) 为估计量 2 的标准误的估计值(estimated standard error)。
于是有:
Pr[ t / 2
整理得:
ˆ 2 2 t / 2 ] 1 ˆ se( 2 )
(5.3.4)
ˆ ˆ ˆ ˆ Pr[ 2 t / 2 se( 2 ) 2 2 t / 2 se( 2 )] 1 (5.3.5)
2 的置信区间:
Pr(
2 1 / 2
/ 2 ) 1
2 2
(5.4.2)
2 2 值由(5.4.1)式给出,12 / 2和 / 2 可以查表得 其中的
到,自由度为n-2,见P125 Figure 5.1。 把(5.4.1)式中的 2 代入(5.4.2)式
参数的区间估计主要解答某一总体参数真值落在什么区间 内的问题; 而假设检验就是要对一个已知估计值或已得出的数据进行 检验,判断它是否与某一个指定的假设(stated hypothesis)相容 或一致(compatible)。所谓相容或一致,是指某一已知估计值 充分地接近其假设的数值,从而导致接受新指定的假设。
我们的任务就是求出两个正数 和 , ,使得随 0 1 的概率 机区间(random interval) 包含 ˆ ˆ 为 : ( 2 , 2 ) 2
1
ˆ ˆ Pr( 2 2 2 ) 1
(5.2.1)
这样的区间称为置信区间(confidence interval); 称为置 1 信系数(confidence coefficient);而 称为显著性水平(level of significance)。置信区间的端点称置信限(confidence limits)也 称临界值(critical values)。
(5.2.1)式表示的是:随机区间包含真实 2 的概率为 1 。区 间估计量给出了一个真实 2 会落入其中的数值范围。 点估计与区间估计: 单一的点估计量可能不同于总体真值,即存在估计误差。点 估计既不能给出误差范围的大小,也没有给出估计的可靠程度。 ˆ ˆ 区间估计则可以显示 1和 2 是怎样的接近总体真值 1 和 2 , 以及这种接近的可靠性。
整理得:
ˆ ˆ 2 2 2 Pr[( n 2) 2 (n 2) 2 ] 1 1 / 2
2
(5.4.3)
该式给出了 2 的置信系数为 100 (1 )% 的置信区间。 §5.5 假设检验(Hypothesis Testing):概述
参数估计与假设检验都是在样本分布基础上作出概率性判 断,两者既有联系又有区别,但其基本原理则是一致的。
在假设 H 0下,落入此区间
