实验设计习题课
实验设计课练习

练习一、表头设计1、 某二水平试验要求考察A 、B 、C 、D 、E 五个因素及交互作用 A ×B 、A ×C 、C ×D ;2、 某二水平试验要求考察A 、B 、C 、D 、E 五个因素及交互作用A ×C 、C ×D 、A ×E ;请根据L 16(215)交互作用表对上述四种情况进行表头设计。
表头设计3、某二水平试验要求考察A 、B 、C 三个因素及交互作用B ×C 、A ×B 和A ×C 。
4、某二水平试验要求考察A 、B 、C 三个因素及交互作用A ×B 和B ×C 。
请根据L 8(27)交互作用表对上述四种情况进行表头设计。
表头设计5、某三水平试验要求考察A 、B 、C 、D 、E 五个因素及交互作用A ×B 、A ×C 和A ×D ;请根据L 27(313)交互作用表对上述情况进行表头设计。
二、一元线性回归分析1、为了明确某种食品添加剂凝胶强度y(g/cm2)与食品添加剂添加量x(%)之间的关系,试验结果如下表,试建立y与x的回归方程,并进行F检验。
表1 食品添加剂添加量(x)与凝胶强度(y)的测定结果1、为了提高某化工产品的转化率,选择反应温度A、加碱量B、催化剂种类C为实验因素,实验方案及结果见下表,试作极差分析,判断因素主次顺序,各因素优水平,优组合。
表2 试验方案与试验结果1、在双歧杆菌酸奶研制中,为确定最佳发酵条件,用L8(27)正交表安排正交试验,试验因素与水平,试验方案和结果分析见下表,试对试验结果进行方差分析。
五、假设检验1、关中地区小麦良种的蛋白质含量平均值为μ0=14.5%,现自外地引入一高产品种,在8个小区种植,得其蛋白质含量(%)为:15.6, 17.6, 13.4, 15.1, 12.7, 16.8, 15.9, 14.6,问新引入品种的蛋白质含量与当地良种有无显著差异?六、名词解释和简答题1.总体:2.样本:3.实验指标:4. 水平:5.处理:6.全面实验:7. 什么是实验因素?包括哪几种?8.标准正态分布的表达式9.方差分析的适用对象和目的?10.误差的来源有哪些?11.如何减少随机误差?12.实验的三个基本原则(Fisher三原则)?13.正交表的等价变换方式有哪些?14.正交表有哪些基本性质?。
习题课教学设计(终稿)

习题课教学设计(终稿)一、教材依据:采用义务教育课程标准实验教科书数学(人教版)八年级上册,第十一章复习题11拓广探索第12题改编“中线”为“高”。
二、设计思想:1、教学指导思想:体现新课程标准的基本理念,以生为本,有效地发挥学生的主体、教师的主导作用。
2、教材分析:全等三角形的证明是初二几何学习的重要内容之一,这节课探究的是如何从运动的角度来看待三角形全等证明的问题,通过类比迁移的思想,使学生在学习过程中,进一步提高学数学、用数学的能力。
在教学中有针对性地对学生进行数学思想方法――由特殊到一般的数学思想方法的渗透,这有利于学生数学思维能力的提高。
通过本节课的学习,将对今后学好几何证明打下一定的基础。
3、设计理念:(1)、让学生通过主动参与、自主探究、合作学习的过程,经历动手、动脑,学会观察、发现、分析、概括的学习方法,创设问题情境,激发学生思维的主动性。
(2)、注重知识的产生、转化和迁移的过程,强调对问题的分析、处理,渗透数学思想。
(3)、给学生提供探索和交流的空间,培养学生的数学思维,同时增强师生间的情感交流。
(4)引导学生从实际问题转化为数学问题,回顾所学的知识,并利用所学知识解决问题,从而快乐的学习数学,这对于学生今后的学习有着积极的意义。
三、学情分析:学生在全等三角形的证明己有一定的认识,学生在一般情况下,对简单的几何证明不会有什么问题,但在特定的条件下,证明两次三角形全等,还有点困难这有一个学生学习上数学思维的转变过程。
由于我校学生主要来自农村,学生的学习素养普遍较低,教学中面对大多数学生,因此,教学起点不易定得太高,而选择引导学生从特殊到一般的数学思想方法,就是想通过剪纸活动去探寻证明途径,降低教学难度,这也完全符合学生的认知规律。
四、学习目标:1、知识技能:经历探索三角形全等条件的过程,掌握三角形全等的“角边角”“HL”判定方法,培养学生的空间观念,推理能力,发展有条理地表达能力在具体情境中。
实验设计与数据处理第五章例题及课后习题答案

习题5.1、
优选过程:
1、首先在试验范围0.618处做第一个实验,这一点的温度为:x1=340+(420-340)×
0.618=389.44.
2、在这点的对称点,即0.382处做一个实验,这一点的温度为:x2=420-(420-340)×0.618=370.56.
3、比较两次的实验结果,发现第一点比第二点的合成率高,故舍去370.56以下部分,在
370.56-420之间,找x1的对称点:x3=420-(420-370.56)×0.618=389.44608.
4、比较两次的实验结果,发现第一点比第三点的合成率高,故舍去389.44608以下部分,
在389.44608-420之间,找x1的对称:x4=420-(420-389.44608)×0.618=401.11767744. 5、比较两次的实验结果,得到最佳点为401.1177。
习题5.2、
优选过程:
1、首先在试验范围3/5处做第一个实验,这一点加入的白砂糖桶数为:
x1=3+3/5*(8-3)=6桶
2、在这点的对称点,即2/5处做一个实验,这一点加入的白砂糖桶数为:
x2=8-3/5*(8-3)=5桶
3、比较两次的实验结果,发现第一点比第二点的实验结果好,故舍去5以下的部分,在5-8之间,找x1的堆成点
习题5.3
目标函数。
化工原理实验课课后习题答案

《化工原理实验课后习题答案》一、流体流动阻力的测定1.如何检验系统内的空气已经被排除干净?答:可通过观察离心泵进口处的真空表和出口处压力表的读数,在开机前若真空表和压力表的读数均为零,表明系统内的空气已排干净;若开机后真空表和压力表的读数为零,则表明,系统内的空气没排干净。
2.U行压差计的零位应如何校正?答:先打开平衡阀,关闭二个截止阀,即可U行压差计进行零点校验3.进行测试系统的排气工作时,是否应关闭系统的出口阀门?为什么?答:在进行测试系统的排气时,不应关闭系统的出口阀门,因为出口阀门是排气的通道,若关闭,将无法排气,启动离心泵后会发生气缚现象,无法输送液体。
4.待测截止阀接近出水管口,即使在最大流量下,其引压管内的气体也不能完全排出。
试分析原因,应该采取何种措施?答:待截止阀接近进水口,截止阀对水有一个阻力,若流量越大,突然缩小直至流回截止阀,阻力就会最大,致使引压管内气体很难排出。
改进措施是让截止阀与引压阀管之间的距离稍微大些。
5.测压孔的大小和位置,测压导管的粗细和长短对实验有无影响?为什么?答:由公式??2?p可知,在一定u下,突然扩大ξ,Δp增大,则压差计读数变大;2u?反之,突然缩小ξ,例如:使ξ=0.5,Δp减小,则压差计读数变小。
6.试解释突然扩大、突然缩小的压差计读数在实验过程中有什么不同现象?答:hf与很多值有关,Re是其中之一,而λ是为了研究hf而引入的一个常数,所以它也和很多量有关,不能单单取决于Re,而在Re在一定范围内的时候,其他的变量对于λ处于一个相对较差的位置,可以认为λ与Re关系统一。
7.不同管径、不同水温下测定的?~Re曲线数据能否关联到同一曲线?答:hf与很多值有关,Re是其中之一,而λ是为了研究hf而引入的一个常数,所以它也和很多量有关,不能单单取决于Re,而在Re在一定范围内的时候,其他的变量对于λ处于一个相对较差的位置,可以认为λ与Re关系统一。
正如Re在3×103~105范围内,λ与Re的关系遵循Blasius 关系式,即λ=0.3163/Re0.258.在?~Re曲线中,本实验装置所测Re在一定范围内变化,如何增大或减小Re的变化范围?答:Re?du?,d为直管内径,m;u为流体平均速度,m/s;?为流体的平均密度,kg/m3;s。
程序设计实验及在线指导课后习题答案

第二章/*一:求平均年龄描述班上有学生若干名,给出每名学生的年龄(整数),求班上所有学生的平均年龄,保留到小数点后两位。
输入第一行有一个整数n(1<= n <= 100),表示学生的人数。
其后n行每行有1个整数,取值为15到25。
输出输出一行,该行包含一个浮点数,为要求的平均年龄,保留到小数点后两位。
样例输入21817样例输出17.50提示要输出浮点数、双精度数小数点后2位数字,可以用下面这种形式:printf("%.2f", num);#include<stdio.h>int main(){int n,i,age;double sum,average;sum=0.00;scanf("%d",&n);for(i=1;i<=n;i++){scanf("%d",&age);sum+=age;}average=sum/n;printf("%.2f\n",average);}/*二:数字求和描述给定一个正整数a,以及另外的5个正整数,问题是:这5个整数中,小于a的整数的和是多少?输入输入一行,只包括6个小于100的正整数,其中第一个正整数就是a。
输出输出一行,给出一个正整数,是5个数中小于a的数的和。
样例输入10 1 2 3 4 11样例输出10#include<stdio.h>int main(){int a,i,s[5];int sum;sum=0;scanf("%d",&a);for(i=0;i<5;i++){scanf("%d",&s[i]);}for(i=0;i<5;i++){if(s[i]<a)sum+=s[i];}printf("%d\n",sum);}/*三:两倍:描述给定2到15个不同的正整数,你的任务是计算这些数里面有多少个数对满足:数对中一个数是另一个数的两倍。
程序设计1实验习题实验一

程序设计(1)实验习题实验一(1)运行以下程序,并解释运行结果。
# include <stdio.h>int main(void){ int x = –1;unsigned u = ;printf ( “x = %u = %d\n”, x, x);printf ( “u = %u = %d\n”, u, u);return 0;}(2)运行以下程序,解释运行结果,并修改程序以使结果正确。
# include <stdio.h>int main(void){ int x = ;printf ( “x + 1 = %d\n”, x + 1);return 0;}(3)运行以下程序,解释运行结果。
程序1:#include <stdio.h>int main(void){ float a;double b;a = 123456.789e4;b = 123456.789e4;printf(“%f\n%f\n”,a,b);return 0;}程序2:# include <stdio.h>int main(){ float a,b;a=123456.789e5;b=a+20;printf("%f\n",a);printf("%f\n",b);return 0;}(4)求平方根:输入1 个实数x,计算并输出其平方根(保留1 位小数)。
(5)华氏温度转换为摄氏温度:输入华氏温度f,计算并输出相应的摄氏温度c(保留2 位小数)。
c = 5/9(f-32).(6)三天打鱼两天晒网:中国有句俗语叫“三天打鱼两天晒网”。
假设某人从某天起,开始“三天打鱼两天晒网”,问这个人在以后的第n天中是“打鱼”还是“晒网”?编写相应程序(第一天就是当天)。
例如:输入:103输出:Fishing in day 103输入:35输出:Drying in day 35(7)按照规定,在高速公路上行使的机动车,达到或超出本车道限速的10%则处200元罚款;若达到或超出50%,就要吊销驾驶证。
实验设计方法课后习题答案46章

▪ 习题不能用正交表78(2)L ,因为会产生混杂。
需选用正交表1516(2)L 。
表头设计如下:▪ 说明:也可有其他不同的表头设计(试验方案)。
▪ 习题 由于1AB C D A B A C B C f f f f f f f ⨯⨯⨯=======, 7f =总,故可选用正交表78(2)L ,且不会产生混杂。
表头设计如下:根据直观分析结果,因素的主次顺序为:AXB AXC C B BXC A D A 与B 的二元表,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,A 与C 的二元表,▪根据A与B的二元表,A1 B2的效果最好;▪根据A与C的二元表,A1 C2的效果最好;▪从直观分析结果可以得到,D1效果最好;▪故最优生产条件为:A1 B2 C2 D1▪(3)方差分析由于没有误差列,故不能对各因素进行显著性检验。
但是,我们选择离差平方和最小的因素D所在的列作为误差列,对各因素进行显著性检验,得到结果如下:因素的主次顺序与直观分析的一样,从显著性来看,只有AXB显著,其他的因素或交互作用都不显著。
▪习题其中A ×B 的离差平方和349.85222.29632.148A B SS SS SS ⨯=+=+=A ×B 的自由度,,,,,,344A B f f f ⨯=+=32.14841.973 5.14024.446A B F ⨯==<故A ×B 不显著。
B ×C 的离差平方和81134.7417.6342.371B C SS SS SS ⨯=+=+=B ×C 的自由度,,,,,,8114B C f f f ⨯=+=42.3714 2.601 5.14024.446B CF ⨯==<故B ×C 不显著。
▪ 因素的主次顺序(根据极差大小或F 值大小) A D F BXC AXB B E C ▪ 最优工艺条件的确定:可以根据直观分析结果选择每个因素的最优水平,得到最优工艺条件为:,,,,,,,,,,,,,,,A1,D1,F1,E0,B0,C0,,.,,,,,,,,,,也可以计算各因素的水平效应 根据水平效应来确定,具体如下: 对于因素A ,,,,115221319ˆ9.148927927A K T a=-=-= 224251319ˆ 1.630927927A K T a =-=-=-333721319ˆ7.519927927A K T a =-=-=-故A 的第1水平的效应最大。
实验设计与数据处理第八章例题及课后习题答案doc资料
0
428
0 1.162084
492
0 1.162084
512
0
0
509
0
0
Signific ance F
7.93E-05
Lower Upper 下限 上限
95%
95% 95.0% 95.0%
465.4405 471.5595 465.4405 471.5595
5.242078 12.93644 5.242078 12.93644
0.002795085 2.593838854 0.122018
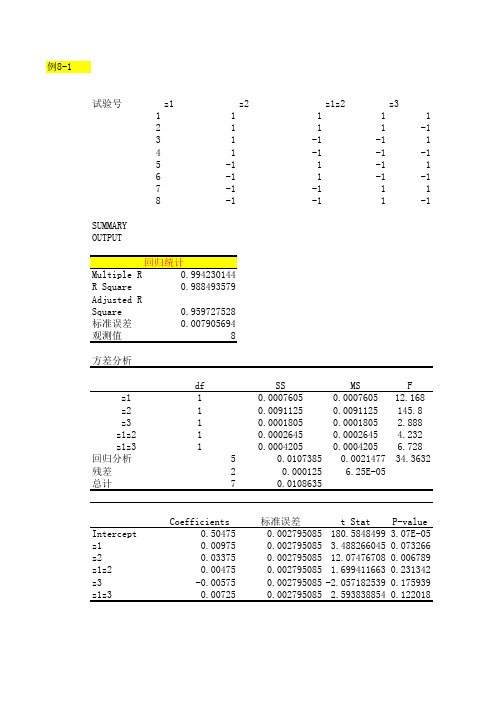
例8-2
回归方程: 由该回归方程 中偏回归系数 绝对值的大 小,可以得到 各因素和交互 作用的主次顺 序为:
y=0.50475+0.00 975z1+0.03375z 2+0.00475z1z20.00575z3+0.00 725z1z3
0 0 -41.73590203
y=468.5+9.09z1 -26.56z2+z3
标准误差
t Stat P-value
1.10193312 425.1619191 1.84E-10
1.385649972 6.55956341 0.002794
1.385649972 -19.17042163 4.36E-05
SS 0.0091125
0.001626 0.0108635
MS
F
0.0091125 33.62546
0.000271
试验号
z1 1 2 3 4 5 6 7 8 9 10 11
z2 1 1 1 1 -1 -1 -1 -1 0 0 0
z3 1 1 -1 -1 1 1 -1 -1 0 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验设计练习题
1.用一种复合饲料饲养动物,每天增重的kg数及其相应的概率如下:
问:(1)每天增重的数学期望是多少?(2)方差是多少?
2.在容量分析中,计算组分含量的公式为W=Vc,其中V是滴定时消耗滴定液的体积,c是滴定液的浓度。
今用浓度为(1.000±0.001)mg/mL的标准溶液滴定某试液,滴定时消耗滴定液的体积为(20.00±0.02)mL,试求滴定结果的绝对误差和相对误差。
3.甲、乙两发酵法生产青霉素的工厂,其产品收率的方差分别为S12=0.46S22=0.37.现甲工厂测得25个数据,X=3.71g/L,乙工厂测得30个数据,Y=3.46g/L,问它们的收率是否相同?
4.为检验某种血清预防感冒的作用,将用了血清的500人与未用血清的另500人在一年中的医疗记录进行比较,统计它们是否曾患感冒,得下表中的数据。
问这种血清对预防感冒是否有效?
5.某城市从4个排污口取水,经两种不同方法处理后,检测大肠杆菌数量,单位面积内菌落数列于下表。
请检验它们是否有差别。
6.用两种不同的实验方法,测定同一种材料,得到以下两组数据,试进行回归分析。
7.茵陈蒿是由茵陈、栀子和大黄3味药组成。
为研究这3味药对利胆作用的最佳配方,取成年大白鼠做正交实验。
以引流胆汁的充盈长度(cm)为指标(给药前与给药后毎10分钟的均数之差作为统计分析的实验指标值)。
考察的因素与水平如下:
8.用三种方法从一种野生植物中提取有效成分,按4种不同浓度加入培养基,观察该成分刺激细胞转化的作用,由于条件有限,每天只完成一个重复,三天完成全部实验。
试进行数据分析.
9.某啤酒厂在实验用不发芽的大麦制造啤酒的新工艺过程中,选择因素及其水平如下表,不考虑因素间的交互作用。
考察指标Yi为粉状粒,越高越好。
采用拟水平法将因素D的第一水平136重复一次作为第3水平,按L9(34)安排实验,得实验结果如下表,试进行方差分析,并找出好的工艺条件。
10.根据下表数据计算蛋白质和赖氨酸的相关系数,并进行显著性检验
11.用容量法测定某样品中的锰,8次平行测定数据为:10.29, 10.33, 10.38, 10.40, 10.43, 10.46, 10.52, 11.82 (%),试问是否有数据应被剔除?
12.在饮料质量检查中常常需要检查饮料中的细菌个数。
设某400mL 饮料中细菌浓度为0.5个细菌/mL ,摇匀后从中随机抽取溶液1mL ,问其中包含有3个以及3个以上细菌的概率有多大?并求出该分布的平均数和方差。
13.已计算出4种不同饮料的平均增重(1x =43.8,2x =71.0,3x =81.4,4x =142.6),总平均数
x =84.7,重复数r=5,误差均方e V =719.2,其自由度为16,试对这四种饲料的增重平均数
进行多重比较。
14.某单位在大田对稀播条件下荞麦植株干重(y )与生长时间(x )的关系进行了研究。
从出苗以后开始,每4天随机从大田抽样一定数目的个体测定其植株干重,重复3次。
共进行6次记载,所得数据列于下表。
请利用原始数据及其对数变换资料分别进行回归分析,计算回归方程和相关系数,检验显著性,并比较那个方程较好。
15.某厂在某电解工艺技术改进时,希望提高电解率,做了初步的实验,结果如下表所示。
试利用抛物线法确定下一个实验点。
16.某产品的得率y与反应温度x1,反应时间x2及其反应物的含量X3有关,今得如表所示的实验结果,设y与x1,x2和x3之间呈线性关系,试求y与x1,x2和x3之间呈线性关系,试求y与x1,x2和x3之间的三元线性回归方程。
