水箱液位matlab模糊控制例程sltank详解
基于MATLAB的水箱水位模糊控制系统的设计

小相位特性、不稳定性、时滞和负荷干扰等。若采用单一的水位反馈控制难以达到预期的控 制效果,所以采用了仿人的模糊控制方法依据操作人员的现场经验制成模糊控制表,通过判 断水位的偏差及偏差变化率来控制输出,并易于在 PLC 上实现。模糊 PID 控制器的特点是在 大范围内利用模糊推理的方法调整系统的控制量 U,而在小偏差范围内转换成 PID 控制,两 者的转换根据事先给定的偏差范围自动实现[3]。这样做的好处是:既保证动态响应效果,又 能改善稳态控制精度。图 3 为模糊 PID 控制器的系统方框图。
r
+ _
PID 控制器 e
ec 模糊控制器 d/dt
e y
对象 U
变送器
图 3 模糊 PID 控制器系统方框图
其中,模糊控制器和 PID 控制器的切换是通过在 MATLAB 的 M 文件中事先设定误差 e 的 范围来自动实现的[4]。选取水位误差 e 的基本论域为[-10cm,10cm],选取误差变化率 ec 的 基本论域为[-4,4],选取控制量 u 的基本论域为[0,4000]。e、ec、u 的语言变量值分别 为:e={NB,NM,NS,ZE,PS,PM,PB},ec={NB,NM,NS,ZE,PS,PM,PB},u={NB,NM, NS,ZE,PS,PM,PB}。
在现代工业生产及日常生活中,有很多方面都会涉及到水位控制这个问题。而在绝大多 数情况下,我们是很难或是不可能得到被控对象的精确数学模型的,因此采用数学工具或计 算机仿真技术的传统控制理论已经无法解决此类系统的控制问题。[1]智能控制的概念主要是 针对控制对象及其环境、目标和任务的不确定性和复杂性而提出来的,而模糊逻辑控制则作 为一种新颖的智能控制方式越来越受到人们的重视。模糊逻辑控制是智能控制领域的重要发 展方向,模糊控制技术被称为“21 世纪的核心技术”。
水箱液位模糊控制

水箱液位模糊控制器的设计1.水箱液位控制系统已知一个容器中液体的流出是随机变化的,无法建立它的数学模型。
但是,通过人工控制进液阀门的开度和进液流速,却能调节容器中液位的高低,保持液位恒定。
根据人工操作经验,我们已经归纳出如下保持液位恒定的操作规则:①如果液位偏低,则快开阀门;②如果液位正好,则阀门开度不变;③如果液位偏高,则快关阀门;④如果液位正好而进液流速慢,则慢关阀门;⑤如果液位正好而进液流速快,则慢开阀门。
图1-1 水箱液位控制系统原理图为此,我们可以设计如图1-2所示的双输入--单输出模糊控制系统:k 1k 2D/FD/F RF/D 控制对象k u 模糊控制器u e ec图1-2 二维模糊控制系统原理框图模糊控制器的两个输入变量分别为液位差e (设定液位高度r -实测液位高度M模糊控制器反馈 压力传感器控制量设定y)和液位差变化率ec(单位时间内的偏差改变量),输出模糊变量为u。
输入变量e和ec、输出变量u的论域、覆盖变量论域的模糊子集明朝、隶属度函数类型及拐点参数等,初步设定为表1-1所列的数值。
表1-1 覆盖输入变量、输出变量的模糊子集设定值2.构建模糊控制器的FIS结构文件2.1编辑出名称为“tank”的液位模糊控制系统FIS启动Matlab后,在主窗口中键入fuzzy回车,进入“FIS Editor”编辑器界面,完成下列任务:①增加一个输入变量;②将输入、输出变量的名称分别改成e、ec和u;③将这个FIS文件名定为“tank”并予以存盘。
得出如图2-1所示的FIS编辑器界面。
图2-1 液位模糊控制FIS编辑器2.2 编辑覆盖输入、输出变量的模糊子集在图2-1所示的FIS编辑器上,单机输入变量e模框,按表1-1列出的数据编辑e、ec和u的模糊子集。
在FIS编辑器界面上,双击输入量或输出量模框中的任何一个,都会弹出隶属函数编辑器,简称MF编辑器。
在MF编辑器界面上,单击“变量模框索引区”中待编辑变量的小模框,使其边框变粗、变红,则界面下部“当前变量区”内就显示该变量的性态,以供编辑。
模糊控制水箱液位调节

实验二:模糊控制水箱液位调节一实验目的1.掌握模糊控制的原理2.加强模糊控制在实践中的应用二实验器材装有Matlab软件PC电脑一台三实验原理模糊控制的基本原理:它的核心部分为模糊控制器,模糊控制器的控制规律由有计算机程序实现。
详见P32(模糊控制原理)。
四原代码clear allclose allq1=0; %定义第一个水箱的入水量q2=0; %定义第一个水箱的出水量q3=0; %定义第二个水箱的出水量q4=0; %定义第三个水箱的出水量b=1.4; %定义第一个水箱入水量的控制系数a1=8.6; %定义第一个水箱出水量的控制系数a2=8.6; %定义第一个水箱出水量的控制系数h1=100; %定义第一个水箱中水的初始高度h2=100; %定义第二个水箱中水的初始高度h3=100; %定义第三个水箱中水的初始高度v=119; %定义sin函数的系数s=190; %定义水箱底面积k=10; %定义开关控制量e=0; %定义误差e_1=0;ec=0;H=130; %定义第三个水箱的期望高度e=H-h1;a=newfis('fuzz'); %误差函数a=addvar(a,'input','e',[-25,25]);a=addmf(a,'input',1,'NB','zmf',[-25,-10]);a=addmf(a,'input',1,'PS','trimf',[-25,-10,0]);a=addmf(a,'input',1,'Z','trimf',[-10,0,10]);a=addmf(a,'input',1,'PS','trimf',[0,10,25]);a=addmf(a,'input',1,'PB','smf',[10,25]);a=addvar(a,'output','u',[0,100]); %控制量输出函数a=addmf(a,'output',1,'NB','zmf',[0,30]);a=addmf(a,'output',1,'NS','trimf',[0,30,50]);a=addmf(a,'output',1,'Z','trimf',[30,50,70]);a=addmf(a,'output',1,'PS','trimf',[50,70,100]);a=addmf(a,'output',1,'PB','smf',[70,100]);rulelist=[1 1 1 1;2 2 1 1;3 3 1 1;4 4 1 1;5 5 1 1];a = addrule(a, rulelist);for i=1:1:8000tt(i)=i; %时间轴q1=b*k; %第一个水箱的进水量q2=a1*sqrt(h1); %第一个水箱的出水量h1=h1+(q1-q2)/s; %第一个水箱中水的高度q3=a2*sqrt(h2); %第二个水箱的进水量h2=h2+(q2-q3)/4; %第二个水箱中水的高度q4=v*abs(sin(2.3*pi*i+0.35)); %第二个谁想的出水量h3=h3+(q3-q4)/s; %第三个水箱中的高度hh(i)=h3;k=evalfis(e,a);e=H-h3;endplot(tt,hh)五、插图。
水箱水位恒定的模糊PID控制(2)
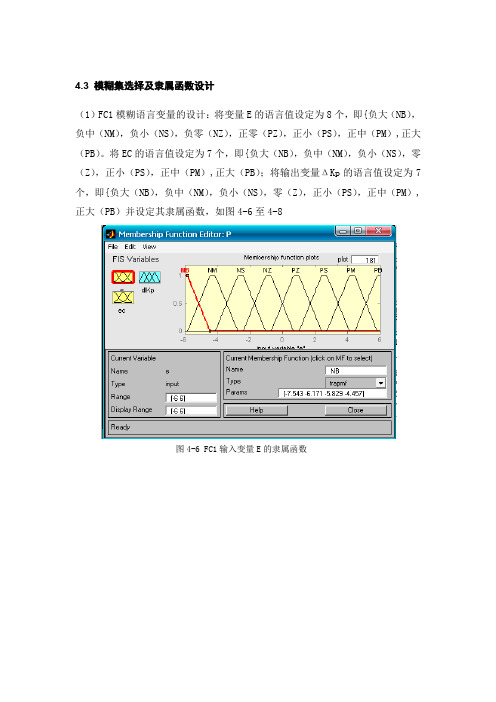
4.3 模糊集选择及隶属函数设计(1)FC1模糊语言变量的设计:将变量E的语言值设定为8个,即{负大(NB),负中(NM),负小(NS),负零(NZ),正零(PZ),正小(PS),正中(PM),正大(PB)。
将EC的语言值设定为7个,即{负大(NB),负中(NM),负小(NS),零(Z),正小(PS),正中(PM),正大(PB);将输出变量ΔKp的语言值设定为7个,即{负大(NB),负中(NM),负小(NS),零(Z),正小(PS),正中(PM),正大(PB)并设定其隶属函数,如图4-6至4-8图4-6 FC1输入变量E的隶属函数图4-7 FC1输入变量EC的隶属函数图4-8FC1输出变量△Kp的隶属函数(2)FC2模糊语言变量的设计:将输入模糊变量E、EC和输出模糊变量ΔKi 的语言值都设定为7个,即{负大(NB),负中(NM),负小(NS),零(Z),正小(PS),正中(PM),正大(PB)。
模糊控制器FC2的输入输出模糊语言变量值隶属函数如图4-9至4-11图4-9 FC2输入变量E的隶属函数图4-10 FC2输入变量EC的隶属函数图4-11 FC2输出变量△Ki的隶属函数(3)FC3模糊语言变量设计:将变量E的语言值设定为6个,即{负大(NB),负中(NM),负小(NS),正小(PS),正中(PM),正大(PB)。
将EC的语言值设定为7个,即{负大(NB),负中(NM),负小(NS),零(Z),正小(PS),正中(PM),正大(PB);将输出变量ΔKd的语言值设定为7个,即{负大(NB),负中(NM),负小(NS),零(Z),正小(PS),正中(PM),正大(PB)并设定其隶属函数如图4-12至4-14图4-12 FC3输入变量E的隶属函数图4-13 FC3输入变量EC的隶属函数图4-14 FC3输出变量△Kd的隶属函数4.4 模糊规则集的设定参数Kp 、Ki 、Kd在不同的e 和ec 下的自调整要满足如下调整原则: (1) 当e 较大时,为加快系统的响应速度,防止因开始时e 的瞬间变大可能会引起的微分溢出,应取较大的Kp 和较小的Kd ,同时由于积分作用太强会使系统超调加大,因而要对积分作用加以限制,通常取较小的Ki值;(2) 当 e 中等大小时,为减小系统的超调量, 保证一定的响应速度, Kp 应适当减小;同时Kd 和Ki的取值大小要适中;(3) 当e 较小时,为了减小稳态误差, Kp 与Ki 应取得大些,为了避免输出响应在设定值附近振荡,同时考虑系统的抗干扰性能, Kd 值的选择根据|ec|值而定,ec较大时,Kd 取较小值,ec较小时,Kd取较大值,通常Kd 为中等大小。
智能控制及MATLAB实现—水箱液位模糊控制仿真设计

智能控制及MATLAB实现—水箱液位模糊控制仿真设计智能控制是一种利用先进的智能技术和算法来实现自动控制的方法。
在智能控制中,模糊控制是一种常见且有效的方法之一、模糊控制通过将模糊逻辑应用于控制系统中的输入和输出,根据模糊规则来进行决策和控制。
水箱液位控制是一个典型的控制问题,常常用于工业和民用领域中的自动化系统。
在许多控制应用中,水箱液位的控制是一个关键的问题,因为它需要根据系统的液位情况来实现稳定的控制。
在模糊控制中,首先需要建立一套模糊规则系统,该系统包括模糊化、模糊推理和解模糊化这三个步骤。
模糊化是将实际输入转换为模糊集合的过程。
在水箱液位控制中,可以将液位分为低、中和高三个模糊集合。
通过将实际液位值映射到这些模糊集合中的一个,来表示液位状态。
模糊推理是根据一组模糊规则,将模糊输入转换为模糊输出的过程。
通过将输入和规则进行匹配,确定输出的模糊集合。
在水箱液位控制中,可以使用如下规则:如果液位低且液位变化小,则控制信号为增大水流量;如果液位高且液位变化大,则控制信号为减小水流量;如果液位中等且液位变化适中,则控制信号为不变。
解模糊化是将模糊输出转换为实际的控制信号的过程。
在水箱液位控制中,可以使用模糊加权平均值的方法来进行解模糊化。
通过将模糊集合和其对应的权重进行加权平均计算,得到最终的控制信号。
在MATLAB中,可以使用Fuzzy Logic Toolbox来实现水箱液位模糊控制仿真设计。
首先需要建立输入和输出的模糊化和解模糊化函数,然后根据实际的模糊规则,构建模糊系统。
最后通过设定输入的模糊值,使用模糊系统进行推理和解模糊,得到最终的控制信号。
总结起来,智能控制及MATLAB实现水箱液位模糊控制仿真设计包括建立模糊规则系统,进行模糊化、模糊推理和解模糊化三个步骤,通过Fuzzy Logic Toolbox来实现模糊控制系统的构建和仿真。
通过利用模糊控制的方法,可以实现水箱液位的自动稳定控制,并提高了控制系统的鲁棒性和适应性。
水箱液面模糊控制及Matlab仿真实现

水箱液面模糊控制及Matlab仿真实现
刘淑荣;袁铮;高俊明
【期刊名称】《微计算机信息》
【年(卷),期】2005(000)031
【摘要】对于不确定输入的水箱液面控制问题,由于输入的不确定性,应用传统的PID控制方法很难达到理想的效果.因此,实际应用中常采用模糊控制的算法.本文介绍了一种基于模糊算法的水箱液面模糊控制系统,并在Matlab的环境下对该系统的实际运行效果进行了仿真模拟,结果显示此种控制方法很好的完成了控制任务.【总页数】5页(P39-43)
【作者】刘淑荣;袁铮;高俊明
【作者单位】130012,吉林,长春,长春工程学院电气工程系;130022,吉林长春吉林大学电子科学与工程学院;130022,吉林长春吉林大学通信工程学院
【正文语种】中文
【中图分类】TP273+.4
【相关文献】
1.白泥回转窑模糊控制及MATLAB仿真实现 [J], 李伟;董继先;汤伟;李明辉
2.定量排料控制系统模糊控制MATLAB仿真研究与实现 [J], 何胜方
3.模糊控制在双螺杆挤出压片机中的应用及MATLAB仿真实现 [J], 刘海燕;周萍;景新幸;陈超
4.水箱液面模糊控制及Matlab仿真实现 [J], 刘淑荣;袁铮;高俊明
5.用ControlLogix实现双容水箱液位系统的模糊控制 [J], 高宏岩
因版权原因,仅展示原文概要,查看原文内容请购买。
模糊控制及matlab仿真

模糊控制及matlab仿真1 .实例某个液位控制系统的液体容器中,液体的流出量变化无常,无法建立起数学模型,只能通过控制进液阀门开度调节液位,使容器中的液位保持平衡。
根据积累的操作经验,归纳总结出使液体容器液位保持恒定的下述几条操作规律。
1.如果液位正好,则阀门开度不变;If level is okay then value is no change2.如果液位偏低,则增大阀门开度;If level is low then value is open fast3.如果液位偏高,则减小阀门开度;If level is high then value is close fast4.如果液位正好而进液流速快,则逐渐减小阀门开度;If level is okay and rate is positive then value is close slow5.如果液位正好而进液流速慢,则逐渐增大阀门开度;If level is okay and rate is negation then value is open slow 2. simulink模块及fis文件本系统采用曼达尼模型进行仿真,通过matlab模糊控制编辑器进行控制规则的建立,以及模糊控制器的搭建。
Fis编辑器如下图所示,该控制器为两输入一输出系统。
其中两输入分别为液位高度,及液位变化速率,输出为阀门开度。
“与”算法用求积来表达,“或”算法用代数和来表达,“蕴含”算法用求积来表达,“综合”算法为各条模糊规则结果取并,“清晰化”算法用面积中心法来描述。
隶属函数编辑器液位隶属函数液位变化速率隶属函数阀门开度隶属函数控制规则编写Simulink模块3. 仿真及结果分析液位初始波动与经过阀门调节后系统液位曲线比较。
智能控制及MATLAB实现—水箱液位模糊控制仿真设计

水箱水位模糊控制系统设计一.在MATLAB命令窗口中输入sltank,便可打开如图所示的模型窗口。
图1 sltank仿真图(1)打开MATLAB,输入指令fuzzy,打开模糊逻辑工具箱的图形用户界面窗口,新建一个Mamdani模糊推理系统。
(2)增加一个输入变量,将输入变量命名为水位误差、误差变化,将输出变量命名为阀门开关速度。
这样就建立了一个两输入单输出的模糊推理系统,保存为shuiwei1。
图2 增加一个输入变量(3)设计模糊化模块;设水位误差level的论域为[2、95 3、05],误差变化率rate的论域为[-0、2 0、2];两个输入量的模糊集为level设为为7个,rate设为5个:其中水位误差level定为NB、NM、NS、ZE、PS、PM、PB;参数分别为[0、01 2、95]、[0、01 2、97],[0、01 2、99]、[0、01 3]、[0、01 3、01]、[0、01 3、03]、[0、01 3、05],隶属度均为高斯函数;图3 输入量level的参数设定误差变化率rate分别为负大,负小,不变,正小,正大。
参数分别为,[0、03 -0、2]、[0、03 -0、1]、[0、03 0]、[0、03 0、1]、[0、03 -0、2],隶属度函数均为高斯函数。
图4 误差变化率rate的参数设定阀门的开关速度设为七个等级:快关,中关,慢关,不动,慢开,中开,快开,其论域为[2、95 3、05]。
参数分别为;[2、94 2、95 2、96]、[2、965 2、97 2、975]、[2、99 2、99 2、995]、[2、999 3 3、001]、[3、005 3、01 3、015]、[3、02 3、03 3、035]、[3、04 3、05 3、06],隶属函数为三角形函数。
图5 输出量valve的参数设定(4)设计模糊规则打开Ruel Editor窗口,通过选择添加模糊规则;1)If (level is NB) and (rate is 负大) then (valve is 快关) (1)2)If (level is NB) and (rate is 负小) then (valve is 快关) (1) 3)If (level is NB) and (rate is 不变) then (valve is 快关) (1) 4)If (level is NB) and (rate is 正小) then (valve is 中关) (1)5)If (level is NB) and (rate is 正大) then (valve is 不动) (1) 6)If (level is NM) and (rate is 负大) then (valve is 快关) (1) 7)If (level is NM) and (rate is 负小) then (valve is 快关) (1) 8)If (level is NM) and (rate is 不变) then (valve is 快关) (1) 9)If (level is NM) and (rate is 正小) then (valve is 中关) (1)10)If (level is NM) and (rate is 正大) then (valve is 不动) (1) 11)If (level is NS) and (rate is 负大) then (valve is 中关) (1) 12)If (level is NS) and (rate is 负小) then (valve is 中关) (1) 13)If (level is NS) and (rate is 不变) then (valve is 中关) (1) 14)If (level is NS) and (rate is 正小) then (valve is 不动) (1) 15)If (level is NS) and (rate is 正大) then (valve is 慢开) (1) 16)If (level is ZE) and (rate is 负大) then (valve is 中关) (1) 17)If (level is ZE) and (rate is 负小) then (valve is 慢关) (1) 18)If (level is ZE) and (rate is 不变) then (valve is 不动) (1)19)If (level is ZE) and (rate is 正小) then (valve is 慢开) (1) 20)If (level is ZE) and (rate is 正大) then (valve is 中开) (1) 21)If (level is PS) and (rate is 负大) then (valve is 慢关) (1) 22)If (level is PS) and (rate is 负小) then (valve is 不动) (1) 23)If (level is PS) and (rate is 不变) then (valve is 中开) (1) 24)If (level is PS) and (rate is 正小) then (valve is 中开) (1) 25)If (level is PS) and (rate is 正大) then (valve is 中开) (1) 26)If (level is PM) and (rate is 负大) then (valve is 不动) (1) 27)If (level is PM) and (rate is 负小) then (valve is 中开) (1) 28)If (level is PM) and (rate is 不变) then (valve is 快开) (1) 29)If (level is PM) and (rate is 正小) then (valve is 快开) (1) 30)If (level is PM) and (rate is 正大) then (valve is 快开) (1) 31)If (level is PB) and (rate is 负大) then (valve is 不动) (1) 32)If (level is PB) and (rate is 负小) then (valve is 中开) (1) 33)If (level is PB) and (rate is 不变) then (valve is 快开) (1) 34)If (level is PB) and (rate is 正小) then (valve is 快开) (1) 35)If (level is PB) and (rate is 正大) then (valve is 快开) (1) 这35条模糊控制规则的权重都为1、图6 模糊控制规则的设定(5)利用编辑器的 to Workspace, 将当前的模糊推理系统,以shuiwei1保存到工作空间中。
基于DCS平台的水箱液位控制系统的模糊控制算法

0 引
言
集散控制系统 ( dist ribut ed cont ro l syst em, DCS) 是一种 以微处理器为基础的分散型综合控 制系统。 DCS 综合了计算机技术、 网络通讯技术、 自动控制技术、 冗余及自诊断技术等先进技术, 采用多层分级的结 构形式, 适应现代化生 பைடு நூலகம்的控制与管理需求, 目前 已成为工业过程控制的主流系 统。但多数 企业开发的 DCS 控制算法仍停留在常规控制阶段 , 因此进一步开发及挖掘其潜力具有重大的意义, 其中先进控制的研 究就是很重要的一部分。水箱液位对象是具有大惯性、 大滞后动态特性的系统 , 在工业生产过程中, 广泛存 在于石油化工过程中的蒸馏塔、 化学反应器、 液体传输设备及热工过程中的锅炉、 热交换器等对象中[ 1] 。通 常液位控制采用 P ID 或模糊 P ID, 但是传统控制需要精确的数学模型 , 而且对于大滞后动态特性的系统控 制效果不是很好。模糊控制不需要精确的数学模型, 而且一些模糊控制器可以等效为变增益的非线性 P I 或 PD 控制器[ 3] , 因此得到广泛的关注和应用。 本文以 CS4000 装置的单容、 双容水箱为实验对象 , 基于 JX 300X DCS 控 制平台, 利用 SCX 语言开发相应的模糊控制算法对水箱液位控制系统进行研 究。 SU PCON JX 300X DCS 由工程师站、 操作站、 控制站、 过程控制网络等组 成, 如图 1 所示。
1 基于 DCS 水箱液位控制系统的模糊控制的设计
文中采用双输入单输出模糊控制器 , 将误差及误差变化作为模糊控制器输入 , 调节阀开度作为控制器 输出。
收稿日期 : 2008- 10- 08 基金项目 : 浙江省科技计划项目 ( 2006C31016) ; 浙江省科技计划项目( 021101039) 作者简介 : 苏 洁 ( 1980) , 女 , 内蒙古巴彦淖尔人 , 硕士研究生 , 研究方向为自结构模糊控制及其应用。
Matlab 水位控制仿真
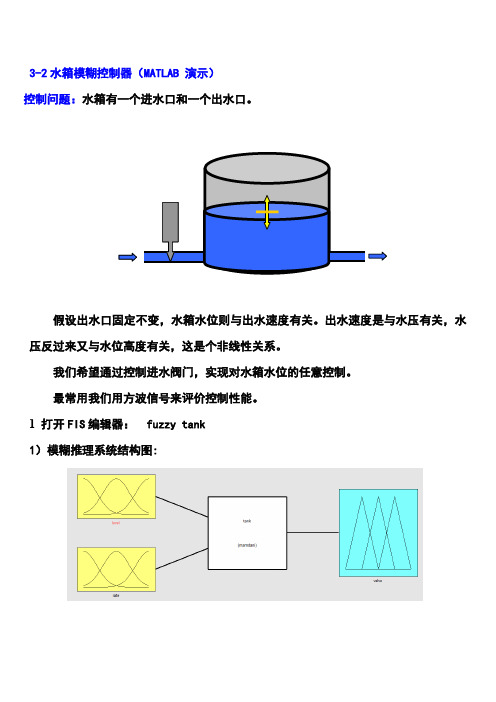
3-2水箱模糊控制器(MATLAB 演示)控制问题:水箱有一个进水口和一个出水口。
假设出水口固定不变,水箱水位则与出水速度有关。
出水速度是与水压有关,水压反过来又与水位高度有关,这是个非线性关系。
我们希望通过控制进水阀门,实现对水箱水位的任意控制。
最常用我们用方波信号来评价控制性能。
1 打开FIS编辑器: fuzzy tank1)模糊推理系统结构图:2)水箱FIS系统结构参数:-----------------------------------a=readfis('tank')---------------------------------a =name: 'tank'type: 'mamdani'andMethod: 'prod'orMethod: 'probor'defuzzMethod: 'centroid'impMethod: 'prod'aggMethod: 'max'input: [1x2 struct]output: [1x1 struct]rule: [1x5 struct]3)水箱FIS详细参数--------------------------------------a=readfis('tank')showfis(a)---------------------------------------1. Name tank2. Type mamdani3. Inputs/Outputs [2 1]4. NumInputMFs [3 3]5. NumOutputMFs 56. NumRules 57. AndMethod prod ;求积运算8. OrMethod probor ;代数和运算9. ImpMethod prod10. AggMethod max11. DefuzzMethod centroid12. InLabels level 输入变量名13. rate14. OutLabels valve 输出变量名15. InRange [-1 1] ;输入论域16. [-0.1 0.1]17. OutRange [-1 1] 输出论域18. InMFLabels high 输入1模糊参考集名称19. okay20. low21. negative 输入2模糊参考集名称22. none23. positive24. OutMFLabels close_fast ;输出模糊参考集名称25. close_slow26. no_change27. open_slow28. open_fast29. InMFTypes gaussmf ;输入模糊参考集形状,高斯型30. gaussmf31. gaussmf32. gaussmf33. gaussmf34. gaussmf35. OutMFTypes trimf ;输出模糊参考集形状,三角形36. trimf37. trimf38. trimf39. trimf40. InMFParams [0.3 -1 0 0] 模糊参考集形状参数41. [0.3 0 0 0]42. [0.3 1 0 0]43. [0.03 -0.1 0 0]44. [0.03 0 0 0]45. [0.03 0.1 0 0]46. OutMFParams [-1 -0.9 -0.8 0]47. [-0.6 -0.5 -0.4 0]48. [-0.1 0 0.1 0]49. [0.2 0.3 0.4 0]50. [0.8 0.9 1 0]51. Rule Antecedent [2 0] 模糊规则前件52. [3 0]53. [1 0]54. [2 3]55. [2 1]51. Rule Consequent 3 模糊规则后件52. 553. 154. 255. 451. Rule Weight 152. 153. 154. 155. 151. Rule Connection 152. 153. 154. 155. 14)列出水箱FIS的模糊规则------------------------------------a=readfis('tank');showrule(a)------------------------------------ans =1. If (level is okay) then (valve is no_change) (1)2. If (level is low) then (valve is open_fast) (1)3. If (level is high) then (valve is close_fast) (1)4. If (level is okay) and (rate is positive) then (valve is close_slow) (1)5. If (level is okay) and (rate is negative) then (valve is open_slow) (1) 5)隶属函数形状6)模糊推理过程图7)模糊推理输入输出关系图sltank,进入Simlink环境观察输入与输出的关系(1)模糊控制器与PID控制器作比较将开关选择“const”, 由-1改为1,表示PID控制器工作观察输出响应情况(4)观察模糊规则变化的影响键入命令:ruleedit tank删除最后两条规则,将结果临时存入工作空间: File /Export / To workspace(退出ruleedit窗口时不要选择保存选择,否则会破坏源程序设置)1. If (level is okay) then (valve is no_change) (1)2. If (level is low) then (valve is open_fast) (1)3. If (level is high) then (valve is close_fast) (1)4. If (level is okay) and (rate is positive) then (valve is close_slow) (1)5. If (level is okay) and (rate is negative) then (valve is open_slow) (1)(c)切换到sltank的Simlink环境,观察结果。
水箱液位matlab模糊控制例程sltank详解
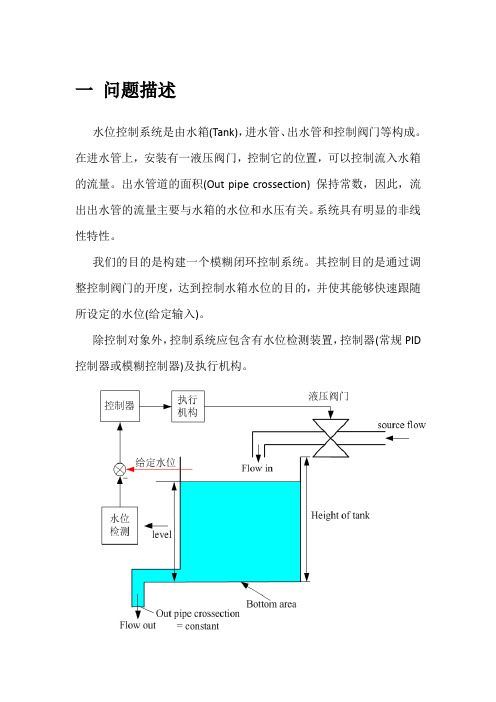
一问题描述水位控制系统是由水箱(Tank),进水管、出水管和控制阀门等构成。
在进水管上,安装有一液压阀门,控制它的位置,可以控制流入水箱的流量。
出水管道的面积(Out pipe crossection) 保持常数,因此,流出出水管的流量主要与水箱的水位和水压有关。
系统具有明显的非线性特性。
我们的目的是构建一个模糊闭环控制系统。
其控制目的是通过调整控制阀门的开度,达到控制水箱水位的目的,并使其能够快速跟随所设定的水位(给定输入)。
除控制对象外,控制系统应包含有水位检测装置,控制器(常规PID 控制器或模糊控制器)及执行机构。
二控制系统动态结构图流速计算依据为简化伯努利方程或托里拆利定律,二者结论一致。
其中托里拆利定律内容为:忽略粘滞性,任何液体止点从小孔中流出的速度与它从h高度处自由落下的速度相等。
Level flow out动态模型中主要用到的计算关系式如下:液位=容积/底面积level=tank volume/area流量=流速*出水口面积流速=(2*g*level)^0.5被控对象水箱模型搭建按照上述动态结构图进行,实际设计的水箱模型如下:封装后执行机构:VALVE三水位控制系统模型四模型使用方法启动matlab,命令行输入sltank,既可打开水位模糊控制仿真模型。
设置const大于等于0,系统工作于PID控制模式设置const小于0,系统工作于模糊控制模式模糊控制时液位输入输出关系(双击Comparison示波器)液位动画PID控制时液位的输入输出关系比较两种控制模式下液位曲线可以发现PID控制有超调,这一点在液位动画中也有体现。
修改模型参数PID参数的调整可以直接双击PID Controller模块设置,这里着重介绍模糊控制器参数的修改。
用到的主要命令如下:例如可通过以下代码以文本形式显示tanka=readfis('tank') %读取tank文件showfis(a); %显示在这里通过模糊推理的用户界面来修改水位控制的规则库,查看对控制效果的影响。
-基于MATLAB的双容水箱液位的模糊神经控制

自 1932 年奈魁斯特(H.Nyquist)的有关反馈放大器稳定性论文发表以来,控制理 论的发展已走过了近 80 年的历程。前 30 年是经典控制理论的发展和成熟阶段,后 50 年是现代控制理论的形成和发展阶段。随着研究的对象和系统越来越复杂,借助 于数学模型描述和分析的传统控制理论已难以解决复杂系统的控制问题。智能控制是 针对控制对象及其环境、目标和任务的不确定性和复杂性而产生和发展起来的。从 20 世纪 60 年代起,计算机技术和人工智能技术迅速发展,为了提高控制系统的自主 学习能力,人工智能技术被学者们提出并广泛应用于控制系统。1965 年,美籍华裔 科学家傅京孙教授首先把人工智能的启发式推理规则用于学习控制系统;1966 年,
2 系统建模与 MATLAB 环境 ......................................................................................4 2.1 过程控制系统的建模方法..................................................................................4 2.1.1 机理法 ...........................................................................................................4 2.1.2 测试法 ...........................................................................................................4 2.2 双容水箱液位控制系统的建模..........................................................................4 2.3 MATLAB 环境及 Simulink 模型 .......................................................................8 2.3.1 MATLAB 软件简介 .....................................................................................8 2.3.2 Simulink 模型................................................................................................8
基于MATLAB水箱液位控制系统的设计

基于MATLAB水箱液位控制系统的设计水箱液位控制系统是水处理领域的一个重要应用,可以实现对水箱液位的监测和控制。
本文将基于MATLAB平台设计一个水箱液位控制系统,并详细介绍其工作原理、设计步骤和实现方法。
1.设计目标和原理设计目标是实现水箱液位的实时监测和自动控制,保持液位在设定值附近波动。
系统原理是通过传感器实时检测水箱液位,将液位信号传输给控制器进行处理,控制器根据设定值和实际液位偏差调整执行机构的动作,使液位保持在设定值范围内。
2.设计步骤(1)确定传感器和执行机构:选择合适的液位传感器和执行机构,如浮球传感器和电动阀门。
(2)建立数学模型:根据系统特性建立数学模型,描述液位与传感器输出和执行机构控制信号之间的关系。
(3)设计控制器:根据液位模型设计控制器,如PID控制器。
(4)编写MATLAB程序:使用MATLAB编写程序,实现液位监测、控制器设计和控制信号输出。
3.系统实现方法(1)建立模拟环境:在MATLAB中建立水箱液位模拟环境,包括液位模型、传感器模型和执行机构模型。
(2)液位监测:读取传感器输出信号,获取实时液位信息。
(3)控制器设计:根据实时液位和设定值计算控制信号,可以使用PID控制器进行设计。
(4)控制信号输出:将控制信号发送给执行机构,实现对阀门的开关控制。
(5)反馈调整:根据执行机构的反馈信号对控制器参数进行调整,以进一步优化系统性能。
4.系统性能指标和优化(1)稳定性:控制系统在干扰的情况下能够保持液位稳定。
(2)响应速度:控制系统对液位变化的响应速度,可以通过调整控制器参数来实现快速响应。
(3)偏差:控制系统的液位偏差大小,可以通过调整控制器参数和设定值来控制偏差范围。
(4)抗干扰性能:控制系统对外界干扰(如水源变化)的抵抗能力。
(5)稳定性分析:通过系统稳定性分析,确定系统参数的合理范围。
(6)优化方法:通过试验和仿真,不断调整控制器参数和设定值,以实现最佳控制效果。
模糊控制的Matlab仿真实例分析

.
18
在Simulink编辑窗口左边的模块浏览区可以看 到在水箱仿真系统中包括水箱子模型、阀门子 模型及 PID 控制子模型。直接在浏览区中点 击或右键点击它们,并在弹出菜单中选择 [ look under mask 】 ,可以看到这些模块实 现的细节结构,如图 所示。
.
19
.
20
.
21
这里暂时不讨论具体的系统模型的构造问题,我们可 以先在这个已经建立好的系统模型上进行修改,体验 模糊逻辑与仿真环境结合使用的优势。
字分别代表服务和食
物的质量( 10 表示
非常好, 0 表示非常
差),这时小费与它
.
们之间的关系又应4当8
如何反映呢?
假设是二元线性关系 用下列 MATLAB 语句可绘出下图 。
.
49
.
50
可以看到,如果不考虑服务质量因素比食物质量因素对 于小费的支付占有更大的比重,上面的关系图形已经能 够反映一些实际的情况了。假如希望服务质量占小费的 80 % , 而食物仅占 20 %。这里可以设定权重因子:
注意将鼠标箭头放置图内,移动鼠标可得到不同 角度的视图,如下图所示。
.
15
Matlab模糊控制仿真演示例子
模型sltank.mdl ——使用模糊控制器对水箱水位进 行控制。
假定水箱有一个进水口和一个出水口,可以通过控 制一个阀门来控制流入的水量(即水位高度),但 是流出的速度取决于出水口的半径(定值)和水箱 底部的压力(随水箱中的水位高度变化)。系统有 许多非线性特性。
真。
.
31
学习 MATLAB 仿真工具的一个快速有效的方法就 是学习示例模型,通过看懂这些模型和模块的功
能以及搭建过程,可以很快熟悉和掌握如何使用 MATLAB 仿真工具来设计和搭建自己独特的模型。
现代计算方法—水箱水位模糊控制

水箱水位模糊控制控制130337杨康一、问题描述1.使用MATLAB的模糊逻辑工具箱,建立模糊推理系统,进行水位系统的模糊控制。
受控对象为二阶有自平衡能力的对象,h(s)/Q(s)=2/(s^2+1.2s+4),其中h(s)是水位偏差,Q(s)是入口阀门开度偏差。
2.模糊控制规则参考如下:IF(水位低)then(阀门迅速打开)IF(水位高)then(阀门迅速关闭)IF(水位偏差小且变化率为零)then(阀门大小不变)IF(水位偏差小且变化率为负)then(阀门缓慢关闭)IF(水位偏差小且变化率为正)then(阀门缓慢打开)二、解决方案熟悉模糊逻辑工具箱,通过工具箱并按照规则参考设计模糊控制逻辑;在Simulink工具箱中加载模糊控制逻辑完成仿真。
通过与传统PID控制的比较,来分析各自的优缺点,加强对控制算法的认识。
三、算法实现1、模糊控制逻辑实现按照上述模糊控制规则分别对水位(level)、水位变化(levelrate)和阀门动作(output)三个变量进行设计。
(1)在水位变量设计时,范围为[-1 1],其模糊子集为{high,okay,low},其隶属度函数如图所示:图一、水位变量设计(2)在水位速率变化设计时,范围为[-1 1],其模糊子集为{negative,none,positive},其隶属度函数如下图所示:图二、水位变化速率设计(3)在阀门变化设计时,范围为[-7 7],其模糊子集为{close fast, close slow, no change, open slow, open fast},其隶属度函数如下图所示:图三、阀门变化设计(4)按照参考的规则设计模糊推理决策的算法:图四、模糊推理设计(5)对输出模糊量的解模糊:模糊控制器的输出量是一个模糊集合,通过反模糊化方法判决出一个确切的精确量,凡模糊化方法很多,我们这里选取重心法。
如图所示:图五、模糊量解模糊2、Simulink平台搭建将设计好的模糊控制器导入到workspace中,并搭建好仿真控制系统,如图所示:图六、模糊逻辑控制仿真平台其中,参考选为正弦波信号,并将误差值及其变化率信号输入到模糊逻辑控制器中进行处理;对象的传递函数为h(s)/Q(s)=2/(s^2+1.2s+4),四、结果分析与比较当参考信号为正选函数时,传统的PID控制会产生一定的相位差,从而导致控制效果变差,若采用模糊逻辑控制可以大大减少相位差。
模糊控制在matlab中的实例

模糊控制在matlab中的实例以下是一个模糊控制在MATLAB中的简单实例:假设我们要设计一个模糊控制器来控制一个水箱中水位的高低。
我们可以先建立一个模糊推理系统,其中包含输入和输出变量以及规则。
1. 输入变量:水箱中的水位(假设范围为0到100)。
2. 输出变量:水泵的流量(假设范围为0到10)。
我们需要定义一组模糊规则,例如:如果水箱中的水位为低,则水泵的流量为低。
如果水箱中的水位为中等,则水泵的流量为中等。
如果水箱中的水位为高,则水泵的流量为高。
将这些规则转换成模糊集合,如下所示:输入变量:- 低:[0, 30]- 中等:[20, 50]- 高:[40, 100]输出变量:- 低:[0, 3]- 中等:[2, 6]- 高:[4, 10]接下来,我们可以使用MATLAB的Fuzzy Logic Toolbox来建立模糊推理系统。
以下是一个简单的MATLAB脚本:```% 定义输入变量water_level = fisvar("input", "Water Level", [0 100]); water_level.addmf("input", "low", "trapmf", [0 0 30 40]); water_level.addmf("input", "medium", "trimf", [20 50 80]);water_level.addmf("input", "high", "trapmf", [60 70 100 100]);% 定义输出变量pump_flow = fisvar("output", "Pump Flow", [0 10]);pump_flow.addmf("output", "low", "trapmf", [0 0 3 4]); pump_flow.addmf("output", "medium", "trimf", [2 6 8]); pump_flow.addmf("output", "high", "trapmf", [7 8 10 10]); % 建立模糊推理系统rule1 = "If Water Level is low then Pump Flow is low"; rule2 = "If Water Level is medium then Pump Flow is medium"; rule3 = "If Water Level is high then Pump Flow is high"; rules = char(rule1, rule2, rule3);fis = newfis("Water Tank Fuzzy Controller");fis = addvar(fis, water_level);fis = addvar(fis, pump_flow);fis = addrule(fis, rules);% 模糊控制器输入water_level_value = 70;% 运行模糊推理系统pump_flow_value = evalfis([water_level_value], fis);disp(["Water level: " num2str(water_level_value) "%"]); disp(["Pump flow: " num2str(pump_flow_value)]);```在这个简单的例子中,我们使用了Fuzzy Logic Toolbox来定义输入和输出变量以及规则,并运行模糊推理系统来计算输出值。
水箱液位控制器matlab

figure(1); plotfis(a2); figure(2); plotmf(a,'input',1); figure(3); plotmf(a,'output',1);
showrule(a); ruleview('tank');
for i=1:1:7 e(i)=i-4; Ulist(i)=evalfis([e(i)],a2);
end Ulist = round(Ulist);
disp('------------------------------------------------------'); disp('----------模糊控制表:e =[-3,3], u = [-4,4]-----------'); disp('------------------------------------------------------'); fprintf('| a |'); fprintf(' %d |',e); fprintf('\n'); fprintf('| u |'); fprintf(' %d |',Ulist); fprintf('\n');
基于MATLAB的水箱水位模糊控制

目录前言1.模糊控制概述模糊控制的产生及特点 (3)模糊控制技术的发展 (4)模糊控制理论的研究现状 (5)2.模糊推理原理模糊控制的基本工作原理 (6)3.基于MATLAB的水箱供水模糊控制水箱水位模糊控制系统设计 (8)小结............ ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・16参考文献 (17)-•、—1—冃IJ §随着社会经济的迅速发展,水对人们生活与工业生产的影响越来越重要,尤其是近儿年,随着居民生活水平的显著提高和城市化进程的加快,居民生活用水和工业用水增长幅度加大,原有的供水系统已经不能满足人们的需求。
为了保证正常的供水,这里应用模糊控制技术,实现对水箱水位的自动控制。
3、基于MATLAB的水箱供水模糊控制水箱水位模糊控制系统设计本系统设计基于MATLAB图形模糊推理系统,设计步骤如下:(1)打开MATLAB,输入指令fuzzy,打开模糊逻辑工具箱的图形用户界面窗口,新建一个Mamdani模糊推理系统。
图FIS Editor窗口中新建水位控制模糊推理系统(2)增加一个输入变量,将输入变量命名为水位误差、误差变化,将输出变量命名为阀门开关速度。
这样就建立了一个两输入单输出的模糊推理系统,保存为。
图增加一个输入变量(3) 设计模糊化模块:设水位误差的论域为[-1 1],误差变化 的论域为[];两个输入量的模糊集都定为5个:其中水位误差定为高、偏 高、合适、偏低、低五等;参数分别为[-1]、[ ]、[0]、[]、 [1]; Current Varidbte Nome Tpqe £yVcm ^huiMono : 2 inpdts, 1 oulpU z ord 24 ruleI rrin I max ceriroid rnn And method Or methodImplicationAggregalbn Dcfuzzficotion input (11) |水位魅 FIS Name: shuxiara FIS Tvpe: maiidcniCloseRange图设汁水位误差模块误差变化分为大、偏大、合适、偏小、小五等。
水箱液面模糊控制及Matlab仿真实现

!"#$
图 " 模糊控制系统结构图
由 图 " 可 知< 要 想 实 现 控 制 目 标< 关 键 在 于 以 下 的三个 步骤 < 即输入 变 量 的 模 糊 化 < 模 糊 关 系 矩 阵 的 获取 < 模糊结果的获 得 以 及 其 输 出 的 去 模 糊 化 D 模 糊 控制系统首先将输入量 M 和 !M 经过模糊化处理< 然 后送到模糊推理环节进行推理 < 推理后得出的输出模 糊量再进行精确化处理 < 最后输出到控制执行环节中 控制被控对象 % 根 据 模 拟 的 实 际 情 况 及 要 求 水 箱 液 面 在 HDICJ "DKC 内波动 < 理想的状态是 "D%C< 易知液面偏差 M 的 基本论域为 PJHDI< HDIQ< 量化为 PJR JS J% J" H " % S RQ T 个 等 级 < 定 义 L 个 模 糊 语 言 变 量 U V 正 大 VNW’XY< V 正 小 V!W’WZ< V 零V!W[MZ< V 负小V!W\WZ< V负大 V!W\XZD
在线推理法模糊控制器实验报告

在线推理式模糊逻辑控制器设计实验报告学院:电力学院专业:自动化学号:姓名:时间:2013年11月16日一、实验目的利用Matlab软件实现模糊控制系统仿真实验,了解模糊控制的在线推理方法的基本原理及实现过程。
二、实验要求以matlab模糊工具箱中提供的一个水位模糊控制系统仿真的实例,定义语言变量的语言值,设置隶属度函数,根据提供的规则建立模糊逻辑控制器。
最后启动仿真,观察水位变化曲线。
三、实验步骤叙述在线推理模糊控制的仿真的主要步骤。
1)在matlab命令窗口输入:sltank,打开水位控制系统的simulink仿真模型图,如图;2)在matlab的命令窗口中,输入指令:fuzzy,便打开了模糊推理系统编辑器(FIS Editor),如图;3)利用FIS Editor编辑器的Edit/Add variable/input菜单,添加一条输入语言变量,并将两个输入语言和一个输出语言变量的名称分别定义为:level;rate;valve。
其中,level代表水位(三个语言值:低,高,正好),rate代表变化率(三个语言值:正,不变,负),valve代表阀门(五个语言变量:不变,迅速打开,迅速关闭,缓慢打开,缓慢关闭);4)①利用FIS Editor编辑器的Edit/membership function菜单,打开隶属度函数编辑器,如下图,将输入语言变量level的取值范围(range)和显示范围(display range)设置为[-1,1],隶属度函数类型(type)设置为高斯型函数(gaussmf),而所包含的三条曲线的名称(name)和参数(parameters)([宽度中心点])分别设置为:high,[0.3 -1];okay [0.3 0];low [0.3 1]。
其中high 、okay、low分别代表水位高、正好、低;②将输入语言变量rate的取值范围(range)和显示范围(display range)设置为[-0.1,0.1],隶属度函数类型(type)设置为高斯型函数(gaussmf),而所包含的三条曲线的名称(name)和参数(parameters)([宽度中心点])分别设置为:negative,[0.03 -0.1];none [0.03 0];positive [0.03 0.1]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一问题描述
水位控制系统是由水箱(Tank),进水管、出水管和控制阀门等构成。
在进水管上,安装有一液压阀门,控制它的位置,可以控制流入水箱的流量。
出水管道的面积(Out pipe crossection) 保持常数,因此,流出出水管的流量主要与水箱的水位和水压有关。
系统具有明显的非线性特性。
我们的目的是构建一个模糊闭环控制系统。
其控制目的是通过调整控制阀门的开度,达到控制水箱水位的目的,并使其能够快速跟随所设定的水位(给定输入)。
除控制对象外,控制系统应包含有水位检测装置,控制器(常规PID 控制器或模糊控制器)及执行机构。
二控制系统动态结构图
流速计算依据为简化伯努利方程或托里拆利定律,二者结论一致。
其中托里拆利定律内容为:忽略粘滞性,任何液体止点从小孔中流出的速度与它从h高度处自由落下的速度相等。
Level flow out
动态模型中主要用到的计算关系式如下:
液位=容积/底面积level=tank volume/area
流量=流速*出水口面积
流速=(2*g*level)^0.5
被控对象水箱模型
搭建按照上述动态结构图进行,实际设计的水箱模型如下:
封装后
执行机构:
VALVE
三水位控制系统模型
四模型使用方法
启动matlab,命令行输入sltank,既可打开水位模糊控制仿真模型。
设置const大于等于0,系统工作于PID控制模式
设置const小于0,系统工作于模糊控制模式
模糊控制时液位输入输出关系(双击Comparison示波器)
液位动画
PID控制时液位的输入输出关系
比较两种控制模式下液位曲线可以发现PID控制有超调,这一点在液位动画中也有体现。
修改模型参数
PID参数的调整可以直接双击PID Controller模块设置,这里着重介绍模糊控制器参数的修改。
用到的主要命令如下:
例如可通过以下代码以文本形式显示tank
a=readfis('tank') %读取tank文件
showfis(a); %显示
在这里通过模糊推理的用户界面来修改水位控制的规则库,查看对控制效果的影响。
具体步骤如下:
(1)输入sltank打开simulink仿真界面
(2)输入fuzzy tank打开FIS界面,可编辑变量和推理规则。
(3)打开tank的模糊规则编辑界面,将规则4和5删除,新的规则如下:
(4)单击File —Export—to workspace,弹出的对话框直接点ok。
注意:建议不要选to file,因为会改变原始文件。
(5)运行sltank,控制效果如下,可见调节效果比PID控制还差。
(6)关闭sltank模型和tank fis界面,均选择不保存修改,以保
证例程的完整性。
五结论
模糊控制效果取决于模糊推理规则,如果规则设置不当,则控制效果会比传统PID控制效果更差。
模糊控制一般和其他智能控制算法结合使用,比如模糊PID,模糊神经网络等,其主要作用是智能控制算法中的一些控制参数进行模糊调节。
伍银波2012年11月13日星期二。
