弹性力学期末考试卷及答案
《弹性力学》试题参考答案

《弹性力学》试题参考答案(答题时间:100分钟)一、填空题(每小题4分)1.最小势能原理等价于弹性力学基本方程中: 平衡微分方程 , 应力边界条件 。
2.一组可能的应力分量应满足: 平衡微分方程 ,相容方程(变形协调条件) 。
3.等截面直杆扭转问题中, M dxdy D=⎰⎰2ϕ的物理意义是 杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M 。
4.平面问题的应力函数解法中,Airy 应力函数ϕ在边界上值的物理意义为 边界上某一点(基准点)到任一点外力的矩 。
5.弹性力学平衡微分方程、几何方程的张量表示为:0,=+i j ij X σ ,)(21,,i j j i ij u u +=ε。
二、简述题(每小题6分)1.试简述力学中的圣维南原理,并说明它在弹性力学分析中的作用。
圣维南原理:如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢与主矩相同),则近处的应力分布将有显著的改变,但远处的应力所受影响可以忽略不计。
作用:(1)将次要边界上复杂的面力(集中力、集中力偶等)作分布的面力代替。
(2)将次要的位移边界条件转化为应力边界条件处理。
2.图示两楔形体,试分别用直角坐标和极坐标写出其应力函数ϕ的分离变量形式。
题二(2)图(a )⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x (b )⎩⎨⎧=+++=)(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3.图示矩形弹性薄板,沿对角线方向作用一对拉力P ,板的几何尺寸如图,材料的弹性模量E 、泊松比 μ 已知。
试求薄板面积的改变量S ∆。
题二(3)图设当各边界受均布压力q 时,两力作用点的相对位移为l ∆。
由q E)1(1με-=得,)1(2222με-+=+=∆Eb a q b a l设板在力P 作用下的面积改变为S ∆,由功的互等定理有:l P S q ∆⋅=∆⋅将l ∆代入得:221b a P ES +-=∆μ显然,S ∆与板的形状无关,仅与E 、μ、l 有关。
弹性力学考试和答案

弹性力学考试和答案一、单项选择题(每题2分,共20分)1. 弹性力学中,应力状态的基本方程是()。
A. 平衡方程B. 几何方程C. 物理方程D. 边界条件答案:A2. 弹性力学中,位移场的三个基本方程是()。
A. 平衡方程B. 几何方程C. 物理方程D. 边界条件答案:B3. 弹性力学中,平面应力问题与平面应变问题的主要区别是()。
A. 应力分量不同B. 位移分量不同C. 应变分量不同D. 边界条件不同答案:C4. 弹性力学中,圣维南原理是指()。
A. 应力集中现象B. 应力释放现象C. 应力平衡现象D. 应力松弛现象答案:B5. 弹性力学中,莫尔圆表示的是()。
A. 应力状态B. 应变状态C. 位移状态D. 应力-应变关系答案:A6. 弹性力学中,平面问题的基本解法有()。
A. 直接积分法B. 叠加原理C. 变分法D. 能量法答案:A7. 弹性力学中,轴对称问题的基本解法是()。
A. 直接积分法B. 叠加原理C. 变分法D. 能量法答案:A8. 弹性力学中,扭转问题的解法是()。
A. 直接积分法B. 叠加原理C. 变分法D. 能量法答案:A9. 弹性力学中,平面应力问题的应力函数是()。
A. 单一函数B. 两个函数C. 三个函数D. 四个函数答案:A10. 弹性力学中,平面应变问题的应力函数是()。
A. 单一函数B. 两个函数C. 三个函数D. 四个函数答案:B二、多项选择题(每题3分,共15分)11. 弹性力学中,应力状态的基本方程包括()。
A. 平衡方程B. 几何方程C. 物理方程D. 边界条件答案:AC12. 弹性力学中,位移场的三个基本方程包括()。
A. 平衡方程B. 几何方程C. 物理方程D. 边界条件答案:BC13. 弹性力学中,平面应力问题与平面应变问题的主要区别包括()。
A. 应力分量不同B. 位移分量不同C. 应变分量不同D. 边界条件不同答案:AC14. 弹性力学中,圣维南原理包括()。
弹性力学试题及答案

弹性力学试题及答案一、选择题(每题5分,共20分)1. 弹性力学中,描述材料弹性特性的基本物理量是()。
A. 应力B. 应变C. 弹性模量D. 泊松比答案:C2. 在弹性力学中,下列哪项不是胡克定律的内容?()A. 应力与应变成正比B. 材料是均匀的C. 材料是各向同性的D. 材料是线性的答案:B3. 弹性模量E和泊松比ν之间的关系是()。
A. E = 2(1 + ν)B. E = 3(1 - 2ν)C. E = 3(1 + ν)D. E = 2(1 - ν)答案:D4. 根据弹性力学理论,下列哪种情况下材料会发生塑性变形?()A. 应力小于材料的弹性极限B. 应力达到材料的弹性极限C. 应力超过材料的屈服强度D. 应力小于材料的屈服强度答案:C二、填空题(每题5分,共20分)1. 弹性力学中,应力的定义是单位面积上的______力。
答案:内2. 弹性力学的基本假设之一是______连续性假设。
答案:材料3. 弹性力学中,应变的量纲是______。
答案:无4. 弹性力学中,当外力撤去后,材料能恢复原状的性质称为______。
答案:弹性三、简答题(每题10分,共30分)1. 简述弹性力学中应力和应变的区别。
答案:应力是描述材料内部单位面积上受到的内力,而应变是描述材料在受力后形状和尺寸的变化程度。
2. 解释弹性力学中的杨氏模量和剪切模量。
答案:杨氏模量(E)是描述材料在拉伸或压缩过程中应力与应变比值的物理量,反映了材料的刚度;剪切模量(G)是描述材料在剪切应力作用下剪切应变与剪切应力比值的物理量,反映了材料抵抗剪切变形的能力。
3. 弹性力学中,如何理解材料的各向异性和各向同性?答案:各向异性是指材料的物理性质(如弹性模量、热膨胀系数等)在不同方向上具有不同的值;而各向同性则是指材料的物理性质在各个方向上都是相同的。
四、计算题(每题15分,共30分)1. 已知一圆柱形试件,其直径为50mm,长度为100mm,材料的弹性模量E=210GPa,泊松比ν=0.3。
期末考试试卷A答案—弹性力学

,考试作弊将带来严重后果!华南理工大学2011年期末考试试卷(A )卷《弹性力学》1. 考前请将密封线内各项信息填写清楚; 所有答案请直接答在答题纸上; .考试形式:闭卷;20分)、五个基本假定在建立弹性力学基本方程时有什么用途?(10分)答:1、连续性假定:引用这一假定后,物体中的应力、应变和位移等物理量就可以看成是连续的,因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
(2分) 2、完全弹性假定:引用这一完全弹性的假定还包含形变与形变引起的正应力成正比的含义,亦即二者成线性的关系,符合胡克定律,从而使物理方程成为线性的方程。
(4分) 3、均匀性假定:在该假定下,所研究的物体内部各点的物理性质显然都是相同的。
因此,反映这些物理性质的弹性常数(如弹性模量E 和泊松比μ等)就不随位置坐标而变化。
(6分) 4、各向同性假定:所谓“各向同性”是指物体的物理性质在各个方向上都是相同的。
进一步地说,就是物体的弹性常数也不随方向而变化。
(8分)5、小变形假定:我们研究物体受力后的平衡问题时,不用考虑物体尺寸的改变而仍然按照原来的尺寸和形状进行计算。
同时,在研究物体的变形和位移时,可以将他们的二次幂或乘积略去不计,使得弹性力学中的微分方程都简化为线性微分方程。
在上述假定下,弹性力学问题都化为线性问题,从而可以应用叠加原理。
(10分)2、试分析简支梁受均布荷载时,平面截面假设是否成立?(5分)解:弹性力学解答和材料力学解答的差别,是由于各自解法不同。
简言之,弹性力学的解法,是严格考虑区域内的平衡微分方程,几何方程和物理方程,以及边界上的边界条件而求解的,因而得出的解答是比较精确的。
而在材料力学中没有严格考虑上述条件,因而得出的是近似解答。
例如,材料力学中引用了平面假设而简化了几何关系,但这个假设对一般的梁是近似的。
所以,严格来说,不成立。
3、为什么在主要边界(占边界绝大部分)上必须满足精确的应力边界条件,教材中式(2-15),而在次要边界(占边界很小部分)上可以应用圣维南原理,用三个积分的应力边界条件(即主矢量、主矩的条件)来代替?如果在主要边界上用三个积分的应力边界条件代替教材中式(2-15),将会发生什么问题?(5分)解:弹性力学问题属于数学物理方程中的边值问题,而要边界条件完全得到满足,往往遇到很大的困难。
《弹性力学及有限单元法》期末考试试卷

《弹性力学及有限元基础》期末考试班级: 姓名: 学号:一.填空题(37分)1(9分). 杆件在竖向体力分量f (常量)的作用下,其应力分量为:x C x 1=σ;32C y C y +=σ;0=xy τ。
支承条件如图所示,C 1 =______ ;C 2=______; C 3=______。
2(12分). 一无限长双箱管道,深埋在地下,如图2所示,两箱中输送的气体压强均为σ0,设中间隔板AB (图中阴影所示)的位移分量为:u = Cx , v = 0,隔板材料模量为E 和μ。
计算隔板上各点的应力分量:σx = _______, σy ,= ______, σz =______。
3(9分). 圆环的内半径为r ,外半径为R ,受内压力q 1及外压力q 2的作用。
若内表面的环向应力为0,则内外压力的关系是:_________________。
4(10分).等截面实心直杆受扭矩的作用,假设应力函数为:()()222222y bx a by x a k -++-=Φ,扭矩引起的单位长度扭转角测得为θ,材料的剪切弹性模量为G ,a 、b 均为常数,则k = _____ 二.分析题5.(20分)一宽度为b 的单向薄板,两长边简支,横向荷载为⎪⎭⎫⎝⎛=b y p p πsin 0,计算板的挠度方程。
(设材料的弹性模量为E ,泊松比为μ,薄板的弯曲刚度为D )6.(20分)如图,一长度为l 的简支梁,在距右端为c 的位置作用一集中荷载P ,请用里兹法计算梁的挠度曲线。
(设挠度曲线为)(x l ax w -=,a 为代求系数)7.(23分)1cm 厚的三角形悬臂梁,长4m ,高2m 。
其三个顶点i , j , k 及内部点m 的面积坐标如图所示。
在面积坐标(1/8,1/2,3/8)处和j 节点处受到10kN 的集中力的作用,在jk 边受到垂直于斜边的线性分布力的作用。
用一个4节点的三角形单元对此题1图 题2图 x 题5图悬臂梁进行有限元分析,域内任一点的位移都表示成⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+++=+++=m m k k j j i i m m k k j j i i v N v N v N v N v u N u N u N u N u 。
(完整版)弹性力学期末考试练习

1、弹性力学的基本假设是什么?弹性力学的基本假设是:连续性、完全弹性、均匀性、各向同性、小变形假定。
2、简述什么是弹性力学?弹性力学与材料力学的主要区别?弹性力学又称为弹性理论,事固体力学的一个分支,其中研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变何位移。
弹性力学与材料力学的区别:从研究对象看;材料力学主要研究杆件,在拉压、剪、弯、扭转等作用下的应力、形变何位移。
弹性力学研究各种形状的弹性体,出杆件外,还研究平面体、空间体、平板和壳体等。
从研究方法看;弹性力学的研究方法是;在弹性体区域内必须严格地考虑静力学、几何学和物理学;而材料力学中虽然也考虑这几方面的条件,但不是十分严密。
3、如图所示悬臂梁,试写出其边界条件。
解:(1)x a =,1,00,0x y l m f f ==⎧⎪⎨==⎪⎩由()()()()x s xy s xy s xy s yl m f m l f στστ+=+=得()()0,0x xy s s στ==(2),y h =-0,10,x y l m f f q==-⎧⎪⎨==⎪⎩()()()()0(1)0(1)0x xy s s y xy ssqστστ⋅+⋅-=⋅-+⋅=则()(),0y xy s s q στ=-=(3),y h =+0,10,0x y l m f f ==+⎧⎪⎨==⎪⎩()()()()0(1)0(1)00x xy s s y xy ssστστ⋅+⋅+=⋅++⋅=得()()0,0y xy s s στ==(4)0,x =00s su v =⎧⎨=⎩4、已知下列位移,试求在坐标为(2,6,8)的P 点的应变状态()32103012-⨯+=x u ,31016-⨯=zy v ,()321046-⨯-=xy z w解:根据⎪⎭⎫ ⎝⎛∂∂+∂∂==∂∂=∂∂+∂∂==∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂==∂∂=z u x w zw z v y w y v x v y u x u zx zx z yz yz y xy xy x 2121,)(2121,2121,εγεεγεεγε 得到-34801201284410124496ij ε-⎡⎤⎢⎥=⨯⎢⎥⎢⎥-⎣⎦5、图示平面薄板,弹性模量E=200GPa ,泊松比v=0.3,求各应变分量()[]()[]()[]⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=+-=+-=yx z z x z y y z y x x v E v E v E σσσεσσσεσσσε111⎪⎪⎪⎩⎪⎪⎪⎨⎧===G G G zx zx yz yz xy xy τγτγτγ 得到100MPa50MPa41075.5-⨯=x ε,4104-⨯-=y ε, 41075.0-⨯-=z ε,0===yz xz xy γγγ6、下面给出平面应力问题(单连通域)的应力场,试分别判断它们是否为可能的应力场(不计体力)。
弹性力学期末考试试题及答案

弹性力学期末考试试题及答案一、名词解释(每题5分,共25分)1. 弹性力2. 弹簧常数3. 应力4. 应变5. 胡克定律6. 弹性模量7. 弹性体的形变8. 弹性位移9. 弹性能量10. 弹性碰撞二、选择题(每题2分,共20分)1. 以下哪种材料不属于弹性材料?A. 钢铁B. 橡胶C. 玻璃D. 水2. 在弹性限度内,弹性力与形变量之间的关系遵循哪一定律?A. 平方律B. 立方律C. 直线律D. 反比律3. 一弹簧的弹簧常数为50N/m,当一个力作用于弹簧上使其压缩0.1m时,弹簧的弹性势能为多少?A. 0.5JB. 1JC. 2JD. 5J4. 下列哪种情况下,弹簧的弹性力最大?A. 弹簧处于自然长度时B. 弹簧被压缩时C. 弹簧被拉伸时D. 弹簧被压缩或拉伸到极限时5. 两个相同的弹性球碰撞,如果它们的弹性系数不同,那么碰撞后它们的速度关系是?A. 速度大小不变,方向相反B. 速度大小不变,方向相同C. 速度大小发生变化,方向相反D. 速度大小发生变化,方向相同三、填空题(每题5分,共25分)1. 一弹性体的形变是指其_________的变化。
2. 在弹性碰撞中,两个物体的速度满足_________定律。
3. 弹簧的弹簧常数_________,表示弹簧的_________。
4. 当一个力作用于弹性体上时,该力与弹性体的_________之比称为应力。
5. 弹性模量是衡量材料_________的物理量。
四、计算题(共40分)1. 一弹簧的弹簧常数为200N/m,当一个力作用于弹簧上使其压缩0.5m时,求弹簧的弹性势能。
(5分)2. 质量为2kg的物体从静止开始沿斜面滑下,斜面与水平面的夹角为30°,斜面长度为10m,摩擦系数为0.2。
求物体滑到斜面底部时的速度。
(5分)3. 两个弹性球A和B,质量分别为m1和m2,弹性系数分别为k1和k2。
它们从静止开始相互碰撞,求碰撞后A和B的速度。
弹性力学试题及答案

弹性力学试题及答案一、选择题(每题5分,共20分)1. 弹性力学中,下列哪一项不是应力状态的描述?A. 正应力B. 剪应力C. 拉应力D. 弯矩答案:D2. 弹性体在外力作用下产生变形,当外力移除后,若能恢复到原始形状,则称为:A. 塑性变形B. 弹性变形C. 永久变形D. 非弹性变形答案:B3. 弹性模量是描述材料弹性特性的物理量,它与下列哪一项无关?A. 杨氏模量B. 泊松比C. 剪切模量D. 热膨胀系数答案:D4. 在弹性力学中,下列哪一项不是材料的本构关系?A. 胡克定律B. 牛顿流体定律C. 圣维南原理D. 弹性模量答案:B二、填空题(每题5分,共20分)1. 弹性力学中,______是指材料在外力作用下发生形变,当外力移除后,材料能够恢复到原始形状的能力。
答案:弹性2. 弹性力学中,______是指材料在外力作用下发生形变,当外力移除后,不能恢复到原始形状的能力。
答案:塑性3. 在弹性力学中,______是指材料在受到剪切力作用时,单位面积上的剪切力与剪切变形的比值。
答案:剪切模量4. 弹性力学中,______是指材料在受到拉伸或压缩时,单位面积上的正应力与正应变的比值。
答案:杨氏模量三、简答题(每题10分,共40分)1. 简述弹性力学中的应力和应变的概念。
答案:应力是指材料内部由于外力作用而产生的内部相互作用力,通常用单位面积上的力来表示。
应变则是指材料在受力后发生的形变程度,通常用形变与原始尺寸的比值来表示。
2. 描述弹性力学中的胡克定律,并说明其适用范围。
答案:胡克定律是描述线性弹性材料应力与应变之间关系的定律,它指出在弹性范围内,材料的应力与应变成正比。
胡克定律的适用范围是材料处于弹性阶段,即材料的应变在很小的范围内,且材料未发生永久变形。
3. 弹性力学中的泊松比有何意义?请举例说明。
答案:泊松比是描述材料在受到拉伸或压缩时,横向应变与纵向应变之比的物理量。
它反映了材料在受力时的侧向膨胀或收缩特性。
本科弹性力学试题及答案

本科弹性力学试题及答案一、选择题(每题2分,共20分)1. 弹性力学中,下列哪一项不是基本假设?A. 连续性假设B. 均匀性假设C. 各向异性假设D. 小变形假设答案:C2. 在弹性力学中,下列哪一项不是应力的类型?A. 正应力B. 剪应力C. 拉应力D. 弯应力答案:D3. 弹性模量E和泊松比μ之间存在以下哪种关系?A. E = 2G(1+μ)B. E = 3G(1-2μ)C. E = 3G(1+μ)D. E = 2G(1-μ)答案:C4. 弹性力学中的圣维南原理适用于以下哪种情况?A. 仅适用于平面应力问题B. 仅适用于平面应变问题C. 适用于平面应力和平面应变问题D. 不适用于任何情况答案:C5. 弹性力学中,下列哪一项不是位移场的基本方程?A. 几何方程B. 物理方程C. 运动方程D. 边界条件答案:D6. 弹性力学中,下列哪一项不是平面应力问题的特点?A. 应力分量σz=0B. 应变分量εz≠0C. 应力分量τxz=τyz=0D. 应变分量γxz=γyz=0答案:B7. 弹性力学中,下列哪一项不是平面应变问题的特点?A. 应力分量σz≠0B. 应变分量εz=0C. 应力分量τxz=τyz=0D. 应变分量γxz=γyz=0答案:A8. 弹性力学中,下列哪一项不是应力集中的类型?A. 几何不连续引起的应力集中B. 材料不连续引起的应力集中C. 载荷不连续引起的应力集中D. 温度不连续引起的应力集中答案:D9. 弹性力学中,下列哪一项不是弹性常数?A. 杨氏模量EB. 泊松比μC. 剪切模量GD. 体积模量K答案:D10. 弹性力学中,下列哪一项不是弹性体的基本性质?A. 均匀性B. 连续性C. 各向同性D. 各向异性答案:D二、填空题(每题2分,共20分)1. 弹性力学中,应力状态的基本方程包括______、______和______。
答案:几何方程、物理方程、平衡方程2. 弹性力学中,应变能密度W与应力分量和应变分量的关系为W=______。
弹性力学复习题参考答案(部分)

x cos xy sin 1 gy cos y sin xy cos 1 gy sin 右边界, l cos , m sin , y x cot x cos xy sin 0 y sin + xy cos 0
h 2 x x0 dy FN , h 2 x x0 ydy M , h 2 xy x0 dy FS
h 2 h 2
在次要边界 x l 上,有位移边界条件: u xl 0 , v xl 0 。这两个位移边界条件可以改用三个积 分的应力边界条件代替:
(2) ra
0
a
b
a
b b dr P cos ; r dr P sin ; rdr P cos a b a
2
17、解: (1)相容条件:将 cxy 代入相容方程
3
2 2 2 4 0 ,显然满足。 4 y x y x
严格;近似 位移单值条件 零 平衡微分方程;应力表达的相容方程;边界上的应力边界条件 -2 -2 -1 -2 -1 -2 L MT ;L MT ;沿坐标轴正向;L MT ;正面正向、负面负向为正,反之为负 集中性;局部性 外法线方向沿坐标轴正向;外法线方向沿坐标轴负向 结构离散化;单元分析;整体分析 原荷载与结点荷载在任意虚位移上的虚功相等。 把环绕某一结点的个单元中的常量应力加以平均用来表征该结点处的应力;把相邻两单元的常量 应力加以平均用来表征公共边中点处的应力。 20、 当 i 结点发生单位位移时在 j 结点引起的结点力;形状;方位;弹性常数;位置。 21、 减小单元尺寸;采用更高次的单元。 22、 几何形状;应力边界条件 23、 差分法;变分法;有限单元法。 三、简答题 1、 答:弹性力学中主要引用的五个基本假定及各假定用途为: 1)连续性假定:引用这一假定后,物体中的应力、应变和位移等物理量就可看成是连续的,因此, 建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。 2)完全弹性假定:这一假定包含应力与应变成正比的含义,亦即二者呈线性关系,复合胡克定律, 从而使物理方程成为线性的方程。 3)均匀性假定:在该假定下,所研究的物体内部各点的物理性质显然都是相同的。因此,反应这些 物理性质的弹性常数(如弹性模量 E 和泊松比μ等)就不随位置坐标而变化。 4)各向同性假定:各向同性是指物体的物理性质在各个方向上都是相同的,也就是说,物体的弹性 常数也不随方向变化。 5)小变形假定:研究物体受力后的平衡问题时,不用考虑物体尺寸的改变,而仍然按照原来的尺寸 和形状进行计算。同时,在研究物体的变形和位移时,可以将它们的二次幂或乘积略去不计,使得弹性力 学的微分方程都简化为线性微分方程。 2、 详见课本。 3、 略 4、 答:弹性力学分析问题,要从 3 方面来考虑:静力学方面、几何学方面、物理学方面。平面问题的静 力学方面主要考虑的是应力分量和体力分量之间的关系也就是平面问 题的平衡微分方程。 平面问
《弹性力学及有限单元法》期末考试试卷及答案(1)
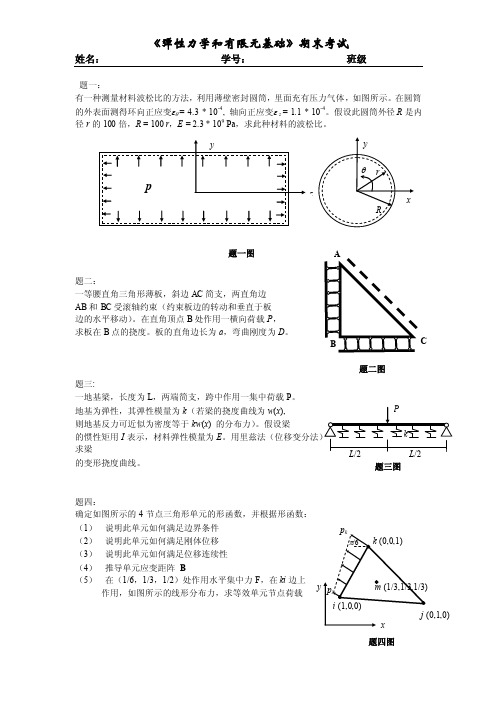
题一:有一种测量材料波松比的方法,利用薄壁密封圆筒,里面充有压力气体,如图所示。
在圆筒的外表面测得环向正应变εθ= 4.3 * 10-4, 轴向正应变ε z= 1.1 * 10-4。
假设此圆筒外径R是内径r的100倍,R = 100 r,E = 2.3 * 109 Pa,求此种材料的波松比。
题二:一等腰直角三角形薄板,斜边AC简支,两直角边AB和BC受滚轴约束(约束板边的转动和垂直于板边的水平移动)。
在直角顶点B处作用一横向荷载P,求板在B点的挠度。
板的直角边长为a,弯曲刚度为D。
题三:一地基梁,长度为L,两端简支,跨中作用一集中荷载P。
地基为弹性,其弹性模量为k(若梁的挠度曲线为w(x),则地基反力可近似为密度等于kw(x) 的分布力)。
假设梁的惯性矩用I表示,材料弹性模量为E求梁的变形挠度曲线。
题四:确定如图所示的4节点三角形单元的形函数,并根据形函数:(1)说明此单元如何满足边界条件(2)说明此单元如何满足刚体位移(3)说明此单元如何满足位移连续性(4)推导单元应变距阵B(5)在(1/6,1/3,1/2)处作用水平集中力F,在ki边上作用,如图所示的线形分布力,求等效单元节点荷载z题一图题二图题三图题四图试题答案题一:由于R >> t ,可以假设σz 沿厚度方向均匀分布。
设内压强为p ,则:Rtpr z 22=σ 由轴对称圆筒的应力计算公式可得:)~0(112222p p r R R -=---=ρσρ;p Rtr p rR R 2222211=-+=ρσφ由于σz ,σφ和远大于σρ,所以σρ可假设为0。
由虎克定律:()φσσεv E z z -=1;()z v Eσσεφφ-=1,再加上z σσφ2=可推导出:zzv εεεεφφ--=22=0.28题二:由对称性可知,所求的B 点挠度即为四边简直方板的中心点的挠度,方板的边长为a 2,在中心位置受到的横向集中力为4F 。
三角级数解为;()∑∑∑∑∞=∞=∞=∞=+=⎪⎪⎭⎫⎝⎛+=..5,3,1,...5,3,1222211222222224132222sin 2sin 216m n m n nmD Faa n a m n m D a Fw ππππ题三:设梁的挠度为:∑∞==1sinm m lxm B w π,此挠度曲线满足边界条件。
弹性力学期末考试卷及答案

名词解释(共10分,每小题5分)1.弹性力学:研究弹性体由于受外力作用或温度改变等原因而发生的应力、应变和位移。
2. 圣维南原理:如果把物体的一小部分边界上的面力,变换为分布不同但静力等效的面力(主矢量相同,对于同一点的主矩也相同),那么近处的应力分布将有显著的改变,但是远处所受的影响可以不计。
一. 填空(共20分,每空1分)1.边界条件表示在边界上位移与约束,或应力与面力之间的关系式,它可以分为位移边界条件、应力边界条件和混合边界条件。
2.体力是作用于物体体积内的力,以单位体积力来度量,体力分量的量纲为L-2MT-2;面力是作用于物体表面上力,以单位表面面积上的力度量,面力的量纲为L-1MT-2;体力和面力符号的规定为以沿坐标轴正向为正,属外力;应力是作用于截面单位面积的力,属内力,应力的量纲为L-1MT-2,应力符号的规定为:正面正向、负面负向为正,反之为负。
3.小孔口应力集中现象中有两个特点:一是孔附近的应力高度集中,即孔附近的应力远大于远处的应力,或远大于无孔时的应力。
二是应力集中的局部性,由于孔口存在而引起的应力扰动范围主要集中在距孔边1.5倍孔口尺寸的范围内。
4. 弹性力学中,正面是指外法向方向沿坐标轴正向的面,负面是指外法向方向沿坐标轴负向的面。
5. 利用有限单元法求解弹性力学问题时,简单来说包含结构离散化、单元分析、整体分析三个主要步骤。
二. 绘图题(共10分,每小题5分)分别绘出图3-1六面体上下左右四个面的正的应力分量和图3-2极坐标下扇面正的应力分量。
图3-1图3-2三. 简答题(24分)1. (8分)弹性力学中引用了哪五个基本假定?五个基本假定在建立弹性力学基本方程时有什么用途?答:弹性力学中主要引用的五个基本假定及各假定用途为:(答出标注的内容即可给满分)1)连续性假定:引用这一假定后,物体中的应力、应变和位移等物理量就可看成是连续的,因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
弹性力学期末考试试题及答案

弹性力学期末考试试题及答案一、选择题(每题2分,共20分)1. 下列哪种材料不具有弹性特性?A. 钢材B. 橡胶C. 水泥D. 玻璃答案:C2. 弹性力学中的胡克定律描述了什么关系?A. 应力与应变的关系B. 应力与位移的关系C. 应变与位移的关系D. 应力与应变能的关系答案:A3. 在弹性力学中,下列哪个物理量表示单位体积内的应变能?A. 应力B. 应变C. 应变能密度D. 弹性模量答案:C4. 下列哪个物理量表示材料的抗拉强度?A. 弹性模量B. 泊松比C. 屈服强度D. 抗拉强度答案:D5. 在弹性力学中,下列哪个物理量表示单位长度上的位移?A. 应变B. 位移C. 位移梯度D. 位移矢量答案:C二、填空题(每题2分,共20分)1. 胡克定律表达式为:σ = Eε,其中σ表示____,E 表示____,ε表示____。
答案:应力、弹性模量、应变2. 在三维应力状态下,应力张量的分解表达式为:σ = σ_0 + σ_1 + σ_2,其中σ_0表示____,σ_1表示____,σ_2表示____。
答案:平均应力、最大切应力、最小切应力3. 下列物理量中,表示单位体积内应变能的物理量为____。
答案:应变能密度4. 在弹性力学中,泊松比μ表示____与____的比值。
答案:横向应变、纵向应变5. 在弹性力学中,下列物理量中与应力状态无关的是____。
答案:位移三、计算题(每题20分,共60分)1. 已知一矩形截面梁,截面尺寸为10cm×20cm,受到均匀分布载荷q=10kN/m,求梁的弯曲应力σ和挠度w。
答案:σ = 5MPa,w = 0.0025m2. 一根长为2m的杆件,弹性模量E=200GPa,泊松比μ=0.3,两端受到轴向拉力F=100kN,求杆件的伸长量Δl。
答案:Δl = 0.005m3. 一圆形截面杆,直径d=10cm,受到扭矩M=2kN·m,弹性模量E=200GPa,泊松比μ=0.3,求杆件的扭转角φ。
弹性力学试题及答案

一、选择题1. 在弹性力学中,下列哪个物理量表示应变能密度?A. 应力B. 应变C. 位移D. 应力能密度答案:D2. 在平面应力状态下,下列哪个方程是正确的?A. σx + σy = 0B. σx + σy = σzC. σx + σy = τxyD. σx + σy = 0答案:A3. 在弹性体中,应力与应变之间的关系可以用下列哪个关系式表示?A. σ = EεB. σ = GγC. τ = μγD. σ = λε答案:A4. 在弹性力学中,下列哪个方程表示平衡方程?A. σij,j = PiB. εij = (σij + σji) / 2C. τ = GγD. σ = Eε答案:A5. 弹性力学中的胡克定律描述的是:A. 应力与位移的关系B. 应力与应变的关系C. 应变与位移的关系D. 位移与力的关系答案:B6. 以下哪个不是弹性力学的基本假设?A. 连续性假设B. 均匀性假设C. 各向同性假设D. 各向异性假设答案:D7. 弹性模量和泊松比的关系是:A. E = 2G(1+ν)B. E = 3K(1-2ν)C. E = 3K(1+ν)D. E = 2G(1-ν)答案:D8. 以下哪种材料可以看作是各向同性材料?A. 木材B. 钢筋混凝土C. 单晶硅D. 多晶硅答案:D9. 应力集中现象通常发生在:A. 均匀受力区域B. 截面突变处C. 材料内部均匀区D. 外部载荷作用点答案:B10. 如果一个物体受到均匀分布的压力作用,则其内部的应力状态为:A. 单向应力状态B. 平面应力状态C. 三向应力状态D. 纯剪应力状态答案:C二、填空题11. 弹性力学中的最小势能原理等价于弹性力学基本方程中的_________。
答案:平衡微分方程12. 一组可能的应力分量应满足:_________,相容方程(变形协调条件)。
答案:平衡微分方程13. 等截面直杆扭转问题中,应力函数的物理意义是杆端截面上剪应力对转轴的矩等于_________。
弹性力学复习题期末考试集锦 (2)

弹性力学复习题(06水工本科)一、选择题1. 下列材料中,()属于各向同性材料。
A. 竹材;B. 纤维增强复合材料;C. 玻璃钢;D. 沥青。
2 关于弹性力学的正确认识是()。
A. 计算力学在工程结构设计的中作用日益重要;B. 弹性力学从微分单元体入手分析弹性体,与材料力学不同,不需要对问题作假设;C. 任何弹性变形材料都是弹性力学的研究对象;D. 弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析。
3. 弹性力学与材料力学的主要不同之处在于()。
A. 任务;B. 研究对象;C. 研究方法;D. 基本假设。
4. 所谓“完全弹性体”是指()。
A. 材料应力应变关系满足胡克定律;B. 材料的应力应变关系与加载时间历史无关;C. 本构关系为非线性弹性关系;D. 应力应变关系满足线性弹性关系。
5. 所谓“应力状态”是指()。
A. 斜截面应力矢量与横截面应力矢量不同;B. 一点不同截面的应力随着截面方位变化而改变;C. 3个主应力作用平面相互垂直;D. 不同截面的应力不同,因此应力矢量是不可确定的。
6. 变形协调方程说明()。
A. 几何方程是根据运动学关系确定的,因此对于弹性体的变形描述是不正确的;B. 微分单元体的变形必须受到变形协调条件的约束;C. 变形协调方程是保证所有弹性体变形协调条件的必要和充分条件;D. 变形是由应变分量和转动分量共同组成的。
7. 下列关于弹性力学基本方程描述正确的是()。
A. 几何方程适用小变形条件;B. 物理方程与材料性质无关;C. 平衡微分方程是确定弹性体平衡的唯一条件;D. 变形协调方程是确定弹性体位移单值连续的唯一条件;8、弹性力学建立的基本方程多是偏微分方程,最后需结合()求解这些微分方程,以求得具体问题的应力、应变、位移。
A .几何方程B .边界条件C .数值方法D .附加假定9、弹性力学平面问题的求解中,平面应力问题与平面应变问题的三类基本方程具有下列关系 ( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h 2
x x 0
dy FN ,
x x0 ydy M , h 2 xy x 0 dy FS h 2
h 2
h 2
在次要边界 x l 上,有位移边界条件: u x l 0 , v xl 0 。这两个位移边界条件可以改用三 个积分的应力边界条件代替:
图 5-1 解:在主要边界 y h 2 上,应精确满足下列边界条件:
h 2
y y h 2
qx l , yx
y h 2
0;
y y h 2
0 , yx
y h 2
q1
在次要边界 x 0 上,应用圣维南原理列出三个积分的应力边界条件,当板厚 1 时,
2 y 2
2 f x , 0 对 x 积分,得 2 y y
(a) (b)
yf x f1 x 。
其中 f x , f1 x 都是 x 的待定函数。 (3)由相容方程求解应力函数。将式(b)代入相容方程 4 0 ,得
2
ql h 2 x x0 dy FN q1l , h 2 x x0 ydy M FS l
h 2
h 2
6
h 2 qlh ql , xy x0 dy FS h 2 2 2
2. (10 分)试考察应力函数 cxy 3 , c 0 ,能满足相容方程,并求出应力分量(不计体力) ,画出 图 5-2 所示矩形体边界上的面力分布,并在次要边界上表示出面力的主矢和主矩。
共 6 页 第 3 页
在次要边界 x 0, x l 上,面力的主失和主矩为
h 2 dy h 26clydy 0 h 2 dy 0 h 2 h 2 x xl h 2 x x0 h 2 h 2 h 2 clh 3 2 y dy 0 h 2 x x0 h 2 x xl ydy h 2 6cly dy 2 h 2 h 2 h 2 h 2 c xy x0 dy h 2 3cy 2 dy h3 xy x0 dy h 2 3cy 2 dy c h3 h 2 h 2 4 4 弹性体边界上的面力分布及在次要边界 x 0, x l 上面力的主失量和主矩如解图所示。
d 4 f x d 4 f1 x y 0 dx 4 dx 4
这是 y 的一次方程,相容方程要求它有无数多的根(全部竖柱内的 y 值都应该满足) ,可见它的
共 6 页 第 4 页
系数和自由项都必须等于零。
d 4 f x d 4 f1 x 0 , 0 ,两个方程要求 dx 4 dx 4
共 6 页 第 2 页
4
l x m yx s f x m y l xy s f y
在s s 上
(3)若为多连体,还须满足位移单值条件。 四. 问答题(36) 1. (12 分)试列出图 5-1 的全部边界条件,在其端部边界上,应用圣维南原理列出三个积分的应力边界 条件。 (板厚 1 )
共
6
页
第 6 页
(4)由应力函数求应力分量。
(d)
x
2 xf x 0 , y 2
(e)
2 y 2 yf y 6 Axy 2 By 6 Dx 2 E gy , x
(f)
xy
2 3 Ax 2 2 Bx C . xy
2. 体力是作用于物体体积内的力,以单位体积力来度量,体力分量的量纲为 L-2MT-2 ;面力是 -1 -2 作用于物体表面上力,以单位表面面积上的力度量,面力的量纲为 L MT ;体力和面力符号 的规定为以 沿坐标轴正向 为正,属 外 力;应力是作用于截面单位面积的力,属 内 力,应 力的量纲为 L-1MT-2 ,应力符号的规定为: 正面正向、负面负向为正,反之为负 。 3. 小孔口应力集中现象中有两个特点: 一是 孔附近的应力高度集中 远处的应力,或远大于无孔时的应力。二是 应力集中的局部性 的应力扰动范围主要集中在距孔边 1.5 倍孔口尺寸的范围内。 4. 弹性力学中,正面是指 的面 。 5. 外法向方向沿坐标轴正向 的面,负面是指 结构离散化 、 , 即孔附近的应力远大于 ,由于孔口存在而引起 外法向方向沿坐标轴负向 单元分析 、
(g)
(5) 考察边界条件。利用边界条件确定待定系数 先来考虑左右两边 x b 2 的主要边界条件:
x xb 2 0 , xy x b 2 0 , xy x b 2 q 。
将应力分量式(e)和(g)代入,这些边界条件要求:
x xb 2 0 ,自然满足;
b 2
y 0
dx
b 2
b 2
6 Dx 2 E dx 2 Eb 0 ;
3
得
E0
b 2 y
b 2
b 2
y 0
xdx
Db 6 Dx 2 E xdx b 2
b 2
2
0,
得
D0
q Ab3 2 3 Ax x C dx bC 0 b 2 xy y0 dx b 2 b 4
图 5-2 解: (1)相容条件:将 cxy 代入相容方程 (2)应力分量表达式: x
3
4 4 2 0 ,显然满足。 x 4 x 2y 2 y 4
4
2 6cxy , y 0 , xy 3cy 2 y 2 h 3 (3)边界条件:在主要边界 y 上,即上下边,面力为 y y h 2 3chx , xy y h 2 ch 2 2 4
xy x b 2
3 2 Ab Bb C 0 4
(h)
xy x b 2
3 2 Ab Bb C q 4 B q 2b
(i)由(h) (i)得(j)考察次要边界 y 0 的边界条件,应用圣维南原理,三个积分的应力边界条件为
b 2 y
名词解释(共 10 分,每小题 5 分) 1. 弹性力学:研究弹性体由于受外力作用或温度改变等原因而发生的应力、应变和位移。 2. 圣维南原理:如果把物体的一小部分边界上的面力,变换为分布不同但静力等效的面力(主矢量相同, 对于同一点的主矩也相同) ,那么近处的应力分布将有显著的改变,但是远处所受的影响可以不计。 一. 填空(共 20 分,每空 1 分) 1. 边界条件表示在边界上 位移 与 分为 位移 边界条件、 应力 约束 ,或 边界条件和 应力 与 面力 混合 边界条件。 之间的关系式,它可以
利用有限单元法求解弹性力学问题时,简单来说包含 整体分析 三个主要步骤。
二. 绘图题(共 10 分,每小题 5 分) 分别绘出图 3-1 六面体上下左右四个面的正的应力分量和图 3-2 极坐标下扇面正的应力分量。
图 3-1
共
6
页
第 1 页
图 3-2 三. 简答题(24 分) 1. (8 分)弹性力学中引用了哪五个基本假定?五个基本假定在建立弹性力学基本方程时有什么用途? 答:弹性力学中主要引用的五个基本假定及各假定用途为: (答出标注的内容即可给满分) 1)连续性假定:引用这一假定后,物体中的应力、应变和位移等物理量就可看成是连续的,因此, 建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。 2)完全弹性假定:这一假定包含应力与应变成正比的含义,亦即二者呈线性关系,复合胡克定律, 从而使物理方程成为线性的方程。 3)均匀性假定:在该假定下,所研究的物体内部各点的物理性质显然都是相同的。因此,反应这些 物理性质的弹性常数(如弹性模量 E 和泊松比μ等)就不随位置坐标而变化。 4)各向同性假定:各向同性是指物体的物理性质在各个方向上都是相同的,也就是说,物体的弹性 常数也不随方向变化。 5)小变形假定:研究物体受力后的平衡问题时,不用考虑物体尺寸的改变,而仍然按照原来的尺寸 和形状进行计算。同时,在研究物体的变形和位移时,可以将它们的二次幂或乘积略去不计,使得弹性力 学的微分方程都简化为线性微分方程。 2. (8 分)弹性力学平面问题包括哪两类问题?分别对应哪类弹性体?两类平面问题各有哪些特征? 答:弹性力学平面问题包括平面应力问题和平面应变问题两类,两类问题分别对应的弹性体和特征分 别为: 平面应力问题:所对应的弹性体主要为等厚薄板,其特征是:面力、体力的作用面平行于 xy 平面,外 力沿板厚均匀分布,只有平面应力分量 x , y , xy 存在,且仅为 x,y 的函数。 平面应变问题:所对应的弹性体主要为长截面柱体,其特征为:面力、体力的作用面平行于 xy 平面, 外力沿 z 轴无变化,只有平面应变分量 x , y , xy 存在,且仅为 x,y 的函数。 3. (8 分)常体力情况下,按应力求解平面问题可进一步简化为按应力函数 求解,应力函数 必须满 足哪些条件? 答: (1)相容方程: 0 (2)应力边界条件(假定全部为应力边界条件, s s ) :
b 2
(k)
由(h) (j) (k)得
A
q , b2
C
q 4
将所得 A、B、C、D、E 代入式(e) (f) (g)得应力分量为:
共
6
页
第 5 页
x 0 , y 6
q q q q q xy y gy , xy 3 2 x 2 x 2 b b b b 4
(c)
f x Ax 3 Bx 2 Cx , f1 x Dx 3 Ex 2
次和常数项,不影响应力分量。得应力函数
f x 中的常数项, f1 x 中的一次和常数项已被略去,因为这三项在 的表达式中成为 y 的一
