小波作业matlab程序
(完整word版)MATLAB小波变换指令及其功能介绍(超级有用)

MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能:一维离散小波变换格式:[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维 DFT说明:[cA,cD]=dwt(X,’wname’) 使用指定的小波基函数’wname’ 对信号X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数功能:一维离散小波反变换格式:X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明:X=idwt(cA,cD,’wname’) 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname’为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R)用指定的重构滤波器 Lo_R 和 Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,’wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L)指定返回信号 X 中心附近的 L 个点。
2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能—-————---—--—---——---—---—-—---—-——----——-----—————dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换—-----—-—-—-—-—-—--—-—-------—-——-—-————-———-—-——-——-—-----(1) wcodemat 函数功能:对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式:Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明:Y=wcodemat(X,NB,OPT,ABSOL)返回数据矩阵 X 的编码矩阵 Y ;NB 伪编码的最大值,即编码范围为 0~NB,缺省值 NB=16;OPT 指定了编码的方式(缺省值为 'mat'),即:别可以实现一维、二维和 N 维 DFTOPT='row’ ,按行编码OPT='col' ,按列编码OPT=’mat’ ,按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数(缺省值为’1'),即:ABSOL=0 时,返回编码矩阵ABSOL=1 时,返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的Matlab实现(2) dwt2 函数功能:二维离散小波变换格式:[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明:[cA,cH,cV,cD]=dwt2(X,'wname’)使用指定的小波基函数'wname’ 对二维信号 X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。
小波 matlab 代码

小波matlab 代码[x,map]=imread('MUCS_新建文件夹_32603.ptl_208.bmp');subplot(1,2,1);imshow(x);[c,s]=wavedec2(x,3,'sym4');Csize=size(c);for i=1:Csize(2)if(c(i)>100) %低频分量----s中第一维的长度c(i)=1*c(i);elsec(i)=0.9*c(i); %高频分量endendx1=waverec2(c,s,'sym4');im=uint8(x1);subplot(1,2,2);imshow(im);[c,s]=wavedec2(X,2,'bior3.7');%对图像用小波进行层分解cal=appcoef2(c,s,'bior3.7',1);%提取小波分解结构中的一层的低频系数和高频系数ch1=detcoef2('h',c,s,1);%水平方向cv1=detcoef2('v',c,s,1);%垂直方向cd1=detcoef2('d',c,s,1);%斜线方向a1=wrcoef2('a',c,s,'bior3.7',1);%各频率成份重构[c,s]=wavedec2(X,1,'sym4');a1=appcoef2(c,s,'sym4',1);%小波分解结构中的一层的低频系数,下面是3个高频系数a1=2*a1;h1=detcoef2('h',c,s,1);v1=detcoef2('v',c,s,1);d1=detcoef2('d',c,s,1);h1=0.5*h1;v1=0.5*v1;d1=0.5*d1;y=idwt2(a1,h1,v1,d1,'sym4');load wbarb;X1=X;map1=map;subplot(2,2,1);image(X1);colormap(map1);title('图像wbarb');load woman;X2=X;map2=map;subplot(2,2,2);image(X2);colormap(map2);title('图像woman');%===================================== %对上述二图像进行分解[c1,l1]=wavedec2(X1,2,'sym4');[c2,l2]=wavedec2(X2,2,'sym4');%对分解系数进行融合c=c1+c2;%===================================== %应用融合系数进行图像重构并显示XX=waverec2(c,l1,'sym4');subplot(2,2,3);image(XX);title('融合图像1');Csize1=size(c1);%=====================================%对图像进行增强处理for i=1:Csize1(2)c1(i)=1.2*c1(i);endCsize2=size(c2);for j=1:Csize2(2)c2(j)=0.8*c2(j);end%===================================== %通过减小融合系数以减小图像的亮度c=0.5*(c1+c2);%===================================== %对融合系数进行图像重构XXX=waverec2(c,l2,'sym4');%===================================== %显示重构结果subplot(2,2,4);image(XXX);title('融合图像2');%本程序实现下述功能:首先读入原始图像,并对它使用db3小波进行2层分解,%然后对分解系数进行处理突出所需,弱化不需要的部分%装载并显示原始图像clear all;clc;load flujet;subplot(1,2,1);image(X);colormap(map);title('原始图像');%=====================================%对图像X用小波db3进行2层分解[c,l]=wavedec2(X,2,'db3');Csize=size(c);%=====================================%对分解系数作处理以突出所需部分并弱化不需要部分for i=1:Csize(2)if(c(i)>300) %低频分量c(i)=2*c(i);elsec(i)=0.5*c(i); %高频分量endend%===================================== %重构图像并显示X1=waverec2(c,l,'db3');subplot(1,2,2);image(X1);colormap(map);title('增强图像');[c,s]=wavedec2(x,2,'sym4');Csize=size(c);for i=1:Csize(2)if(c(i)>169) %低频分量----s中第一维的长度c(i)=2*c(i);elsec(i)=0.3*c(i); %高频分量endendx1=waverec2(c,s,'sym4');im=uint8(x1);imshow(im);二维小波变换的Matlab 实现y j v z w %o u n\ { K*Y二维小波变换的函数a r T Q3Y r -------------------------------------------------5B Y0x!Z9a9] 函数名函数功能h$H9q ` \ ---------------------------------------------------'d3d t Be'x6gdwt2 二维离散小波变换!t2B!I9L5S;q:r X wavedec2 二维信号的多层小波分解!D o4B @2U Y,o!H#M l idwt2 二维离散小波反变换o l!R H N_ G4M waverec2 二维信号的多层小波重构z H!f6~)}-P _wrcoef2 由多层小波分解重构某一层的分解信号0E,\ |.o | D T2@2b2K$Uupcoef2 由多层小波分解重构近似分量或细节分量*^ Y4? T3R x(k3v detcoef2 提取二维信号小波分解的细节分量2~ U W L8V appcoef2 提取二维信号小波分解的近似分量0q l N7p a @ i Y C ] c b upwlev2 二维小波分解的单层重构2y W_ ] h-i~ m(~ dwtpet2 二维周期小波变换4Y/aN&G q ] E B"H)Widwtper2 二维周期小波反变换7h"| Iv e -------------------------------------------------------------9O d7D ` b y&lX { I g u s I `(1) wcodemat 函数` T f ?-[ c*e$M c d 功能:对数据矩阵进行伪彩色编码|4X C i5R$x6g 格式:Y=wcodemat(X,NB,OPT,ABSOL)'k#e C a I%HY=wcodemat(X,NB,OPT) i)E)p _!O-k j J ^Y=wcodemat(X,NB)A2z,q D'u'z*_.~/U Y=wcodemat(X)Z5D"^ e5i |L'^4` 说明:Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵X 的编码矩阵Y ;NB 伪编码的最大值,即编码范围为0~NB,缺省值NB=16;@ N6C Y p Y E OPT 指定了编码的方式(缺省值为'mat'),即:r(o ? L j(y e f NOPT='row' ,按行编码-y q i H { o5e OPT='col' ,按列编码8X N*\.Z/c @ OPT='mat' ,按整个矩阵编码e j!l W b L ABSOL 是函数的控制参数(缺省值为'1'),即:i x"^:| ~5{ABSOL=0 时,返回编码矩阵2z x;^ l$q | _ Z ABSOL=1 时,返回数据矩阵的绝对值ABS(X)V l U1e r g3x'O%I9z&c,A ]!T%y d s \.s (2) dwt2 函数D J ~0D/m S:O S"I 功能:二维离散小波变换 B c t _)h O X I格式:[cA,cH,cV,cD]=dwt2(X,'wname')3A N _ W F[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)m(E j"[ _ @ 说明:[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分.g(R @ E E Y'n 量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器Lo_D 和Hi_D 分j4F2} ~ Q e W 解信号X 。
MATLAB小波变换指令及其功能介绍(超级有用)解读

MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能:一维离散小波变换格式:[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维DFT说明:[cA,cD]=dwt(X,'wname') 使用指定的小波基函数 'wname'对信号X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数功能:一维离散小波反变换格式:X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明:X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname' 为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,'wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。
2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能---------------------------------------------------dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换----------------------------------------------------------- (1) wcodemat 函数功能:对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式:Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明:Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵 X 的编码矩阵Y ;NB 伪编码的最大值,即编码范围为 0~NB,缺省值 NB=16;OPT 指定了编码的方式(缺省值为 'mat'),即:别可以实现一维、二维和 N 维 DFTOPT='row' ,按行编码OPT='col' ,按列编码OPT='mat' ,按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数(缺省值为 '1'),即:ABSOL=0 时,返回编码矩阵ABSOL=1 时,返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的 Matlab实现(2) dwt2 函数功能:二维离散小波变换格式:[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明:[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号 X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。
小波分析中matlab阈值获取函数及其应用附程序代码

⼩波分析中matlab阈值获取函数及其应⽤附程序代码1、⼩波分析中MATLAB阈值获取函数MATLAB中实现阈值获取的函数有ddencmp、thselect、wbmpen和wwdcbm,下⾯对它们的⽤法进⾏简单的说明。
⼀、ddencmp的调⽤格式有以下三种:(1)[THR,SORH,KEEPAPP,CRIT]=ddencmp(IN1,IN2,X)(2)[THR,SORH,KEEPAPP,CRIT]=ddencmp(IN1,'wp',X)(3)[THR,SORH,KEEPAPP,CRIT]=ddencmp(IN1,'wv',X)函数ddencmp⽤于获取信号在消噪或压缩过程中的默认阈值。
输⼊参数X 为⼀维或⼆维信号;IN1取值为'den'或'cmp','den'表⽰进⾏去噪,'cmp'表⽰进⾏压缩;IN2取值为'wv'或'wp',wv表⽰选择⼩波,wp表⽰选择⼩波包。
返回值THR是返回的阈值;SORH是软阈值或硬阈值选择参数;KEEPAPP表⽰保存低频信号;CRIT是熵名(只在选择⼩波包时使⽤)。
例题1:clear allclcload noisbump;x=noisbump;[c,l]=wavedec(x,5,'sym6'); %对⼩波进⾏5层分解[thr,sorh,keepapp]=ddencmp('den','wv',x)xd=wdencmp('gbl',c,l,'sym6',5,thr,sorh,keepapp);%显⽰降噪信号subplot(211),plot(x),title('x','fontsize',10);subplot(212),plot(xd),title('xd','fontsize',10);xxdthr =3.7856;sorh =s;keepapp=1.Err=39.3060⼆、函数wbmpen的调⽤格式如下:THR=wbmpen(C,L,SIGMA,ALPHA);THR=wbmpen(C,L,SIGMA,ALPHA)返回去噪的全局阈值THR。
小波变换的matlab实现

举例: A1=upcoef('a','cA1','db1',1,ls); D1=upcoef('d','cD1','db1',1,ls);
subplot(1,2,1);plot(A1);title('Approximation A1')
subplot(1,2,2);plot(D1);title('Detail D1')
重构原始信号
*
2D图形接口
*
显示
*
小波分析用于信号处理
01
信号的特征提取
信号处理
常用信号的小波分析
GUI进行信号处理
*
正弦波的线性组合
S(t)=sin(2t)+sin(20t)+sin(200t)
*
2019
间断点检测
01
2020
波形未来预测
02
2021
各分信号的频率识别
03
2022
信号从近似到细节的迁移
*
多尺度二维小波
命令:wavedec2
格式: [C, S]=wavedec2(X,N,’wname’) [C, S]=wavedec2(X,N,Lo_D,Hi_D)
*
[C,S] = wavedec2(X,2,'bior3.7'); %图像的多尺度二维小波分解
提取低频系数
命令:appcoef2 格式: 1. A=appcoef2(C,S,’wname’,N) 2. A=appcoef2(C,S,’wname’) 3. A=appcoef2(C,S,Lo_R,Hi_R) 4. A=appcoef2(C,S,Lo_R,Hi_R,N) cA2 = appcoef2(C,S,'bior3.7',2); %从上面的C中提取第二层的低频系数
小波分析信号处理matlab

时间采样频率是频谱信号的信号周期 频率离散间隔对应时间信号的信号同期
15
2. f(t) 的频谱(线频谱)
f(t)分解为傅氏级数后包含哪些频率分量和各分量所占“比重 ”用长度与各次谐波振幅大小相对应的线段进行表示,并按频率的 高低把它们依次排列起来所得到的图形,称为 f(t) 的频谱。
幅度 X(k)谱 X : R 2(k)XI2(k)
相位谱 (k): arcXtI(g k)
XR(k)
利用 FFT 进行频谱分析的实现过程框图为:
17
离散时间、连续频率—序列的傅里叶变换
X(ej) x(n)ejn n
x(n)21 X(ej)ejnd
时域的离散化造成频域的周期 延拓,而时域的非周期对应于 频域的连续
小波分析信号处理matlab
Linear space(线性空间)
S is a set, if a S and b S a+b S ( 加法满足对称性、交换律和结合律)
R(or C), a S a S
(数乘满足结合律和分配律,有0元) We call S a linear space.
Y=kx与y=kx+b
(标准正交系 ), alsocalledorthonormalsystem.
7
Basis(基)
xk is a subset of Hilbert space X, if
1. x X , x ck xk where ck are numbers 线性表出 2. ck xk 0 ck 0 线性无关向量
28
小波分析在一维信号处理中的应用
小波变换就是将 “ 原始信号 s ” 变换 成 “ 小波 系数 w ” ,w=[wa , wd] 包括近似(approximation)系数wa 与细节(detail)系数wd 近似系数wa---平均成分(低频) 细节系数wd---变化成分(高频)
小波去噪matlab程序代码

axis square %产生含噪声图像 init = 2055615866; randn(seed,init); x = X + 50*randn(size(X) ); subplot(2,2,2);image(x); colormap(map); xlabel((b)含噪声图像);
%对三个方向高频系数进行阈值处理 nc = wthcoef2(h,c,s,n,p,s); nc = wthcoef2(v,nc,s,n,p,s); nc = wthcoef2(d,nc,s,n,p,s); %对新的小波分解结构[c,s]进行重构 x1 = wavee(x1); colormap(map);
小波去噪 matlab 程序代码
1、小波去噪实现步骤 (1)二维信号的小波分解。选择一个小波和小波分解的层次 N,然后计 算信号 s 到第 N 层的分解。 (2)对高频系数进行阈值量化。对于从 1~N 的每一层,选择一个阈值, 并对这一层的高频系数进行软阈值量化处理。 (3)二维小波重构。根据小波分解的第 N 层的低频系数和经过修改的从 第一层到第 N 的各层高频系数,计算二维信号的小波重构 2、Matlab 函数介绍 (1)wavedec2 函数 该函数用于对多尺度二维小波进行分解,其常用调用格式:
xlabel((c)第一次去噪图像); axis square %对 nc 再次进行滤波去噪 xx = wthcoef2(v,nc,s,n,p,s); x2 = waverec2(xx,s,coif3); subplot(2,2,4);image(x2); colormap(map); xlabel((d)第二次去噪图像);
axis square《span style=font-size:14px》 《span style=font-size:14px》 《span style=font-size:18px; color:#3366ff》
matlab小波工具箱小波分析步骤
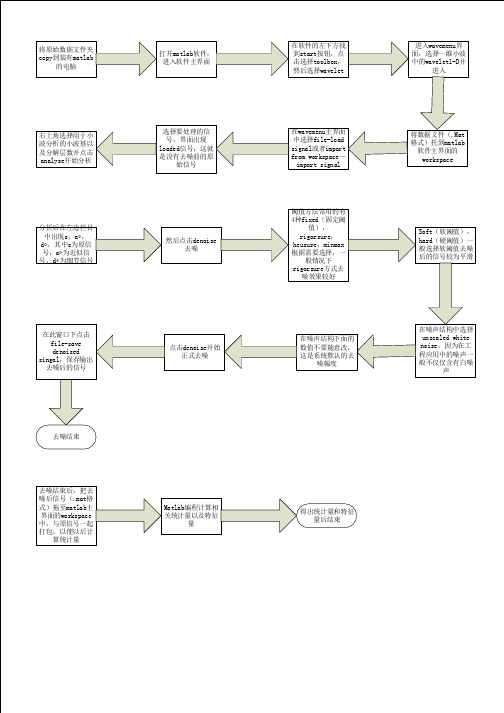
选择要处理的信 号,界面出现 loaded信号,这就 是没有去噪前的原 始信号
在wavemenu主界面 中选择file-load signal或者import from workspace— import signal
将数据文件(.Mat 格式)托到matlab 软件主界面的 workspace
分析后在左边栏目 中出现s,a*, d*,其中s为原信 号,a*为近似信 号,d*为细节信号
点击denoise开始 正式去噪
在噪声结构下面的 数值不要随意改, 这是系统默认的去 噪幅度
在噪声结构中选择 unscaled white noise,因为在工 程应用中的噪声一 般不仅仅含有白噪 声
去噪结束
去噪结束后,把去 噪后信号(.mat格 式)拖至matlab主 界面的workspace 中,与原信号一起 打包,以便以后计 算统计量
Matlab编程计算相 关统计量以及特征 量
得出统计量和特征 量后结束
将原始数据文件夹 copy到装有matlab 的电脑
打开matlab软件, 进入软件主界面
在软件的左下方找 到start按钮,点 击选择toolbox, 然后选择wavelet
Hale Waihona Puke 进入wavemenu界 面,选择一维小波 中的wavelet1-D并 进入
右上角选择用于小 波分析的小波基以 及分解层数并点击 analyse开始分析
然后点击denoise 去噪
阈值方法常用的有 4种fixed(固定阈 值), rigorsure, heusure,minmax 根据需要选择,一 般情况下 rigorsure方式去 噪效果较好
Soft(软阈值), hard(硬阈值)一 般选择软阈值去噪 后的信号较为平滑
matlab小波滤波器代码 -回复

matlab小波滤波器代码-回复在MATLAB中实现小波滤波器的代码,可以通过以下步骤来完成:第一步:导入信号数据在MATLAB中,首先需要导入待处理的信号数据。
可以使用`wavread`函数读取声音文件,或者使用`load`函数导入其他格式的数据。
matlab[data, fs] = wavread('sound.wav');这里`data`是读取到的信号数据,`fs`是采样率。
第二步:选择小波基函数小波滤波器通过对信号进行小波变换来实现滤波效果。
在MATLAB 中,可以选择不同的小波基函数进行变换。
常用的小波基函数包括`haar`、`dbN`(N是小波基的阶数)、`coifN`、`symN`等。
这里以`haar`小波基为例。
matlabwaveletName = 'haar';第三步:进行小波变换使用`wavedec`函数进行小波变换,将信号分解为多个尺度的小波系数。
matlab[level1, level2, level3, level4] = wavedec(data, 4, waveletName);这里将信号分解为4个尺度的小波系数,分别存储在`level1`、`level2`、`level3`和`level4`变量中。
第四步:滤波在小波变换后,可以对小波系数进行滤波操作。
可以通过设定一个阈值,将小波系数中小于该阈值的部分设为0,从而达到去噪的效果。
matlabthreshold = 0.5;level1(filteredLevel1 < threshold) = 0;level2(filteredLevel2 < threshold) = 0;level3(filteredLevel3 < threshold) = 0;level4(filteredLevel4 < threshold) = 0;这里使用了一个阈值为0.5的例子,小于该阈值的小波系数将被设为0。
matlab 小波变换时频

matlab 小波变换时频Matlab小波变换是一种在时频域中分析信号的方法。
它将信号划分为不同的频率区间,并在每个频率区间内进行时域分析。
这使得我们可以同时获得信号的时间和频率信息,从而更好地理解信号的特性。
在Matlab中,我们可以使用`cwt`函数来执行小波变换。
该函数需要输入待分析的信号和小波的类型以及其他参数。
在本文中,我们将逐步展示如何执行小波变换以及如何分析得到的时频表示。
首先,我们需要准备一个示例信号,以便进行小波变换。
假设我们有一个正弦信号,频率为10Hz,采样频率为1000Hz,持续时间为1秒。
可以使用以下代码生成这个信号:matlabfs = 1000; 采样频率为1000Hzt = 0:1/fs:1-1/fs; 时间向量,从0s到1sf = 10; 正弦信号频率为10Hzx = sin(2*pi*f*t); 生成正弦信号接下来,我们可以使用`cwt`函数进行小波变换。
我们可以选择不同的小波函数来适应信号的特性。
在这个例子中,我们选择使用'Morlet'小波函数。
可以使用以下代码执行小波变换:matlabscales = 1:64; 尺度向量,设置小波变换尺度coefs = cwt(x, scales, 'morl'); 执行小波变换在上述代码中,我们创建了一个尺度向量来定义小波变换的尺度范围。
在这个例子中,我们选择了1到64的尺度范围。
然后,我们使用`cwt`函数对信号进行小波变换,并指定了使用'Morlet'小波函数。
执行上述代码之后,我们将得到一个时频矩阵`coefs`,其中存储了小波变换的结果。
该矩阵的行数对应于尺度向量的长度,列数对应于信号的样本数。
为了更好地理解时频表示,我们可以绘制小波系数矩阵的图像。
可以使用以下代码将小波系数图像化:matlabimagesc(abs(coefs)); 绘制小波系数图像colormap jet; 使用彩虹色调来表示幅度colorbar; 添加颜色刻度在上述代码中,我们使用`imagesc`函数绘制小波系数的幅度图像。
(完整word版)MATLAB小波变换指令及其功能介绍(超级有用)

MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能:一维离散小波变换格式:[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维DFT说明:[cA,cD]=dwt(X,'wname') 使用指定的小波基函数 'wname'对信号X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数功能:一维离散小波反变换格式:X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明:X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname' 为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,'wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。
2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能---------------------------------------------------dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换----------------------------------------------------------- (1) wcodemat 函数功能:对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式:Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明:Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵 X 的编码矩阵Y ;NB 伪编码的最大值,即编码范围为 0~NB,缺省值 NB=16;OPT 指定了编码的方式(缺省值为 'mat'),即:别可以实现一维、二维和 N 维 DFTOPT='row' ,按行编码OPT='col' ,按列编码OPT='mat' ,按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数(缺省值为 '1'),即:ABSOL=0 时,返回编码矩阵ABSOL=1 时,返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的 Matlab实现(2) dwt2 函数功能:二维离散小波变换格式:[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明:[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号 X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。
matlab小波特征提取 -回复

matlab小波特征提取-回复Matlab小波特征提取小波变换是一种在信号处理中常用的技术,可以将信号在时域和频域之间进行转换。
在Matlab中,小波变换可以通过使用Wavelet Toolbox 来实现,该工具箱提供了一系列小波函数和工具,可以方便地进行小波分析和特征提取。
本文将详细介绍在Matlab中使用小波变换进行特征提取的方法和步骤。
我们将通过以下四个步骤来实现:1. 导入信号数据2. 选择合适的小波函数3. 进行小波分解4. 提取小波特征Step 1: 导入信号数据在Matlab中,我们可以使用`load`函数将信号数据从文件中导入到工作空间。
例如,如果信号数据保存在名为`signal_data.mat`的MAT文件中,我们可以使用以下代码将其导入:matlabload('signal_data.mat');导入信号数据后,我们可以使用`plot`函数来可视化信号,以便更好地了解其特征。
Step 2: 选择合适的小波函数在小波变换中,我们需要选择适合信号类型的小波函数。
Matlab的Wavelet Toolbox提供了一系列小波函数,如Daubechies、Haar、Coiflets等。
你可以根据你的信号类型和特征要求选择适当的小波函数。
例如,如果你的信号是离散的,并且你希望在分析中具有较好的低频和高频分辨率,那么Daubechies小波函数是一个不错的选择。
Step 3: 进行小波分解一旦你选择了适当的小波函数,就可以使用`wavedec`函数进行小波分解。
`wavedec`函数接受一个信号向量和小波函数作为输入,并返回小波系数和逼近系数。
matlab[coefficients, approximations] = wavedec(signal, level,'wname');其中,`signal`是输入信号,`level`是小波分解的层数,`wname`是选择的小波函数名称。
小波函数及Matlab常用指令

小波包分析能够更全面地揭示信号的细节特征,对于非平稳信号的处理效果尤为突出。此 外,小波包分析还可以根据实际需求选择合适的小波基函数,从而更好地满足信号处理的 需求。
小波包分析的应用
小波包分析在信号处理、图像处理、语音识别等领域有着广泛的应用。例如,在信号处理 中,小波包分析可以用于信号去噪、特征提取、故障诊断等;在图像处理中,小波包分析 可以用于图像压缩、图像增强、图像恢复等。
信号的小波重构是将小波分解后的系数重新组合成原始信号的 过程。
02
在Matlab中,可以使用`waverec`函数对小波系数进行重构,该
函数可以根据小波分解的层次和系数重建原始信号。
小波重构的结果可以用于验证小波分解的正确性和完整性,以
03
及评估去噪等处理的效果。
信号的小波去噪
信号的小波去噪是一种利用小波 变换去除信号中噪声的方法。
小波函数及Matlab常用指 令
• 小波函数简介 • Matlab中小波函数的常用指令 • Matlab中信号的小波分析 • Matlab中小波变换的应用实例 • Matlab中小波函数的进阶使用
01
小波函数简介
小波函数的定义
小波函数是一种特殊的函数,其时间频率窗口均有限,具有良好的局部化 特性。
金融数据分类与聚类
利用小波变换的特征提取能力,可以对金融数据进行分类或聚类, 用于市场趋势预测等。
05
Matlab中小波函数的进阶使用
小波包分析
小波包分析
小波包分析是一种更为精细的信号分析方法,它不仅对信号进行频域分析,还对信号进行 时频分析。通过小波包分析,可以更准确地提取信号中的特征信息,为信号处理提供更全 面的数据支持。
THANKS
小波变换matlab程序

小波变换matlab程序小波变换是一种信号处理技术,它可以将信号分解成不同频率的成分,并且可以在不同时间尺度上进行分析。
在Matlab中,可以使用内置的小波变换函数来实现这一技术。
下面是一个简单的小波变换Matlab程序示例:matlab.% 生成一个示例信号。
t = 0:0.001:1; % 时间范围。
f1 = 10; % 信号频率。
f2 = 50; % 信号频率。
y = sin(2pif1t) + sin(2pif2t); % 信号。
% 进行小波变换。
[c, l] = wavedec(y, 3, 'db1'); % 进行3层小波分解,使用db1小波基函数。
% 重构信号。
yrec = waverec(c, l, 'db1'); % 使用小波系数和长度进行信号重构。
% 绘制原始信号和重构信号。
subplot(2,1,1);plot(t, y);title('原始信号');subplot(2,1,2);plot(t, yrec);title('重构信号');这个程序首先生成了一个包含两个频率成分的示例信号,然后使用`wavedec`函数对信号进行小波分解,得到小波系数和长度。
接着使用`waverec`函数对小波系数和长度进行信号重构,最后绘制了原始信号和重构信号的对比图。
小波变换在信号处理、图像处理等领域有着广泛的应用,可以用于信号去噪、特征提取、压缩等方面。
通过Matlab中的小波变换函数,我们可以方便地进行小波分析和处理,从而更好地理解和利用信号的特性。
使用小波包变换分析信号的MATLAB程序

使用小波包变换分析信号的MATLAB程序,下面是使用小波包变换分析两个信号的特征向量和各频率成分的功率谱%t=0.001:0.001:1;t=1:1000;s1=sin(2*pi*50*t*0.001)+sin(2*pi*120*t*0.001)+rand(1,leng th(t));for t=1:500;s2(t)=sin(2*pi*50*t*0.001)+sin(2*pi*120*t*0.001)+rand(1,l ength(t));endfor t=501:1000;s2(t)=sin(2*pi*200*t*0.001)+sin(2*pi*120*t*0.001)+rand(1, length(t));endsubplot(9,2,1)plot(s1)title('原始信号')ylabel('S1')subplot(9,2,2)plot(s2)title('故障信号')ylabel('S2')wpt=wpdec(s1,3,'db1','shannon');%plot(wpt);s130=wprcoef(wpt,[3,0]);s131=wprcoef(wpt,[3,1]);s132=wprcoef(wpt,[3,2]);s133=wprcoef(wpt,[3,3]);s134=wprcoef(wpt,[3,4]);s135=wprcoef(wpt,[3,5]);s136=wprcoef(wpt,[3,6]);s137=wprcoef(wpt,[3,7]);s10=norm(s130);s11=norm(s131);s12=norm(s132);s13=norm(s133);s14=norm(s134);s15=norm(s135);s16=norm(s136);s17=norm(s137);st10=std(s130);st11=std(s131);st12=std(s132);st13=std(s133);st14=std(s134);st15=std(s135);st16=std(s136);st17=std(s137);disp('正常信号的特征向量');snorm1=[s10,s11,s12,s13,s14,s15,s16,s17]std1=[st10,st11,st12,st13,st14,st15,st16,st17]subplot(9,2,3);plot(s130);ylabel('S130');subplot(9,2,5);plot(s131);ylabel('S131');subplot(9,2,7);plot(s132);ylabel('S132');subplot(9,2,9);plot(s133);ylabel('S133');subplot(9,2,11);plot(s134);ylabel('S134');subplot(9,2,13);plot(s135);ylabel('S135');subplot(9,2,15);plot(s136);ylabel('S136');subplot(9,2,17);plot(s137);ylabel('S137');wpt=wpdec(s2,3,'db1','shannon');%plot(wpt);s230=wprcoef(wpt,[3,0]);s231=wprcoef(wpt,[3,1]);s232=wprcoef(wpt,[3,2]);s233=wprcoef(wpt,[3,3]);s234=wprcoef(wpt,[3,4]);s235=wprcoef(wpt,[3,5]);s236=wprcoef(wpt,[3,6]);s237=wprcoef(wpt,[3,7]);s20=norm(s230);s21=norm(s231);s22=norm(s232);s23=norm(s233);s24=norm(s234);s25=norm(s235);s26=norm(s236);s27=norm(s237);st20=std(s230);st21=std(s231);st22=std(s232);st23=std(s233);st24=std(s234);st25=std(s235);st26=std(s236);st27=std(s237);disp('故障信号的特征向量');snorm2=[s20,s21,s22,s23,s24,s25,s26,s27]std2=[st20,st21,st22,st23,st24,st25,st26,st27]subplot(9,2,4);plot(s230);ylabel('S230');subplot(9,2,6);plot(s231);ylabel('S231');subplot(9,2,8);plot(s232);ylabel('S232');subplot(9,2,10);plot(s233);ylabel('S233');subplot(9,2,12);plot(s234);ylabel('S234');subplot(9,2,14);plot(s235);ylabel('S235');subplot(9,2,16);plot(s236); ylabel('S236');subplot(9,2,18);plot(s237); ylabel('S237');%fftfigurey1=fft(s1,1024);py1=y1.*conj(y1)/1024;y2=fft(s2,1024);py2=y2.*conj(y2)/1024;y130=fft(s130,1024);py130=y130.*conj(y130)/1024; y131=fft(s131,1024);py131=y131.*conj(y131)/1024; y132=fft(s132,1024);py132=y132.*conj(y132)/1024; y133=fft(s133,1024);py133=y133.*conj(y133)/1024; y134=fft(s134,1024);py134=y134.*conj(y134)/1024; y135=fft(s135,1024);py135=y135.*conj(y135)/1024; y136=fft(s136,1024);py136=y136.*conj(y136)/1024; y137=fft(s137,1024);py137=y137.*conj(y137)/1024;y230=fft(s230,1024);py230=y230.*conj(y230)/1024; y231=fft(s231,1024);py231=y231.*conj(y231)/1024; y232=fft(s232,1024);py232=y232.*conj(y232)/1024; y233=fft(s233,1024);py233=y233.*conj(y233)/1024; y234=fft(s234,1024);py234=y234.*conj(y234)/1024; y235=fft(s235,1024);py235=y235.*conj(y235)/1024; y236=fft(s236,1024);py236=y236.*conj(y236)/1024; y237=fft(s237,1024);py237=y237.*conj(y237)/1024;f=1000*(0:511)/1024;subplot(1,2,1);plot(f,py1(1:512));ylabel('P1');title('原始信号的功率谱')subplot(1,2,2);plot(f,py2(1:512));ylabel('P2');title('故障信号的功率谱')figuresubplot(4,2,1);plot(f,py130(1:512));ylabel('P130');title('S130的功率谱')subplot(4,2,2);plot(f,py131(1:512));ylabel('P131');title('S131的功率谱')subplot(4,2,3);plot(f,py132(1:512));ylabel('P132');subplot(4,2,4);plot(f,py133(1:512));ylabel('P133');subplot(4,2,5);plot(f,py134(1:512));ylabel('P134');subplot(4,2,6);plot(f,py135(1:512));ylabel('P135');subplot(4,2,7);plot(f,py136(1:512));ylabel('P136');subplot(4,2,8);plot(f,py137(1:512)); ylabel('P137');figuresubplot(4,2,1);plot(f,py230(1:512)); ylabel('P230');title('S230的功率谱')subplot(4,2,2);plot(f,py231(1:512)); ylabel('P231');title('S231的功率谱')subplot(4,2,3);plot(f,py232(1:512)); ylabel('P232'); subplot(4,2,4);plot(f,py233(1:512)); ylabel('P233'); subplot(4,2,5);plot(f,py234(1:512)); ylabel('P234'); subplot(4,2,6);plot(f,py235(1:512)); ylabel('P235'); subplot(4,2,7);plot(f,py236(1:512)); ylabel('P236'); subplot(4,2,8);plot(f,py237(1:512)); ylabel('P237');figure%plottree(wpt)。
小波分析Matlab程序

1 绪论1.1概述小波分析是近15年来发展起来的一种新的时频分析方法。
其典型应用包括齿轮变速控制,起重机的非正常噪声,自动目标所顶,物理中的间断现象等。
而频域分析的着眼点在于区分突发信号和稳定信号以及定量分析其能量,典型应用包括细胞膜的识别,金属表面的探伤,金融学中快变量的检测,INTERNET 的流量控制等。
从以上的信号分析的典型应用可以看出,时频分析应用非常广泛,涵盖了物理学,工程技术,生物科学,经济学等众多领域,而且在很多情况下单单分析其时域或频域的性质是不够的,比如在电力监测系统中,即要监控稳定信号的成分,又要准确定位故障信号。
这就需要引入新的时频分析方法,小波分析正是由于这类需求发展起来的。
在传统的傅立叶分析中,信号完全是在频域展开的,不包含任何时频的信息,这对于某些应用来说是很恰当的,因为信号的频率的信息对其是非常重要的。
但其丢弃的时域信息可能对某些应用同样非常重要,所以人们对傅立叶分析进行了推广,提出了很多能表征时域和频域信息的信号分析方法,如短时傅立叶变换,Gabor 变换,时频分析,小波变换等。
其中短时傅立叶变换是在傅立叶分析基础上引入时域信息的最初尝试,其基本假定在于在一定的时间窗内信号是平稳的,那么通过分割时间窗,在每个时间窗内把信号展开到频域就可以获得局部的频域信息,但是它的时域区分度只能依赖于大小不变的时间窗,对某些瞬态信号来说还是粒度太大。
换言之,短时傅立叶分析只能在一个分辨率上进行。
所以对很多应用来说不够精确,存在很大的缺陷。
而小波分析则克服了短时傅立叶变换在单分辨率上的缺陷,具有多分辨率分析的特点,在时域和频域都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态动态调整,在一般情况下,在低频部分(信号较平稳)可以采用较低的时间分辨率,而提高频率的分辨率,在高频情况下(频率变化不大)可以用较低的频率分辨率来换取精确的时间定位。
因为这些特定,小波分析可以探测正常信号中的瞬态,并展示其频率成分,被称为数学显微镜,广泛应用于各个时频分析领域。
小波分析的应用及其MATLAB程序的实现

小波分析的应用及其MATLAB 程序的实现 摘要:在简单介绍小波分析的发展的基础上,对傅立叶变换和小波变换比较分析,介绍了小波分析在实际生活中的应用,重点阐述了MA 的应用研究现存的几个TLAB 小波分析信号处理的方法.分析了小波分析在故障诊断中问题,并对解决这些问题和未来的发展进行了探讨。
关键词:小波分析;信号处理;MATLAB1.引言故障诊断中的首要问题就是对观测信号的故障特征提取,即对观测信号进行信号处理,从中获取反映故障信息的特征。
由于故障诊断中所遇到的信号绝大多数都是非平稳信号,而特别适用于非平稳信号处理的工具就是小波分析,所以小波分析在故障诊断中的应用越来越受到人们的青睬。
小波变换的基本思想类似于傅立叶变换,小波分析优于博立叶之处在于它能够实现时域和频域的局部分析,即通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析,从而可以聚焦到信号的任意细节。
因此,小波变换被誉为分析信号的微镜。
现在,小波分析技术在信号处理、图像处理、语音分析、模识别、量子物理、生物医学工程、计算机视觉、故障诊断及众多非线性科学领域都有广泛的应用。
2、从傅立叶变换到小波变换小波分析属于时频分析的一种,传统的信号分析是建立在傅立叶变换的基础上的,由于傅立叶分析使用的是一种全局的变换,要么完全在时域,要么完全在时域,要么完全在频域,因此无法表述信号的时频局域性质,而这种性质恰恰是非平稳信号最根本和最关键的性质。
为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并发展了一系列新的信号分析理论:短时傅立叶变换、Gabor 变换、时频分析、小波变换、分数阶傅立叶变换、线调频小波变换、循环统计量理论和调幅-调频信号分析等。
其中,短时傅立叶变换和小波变换也是应传统的傅立叶变换不能够满足信号处理的要求而产生的。
短时傅立叶变换分析的基本思想是:假定非平稳信号在分析窗函数g (t )的一个短时间间隔内是平稳(伪平稳)的,并移动分析窗函数,使)()(τ-t g t f 在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的功率谱。
同步压缩小波变换matlab程序

同步压缩小波变换matlab程序英文回答:Wavelet transform is a powerful tool in signal processing and data compression. It is widely used in various fields such as image and audio compression, denoising, and feature extraction. In MATLAB, there are built-in functions and toolboxes that can be used to perform wavelet transform and compression.To perform synchronous wavelet compression in MATLAB, we can follow these steps:1. Load the signal or image data: We first need to load the signal or image data that we want to compress. This can be done using the appropriate MATLAB functions, such as`audioread` for audio signals or `imread` for images.2. Choose a wavelet: Next, we need to choose a suitable wavelet for the compression. MATLAB provides a variety ofwavelets, such as Daubechies, Coiflets, and Symlets. We can use the `wfilters` function to obtain the coefficients of a specific wavelet.3. Perform wavelet decomposition: We can use the`wavedec` function to decompose the signal or image into different frequency subbands using the chosen wavelet. This will result in a set of approximation and detail coefficients.4. Set a compression threshold: In order to reduce the amount of data to be stored or transmitted, we can set a compression threshold to discard or truncate the detail coefficients with small magnitudes. This can be done by comparing the magnitude of each coefficient with the threshold value.5. Reconstruct the compressed signal or image: After discarding or truncating the detail coefficients, we can use the `waverec` function to reconstruct the compressed signal or image using the remaining approximation anddetail coefficients.6. Evaluate the compression performance: Finally, wecan evaluate the compression performance by comparing the quality of the reconstructed signal or image with the original data. This can be done using various metrics such as peak signal-to-noise ratio (PSNR) or mean squared error (MSE).中文回答:小波变换是信号处理和数据压缩中的一种强大工具。
MATLAB小波变换指令及其功能介绍(超级有用)

MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能:一维离散小波变换格式:[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维DFT说明:[cA,cD]=dwt(X,'wname') 使用指定的小波基函数 'wname'对信号X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数功能:一维离散小波反变换格式:X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明:X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname' 为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,'wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。
2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能---------------------------------------------------dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换----------------------------------------------------------- (1) wcodemat 函数功能:对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式:Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明:Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵 X 的编码矩阵Y ;NB 伪编码的最大值,即编码范围为 0~NB,缺省值 NB=16;OPT 指定了编码的方式(缺省值为 'mat'),即:别可以实现一维、二维和 N 维 DFTOPT='row' ,按行编码OPT='col' ,按列编码OPT='mat' ,按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数(缺省值为 '1'),即:ABSOL=0 时,返回编码矩阵ABSOL=1 时,返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的 Matlab实现(2) dwt2 函数功能:二维离散小波变换格式:[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明:[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号 X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。
关于小波分析的matlab程序

关于小波分析的matlab程序小波分析是一种在信号处理和数据分析领域中广泛应用的方法。
它可以帮助我们更好地理解信号的时域和频域特性,并提供一种有效的信号处理工具。
在本文中,我将介绍小波分析的基本原理和如何使用MATLAB编写小波分析程序。
一、小波分析的基本原理小波分析是一种基于窗口函数的信号分析方法。
它使用一组称为小波函数的基函数,将信号分解成不同频率和不同时间尺度的成分。
与傅里叶分析相比,小波分析具有更好的时频局部化性质,可以更好地捕捉信号的瞬时特征。
小波函数是一种具有局部化特性的函数,它在时域上具有有限长度,并且在频域上具有有限带宽。
常用的小波函数有Morlet小波、Haar小波、Daubechies小波等。
这些小波函数可以通过数学运算得到,也可以通过MATLAB的小波函数库直接调用。
小波分析的基本步骤如下:1. 选择合适的小波函数作为基函数。
2. 将信号与小波函数进行卷积运算,得到小波系数。
3. 根据小波系数的大小和位置,可以分析信号的时频特性。
4. 根据需要,可以对小波系数进行阈值处理,实现信号的去噪和压缩。
二、MATLAB中的小波分析工具MATLAB提供了丰富的小波分析工具箱,可以方便地进行小波分析的计算和可视化。
下面介绍几个常用的MATLAB函数和工具箱:1. `waveinfo`函数:用于查看和了解MATLAB中可用的小波函数的信息,如小波函数的名称、支持的尺度范围等。
2. `wavedec`函数:用于对信号进行小波分解,得到小波系数。
3. `waverec`函数:用于根据小波系数重构原始信号。
4. `wdenoise`函数:用于对小波系数进行阈值处理,实现信号的去噪。
5. 小波分析工具箱(Wavelet Toolbox):提供了更多的小波分析函数和工具,如小波变换、小波包分析、小波阈值处理等。
可以通过`help wavelet`命令查看工具箱中的函数列表。
三、编写小波分析程序在MATLAB中编写小波分析程序可以按照以下步骤进行:1. 导入信号数据:首先需要导入待分析的信号数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业一
读入一个一维非平稳信号,对其进行3层小波分解与重构,提取指定尺度上的低频,高频系数。
保留10%,80%的模极大系数,进行重构,并做分析比较。
在一副图中显示出原始信号,分解后第2,3尺度上的高频,第3尺度上的低频,以及重构信号。
Matlab程序如下:
clear
clc
load noisdopp;
s=noisdopp;
[c,l]=wavedec(s,3,'db3');
ca1=appcoef(c,l,'db3',1);
ca2=appcoef(c,l,'db3',2);
ca3=appcoef(c,l,'db3',3);
%提取低频分量
cd1=detcoef(c,l,1);
cd2=detcoef(c,l,2);
cd3=detcoef(c,l,3);
%提取高频分量
coef1=0.1;
coef2=0.8;
%定义模值系数
[~,id1] = sort(abs(cd1),'descend');%对第一尺度高频信号排序并记录下其索引[m1,n1]=size(cd1);
number=round(n1*coef1);
nid1=id1(1:number);%取前10%的模值个数
ncd1=zeros(m1,n1);
for i=1:n1
if ismember(i,nid1)==1
ncd1(m1,i)=cd1(m1,i);
end
end
%第一尺度高频的10
[~,id2] = sort(abs(cd2),'descend');
[m2,n2]=size(cd2);
number=round(n2*coef1);
nid2=id2(1:number);
ncd2=zeros(m2,n2);
for i=1:n2
if ismember(i,nid2)==1
ncd2(m2,i)=cd2(m2,i);
end
end
%第二尺度高频的10%
[~,id3] = sort(abs(cd3),'descend'); [m3,n3]=size(cd3);
number=round(n3*coef1);
nid3=id3(1:number);
ncd3=zeros(m3,n3);
for i=1:n3
if ismember(i,nid3)==1
ncd3(m3,i)=cd3(m3,i);
end
end
%第三尺度高频的10%
[~,ia3] = sort(abs(ca3),'descend'); [ma3,na3]=size(ca3);
number=round(na3*coef1);
nia3=ia3(1:number);
nca3=zeros(ma3,na3);
for i=1:na3
if ismember(i,nia3)==1
nca3(ma3,i)=ca3(ma3,i);
end
end
%第三尺度低频的10%
c1=[nca3 ncd3 ncd2 ncd1];
x1=waverec(c1,l,'db3');%小波重构
[~,id11] = sort(abs(cd1),'descend'); [m11,n11]=size(cd1);
number2=round(n11*coef2);
nid11=id11(1:number2);
ncd11=zeros(m11,n11);
for i=1:n11
if ismember(i,nid11)==1
ncd11(m11,i)=cd1(m11,i);
end
end
%第一尺度高频的80%
[~,id21] = sort(abs(cd2),'descend'); [m21,n21]=size(cd2);
number2=round(n21*coef2);
nid21=id21(1:number2);
ncd21=zeros(m21,n21);
for i=1:n21
if ismember(i,nid21)==1
ncd21(m21,i)=cd2(m21,i);
end
end
%第二尺度高频的80%
[~,id31] = sort(abs(cd3),'descend'); [m31,n31]=size(cd3);
number2=round(n31*coef2);
nid31=id31(1:number2);
ncd31=zeros(m31,n31);
for i=1:n31
if ismember(i,nid31)==1
ncd31(m31,i)=cd3(m31,i);
end
end
%第三尺度高频的80%
[~,ia31] = sort(abs(ca3),'descend'); [ma31,na31]=size(ca3);
number=round(na31*coef2);
nia31=ia31(1:number);
nca31=zeros(ma31,na31);
for i=1:na31
if ismember(i,nia31)==1
nca31(ma31,i)=ca3(ma31,i);
end
end
%第三尺度低频的80%
cl2=[nca31 ncd31 ncd21 ncd11];
x2=waverec(cl2,l,'db3');%小波重构
subplot(421),plot(s);
subplot(422),plot(ca3);
subplot(423),plot(cd2);
subplot(424),plot(cd3);
subplot(425),plot(x1);
subplot(426),plot(x2);
结果如下图所示:
从图中可以看出,只保留10%模值极大系数,重构的信号与原信号相比偏差较大,保留80%模值极大系数,重构信号与原信号基本一致。
作业四
读入二维信号,加入高斯噪声,对其进行3层小波分解,并用小波阈值进行去噪。
选取两种不同的阈值:一是取Matlab中的阈值,二是自己给定阈值(如根据不同尺度上信号的方差,小波系数相关性等)。
计算均方误差,并比较分析两种不同去噪方法。
显示原始信号,第2,3尺度上的低频,以及硬,软阈值去噪后的图像。
Matlab程序如下:
clear
clc
load woman;
f=X;
x1=X+randn(size(X))*20;
[c,s]=wavedec2(x1,3,'db4');
a2=appcoef2(c,s,'db4',2);
a3=appcoef2(c,s,'db4',3); %提取低频分量
n=[1 2 3];%设置尺度向量
p=[80 23 10];%设置阈值向量
nc=wthcoef2('h',c,s,n,p,'s');
x0=waverec2(nc,s,'db4');%重构信号
[thr, sorh, keepapp] = ddencmp('den','wv',x1);
t = thselect(x1,'sqtwolog');
xd1 = wdencmp('gbl',x1,'db4',3,t,'h','1');%硬阈值去噪
xd2 = wdencmp('gbl',x1,'db4',3,t,'s','1');%软阈值去噪figure;
subplot(421),imshow(f,[]);title('原图')
subplot(422),imshow(x1,[]);title('加噪声后图')
subplot(423),imshow(a2,[]);title('第二尺度低频') subplot(424),imshow(a3,[]);title('第三尺度低频') subplot(425),imshow(xd1,[]);title('硬阈值去噪') subplot(426),imshow(xd2,[]);title('软阈值去噪') subplot(427),imshow(x0,[]);title('自设阈值去噪')
nf=norm(x1-f);%加入噪声的图均方误差
dnf1=norm(xd1-f);%硬阈值去噪后的均方误差
dnf2=norm(xd2-f);软阈值去噪后的均方误差
dnf3=norm(x0-f);%自设阈值去噪后的均方误差
加入噪声的图像与原图相比均方误差为:636.2014
硬阈值去噪后的均方误差为:633.8073
软阈值去噪后的均方误差为:558.2569
自设阈值去噪后的均方差为:589.4099
评价:自设的阈值去噪因为可以自己更改阈值向量的值,使得图像去噪效果向好的方向变换。
从主观视觉上来看,自设阈值的方法和软阈值去噪方法都比硬阈值的方法要好一些。
从客观评价指标,与原图的均方误差值来比较,自设阈值的方法比硬阈值方法要好,但不如matlab自带的软阈值方法。
