教育事业发展全国及各地省市区统计数据:中国2018年普通高中学生数统计(乡村)
江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(七)

一、单选题二、多选题1. 设命题,使得,则为( )A .使得B .都有C .使得D .都有2.已知函数,,若函数有6个零点,则实数的取值范围为A.B.C.D.3.已知向量满足,则( )A .3B.C .7D.4. 已知椭圆的左、右焦点分别为,,过的直线交椭圆于,两点,若的最大值为10,则的值是( )A.B.C.D.5. 将函数的图象向左平移个单位长度,向下平移个单位长度后,得到的图象,若对于任意的实数,都单调递增,则正数的最大值为A.B.C.D.6. 函数的最小正周期为,则的值为( ).A .2B .4C .1D.7. 已知复数在复平面内对应的点都在射线上,且,则的虚部为( )A .3B.C.D.8.若函数,对任意的都有,则等于( )A.B .0C.D.9. 下图是《2018年全国教育事业发展统计公报》中1949-2018年我国高中阶段在校生数条形图和毛入学率的折线图,根据下图可知在1949-2018年()高中阶段在校生数和毛入学率A .1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高B .从1990年开始,我国高中阶段的在校生数和毛入学率在逐年增高C .2010年我国高中阶段在校生数和毛入学率均达到了最高峰D .2018年高中阶段在校生数比2017年下降了约0.91%,而毛入学率提高了0.5个百分点10. 已知函数,则( )A .函数在区间上单调递减江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(七)三、填空题四、填空题五、填空题六、解答题七、解答题B .函数在区间上的最大值为1C .函数在点处的切线方程为D .若关于的方程在区间上有两解,则11. 设O 为坐标原点,直线l 过抛物线C :的焦点F 且与C 交于A ,B 两点(点A 在第一象限),,l 为C 的准线,,垂足为M ,,则下列说法正确的是( )A.B .的最小值为C .若,则D .x 轴上存在一点N ,使为定值12. 已知x ,y 的取值如下表:x 0134y2.24.34.86.7若x ,y具有线性相关关系,且回归方程为,则的值为______.13. 已知是空间单位向量,若空间向量满足,,且对于任意x ,y ∈R,,则=______.14. 若,,且,则的最大值为______.15. 在长方体中,,,,为线段的中点,一质点从点出发,沿长方体表面运动到达点处,则质点从到的最短距离为___________;若沿质点的最短运动路线截长方体,则所得截面的面积为___________.16.已知数列的前项和为,且,记,则________;若数列满足,则的最小值是________.17. 用表示不超过的最大整数,已知数列满足:,,.若,,则________;若,则________.18. 化简(I)(Ⅱ).19. 某校从参加高一年级期末考试的学生中抽出名学生,将其成绩(均为整数)分成六段,后画出如图的频率分布直方图.八、解答题九、解答题十、解答题观察图形的信息,回答下列问题:(1)估计这次考试成绩的众数;(2)估计这次考试成绩的及格率(分及以上及格).20. 在三棱锥中,.(1)求证:;(2)求直线与平面所成角的正弦值.21. 某创业团队拟生产A 、B 两种产品,根据市场预测,A 产品的利润与投资额成正比(如图1),B 产品的利润与投资额的算术平方根成正比(如图2),(注:利润与投资额的单位均为万元)(1)分别将A 、B 两种产品的利润、表示为投资额x 的函数;(2)该团队已筹集到10万元资金,并打算全部投入A 、B 两种产品的生产,问:当B 产品的投资额为多少万元时,生产A 、B 两种产品能获得最大利润,最大利润为多少?22. 已知a 、b 、c分别为三内角A 、B 、C 所对的边,且.(1)求A ;(2)若,且,求c 的值.。
教育事业发展全国及各地省市区统计数据:中国2018年分举办者研究生数统计(普通高校)

中国2
学校(机构)数 毕业生数 合计
博士
总计
580
597503
59503
一.中央
111
290946
47272
1.教育部
76
238727
36005
2.其他部门
35
52219
11267
二.地方
469
306557
12231
1.教育部门
444
302384
12166
2.其他部门
20
3907
65
3.地方企业
0
0
0
4.民办
5
266
0
注5:.2具01有7独年立起法.研人究资生格招的生中.在外校合生作指办标内涵发生变化0.招生包含全日制和0非全日制研究生;在校0 生.授予学位数包含全日制.非全日制研究
中国2018年分举办者研究生数统计(普通高校)
硕士
招生数 合计
博士
538000
849176
93802
243674
预计毕业生数 合计
808799 422738 348889 73849 386061 380487 5060 0 514 0
博士
169435 128685 103578 25107 40750 40455 295 0 0 0
硕士
639364 294053 245311 48742 345311 340032 4765 0 514 0
在校生数 合计
2703411 1419258 1175323 243935 1284153 1266139 16524 0 1490 0
摘编自《中国教育统计年鉴2018》
河南省南阳市2024高三冲刺(高考数学)人教版模拟(评估卷)完整试卷

河南省南阳市2024高三冲刺(高考数学)人教版模拟(评估卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知,函数在区间上单调递增,则的取值范围是()A.B.C.D.第(2)题双曲线左、右焦点坐标分别是()A.,B.,C.,D.,第(3)题已知函数,若对任意、、,总有、、为某一个三角形的边长,则实数的取值范围是A.B.C.D.第(4)题在复数范围内方程的解为()A.B.C.D.第(5)题已知,为锐角,,,则()A.B.C.D.第(6)题设集合,,,则A.B.C.D.第(7)题设全集,集合,则()A.B.C.D.第(8)题已知函数,若,则的取值范围是()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题下图是《2018年全国教育事业发展统计公报》中1949-2018年我国高中阶段在校生数条形图和毛入学率的折线图,根据下图可知在1949-2018年()高中阶段在校生数和毛入学率A.1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高B.从1990年开始,我国高中阶段的在校生数和毛入学率在逐年增高C.2010年我国高中阶段在校生数和毛入学率均达到了最高峰D.2018年高中阶段在校生数比2017年下降了约0.91%,而毛入学率提高了0.5个百分点第(2)题设函数,则()A.有三个零点B .是的极大值点C.曲线为轴对称图形D .为曲线的对称中心第(3)题已知函数在上有且仅有5个零点,则( )A .的取值范围是B .的图象在上有且仅有3个最高点C.的图象在上最多有3个最低点D .在上单调递增三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题某学校每天安排4项课后服务供学生自愿选择参加.学校规定:(1)每位学生每天最多选择1项;(2)每位学生每项一周最多选择1次.学校提供的安排表如下:时间周一周二周三周四周五课后服务音乐、阅读、体育、编程口语、阅读、编程、美术手工、阅读、科技、体育口语、阅读、体育、编程音乐、口语、美术、科技若某学生在一周内共选择了阅读、体育、编程3项,则不同的选择方案共有______种.(用数值表示)第(2)题执行如图所示的程序框图,输入l=2,m=3,n=5,则输出的y 的值____第(3)题已知为虚数单位,复数,则______.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题某学校有1000人,想通过验血的方式筛查出某种病毒的携带者,如果对每个人的血样逐一化验,需要化验1000次,统计专家提出了一种方法:随机地按10人一组分组,然后将各组10个人的血样混合再化验,如果混合血样呈阴性,说明这10个人全部阴性;如果混合血样呈阳性,说明其中至少有一个人呈阳性,就需要对这组的每个人再分别化验一次.假设某学校携带病毒的人数有10人.()(1)用样本的频率估计概率,若5个人一组,求一组混合血样呈阳性的概率;(2)用统计专家这种方法按照5个人一组或10个人一组,问哪种分组方式筛查出这1000人中该病毒携带者需要化验次数较少?为什么?第(2)题在直角坐标系中,圆的参数方程为(为参数).以坐标原点为极点,轴的正半轴为极轴建立极坐标系,直线的极坐标方程为.(1)求圆的普通方程和直线的直角坐标方程;(2)若直线与圆相交于两点,点的直角坐标为,求的值.第(3)题已知点在抛物线上,且到抛物线的焦点的距离为2.(1)求抛物线的标准方程;(2)过点向抛物线作两条切线,切点分别为,若直线与直线交于点,且点到直线、直线的距离分别为.求证:为定值.第(4)题新冠病毒奥密克戎毒株开始流行后,为了控制新冠肺炎疫情,杭州某高中开展了每周核酸检测工作.周一至周五,每天中午13:30开始,安排位师生进行核酸检测,教职工每天都要检测,用五天时间实现全员覆盖.(1)该校教职工有人,高二学生有人,高三学生有人.①用分层抽样的方法,求高一学生每天的检测人数.②高一年级共个班,该年级每天进行核酸检测的学生有两种安排方案.方案一:集中来自部分班级;方案二:分散来自所有班级.你认为哪种方案更合理?给出理由.(2)学校开展核酸检测的第一周,周一至周五核酸检测用时记录如下表.第天用时①计算变量和的相关系数(精确到),并说明两变量的线性相关程度;②根据①中的计算结果,判定变量和是正相关还是负相关,并给出可能的原因.参考数据和公式:,相关系数.第(5)题已知数列的前项和为,,.(1)求数列的通项公式;(2)若,求数列的前项和.。
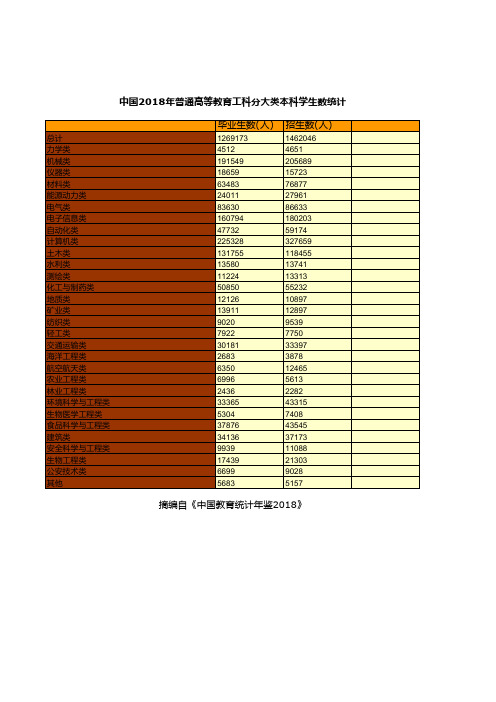
教育事业发展全国及各地省市区统计数据:中国2018年普通高等教育工科分大类本科学生数统计
在校生数(人)
5692317 18620 830427 70429 286231 106604 360402 712988 220251 1195726 492657 55675 49433 213427 43091 47960 37468 30666 134064 13626 38609 26154 9620 156752 26709 168203 167160 42103 81365 33111 22786
单位:人
总计 力学类 机械类 仪器类 材料类 能源动力类 电气类 电子信息类 自动化类 计算机类 土木类 水利类 测绘类 化工与制药类 地质类 矿业类 纺织类 轻工类 交通运输类 海洋工程类 航空航天类 农业工程类 林业工程类 环境科学与工程类 生物医学工程类 食品科学与工程类 建筑类 安全科学与工程类 生物工程类 公安技术类 其他
摘编自《中国教育统计年鉴2018》
Байду номын сангаас
中国2018年普通高等教育工科分大类本科学生数统计
毕业生数(人)
1269173 4512 191549 18659 63483 24011 83630 160794 47732 225328 131755 13580 11224 50850 12126 13911 9020 7922 30181 2683 6350 6996 2436 33365 5304 37876 34136 9939 17439 6699 5683
招生数(人)
1462046 4651 205689 15723 76877 27961 86633 180203 59174 327659 118455 13741 13313 55232 10897 12897 9539 7750 33397 3878 12465 5613 2282 43315 7408 43545 37173 11088 21303 9028 5157
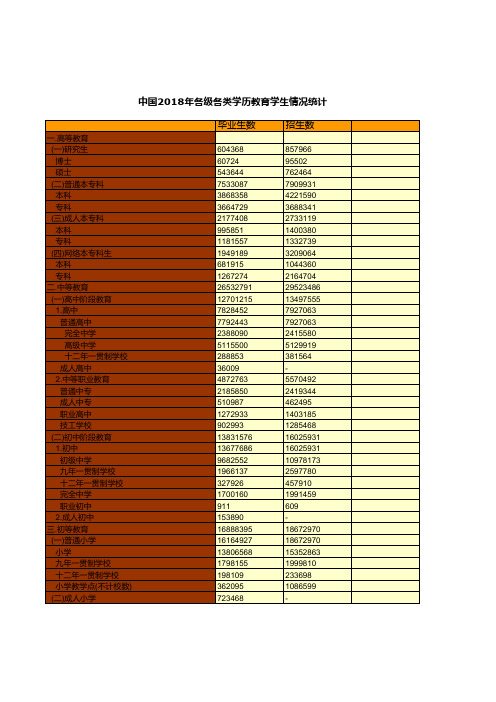
教育事业发展全国及各地省市区统计数据:中国2018年各级各类学历教育学生情况统计
招生数
857966 95502 762464 7909931 4221590 3688341 2733119 1400380 1332739 3209064 1044360 2164704 29523486 13497555 7927063 7927063 2415580 5129919 381564 5570492 2419344 462495 1403185 1285468 16025931 16025931 10978173 2597780 457910 1991459 609 18672970 18672970 15352863 1999810 233698 1086599 -
三.初等教育 (一)普通小学 小学 九年一贯制学校 十二年一贯制学校 小学教学点(不计校数) (二)成人小学
毕业生数
604368 60724 543644 7533087 3868358 3664729 2177408 995851 1181557 1949189 681915 1267274 26532791 12701215 7828452 7792443 2388090 5115500 288853 36009 4872763 2185850 510987 1272933 902993 13831576 13677686 9682552 1966137 327926 1700160 911 153890 16888395 16164927 13806568 1798155 198109 362095 723468
2.完全中学.九年一贯制学校和十二年一贯制学校的学生数按教育层次分别计入对应教育阶段的学生数中
3.特殊教育学生数中包括义务教育阶段随班就读.其他学校附设特教班和送教上门的学生.
摘编自《中国教育统计年鉴2018》
安徽省巢湖市(新版)2024高考数学统编版质量检测(预测卷)完整试卷

安徽省巢湖市(新版)2024高考数学统编版质量检测(预测卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知函数有唯一零点,则A.B.C.D.1第(2)题设集合则A.B.C.D.第(3)题复数的值是A.-1B.1C.-D.第(4)题已知集合,则()A.B.C.D.第(5)题如图,在半径为3的球面上有三点,,球心到平面的距离是,则两点的球面距离是A.B.C.D.第(6)题小明爬楼梯每一步走1级台阶或2级台阶是随机的,且走1级台阶的概率为,走2级台阶的概率为.小明从楼梯底部开始往上爬,在小明爬到第4级台阶的条件下,他走了3步的概率是()A.B.C.D.第(7)题已知集合,则实数m的取值范围是().A.或B.C.或D.第(8)题设直线:,一束光线从原点出发沿射线向直线射出,经反射后与轴交于点,再次经轴反射后与轴交于点.若,则的值为()A.B.C.D.2二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题下图是《2018年全国教育事业发展统计公报》中1949-2018年我国高中阶段在校生数条形图和毛入学率的折线图,根据下图可知在1949-2018年()高中阶段在校生数和毛入学率A.1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高B.从1990年开始,我国高中阶段的在校生数和毛入学率在逐年增高C.2010年我国高中阶段在校生数和毛入学率均达到了最高峰D.2018年高中阶段在校生数比2017年下降了约0.91%,而毛入学率提高了0.5个百分点第(2)题如图甲所示,古代中国的太极八卦图是以同圆内的圆心为界,画出相等的两个阴阳鱼,阳鱼的头部有眼,阴鱼的头部有个阳殿,表示万物都在相互转化,互相涉透,阴中有阳,阳中有阴,阴阳相合,相生相克,蕴含现代哲学中的矛盾对立统一规律,其平面图形记为图乙中的正八边形,其中,则()A.B.C.D.第(3)题甲乙两队进行比赛,若双方实力随时间的变化遵循兰彻斯特模型:其中正实数分别为甲、乙两方初始实力,为比赛时间;分别为甲、乙两方时刻的实力;正实数分别为甲对乙、乙对甲的比赛效果系数.规定当甲、乙两方任何一方实力为0时比赛结束,另一方获得比赛胜利,并记比赛持续时长为.则下列结论正确的是()A.若且,则B.若且,则C.若,则甲比赛胜利D.若,则甲比赛胜利三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题在中,角所对的边分别为,若.当时,的面积是__________.第(2)题函数的单调增区间是_______.第(3)题如图所示是某市2016年2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某同志随机选择2月1日至2月12日中的某一天到达该市,并停留3天.该同志到达当日空气质量优良的概率______________________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知直线为参数,,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为,圆与极轴和直线分别交于点,点(异于坐标原点).(1)写出点的极坐标及圆的参数方程;(2)求的最大值.第(2)题溺水、校园欺凌、食品卫生、消防安全、道路交通等与学生安全有关的问题越来越受到社会的关注和重视.学校安全工作事关学生的健康成长,关系到千万个家庭的幸福和安宁,关系到整个社会的和谐稳定.为了普及安全教育,某市准备组织一次安全知识竞赛.某学校为了选拔学生参赛,按性别采用分层抽样的方法抽取200名学生进行安全知识测试,根据200名同学的测试成绩得到如下表格:性别了解安全知识的程度得分不超过85分的人数得分超过85分的人数男生20100女生3050(1)现从得分超过85分的学生中根据性别采用分层随机抽样抽取6名学生进行安全知识培训,再从这6名学生中随机抽取3名学生去市里参加竞赛,求这3名学生中有至少一名女生的概率;(2)根据小概率值的独立性检验,能否推断该校男生和女生在了解安全知识的程度与性别有关?附:参考公式,其中.下表是独立性检验中几个常用的小概率值和相应的临界值a0.10.050.010.0050.0012.7063.8416.6357.87910.828第(3)题已知.(1)求;(2)证明:是等差数列,并求出;(3)设,求的前项和.第(4)题在中,角、、所对的边分别为、、.已知,,.(1)求的值;(2)求的值;(3)求的值.第(5)题已知函数,.(1)若函数在定义域内恒成立,求实数m的取值范围;(2)证明:.。
教育事业发展全国及各地省市区统计数据:中国2018年各级各类学校少数民族学生数统计

少数民族学生 人数
138593 23006 115587 2697534 1604699 1092835 529290 263243 266047 578550 188470 390080 2584317 735635 1788144 60538 1613 785300 113512 419991 5274704 3958837 671310 69524 574393 640 12261088 11156967 1028246 75875 99459
占学生总数的
5.07 5.91 4.94 9.53 9.45 9.64 8.96 8.86 9.05 7.01 6.67 7.18 10.88 10.15 11.57 5.72 0.83 11.23 10.03 10.47 11.34 12.28 9.25 5.51 9.98 31.22 11.86 12.26 9.23 6.00 13.58
三.初等教育 (一)普通小学 小学 九年一贯制学校 十二9518 2341739 28310348 16973343 11337005 5909878 2971134 2938744 8256553 2825757 5430796 23753709 7246165 15449469 1058075 194905 6994205 1131250 4010825 46525854 32249484 7256642 1262258 5755420 2050 103392541 90986857 11140679 1265005 732463
扫盲班 四.工读学校 五.特殊教育 六 注.:学 少前 数教 民育 族成人高中数据包括成人初中数据.
665942 46564204
86852 5101737
摘编自《中国教育统计年鉴2018》
2018中国教育事业数据报告

2018年中国教育数据报告2018年,全国共有各级各类学校251.88万所,比上年增加5017所。
全国各级各类学历教育在校生2.76亿人,比上年增加539.40万人,增长2.0%。
全国各级各类学校专任教师1672.85万人,比上年增加45.96万人,增长2.8%。
全国各级各类学校共拥有校舍建筑面积335.73亿平方米,比上年增加1.54亿平方米,增长4.5%;全国各级各类学校教学、科研仪器设备资产总值10218.21亿元,比上年增加1027.26亿元,增长11.2%。
义务教育(一)义务教育规模2018年,全国共有义务教育阶段学校21.38万所,比上年减少5110所;义务教育阶段招生3469.89万人,比上年增加156.11万人,增长4.7%;在校生1.50亿人,比上年增加456.08万人,增长3.1%。
小学招生、在校生人数继续增长,城市小学招生增长较快。
2018年,全国共有普通小学16.18万所,比上年减少5198所;小学招生1867.30万人,比上年增加100.74万人,增长5.7%。
其中,城市小学招生713.51万人,同比增长13.2%,农村小学招生1153.79万,同比增长1.5%。
全国普通小学在校生规模继续增加,为10339.25万人,比上年增加245.56万人,增长2.4%。
初中招生、在校生规模持续增长,城市初中增长较快。
2018全国共有初中阶段学校5.20万所,比上年增加88所。
初中招生1602.59万人,比上年增加55.37万人,增长3.6%。
其中,城市初中招生581.56万人,同比增长5.7%,农村初中招生1021.03万人,同比增长2.4%。
初中阶段在校生4652.59万人,比上年增加210.52万人,增长4.7%。
受在校生规模增长影响,每十万人口中小学在校生人数比上年增加138人,为7438人;每十万人口中初中阶段在校生人数比上年增加134人,为3347人。
(二)义务教育普及与巩固水平2018年,小学学龄儿童净入学率达99.95%,全国及绝大多数省份男女童入学率性别差异已经消除;全国初中阶段毛入学率为100.9% 。
江苏省南京市(新版)2024高考数学统编版真题(综合卷)完整试卷

江苏省南京市(新版)2024高考数学统编版真题(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知球与圆台的上下底面和侧面都相切.若圆台的侧面积为;上、下底面的面积之比为,则球的表面积为().A.B.C.D.第(2)题已知函数,若对任意,恒成立,则实数的取值范围为()A.B.C.D.第(3)题设等差数列的前n项和为,若,则当取得最小值时,n的值为()A.11B.10C.9D.8第(4)题平面直角坐标系中,点、是方程表示的曲线上不同两点,且以为直径的圆过坐标原点,则到直线的距离为( )A.2B.C.3D.第(5)题已知复数满足,则在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限第(6)题点在同一个球的球面上,,若四面体体积的最大值为,则该球的表面积为A.B.C.D.第(7)题“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件第(8)题已知椭圆C:()的左、右焦点分别为,,P为C上一点,满足,以C的短轴为直径作圆O,截直线的弦长为,则C的离心率为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题在对具有相关关系的两个变量进行回归分析时,若两个变量不呈线性相关关系,可以建立含两个待定参数的非线性模型,并引入中间变量将其转化为线性关系,再利用最小二乘法进行线性回归分析.下列选项为四个同学根据自己所得数据的散点图建立的非线性模型,且散点图的样本点均位于第一象限,则其中可以根据上述方法进行回归分析的模型有()A.B.C.D.第(2)题已知,则()A.的最大值为B.的最小值为C.的最大值为2D.的最小值为第(3)题下图是《2018年全国教育事业发展统计公报》中1949-2018年我国高中阶段在校生数条形图和毛入学率的折线图,根据下图可知在1949-2018年()高中阶段在校生数和毛入学率A.1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高B.从1990年开始,我国高中阶段的在校生数和毛入学率在逐年增高C.2010年我国高中阶段在校生数和毛入学率均达到了最高峰D.2018年高中阶段在校生数比2017年下降了约0.91%,而毛入学率提高了0.5个百分点三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知数列的前n项和,记,则数列的前n项和_______.第(2)题随机变量分布列如下表,则______;______.012第(3)题若函数的图象关于点对称,且关于直线对称,则______(写出满足条件的一个函数即可).四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题正四棱锥中,,,其中为底面中心,为上靠近的三等分点.(1)求证:平面;(2)求四面体的体积.第(2)题第22届亚运会在中国杭州举行,中国代表团斩获201枚金牌,稳居榜首.为了普及亚运会知识,某校组织了亚运会知识竞赛,设置了A,B,C三套不同试卷.现将每份试卷分别装入大小、外观均相同的竹筒中,再放入甲、乙两个抽题箱内,其中甲箱装有A卷竹筒4个、B卷竹筒3个、C卷竹筒2个、乙箱装有A卷竹筒2个、B卷竹筒2个、C卷竹筒5个.(1)若从甲箱中取出一个竹筒,求该竹筒装有A卷的概率.(2)若从甲、乙箱中各取出一个竹筒,记取出的装有B卷的竹筒数为随机变量,求的分布列与数学期望.(3)若先从甲箱中随机取出一个竹筒放入乙箱,再从乙箱中随机取出一个竹筒,求从乙箱取出的竹筒装有C卷的概率.第(3)题已知双曲线的右焦点为,过与轴垂直的直线交于两点,且,离心率为.(1)求的方程;(2)已知圆上点处的切线方程是,利用类比思想可知双曲线上点处的切线方程为.过点分别作双曲线的左、右两支的切线,切点分别为,连接,并过线段的中点分别再作双曲线左、右两支的切线,切点分别为,证明:点在同一条直线上.第(4)题记为数列的前n项和,时,满足,.(1)求的通项公式;(2)求.第(5)题已知函数的一个极值点是.(1)求a与b的关系式,并求的单调区间;(2)设,,若存在,,使得成立,求实数a的范围.。
