垂直与平行的概念t
立体几何平行,垂直的判定定理和性质定理

你应to果的卅个麻平行、&的熾碇理判左罡王里L直空3平血形r曲判宦宝理.(1罡理肉客'姐果舷丼-<亘兰£和世十平阪貝附一余直兰£平行丿瞅£条盘绞*9冷巧S平愆⑴.疥号侶4・Ta《d"d,q//6<\ a//d2直喪才平血垂直的判定理理、、俶企理内埜期果一条•直兰戋和一个平厨内的嗽木胶直孜劭重X労吆史条直我舷于笛个平因.⑴'相施T C丄scd£, aud,gda砒=0 八u丄d(3J、英何两种判宜方叫。
.方妊一「如杲两糸平行直M中的一隶直兰戋垂直于一于平虬声昭另一糸直三士史邑厘于千血.' 然绘养\yj.d,a//b八6丄d@.方址二、、一余直兰吳垂直于丐亍平行乎面中曲一亍平廚」月曲宓坦僉演一今陋・ "舸瓯打仲,a丄d八a±p3网个平血平行加判定览理、・(0•皇理内乱炉果一个平囲团有两糸木瓦或直兰£ tWj 芋另一丁ZPA 7®其把两釉刊定方坯、・“ ----- —I@方辽一、、垂直于同TL 孜他題个平血平行 骨号常吉丨T a丄d , a 丄p•\ 4 lip_©誌席二、、平彳了于闸一平血怕两T 平面平行 箝宕诸盲、.•? diip . ai/r庄二7•\ mp*两I s 平面垂直釣判定罡理、・(认定理内站 如果-个平预々生JS 另一于平面的一気垂兰色另腕虫颅个平同艺相垂直.g 瘠号绘宜「I old 」ac.p八卩丄d平血,更吆咚料丁于適平行. 曲斛也MudMud, an^O allR Jh/ip性质罡理”/.直峯牙平页平行餡"生员览理、'(U隹理内密J如果~杀直起和-? fffi平行,俎的平页承血个刊S相丸为艺七逋兰电心M壬平红3符号垢1 T Q〃d,au*, 4仲二b.\ al/b2、直兰 < 平血垂直怕彳土腹定理、.(小罡理内瓠如杲两聚直孜同巧垂直于一个平页丿刃滋虫两棗盘兰戋平行⑴.看呂第盲、‘ T a丄dj b丄d.;allb⑶、推盘果一余直呈爰垂直于一个平面〉另曲危亲直空垂直于直个平囲用曲任直 V童兰电鯛H乳T a丄d,bG「、a丄右3. Mt平囲平行的性浚建理、・©定启沁星步果两T平行平廊阖吋和第三个平两相娄刃吆如戈平行.’"Pnr^b•* am心鉀按如榨酎陋平彷舷其二个平血内倒径何一亲童兰吳考户平行于另一平面.. Td〃P z_______ 7心h一”•\ a〃0 I ----- 斗两亍平页垂直的灶戾崖锂、、隹 ---- ' "J,定理内琵丈口果网个尧®童贞,另以;在-个平两内垂直T宓们交兰£曲直2空垂点于另一个平向.⑴搭号堰弐・心丄p, dnp=bQud , q丄bJ、q_Lj3如有侵权请联系告知删除,感谢你们的配合!。
平行线与垂直线的认识及性质

平行线与垂直线的认识及性质一、平行线的认识1.平行线的定义:在同一平面内,永不相交的两条直线叫做平行线。
2.平行线的符号表示:用“//”表示平行线。
3.平行线的性质:a.平行线永不相交。
b.平行线之间的距离相等。
c.平行线上的对应角相等。
d.平行线上的内错角相等。
e.平行线上的同位角相等。
二、垂直线的认识1.垂直线的定义:两条相交成90度角的两条直线叫做垂直线。
2.垂直线的符号表示:用“⊥”表示垂直线。
3.垂直线的性质:a.垂直线相交成90度角。
b.垂直线之间的距离相等。
c.垂直线上的对应角相等。
d.垂直线上的内错角相等。
e.垂直线上的同位角相等。
三、平行线与垂直线的相互关系1.平行线与垂直线的判定:a.如果两条直线相交成90度角,那么这两条直线一定垂直。
b.如果两条直线永不相交,那么这两条直线一定平行。
2.平行线与垂直线的性质:a.平行线垂直于同一条直线时,相互平行。
b.垂直线平行于同一条直线时,相互垂直。
四、平行线与垂直线的应用1.生活中的应用:a.建筑设计中的墙体垂直度检查。
b.道路建设中,道路的直线与交叉线的规划。
c.家电产品中的平行与垂直设计,如电视、冰箱等。
2.数学中的应用:a.在坐标系中,平行线与垂直线用于确定点的坐标位置。
b.在几何题中,平行线与垂直线用于求解角度和距离。
c.在函数题中,平行线与垂直线用于确定函数的图像。
五、学习平行线与垂直线的方法1.观察实物:通过观察生活中的实物,了解平行线与垂直线的应用。
2.画图实践:通过画图,掌握平行线与垂直线的性质和判定方法。
3.理论学习:通过学习相关知识点,理解平行线与垂直线的理论基础。
4.练习题目:通过做练习题,巩固平行线与垂直线的知识和应用能力。
知识点:__________平行线与垂直线是数学中的基本概念,掌握它们的性质和判定方法对于学习几何和其他数学分支有很大帮助。
通过观察实物、画图实践、理论学习和练习题目,可以更好地理解和应用平行线与垂直线。
直线平面平行、垂直地判定及其性质的知识点
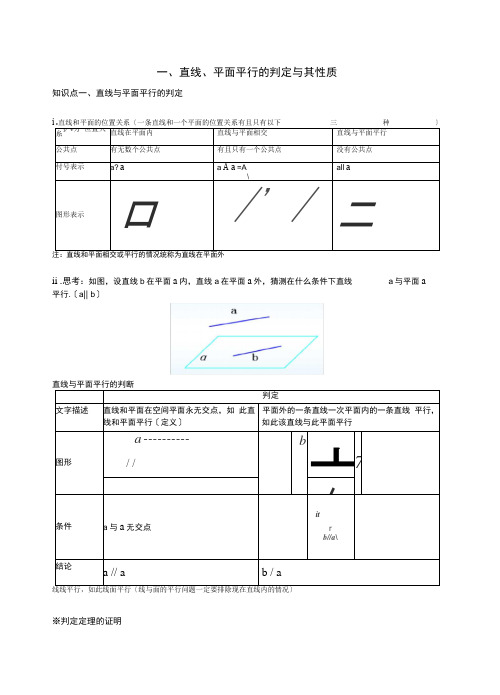
一、直线、平面平行的判定与其性质知识点一、直线与平面平行的判定ii .思考:如图,设直线b在平面a内,直线a在平面a外,猜测在什么条件下直线a与平面a 平行.〔a|| b〕※判定定理的证明特别提示证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线平行,证得“线面〃平行;②利用两平面平行的性质定理,通过“面面〃平行,证得“线面〃平行. 知识点三、平面与平面平行的判定、直线、平面垂直的判定与其性质知识点一、直线和平面垂直的定义与判定要点诠释:定义中“平面-内的任意一条直线"就是指“平面二:内的所有直线",这与“无数条直线〃不同〔线线垂直线面垂直〕知识点二、二面角I.二面角::从一条直线出发的两个半平面所组成的图形叫二面角〔dihedral angle 〕.这条直线叫做二面角的棱,这两个半平面叫做二面角的面•记作二面角一AB —.〔简记P —AB —Q〕.面角的平面角的三个特征:i .点在棱上ii.线在面内iii.与棱垂直n .二面角的平面角:在二面角一I —的棱I上任取一点O ,以点O为垂足,在半平面,内分别作垂直于棱丨的射线OA和0B,如此射线OA和0B构成的AOB叫做二面角的平面角• 作用:衡量二面角的大小;X 围:0°180°.2能保证直线 a 与平面a 平行的条件是〔A 〕 A.a a ,b a ,a / bB .b a ,a / b知识点四、平面和平面垂直的定义和判定定义 判定文字描述 两个平面相交,如果它们所成的二面角是 直二面角,就说这两个平面垂直 .一个平面过另一个平面的垂线,如此这两 个平面垂直 图形 k z结果aAp = l a -l- B =90° 戸 a 丄 B 1 丄 cxj c a:丄 0〔垂直问题中要注意题目中的文字表述,特别是“任何〃“随意〃“无数〃等字眼〕 知识点五、平面和平面垂直的性质面面垂直 '线面垂直〔如果两个平面垂直,那么一个平面内垂直于它们交线的直线与一个面平垂直〕例题1.如图,假如 是长方体ABCD-ABCQ 被平面EFGH 截去几何体 EFGHBD 后得到的几 何体,其中E 为线段A i B i 上异于B i 的点,F 为线段BB 上异于B 的点,且EH// A i D i , 如此如下结论中不正确的答案是A. EH // FGB. 四边形EFGH 是矩形C. 是棱柱D.是棱台 C. b a ,c / a ,a / b,a / cD. b a ,A € a,B € a,C € b ,D € b 且 AC = BD3如下命题正确的答案是〔 DF 〕A. 平行于同一平面的两条直线平行B. 假如直线a / a ,如此平面a 内有且仅有一条直线与a 平行 C. 假如直线a / a ,如此平面a 内任一条直线都与a 平行 D. 假如直线a / a ,如此平面a 内有无数条直线与 a 平行E. 如果a 、b 是两条直线,且 a / b ,那么a 平行于经过b 的任何平面F. 如果直线a 、b 和平面a 满足 a / b , a / a ,b a,那么b /a4在空间,如下命题正确的答案是〔A 〕平行直线的平行投影重合〔B 〕平行于同一直线的两个平面平行〔C〕垂直于同一平面的两个平面平行A. m , n〔D〕垂直于同一平面的两条直线平行5m n为两条不同的直线,a、B为两个不同的平面,如此如下命题中正确的答案是B. a m , nm// nC. ml a,m 丄n n / aD. n / m,n丄a m± a〔A〕如果平面丄平面,那么平面内一定直线平行于平面〔B〕如果平面垂直于平面,那么平面内一定不存在直线垂直于平面〔C〕如果平面丄平面,平面丄平面,丨,那么丨丄平面〔D〕如果平面丄平面,那么平面内所有直线都垂直于平面设盘上是悔条直线, 血是两个平酣则a Lb的一个充分条件是(A) a ± a.bll(i.Q1 /J (B) □丄a少丄p(C) a c a,b丄(D)a c a.bll丄08. 求证:空间四边形相邻两边中点的连线,平行于经过另外两边的平面:空间四边形ABCD中, E、F分别是AB AD的中点求证:EF”平面BCD9. 如图,在椎体P-ABCD中,ABCD1边长为1的棱形,且/ DAB=60, ,PB=2,E,F分别是BC,PC的中点.⑴证明:AD丄平面DEF;(2)求二面角P-AD-B的余弦值.课堂练习A组1已知砌理是两条不冋宜线,a t j8,y是三个不同平面'下列命题中正确的是()A•若fn\\ ay/II a,则加“舟 B.若c(一丁』丄人则口"0C*若卅队则伉//爪 D.若仍丄丄<7,则朋“料4.已拓两荼直线,阳个平和。
平行线和垂直线的判断知识点总结

平行线和垂直线的判断知识点总结在几何学中,平行线和垂直线是两个重要的线性概念。
它们的判断是我们解决几何问题的基础,因此掌握相关的判断知识点非常重要。
本文将从几何学的角度总结平行线和垂直线的判断知识点,帮助读者加深理解和运用。
1. 平行线的判断知识点平行线是指在同一个平面内,永远不会相交的两条直线。
下面是判断平行线的几个要点:(1) 对于两条直线来说,如果它们的斜率相等,那么它们是平行线。
斜率的计算公式是:斜率k = (y2 - y1) / (x2 - x1),其中(x1, y1)和(x2, y2)分别是直线上的两个点。
(2) 如果两条直线的斜率乘积为-1,则它们是互相垂直的。
例如,如果直线L1的斜率为m1,直线L2的斜率为m2,那么若m1 * m2 = -1,则L1和L2是互相垂直的。
(3) 如果两条直线的对应角或同位角是等于的,则这两条直线是平行线。
对应角指的是两条平行线被一条横截线所截得的角,同位角指的是两条平行线的对应角中的一组相等的角。
(4) 对于平行线L和一条横截线T来说,如果对于横截线上的两条线段的内角、外角关系满足:内角之和为180度,外角之和为360度,则L与T平行。
该性质被称为同旁内角和定理和同旁外角和定理。
2. 垂直线的判断知识点垂直线是指与另一条直线之间的夹角为90度的直线。
以下是判断垂直线的几个要点:(1) 对于两条直线来说,如果它们的斜率乘积为-1,则它们是互相垂直的。
这一点在判断平行线时已经提到过。
(2) 如果两条直线的斜率分别为k1和k2,那么它们是互相垂直的当且仅当k1 * k2 = -1。
(3) 如果两条直线是互相垂直的,那么它们的对应角也是互相垂直的。
(4) 垂直平分定理指出,若一条直线平分了另一条直线上的一段线段且垂直于该线段,那么该直线与该线段是垂直的。
综上所述,判断平行线和垂直线的方法有很多,但是其中最常用的是斜率和角度的关系。
通过计算斜率、对应角或同位角之间的关系,我们可以准确判断两条直线是平行的还是垂直的。
人教新课标四年级数学上册5.1《平行与垂直——垂线的画法》说课稿

人教新课标四年级数学上册5.1《平行与垂直——垂线的画法》说课稿一. 教材分析《平行与垂直——垂线的画法》这一节是人教新课标四年级数学上册第五章第一节的内容。
本节课主要让学生掌握垂线的定义和画法,理解垂直与平行的概念,并能够运用垂线和平行线的知识解决实际问题。
教材通过丰富的图片和生活实例,激发学生的学习兴趣,引导学生通过观察、操作、思考、交流等活动,掌握垂线的画法和垂直与平行的特征。
二. 学情分析四年级的学生已经具备了一定的观察能力、操作能力和表达能力,对于生活中的垂直和水平的概念有一定的认识。
但学生在画垂线方面可能还存在一定的困难,因此,在教学过程中,教师需要耐心引导,让学生充分理解和掌握垂线的画法。
三. 说教学目标1.知识与技能目标:学生能够理解垂线的定义,学会用三角板画垂线,掌握垂直与平行的特征。
2.过程与方法目标:通过观察、操作、思考、交流等活动,培养学生解决问题的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的合作意识。
四. 说教学重难点1.教学重点:垂线的定义,垂线的画法,垂直与平行的特征。
2.教学难点:垂线的画法,垂直与平行的应用。
五. 说教学方法与手段本节课采用情境教学法、启发式教学法、合作学习法等多种教学方法,并结合多媒体课件、实物模型、三角板等教学手段,引导学生主动参与,提高学生的学习兴趣和效果。
六. 说教学过程1.导入新课:通过展示生活中的垂直和平行现象,引导学生发现数学与生活的联系,激发学生的学习兴趣。
2.探究新知:引导学生观察、操作,发现垂线的特征,学会用三角板画垂线。
3.巩固新知:通过练习题,让学生运用垂线和平行线的知识解决问题。
4.课堂小结:总结本节课的学习内容,强化垂直与平行的概念。
5.布置作业:布置适量的课后练习,巩固所学知识。
七. 说板书设计板书设计要简洁明了,突出本节课的主要内容。
可以设计如下板书:垂线:垂直于水平线的线段画垂线:用三角板,沿水平线画垂直线段平行线:在同一平面内,不相交的两条直线八. 说教学评价本节课的教学评价主要从学生的知识掌握、能力培养、情感态度三个方面进行。
人教A版数学必修二课件:3.1.2 两条直线平行与垂直的判定

阅读页去广告
VIP有效期内享有搜索结果页以及文档阅读页免广告特权,清爽阅读没有阻碍。
多端互通
VIP有效期内可以无限制将选中的文档内容一键发送到手机,轻松实现多端同步。
抽奖特权
福利特权
知识影响格局,格局决定命运!
其他特 VIP专享精彩活动
α2tan α1=-1,
1
所以 tan α2=-tan
1
.
又0°≤α1<180°,0°≤α2<180°,
所以tan α2=tan(90°+α1),
则α2=90°+α1,所以l1⊥l2.
3.对任意两条直线,如果l1⊥l2,一定有k1·k2=-1吗?为什么?
提示:不一定,因为如果直线l1和l2分别平行于x,y轴,则k2不存在,所
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档(不含付费文档和VIP专享文档),每下载一篇共享文
档消耗一个共享文档下载特权。
年VIP
月VIP
连续包月VIP
服务特
权
共享文档下载特权
赠送每月15次共享文档下载特权,自
赠送的共享文档下载特权自VIP生效起每月发放一次,
享受100次共享文档下载特权,一次
综上所述,a的值为0或5.
反思感悟反思感悟两直线垂直的判定方法
两条直线垂直需判定k1k2=-1,使用它的前提条件是两条直线斜率
都存在,若其中一条直线斜率不存在,另一条直线斜率为零,此时两
直线也垂直,注意讨论的全面性.
-14-
3.1.2
两条直线平行与垂直的判定
探究一
探究二
机械设计平行度、垂直度公差等级

机械设计平行度、垂直度公差等级机械设计中的平行度和垂直度公差是非常重要的概念,它们在制造过程中对于零件的精度和质量起着至关重要的作用。
平行度和垂直度公差级别的确定对于机械零件的功能性和可靠性有着直接的影响。
本文将就机械设计中的平行度和垂直度公差等级进行详细的介绍和分析。
我们来介绍一下平行度和垂直度的概念。
平行度是指两个平面或者轴线之间的平行程度,而垂直度是指两个平面或者轴线之间的垂直程度。
在机械制造中,零件的平行度和垂直度公差级别的确定需要考虑到零件的具体用途和使用条件,以及制造成本等因素。
根据《GB/T1184-1986》标准,平行度和垂直度公差按照精度等级可分为IT级和数字级。
在IT级中,平行度和垂直度公差被分为IT01、IT0、IT1、IT2、IT3、IT4、IT5、IT6、IT7、IT8、IT9、IT10共12个等级。
其中IT01等级的平行度和垂直度公差最严格,IT10等级的平行度和垂直度公差最宽松。
IT级的平行度和垂直度公差适用于对于精度要求较高的机械零件,如精密仪器、汽车发动机零件等。
而在数字级中,平行度和垂直度公差被分为数字01、02、03、04、05、06、07、08、09、10、11、12、13、14、15、16共16个等级。
同样地,数字级的平行度和垂直度公差也是按照严格度递减的原则,数字01级的公差最小,数字16级的公差最大。
数字级的平行度和垂直度公差适用于对精度要求不是很高的机械零件,如一般机械设备的零部件。
在实际的机械设计和制造过程中,平行度和垂直度公差等级的选择需要综合考虑零件的功能要求、使用条件、制造工艺和成本等因素。
合理确定平行度和垂直度公差等级可以保证零件的尺寸精度、装配配合的合理性,从而提高零件的可靠性和使用寿命。
换言之,在满足机械设计要求的前提下,需根据实际情况灵活判断平行度和垂直度公差等级,以满足零件的使用要求,提高零部件的性能。
平行度和垂直度公差等级在机械设计中具有重要的地位,它直接影响了零件的准确度和稳定性。
四年级上册数学教案7.2:平行和垂直关系的认识

四年级上册数学教案-7.2:平行和垂直关系的认识数学是一门重要的学科,学生在学习数学的过程中,需要掌握的知识点很多,其中平行和垂直关系的认识是非常重要的一部分。
平行和垂直的关系是我们日常生活中经常遇到的,学生通过课堂学习,可以更好的理解这些关系,在应用中更加自如地运用。
学习目标:1.能够正确理解平行和垂直的概念,并能够运用所学知识在生活中解决问题。
2.能够准确判断平行和垂直的关系,并在图形中标示出来。
3.能够根据所学知识解决平行和垂直的问题,形成自己的思维方式。
教学重点:1.平行和垂直关系的概念、特点以及判断方法。
2.平行和垂直关系在生活中的应用。
3.帮助学生形成正确的思维方式,能够解决实际问题。
教学难点:1.学生对概念的理解和形象化的表示。
2.学生对平行与垂直之间相互转化的认识。
3.能否灵活运用所学知识的能力。
教学方法:1.情境化教学。
通过具体例子告诉学生何时需要用到平行和垂直关系。
2.教学实例化。
通过举例子来让学生感受平行和垂直的特点和应用。
3.引导探索。
让学生自己发现问题,引导学生进行思考和探究。
教学过程:一、自然情境引入一名学生在黑板上画了一个平行四边形和一个正方形。
教师引导学生看一下图形,询问学生这两个图形有何不同?询问学生是否知道这两个图形之间的关系,引导学生进行讨论,从而引出本节课的主题——平行和垂直关系。
二、概念理解1、平行线引导学生看图自己发现什么是平行线。
定义平行线:在同一平面内,永远不会相交的两条直线互相平行。
示意图2、垂直线引导学生看小视频,介绍垂直线。
定义垂直线:在同一平面内,相交而成的直角互相垂直。
示意图三、特点探究1、平行线:引导学生发现平行线的特点。
做以下实验:1.平面上各两条不同的平行线如下图,用直尺合成平行线的特点。
示意图2.再分别画两条新线,如上图,比较新线和原线之间的关系。
探究结果:所有新线都与原线平行。
2、垂直线:引导学生发现垂直线的特点。
做以下实验:1.在黑板上画正方形,选取一个角度,用直尺慢慢调整角度,使直尺和边都与原边相交成直角,这时把直尺固定住外围,再连接两个交点,如下图,便得到了垂直线。
人教版数学四年级上册第五单元第一课《平行与垂直》精品PPT课件

直线 可以向两端无限延长
在纸上任意画两条直线, 会有哪几种情况?
①
②
③
④
⑤
⑥
⑦ (1)、这几个图行怎么分类?
相交
①
③
⑥
不相交
②
④
⑤
⑦
②
④
⑦
⑤
相交
①
③
不相交
④
⑥ ⑦
②
⑤
永不相交
A
B
在同一平面内,不相交的两条直线叫平行 线,也可以说这两条直线互相平行。 其中一条直线是另一条的平行线。
———————— A
———————— B
直线A是直线B的平行线
直线B是直线A的平行线
直线A和直线B互相平行
———————— A
———————— B
直线A是直线B的平行线
直线B是直线A的平行线
直线A和直线B互相平行
———————— A
———————— B
直线A是直线B的平行线
直线B是直线A的平行线
直线A和直线B互相平行
相交
①
③
⑥
④
⑦
如果两条直线相交成直角,就说这两条 直线互相垂直,其中一条直线叫做另一条直 线的垂线,这两条直线的交点叫做垂足。
在同一平面内,如果两条 直线相交成直角,就说这 两条直线互相垂直。
其中一条直线叫做另一条 直线的垂线。
A⊥B
两条直线的交点叫做垂足。
B
A
O 垂足
(×)
判断下面的直线是平行还是 垂直。
平行
~ ~
垂直
平行
平行和垂直
看看几何图形中有没有垂直和平行的现象?
A
四年级上册数学说课稿-4.3 《垂直与平行》 ︳青岛版

四年级上册数学说课稿-4.3 《垂直与平行》︳青岛版一、教学目标 1. 知识与技能:掌握平行线和垂直线的基本概念;会判断平行线和垂直线;会根据图形特点判断两线的关系。
2. 过程与方法:通过观察实物,完成图形结构,引导学生归纳并发现新知,锻炼学生的观察与分析能力;采用竞赛、互动等活动形式,培养学生积极参与、团结合作的精神。
3. 情感态度与价值观:通过教学过程使学生感受到数学知识的实际应用及重要性,提高他们对学习数学的兴趣和自信心。
二、教学重难点重点1:垂直与平行的基本概念。
重点2:判断两条线是否垂直或平行。
难点1:在实际问题中如何判断两线的关系。
难点2:如何利用视频和实际事例引领学生理解垂直,平行的概念。
三、教学过程一、引入 1. 教师出示垂线、竖线、水平线等图形,引发学生对科技中直线的认识。
2. 让学生来描述这些直线的共性和区别。
二、学习新知 1. 垂线、竖线、水平线的概念 2. 平行线和垂直线的概念以及二者之间区别。
3. 判断平行线和垂直线的方法。
如先画线必须两条线都是平行的,两条线是垂直的时候也要使用画线方法,学生应该能清楚地看到线条是平行的或者互相垂直的。
4. 利用视频、实例等教材带领学生观察图形特点,判定两线之间的关系。
三、巩固练习 1. 将课上知识运用到实际问题中进行讨论,如描述两条线的关系、线条在图形中的位置等。
2. 利用小组竞赛和互动模拟等形式,使学生能够深入掌握并应用所学的知识。
四、课堂扩展 1. 教学媒体等方式展现与直线相关的图形。
2. 带领学生进行探究,让学生进行更深入的掌握和思考。
四、教学总结 1. 总结平行线和垂直线的基本概念、判断平行线和垂直线的方法以及如何应用图形特点判断两线之间的关系。
2. 让学生感受到数学知识的实际应用及重要性,并提高他们对学习数学的兴趣和自信心。
五、课后作业练习册上与本节课相关的题目练习,帮助学生巩固所学的知识点。
六、板书设计垂直、平行竖线、水平线判断平行线和垂直线的方法七、教学反思本堂课通过让学生观察实物、判断图形特点,引导学生进入数学知识学习的世界,同时让学生感到数学知识的实际应用及重要性,提高了学生对学习数学的兴趣和自信心。
新教材人教A版高中数学选择性必修第一册2.1.2 两条直线平行和垂直的判定 精品教学课件

由 AB⊥CD,且 AD∥BC, 得y-x 4×1=-1,
-23=x-y 1, 解得xy= =-10, 6, 所以点 D 的坐标为(10,-6).
角度2 平行、垂直在图形中的应用 典例 4 如图所示,在平面直角坐标系中,
四边形OPQR的顶点坐标按逆时针顺序依次为 O(0,0),P(1,t),Q(1-2t,2+t),R(-2t,2), 其中t>0.试判断四边形OPQR的形状.
题型探究
题型一Βιβλιοθήκη 两直线平行典例 1判断下列各小题中的直线l1与l2是否平行: (1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1); (2)l1的斜率为1,l2经过点A(1,1),B(2,2); (3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0); (4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5). [分析] 斜率存在的直线求出斜率,利用l1∥l2⇔k1=k2进行判断, 若两直线斜率都不存在,可通过观察并结合图形得出结论.
题型二
两直线垂直
典例 2 (1)直线l1经过点A(3,2),B(3,-1),直线l2经过点 M(1,1),N(2,1),判断l1与l2是否垂直; (2)已知直线l1经过点A(3,a),B(a-2,3),直线l2经过点C(2,3), D(-1,a-2),若l1⊥l2,求a的值. [分析] (1)若斜率存在,求出斜率,利用垂直的条件判断; 若一条直线的斜率不存在,再看另一条直线的斜率是否为0, 若为0,则垂直.
[规律方法] 关于直线平行,垂直的综合应用
(1)设出点的坐标,利用平行、垂直时的斜率关系建立方程(组) 去解.
(2)图形中的平行与垂直问题要充分利用图形性质求解,图形 的形状不确定时要分情况讨论.
两条直线平行与垂直的判定 课件

3.1.2 两条直线平行与垂直的判定
• ●知识衔接
• 1.直线的倾斜角与斜率. • 当直线倾斜角α≠90°时,斜率k=_____t_an_α___.当直线倾斜
角α=90°时,斜率k_不__存__在_____. • 直线倾斜角的范围是_0_°__≤_α_<_1_8_0_°______,直线斜率的取值
(4)l1 的斜率不存在,k2=12--11=0,画出图形,如下图所示,
则 l1⊥x 轴,l2⊥y 轴,∴l1⊥l2.
• 平面内两条直线相交,而且它们的夹角是___直__角_____,那 么这两条直线垂直.
• 4.已知直线l1的斜率为0,且直线l1⊥l2,则直线l2的倾斜角 为( )
• A.0° B.135° • C.90° D.180° • [答案] C • 5.直线l1的倾斜角为45°,l2∥l1,则l2的倾斜角为
[解析] 由题意知 A,B,C,D 四点在坐标平面内的位置, 如右图,
由斜率公式可得 kAB=2-5--34=13, kCD=-0-3-36=13, kAD=-30--3-4=-3, kBC=36--52=-12.
所以 kAB=kCD,由图可知 AB 与 CD 不重合, 所以 AB∥CD,由 kAD≠kBC,所以 AD 与 BC 不平行. 又因为 kAB·kAD=13×(-3)=-1, 所以 AB⊥AD, 故四边形 ABCD 为直角梯形.
两直线的倾斜角不相等,则一定 ③√
相交,故③正确
• 2.直线l1的斜率为k1=-3,直线l2的斜率为k2=-3,则l1与 l2( )
• A.平行 B.垂直
• C.重合 D.平行或重合
• [答案] D
3.已知直线 l1 的斜率为 a,l2⊥l1,则 l2 的斜率为( )
t字之谜 (2)

T字之谜引言T字,是一个字母和符号中具有特殊意义和用途的一个字符。
它在各种领域中都有着重要的作用,如数学、计算机科学和语言学等。
本文将探讨T字的起源、应用和神秘之处。
起源T字最早可追溯到古代文字和象形文字的演变。
根据历史学家的研究,T字最初是一种象征着天空和神圣的符号。
在许多文明中,T字被认为是连接天堂与人类的桥梁,象征着信仰和力量。
在古希腊,T字是Theta(Θ)的形式,代表着神秘和智慧。
它被用来表示希腊神话中的一些重要神祇,如智慧女神雅典娜。
在数学上,T字也被用来表示角度和三角函数等概念。
数学中的T字在数学领域,T字有着重要的意义。
它代表着垂直和平行的概念。
例如,在几何学中,T字被用来表示垂直线和直角。
此外,T字还被用来表示平面直角坐标系中的X轴和Y轴。
在代数学中,T字被用来表示变量或未知数。
当一个方程中有未知数时,我们通常用T字表示该未知数。
例如,方程2T + 5 = 15中,T就代表了一个未知数。
计算机科学中的T字T字在计算机科学中也有广泛的应用。
在编程语言中,T字常用来表示泛型类型。
泛型类型可以适用于不同的数据类型,使程序具有更高的灵活性和可重用性。
此外,T字还用于描述树形结构中的子树。
当一个树状结构中包含多个子树时,我们可以用T字来表示每个子树的根节点。
语言学中的T字在语言学中,T字代表着时间。
它常被用来表示动词的时态,如过去时(T1)和现在时(T2)。
通过使用T字,我们可以清晰地表示事件发生的时间顺序。
此外,在语义学中,T字还用来表示真值。
当一个陈述为真时,我们用T字来表示其真值为真。
T字的神秘之处虽然T字在不同领域中有着各种应用,但它也有一些神秘的特性。
许多人认为,T字象征着平衡和完美。
它的两条直线形成了一个稳定的结构,具有固有的坚韧性。
另外,一些研究人员认为,T字还具有宇宙的秘密。
他们认为,T字代表着宇宙中的时间和空间,是连接和统一一切的力量。
结论T字作为一个字母和符号,具有着多种意义和应用。
理解平行线与垂直线的性质

理解平行线与垂直线的性质在数学中,平行线和垂直线是两种常见的线性关系。
它们有各自独特的性质与特点。
理解这些性质对于解决几何问题以及应用数学在实际生活中具有重要意义。
本文将深入探讨平行线和垂直线的性质,以及它们在数学和实际应用中的重要性。
一、平行线的性质平行线是指在同一平面中永远不会相交的两条直线。
它们具有以下的性质:1. 平行线具有相同的斜率:在直角坐标系中,平行线的斜率是相同的。
假设有两条平行线L1和L2,它们的斜率分别为m1和m2,则m1 = m2。
2. 平行线的对应角相等:当一条直线与两条平行线相交时,对应角是相等的。
例如,对于平行线L1和L2,以及与它们相交的直线T,∠A = ∠D,∠B = ∠E,∠C = ∠F。
3. 平行线之间的距离相等:对于平行线L1和L2上的任意一点A和B,它们到一条直线上的垂直距离是相等的。
这些性质使得平行线在几何证明中起到重要的作用。
通过应用这些性质,可以解决各种与平行线相关的问题,如等腰三角形、相似三角形以及平行线切割定理等。
二、垂直线的性质垂直线是指在同一平面中与另一条线段或直线相交,且交角为90度的直线。
以下是垂直线的性质:1. 垂直线的斜率之乘积为-1:如果一条直线的斜率为m,则与其垂直的直线的斜率为-1/m。
这一性质在解决垂直线相关问题时很有帮助。
2. 垂直线相交角为90度:当两条直线相交且交角为90度时,它们被定义为垂直线。
这样的两条线段或直线在几何学中起到重要的作用,例如构成直角三角形以及垂直平分线等。
垂直线的性质也被广泛应用于实际生活中。
例如,在建筑设计中,垂直线的概念用于确保房屋的立柱或墙壁垂直于地面。
在地图绘制中,垂直线用于标记和测量地理位置以及确定方向。
三、平行线与垂直线的重要性正确理解和应用平行线和垂直线的性质具有重要的意义:1. 解决几何问题:平行线和垂直线的性质是解决几何问题的基础。
通过应用这些性质,可以进行线段比较、三角形相似性判断、角度测量等,从而解决各种几何问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、垂直和平行
课题:垂直与平行的概念
教学内容:
同一平面内两条直线的特殊位置关系,垂直与平行。
(课文第56页57页的例1,及相应的“做一做”及练习)
教学目标:
1、初步理解垂直与平行是在同一平面内两条直线的两种特殊的位置关系。
2、初步认识垂直与平行线线
3、培养学生的观察能力,空间想象能力和抽象概括能力。
教学重点:理解垂直与平行的概念。
教学难点:理解平行与垂直这两种关系的界定前提是同一平面。
教具准备:课件、三角板、直尺、手工纸、挂图学具准备。
教学过程:
一、创设情境,引入新课
1口答
直线的特点是什么?
2谈话
两根铅笔落在地上后可能会形成哪些图形?
二、探索比较,掌握特征
(一)、学习平行线
1、学习平行线
把可能出现的图形用铅笔摆一摆,摆完后,小组长组织大家把可能出现的图形用小棒摆在展示板上。
2、教师巡视,参与讨论,了解情况。
3、提出平行意义
4、举例;说一说生活中的平行
5、提问:平行有什么特点?
6、完整概括平行线的概念。
7、质疑
三条或更多条直线不想交,是否也叫平行线?
(二)、学习垂直
1、两支铅笔相交会出现两种情况
2、观察一下各是什么角?
3、相交的两条直线形成的四个角,如果都是90度,就说这两条直线相互垂直,其中一条叫另外一条的垂线,这两条直线的焦点叫做垂足。
4、练习
观察下面向组图形,看哪两条直线相交成直角,哪两直线是互相垂直的?
①②③④
问:两条直线互相垂直的关键是什么?引导学生明确:两条直线互相垂
5、找一找、想一想你的身边还有哪些物体的边是互相垂直的?
6、小结
师归纳总结并板书,互相垂直、垂线和垂足的概念
三、发现两条平行线间的距离处处相等
1、在平行线间画出几条垂直线段
2、观察,度量这些垂直线段的长度,有什么发现?
3、汇报
四、全课总结,完善认知。
同学们,你觉得这节课里你表现怎样?你有什么收获和体会?
五、课后作业
六、课后反思:。
