冀教版九年级数学下册《直线与圆的位置关系》PPT课件(3篇)
合集下载
新冀教版九年级下册数学课件(第29章 直线与圆的位置关系)

思考: 足球运动员踢出的足球在球场上滚动,在足球
穿越中圈区(中间圆形区域)的过程中,可将足球 看成一个点,这个点与圆具有怎样的位置关系?
在同一个平面内,点与圆有三种位置关系: 点在圆外、点在圆上和点在圆内. 点P与☉O的位置关系如图所示.
知1-导
知1-导
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
知2-练
1 已知一个圆的直径为10. 如果这个圆的圆心到一条 直线的距离分别等于3,5,6,那么这条直线与这个圆 的位置关系分别是怎样的?
解:因为圆的直径为10,所以圆的半径为5.当直线与圆 心的距离等于3时,因为3<5,所以直线与圆相交; 当直线与圆心的距离等于5时,因为5=5,所以直 线与圆相切; 当直线与圆心的距离等于6时,因为6>5,所以直 线与圆相离.
B.点P法确定
知1-练
4 【中考·宜昌】在公园的O处附近有E,F,G,H 四棵树,位置如图所示(图中小正方形的边长均相 等).现计划修建一座以O为圆心,OA为半径的圆 形水池,要求池中不留树木,则E,F,G,H四棵 树中需要被移除的为( A ) A.E,F,G B.F,G,H C.G,H,E D.H,E,F
解:如图,过点A作AC⊥ON于C, 以点A为圆心,200米为半径作 圆,与MN交于点B,D,连接 AB,AD,则AB=AD=200米,
知2-讲
∵∠QON=30°,OA=240米, ∴AC=120米. 当火车到B点时对A处产生噪音影响, ∵AB=200米,AC=120米, ∴由勾股定理得BC=160米,同理可得CD=160米, ∴BD=320米. ∵72千米/时=20米/秒, ∴A处受到噪音影响的时间应是320÷20=16(秒).
的公共点个数有____三____种情况.
冀教版九年级下册 数学 课件 29.2 直线与圆的位置关系2(18张PPT)

,以C为圆心,分别以2cm,2.4cm,3cm为半径 画⊙C,斜边AB与⊙C分别有怎样的位置关系? 为什么?
分析
B
根据圆心到直线的距离d与半
径r的大小在进R行t比△较A:BC中, 距离关Ad,B键这=是个确距定离2圆是心什C到2么直呢线?A怎2B么的 求这=个距=5离(呢c?m)
根据三角形面积公式有
(2)当r=2.4cm时, 有d=r, 因此⊙C和AB相切.
D
d
(3)当r=3cm时,有d<r, 因此,⊙C和AB相交.
D
d
深入思考
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm, 以C为圆心,r为半径作圆. (1)当r满足0cm<r<2.4cm 时,
⊙C与直线AB相离.
(2)当r满足 r>2.4cm 时, ⊙C与直线AB相交.
(3) 如图,假设拖拉机在公路MN上沿PN方向行驶到点C处学校开始受到影响,
那么AC=100(m),
BC2 1002 802由 3勾60股0定理得:
,∴ BC=60。
同理,拖拉机行驶到点D处学校开始脱离影响, 那么,AD=100(m), BD=60(m), ∴CD=120(m)。
拖拉机行驶的速度为 : t=120m÷6m/s=20s。
这节课你学会了什么? 有什么感想?
课后作业
必做题:A组1、2题 B组1题
选做题:B组2题
谢谢
走入生活
如图,公路MN和公路PQ在P点相交, ∠QPN=30°,点A处有一所幼儿园,AP=160m,假 设拖拉机行驶时周围100m以内会受到噪音的影响.
(1)画出幼儿园到公路MN的距离.
(2)求出幼儿园到公路MN的距离
,并说明拖拉机行驶时,学校
分析
B
根据圆心到直线的距离d与半
径r的大小在进R行t比△较A:BC中, 距离关Ad,B键这=是个确距定离2圆是心什C到2么直呢线?A怎2B么的 求这=个距=5离(呢c?m)
根据三角形面积公式有
(2)当r=2.4cm时, 有d=r, 因此⊙C和AB相切.
D
d
(3)当r=3cm时,有d<r, 因此,⊙C和AB相交.
D
d
深入思考
在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm, 以C为圆心,r为半径作圆. (1)当r满足0cm<r<2.4cm 时,
⊙C与直线AB相离.
(2)当r满足 r>2.4cm 时, ⊙C与直线AB相交.
(3) 如图,假设拖拉机在公路MN上沿PN方向行驶到点C处学校开始受到影响,
那么AC=100(m),
BC2 1002 802由 3勾60股0定理得:
,∴ BC=60。
同理,拖拉机行驶到点D处学校开始脱离影响, 那么,AD=100(m), BD=60(m), ∴CD=120(m)。
拖拉机行驶的速度为 : t=120m÷6m/s=20s。
这节课你学会了什么? 有什么感想?
课后作业
必做题:A组1、2题 B组1题
选做题:B组2题
谢谢
走入生活
如图,公路MN和公路PQ在P点相交, ∠QPN=30°,点A处有一所幼儿园,AP=160m,假 设拖拉机行驶时周围100m以内会受到噪音的影响.
(1)画出幼儿园到公路MN的距离.
(2)求出幼儿园到公路MN的距离
,并说明拖拉机行驶时,学校
《直线与圆的位置关系》PPT课件下载-冀教版九年级数学下册

2:已知圆x2+y2=8, 定点p(4,0), 问过p点的 直线的倾斜角在什么范围内取值时, 这条直线 与圆(1)相切, (2)相交, (3)相离
3:已知直线L:kx-y+6=0被圆 x2+y2=25截得的弦长为8,求k值
; 带电清洗剂 http://www.hnlqhg.com 带电清洗剂 ;
4.2 直线与圆的位置关系
4.2.1 直线与圆的位置关系
直线与圆的位置关系:
(1)直线与圆相交, 有两个公共点; (2)直线与圆相切, 只有一个公共点; (3)直线与圆相离, 没有公共点;
问题:如何用直线和圆的方程判断它们之 间的位置关系?
直线与圆的位置关系的判定方法:
直线l:Ax+By+C=0
Y
2、判断直线3x+4y+2=0与 圆x2+y2-2x=0的位置关系. C(1、3)
0
X
3x-4y-6=0
例2、已知过点M(-3,-3)的直线l被圆
x2+y2+4y-21=0所截得的弦长为4 5,求直线l的
方程。
yM. .OFra bibliotekxE
F
问题:一艘轮船在沿直线返回港口的途中, 接
到气象台的台风预报:台风中心位于轮船正西
圆C:(x-a)2+(y-b)2=r2(r>0)
(1)利用圆心到直线的距离d与半径r的大小关
系判断:
aA bB C
d
A2 B2
d >r
直线与圆相离
d =r
直线与圆相切
d <r
直线与圆相交
(2) 利用直线与圆的公共点的个数进行判断:
设方程组(AxxaB)2y
3:已知直线L:kx-y+6=0被圆 x2+y2=25截得的弦长为8,求k值
; 带电清洗剂 http://www.hnlqhg.com 带电清洗剂 ;
4.2 直线与圆的位置关系
4.2.1 直线与圆的位置关系
直线与圆的位置关系:
(1)直线与圆相交, 有两个公共点; (2)直线与圆相切, 只有一个公共点; (3)直线与圆相离, 没有公共点;
问题:如何用直线和圆的方程判断它们之 间的位置关系?
直线与圆的位置关系的判定方法:
直线l:Ax+By+C=0
Y
2、判断直线3x+4y+2=0与 圆x2+y2-2x=0的位置关系. C(1、3)
0
X
3x-4y-6=0
例2、已知过点M(-3,-3)的直线l被圆
x2+y2+4y-21=0所截得的弦长为4 5,求直线l的
方程。
yM. .OFra bibliotekxE
F
问题:一艘轮船在沿直线返回港口的途中, 接
到气象台的台风预报:台风中心位于轮船正西
圆C:(x-a)2+(y-b)2=r2(r>0)
(1)利用圆心到直线的距离d与半径r的大小关
系判断:
aA bB C
d
A2 B2
d >r
直线与圆相离
d =r
直线与圆相切
d <r
直线与圆相交
(2) 利用直线与圆的公共点的个数进行判断:
设方程组(AxxaB)2y
【精品课件】九年级数学下册 直线与圆的位置关系 课件(共22张PPT)
知识点 正多边形及其外接圆
不是任何多边形(边数大于3)都有外接圆和内 切圆,但任何正多边形都有一个外接圆和一个内切 圆,这两个圆是同心圆.
知识点 正多边的有关计算
利用正多边形的有关数据,我们可以进行平面图形的镶嵌.
知识点 正多边形的画法
设计美丽的图案: (1)以圆的三等分点为圆心,圆的半径为半径作三条弧; (2)以正六边形各边的中点为圆心,正六边形的边长为直径向圆外画半圆; (3)作圆的内接正五边形,再以正五边形的各个顶点为圆心,边长为半径画 十条弧.
下雨天,当你快速转动雨伞时, 雨伞上的水珠就是顺着伞边切线 方向飞出去的(把伞面抽象成一个 圆).
知识点 切线的判定定理
圆的切线必须同时具备两个条件: (1)经过半径的外端; (2)垂直于这条半径.
第二十九章 直线与圆的位置关系
29.4 切线长定理*
知识点 切线长及切线长定理
如果将人的手臂看作是 一条直线,身体也成一条线,画 出这个造型的截面图如图所 示,即切线长定理的基本几何 模型.
知识点 三角形的内切圆
图中这条美丽的花边中三角形的各边都和圆 相切,这个三角形是圆的外切三角形,这个圆是三 角形的内切圆.
知识点 三角形的内切圆
三角形的内心是三角形三个内角的平分线的交点,通过作 出三角形三个内角的平分线,可以找到内心.在实际操作过程中, 画出两个内角的平分线,找到交点,该交点就是三角形的内心.
学科素养课件
冀教版·数学 九年级下
第二十圆的位置关系
知识点 点和圆的位置关系
足球运动员踢出的足球在球场 上滚动,在足球穿越中圈区(中间圆形 区域)的过程中,可将足球看成一个点, 这个点与圆就体现了点在圆内、点 在圆上、点在圆外三种位置关系.
2直线与圆的位置关系 课件冀教版数学九年级下册

问题2:请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上
移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点 个数最少时有几个?最多时有几个?
● ● ●
l
最少0个 最多2个
学习目标
自主学习
填一填:
直线与圆的 位置关系
合作探究 相离
当堂检测 相切
课堂总结 相交
图形
公共点个数
0个
公共点名称
直线名称
(1)
(2)
(3)
.O
.O
.O
相离
相交
相切
(4) .O
相交
(5) ? .O 相交
注意:直线是可 以无限延伸的.
学习目标
自主学习
合作探究
当堂检测
课堂总结
探究二:用数量关系判断直线与圆的位置关系
问题1:同学们用直尺在圆上移动的过程中,除了发现公共点的个数产生了 变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
第二十九章 直线与圆的位置关系 29.2 直线与圆的位置关系
学习目标
自主学习
合作探究
当堂检测
课堂总结
1.理解掌握直线与圆的三种位置关系 2.理解直线与圆三种位置关系的性质,并解决简单问题(重点)
学习目标
自主学习
合作探究
当堂检测
课堂总结
复习回顾
点和圆的位置关系有几种?
⑴点在圆内
·P r O
用数量关系如何来判断呢? (令OP=d )
d<r
⑵点在圆上
P· O r
d=r
⑶点在圆外
r
P·
O
d>r
学习目标
自主学习
冀教版数学九年级下册全套ppt课件精选全文

∴OA⊥PA,OB⊥PB
又∵ ∠APB=40°,∴∠AOB=140°
︵ ︵
又∵AB=AB
∴∠AOB=2∠ACB
∴∠ACB=70°
B
C
练 习
如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
A
求证:PE是⊙O的切线。
O
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
A
d
C
O
B
点到圆心距离为d
⊙O半径为r.
(1)d<r
点A在圆内
(2)d=r
点B在圆上
(3)d>r
点C在圆外
三种位置关系
观察探究一
你发现这个自然现象反映出直线和圆的公共点
个数有几种情况?
探究活动二
请同学们在练习本上画一个圆,把直尺边缘看成一条直线,
平移直尺。
直线和圆分别有几个公共点?
两个公共点
●O
这点和切点之间的线段的长。
B
P
O
C
小结:切线是直线,不可以度量;切线长是指切线
上的一条线段的长,可以度量。
下面进一步探讨,先请一些同学做小实验:
(1)请同学们观察当圆变化时,切线长PA、PB之间
的关系,同时注意 1、2 之间的关系。
(2)请根据你的观察尝试总结它们之间的关系。
A
1
2
O
B
p
A
你能不能用所
2.用图形表示如下:
有两个公共点
有一个公共点
.o
.o
.
l
.o
l
l
相切
相交
又∵ ∠APB=40°,∴∠AOB=140°
︵ ︵
又∵AB=AB
∴∠AOB=2∠ACB
∴∠ACB=70°
B
C
练 习
如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,
PE⊥AC于E。
A
求证:PE是⊙O的切线。
O
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
A
d
C
O
B
点到圆心距离为d
⊙O半径为r.
(1)d<r
点A在圆内
(2)d=r
点B在圆上
(3)d>r
点C在圆外
三种位置关系
观察探究一
你发现这个自然现象反映出直线和圆的公共点
个数有几种情况?
探究活动二
请同学们在练习本上画一个圆,把直尺边缘看成一条直线,
平移直尺。
直线和圆分别有几个公共点?
两个公共点
●O
这点和切点之间的线段的长。
B
P
O
C
小结:切线是直线,不可以度量;切线长是指切线
上的一条线段的长,可以度量。
下面进一步探讨,先请一些同学做小实验:
(1)请同学们观察当圆变化时,切线长PA、PB之间
的关系,同时注意 1、2 之间的关系。
(2)请根据你的观察尝试总结它们之间的关系。
A
1
2
O
B
p
A
你能不能用所
2.用图形表示如下:
有两个公共点
有一个公共点
.o
.o
.
l
.o
l
l
相切
相交
29.2 直线与圆的位置关系-2021春冀教版九年级数学下册课件

归纳:直线l和⊙O相交____d_<_r_____ 直线l和⊙O相切____d_=_r_____ 直线l和⊙O相离____d_>_r_____
目录
新知导入 课程讲授 随堂练习 课堂小结
目录
直线与圆的位置关系的数量表示
例 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,2cm, 2.4cm,3cm为半径画⊙C,斜边AB分别与⊙C有怎样的位置关系? 为什么?
6.在直角坐标系中,⊙M的圆心坐标是(m,0),半径是2,如果 ⊙M与y轴所在的直线相切,那么m=__±__2_;如果⊙M与y轴所 在的直线相交,那么m的取值范围是__-_2_<__m_<__2___.
目录
新知导入 课程讲授 随堂练习 课堂小结
目录
CONTENTS
4
新知导入 课程讲授 随堂练习 课堂小结
AC BC=ABCD
∴ CD AC BC 3 4 2.4(cm),
AB
5
即圆心C到AB的距离d=2.4cm.
当r=2cm时,d >r, 斜边AB⊙C和相离.
当r=2.4cm时, d =r, 斜边AB⊙C和相切.
当r=3cm时,d <r, 斜边AB⊙C和相交.
C AD
目录
B
新知导入 课程讲授 随堂练习 课堂小结
直线与圆的 位置关系
相离
定义 相切
性质
相交 公共点的个数
d与r的数量关系
相离:0个 相切:1个 相交:2个
相离:d>r 相切:d=r 相交:d<r
定义法
0个:相离; 1个:相切; 2个:相交
判定 性质法
d>r:相离 d=r:相切 d<r:相交
目录
新知导入 课程讲授 随堂练习 课堂小结
目录
直线与圆的位置关系的数量表示
例 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,2cm, 2.4cm,3cm为半径画⊙C,斜边AB分别与⊙C有怎样的位置关系? 为什么?
6.在直角坐标系中,⊙M的圆心坐标是(m,0),半径是2,如果 ⊙M与y轴所在的直线相切,那么m=__±__2_;如果⊙M与y轴所 在的直线相交,那么m的取值范围是__-_2_<__m_<__2___.
目录
新知导入 课程讲授 随堂练习 课堂小结
目录
CONTENTS
4
新知导入 课程讲授 随堂练习 课堂小结
AC BC=ABCD
∴ CD AC BC 3 4 2.4(cm),
AB
5
即圆心C到AB的距离d=2.4cm.
当r=2cm时,d >r, 斜边AB⊙C和相离.
当r=2.4cm时, d =r, 斜边AB⊙C和相切.
当r=3cm时,d <r, 斜边AB⊙C和相交.
C AD
目录
B
新知导入 课程讲授 随堂练习 课堂小结
直线与圆的 位置关系
相离
定义 相切
性质
相交 公共点的个数
d与r的数量关系
相离:0个 相切:1个 相交:2个
相离:d>r 相切:d=r 相交:d<r
定义法
0个:相离; 1个:相切; 2个:相交
判定 性质法
d>r:相离 d=r:相切 d<r:相交
精品九年级数学下册29直线与圆的位置关系小结与复习课件新版冀教版精品ppt课件
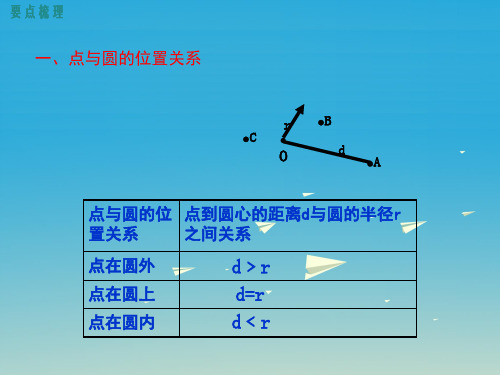
图2
方法总结
本题之类的题目中,常因混淆了“直线与圆只有一个交点 ”和“线段与圆只有一个交点”或“射线与圆只有一个交点”的区 别.实际上,当直线与圆只有一个交点时,直线与圆一定相切 ,而线段与圆只有一个交点或射线与圆只有一个交点时,它 们与圆的位置关系可能相切,也可能是相交.
针对训练
1.如图,直线l:y=x+1M为圆心,2个单位长度为
针对训练
4. 如图,正六边形ABCDEF内接于半径为 5的⊙O,四边形EFGH是正方形.
⑴求正方形EFGH的面积;
⑵连接OF、OG,求∠OGF的度数.
解:⑴∵正六边形的边长与其半径相等,∴EF=OF=5.
∵四边形EFGH是正方形,∴FG=EF=5,∴正方形EFGH
的面积是25.
⑵∵正六边形的边长与其半径相等,∴∠OFE=600.
点和圆的位置关系
与圆有关的位置关系
直线和圆的位置关系 切线的判定与性质
三角形的内切圆
圆
正多边形和圆
等分圆
中心角及内角和的计算
课后作业
见《学练优》河北中考热点专练
半径作⊙M,当⊙M与直线l相切时,则m的值为_2__5___2_.
考点二 切线的性质与判定
例2 如图,以△ABC的边AB为直径的⊙O交边AC于点D, 且过点D的切线DE平分边BC. 问:BC与⊙O是否相切?
解:BC与⊙O相切. 理由:连接OD,BD, ∵DE切⊙O于D,AB为直径, ∴∠EDO=∠ADB=90°. 又DE平分CB,∴DE=2(1)BC=BE. ∴∠EDB=∠EBD. 又∠ODB=∠OBD,∠ODB+ ∠EDB=90°,∴∠OBD+∠DBE=90°, 即∠ABC=90°. ∴BC与⊙O相切.
公共点,求r的值或取值范围. 解:当射线OM与⊙P相切时,射线OM与⊙P只有 一个公共点. 过点P作PA⊥OM于A,如图1所示. 在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
方法总结
本题之类的题目中,常因混淆了“直线与圆只有一个交点 ”和“线段与圆只有一个交点”或“射线与圆只有一个交点”的区 别.实际上,当直线与圆只有一个交点时,直线与圆一定相切 ,而线段与圆只有一个交点或射线与圆只有一个交点时,它 们与圆的位置关系可能相切,也可能是相交.
针对训练
1.如图,直线l:y=x+1M为圆心,2个单位长度为
针对训练
4. 如图,正六边形ABCDEF内接于半径为 5的⊙O,四边形EFGH是正方形.
⑴求正方形EFGH的面积;
⑵连接OF、OG,求∠OGF的度数.
解:⑴∵正六边形的边长与其半径相等,∴EF=OF=5.
∵四边形EFGH是正方形,∴FG=EF=5,∴正方形EFGH
的面积是25.
⑵∵正六边形的边长与其半径相等,∴∠OFE=600.
点和圆的位置关系
与圆有关的位置关系
直线和圆的位置关系 切线的判定与性质
三角形的内切圆
圆
正多边形和圆
等分圆
中心角及内角和的计算
课后作业
见《学练优》河北中考热点专练
半径作⊙M,当⊙M与直线l相切时,则m的值为_2__5___2_.
考点二 切线的性质与判定
例2 如图,以△ABC的边AB为直径的⊙O交边AC于点D, 且过点D的切线DE平分边BC. 问:BC与⊙O是否相切?
解:BC与⊙O相切. 理由:连接OD,BD, ∵DE切⊙O于D,AB为直径, ∴∠EDO=∠ADB=90°. 又DE平分CB,∴DE=2(1)BC=BE. ∴∠EDB=∠EBD. 又∠ODB=∠OBD,∠ODB+ ∠EDB=90°,∴∠OBD+∠DBE=90°, 即∠ABC=90°. ∴BC与⊙O相切.
公共点,求r的值或取值范围. 解:当射线OM与⊙P相切时,射线OM与⊙P只有 一个公共点. 过点P作PA⊥OM于A,如图1所示. 在Rt△AOP中,r=PA=OP·sin∠POA=2.5(㎝).
冀教版初中九年级下册数学课件 《直线与圆的位置关系》PPT1

∴AB是⊙O的切线
∵OC为⊙O的半径
如果知道直线是圆的切线,有什么性质定理呢?
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并 说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E 作⊙O的切线交AC的延长线于点D,试判断△AED的 形状,并说明理由.
.B1
.O
.A
.B
.B2
.A2
是是非非
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。()
.
O
判断 1.经过半径外端的直线是圆的切线() 2.与半径垂直的直线是圆的切线()
l
注意:若直线满足①, 而不满足②;
若直线满足②, 而不满足①。
×
×
例1直线AB经过⊙O上的点C,并且OA=OB,CA=CB, 求证:直线AB是⊙O的切线.
证明:连接OC
∵在△OAB中,OA=OB, CA=CB
∴OC⊥AB
随堂练习
1.已知圆的半径等于5厘米,圆心到直线l的距离是:(1)4厘米;(2)5厘米;(3)6厘米.直线l与圆分别有几个公共点?分别说出直线l和圆的位置关系. 2.已知圆的半径等于10厘米,直线l和圆只有一个公共点,求圆心到直线l的距离. 3.如果⊙O的直径为10厘米,圆心O到直线AB的距离为10厘米,那么⊙O和直线AB有怎样的位置关系?
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
直线与圆的 位置关系
相离
相切
相交
图 形
公共点个数
公共点名称
∵OC为⊙O的半径
如果知道直线是圆的切线,有什么性质定理呢?
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并 说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E 作⊙O的切线交AC的延长线于点D,试判断△AED的 形状,并说明理由.
.B1
.O
.A
.B
.B2
.A2
是是非非
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。()
.
O
判断 1.经过半径外端的直线是圆的切线() 2.与半径垂直的直线是圆的切线()
l
注意:若直线满足①, 而不满足②;
若直线满足②, 而不满足①。
×
×
例1直线AB经过⊙O上的点C,并且OA=OB,CA=CB, 求证:直线AB是⊙O的切线.
证明:连接OC
∵在△OAB中,OA=OB, CA=CB
∴OC⊥AB
随堂练习
1.已知圆的半径等于5厘米,圆心到直线l的距离是:(1)4厘米;(2)5厘米;(3)6厘米.直线l与圆分别有几个公共点?分别说出直线l和圆的位置关系. 2.已知圆的半径等于10厘米,直线l和圆只有一个公共点,求圆心到直线l的距离. 3.如果⊙O的直径为10厘米,圆心O到直线AB的距离为10厘米,那么⊙O和直线AB有怎样的位置关系?
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
直线与圆的 位置关系
相离
相切
相交
图 形
公共点个数
公共点名称
冀教版数学九下2直线与圆的位置关系教学课件

在Rt△ABC中,∠C=90°,AC=3cm, BC=4cm,以C为圆心,r为半径作圆.
1、当r满足_0__c_m_<__r_<__2_._4_c_m__时,
⊙C与直线AB相离.
B
d=2.4c m
2、当r满足_r_=__2_.4__c_m____ 时,
⊙C与直线AB相切.
5
3、当r满足__r_>___2_.4__c_m__时,
系?若把 A向左平移呢? ⊙
[z x x k 学科网]
(2)若要使⊙A与x轴、y轴都相切,则圆心A应当移到
什么位置?请写出点A所有可能位置的坐标. [zxxk学科网]
是方程X2-4x+m=0的两根,且直线m与⊙O相
切,则m的值为__4_____。
4、选择题:
(1)已知∠OAB = 30°,OA = 10,则以O为圆心,6为半径 的圆与射线AB的位置关系是(A )
A.相交 B.相切 C.相离 D.不能确定
(2)设圆的直径长为a,一条直线和圆有公共点,直线和圆心 的距离为d,则(B )
解:过点M作MC⊥OA于C ,
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm ⑴ ∵ d=MC=2.5, r=2 即r=4 即d < r
O
∴ ⊙O与OA相交;
A C
.
MB
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.
随堂检测
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( A):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( C ):
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
d
1 CD AB 1 AC BC
2
2
∴ CD AC BC 3 4 2.4(cm)
AB
5
即圆心C到AB的距离d=2.4cm
所以 (1)当r=2cm时,有d>r,因此⊙C和AB相离.
(2)当r=2.4cm时,有d=r, 因此⊙C和AB相切.
D
d
(3)当r=3cm时,有d<r, 因此,⊙C和AB相交.
灵活应用
1. 如图:∠AOB = 30°M是OB上的一点,且OM =5 cm 以M为 圆心,以r 为半径的圆与 直线OA 有怎样的关系?为什么?A (1)r = 2 cm ; (2) r = 4 cm ; (3) r = 2.5 cm .
解: 过 M 作 MC⊥OA 于 C,在 Rt C
△OMC 中, ∠AOB = 30°
O 30°
2.5
MC= 1 OM= 1 x5=2.5
2
2
5M
B
即圆心 M 到OA的距离 d = 2.5 cm.
(1) 当 r = 2 cm 时,有 d > r, 因此⊙M 和 直线OA 相离. (2) 当 r = 4 cm 时,有 d < r, 因此⊙M 和直线O A 相交.
(3) 当 r = 2.5cm 时,有 d = r ,因此⊙M 和直线 OA 相切.
D
d
知识小结 直线与圆的位置关系:
图形
.O r d┐ l
直线与圆的 位置关系
相离
公共点的个数 0
圆心到直线的距离
d 与半径 r 的关系 d>r
公共点的名称
直线名称
.o
.O
d .┐r l
A
. r ┐d .
B
lC
相切 相交
1
2
d=r 切点 切线
d<r 交点 割线
拓展练习
如图:AB=8是大圆⊙O的弦,大圆半径为R=5, 则以O为圆心,半径为3的小圆与A B的位置关系 是( B )
直线与圆的位置关系
复习回顾 点和圆的位置关系有哪几种?
A
d
B
C
O
点到圆心距离为d
⊙O半径为r
(1)d<r (2)d=r (3)d>r
点A在圆内
点B在圆上 点C 在圆外
三种位置关系
观察探究一
把太阳看成一个圆,地平线看成一条直线,注 意观察直线与圆的公共点的个数
a(地平线)
●
●
●
●
a(地平线)
•你发现这个自然现象反映出直线和圆的公共点个数有 三
种情况
探究活动二
• 请同学们在练习本上画一个圆,把直尺边缘看成 一条直线,平移直尺,
直线和圆分别有几个公共点?
没有公共点
两个公共点
●O
一个公共点
●O 直线与圆的交
●O
点个数可判定
它们关系
相交
相切
相离
直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条 PPT模板:/moban/ PPT背景:/beijing/ PPT下载:/xiazai/ 资料下载:/ziliao/ 试卷下载:/shiti/ PPT论坛:
2.在Rt△ABC中,∠C=90°,AC=3cm, BC=4cm,以C为圆心,r为半径的圆与AB 有怎样的位置关系?为什么? (1)r=2cm;(2)r=2.4cm (3)r=3cm.
B
பைடு நூலகம்
4
D
d
C
A
3
解:过C作CD⊥AB,垂足为D
在△ABC中,
AB= AC2 BC2 32 42 5 根据三角形的面积公式有
科学课件:/kejian/kexue/ 物理课件:/kejian/wuli/
化学课件:/kejian/huaxue/ 生物课件:/kejian/shengwu/
地理课件:/kejian/dili/
历史课件:/kejian/lishi/
直线叫做圆的割线
直线和圆只有一个公共点,这时我们就说这条直线和圆相切, 这条直线叫做圆的切线,这个点叫做切点.
PPT素材:/sucai/ PPT图表:/tubiao/ PPT教程: /powerpoint/ 范文下载:/fanwen/ 教案下载:/jiaoan/
PPT课件:/kejian/
语文课件:/kejian/yuwen/ 数学课件:/kejian/shuxue/
英语课件:/kejian/yingyu/ 美术课件:/kejian/meishu/
(2)
(3)
l
·O
·O
l
·O
l
相离 (4)
相交
相切
·O
相交
l
思考讨论
O
l
相交
O
Al
相切
O
l
相离
上述变化过程中,除了公共点的个数发生了变化, 还有什么量在改变?你能否用数量关系来判别直线 与圆的位置关系?
温馨提示
过直线外一点作这条直线的垂线段, 垂线段的长度叫点到直线 的距离.
.A
D
l
二、直线与圆的位置关系量化
1)若AB和⊙O相离,则 d > 6cm ; 2)若AB和⊙O相切,则 d = 6cm ; 3)若AB和⊙O相交,则 0cm≤ d < 6cm .
2.直线和圆有2个交点,则直线和圆__相__交_____; 直线和圆有1个交点,则直线和圆__相__切_____; 直线和圆有没有交点,则直线和圆__相__离_____;
A相离 B相切 C相交 D都有可能
O
5
3
A
4B
D
8
课后作业
必做题:A组1题 B组1题
选做题:B组2题
4.2 直线与圆的位置关系
4.2.1 直线与圆的位置关系
直线与圆的位置关系:
(1)直线与圆相交,有两个公共点; (2)直线与圆相切,只有一个公共点; (3)直线与圆相离,没有公共点;
问题:如何用直线和圆的方程判断它们之 间的位置关系?
(1)根据定义,由_直__线___与__圆___的__公__共_ 点 的个数来判断;
(2)由_圆__心__到__直__线__的__距__离__d与半径r 的大小关系来判断.
在实际应用中,常采用第二种方法判定.
当堂检测
1、已知⊙O的半径为6cm,圆心O与直线AB的距离为d, 根据 条件填写d的范围:
你能根据d与r的大小关系确定直线与圆的位置关系吗?
d:圆心O到直线的距离为d 过圆心作直线的垂线段
r ●O ┐d
相交
(1)直线和圆相交 (2)直线和圆相切 (3)直线和圆相离
r ●O
d ┐ 相切
d < r;
d = r;
d > r;
r ●O
d
┐ 相离
尝试归纳
判定直线 与圆的位置关系的方法有__两__种:
直线和圆没有公共点,这时我们就说这条直线和圆相离.
一、直线与圆的位置关系(公共点的个数)
1.直线和圆的位置关系有三种(从直线与圆
公共点的个数) 2.用图形表示如下:
有两个公共点
有一个公共点
没有公共点
.o
l
相交
.o
.
.o
l
l
相切
相离
交 点
割 线
切 点
切 线
请你判断
看图判断直线l与⊙O的位置关系.
(1)
