数理逻辑习题部分解答
初中数理逻辑试题及答案

初中数理逻辑试题及答案一、选择题(每题2分,共10分)1. 如果一个数的平方等于它本身,那么这个数是()A. 0或1B. 0或-1C. 1或-1D. 无法确定2. 下列哪个选项是偶数()A. 2B. 3C. 4D. 53. 一个三角形的三个内角之和等于()A. 90°B. 180°C. 270°D. 360°4. 一个数的相反数是它本身,这个数是()A. 0B. 1C. -1D. 无法确定5. 一个数的绝对值是它本身,这个数是()A. 非负数B. 非正数C. 非负数或非正数D. 无法确定二、填空题(每题2分,共10分)1. 一个数的平方是25,那么这个数是_________。
2. 一个数的立方是-8,那么这个数是_________。
3. 一个数的倒数是1/2,那么这个数是_________。
4. 一个数的绝对值是5,那么这个数是_________。
5. 如果一个数的平方根是3,那么这个数是_________。
三、解答题(每题5分,共30分)1. 证明:对于任意实数a和b,(a+b)² = a² + 2ab + b²。
2. 已知一个数的平方是16,求这个数。
3. 一个等腰三角形的底角是45°,求顶角的度数。
4. 一个数的立方是27,求这个数。
5. 一个数的绝对值是3,求这个数。
四、逻辑推理题(每题5分,共10分)1. 如果一个数既是偶数又是质数,那么这个数是()A. 2B. 4C. 6D. 82. 如果一个数的绝对值是它本身,那么这个数是()A. 正数B. 负数C. 零D. 正数或零五、应用题(每题10分,共20分)1. 一个长方形的长是宽的两倍,如果宽是5cm,求长方形的周长。
2. 一个数的平方比它的立方小64,求这个数。
答案:一、选择题1. A2. A3. B4. A5. A二、填空题1. ±52. -23. 24. ±55. 9三、解答题1. 证明:(a+b)² = (a+b)(a+b) = a² + ab + ba + b² = a² + 2ab + b²。
数理逻辑练习题及答案-3

命题逻辑的推理1.判断下面推理是否正确。
先将简单命题符号化,再写出前提、结论、推理的形式结构(以蕴涵式的形式给出)和判断过程(至少给出两种判断方法):(1)若今天是星期一,则明天是星期三;今天是星期一。
所以明天是星期三。
(2)若今天是星期一,则明天是星期二;明天是星期二。
所以今天是星期一。
(3)若今天是星期一,则明天是星期三;明天不是星期三。
所以今天不是星期一。
(4)若今天是星期一,则明天是星期二;今天不是星期一。
所以明天不是星期二。
(5)若今天是星期一,则明天是星期二或星期三。
(6)今天是星期一当且仅当明天是星期三;今天不是星期一。
所以明天不是星期三。
2.构造下面推理的证明:(1)前提:p→(q→r), p, q结论:r∨s(2)前提:p→q, ┐(q∧r), r结论:┐p(3)前提:p→q结论:p→(p∧q)(4)前提:q→p, q s, s t, t∧r结论:p∧q(5)前提:p→r, q→s, p∧q结论:r∧s(6)前提:┐p∨r, ┐q∨s, p∧q结论:t→(r∨s)3.用附加前提法证明下面各推理:(1)前提:p→(q→r), s→p, q结论:s→r(2)前提:(p∨q)→(r∧s), (s∨t)→u结论:p→u4.用归谬法证明下面推理:(1)前提:p→┐q, ┐r∨q, r∧┐s结论:┐p(2)前提:p∨q, p→r, q→s结论:r∨s5.构造下面推理的证明。
(1)如果小王是理科学生,他必学好数学;如果小王不是文科生,他必是理科生;小王没学好数学。
所以,小王是文科生。
(2)明天是晴天,或是雨天;若明天是晴天,我就去看电影;若我看电影,我就不看书。
所以,如果我看书,则明天是雨天。
答案1.设p:今天是星期一,q:明天是星期二,r:明天是星期三。
(1)推理的形式结构为(p→r)∧p→r此形式结构为重言式,即(p→r)∧p r所以推理正确。
(2)推理的形式结构为(p→q)∧q→p此形式结构不是重言式,故推理不正确。
数理逻辑课后习题答案

数理逻辑课后习题答案数理逻辑课后习题答案数理逻辑是一门研究推理和思维的学科,它涉及到数学和哲学的交叉领域。
在学习数理逻辑的过程中,课后习题是巩固知识和提高能力的重要途径。
本文将为你提供一些数理逻辑课后习题的答案,希望能够帮助你更好地理解和应用这门学科。
1. 逻辑符号的运用习题:将以下自然语言句子转化为逻辑符号表示:a) 如果今天下雨,那么我就带伞。
b) 所有猫都喜欢吃鱼。
c) 除非你努力学习,否则你不会成功。
答案:a) p: 今天下雨q: 我带伞逻辑符号表示:p → qb) p: x是猫q: x喜欢吃鱼逻辑符号表示:∀x(p → q)c) p: 你努力学习q: 你成功逻辑符号表示:p → q2. 命题逻辑推理习题:使用命题逻辑进行推理,判断以下论断是否成立:a) 如果今天是周末,那么我会去看电影。
今天是周末,所以我会去看电影。
b) 如果这只猫是黑色的,那么它是一只黑猫。
这只猫是黑色的,所以它是一只黑猫。
答案:a) 论断成立。
根据前提条件,今天是周末,可以推出结论我会去看电影。
b) 论断不成立。
虽然前提条件是这只猫是黑色的,但不能推出结论它是一只黑猫,因为黑色的猫不一定全身都是黑色的。
3. 谓词逻辑推理习题:使用谓词逻辑进行推理,判断以下论断是否成立:a) 所有猫都喜欢吃鱼。
汤姆是一只猫,所以汤姆喜欢吃鱼。
b) 所有学生都喜欢音乐。
小明是学生,所以小明喜欢音乐。
答案:a) 论断成立。
根据前提条件,所有猫都喜欢吃鱼,可以推出结论汤姆喜欢吃鱼。
b) 论断成立。
根据前提条件,所有学生都喜欢音乐,可以推出结论小明喜欢音乐。
4. 范式化和归结习题:使用范式化和归结法解决以下逻辑问题:a) 给定前提条件:p → q, ¬q → r, ¬r。
证明结论:¬p。
答案:首先,根据前提条件,我们可以得到以下逻辑式:1. p → q2. ¬q → r3. ¬r然后,我们可以将逻辑式1和3应用范式化规则,得到新的逻辑式:4. ¬p → ¬q接下来,我们将逻辑式4和逻辑式2应用归结规则,得到新的逻辑式:5. ¬p → r最后,我们将逻辑式5和前提条件的逻辑式3应用归结规则,得到最终的结论:6. ¬p通过范式化和归结法,我们证明了结论¬p成立。
数理逻辑参考答案

以下是参考答案。
对于较长的答案,只要回答出要点即可。
每题10分。
酌情评分。
1(A)、答案:300元。
源源,田田,晖晖每人拿出100元即可。
1(B)、答案:故选派方案有:(1)派A、C出差;(2)派A、D出差;(3)派A、B、D出差;(4)派C出差(5)派D出差;(6)派B出差;(7)派B、D出差由于题目要派两个人去出差,因此只有方案(1)、(2)、(7)满足要求,即:派A、C出差;派A、D出差;派B、D出差。
2(A)、答案:底下放一个1,然后2 3放在1上面,另外的4 5竖起来放在1的上面。
另外参考:要两人才能做到,先在平面上摆放一枚,再在这枚硬币的正面立着放两枚(这两枚是侧面接触的),这样,这三枚硬币之间形成一个三角形空隙。
剩下的两枚在空隙处交叉就行了,注意这两枚同样是平躺着,但可能需要翘起一定的角度。
2(B)、答案:a=a+b;b=a-b;a=a-b;3(A)、答案:根据I,每条供词都是由供词中没有提到的怀疑对象所作的。
因此,供词与怀疑对象之间的对应关系只有两种可能:A B(1)布拉德:亚当是无辜的。
(1)科尔:亚当是无辜的6(2)科尔:布拉德说的是真话。
(2)亚当:布拉德说的是真话。
(3)亚当:科尔在撒谎。
(3)布拉德:科尔在撒谎。
对于A,(2)支持(1);而(3)否定(2),进而否定(1)。
事实上,供词变成了:(1)布拉德:亚当是无辜的。
(2)科尔:亚当是无辜的。
(3)亚当:亚当有罪。
如果“亚当有罪”是真话,那么亚当说了真话而且是有罪的。
根据Ⅱ,这是不可能的。
如果“亚当是无辜的”是真话,那么布拉德和科尔说了真话,而且其中有一人是有罪的。
根据Ⅱ,这也是不可能的。
因此,A是不可能的。
对于B,(3)否定(1);而(2)支持(3),进而否定(1)。
事实上,供词变成了:(1)科尔:亚当是无辜的。
(2)亚当:亚当有罪。
(3)布拉德:亚当有罪。
如果“亚当有罪”是真话,那么亚当说了真话而且是有罪的。
根据Ⅱ。
离散数学 练习-第1部分 数理逻辑(解答)

5、下列命题公式为重言式的是( D ),为矛盾式的是( C )
A、(P→Q)⋀Q⋀R
B、(P→P)→Q
C、(Q⋁R)⋀R
D、((P→Q)⋀(Q→R))→(P→R)
6、命题公式 (P→Q) 的主合取范式中含有( D )个极大项, 主析取范式中含有( B )个极小项 A、0 B、1 C、2 D、3
7、下列式子不正确的是( D ) A、∃xA(x) ⇔ ∀xA(x) B、∃x(A→B(x)) ⇔ A→∃xB(x) C、∀xA(x) ⇔ ∃xA(x) D、∀x(A(x)→B) ⇔ ∀xA(x)→B
以下方案任选一:①A不去,B不去,C去;②A不去,B去,C不去; ③A去,B不去,C去
9、证明下列谓词公式为永真式
(xF( x) yG( y)) (yG( y) xF( x))
证明:题中的谓词公式为 (P Q) (Q P) 的代换实例
(P Q) (Q P) (P Q) (Q P) (P Q) (P Q) 1 (A A 1)
(P Q R) (P Q R) (P Q R) (P Q R) (P Q R) (P Q R) (P Q R) (P Q R) m001 m000 m011 m111 m0 m1 m3 m(7 主析取范式) M2 M4 M5 M(6 主合取范式) (P Q R) (P Q R) (P Q R) (P Q R)
命题“并不是所有汽车都比火车跑得慢”可符号化为( C )
命题“说汽车都比火车快是不对的”可符号化为( C ) A、∃x(F(x)∧∀y(G(y)→H(x,y))) B、∃x∃y(F(x)∧G(y)→H(x,y)) C、∀x∀y(F(x)∧G(y)→H(x,y)) D、∀x(F(x)∧∃y(G(y)→H(x,y)))
数理逻辑部分参考答案

4.下面的推理是否正确,请给予说明. (1) (x)A(x) B(x) (2) A(y) B(y) 前提引入 US (1)
错误。 因为(1)中(x)的辖域仅是 A(x),而不是 A(x) B(x)
四.计算题 1. 求 PQR 的析取范式,合取范式、主析取范式,主合取范式.
解:由于 P Q R P Q R 析取范式: P Q R 合取范式: P Q R 主析取范式 P Q R P Q R (P 1 1) (1 Q 1) (1 1 R) (P (Q Q) (R R)) (( P P) Q (R R)) (( P P) (Q Q) R) (P Q R) (P Q R) (P Q R) (P Q R) ( P Q R) ( P Q R) ( P Q R)
( A(a) A(b)) (B(a) B(b))
.
6.设个体域 D={1, 2, 3},A(x)为“x 大于 3”,则谓词公式(x)A(x) 的真值 为 0 . 7.谓词命题公式(x)((A(x)B(x)) C(y))中的自由变元为 8. 谓词命题公式(x)(P(x) Q(x) R(x, y))中的约束变元为 y x . .
三、公式翻译题 1.请将语句“今天是天晴”翻译成命题公式. 设 P:今天是天晴 则该语句符号化为 P 2.请将语句“小王去旅游,小李也去旅游.”翻译成命题公式. 设 P:小王去旅游,Q:小李也去旅游 则该语句符号化为 P∧Q
3.请将语句“他去旅游,仅当他有时间.”翻译成命题公式. 设: P:他去旅游 Q:他有时间 则该语句符号化为 P->Q 4.将语句“41 次列车下午五点开或者六点开.”翻译成命题公式. 设:
数理逻辑考试题及答案

数理逻辑考试题及答案一、单项选择题(每题2分,共20分)1. 以下哪个选项不是命题逻辑中的联结词?A. 与B. 或C. 非D. 存在答案:D2. 在布尔代数中,以下哪个表达式是正确的?A. ¬(A∧B) = ¬A∨¬ BB. A∧¬ A = AC. A∨¬ A = 1D. A∧(A∨B) = A答案:C3. 以下哪个命题是真命题?A. 如果今天是星期一,那么明天是星期二。
B. 所有的鸟都会飞。
C. 所有的人都是哲学家。
D. 2+2=5答案:A4. 在命题逻辑中,以下哪个命题的否定是正确的?A. 如果A,则B。
B. A且B。
C. A或B。
D. A当且仅当B。
答案:A5. 以下哪个选项是谓词逻辑中的量词?A. 与B. 或C. 存在D. 非答案:C6. 在谓词逻辑中,以下哪个表达式表示“存在一个x,使得x是学生”?A. ∀x (x 是学生)B. ∃x (x 是学生)C. ¬∃x (x 是学生)D. ¬∀x (x 是学生)答案:B7. 以下哪个选项是模态逻辑中的模态词?A. 与B. 或C. 可能D. 非答案:C8. 在模态逻辑中,以下哪个命题表示“必然P”?A. PB. ¬PC. ◊PD. □P答案:D9. 以下哪个命题是逻辑等价的?A. A∧BB. A∨BC. ¬A∧¬ BD. ¬(A∧¬B)答案:C10. 在逻辑推理中,以下哪个选项是演绎推理?A. 归纳推理B. 演绎推理C. 溯因推理D. 类比推理答案:B二、多项选择题(每题3分,共15分)1. 以下哪些选项是命题逻辑中的有效推理形式?A. 从A∧B,可以推出A。
B. 从A∨B,可以推出A。
C. 从A,可以推出A∨B。
D. 从A∧B,可以推出B。
答案:A, C, D2. 在布尔代数中,以下哪些表达式是等价的?A. A∧(B∨¬A)B. A∨(B∧¬A)C. A∧¬ BD. A∨¬ B答案:A, C3. 以下哪些命题是真命题?A. 如果A则B,且A为真,那么B也为真。
最新数理逻辑考试题及答案

“离散数学”数理逻辑部分考核试题答案━━━━━━━━━━━━━━━━━━★━━━━━━━━━━━━━━━━━━数理逻辑考试题及答案一、命题逻辑基本知识(5分)1、将下列命题符号化(总共4题,完成的题号为学号尾数取4的余,完成1题。
共2分)(0)小刘既不怕吃苦,又爱钻研。
解:⌝p∧q,其中,P:小刘怕吃苦;q:小刘爱钻研。
(1)只有不怕敌人,才能战胜敌人。
解:q→⌝p,其中,P:怕敌人;q:战胜敌人。
(2)只要别人有困难,老张就帮助别人,除非困难已经解决了。
解:⌝r→(p→p),其中,P:别人有困难;q:老张帮助别人;r:困难解决了。
(3)小王与小张是亲戚。
解:p,其中,P:小王与小张是亲戚。
2、判断下列公式的类型(总共5题,完成的题号为学号尾数取5的余,完成1题。
共1分)(0)A:(⌝(p↔q)→((p∧⌝q) ∨(⌝p∧q)))∨ r(1)B:(p∧⌝(q→p)) ∧(r∧q)(2)C:(p↔⌝r) →(q↔r)(3)E:p→(p∨q∨r)(4)F:⌝(q→r) ∧r解:用真值表判断,A为重言式,B为矛盾式,C为可满足式,E为重言式,F为矛盾式。
3、判断推理是否正确(总共2题,完成的题号为学号尾数取2的余,完成1题。
共2分)(0)设y=2|x|,x为实数。
推理如下:如y在x=0处可导,则y在x=0处连续。
发现y在x=0处连续,所以,y在x=0处可导。
解:设y=2|x|,x为实数。
令P:y在x=0处可导,q:y在x=0处连续。
由此,p为假,q为真。
本题推理符号化为:(p→q) ∧q→p。
由p、q的真值,计算推理公式真值为假,由此,本题推理不正确。
(1)若2和3都是素数,则6是奇数。
2是素数,3也是素数。
所以,5或6是奇数。
解:令p:2是素数,q:3是素数,r:5是奇数,s:6是奇数。
由此,p=1,q=1,r=1,s=0。
本题推理符号化为:((p ∧ q) →s) ∧p ∧q) →(r ∨ s)。
数理逻辑练习题及答案

数理逻辑练习题及答案-4(共4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一阶逻辑基本概念1.在一阶逻辑中将下面命题符号化,并分别讨论个体域限制为(a),(b)时命题的真值:(1)凡有理数都能被2整除。
(2)有的有理数能被2整除。
其中(a)个体域为有理数集合,(b)个体域为实数集合。
2.在一阶逻辑中将下面命题符号化,并分别讨论个体域限制为(a),(b)时命题的真值:(1)对于任意的x,均有x2-2= (x+)(x-)。
(2)存在x,使得x+5=9。
其中(a)个体域为自然数集合,(b)个体域为实数集合。
3.在一阶逻辑中将下列命题符号化:(1)没有不能表示成分数的有理数。
(2)在北京卖菜的人不全是外地人。
(3)乌鸦都是黑色的。
(4)有的人天天锻炼身体。
4.在一阶逻辑中将下列命题符号化:(1)火车都比轮船快。
(2)有的火车比有的汽车快。
(3)不存在比所有火车都快的汽车。
(4)“凡是汽车就比火车慢”是不对的。
5.给定解释I如下:(a)个体域D I为实数集合R。
(b)D I中特定元素=0。
(c)特定函数(x,y)=x-y,x,y∈D I。
(d)特定谓词(x,y):x=y,(x,y):x<y,x,y∈D I。
说明下列公式在I下的含义,并指出各公式的真值:(1)x y(G(x,y)→┐F(x,y))(2)x y(F(f(x,y),a)→G(x,y))(3)x y(G(x,y)→┐F(f(x,y),a))(4)x y(G(f(x,y),a)→F(x,y))6.给定解释I如下:(a)个体域D=N(N为自然数)。
(b)D中特定元素=2。
(c)D上函数(x,y)=x+y,(x,y)=x·y。
(d)D上谓词(x,y):x=y。
说明下列公式在I下的含义,并指出各公式的真值:(1)xF(g(x,a),x)(2)x y(F(f(x,a),y)→F(f(y,a),x))(3)x y z(F(f(x,y),z)(4)xF(f(x,x),g(x,x))7.证明下面公式既不是永真式也不是矛盾式:(1)x(F(x)→y(G(y)∧H(x,y)))(2)x y(F(x)∧G(y)→H(x,y))1.(1)(a)中,xF(x),其中,F(x):x能被2整除,真值为0。
数理逻辑期末考试题及答案

数理逻辑期末考试题及答案一、选择题(每题2分,共20分)1. 以下哪个命题与“所有猫都怕水”是等价的?A. 没有猫不怕水B. 所有不怕水的都不是猫C. 有些猫不怕水D. 有些猫怕水2. 如果命题P:x > 0,命题Q:x^2 > 0,那么P是Q的什么条件?A. 充分条件B. 必要条件C. 充分必要条件D. 既不充分也不必要条件3. 逻辑运算符“与”(AND)的真值表中,当两个输入都为真时,输出是什么?A. 假B. 真C. 随机D. 无定义4. 以下哪个是命题逻辑中的有效论证?A. 如果今天是星期一,那么明天是星期二B. 如果今天是星期一,那么明天是星期三C. 如果今天是星期一,那么明天是星期五D. 如果今天是星期一,那么今天是星期二5. 以下哪个命题是真命题?A. 2 + 2 = 5B. 2 + 2 = 4C. 2 + 2 > 4D. 2 + 2 < 46. 以下哪个命题与“如果今天是星期五,那么明天是星期六”是逆命题?A. 如果明天是星期六,那么今天是星期五B. 如果明天不是星期六,那么今天不是星期五C. 如果今天是星期五,那么明天是星期六D. 如果明天是星期六,那么今天是星期六7. 以下哪个命题与“所有的狗都是哺乳动物”是矛盾命题?A. 有些狗不是哺乳动物B. 所有的狗都是哺乳动物C. 所有的哺乳动物都是狗D. 有些哺乳动物不是狗8. 以下哪个命题是假命题?A. 0是自然数B. 1是最小的正整数C. 0是最小的自然数D. 1是最小的正整数且0是最小的自然数9. 以下哪个命题是真命题?A. 所有的偶数都是整数B. 所有的整数都是偶数C. 所有的奇数都是整数D. 所有的整数都是奇数10. 以下哪个命题与“如果今天是星期三,那么明天是星期四”是同一律命题?A. 如果今天是星期三,那么明天是星期四B. 如果明天是星期四,那么今天是星期三C. 如果今天是星期四,那么明天是星期三D. 如果明天不是星期四,那么今天不是星期三答案:1. A2. B3. B4. A5. B6. A7. A8. D9. A10. A二、填空题(每空2分,共20分)1. 命题逻辑中的“或”运算符可以表示为________。
数理逻辑习题答案

P184 习题10.110.1.1 解:⑴①⌝P∧R→Q ;② Q→R ;③ P∧⌝Q⑵①我去镇上,当且仅当我有时间且天不下雪。
②我若去镇上则我有时间,并且我若有时间则去镇上。
③我有时间或我去镇上,此话不对。
(并非如此)10.1.2 解:⑴⇔T∨T∧F⇔T∨F⇔T⑵⇔T∧T∧F∨⌝(T∨T∧(F∨F)) ⇔F∨⌝(T∨T∧F) ⇔F∨F⇔F⑶⇔ (F∧T∨T)∧F∨(⌝(T∧T)∨T) ⇔F∨(F∨T) ⇔T⑷⇔⌝(T∧T)∨T∨( ) ⇔T⑸⇔ (T↔F)∧(F→F) ⇔F∧T⇔F⑹⇔T∨( )↔T∨T⇔T↔T⇔T10.1.3 解:⑴ P:天下雨;Q:我不去;正:⌝P→⌝Q ;逆:⌝Q→⌝P ;反:P→Q 。
⑵ P:你去; Q:我逗留;正:Q→P ;逆:P→Q ;反:⌝Q→⌝P 。
⑶ P:n是大于2的正整数; Q:方程x n+y n=z n无正整数解。
正:P→Q ;逆:Q→P ;反:⌝P→⌝Q。
P201 习题10.210.2.1 解:⑴⑵⑶⑷10.2.2 解:⑴ 否。
∵无论基础条款还是归纳条款都不能产生P ,Q 连在一起的情况。
⑵ 是。
根据基础,P ,Q ,R 是; 根据归纳,⌝P ,(P ∧Q) 皆是;又根据归纳,⌝P →(P ∧Q) 是; 又根据归纳,(⌝P →(P ∧Q))∨R 是。
⑶ 否。
∵无论基础条款还是归纳条款都不能产生∨∧。
⑷ 是。
根据基础,P ,Q ,R 是; 根据归纳,R →P 是;又根据归纳,Q ∧(R →P) 是; 又根据归纳,(Q ∧(R →P))→P 是。
10.2.3 解:⑴ P ∧(P →Q)→Q 36E ⇔⌝(P ∧(⌝P ∨Q))∨Q 7E ⇔⌝((P ∧⌝P)∨(P ∧Q))∨Q 19E ⇔⌝(F ∨(P ∧Q))∨Q 29E ⇔⌝(P ∧Q)∨Q 13E ⇔(⌝P ∨⌝Q)∨Q 4E ⇔⌝P ∨(⌝Q ∨Q) 20E ⇔⌝P ∨T 28E ⇔T⑵ (P →Q)∧(Q →R)→(P →R)36E ⇔⌝[(⌝P ∨Q)∧(⌝Q ∨R)]∨(⌝P ∨R) 7E ⇔⌝[(⌝P ∧⌝Q)∨(⌝P ∧R)∨(Q ∧⌝Q)∨(Q ∧R)]∨(⌝P ∨R) 19E ⇔⌝[(⌝P ∧⌝Q)∨(⌝P ∧R)∨F ∨(Q ∧R)]∨(⌝P ∨R) 29E ⇔⌝[(⌝P ∧⌝Q)∨(⌝P ∧R)∨(Q ∧R)]∨(⌝P ∨R) 14E ⇔[⌝(⌝P ∧⌝Q)∧⌝(⌝P ∧R)∧⌝(Q ∧R)]∨(⌝P ∨R) 13E ⇔[(P ∨Q)∧(P ∨⌝R)∧(⌝Q ∨⌝R)]∨(⌝P ∨R)8E ⇔(P ∨Q ∨⌝P ∨R)∧(P ∨⌝R ∨⌝P ∨R)∧(⌝Q ∨⌝R ∨⌝P ∨R) 20E ⇔(T ∨Q ∨R)∧(T ∨T )∧(T ∨⌝Q ∨⌝P)28E ⇔T ∧T ∧T ⇔ T ⑶ (P →Q)→(⌝P ∨Q)36E ⇔(P →Q)→(P →Q)21E ⇔T ⑷ (P ↔Q)↔(P ∧Q ∨⌝P ∧⌝Q)36E ⇔(P ↔Q)↔(P ↔Q)24E ⇔TP189 习题10.310.3.1 解:⌝P ⇔ P ↓PP ∧Q ⇔ (P ↓P)↓(Q ↓Q) P ∨Q ⇔ (P ↓Q)↓(P ↓Q) P →Q ⇔ (P ↓P ↓Q)↓(P ↓P ↓Q) P ↔Q ⇔ (P ↓P ↓Q)↓(Q ↓Q ↓P) 10.3.2 解:⌝P ⇔ P ↑PP ∧Q ⇔ (P ↑Q)↑(P ↑Q) P ∨Q ⇔ (P ↑P)↑(Q ↑Q)P →Q ⇔ P ↑(Q ↑Q) ⇔ P ↑(P ↑Q) P ↔Q ⇔ (P ↑Q)↑((P ↑P)↑(Q ↑Q)) 10.3.3 解:P ∧Q ⇔ ⌝(⌝P ∨⌝Q) ⇔ ⌝(P →⌝Q) P ∨Q ⇔ ⌝P →QP ↔Q ⇔(P →Q)∧(Q →P)⇔⌝(⌝(P →Q)∨⌝(Q →P))⇔ ⌝((P →Q)→⌝(Q →P)) T ⇔ P →P F ⇔ ⌝(P →P)10.3.4 解:P ∧Q ⇔ ⌝(⌝P ∨⌝Q) ⇔ ⌝(P →⌝Q) ⇔ (P →(Q →F ))→F P ∨Q ⇔ ⌝P →Q ⇔ (P →F ) →Q ⌝P ⇔ P →F T ⇔ P →PP ↔Q ⇔ (P →Q)∧(Q →P) ⇔ ((P →Q)→((Q →P)→F ))→F 10.3.5 解:⌝P ⇔ T PP ∧Q ⇔ P (T Q) P ∨Q ⇔ T ((T P)Q)P ↔Q ⇔ (T (P Q))(T (T (Q P))) F ⇔ T T10.3.6 证:⑴ P ↑Q ⇔⌝(P ∧Q)⇔⌝(Q ∧P)⇔Q ↑P 。
数理逻辑考试题目及答案

数理逻辑考试题目及答案一、单项选择题(每题3分,共30分)1. 在命题逻辑中,下列哪个命题是永真命题?A. (P → Q) ∧ (Q → R) → (P → R)B. (P → Q) ∧ (¬Q → ¬R) → (P → R)C. (P → Q) ∧ (¬Q → R) → (P → ¬R)D. (P → Q) ∧ (¬Q → ¬P) → (P → ¬Q)答案:A2. 谓词逻辑中的量词“∀”表示什么?A. 存在B. 任意C. 所有D. 唯一答案:C3. 以下哪个命题是命题逻辑中的矛盾命题?A. P ∧ ¬PB. P ∨ ¬PC. P → QD. P ↔ ¬P答案:A4. 在谓词逻辑中,下列哪个量词是存在量词?A. ∀xB. ∃xC. ∀yD. ∃y答案:B5. 以下哪个命题是命题逻辑中的等价命题?A. P → QB. ¬P → ¬QC. P ↔ QD. P ∨ Q答案:C6. 以下哪个命题是命题逻辑中的蕴含命题?A. P ∧ QB. P ∨ QC. P → QD. P ↔ Q答案:C7. 在谓词逻辑中,以下哪个符号表示存在量词?A. ∀B. ∃C. ¬D. →答案:B8. 以下哪个命题是命题逻辑中的析取命题?A. P ∧ QB. P ∨ QC. P → QD. P ↔ Q答案:B9. 在命题逻辑中,以下哪个命题是永假命题?A. P ∧ ¬PB. P ∨ ¬PC. P → QD. P ↔ ¬P答案:A10. 在谓词逻辑中,以下哪个命题是全称量化?A. ∃x P(x)B. ∀x P(x)C. ¬∀x P(x)D. ¬∃x P(x)答案:B二、填空题(每题2分,共20分)11. 在命题逻辑中,命题“如果P,则Q”的符号表示为______。
大学数学数理逻辑练习题及答案

大学数学数理逻辑练习题及答案第一题:简述“蕴涵”与“等价”的概念及其区别,并给出一个例子进行说明。
蕴涵和等价是数理逻辑中常用的两个概念,它们主要用于描述命题之间的逻辑关系。
蕴涵是指一个命题可以推出另一个命题,也可以理解为一个命题包含了另一个命题。
记作p→q,读作p蕴涵q。
当p为真时,q必为真;当p为假时,q可以为真也可以为假。
蕴涵关系可以用真值表来表示。
等价是指两个命题具有相同的真值,即当其中一个命题为真时,另一个命题也为真;当其中一个命题为假时,另一个命题也为假。
记作p↔q,读作p等价于q。
等价关系也可以通过真值表来表示。
例子:命题p:如果今天下雨,那么地面湿润。
命题q:地面湿润的话,那么今天一定下雨。
根据上述命题可以得出以下结论:p蕴涵q:如果今天下雨,那么地面湿润。
即p→q。
q蕴涵p:如果地面湿润,那么今天下雨。
即q→p。
p等价于q:今天下雨当且仅当地面湿润。
即p↔q。
以上例子通过逻辑关系中的蕴涵和等价来描述了“下雨”和“地面湿润”之间的关系。
第二题:证明蕴涵的逆否命题成立。
蕴涵的逆否命题是由蕴涵命题转化得到的。
对于蕴涵命题p→q,其逆否命题为非q→非p。
假设p为真,q为假。
根据蕴涵命题的定义,当p为真时,q为假,则非q为真,非p也为真。
所以非q→非p成立。
假设p为真,q为真。
根据蕴涵命题的定义,当p为真时,q为真,则非q为假,非p也为假。
所以非q→非p成立。
假设p为假,q为真。
根据蕴涵命题的定义,当p为假时,q可以为真也可以为假,所以非q为假,非p也为假。
所以非q→非p成立。
假设p为假,q为假。
根据蕴涵命题的定义,当p为假时,q可以为真也可以为假,所以非q为真,非p也为真。
所以非q→非p成立。
综上所述,蕴涵的逆否命题非q→非p成立。
第三题:使用真值表判断以下复合命题的真假,并给出判断步骤:命题:(p∧q)∨(¬p∧¬q)为了判断复合命题的真假,我们可以使用真值表。
真值表的步骤如下:1. 写出各命题变量p和q的所有可能的真值组合。
数理逻辑考试题目及答案

数理逻辑考试题目及答案一、单项选择题(每题2分,共20分)1. 以下哪个命题是真命题?A. 所有的狗都会游泳。
B. 所有的天鹅都是白色的。
C. 有些猫是黑色的。
D. 所有的人都是不朽的。
答案:C2. 若命题P为真,则以下哪个命题也为真?A. 非PB. P且QC. P或QD. 非(P且Q)答案:C3. 逻辑等价的两个命题具有相同的真值表。
以下哪对命题是逻辑等价的?A. P且Q,P或QB. 非P,PC. P且非Q,非(P或Q)D. P或Q,非(非P且非Q)答案:D4. 以下哪个命题是永真命题?A. P且非PB. P或非PC. 非(P且Q)或(P且Q)D. P且Q或非P且非Q答案:B5. 以下哪个命题是永假命题?A. P且非PB. P或非PC. 非(P且Q)或(P且Q)D. P且Q或非P且非Q答案:A6. 以下哪个命题是矛盾命题?A. P且非PB. P或非PC. 非(P且Q)或(P且Q)D. P且Q或非P且非Q答案:A7. 以下哪个命题是充分不必要条件?A. 如果下雨,则地面湿。
B. 如果地面湿,则下雨。
C. 如果下雨,则地面干。
D. 如果地面干,则下雨。
答案:A8. 以下哪个命题是必要不充分条件?A. 如果下雨,则地面湿。
B. 如果地面湿,则下雨。
C. 如果下雨,则地面干。
D. 如果地面干,则下雨。
答案:B9. 以下哪个命题是充要条件?A. 如果下雨,则地面湿。
B. 如果地面湿,则下雨。
C. 如果下雨,则地面干。
D. 如果地面干,则下雨。
答案:A10. 以下哪个命题是既不充分也不必要条件?A. 如果下雨,则地面湿。
B. 如果地面湿,则下雨。
C. 如果下雨,则地面干。
D. 如果地面干,则下雨。
答案:C二、多项选择题(每题3分,共15分)11. 以下哪些命题是永真命题?A. P且非PB. P或非PC. 非(P且Q)或(P且Q)D. P且Q或非P且非Q答案:BC12. 以下哪些命题是永假命题?A. P且非PB. P或非PC. 非(P且Q)或(P且Q)D. P且Q或非P且非Q答案:A13. 以下哪些命题是矛盾命题?A. P且非PB. P或非PC. 非(P且Q)或(P且Q)D. P且Q或非P且非Q答案:A14. 以下哪些命题是充分不必要条件?A. 如果下雨,则地面湿。
离散数学及其应用数理逻辑部分课后习题答案

作业答案:数理逻辑部分P14:习题一1、下列句子中,哪些是命题?在是命题的句子中,哪些是简单命题?哪些是真命题?哪些命题的真值现在还不知道?(3 答:简单命题,真命题。
(9)吸烟请到吸烟室去! 答:不是命题。
(12)8是偶数的充分必要条件是8能被3整除。
答:复合命题,假命题。
14、讲下列命题符号化。
(6)王强与刘威都学过法语。
答::p 王强学过法语;:q 刘威学过法语。
符号化为:p q ∧(10)除非天下大雨,他就乘班车上班。
答::p 天下大雨;:q 他乘班车上班。
符号化为:p q →(13)“2或4是素数,这是不对的”是不对的。
答::p 2是素数;:q 4是素数。
符号化为:(())p q ⌝⌝∨15、设:p 2+3=5. :q 大熊猫产在中国。
:r 太阳从西方升起。
求下列复合命题的真值。
(2)(())r p q p →∧↔⌝(4)()(())p q r p q r ∧∧⌝↔⌝∨⌝→ 解答: p 真值为1;q 真值为1;r 真值为0.(2)p q ∧真值为1;()r p q →∧真值为1;p ⌝真值为0;所以(())r p q p →∧↔⌝真值为0.(4)p q r ∧∧⌝真值为1,p q ⌝∨⌝真值为0,()p q r ⌝∨⌝→真值为1;所以()(())p q r p q r ∧∧⌝↔⌝∨⌝→真值为1.19、用真值表判断下列公式的类型。
(4)()()p q q p →→⌝→⌝所以为重言式。
(7)所以为可满足式。
P36:习题二3、用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出其成真赋值。
(1)()p q q ⌝∧→ 解答:()(())(())()10p q q p q q p q q p q q ⌝∧→⇔⌝⌝∧∨⇔⌝⌝∨⌝∨⇔⌝⌝∨⌝∨⇔⌝⇔所以为永假式。
(2)(())()p p q p r →∨∨→ 解答:(())()(())()()()1()1p p q p r p p q p r p p q p r p r →∨∨→⇔⌝∨∨∨⌝∨⇔⌝∨∨∨⌝∨⇔∨⌝∨⇔ 所以因为永真式。
数理逻辑考试题目及答案

数理逻辑考试题目及答案一、单项选择题(每题2分,共20分)1. 命题逻辑中的“与”运算符用符号表示为:A. ∨B. ∧C. →D. ¬答案:B2. 如果命题P为真,命题Q为假,则命题P∨Q的真值是:A. 真B. 假C. 未知D. 既非真也非假答案:A3. 以下哪个是命题逻辑中的有效论证?A. P → Q, ¬Q → ¬P, 因此P → ¬QB. P → Q, ¬P → Q, 因此QC. P → Q, Q → R, 因此P → RD. P ∧ Q, ¬P, 因此¬Q答案:C4. 命题逻辑中的“非”运算符用符号表示为:A. ∨B. ∧C. →D. ¬答案:D5. 如果命题P为假,命题Q为真,则命题P∧Q的真值是:A. 真B. 假C. 未知D. 既非真也非假答案:B6. 以下哪个是谓词逻辑中的量词?A. ∀B. ∃C. ∧D. ¬答案:A7. 在谓词逻辑中,全称量词“∀”表示:A. 存在B. 对所有C. 对某些D. 非答案:B8. 在谓词逻辑中,存在量词“∃”表示:A. 存在B. 对所有C. 对某些D. 非答案:A9. 以下哪个是谓词逻辑中的等价关系?A. 传递性B. 对称性C. 自反性D. 所有选项都是答案:D10. 以下哪个是谓词逻辑中的偏序关系?A. 传递性B. 对称性C. 自反性D. 所有选项都是答案:A二、多项选择题(每题3分,共15分)11. 以下哪些是命题逻辑中的联结词?A. ∨B. ∧C. →D. ¬答案:ABCD12. 以下哪些是谓词逻辑中的量词?A. ∀B. ∃C. →D. ¬答案:AB13. 以下哪些是谓词逻辑中的等价关系的性质?A. 自反性B. 对称性C. 传递性D. 非对称性答案:ABC14. 以下哪些是谓词逻辑中的偏序关系的性质?A. 自反性B. 反对称性C. 传递性D. 对称性答案:ABC15. 以下哪些是谓词逻辑中的逻辑推理规则?A. 普遍实例化B. 存在概括C. 模态逻辑D. 条件证明答案:ABD三、填空题(每题2分,共20分)16. 命题逻辑中的“或”运算符用符号________表示。
数理逻辑期末试题及答案

数理逻辑期末试题及答案1. 选择题1.1. 下列哪个符号表示逻辑“与”关系?a) ∨b) ⊕c) ¬d) ∧答案: d) ∧1.2. 如果命题p为真,命题q为假,那么命题“p→q”为:a) 真b) 假c) 不确定d) 无法确定答案: a) 真1.3. 下列哪个逻辑符号表示“或”关系?a) ∨b) ∧c) ¬d) ⊕答案: a) ∨1.4. 命题“¬(p∨q)”的否定形式是:a) p∧qb) ¬p∧¬qc) p∨qd) ¬p∨¬q答案: c) p∨q1.5. 命题“p∨q→r”与下列哪个命题等价?a) (p→r)∧(q→r)b) (p∧q)→rc) p∨(q→r)d) p∧(q∨r)答案: a) (p→r)∧(q→r)2. 填空题2.1. 命题“¬(¬p∧q)”的双重否定形式是________。
答案: p∨¬q2.2. 命题“p∧(¬r∨q)”的否定形式是________。
答案: ¬p∨(r∧¬q)2.3. 命题“p∧¬q∧r”的析取范式是________。
答案: (p∨q∨r)∧(p∨q∨¬r)∧(p∨¬q∨r)2.4. 命题“p→(q→r)”的否定形式是________。
答案: p∧q∧¬r2.5. 下列命题中,为可满足的命题是________。
a) ¬(p∧q)b) p∨(¬q∧r)c) ¬(p∧¬p)d) (p→q)∨(q→p)答案: b) p∨(¬q∧r)3. 简答题3.1. 什么是数理逻辑?答案: 数理逻辑是研究形式逻辑和符号逻辑的数学分支学科。
它通过使用符号和规则来研究命题和推理的规律性质,并利用数学方法来分析和解决逻辑问题。
3.2. 解释命题逻辑中的蕴含关系。
答案: 在命题逻辑中,蕴含关系表示一个命题是否能从另一个或一组命题中推导出来。
数理逻辑考试题及答案.pdf

“离散数学”数理逻辑部分考核试题答案━━━━━━━━━━━━━━━━━━★━━━━━━━━━━━━━━━━━━一、命题逻辑基本知识(5分)1、将下列命题符号化(总共4题,完成的题号为学号尾数取4的余,完成1题。
共2分)(0)小刘既不怕吃苦,又爱钻研。
解:p∧q,其中,P:小刘怕吃苦;q:小刘爱钻研。
(1)只有不怕敌人,才能战胜敌人。
解:q→p,其中,P:怕敌人;q:战胜敌人。
(2)只要别人有困难,老张就帮助别人,除非困难已经解决了。
解:r→(p→p),其中,P:别人有困难;q:老张帮助别人;r:困难解决了。
(3)小王与小张是亲戚。
解:p,其中,P:小王与小张是亲戚。
2、判断下列公式的类型(总共5题,完成的题号为学号尾数取5的余,完成1题。
共1分)(0)A:((p q)((p q) (p q))) r(1)B:(p(q p)) (r q)(2)C:(p r) (q r)(3)E:p(p q r)(4)F:(q r) r解:用真值表判断,A为重言式,B为矛盾式,C为可满足式,E为重言式,F为矛盾式。
3、判断推理是否正确(总共2题,完成的题号为学号尾数取2的余,完成1题。
共2分)(0)设y=2|x|,x为实数。
推理如下:如y在x=0处可导,则y在x=0处连续。
发现y在x=0处连续,所以,y在x=0处可导。
解:设y=2|x|,x为实数。
令P:y在x=0处可导,q:y在x=0处连续。
由此,p为假,q为真。
本题推理符号化为:(p q) q p。
由p、q的真值,计算推理公式真值为假,由此,本题推理不正确。
(1)若2和3都是素数,则6是奇数。
2是素数,3也是素数。
所以,5或6是奇数。
解:令p:2是素数,q:3是素数,r:5是奇数,s:6是奇数。
由此,p=1,q=1,r=1,s=0。
本题推理符号化为: ((p q) →s) p q) →(r s)。
计算推理公式真值为真,由此,本题推理正确。
二、命题逻辑等值演算(5分)1、用等值演算法求下列公式的主析取范式或主合取范式(总共3题,完成的题号为学号尾数取3的余,完成1题。
习题与解答(数理逻辑)
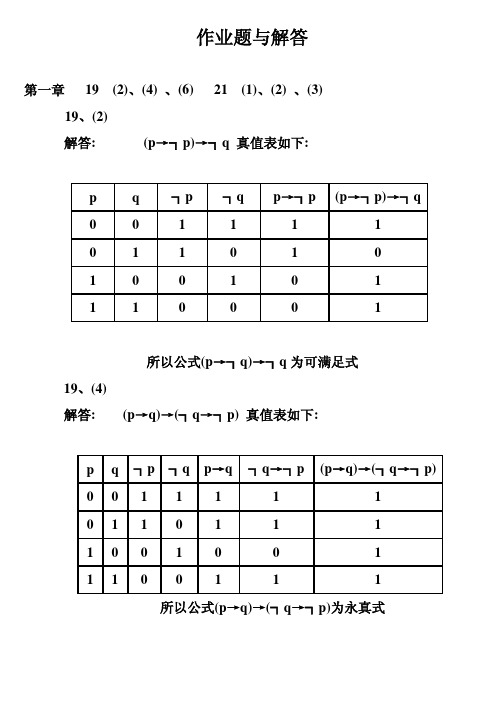
(x,y):x=y。
(2) xy(F(f(x,a),y)→F(f(y,a),x)) xy((x+2=y)→(y+2=x)),真值为 0。 (4) xF(f(x,x),g(x,x)) x(x+x=x·x),真值为 1。 11、判断下列各式的类型
(2) x(F(x)→F(x)) →y(G(y)∧┐G(y))) 此谓词公式前件永为真,而后件永为假,即公式为(1→0) ,此公式为矛盾式,所以原谓词公式为矛盾式。 (6) ┐(xF(x)→yG(y))∧yG(y) 此谓词公式是命题公式┐(p→q)∧q 的代换实例,而该命 题公式是矛盾式,所以此谓词公式是矛盾式。 第五章 15 (1)(2)(3)(4) 20 (1) (2) 23 (1) (2)
16、在自然推理系统 P 中用归谬法证明下面推理: (1) 前提:p→┐q, ┐r∨q, r∧┐s
结论:┐p 证明: ①p ②p→┐q ③┐q ④┐r∨q ⑤┐r ⑥r∧┐s ⑦r ⑧┐r∧r 结论否定引入 前提引入 ①②假言推理 前提引入 ③④析取三段论 前提引入 ⑥化简 ⑤⑦合取(矛盾)
⑧为矛盾式,由归谬法可知,推理正确。 第四章 5、(1) (2) (3) (4) 10、(2) (4) 11、(2) (6)
(3) 不存在比所有火车都快的汽车。 ┐x(F(x)∧y(G(y)→H(x,y))) 或x(F(x)→y(G(y)∧┐H(x,y))), 其中,F(x): x 是汽车,G(y):y 是火车,H(x,y):x 比 y 快。 (4) 说凡是汽车就比火车慢是不对的。 ┐xy(F(x)∧G(y)→H(x,y)) 或xy(F(x)∧G(y)∧┐H(x,y) ), 其中,F(x): x 是汽车,G(y):y 是火车,H(x,y):x 比 y 慢。 10、给定解释 I 如下: (a) 个体域 D=N(N 为自然数)。 (b) D 中特定元素 =2。 (c) D 上函数 D 上谓词 (x,y)=x+y, (x,y)=x·y。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
百度文库- 让每个人平等地提升自我一、命题逻辑3.将下列命题符号化。
(3)如果公用事业费用增加或者增加基金的要求被否定,那么当且仅当现有计算机设不适用的时候,才需购买一台新计算机;(5)虽然天气很好,老王还是不来;(7)停机的原因在于语法错误或程序错误;解:(3)设P:公用事业费用增加;Q:要求增加基金;R:现有计算机设备适用;S:购买一台计算机;则命题可符号化为:()()P Q R S∨⌝→⌝↔。
(5)设P:天气很好;Q:老王来;则命题可符号化为:P Q∧⌝。
(7)设P:停机的原因在于语法错误;Q:停机的原因在于程序错误。
则命题可符号化为:P Q∨。
4.设命题P:这个材料很有趣;Q:这些习题很难;R:这门课程使人喜欢。
将下列句子符号化。
(4)这个材料很有趣意味着这些习题很难,反之亦然;(5)或者这个材料很有趣,或者这些习题很难,并且两者恰具其一。
解:(4)P Q↔(5)()()P Q P Q∧⌝∨⌝∧或者()()P Q P Q∨∧⌝∨⌝12.用基本等价公式的转换方法验证下述论断是否有效。
(1)P→Q,R∧S,┐Q⇒P∧S;(2)┐(P∧┐Q),┐Q∨R,┐Q⇒┐P;(3)P,Q→R,R∨S⇒Q→S。
解:(1)()()()(()())()P Q R S Q P S P Q R S Q P S→∧∧∧⌝→∧=⌝⌝∨∧∧∧⌝∨∧()()1P Q R S Q P S P Q R S=∧⌝∨⌝∨⌝∨∨∧=∨∨⌝∨⌝≠(2)(()())()()P Q Q R Q P P Q Q R Q P⌝∧⌝∧⌝∨∧⌝→⌝=∧⌝∨∧⌝∨∨⌝()()()1P Q Q P P Q P Q=∧⌝∨∨⌝=∧⌝∨⌝∧⌝=(3)(()())()()()()P Q R R S Q S P Q R R S Q S∧→∧∨→→=⌝∨∧⌝∨⌝∧⌝∨⌝∨(())()1P R Q S Q S P R Q S=⌝∨⌝∧∨⌝∨⌝∨=⌝∨⌝∨⌝∨≠14.符号化下列论断,并用演绎法验证论断是否正确。
(1)有红、黄、蓝、白四队参加足球联赛。
如果红队第三,则当黄队第二时,蓝队第四;或者白对不是第一,或者红队第三;事实上,黄队第二。
因此,如果白队第一,那么蓝队第四;证明:设P:红队第三;Q:黄队第二;R:蓝队第四;S:白队第一。
则上述句子可符号为:()P Q R→→,S R⌝∨,Q S R⇒→①S P⌝∨②S③P④()P Q R→→⑤Q R→⑥Q⑦R⑧S R→PP(附加前提)T,①,②,I PT,③,④,I PT,⑤,⑥,I CP,②,⑦(2)如果6是偶数,则2不能整除7;或者5不是素数,或者2整除7;5是素数。
因此,6是奇数;证明:设P:6是偶数;Q:2整除7;R:5是素数则上述句子可符号化为:P Q→⌝,R Q⌝∨,R P⇒⌝①()P⌝⌝②P③P Q→⌝④Q⌝⑤R Q⌝∨⑥R⌝⑦R⑧R R⌝∧P(附加前提)T,①,EPT,②,③,I PT,④,⑤,I PT,⑥,⑦,I(3)若今天是星期二,那么我要考计算机科学或经济学;若经济学教授病了,就不考经济学;今天是星期二,并且经济学教授病了。
所以,我要考计算机科学;证明:设P:今天是星期二;Q:我要考计算机科学;R:我要考经济学;S:经济学教授病了。
则上述句子可符号化为:()P Q R→∨,S R→⌝,P S∧Q⇒①P S∧②S③S R→⌝④R⌝⑤()P Q R→∨⑥P⑦Q R∨⑧Q PT,①,I PT, ②,③,I PT, ①,I T, ⑤,⑥,I T, ④,⑦,I二、谓词逻辑1.用谓词和量词,将下列命题符号化。
(4)会叫的狗未必会咬人;(5)每个人的外祖母都是他母亲的母亲;(6)任何金属均可溶解于某种液体之中;解:(4)设:D(x):x是会叫的狗,R(x):x是会咬人的狗。
则上述句子可符号化为:()(()())x D x R x∃∧⌝(5)设H(x):x是人,G(x,y):x是y的外祖母,M(x,y):x是y的母亲。
则上述句子可符号化为:()()(()()(,)()(()(,)(,)))x y H x H y G x y z H z M x z M z y∀∀∧∧→∃∧∧(6)设:P(x):x是液体,G(x):x是金属,R(x,y):x溶解y。
则上述句子可符号化为:()(()()(()(,)))x G x y P y R y x∀→∃∧8.求下述公式的前束范式和Skolem范式。
(1)(∀y) (P(x)→(∃y)Q(x, y));(3)(∃x) P(x,y)↔(∀z)Q(z);(5)(∃y)(∀x)(∀z)(∃u)(∀v)P(x, y, z, u, v)。
解:(1)求前束范式()(()()(,))()(()()(,))()()(()(,))x P x y Q x y x P x y Q x y x y P x Q x y∀→∃=∀⌝∨∃=∀∃⌝∨求Skolem范式()(()()(,))()()(()(,))()(,())x P x y Q x y x y P x Q x y P x Q x f x∀→∃=∀∃⌝∨=⌝∨(3)求前束范式()((,)()())()((,)()())(()()(,)))()((,)()())(()()(,)))()((,)()())(()()(,)))()()()(((,)())(()(,)))x P x y z Q z x P x y z Q z z Q z P x y x P x y z Q z z Q z P x y x P x y z Q z u Q u P x y x z u P x y Q z Q u P x y ∃↔∀=∃⌝∨∀∧⌝∀∨=∃⌝∨∀∧∃⌝∨=∃⌝∨∀∧∃⌝∨=∃∀∃⌝∨∧⌝∨ 求Skolem 范式()((,)()())()()()(((,)())(()(,)))((,)())(((,))(,))x P x y z Q z x z u P x y Q z Q u P x y P a y Q z Q f y z P a y ∃↔∀=∃∀∃⌝∨∧⌝∨=⌝∨∧⌝∨11.指出下列推导中的错误,并加以改正。
(1)① (∀x)P(x)→Q(x) P② P(y)→Q(y) US,①解:,在第①步中的量词(∀x)就辖域为P(x),而非P(x)→Q(x),所以消去量词时,不能直接使用US 规则。
正确的推导可为:① (∀x)(P(x)→Q(x)) P② P(y)→Q(y) US,①(2)① P(x)→Q(c) P② (∃x)(P(x)→Q(x)) EG,①解:在第①步中x 是以自由变元的身份出现,所以在对个体常量加入量词时,该量词的变元符号不能在原公式中以自由变元的身份出现。
正确的推导可为:① P(x)→Q(c) P② (∃y)(P(x)→Q(y)) EG,①(3)① (∀x)(∃y)(x >y) P② (∃y)(z >y) US,①③ (z >c) ES,②④ (∀x)(x >c) UG,③⑤ c >c US,④解:由于在第②步中含有自由变元符号z ,所以在消去量词(∃y)时,应选的常量符号为含有z 作为下标的常量符号z c 。
正确的推导可为:① (∀x)(∃y)(x >y) P② (∃y)(z >y) US,①③ (z >z c ) ES,②(4)① (∀x)(∃y)(x >y) P② (∃y)(z >y) US,①③ (z >c Z ) ES,②④ (∀x)(x >x) UG,③解:在第③步中,常量符号z c 中的z 是一个下标符号,因此,不能对下标z 使用UG 规则。
正确的推导可为:① (∀x)(∃y)(x >y) P② (∃y)(z >y) US,①③ (z >c Z ) ES,②12.将下列命题符号化,并用演绎法证明其论证是否正确。
(1)每一个大学生,不是文科学生,就是理工科学生;有的大学生是优等生;小张不是 文科生,但他是优等生。
因而,如果小张是大学生,他就是理工科学生;(2)伟大的物理学家都具有广博的知识;新闻记者具有广博的知识。
所以新闻记者是伟大的物理学家;(3)不存在白色的乌鸦;北京鸭是白色的。
因此,北京鸭不是乌鸦;(4)所有的有理数都是实数;所有的无理数也是实数;虚数不是实数。
因此,虚数即不是有理数也不是无理数;解:(1)设P(x):x是一个大学生;Q(x):x是文科生;S(x):x是理科生;T(x):x是优等生;c:小张;则上述句子可符号为:()(()(()()))x P x Q x S x∀→∨,()(()())x P x T x∃∧,()()Q c T c⌝∧()()P c S c⇒→①()()Q c T c⌝∧②()(()(()()))x P x Q x S x∀→∨③()(()())P c Q c S c→∨④()P c⑤()()Q c S c∨⑥()Q c⌝⑦()S c⑧()()P c S c→PPUS,②P(附加前提) T,③,④,I T,①,IT,⑤,⑥,I CP,④,⑦(2)设P(x):x是伟大的物理学家;Q(x):x是新闻工作者;S(x):x具有广博的知识;则上述句子可符号化为:()(()())x P x S x∀→,()(()())x Q x S x∀→()(()())x Q x P x⇒∀→①()(()())x P x S x∀→②()(()())x Q x S x∀→③()()P y S y→④()()Q y S y→PP US,①US,②上述公式无法推出()()Q y P y→,即无法推出()(()())x Q x P x∀→。
所以,此论证并非是正确的。
(3)设W(x):x是白色的;Q(x):x是乌鸦;R(x):x是北京鸭;则上述句子可符号化为:()(()())x W x Q x⌝∃∧,()(()())x R x W x∀→()(()())x R x Q x⇒∀→⌝①()(()())x R x W x∀→②()()R x W x→③()(()())x W x Q x⌝∃∧④()(()())x W x Q x∀⌝∨⌝⑤()()W x Q x⌝∨⌝⑥()()W x Q x→⌝⑦()()R x Q x→⌝⑧()(()())x R x Q x∀→⌝PUS,①PT,③,E US,④T,⑤,ET,②,⑥,I UG,⑦(4)设Q(x):x是有理数;R(x):x是实数;N(x):x是无理数;C(x):x是虚数;则上述句子可符号化为:()(()())x Q x R x∀→,()(()())x N x R x∀→,()(()())x C x R x∀→⌝()(()(()()))x C x Q x N x⇒∀→⌝∧⌝①()(()())x Q x R x∀→②()()Q x R x→③()(()())x N x R x∀→④()()N x R x→⑤()(()())x C x R x∀→⌝⑥()()C x R x→⌝⑦()()R x C x→⌝⑧()()Q x C x→⌝PUS,①PUS,③PUS,⑤T,⑥,ET,②,⑦,I⑨()()N x C x→⌝⑩(()())(()()) Q x C x N x C x→⌝∧→⌝○11(()(()()))C x Q x N x→⌝∧⌝○12()(()(()()))x C x Q x N x∀→⌝∧⌝T,④,⑦,I T,⑧,⑨,I T,⑩,E UG,○11。
