二叉树及其先序遍历
二叉树的遍历和应用

内蒙古科技大学本科生课程设计说明书题目:数据结构课程设计——二叉树的遍历和应用学生姓名:学号:专业:班级:指导教师:2013年5月29日内蒙古科技大学课程设计说明书内蒙古科技大学课程设计任务书I内蒙古科技大学课程设计说明书目录内蒙古科技大学课程设计任务书..............................................................错误!未定义书签。
目录 (II)第一章需求分析 (3)1.1课程设计目的 (3)1.2任务概述 (3)1.3课程设计内容 (3)第二章概要设计 (5)2.1设计思想 (5)2.2二叉树的遍历 (5)2.3运行界面设计 (6)第三章详细设计 (7)3.1二叉树的生成 (7)3.2二叉树的先序遍历 (7)3.3 二叉树的中序遍历 (8)3.4二叉树的后续遍历 (8)3.5主程序的设计 (8)第四章测试分析 (11)4.1二叉树的建立 (11)4.2二叉树的先序、中序、后序遍历 (11)第五章课程设计总结 (12)附录:程序代码 (13)致谢 ···········································································································错误!未定义书签。
完全二叉树非递归无堆栈先序遍历算法的研究

又 被 Mateti等人于 1988年改进 0 。国内也一直有 学者在做 相 关 的 研 究 。可 从 文 献 [4.12]的研 究 主 题 可 以看 出 ,近 10年 来 对 此 主 题 的研 究 从 未 间 断 ,并 且 近 几 年 的 关 注 度 更 高 。
0 引 言
二 叉 树 作 为 一种 重 要 的 数 据 结 构 是 工农 业 应 用 与 开 发 的 重要工 具。满 二叉树 的中序序列 能够与一 条有 向连续 曲线上 的 点 列 建 立 自起 点 到 终 点 的 一 一 对 应 的 关 系 ;二 叉 树 的 先 序 序 列 ,能 与 植 物 从 根 部 向枝 叶 的生 长 发 育 过 程 建 立 关 联 ,可 作 为 植 物 生 产 建 模 的 基 本 数 据 结 构 模 型 。因 此 ,研 究 二 叉 树 的 先 序 、中序 相 关 算 法 成 为 工 农 业 信 息 技 术 领 域 的关 注 点 。
Abstract: Through a study on the analytic relationship am ong a full binary tree, its sequential storage sequence a n d its preorder-traversal sequence, a algorithms is obtained,which can conve ̄ a full binary t ree a n d its sequential storage sequence into its preorder-traversal se· quence. Consequentl ̄ non—recursive and stack-free algorithms are deduced for preorder t raversal ofa complete binary tree and for inter- conversionsbetweenthe sequential storage sequen ce andthepreorder-tmversal seque n ce. The algor ithms carla1]SWe r a quer y ofanode in constant tim e an d perform a traversal in linear tim e. Being derived from exact m athem atical a n alysis and inosculated with deductions ofbinary encodes that naturally fit the bitwise operation, the algorithms are available for both conventional programming and professional developments such as embedded system and SO on. A sample example is presented to demonstrate the application of the algorithms in virtual-plants modeling. Key words: binary t ree; sequential storage m odel; preorder traversal; non--recursive and stack--free; virtual pla n ts
数据结构应用-二叉树

数据结构应⽤-⼆叉树1.表达式树描述:表达式树的叶节点为操作数,其他节点为运算符。
对表达式式树采⽤不同的遍历策略可以分别得到前中后缀三种表达式。
先序遍历:前缀表达式(不常⽤)中序遍历:中缀表达式后序遍历:后缀表达式构造表达式树:把后缀表达式转化为表达式树(中缀转后缀已经在栈的应⽤中提到过),本质上还是借助了栈。
类似后缀表达式求值,从头开始逐字符读⼊表达式,遇到操作数则建⽴⼀个单节点树,将其指针压⼊栈中,当遇到运算符时,将栈顶的两个指针弹出并作为当前运算符的⼦节点构成⼀棵⼆叉树,将该树的指针压⼊栈中。
读到表达式末尾时,留在栈中的只剩下指向最终的表达式树的指针。
2.编码树编码:将信息转化为⼆进制码传输的过程就是编码。
解码:将接受到的⼆进制码恢复为原信息就是解码。
编码表:字符集中的任意字符都能在编码表中找到唯⼀对应的⼆进制串。
字符集到编码表是单射。
解码歧义:编码可以做到⼀⼀对应,解码却未必。
⽐如,规定S->11,M->111,那么现有⼆进制串“111111”,这个⼆进制串应该解码为SSS还是MM呢?这就产⽣了歧义。
产⽣歧义的根源在于,编码表中的某些编码,是其他编码的前缀。
在上例中,S对应的11就是M对应的111的前缀。
前缀⽆歧义编码(PFC):既然知道了产⽣歧义的根源,就可以针对此根源来避免歧义。
避免歧义的本质要求就是,保证字符集中的每⼀个字符所对应的⼆进制串不是编码表中其他任何⼆进制串的前缀。
⼆叉编码树:⽤⼆叉树来描述编码⽅案。
我们知道从⼆叉树的根节点到任⼀其他节点的通路是唯⼀的,那么如果,我们使每⼀个节点之间的通路都表⽰⼆进制码0和1(左通路0,右通路1),这样从根节点出发到某节点的通路就变成了⼀个唯⼀的⼆进制串。
↑⼀棵普通的⼆叉编码树,来⾃《数据结构(C++语⾔版)》邓俊辉PFC编码树:由上图可以清晰地看出,S所对应的⼆进制码之所以会成为M(所对应的⼆进制码)的前缀,是因为S是M的⼦节点。
二叉树的建立与先序中序后序遍历 求叶子节点个数 求分支节点个数 求二叉树的高度

/*一下总结一些二叉树的常见操作:包括建立二叉树先/中/后序遍历二叉树求二叉树的叶子节点个数求二叉树的单分支节点个数计算二叉树双分支节点个数计算二叉树的高度计算二叉树的所有叶子节点数*/#include<stdio.h> //c语言的头文件#include<stdlib.h>//c语言的头文件stdlib.h千万别写错了#define Maxsize 100/*创建二叉树的节点*/typedef struct BTNode //结构体struct 是关键字不能省略结构体名字可以省略(为无名结构体)//成员类型可以是基本型或者构造形,最后的为结构体变量。
{char data;struct BTNode *lchild,*rchild;}*Bitree;/*使用先序建立二叉树*/Bitree Createtree() //树的建立{char ch;Bitree T;ch=getchar(); //输入一个二叉树数据if(ch==' ') //' '中间有一个空格的。
T=NULL;else{ T=(Bitree)malloc(sizeof(Bitree)); //生成二叉树(分配类型*)malloc(分配元素个数*sizeof(分配类型))T->data=ch;T->lchild=Createtree(); //递归创建左子树T->rchild=Createtree(); //地柜创建右子树}return T;//返回根节点}/*下面先序遍历二叉树*//*void preorder(Bitree T) //先序遍历{if(T){printf("%c-",T->data);preorder(T->lchild);preorder(T->rchild);}} *//*下面先序遍历二叉树非递归算法设计*/void preorder(Bitree T) //先序遍历非递归算法设计{Bitree st[Maxsize];//定义循环队列存放节点的指针Bitree p;int top=-1; //栈置空if(T){top++;st[top]=T; //根节点进栈while(top>-1) //栈不空时循环{p=st[top]; //栈顶指针出栈top--;printf("%c-",p->data );if(p->rchild !=NULL) //右孩子存在进栈{top++;st[top]=p->rchild ;}if(p->lchild !=NULL) //左孩子存在进栈{top++;st[top]=p->lchild ;}}printf("\n");}}/*下面中序遍历二叉树*//*void inorder(Bitree T) //中序遍历{if(T){inorder(T->lchild);printf("%c-",T->data);inorder(T->rchild);}}*//*下面中序遍历二叉树非递归算法设计*/void inorder(Bitree T) //中序遍历{Bitree st[Maxsize]; //定义循环队列,存放节点的指针Bitree p;int top=-1;if(T){p=T;while (top>-1||p!=NULL) //栈不空或者*不空是循环{while(p!=NULL) //扫描*p的所有左孩子并进栈{top++;st[top]=p;p=p->lchild ;}if(top>-1){p=st[top]; //出栈*p节点,它没有右孩子或右孩子已被访问。
《数据结构及其应用》笔记含答案 第五章_树和二叉树

第5章树和二叉树一、填空题1、指向结点前驱和后继的指针称为线索。
二、判断题1、二叉树是树的特殊形式。
()2、完全二叉树中,若一个结点没有左孩子,则它必是叶子。
()3、对于有N个结点的二叉树,其高度为。
()4、满二叉树一定是完全二叉树,反之未必。
()5、完全二叉树可采用顺序存储结构实现存储,非完全二叉树则不能。
()6、若一个结点是某二叉树子树的中序遍历序列中的第一个结点,则它必是该子树的后序遍历序列中的第一个结点。
()7、不使用递归也可实现二叉树的先序、中序和后序遍历。
()8、先序遍历二叉树的序列中,任何结点的子树的所有结点不一定跟在该结点之后。
()9、赫夫曼树是带权路径长度最短的树,路径上权值较大的结点离根较近。
()110、在赫夫曼编码中,出现频率相同的字符编码长度也一定相同。
()三、单项选择题1、把一棵树转换为二叉树后,这棵二叉树的形态是(A)。
A.唯一的B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子解释:因为二叉树有左孩子、右孩子之分,故一棵树转换为二叉树后,这棵二叉树的形态是唯一的。
2、由3个结点可以构造出多少种不同的二叉树?(D)A.2 B.3 C.4 D.5解释:五种情况如下:3、一棵完全二叉树上有1001个结点,其中叶子结点的个数是(D)。
A.250 B. 500 C.254 D.501解释:设度为0结点(叶子结点)个数为A,度为1的结点个数为B,度为2的结点个数为C,有A=C+1,A+B+C=1001,可得2C+B=1000,由完全二叉树的性质可得B=0或1,又因为C为整数,所以B=0,C=500,A=501,即有501个叶子结点。
4、一个具有1025个结点的二叉树的高h为(C)。
A.11 B.10 C.11至1025之间 D.10至1024之间解释:若每层仅有一个结点,则树高h为1025;且其最小树高为⎣log21025⎦ + 1=11,即h在11至1025之间。
已知二叉树的先序遍历和中序遍历画出该二叉树

已知⼆叉树的先序遍历和中序遍历画出该⼆叉树对⼀棵⼆叉树进⾏遍历,我们可以采取3中顺序进⾏遍历,分别是前序遍历、中序遍历和后序遍历。
这三种⽅式是以访问⽗节点的顺序来进⾏命名的。
假设⽗节点是N,左节点是L,右节点是R,那么对应的访问遍历顺序如下:前序遍历 N->L->R中序遍历 L->N->R后序遍历 L->R->N所以,对于以下这棵树,三种遍历⽅式的结果是前序遍历 ABCDEF中序遍历 CBDAEF后序遍历 CDBFEA已知⼆叉树的前序遍历和中序遍历,如何得到它的后序遍历其实,只要知道其中任意两种遍历的顺序,我们就可以推断出剩下的⼀种遍历⽅式的顺序,这⾥我们只是以:知道前序遍历和中序遍历,推断后序遍历作为例⼦,其他组合⽅式原理是⼀样的。
要完成这个任务,我们⾸先要利⽤以下⼏个特性:特性A,对于前序遍历,第⼀个肯定是根节点;特性B,对于后序遍历,最后⼀个肯定是根节点;特性C,利⽤前序或后序遍历,确定根节点,在中序遍历中,根节点的两边就可以分出左⼦树和右⼦树;特性D,对左⼦树和右⼦树分别做前⾯3点的分析和拆分,相当于做递归,我们就可以重建出完整的⼆叉树;我们以⼀个例⼦做⼀下这个过程,假设:前序遍历的顺序是: CABGHEDF中序遍历的顺序是: GHBACDEF第⼀步,我们根据特性A,可以得知根节点是C,然后,根据特性C,我们知道左⼦树是:GHBA,右⼦树是:DEF。
C/ \GHBA DEF第⼆步,取出左⼦树,左⼦树的前序遍历是:ABGH,中序遍历是:GHBA,根据特性A和C,得出左⼦树的⽗节点是A,并且A没有右⼦树。
C/ \A DEF/GBH第三步,使⽤同样的⽅法,前序是BGH,中序是GHB,得出⽗节点是B,GH是左⼦树,没有右⼦树。
C/ \A DEF/B/GH第四步,前序是GH, 中序是GH, 所以 G是⽗节点, H是右⼦树, 没有左⼦树.C/ \A DEF/B/G\H第四步,回到右⼦树,它的前序是EDF,中序是DEF,依然根据特性A和C,得出⽗节点是E,左右节点是D和F。
二叉树的遍历及其应用

0引言
所谓遍历,是指沿着某条搜索路线,依次对树中每个结点均做一次 且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。 遍历 在二叉树上最重要的运算之一,是二叉树上进行其它运算之基础。二叉 树作为一种重要的数据结构是工农业应用与开发的重要工具。遍历是二 叉树算法设计中经典且永恒的话题。经典的算法大多采用递归搜索。递 归算法具有简练、清晰等优点,但因其执行过程涉及到大量的堆栈使 用,难于应用到一些严格限制堆栈使用的系统,也无法应用到一些不支 持递归的语言环境[9]。
由先序序列和中序序列来还原二叉树的过程算法思想[7]: (1)若二叉树空,返回空; (2)若不空,取先序序列第一个元素,建立根节点; (3)在中序序列中查找根节点,以此来确定左右子树的先序序列和中 序序列; (4)递归调用自己,建左子树; (5)递归调用自己,建右子树。
4二叉树的遍历的应用
根据二叉树的遍历算法, 可得出如下规律: 规律1: 前序序列遍历第一个为根结点, 后序遍历的最后一个结点为 根结点。 规律2: 前序序列遍历最后一个为根结点右子树的最右叶子结点, 中 序遍历的最后一个结点为根结点右子树的最右叶子结点。 规律3: 中序序列遍历第一个结点为根结点左子树的最左叶子结点,
1遍历二叉树的概念
所谓遍历二叉树,就是遵从某种次序,访问二叉树中的所有结点, 使得每个结点仅被访问一次。这里提到的“访问”是指对结点施行某种 操作,操作可以是输出结点信息,修改结点的数据值等,但要求这种访
问不破坏它原来的数据结构。在本文中,我们规定访问是输出结点信息 data,且以二叉链表作为二叉树的存贮结构。由于二叉树是一种非线性 结构,每个结点可能有一个以上的直接后继,因此,必须规定遍历的规 则,并按此规则遍历二叉树,最后得到二叉树所有结点的一个线性序 列[1]。
前序后序中序详细讲解

前序后序中序详细讲解1.引言1.1 概述在数据结构与算法中,前序、中序和后序是遍历二叉树的三种基本方式之一。
它们是一种递归和迭代算法,用于按照特定的顺序访问二叉树的所有节点。
通过遍历二叉树,我们可以获取有关树的结构和节点之间关系的重要信息。
前序遍历是指先访问根节点,然后递归地访问左子树,最后递归地访问右子树。
中序遍历是指先递归地访问左子树,然后访问根节点,最后递归地访问右子树。
后序遍历是指先递归地访问左子树,然后递归地访问右子树,最后访问根节点。
它们的不同之处在于访问根节点的时机不同。
前序遍历可以帮助我们构建二叉树的镜像,查找特定节点,或者获取树的深度等信息。
中序遍历可以帮助我们按照节点的大小顺序输出树的节点,或者查找二叉搜索树中的某个节点。
后序遍历常用于删除二叉树或者释放二叉树的内存空间。
在实际应用中,前序、中序和后序遍历算法有着广泛的应用。
它们可以用于解决树相关的问题,例如在Web开发中,树结构的遍历算法可以用于生成网页导航栏或者搜索树结构中的某个节点。
在图像处理中,前序遍历可以用于图像压缩或者图像识别。
另外,前序和后序遍历算法还可以用于表达式求值和编译原理中的语法分析等领域。
综上所述,前序、中序和后序遍历算法是遍历二叉树的重要方式,它们在解决各种与树有关的问题中扮演着关键的角色。
通过深入理解和应用这些遍历算法,我们可以更好地理解和利用二叉树的结构特性,并且能够解决更加复杂的问题。
1.2文章结构文章结构是指文章中各个部分的布局和组织方式。
一个良好的文章结构可以使读者更好地理解和理解文章的内容。
本文将详细讲解前序、中序和后序三个部分的内容和应用。
首先,本文将在引言部分概述整篇文章的内容,并介绍文章的结构和目的。
接下来,正文部分将分为三个小节,分别对前序、中序和后序进行详细讲解。
在前序讲解部分,我们将定义和解释前序的意义,并介绍前序在实际应用中的场景。
通过详细的解释和实例,读者将能更好地理解前序的概念和用途。
数据结构二叉树先序中序后序考研题目

数据结构二叉树先序中序后序考研题目在考研所涉及的数据结构中,二叉树以及与之相关的先序、中序和后序遍历是一个重要的考察点。
通过对二叉树的各种遍历方式的理解和掌握,可以帮助考生更好地理解树这个数据结构,提高解题的效率和正确率。
本文将针对数据结构中关于二叉树先序、中序和后序遍历的考研题目进行深入探讨,并希望能为考生提供一些帮助和启发。
一、先序、中序和后序遍历的概念在开始具体讨论考研题目之前,我们先来回顾一下先序、中序和后序遍历的概念。
在二叉树中,所谓的先序、中序和后序遍历,是指对二叉树中的节点进行遍历的顺序方式。
1. 先序遍历:先访问根节点,然后依次递归地访问左子树和右子树。
在遍历过程中,对于任一节点,先访问该节点,然后再访问其左右子树。
2. 中序遍历:先递归地访问左子树,然后访问根节点,最后再递归地访问右子树。
在遍历过程中,对于任一节点,先访问其左子树,然后访问该节点,最后再访问其右子树。
3. 后序遍历:先递归地访问左子树,然后再递归地访问右子树,最后再访问根节点。
在遍历过程中,对于任一节点,先访问其左右子树,然后再访问该节点。
二、考研题目解析1. 题目一:给出一个二叉树的中序遍历和后序遍历序列,构建该二叉树。
这是一个典型的二叉树重建题目,考查对中序和后序遍历结果的理解和利用。
解题的关键在于根据后序遍历序列确定根节点,在中序遍历序列中找到对应的根节点位置,然后再将中序遍历序列分为左右两个子树部分,分别递归构建左右子树。
考生需要对二叉树遍历的特点有清晰的认识,以及对递归构建树结构有一定的掌握。
2. 题目二:给出一个二叉树的先序遍历和中序遍历序列,构建该二叉树。
这个题目与上一个题目相似,同样是考察对二叉树重建的理解和应用。
解题思路也类似,首先根据先序遍历的结果确定根节点,在中序遍历序列中找到对应的根节点位置,然后递归构建左右子树。
需要注意的是,先序遍历序列的第一个元素即为根节点,而中序遍历序列中根节点的左边是左子树,右边是右子树。
数据结构二叉树习题含答案

第6章树和二叉树1.选择题(1)把一棵树转换为二叉树后,这棵二叉树的形态是()。
A.唯一的B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子(2)由3 个结点可以构造出多少种不同的二叉树?()A.2 B.3 C.4 D.5(3)一棵完全二叉树上有1001个结点,其中叶子结点的个数是()。
A.250 B. 500 C.254 D.501(4)一个具有1025个结点的二叉树的高h为()。
A.11 B.10 C.11至1025之间 D.10至1024之间(5)深度为h的满m叉树的第k层有()个结点。
(1=<k=<h)A.m k-1 B.m k-1 C.m h-1 D.m h-1(6)利用二叉链表存储树,则根结点的右指针是()。
A.指向最左孩子 B.指向最右孩子 C.空 D.非空(7)对二叉树的结点从1开始进行连续编号,要求每个结点的编号大于其左、右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,可采用()遍历实现编号。
A.先序 B. 中序 C. 后序 D. 从根开始按层次遍历(8)若二叉树采用二叉链表存储结构,要交换其所有分支结点左、右子树的位置,利用()遍历方法最合适。
A.前序 B.中序 C.后序 D.按层次(9)在下列存储形式中,()不是树的存储形式?A.双亲表示法 B.孩子链表表示法 C.孩子兄弟表示法D.顺序存储表示法(10)一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足()。
A.所有的结点均无左孩子B.所有的结点均无右孩子C.只有一个叶子结点 D.是任意一棵二叉树(11)某二叉树的前序序列和后序序列正好相反,则该二叉树一定是()的二叉树。
A.空或只有一个结点 B.任一结点无左子树C.高度等于其结点数 D.任一结点无右子树(12)若X是二叉中序线索树中一个有左孩子的结点,且X不为根,则X的前驱为()。
A.X的双亲 B.X的右子树中最左的结点C.X的左子树中最右结点 D.X的左子树中最右叶结点(13)引入二叉线索树的目的是()。
给定一棵二叉树的先序遍历序列和中序遍历序列,要求计算该二叉树的高度

给定一棵二叉树的先序遍历序列和中序遍历序列,要求计算该二叉树的高度.题目描述现给定一棵二叉树的先序遍历序列和中序遍历序列,要求你计算该二叉树的高度。
输入输入包含多组测试数据,每组输入首先给出正整数N(<=50),为树中结点总数。
下面2行先后给出先序和中序遍历序列,均是长度为N的不包含重复英文字母(区别大小写)的字符串。
输出对于每组输入,输出一个整数,即该二叉树的高度。
样例输入9ABDFGHIECFDHGIBEAC7思路见代码#include<bits/stdc++.h>using namespace std;int dfs(char*pre,char*in,int n)//n为中序遍历中的查找个数,即为子树的节点数{if(n==0) return 0;int i;for(i=0;i<n;i++) //找顶点if(pre[0]==in[i])break;int left=dfs(pre+1,in,i);//对左子树//顶点在先序遍历中的位置往后一位//中序查找的起点不变,但结尾处应小于i ,即n=iint right=dfs(pre+i+1,in+i+1,n-i-1);// 对右子树//顶点在先序遍历中的位置要加上其左子树的全部节点数i,再往后移一位//中序查找的位置就从i往后一位,其个数为n-i-1;return max(left,right)+1;//要最深的那个}int main(){int n;while(cin>>n){char pre[n+1],in[n+1];cin>>pre>>in;cout<<dfs(pre,in,n)<<endl; }return 0;}。
数据结构实验三——二叉树基本操作及运算实验报告

《数据结构与数据库》实验报告实验题目二叉树的基本操作及运算一、需要分析问题描述:实现二叉树(包括二叉排序树)的建立,并实现先序、中序、后序和按层次遍历,计算叶子结点数、树的深度、树的宽度,求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目,以及二叉树常用运算。
问题分析:二叉树树型结构是一类重要的非线性数据结构,对它的熟练掌握是学习数据结构的基本要求。
由于二叉树的定义本身就是一种递归定义,所以二叉树的一些基本操作也可采用递归调用的方法。
处理本问题,我觉得应该:1、建立二叉树;2、通过递归方法来遍历(先序、中序和后序)二叉树;3、通过队列应用来实现对二叉树的层次遍历;4、借用递归方法对二叉树进行一些基本操作,如:求叶子数、树的深度宽度等;5、运用广义表对二叉树进行广义表形式的打印。
算法规定:输入形式:为了方便操作,规定二叉树的元素类型都为字符型,允许各种字符类型的输入,没有元素的结点以空格输入表示,并且本实验是以先序顺序输入的。
输出形式:通过先序、中序和后序遍历的方法对树的各字符型元素进行遍历打印,再以广义表形式进行打印。
对二叉树的一些运算结果以整型输出。
程序功能:实现对二叉树的先序、中序和后序遍历,层次遍历。
计算叶子结点数、树的深度、树的宽度,求树的非空子孙结点个数、度为2的结点数目、度为2的结点数目。
对二叉树的某个元素进行查找,对二叉树的某个结点进行删除。
测试数据:输入一:ABC□□DE□G□□F□□□(以□表示空格),查找5,删除E预测结果:先序遍历ABCDEGF中序遍历CBEGDFA后序遍历CGEFDBA层次遍历ABCDEFG广义表打印A(B(C,D(E(,G),F)))叶子数3 深度5 宽度2 非空子孙数6 度为2的数目2 度为1的数目2查找5,成功,查找的元素为E删除E后,以广义表形式打印A(B(C,D(,F)))输入二:ABD□□EH□□□CF□G□□□(以□表示空格),查找10,删除B预测结果:先序遍历ABDEHCFG中序遍历DBHEAGFC后序遍历DHEBGFCA层次遍历ABCDEFHG广义表打印A(B(D,E(H)),C(F(,G)))叶子数3 深度4 宽度3 非空子孙数7 度为2的数目2 度为1的数目3查找10,失败。
二叉树的遍历PPT-课件

4 、二叉树的创建算法
利用二叉树前序遍历的结果可以非常方便地生成给定的
二叉树,具体做法是:将第一个输入的结点作为二叉树的 根结点,后继输入的结点序列是二叉树左子树前序遍历的 结果,由它们生成二叉树的左子树;再接下来输入的结点 序列为二叉树右子树前序遍历的结果,应该由它们生成二 叉树的右子树;而由二叉树左子树前序遍历的结果生成二 叉树的左子树和由二叉树右子树前序遍历的结果生成二叉 树的右子树的过程均与由整棵二叉树的前序遍历结果生成 该二叉树的过程完全相同,只是所处理的对象范围不同, 于是完全可以使用递归方式加以实现。
void createbintree(bintree *t) { char ch; if ((ch=getchar())==' ') *t=NULL; else { *t=(bintnode *)malloc(sizeof(bintnode)); /*生成二叉树的根结点*/ (*t)->data=ch; createbintree(&(*t)->lchild); /*递归实现左子树的建立*/ createbintree(&(*t)->rchild); /*递归实现右子树的建立*/ }
if (s.top>-1) { t=s.data[s.top]; s.tag[s.top]=1; t=t->rchild; }
else t=NULL; }
}
7.5 二叉树其它运算的实现
由于二叉树本身的定义是递归的,因此关于二叉树的许多 问题或运算采用递归方式实现非常地简单和自然。 1、二叉树的查找locate(t,x)
(1)对一棵二叉树中序遍历时,若我们将二叉树严
格地按左子树的所有结点位于根结点的左侧,右子树的所
自考软件基础(数据结构--树与二叉树)

B
C
D
E
F
G
H
I
J
第 5 /209页
第二节 二叉树
一、定义
南昌大学
二叉树是一种重要的树形结构,它的特点是:二叉树可以为空(节点个
数为0),任何一个节点的度都小于或等于2,并且,子树有左、右之分,
其次序不能任意颠倒。 二叉树有5种基本形态,如图10-2所示。
第 6 /209页
第二节 二叉树
南昌大学
struct node
{ datatype data; struct node *Lchild,*rchild:
};
第 15 /209页
第二节 二叉树
南昌大学
例10-5 写出图10-8a所示二叉树的链式存储结构。其链式结构如图10-8b 所示。可以看出:具有n个节点的二叉树链式存储共有2n个链,其中只 有n-1个用来存放该节点的左、右孩子,其余的n +1个指针域为空。
解:第一步:由后序遍历结果确定整个二叉树根为A,由中序结果确定
A的左、右子树。 后序遍历结果: 中序遍历结果:
第 24 /209页
第三节 二叉树的遍历
第二步:确定A的左子树。 1)后序遍历结果:
南昌大学
中序遍历结果:
2)确定B的右子树: ①后序遍历结果:
第 25 /209页
第三节 二叉树的遍历
②中序遍历结果:
南昌大学
第 9 /209页
第二节 二叉树
下面介绍两种特殊的二叉树。
南昌大学
(1) 满二叉树指深度为k,且有2k-1个节点的二叉树。或者说除叶子节点外,
其它节点的度都为2的二叉树。
(2) 完全二叉树一个满二叉树的最下层从右向左连续缺少n (n>=0)个节点 的二叉树。 图10-3为满二叉树和完全二叉树示例。
2023年高考信息技术专题13 树与二叉树 知识点梳理(选修)(浙教版2019)
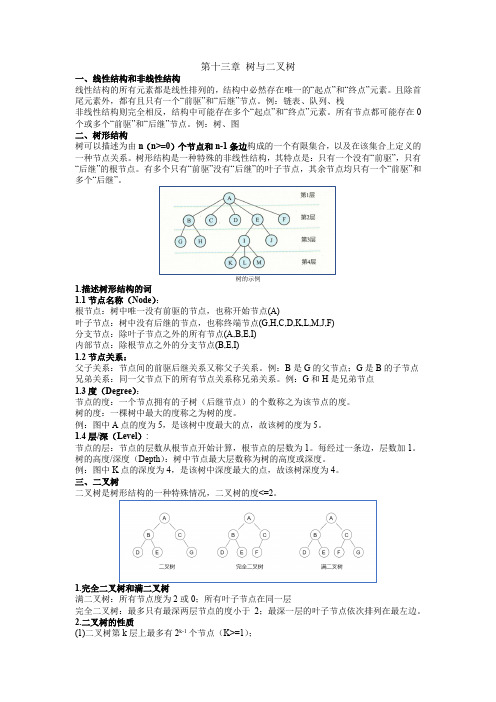
第十三章树与二叉树一、线性结构和非线性结构线性结构的所有元素都是线性排列的,结构中必然存在唯一的“起点”和“终点”元素。
且除首尾元素外,都有且只有一个“前驱”和“后继”节点。
例:链表、队列、栈非线性结构则完全相反,结构中可能存在多个“起点”和“终点”元素。
所有节点都可能存在0个或多个“前驱”和“后继”节点。
例:树、图二、树形结构树可以描述为由n(n>=0)个节点和n-1条边构成的一个有限集合,以及在该集合上定义的一种节点关系。
树形结构是一种特殊的非线性结构,其特点是:只有一个没有“前驱”,只有“后继”的根节点。
有多个只有“前驱”没有“后继”的叶子节点,其余节点均只有一个“前驱”和多个“后继”。
树的示例1.描述树形结构的词1.1节点名称(Node):根节点:树中唯一没有前驱的节点,也称开始节点(A)叶子节点:树中没有后继的节点,也称终端节点(G,H,C,D,K,L,M,J,F)分支节点:除叶子节点之外的所有节点(A,B,E,I)内部节点:除根节点之外的分支节点(B,E,I)1.2节点关系:父子关系:节点间的前驱后继关系又称父子关系。
例:B是G的父节点;G是B的子节点兄弟关系:同一父节点下的所有节点关系称兄弟关系。
例:G和H是兄弟节点1.3度(Degree):节点的度:一个节点拥有的子树(后继节点)的个数称之为该节点的度。
树的度:一棵树中最大的度称之为树的度。
例:图中A点的度为5,是该树中度最大的点,故该树的度为5。
1.4层/深(Level):节点的层:节点的层数从根节点开始计算,根节点的层数为1。
每经过一条边,层数加1。
树的高度/深度(Depth):树中节点最大层数称为树的高度或深度。
例:图中K点的深度为4,是该树中深度最大的点,故该树深度为4。
三、二叉树二叉树是树形结构的一种特殊情况,二叉树的度<=2。
1.完全二叉树和满二叉树满二叉树:所有节点度为2或0;所有叶子节点在同一层完全二叉树:最多只有最深两层节点的度小于2;最深一层的叶子节点依次排列在最左边。
二叉树的三种遍历方法

二叉树的三种遍历方法
二叉树是一种常见的数据结构,它由节点和边组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树的遍历是指按照一定的顺序依次访问二叉树中的所有节点。
常见的二叉树遍历方法有三种,分别是前序遍历、中序遍历和后序遍历。
一、前序遍历
前序遍历是指先访问根节点,再依次访问左子树和右子树。
具体步骤如下:
1. 访问根节点。
2. 前序遍历左子树。
3. 前序遍历右子树。
二、中序遍历
中序遍历是指先访问左子树,再访问根节点,最后访问右子树。
具体步骤如下:
1. 中序遍历左子树。
2. 访问根节点。
3. 中序遍历右子树。
三、后序遍历
后序遍历是指先访问左子树,再访问右子树,最后访问根节点。
具体步骤如下:
1. 后序遍历左子树。
2. 后序遍历右子树。
3. 访问根节点。
以上三种遍历方法都是深度优先遍历,因为它们都是先访问一个节点的所有子节点,再依次访问子节点的子节点。
在实际应用中,不同的遍历方法有不同的应用场景,例如前序遍历可以用于复制一棵二叉树,中序遍历可以用于排序,后序遍历可以用于计算表达式的值。
二叉树的先序遍历和中序遍历的非递归算法

第 1期
电 脑 开 发 与 应 用
文 章编 号 :0 35 5 ( 00 9—0 30 1 0—8 0 2 1 ) 10 5 —3
二 叉树 的先 序 遍 历 和 中序 遍 历 的非 递 归 算 法
Di c s i n a s u s o nd Ana y i n— e u s v g r t m o e r r l s s of No r c r i e Al o ih f r Pr o de
t e S p e r rt a e s la t i r e’ r o de r v r a nd ob an non r c sv l ort o i ar r e’ e r ertav r a i t c A tls obt i ng non e ur i e a g ihm f r b n y t e Spr o d r e s lusng s a k. a t. ani
ta e s . r v r a1 The i p t c s an yssng oft e lf r bi r r e’ S pr or r tav r a d bi r r e’ S i r rt a er a . m oran e i al i i he r a o na y t e e de r e s lan na y t e no de r v s 1 K EYW O RDS bi r t e na y r e’ S pr or e t a r a , bi r t e e d r r ve s l na y r e’ a g ihm l ort
Pr o d ( 一 r hid); e r er bt> c l
从二 叉树 先 序遍 历非 递归 算法 实现 时 系统栈 的变 化情 况 , 我们 不难 看 出 , 二叉 树 先序遍 历 实 际上 是走 丫
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二叉树及其先序遍历
一、实验目的:
1.明确了解二叉树的链表存储结构。
2.熟练掌握二叉树的先序遍历算法。
一、实验内容:
1.树型结构是一种非常重要的非线性结构。
树在客观世界是广泛存在的,在计算
机领域里也得到了广泛的应用。
在编译程序里,也可用树来表示源程序的
语法结构,在数据库系统中,数形结构也是信息的重要组织形式。
2.节点的有限集合(N大于等于0)。
在一棵非空数里:(1)、有且仅
有
一个特定的根节点;(2)、当N大于1时,其余结点可分为M(M大于0)
个互不相交的子集,其中每一个集合又是一棵树,并且称为根的子树。
树
的定义是以递归形式给出的。
3.二叉树是另一种树形结构。
它的特点是每个结点最多有两棵子树,并且,二叉
树的子树有左右之分,其次序不能颠倒。
4.二叉树的结点存储结果示意图如下:
二叉树的存储(以五个结点为例):
三、实验步骤
1.理解实验原理,读懂实验参考程序。
2.
(1)在纸上画出一棵二叉树。
A
B E
C D G F
(2) 输入各个结点的数据。
(3) 验证结果的正确性。
四、程序流程图
先序遍历
五、参考程序
# define bitreptr struct type1 /*二叉树及其先序边历*/ # define null 0
# define len sizeof(bitreptr)
bitreptr *bt;
int f,g;
bitreptr /*二叉树结点类型说明*/
{
char data;
bitreptr *lchild,*rchild;
};
preorder(bitreptr *bt) /*先序遍历二叉树*/
{
if(g==1) printf("先序遍历序列为:\n");
g=g+1;
if(bt)
{
printf("%6c",bt->data);
preorder(bt->lchild);
preorder(bt->rchild);
}
else if(g==2) printf("空树\n");
}
bitreptr *crt_bt() /*建立二叉树*/ {
bitreptr *bt;
char ch;
if(f==1) printf("输入根结点,#表示结束\n"); else printf("输入结点,#表示结束\n");
scanf("\n%c",&ch);
f=f+1;
if(ch=='#') bt=null;
else
{
bt=(bitreptr *)malloc(len);
bt->data=ch;
printf("%c 左孩子",bt->data);
bt->lchild=crt_bt();
printf("%c 右孩子",bt->data);
bt->rchild=crt_bt();
}
return(bt);
}
main()
{
f=1;
g=1;
bt=crt_bt();
preorder(bt);
}
六、思考问题
1. 画出给出的各类型的数据示意图,理解为不同目的而建立的不同数据结构意义。
2. 改写程序完成中、后序遍历。
3. 考虑用非递归算法完成二叉树遍历。
