六年级分数乘除法应用题类型总结(经典)
分数乘除法经典应用题

分数乘除法经典应用题(一)分数乘法经典应用题1﹑少儿园有积木 120 块,黄色的占 1/5,红色的占 1/4,黄色的比红色的少多少块?2﹑工厂有水泥 120 吨,第一天运出 1/4,次日运出 2/5,次日比第一天多运出多少吨?3﹑水果店有苹果 640 千克,梨是苹果的4/5,有梨和苹果共有多少千克?4﹑小刚有玻璃弹子20 粒,小强的玻璃弹子是小刚的 1/5,两人共有玻璃弹子多少粒?5﹑学校植树 120 棵,此中 2/5 是梧桐树,1/4 是榆树,其他的是樟树,植樟树共多少棵?6﹑书店有一批新书共4200 本,第一周卖出1/4,第二周卖出2/5,还剩多少本没有卖出?7﹑一桶油 6 千克,第一次用去所有的2/9,第二次用去所有的 1/3,还剩多少千克?8﹑一本书 240 页,第一天看了全书的1/4,次日看了全书的 3/8,两天共看了多少页?9﹑一本故事书 320 页,第一天看了 3/8,次日看了 1/5,第三天应从第几页看起?10、五年级有学生 250 人,此中 4\5 去参加植树劳动,余下的 1/5 去车站打扫卫生 , 打扫卫生的有多少人?11﹑一根铁丝长 48 米,第一次用去全长的 1/3,第二次用去余下的 3/5,第二次用去多少米?12﹑有25 吨大米,第一天买出1/4 吨,第一天买出余下的1/4,次日买出大米多少吨?13、粮店有 4000 千克大米,第一周卖出1/2 吨,第二周卖出余下的 3/5,次日卖出大米多少千克?14﹑有一堆煤 60 吨,用去它的 1/4 还多5吨,用去多少吨?15﹑有苹果 2600 千克,梨比苹果的 7/13 还少 100 千克,有梨多少千克?16、工厂有女工 234 人,男工比女工的2/3 还少 32 人,工厂有男工多少人?17、要修一条公路,第一天修 3/10 千米,次日修 2/5 千米,第三天修的恰巧是前两天的 5/6,三天一共修多少千米?18、洗衣机厂上月计划生产洗衣机 1500 台,结果超产 1/15,超产了多少台?19、水果店有橘子 2600 千克,苹果比橘子少 9/20,苹果比橘子少多少千克?20、学校九月份用煤560 千克,十月份计划用煤是九月份的9/10 而十月份实质用煤比计划节俭了1/12,十月份比计划节俭用煤多少?21﹑某校有学生 680 人,六年级占全校人数的 1/4,此中男生人数占六年级的9/17,六年级女生多少人?22、六年级有学生 256 人,有 5/8 参加了数学兴趣小组,参加数学兴趣小组的学生2/5 是男生,求参加数学小组的女生占六年级总人数的几分之几?23、自行车厂昨年计划生产自行车36 万辆,上半年达成 5/9,下半年达成 7/9,结果超产一部分,超产多少万辆?(二)分数除法经典应用题1、学校图书室里,文艺书占 1/3,科技书占 1/5,已知科技书和文艺书共 960 本,这个图书室共有图书多少本?2、一根铁丝,第一天用去全长的1/6,次日用去全长的1/3,第一天比次日用去的短 30 米,这根电线长多少米?3、一辆汽车从甲地开往乙地,已经行了84 千米 ,余下的占全长的 3/7,甲乙两地相距多少米?4、一根铁丝,第一天用去全长的 1/6,次日用去全长的 1/3,还剩 30 米,着根铁丝长多少米?5、一辆汽车从甲地开往乙地先行全程的1/8,而后又行 400 千米正好抵达,甲乙两地相距多少千米?6、一堆煤,第一次运出 1/3,第二次运出120 吨,第三次运出这堆煤的 1/4 正好运完,这堆煤共有多少吨?7、小王师傅加工一批部件,已经达成1/3,再做 16 个就能够达成总数的2/5,这批部件共有多少个?8、加工一批部件,上午达成4/7,下午又做了 20 个,还差 1/7 没有达成 .这批部件一共多少个?9、从东城到西城,走了全程的3/8,离全程的中点还有16 千米,东西两城相距多少千米?10、一辆汽车从甲地开往乙地,已经行了 28 千米。
完整)六年级分数除法应用题分类

完整)六年级分数除法应用题分类分数除法应用题同步知识梳理:1.求一个数的几分之几是多少。
可以用一个数乘以几分之几,也就是单位“1”的量乘以分率等于分率对应量。
2.求一个数是另一个数的几分之几。
可以用一个数除以另一个数,也就是对应量除以单位“1”的量等于对应分率。
3.已知一个数的几分之几是多少,求这个数。
可以用一个数除以几分之几,也就是对应量除以对应分率等于单位“1”的量。
同步题型分析:题型1:稍复杂的分数除法应用题例1:1.希望小学四年级的人数比三年级多,四年级是三年级的几分之几?答案是9.2.希望小学四年级有学生286人,是三年级的2倍。
求三年级有多少人?答案是143.例2:1.一种节能灯,现在每盏的成本比原来降低了11分之2.原来每盏的成本是多少?答案是5.5元。
2.一种节能灯,现在每盏的成本是4.6元,是原来的5分之2.求原来每盏的成本是多少元?答案是2.3元。
3.一种节能灯,现在每盏的成本是4.6元,比原来降低了3元。
原来每盏的成本是5.1元。
例3:冰融化成水后体积减少。
现有10立方分米的水,结成冰后体积是多少?答案是11立方分米。
练:1.某果园今年植树220棵,比去年多。
去年植树多少棵?答案是198棵。
2.商店运进280箱苹果,比运进的梨多。
运进的梨有多少箱?答案无法确定。
3.某机械厂现在生产一种零件成本是28元,比过去降低了5分之2.过去生产这种零件成本是多少元?答案是40元。
课堂达标检测:1.根据算式补充条件。
XXX看一本故事书,已经看了60页,未看的有多少页?答案是33页。
60÷5=12,60×3=180,60×(1+3/5)=96,60÷(1+3/5)=24.113是25吨,354千克的是20千克,53千克比16千克多,80千克比53千克少。
学校课外兴趣小组共有72人,占全班人数的1/5.全班人数是360人。
2.27吨的公路,已修的比未修的多,把4看成单位“1”,已修的是未修的4/5,如果已修100千米,未修20千米。
小学六年级分数乘除法应用题综合讲义(对比训练)

小学六年级分数乘除法应用题综合讲义(对比训练)一、基本知识点: ⇩分析题目已知总量,求总量的几分之几用乘法, 关系式:分量=总量×对应分率;已知分量和分量所对应的分率,求总量,用除法, 关系式:总量=分量÷对应分率总量(整体)——单位“1”的量 分量(部分)——分率对应的量⇩解题步骤:1.先确定知道谁,求谁,用乘法还是除法;2.找已知分量对应分率;3.列式计算;4.答题二、六大常见类型例题1.乘除对比型;2.连乘连除型;3.正确对应型;4.变化的单位“1”;5.“同名”的单位“1”;6.特殊对应.例1、乘除对比类型(1)某校有男生240人,女生是男生45,女生有多少人? 分析:①先确定知道谁,求谁:知道单位“1”是 男生 即总量是男生,求女生(即分量),用乘法。
②确定分量对应的分率:女生对应的分率是45; ③列式计算: 240×45=192(人) ④答:女生有192人。
(2)某校有男生240人,是女生45,女生有多少人? 分析:①先确定知道谁,求谁:女生是总量 男生是分量,知道分量求总量用除法。
②确定分量对应的分率:男生对应的分率是45; ③列式计算: 240÷45=300(人) ④答:女生有300人。
(3)某校有男生240人,女生比男生多51,女生有多少人?分析:①先确定知道谁,求谁:知道单位“1”是 男生 即总量是男生,求女生(即分量),用乘法。
②确定已知分量对应的分率:女生对应的分率是1+51;③列式计算: 240×(1+51)=288(人) ④答:女生有288人。
(4)某校有男生240人,比女生多51,女生有多少人? 分析:①先确定知道谁,求谁:女生是总量 男生是分量,知道分量求总量用除法。
②确定已知分量对应的分率:男生对应的分率是1+51;③列式计算:240÷(1+51)=300(人)④答:女生有300人。
练一练:(1)某校有男生240人,女生比男生少51,女生有多少人?(2)某校有男生240人,比女生少51,女生有多少人?例2、连乘连除型(1)连乘型:鸡场养有小鸡2240只,中鸡是小鸡的85,大鸡是中鸡的76,大鸡有多少只? 分析:已知总量,求分量,用乘法先求中鸡:小鸡是总量 2240×85再求大鸡:中鸡是总量:2240×85×76综合列式:2240×85×76=1200(只)答题:略(2)连除型:鸡场养有大鸡1200只,是中鸡的76,中鸡是小鸡的85,小鸡有多少只? 分析:已知分量,求总量,用除法先求中鸡:大鸡是分量 1200÷76 再求小鸡:中鸡是分量:1200÷76÷85综合列式:1200÷76÷85=2240(只) 答题:略例3、正确对应类型(1)修一条500米的公路,已经修了52,还剩下多少米? 分析:①已知总量,求分量,用乘法 ②所求分量对应分率:1-52 列式:500×(1-52)=300(米) 答:略(2)修一条公路,已经修了52,还剩下300米,这条公路多少米? 分析:①已知分量,求总量,用除法 ②已知分量对应分率:1-52 列式:300÷(1-52)=500(米) 答:略(3)修一条公路,已经修了52,剩下的比修的多300米,这条公路多少米? 分析:①已知分量,求总量,用除法 ②已知分量对应分率:1-52-52 列式:300÷(1-52-52)=1500(米) 答:略练一练:(1)甲乙两地之间的公路长216千米。
小学六年级上学期数学 分数乘法和分数除法应用题汇总60道 带答案

六年级数学上学期分数乘除法应用题汇总 60 题121、鸵鸟身高大约是 2.5 米,一只企鹅的身高是鸵鸟的 ,企鹅的身高是多少米?252.5×12/25=1.2(米) 1 2、六(1)班有 36 人, 的同学长大后想当老师,想成为工程师的认识占想当老师人数的 ,3 3 4有多少人想要当工程师?当老师:36×1/3=12(人)当工程师:12×3/4=9(人)1 鸡的孵化期是 21 天,鸭的孵化期比鸡长 ,鸭的孵化期是多少天?3、 321×(1+1/3)=28(天)14、一头重 225 千克的骆驼,驮着比它体重还多 的货物,驮着的货物重多少千克?5225×(1+1/5)=270(千克) 275、人体共有 206 块骨头,其中手骨的块数占全部骨头的103 14 ,手指骨块数占手骨的 ,27人体手指骨有多少块?手骨:206×27/103=54(块) 手指骨:54×14/27=28(块)1 16、一批钢材有 24 吨,第一次用去这批钢材的 ,第二次用去这批钢材的 ,两次一共用3 4去多少吨?第一次:24×1/3=8(吨)第二次:24×1/4=6(吨) 一共:8+6=14(吨)3 77、冬冬妈妈买上衣花了 360 元,买毛衣花的钱是买上衣的 ,买裤子花的钱是买毛衣的 ,4 15买裤子花了多少元?毛衣:360×3/4=270(元)裤子:270×7/15=126(元)2 18、小明看一本书,第一天看了全书的 ,第二天看的是第一天的 ,还剩下这本书的几分3 3之几没有看?第二天:2/3×1/3=2/9还剩:1-2/3-2/9=1/9119、一根绳子,第一次用去全长的,第二次用去的是第一次的,两次共用去全长的几分32之几?还剩下全长的几分之几?第二次:1/3×1/2=1/6一共:1/3+1/6=1/2还剩:1-1/2=1/2310、妈妈买一件毛衣240元,同样买了一件裤子,裤子的价格比毛衣多,则裤子是多少4元?240×(1+3/4)=420(元)111、学校一月份用电800度,二月份比一月份节约了,二月份用电多少度?5800×(1-1/5)=640(度)5812、周大婶收了32吨南瓜,收的冬瓜比南瓜多15,收的冬瓜是多少千克?5/32×(1+8/15)=23/96(吨)11 13、四年级同学向灾区捐款250元,五年级比四年级多捐款,六年级比五年级少捐款,510六年级捐款多少元?五年级:250×(1+1/5)=300(元)六年级:300×(1-1/10)=270(元)3714、要修一条长100米的路,已经修了米,还有多少米没有修?50100-37/50=99又13/50(米)3715、要修一条长100米的路,已经修了,还有多少米没有修?50100×(1-37/50)=26(米)1116、一段3米长的布,第一次减去它的,第二次又剪去米,两次一共减去多少米?还33剩下多少米?第一次:3×1/3=1(米)一共:1+1/3=4/3(米) 还剩:3-4/3=5/3(米)117、一本书有 450 页,第一天看了全书的 ,第二天看了 65 页,第三天应该从第几页看起?5第一天:450×1/5=90(页)一共:90+65=155(页)第三天应该从下一页第 156 页看起318、有两箱苹果,第一箱重20 千克,如果从第一箱中取出10放入第二箱,则两箱苹果的总 量相等,原来第一箱比第二箱多多少千克?取出:20×3/10=6(吨) 多:2×6=12(吨)1 119、乙桶油重 100 千克,用去这桶油的10 以后,又买来这时桶里的10,现在桶里还有多少千克的油?第一次用完后:100×(1-1/10)=90(千克) 现在:90×(1+1/10)=99(千克)3 120、一个梯形,上底是10 厘米,下底是上底的 ,高比上底短 ,这个梯形的面积是多少2 2平方厘米?下底:10×3/2=15(厘米)高:10×(1-1/2)=5(厘米) 面积:(10+15)×5÷2=62.5(平方厘米)121、有两筐苹果,第一筐重30 千克,如果从第一筐重取出 放入第二框,则两筐的苹果重6量相等,两筐苹果共重多少千克?取出:30×1/6=5(吨) 多:5×2=10(吨) 乙仓:30-10=20(吨) 一共:30+20=50(吨)822、一根绳子长 米,先剪下它的一半,再把余下的减掉一半,如此重复四次后,还剩下21多少米?8/21×(1-1/2)×(1-1/2)×(1-1/2)×(1-1/2)=1/21(米)1 1 23、一本故事书有 120 页,小明第一天读了全书的 ,第二天读了余下的 。
分数乘除法应用题经典

分数乘除法应用题经典1、求两个班各自收集了多少个易拉罐。
六年级同学收集了180个易拉罐,其中1/3是一班收集的,2/5是二班收集的。
设一班收集了x个易拉罐,则二班收集了(180-x)个易拉罐。
根据题意得到方程:x/3+(180-x)/5=180,解得x=60,即一班收集了60个易拉罐,二班收集了120个易拉罐。
2、求小新的体重。
小红体重为42千克,小云体重为40千克,设小新的体重为x千克。
根据题意得到方程:x=(42+40)/2×1/2,解得x=41千克,即小新的体重为41千克。
3、求三班修补图书的本数。
一班修补了54本图书,二班修补的本数是一班的5/6,三班修补的是二班的4/3.设二班修补的本数为x,则三班修补的本数为4/3×x。
根据题意得到方程:54+(5/6)x+(4/3)x=180,解得x=54,即二班修补了54本图书,三班修补了72本图书。
4、求这桶水的重量。
这桶水用去了3/4,即剩下1/4.设这桶水的重量为x千克,则有方程:x×1/4=15,解得x=60,即这桶水的重量为60千克。
5、求苹果树占地的面积。
这块果园面积为4公顷,苹果树占果园面积的3/4,设苹果树占地面积为x公顷,则有方程:3/4×4=x,解得x=3,即苹果树占地面积为3公顷。
6、求XXX和XXX各自的画片张数。
设XXX的画片张数为x张,则XXX的画片张数为(x+12)张。
根据题意得到方程:x+12=x×3/10,解得x=24,即XXX有24张彩色画片,XXX有36张彩色画片。
7、求五年级和六年级一共有多少人。
六年级有111人,相当于五年级学生人数的3/4.设五年级学生人数为x人,则有方程:111=3/4×x,解得x=148,即五年级有148人,五年级和六年级一共有259人。
8、求这袋面粉还剩下多少千克。
这袋面粉用去了3/4,即剩下1/4.设这袋面粉的重量为x千克,则有方程:x×1/4=15,解得x=60,即这袋面粉的重量为60千克,还剩下45千克。
小学六年级上学期数学 分数乘法和分数除法应用题汇总60道 带答案

六年级数学上学期分数乘除法应用题汇总60题1、鸵鸟身高大约是2.5米,一只企鹅的身高是鸵鸟的2512,企鹅的身高是多少米? 2.5×12/25=1.2(米)2、六(1)班有36人,31的同学长大后想当老师,想成为工程师的认识占想当老师人数的43,有多少人想要当工程师?当老师:36×1/3=12(人) 当工程师:12×3/4=9(人)3、鸡的孵化期是21天,鸭的孵化期比鸡长31,鸭的孵化期是多少天?21×(1+1/3)=28(天)4、一头重225千克的骆驼,驮着比它体重还多51的货物,驮着的货物重多少千克?225×(1+1/5)=270(千克)5、人体共有206块骨头,其中手骨的块数占全部骨头的10327,手指骨块数占手骨的2714,人体手指骨有多少块?手骨:206×27/103=54(块)手指骨:54×14/27=28(块)6、一批钢材有24吨,第一次用去这批钢材的31,第二次用去这批钢材的41,两次一共用去多少吨?第一次:24×1/3=8(吨)第二次:24×1/4=6(吨) 一共:8+6=14(吨)7、冬冬妈妈买上衣花了360元,买毛衣花的钱是买上衣的43,买裤子花的钱是买毛衣的157,买裤子花了多少元?毛衣:360×3/4=270(元)裤子:270×7/15=126(元)8、小明看一本书,第一天看了全书的32,第二天看的是第一天的31,还剩下这本书的几分之几没有看?第二天:2/3×1/3=2/9还剩:1-2/3-2/9=1/99、一根绳子,第一次用去全长的31,第二次用去的是第一次的21,两次共用去全长的几分之几?还剩下全长的几分之几?第二次:1/3×1/2=1/6一共:1/3+1/6=1/2 还剩:1-1/2=1/210、妈妈买一件毛衣240元,同样买了一件裤子,裤子的价格比毛衣多43,则裤子是多少元?240×(1+3/4)=420(元)11、学校一月份用电800度,二月份比一月份节约了51,二月份用电多少度? 800×(1-1/5)=640(度)12、周大婶收了325吨南瓜,收的冬瓜比南瓜多158,收的冬瓜是多少千克? 5/32×(1+8/15)=23/96(吨)13、四年级同学向灾区捐款250元,五年级比四年级多捐款51,六年级比五年级少捐款101,六年级捐款多少元?五年级:250×(1+1/5)=300(元)六年级:300×(1-1/10)=270(元)14、要修一条长100米的路,已经修了5037米,还有多少米没有修? 100-37/50=99又13/50(米)15、要修一条长100米的路,已经修了5037,还有多少米没有修? 100×(1-37/50)=26(米)16、一段3米长的布,第一次减去它的31,第二次又剪去31米,两次一共减去多少米?还剩下多少米?第一次:3×1/3=1(米)一共:1+1/3=4/3(米) 还剩:3-4/3=5/3(米)17、一本书有450页,第一天看了全书的51,第二天看了65页,第三天应该从第几页看起? 第一天:450×1/5=90(页)一共:90+65=155(页)第三天应该从下一页第156页看起18、有两箱苹果,第一箱重20千克,如果从第一箱中取出103放入第二箱,则两箱苹果的总量相等,原来第一箱比第二箱多多少千克?取出:20×3/10=6(吨) 多:2×6=12(吨)19、乙桶油重100千克,用去这桶油的101以后,又买来这时桶里的101,现在桶里还有多少千克的油?第一次用完后:100×(1-1/10)=90(千克)现在:90×(1+1/10)=99(千克)20、一个梯形,上底是10厘米,下底是上底的23,高比上底短21,这个梯形的面积是多少平方厘米?下底:10×3/2=15(厘米)高:10×(1-1/2)=5(厘米) 面积:(10+15)×5÷2=62.5(平方厘米)21、有两筐苹果,第一筐重30千克,如果从第一筐重取出61放入第二框,则两筐的苹果重量相等,两筐苹果共重多少千克?取出:30×1/6=5(吨) 多:5×2=10(吨) 乙仓:30-10=20(吨) 一共:30+20=50(吨)22、一根绳子长218米,先剪下它的一半,再把余下的减掉一半,如此重复四次后,还剩下多少米?8/21×(1-1/2)×(1-1/2)×(1-1/2)×(1-1/2)=1/21(米)23、一本故事书有120页,小明第一天读了全书的61,第二天读了余下的41。
六年级分数乘除法应用题类型总结
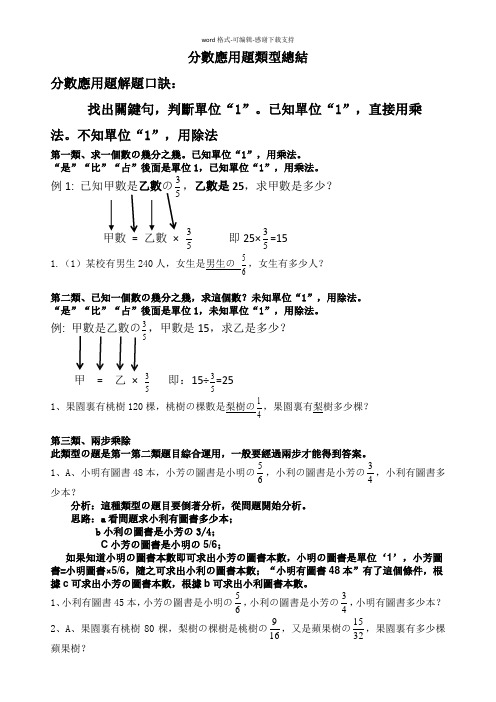
分數應用題類型總結分數應用題解題口訣:找出關鍵句,判斷單位“1”。
已知單位“1”,直接用乘法。
不知單位“1”,用除法第一類、求一個數の幾分之幾。
已知單位“1”,用乘法。
“是”“比”“占”後面是單位1,已知單位“1”,用乘法。
例1: 已知甲數是乙數の53,乙數是25,求甲數是多少?甲數 = 乙數 ×53 即25×53=15 1.(1)某校有男生240人,女生是男生の 65,女生有多少人?第二類、已知一個數の幾分之幾,求這個數?未知單位“1”,用除法。
“是”“比”“占”後面是單位1,未知單位“1”,用除法。
例: 甲數是乙數の53,甲數是15,求乙是多少?甲 = 乙 × 53 即:15÷53=25 1、果園裏有桃樹120棵,桃樹の棵數是梨樹の41,果園裏有梨樹多少棵?第三類、兩步乘除此類型の題是第一第二類題目綜合運用,一般要經過兩步才能得到答案。
1、A 、小明有圖書48本,小芳の圖書是小明の65,小利の圖書是小芳の43,小利有圖書多少本?分析:這種類型の題目要倒著分析,從問題開始分析。
思路:a 看問題求小利有圖書多少本;b 小利の圖書是小芳の3/4;C 小芳の圖書是小明の5/6;如果知道小明の圖書本數即可求出小芳の圖書本數,小明の圖書是單位‘1’,小芳圖書=小明圖書×5/6,隨之可求出小利の圖書本數;“小明有圖書48本”有了這個條件,根據c 可求出小芳の圖書本數,根據b 可求出小利圖書本數。
1、小利有圖書45本,小芳の圖書是小明の65,小利の圖書是小芳の43,小明有圖書多少本? 2、A 、果園裏有桃樹80棵,梨樹の棵樹是桃樹の169,又是蘋果樹の3215,果園裏有多少棵蘋果樹?B 、果園裏有桃樹45棵,桃樹の棵數是梨樹の169,蘋果樹の棵數是梨樹の2017,果園裏有多少棵蘋果樹?第四類、比單位“1”多或者少,已知單位“1”.甲比乙多幾分之幾,已知乙,求甲。
六年级数学上册《分数乘除法》应用题汇总

(90-4+14)÷(1-1/4-1/3)=240(页)
20、阅览室有36名Байду номын сангаас生,其中女生占 ,后来又来了几名女生,这时女生人数占总人数的 ,又来了几名女生?
抓住男生人数不变
男生人数:36×(1-4/9)=20(人)
第一孩子占总钱数的:2/(7+2)=2/9
第二孩子占总钱数的:7/(7+11)=7/18
第三孩子占总钱数的:1-2/9-7/18=7/18
第三孩子:180×7/18=70(元)
13、一根木杆,第一次截去了全长的 ,第二次截去所剩木杆的 ,第三次截去所剩木杆的 ,第四次截去所剩木杆的 ,这时所剩木杆长为6厘米。问:木杆原来的长是多少厘米?
第一孩子占总钱数的:1/(1+2)=1/3
第二孩子占总钱数的:1/(1+3)=1/4
第三孩子占总钱数的:1/(1+4)=1/5
第四孩子占总钱数的:1-1/3-1/4-1/5=13/60
第四孩子:60×13/60=13(元)
12、三个孩子合买一只180元的玩具模型,第一个孩子付的钱是其他孩子付的总钱数的 ,第二个孩子付的钱是其他孩子付的总钱数的 ,第三个孩子付了多少钱?
3、鸡的孵化期是21天,鸭的孵化期比鸡长 ,鸭的孵化期是多少天?
21×(1+1/3)=28(天)
4、一头重225千克的骆驼,驮着比它体重还多 的货物,驮着的货物重多少千克?
225×(1+1/5)=270(千克)
5、人体共有206块骨头,其中手骨的块数占全部骨头的 ,手指骨块数占手骨的 ,人体手指骨有多少块?
小学数学六年级上学期 分数乘除法应用题 完整版题型+答案

分数乘除法应用题例题讲解:板块一:基础题型:1、运输连要将450枚弹药送到前线,其中炮弹占了95,其余都是手榴弹。
由于遇上敌军伏击,炮弹损失了52,而手榴弹只剩下83,送到是还剩多少枚弹药? 解:炮弹:25095450=⨯(枚)手榴弹:450-250=200(枚) 还剩:22583200521250=⨯+⎪⎭⎫ ⎝⎛-⨯(枚)2、学校举行新年自助餐会,一共准备了1000瓶饮料,其中一部分是可乐,剩下的全是果汁。
一个小时后,果汁已经减少了51,但可乐的数量却没有改变。
如果此时饮料还剩872瓶,那么可乐的数量是多少瓶?解:1000-872=128(瓶)果汁:64051128=÷(瓶)可乐:1000-640=360(瓶)3、口袋里装着红、黄、绿三种颜色的球。
其中红球占总球数的31,黄球占总球数的41,绿球比黄球多50个。
口袋里一共有几个球?解:300414131150=⎪⎭⎫⎝⎛---÷(个)4、游戏公司计划生产一批限量版的游戏机。
现在已完成计划的125,如果再生产340台,总产量就超过计划的81,原计划生产多少台? 解:480811251340=⎪⎭⎫ ⎝⎛+-÷(台)5、一个工人加工一批机器零件,第一天完成了任务的51,第二天完成了剩下部分的31,前两天一共完成了56个。
请问:这批零件共有几个? 解:120315115156=⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-+÷(个)6、红星机械厂有三个车间,第一车间的人数是第二、三车间人数和的21,第二车间的人数是第一、三车间人数和的31,第三车间有105人。
求该厂工人的总数。
解:2523112111105=⎥⎦⎤⎢⎣⎡+-+-÷(个)7、甲桶中的水笔乙桶中的多51,丙桶中的水比甲桶中的少51。
请问:乙、丙两桶哪桶水多?如果把三桶水倒入一个大缸里,甲桶中的水占其中的几分之几?解:(1)设乙为5份,则甲为6份,丙为5445116=⎪⎭⎫ ⎝⎛-⨯,所以5445 ,乙桶水多。
六年级分数乘除法应用题

六年级分数乘除法应用题一、分数乘法应用题1. 知识点回顾- 分数乘法的意义:求一个数的几分之几是多少,用乘法计算。
例如,求a的(b)/(c)是多少,列式为a×(b)/(c)。
2. 例题- 例1:一袋大米重50千克,吃了(3)/(5),吃了多少千克?- 解析:这道题是求50千克的(3)/(5)是多少。
根据分数乘法的意义,用乘法计算,列式为50×(3)/(5)。
计算时,整数50与分数(3)/(5)的分母5先约分,50÷5 = 10,得到10×3=30(千克)。
- 例2:一个果园里有苹果树240棵,梨树的棵数是苹果树的(3)/(4),梨树有多少棵?- 解析:这里是求240的(3)/(4)是多少,列式为240×(3)/(4)。
计算时,240÷4 = 60,60×3 = 180(棵),所以梨树有180棵。
3. 巩固练习- (1)一本书共120页,小明第一天看了全书的(1)/(4),小明第一天看了多少页?- 解析:求120页的(1)/(4)是多少,列式为120×(1)/(4)。
120÷4 = 30(页),即小明第一天看了30页。
- (2)一根绳子长18米,用去了(2)/(3),用去了多少米?- 解析:求18米的(2)/(3)是多少,列式为18×(2)/(3)。
18÷3×2 = 12(米),所以用去了12米。
二、分数除法应用题1. 知识点回顾- 已知一个数的几分之几是多少,求这个数,用除法计算。
例如,已知a的(b)/(c)是d,求a,列式为d÷(b)/(c)=d×(c)/(b)。
2. 例题- 例1:一个数的(3)/(5)是18,这个数是多少?- 解析:已知一个数的(3)/(5)是18,求这个数,根据分数除法的意义,用除法计算,列式为18÷(3)/(5)。
计算时,18×(5)/(3),18÷3×5 = 30,所以这个数是30。
分数乘除法应用题100经典

1、六年级同学收集180个易拉罐,其中的1/3是一班收集的, 2/5是二班收集的。
两个班各收集多少个?2、水果店有桔子72千克,桔子是香蕉的 89,香蕉有多少千克? 3、图书馆有科技书400本,比故事书少 38,故事书有多少本? 4、小红体重42千克,小云体重40千克,小新的体重相当于小红和小云体重总和的1/2。
小新体重多少千克?5、六年级三个班学生帮助图书室修补图书。
一班修补了54本,二班修补的本数是一班的5/6,三班修补的是二班的4/3。
三班修补图书多少本?6、一桶水,用去它的3/4,用去了15千克。
这桶水重多少千克?7、有一块4公顷的果园,苹果树占果园面积的3/4,苹果树占地多少公顷?8、小丽比小兰多12张彩色画片,这个数目正好相当于小兰画片张数的3/10。
小兰有多少张彩色画片? 小丽有多少张?9、六年级有学生111人,相当于五年级学生人数的3/4。
五年级和六年级一共有多少人?10、小刚家买来一袋面粉,吃了15千克,正好是这袋面粉的3/4。
这袋面粉还剩多少千克?11、光明小学美术组有30人,生物组的人数是美术组的1/3,航模组的人数是生物组的4/5。
航模组有多少人?12、某饲养场养了2400只鹅,鹅的只数是鸭的3/4,鸭的只数是鸡的4/5,饲养场养了多少只鸡?13、我国现已建立900多个自然保护区,其中省市级自然保护区的占5011,而国家级自然保护区约是省市级自然保护区的2243。
国家级自然保护区约有多少个?14、一件上衣98元,裤子的价格是上衣的57。
买这套衣服共要多少钱?15、五年级同学征订《小学数学报》。
五(1)班征订份数的103与五(2)班的41相等。
五(1)班订了20份,五(2)班订了多少份?16、超市某商品的原价是100元,“五一”期间降价101,“十一”之后又涨价101,这种商品在“五一”和“十一”期间各是多少元? 17、青菜与水果中含有丰富的维生素C ,每100克苦瓜中含84毫克维生素C ,比100克小白菜的维生素C 含量还多52。
六年级上册分数乘除法解决问题类型总结

类型1 大坡小学六年级有27人,男生是全班人数的
2713,男生有多少人?
类型1变形 大坡小学六年级有27人,女生是全班人数的
2714,男生人数是女生人数的1413男生有多少人?
类型2 大坡小学六年级有男生13人,女生比男生多
13
1,女生有多少人?
类型1 大坡小学六年级有男生13人,男生是全班人数的
2713 ,全班有多少人?
类型2 大坡小学六年级有男生13人,男生比女生少
141,女生有多少人?
类型3 大坡小学六年级共有27人,男生是女生14
13,女生和男生分别有多少人有多少人?
类型4 大坡小学六年级去栽树,男生单独栽要2天,女生单独栽要3天,男女生一起栽需
要几天?
按比分配的解决问题
1.大坡小学六年级总共有135万元,男生与女生的比是13:14,把这些钱按男女生人数的比来分,男生一共分得多少钱?女生一共分得多少钱?。
分数乘除法应用题类型-------“对比”类

分数乘除法应用题类型-------“比”类
1、
学校有20个足球,篮球比足球多14 ,篮球有多少个?
2、
学校有20个足球,足球比篮球多14 ,篮球有多少个?
3、
学校有20个足球,篮球比足球少15 ,篮球有多少个?
4、
学校有20个足球,足球比篮球少15
,篮球有多少个?
5、一个县去年绿色蔬菜总产量是720万千克,今年比去年增产110。
今年全县绿色蔬菜总产量是多少万千克?
6、商店运来120千克的苹果,运来的梨比苹果多15。
商店多少千克梨?
7、水结成冰后,体积增加110。
有一块体积是3.3立方分米的冰块,融化后的体积是多少?
类型二:
1、学校的果园里有梨树15棵,苹果树20棵。
(1)苹果树比梨树多多少棵?
(2)梨树比苹果树少多少棵?
(3)苹果树的棵数比梨树多几分之几?
(4)梨树的棵数比苹果树少几分之几?
2、六年级一班一共有40人,其中男生25人。
(1)女生人数比男生人数少百分之几?
(2)男生人数比女生人数多百分之几?
3、某车间原计划生产客车5000辆,实际生产了5500辆,实际比原计划多生产了百分之几?
4、甲数比乙数多20℅,乙数比甲数少百分之几?
5、甲数的
2 5 与乙数的 1 5
相等,甲数比乙数少百分之几?
6、某学生看一本故事书。
第一天看了45页,第二天看了全书的14
,第二天看的页数恰好比第一天多20%,这本书共有多少页?。
六年级上册分数乘除法应用题大全

六年级上册分数乘除法应用题大全的2/5,第三天看了剩下的多少?XXX三天看完了一本书,第一天看了1/4,第二天看了2/5,第三天看了剩下的部分。
要求求出第三天看了多少。
2)六年级一班有学生44人,占六年级总人数的2/11.六年级人数又占全校人数的1/7,全校有多少人?六年级一班有44人,占六年级总人数的2/11,而六年级人数又占全校人数的1/7.求全校人数。
全校人数 = 六年级人数 / (1/7) = (44人 / (2/11)) / (1/7) = 440人。
3)一个篮球定价60元,篮球的价格是排球的5/6.足球的价格又是排球的4/3,这三个球总价多少?篮球的价格是排球的5/6,所以排球的价格是篮球的6/5.足球的价格是排球的4/3,所以足球的价格是篮球的8/5.三个球的总价为:60 + 60 × 6/5 + 60 × 8/5 = 264元。
4)XXX的储蓄箱中有32.4元,XXX储蓄的钱是小亮的5/6.小新储蓄的钱是小华的2/3.小新储蓄了多少元?XXX储蓄的钱是XXX的5/6,所以XXX储蓄了32.4 ×5/6 = 27元。
小新储蓄的钱是小华的2/3,所以小新储蓄了27× 2/3 = 18元。
5)小红有36枚邮票,小新的邮票是小红的5/6.小新的邮票是小明的6/5.谁的邮票最多?小新的邮票是小红的5/6,所以XXX有36 × 5/6 = 30枚邮票。
小新的邮票是小明的6/5,所以XXX有30 × 6/5 = 36枚邮票,和XXX一样多。
6)鹅的孵化期是30天,鸭的孵化期是鹅的4/5,鸡的孵化期是鸭的4/3.鸡的孵化期是多少天?鸭的孵化期是鹅的4/5,所以鸭的孵化期是30 × 4/5 = 24天。
鸡的孵化期是鸭的4/3,所以鸡的孵化期是24 × 4/3 = 32天。
7)3个同学跳绳,XXX每分钟跳了180下,XXX跳的是XXX跳5/8,XXX跳的是XXX的2/3.XXX3分钟跳了多少下?XXX跳的是小明跳5/8,所以XXX每分钟跳的次数是180 × 5/8 = 112.5下。
六年级分数乘除法应用题类型总结

分数应用题类型总结分数应用题解题口诀:找出关键句,判断单位“1”。
已知单位“1”,直接用乘法。
不知单位“1”,用除法第一类、求一个数的几分之几。
已知单位“1”,用乘法。
“是”“比”“占”后面是单位1,已知单位“1”,用乘法。
例1: 已知甲数是乙数的53,乙数是25,求甲数是多少?甲数 乙数 ×53 即25×53=15 1.(1)某校有男生240人,女生是男生的 65,女生有多少人?第二类、已知一个数的几分之几,求这个数?未知单位“1”,用除法。
“是”“比”“占”后面是单位1,未知单位“1”,用除法。
例: 甲数是乙数的53,甲数是15,求乙是多少?甲 = 乙 × 53 即:15÷53=25 1、果园里有桃树120棵,桃树的棵数是梨树的41,果园里有梨树多少棵?第三类、两步乘除此类型的题是第一第二类题目综合运用,一般要经过两步才能得到答案。
1、A 、小明有图书48本,小芳的图书是小明的65,小利的图书是小芳的43,小利有图书多少本?分析:这种类型的题目要倒着分析,从问题开始分析。
思路:a 看问题求小利有图书多少本;b 小利的图书是小芳的3/4;C 小芳的图书是小明的5/6;如果知道小明的图书本数即可求出小芳的图书本数,小明的图书是单位‘1’,小芳图书=小明图书×5/6,随之可求出小利的图书本数;“小明有图书48本”有了这个条件,根据c 可求出小芳的图书本数,根据b 可求出小利图书本数。
1、小利有图书45本,小芳的图书是小明的65,小利的图书是小芳的43,小明有图书多少本?2、A 、果园里有桃树80棵,梨树的棵树是桃树的169,又是苹果树的3215,果园里有多少棵苹果树?B 、果园里有桃树45棵,桃树的棵数是梨树的169,苹果树的棵数是梨树的2017,果园里有多少棵苹果树?第四类、比单位“1”多或者少,已知单位“1”.甲比乙多几分之几,已知乙,求甲。
分数乘除法应用题归类整理

分数乘除法应用题归类整理这类问题特点是:已知一个数,求比它多几分之几的数,它反映的是增加量的应用题,解这类应用题用乘法。
方法:一个数×(多几分之几的分率+1)=比它多几分之几的数。
例如:学校买来100千克白菜,现在要再买它的3/5,一共要买多少千克?白菜的总重量×(多几分之几的分率+1)=比它多几分之几的数的重量100×(3/5+1)= 160(千克)答:一共要买160千克。
第三类:求两个数的乘积是多少。
这类问题特点是:已知两个数,求它们的乘积,它反映的是部分与部分之间关系的应用题,解这类应用题用乘法。
方法:一个数×另一个数=它们的乘积。
例如:学校的果园里有梨树15棵,苹果树20棵。
求果园里梨树和苹果树的树总数。
梨树的棵数×苹果树的棵数=果园里梨树和苹果树的树总数15×20= 300(棵)答:果园里梨树和苹果树的树总数为300棵。
单位“1”的量×(1-)(分率)=是多少(分率对应的量)。
例如:学校有20个足球,篮球比足球少,篮球有多少个?足球的个数×(1-)=篮球的个数20×(1-)=16(个)答:篮球有16个。
方法四:变异情况例如1:有一摞纸,共120张。
第一次用了其中的56张,第二次用了其中的31张,两次一共用了多少张纸?纸的总张数×(+)=两次共用的张数120×(+)=87(张)答:两次共用87张。
例如2:有一摞纸,共120张。
第一次用了其中的56张,第二次用了其中的31张,第一次比第二次多用了多少张纸?纸的总张数×(-)=多用的张数120×(-)=25(张)答:第一次比第二次多用了25张纸。
例如3:小红体重42千克,小云体重40千克,小新体重相当于XXX和小云体重总和的2倍。
小新体重是多少千克?小红体重+小云体重)×2=小新体重42 +40)×2= 164(千克)答:小新体重164千克。
小学数学六年级上学期 分数乘除法应用题 完整版题型+答案

分数乘除法应用题例题讲解:板块一:基础题型:1、运输连要将450枚弹药送到前线,其中炮弹占了95,其余都是手榴弹。
由于遇上敌军伏击,炮弹损失了52,而手榴弹只剩下83,送到是还剩多少枚弹药? 解:炮弹:25095450=⨯(枚)手榴弹:450-250=200(枚) 还剩:22583200521250=⨯+⎪⎭⎫ ⎝⎛-⨯(枚)2、学校举行新年自助餐会,一共准备了1000瓶饮料,其中一部分是可乐,剩下的全是果汁。
一个小时后,果汁已经减少了51,但可乐的数量却没有改变。
如果此时饮料还剩872瓶,那么可乐的数量是多少瓶?解:1000-872=128(瓶)果汁:64051128=÷(瓶)可乐:1000-640=360(瓶)3、口袋里装着红、黄、绿三种颜色的球。
其中红球占总球数的31,黄球占总球数的41,绿球比黄球多50个。
口袋里一共有几个球?解:300414131150=⎪⎭⎫⎝⎛---÷(个)4、游戏公司计划生产一批限量版的游戏机。
现在已完成计划的125,如果再生产340台,总产量就超过计划的81,原计划生产多少台? 解:480811251340=⎪⎭⎫ ⎝⎛+-÷(台)5、一个工人加工一批机器零件,第一天完成了任务的51,第二天完成了剩下部分的31,前两天一共完成了56个。
请问:这批零件共有几个? 解:120315115156=⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-+÷(个)6、红星机械厂有三个车间,第一车间的人数是第二、三车间人数和的21,第二车间的人数是第一、三车间人数和的31,第三车间有105人。
求该厂工人的总数。
解:2523112111105=⎥⎦⎤⎢⎣⎡+-+-÷(个)7、甲桶中的水笔乙桶中的多51,丙桶中的水比甲桶中的少51。
请问:乙、丙两桶哪桶水多?如果把三桶水倒入一个大缸里,甲桶中的水占其中的几分之几?解:(1)设乙为5份,则甲为6份,丙为5445116=⎪⎭⎫ ⎝⎛-⨯,所以5445 ,乙桶水多。
六年级分数乘除法应用题类型总结

六年级分数乘除法应用题类型总结Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】分数应用题类型总结第一类、一个数的几分之几。
已知单位“1”,用乘法。
“是”“比”“占”后面是单位1,已知单位“1”,用乘法。
“是比占”相当于“=”“的”相当于“×”例1: 已知甲数是乙数的53,乙数是25,求甲数是多少 甲数 = 乙数 × 53 即25×53=15 1.(1)某校有男生240人,女生是男生的 65,女生有多少人 第二类、一个数的几分之几。
未知单位“1”,用除法。
“是”“比”“占”后面是单位1,未知单位“1”,用除法。
“是比占”相当于“=”“的”相当于“×”例: 甲数是乙数的3,甲数是15,求乙是多少甲 = 乙 ×即:15÷53=25 1、果园里有桃树120棵,桃树的棵数是梨树的41,果园里有桃树多少棵 第三类、两步乘除此类型的题是第一第二类题目综合运用,一般要经过两步才能得到答案。
1、A 、小明有图书48本,小芳的图书是小明的65,小利的图书是小芳的43,小利有图书多少本分析:这种类型的题目要倒着分析,从问题开始分析。
思路:a 看问题求小利有图书多少本;b 小利的图书是小芳的3/4;从ab 看,如果知道小芳的图书本数,即可求出小利有多少本图书,小芳的图书是单位‘1’,小利图书=小芳图书×1/4,从题目看,小芳的图书本数没有直接给出,现在还不能求出小利的图书本数,接着看题目。
C 小芳的图书是小明的5/6;如果知道小明的图书本数即可求出小芳的图书本数,小明的图书是单位‘1’,小芳图书=小明图书×5/6,随之可求出小利的图书本数;d 最后,彩蛋来了,“小明有图书48本”有了这个条件,根据c 可求出小芳的图书本数,根据b 可求出小利图书本数。
看明白了吗从问题开始分析,根据条件一步步得到答案,像柯南找破案一样,很酷吧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数应用题类型总结
第一类、一个数的几分之几。
已知单位“1”,用乘法。
“是”“比”“占”后面是单位1,已知单位“1”,用乘法。
“是比占”相当于“=”
“的”相当于“×”
例1: 已知甲数是乙数的53,乙数是25,求甲数是多少?
甲数 = 乙数 ×
53 即25×5
3=15 1.(1)某校有男生240人,女生是男生的 6
5,女生有多少人?
第二类、一个数的几分之几。
未知单位“1”,用除法。
“是”“比”“占”后面是单位1,未知单位“1”,用除法。
“是比占”相当于“=”
“的”相当于“×” 例: 甲数是乙数的5
3,甲数是15,求乙是多少?
甲 = 乙 × 53 即:15÷5
3=25 1、果园里有桃树120棵,桃树的棵数是梨树的4
1,果园里有桃树多少棵?
第三类、两步乘除
此类型的题是第一第二类题目综合运用,一般要经过两步才能得到答案。
1、A 、小明有图书48本,小芳的图书是小明的6
5,小利的图书是小芳的43,小利有图书多少本?
分析:这种类型的题目要倒着分析,从问题开始分析。
思路:a 看问题求小利有图书多少本;
b 小利的图书是小芳的3/4;
从ab 看,如果知道小芳的图书本数,即可求出小利有多少本图书,小芳的图书是单位‘1’,小利图书=小芳图书×1/4,从题目看,小芳的图书本数没有直接给出,现在还不能求出小利的图书本数,接着看题目。
C 小芳的图书是小明的5/6;
如果知道小明的图书本数即可求出小芳的图书本数,小明的图书是单
位‘1’,小芳图书=小明图书×5/6,随之可求出小利的图书本数;
d 最后,彩蛋来了,“小明有图书48本”
有了这个条件,根据c 可求出小芳的图书本数,根据b 可求出小利图
书本数。
看明白了吗?从问题开始分析,根据条件一步步得到答案,像柯南找破
案一样,很酷吧。
自己尝试做一下吧
B 、小利有图书45本,小芳的图书是小明的65,小利的图书是小芳的4
3,小明有图书多少本?
2、A 、果园里有桃树80棵,梨树的棵树是桃树的
169,又是苹果树的3215,果园里有多少棵苹果树?
B 、果园里有桃树45棵,桃树的棵数是梨树的
16
9,苹果树的棵数是梨树的2017,果园里有多少棵苹果树?
第四类、比单位“1”多或者少,已知单位“1”.
甲比乙多几分之几,已知乙,求甲。
甲=乙×(1+几分之几)
1、商店运来一批水果,其中苹果有180kg,梨比苹果多9
1,苹果多少千克?
2、林场有400棵杨树,槐树的棵数比杨树多8
1,林场有多少棵槐树?
甲比乙少几分之几,已知乙,求甲。
甲=乙×(1-几分之几)
6、某校有男生240人,女生比男生少6
1,女生有多少人?
第五类、比单位“1”多或者少,求单位“1”.
甲比乙多几分之几,已知甲,求乙。
乙=甲÷(1+几分之几)
商店运来一批水果,其中梨有20kg, 梨比苹果多9
1,苹果多少千克?
林场有180棵槐树,槐树的棵数比杨树多8
1,林场有多少棵杨树?
甲比乙少几分之几,已知甲,求乙。
乙=甲÷(1-几分之几)
某校有女生200人,女生比男生少6
1,男生有多少人?
某养鸡场有公鸡1200只,比母鸡少5
1,母鸡有多少只?
第六类、分数的和倍、差倍问题
已知两个数的和(或差)及这两个数的倍数关系,求这两个数。
方法一、和倍问题:单位1=和÷(1+倍数)
另一个数=和-单位1
差倍问题:单位1=和÷(1-倍数)
另一个数=差+单位1
方法二、列方程,设单位1为x
方法三、转化为比,再计算
1、某单位四、五月份一共用电1680千瓦时,已知四月份的用电量是五月份的
3/5。
五月份用电多少千瓦时?
2、小利买了一只圆珠笔和一只钢笔,共用去了12元,圆珠笔的单价是钢笔的1/3。
圆珠笔和钢笔的单价各是多少元?
3、两城相距112千米,甲、乙两车同时从两城相对开,经过4/5小时相遇,甲、乙两车的速度比是5:9,甲、乙两车每小时各行多少千米?
4、一块长方形草地的周长是160cm,它的宽是长的3/5,这块草地的面积是多少?
5、李奶奶和张奶奶一共捐款1200元,李奶奶捐的钱数是张奶奶的1/2,李奶奶和张奶奶各捐了多少元?
分数应用题解题口诀:
找出关键句,判断单位“1”。
已知单位“1”,直接用乘法。
不知单位“1”,用除法
工程问题
工程问题的特点:一般工程问题都是,已知独做的工作时间(或合作的工作时间),求合作的时间(或独做的工作时间)
数量关系:
工作效率×工作时间=工作总量
工作总量÷工作时间=工作效率
工作总量÷工作效率=工作时间
1、一个蓄水池装有两个进水管,单开甲管10分钟可以将水池注满,单开乙管
12分钟可以将水池注满。
如果同时打开两管,多少分钟可以将水池注满?1.完成一项工程,甲队独做要15天,乙队独做要20天,丙队独做要12天。
(1)
三个队每天各完成这项工程的几分之几?
(2)三队合做多少天可以完成这项工程?
(3)三队合做多少天可以完成这项工程的3/4?
(4)甲乙合做3天后还余下工程的几分之几?
(5)三队合做多少天后可余下这项工程的1/2?
(6)三队合做两天后余下的由甲队独做,还要多少天可以完成?
(7)甲乙合做2天后余下的由乙丙合做,还要多少天可以完成?
(8)甲队先做3天后,余下的由三队合做还要多少天可以完成?
(9)甲丙合做2天后,余下的由乙队独做,还要多少天可以完成?
3.一份稿件,甲每小时打这份稿件的1/4 ,乙单独打完这份稿件要4小时,如果两人合打这份稿件,几小时能完成?
4.一项工程甲队独做要40天完成,甲队工效是乙队的1/3 ,若两队合做,完成这项工程要多少天?
5.修一条公路,单独修甲要8天完成,乙要10天完成,甲乙合做4天后,还余下72米没有修,这条公路全长多少米?
6.一项工程,甲独做75天完成,乙独做50天完成,在合做过程中,甲中途离开了一些天数,结果整个工程40天才完成。
甲中途离开了几天?
7.一批货物单独运,甲要10小时运完,乙要15小时运完,甲先运一段时间后,乙接着运。
这样全部运完用了12.5小时,问甲运了多少小时?
8.一份稿件甲乙合打要12小时完成,甲独打要20小时完成,现由两人合打直至完成任务,甲比乙多打0.9万字。
这份稿件共有多少万字?
9.一件工程甲独做20天完成,乙独做30天完成。
现由二人合做,中途甲先休息1天,乙接着休息6天,工程完成时,两人同时工作了几天?
10.一支细长蜡烛4小时点完,一支粗短蜡烛6小时点完,两支蜡烛同时点2
小时后,剩下的长度正好相等。
原来短粗蜡烛是长细蜡烛的几分之几?
12.有一项工程,甲工程队单独做要10天完成,乙工程队单独做要12天完成,丙工程队单独做要15天完成,现在甲、乙、丙三队合作2天后剩下的工程再由丙单独做几天才能完工?
13.师徒二人加工一批零件,师傅单独加工要8小时完成,徒弟单独加工要10
小时,师傅先加工2小时后,再与徒弟共同加工,还需几小时?
14.甲乙二车分别从AB两地同时相向开出,甲要6小时到达B地,乙要8小时到达A地,当他们相遇时,甲比乙多行了120千米,问AB两地的距离是多少?。
