资料分析公式
资料分析公式汇总

资料分析公式汇总在进行资料分析时,掌握一些关键的公式可以帮助我们更高效、准确地处理和解读数据。
以下是为大家汇总的一些常用公式:一、增长相关公式1、增长量=现期量基期量增长量用于衡量数据在一定时期内的绝对增长幅度。
2、增长率=增长量÷基期量×100%这个公式反映了数据增长的相对速度。
3、基期量=现期量÷(1 +增长率)当我们已知现期量和增长率,要求出之前某个时期的量时,就会用到这个公式。
4、现期量=基期量×(1 +增长率)通过基期量和增长率来计算当前时期的量。
二、比重相关公式1、比重=部分÷整体×100%比重表示部分在整体中所占的比例。
2、整体=部分÷比重已知部分和其占整体的比重,可求出整体的量。
3、部分=整体×比重根据整体的量和部分所占的比重,能计算出部分的量。
三、平均数相关公式1、平均数=总数÷个数这是计算平均数最基本的公式。
2、总数=平均数×个数当已知平均数和个数时,可求出总数。
四、倍数相关公式1、 A 是 B 的几倍:A÷B直接用 A 的数值除以 B 的数值,得到 A 是 B 的倍数。
2、 A 比 B 多几倍:(A B)÷B先计算 A 与 B 的差值,再除以 B 的数值。
五、隔年增长相关公式1、隔年增长率=现期增长率+间期增长率+现期增长率×间期增长率例如,今年的增长率为 r1,去年的增长率为 r2,那么隔年增长率就是 r1 + r2 + r1×r2 。
2、隔年基期量=现期量÷(1 +隔年增长率)六、年均增长相关公式1、年均增长量=(末期量初期量)÷年份差用于计算在一定年份内平均每年的增长量。
2、年均增长率=(末期量÷初期量)^(1÷年份差) 1七、混合增长率相关公式整体增长率介于部分增长率之间,且偏向于基期量大的部分增长率。
资料分析公式汇总

资料分析公式汇总在现代化的信息时代,各行各业都需要对大量数据进行分析和处理。
而对于数据的分析,公式是必不可少的工具。
在这里,我们将分享一些常用的资料分析公式,帮助你更好地理解和应用它们。
1. 平均数平均数是最常见的资料分析公式之一。
它是指将一组数的总和除以这组数的个数,用数学符号表示为:$$\bar{x} = \frac{\sum\limits_{i=1}^n{x_i}}{n}$$其中,$\bar{x}$代表平均数,$x_i$代表数据集中的每个数字,$n$代表数据集的大小。
2. 中位数中位数是将一组数排序后位于中间的数字。
如果数的个数为偶数,则把中间两个数字的平均数作为中位数。
中位数用数学符号表示为:$$\begin{cases}x_{\frac{n+1}{2}} & \text{n为奇数} \\\frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} & \text{n为偶数} \end{cases}$$其中,$x_{\frac{n+1}{2}}$代表第$\frac{n+1}{2}$个数字,$x_{\frac{n}{2}}$和$x_{\frac{n}{2}+1}$代表第$\frac{n}{2}$和第$\frac{n}{2}+1$个数字。
3. 众数众数是一组数中出现次数最多的数字。
如果一组数中有多个数出现次数相同,则它们都是众数。
4. 方差方差衡量的是一组数与其平均数之间的差异程度。
它的数学公式为:$$\sigma^2=\frac{\sum\limits_{i=1}^n(x_i-\bar{x})^2}{n}$$其中,$\sigma^2$代表方差,$x_i$代表数据集中的每个数字,$\bar{x}$代表平均数,$n$代表数据集的大小。
5. 标准差标准差是方差的平方根,用来衡量数据集的离散程度。
标准差的公式为:$$\sigma=\sqrt{\frac{\sum\limits_{i=1}^n(x_i-\bar{x})^2}{n}}$$其中,$\sigma$代表标准差,$x_i$代表数据集中的每个数字,$\bar{x}$代表平均数,$n$代表数据集的大小。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些关键的计算公式是至关重要的。
这些公式能够帮助我们快速、准确地从大量的数据中提取有价值的信息,做出合理的判断和决策。
下面,我将为大家整理一些常见且实用的资料分析计算公式。
一、增长率相关公式1、增长率=(现期量基期量)÷基期量× 100%这是最基本的增长率计算公式。
例如,某公司去年的销售额为 100 万元,今年为 120 万元,那么今年的销售额增长率为(120 100)÷ 100 × 100% = 20%。
2、间隔增长率= r1 + r2 + r1×r2当涉及到间隔年份的增长率计算时,就需要用到这个公式。
假设第一年的增长率为 r1,第二年的增长率为 r2,那么从第一年到第二年的间隔增长率就是 r1 + r2 + r1×r2。
3、年均增长率=\(\sqrtn{\frac{现期量}{基期量}} 1 \)(n 为年份差)如果要计算一段时间内的平均增长率,就用这个公式。
比如,某地区 2010 年的 GDP 为 100 亿元,2020 年为 200 亿元,年份差为 10 年,那么年均增长率=\(\sqrt10{\frac{200}{100}} 1 \)。
1、比重=部分量÷整体量× 100%比如,某班级共有 50 名学生,其中男生 25 人,那么男生在班级中的比重就是 25÷50× 100% = 50%。
2、整体量=部分量÷比重已知部分量和比重,求整体量时使用。
假设某企业某产品的销售额占总销售额的 30%,该产品销售额为 100 万元,那么企业总销售额=100÷30% 。
3、部分量=整体量×比重当已知整体量和比重,求部分量时运用。
比如一个城市总人口为100 万人,其中老年人占比 20%,那么老年人的数量= 100×20% = 20 万人。
资料分析公式汇总

资料分析公式汇总资料分析公式的汇总在社会科学、自然科学、工程技术等领域,资料分析是一项非常重要的研究方法。
通过对大量的数据进行收集、整理和处理,可以得出对问题的解释和预测。
而资料分析公式则是在这个过程中广泛应用的一种工具。
本文将对一些常见的资料分析公式进行汇总和解释。
一、中心趋势测量公式1. 平均数公式:平均数是将一组数据的总和除以数据的个数得出的数值,用来代表这组数据的中心趋势。
计算公式如下:平均数 = 总和 / 数据个数2. 中位数公式:中位数是将一组数据按大小顺序排列后,位于中间位置的数值。
如果数据个数为奇数,则中位数就是中间的数值;如果数据个数为偶数,则中位数是中间两个数值的平均值。
3. 众数公式:众数是指在一组数据中出现频率最高的数值。
有时候一组数据中可能存在多个众数,这时可以将所有的众数列举出来。
二、离散程度测量公式1. 范围(R)公式:范围是用于度量一组数据的离散程度的指标,其计算公式如下:范围 = 最大值 - 最小值2. 方差(S²)公式:方差是一组数据偏离平均数的平方差的平均值,用于度量一组数据的离散程度。
计算公式如下:方差= ∑(Xi - 平均数)² / 数据个数3. 标准差(S)公式:标准差是方差的平方根,用于度量一组数据的离散程度的更常用指标。
计算公式如下:标准差= √方差三、相关关系测量公式1. 相关系数(r)公式:相关系数用于度量两组数据之间的相关性,其取值范围在-1到1之间。
相关系数越接近于1或-1,表示两组数据之间的相关性越强,越接近于0则表示两组数据之间的相关性越弱。
计算公式如下:相关系数r = ∑(Xi - 平均数X)(Yi - 平均数Y)/ √[∑(Xi - 平均数X)²] * √[∑(Yi - 平均数Y)²]2. 斯皮尔曼相关系数公式:斯皮尔曼相关系数也是度量两组数据之间的相关性的指标,但它适用于非线性关系的数据。
计算公式如下:斯皮尔曼相关系数 rs = 1 - 6 * ∑(Di²) / (n³ - n)四、回归关系测量公式1. 简单线性回归公式:简单线性回归是通过拟合一条直线来建立两组数据之间的线性关系,从而进行预测和解释的方法。
资料分析计算公式整理

资料分析计算公式整理在资料分析的过程中,计算公式的整理是非常重要的一步。
通过对数据的系统整理、统计和运算,可以得到准确的结果,进而为决策提供支持。
在这篇文章中,我将介绍一些常用的资料分析计算公式,并给出示例,以便读者更好地理解和应用。
一、平均值计算平均值是资料分析中最基本的计算方式之一,它可以帮助我们了解数据的集中趋势。
在进行平均值计算时,需要先将所有观测值相加,再除以观测值的个数。
示例:假设我们有一组数据:10, 12, 15, 18, 20那么平均值的计算公式为:(10 + 12 + 15 + 18 + 20) / 5 = 75 / 5 = 15二、中位数计算中位数是将一组数据按照大小顺序排列后,处于中间位置的观测值。
它对数据的极值不敏感,可以较好地反映数据的集中趋势。
示例:假设我们有一组数据:10, 12, 15, 18, 20首先将数据从小到大排列:10, 12, 15, 18, 20中位数即为中间位置的观测值,即15。
三、标准差计算标准差是度量数据离散程度的一种指标,它可以帮助我们判断一组数据是否分散或集中。
标准差的计算公式包括多个步骤,首先需要计算出各观测值与平均数的差值,然后求其平方,并对所有平方结果求和,最后将和值除以观测值的个数再开方。
示例:假设我们有一组数据:10, 12, 15, 18, 20首先计算平均值:(10 + 12 + 15 + 18 + 20) / 5 = 75 / 5 = 15然后计算差值的平方并求和:(10-15)^2 + (12-15)^2 + (15-15)^2 + (18-15)^2 + (20-15)^2 = 25 + 9 + 0 + 9 + 25 = 68最后将和值除以观测值的个数再开方:√(68/5) ≈ 3.28四、相关系数计算相关系数可以衡量两组变量之间的线性关系强弱。
它的取值范围在-1到1之间,接近-1表示强负相关,接近1表示强正相关,接近0表示无相关。
资料分析公式汇总.docx
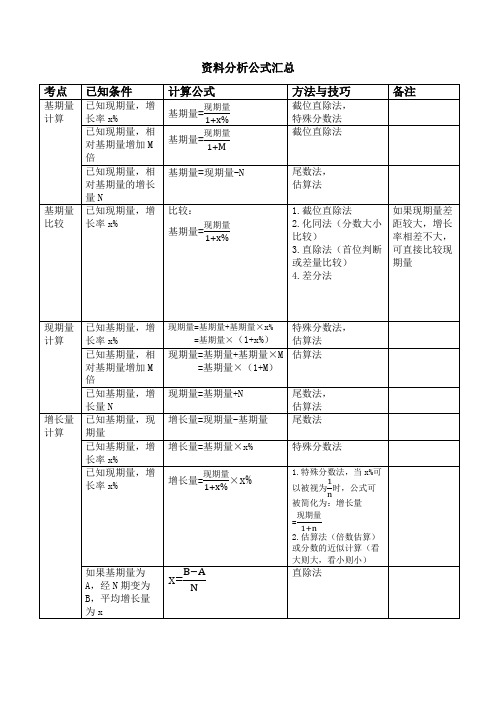
资料分析公式汇总速算技巧一、估算法精度要求不高的情况下,进行粗略估值的速算方式。
选项相差较大,或者在被比较的数字相差必须比较大,差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时,通过“直接相除”的方式得到商的首位(首一位、首两位、首三位),从而得出正确答案的速算方式。
常用形式: 1.比较型:比较分数大小时,若其量级相当,首位最大∕小数为最大∕小数2.计算型:计算分数大小时,选项首位不同,通过计算首位便可得出答案。
难易梯度:1.基础直除法:①可通过直接观察判断首位的情形;②需要通过手动计算判断首位的情形。
2.多位直除法:通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较,若可以找到一个数C,使得A﹥C,而B﹤C,既可以判定A﹥B;若可以找到一个数C,使得A﹤C,而B﹥C,既可以判定A﹤B;2.“计算型”插值法若A﹤C﹤B,则如果f﹥C,则可以得到f=B;如果f﹤C,则可以得到f=A;若A﹥C﹥B,则如果f﹥C,则可以得到f=A;如果f﹤C,则可以得到f=B。
四、放缩法当计算精度要求不高时,可以将中间结果进行大胆的“放”(扩大)或者“缩”(缩小),从而迅速得到精度足够的结果。
常用形式:1. A﹥B,C﹥D,则有A+C﹥B+D;A-D﹥B-C;2. A﹥B﹥0,C﹥D﹥0,则有A×C﹥B×D;A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时,首先选取一个中间值,根据中间值将这组数据“割”(减去)或“补”(追上),进而求取平均值或总和值。
常用形式:1.根据该组数据,粗略估算一个中间值;2.将该组值分别减去中间值得到一组数值;3.将得到的新数值相加得到和值,用和值除以该组数值的项数得到商值,将商值加上中间值,即为该组数值的精确平均值;4.用中间值乘以数据项数再加上最后的和值即为总和值。
资料分析知识点公式总结

资料分析知识点公式总结资料分析是一种通过统计学和概率理论来获得和分析数据的方法。
它主要用于对数据进行模式、趋势和关系的识别。
资料分析通常通过使用数学公式来计算各种参数和统计量,从而得出对数据的解释和预测。
在本文中,我们将总结一些常见的资料分析知识点和公式。
1. 中心趋势中心趋势是数据集中值的度量。
常见的中心趋势包括平均数、中位数和众数。
平均数是一组数据的所有数值之和除以数据个数。
其公式为:\[\bar{x} = \frac{\sum_{i=1}^{n} x_i}{n}\]其中,\(\bar{x}\)代表平均数,\(x_i\)代表第i个数据值,n代表数据个数。
中位数是一组数据中居中位置的数值。
如果数据个数为奇数,中位数为排序后的中间值;如果数据个数为偶数,中位数为排序后中间两个值的平均数。
众数是一组数据中出现频率最高的数值。
2. 离散度离散度用于衡量一组数据的分散程度。
常见的离散度包括极差、方差和标准差。
极差是一组数据中最大值和最小值的差值。
方差是一组数据与其平均数之差的平方和的平均数。
其公式为:\[s^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}\]其中,\(s^2\)代表方差,\(x_i\)代表第i个数据值,\(\bar{x}\)代表平均数,n代表数据个数。
标准差是方差的平方根。
其公式为:\[s = \sqrt{s^2}\]3. 相关性相关性用于衡量两组数据之间的关系。
常见的相关性包括协方差和相关系数。
协方差是一组数据对之间的平均偏差乘积。
其公式为:\[Cov(X, Y) = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{n}\]其中,\(Cov(X, Y)\)代表X和Y的协方差,\(x_i\)和\(y_i\)分别代表两组数据的第i个数值,\(\bar{x}\)和\(\bar{y}\)分别代表两组数据的平均数,n代表数据个数。
资料分析常用基础公式

资料分析常用基础公式在进行数据分析时,有一些常用的基础公式被广泛应用于统计分析和数据建模。
这些公式可以帮助我们理解数据、计算数据的统计特征以及推断数据的模式和趋势。
下面是一些常用的基础公式:1. 平均值(Mean):平均值是数据集所有观测值的总和除以观测值的个数。
平均值常用于描述数据的中心趋势。
公式:Mean = (x₁ + x₂ + ... + xn)/ n2. 中位数(Median):中位数是将数据集的观测值按升序排列后,位于中间位置的值。
中位数可以用来表示数据的中心位置,相比平均值,中位数对于极端值的鲁棒性更强。
公式:Median = ((n + 1)/ 2 )th observation3. 众数(Mode):公式:No explicit formula4. 标准差(Standard Deviation):标准差是观测值与平均值之间的偏离程度的度量。
标准差越大,观测值越分散。
公式:Standard Deviation = sqrt(( (x₁ - x̄)² + (x₂ - x̄)² + ... + (xn - x̄)² ) / n)5. 方差(Variance):方差是标准差的平方,它通过在标准差公式中去掉平方根而得到。
公式:Variance = ( (x₁ - x̄)² + (x₂ - x̄)² + ... + (xn - x̄)² ) / n6. 百分位数(Percentiles):百分位数是对数据集进行排序后的一些百分比处的值。
百分位数常用于描述数据分布的位置和统计特征。
公式:x_p=(p/100)*n(当p为整数时)7. 相关系数(Correlation coefficient):相关系数描述了两个变量之间的线性关系强度和方向。
相关系数的取值范围在-1到1之间,接近-1表示强负相关,接近1表示强正相关,接近0表示无线性关系。
资料分析必备公式

给人改变未来的力量版权所有 翻印必究资料分析必备公式1. 增长量 ①.增长量=增长后的量-增长前的量 ②.本期比上期增长的量= 2. 年均增长量本期的量 × 增长率 1 + 增长率m=b − a 总增长量 = n 增长次数其中,m 代表年均增长量,n 代表增长次数,b 代表增长后的量,a 代表增长前的量 3. 增长率 ①.增长率=增长后的量 − 增长前的量 增长量 × 100% = × 100% 增长前的量 “比”字后面的量 减少前的量 − 减少后的量 减少量 × 100% = × 100% 减少前的量 “比”字后面的量②.减少率=③.总体的增长率数值介于部分增长率之间 一个整体中包含两个部分。
已知总体增长率为 f%,两个部分增长率分别为 x%,y%, 其中 x%<y% 那么它们之间满足关系式:x%<f%<y% 4. 年均增长率 ①.x%= n (b − 1) 100% × a其中 x%代表年均增长率,b 代表增长后的量,a 代表增长前的量,n 代表增长次数 ②.a×(1+x%)n=b 其中 a 代表增长前的量,x%代表年均增长率,n 代表增长次数,b 代笔增长后的量 5. 倍数b ,其中 k 代表 b 是 a 的多少倍(a<b) a b−a b ②. × 100% = − 1 (a<b) a a①.k= 即:增长率 6. 比重 比重= = 倍数-1部分的量 × 100% 整体的量 整体 = 部分的量 部分占整体的比重部分= 整体 × 部分占整体的比重 7. 比重的变化全国客服:4006 300 9991中公教育学员内部专用资料给人改变未来的力量版权所有 翻印必究对比: ①:本期比重=部分的量 × 100% 整体的量增长后的比重=部分的量(1 + x%) × 100% 整体的量(1 + y %)其中 x%代表部分的增长率,y%代表整体的增长率 如果 x%>y%,那么增长后的比重>本期比重 如果 x%<y%,那么增长后的比重<本期比重②:本期比重=部分的量 × 100% 整体的量部分的量 增长前的比重= 1 + x % × 100% 整体的量 1 + y%其中 x%代表部分的增长率,y%代表整体的增长率 如果 x%>y%,那么本期比重>增长前的比重 如果 x%<y%,那么本期比重<增长前的比重 8. 平均数 平均数=总量/份数,人均=总量/人数 9. 计算公式 ①.1 1 ≈ 1 − x%, ≈ 1 + x% ,其中 x%在比较小的情况下的近似,一般 x%<3%。
资料分析公式汇总

资料分析公式汇总欢迎共阅资料分析公式汇总考点基期量计算已知条件已知现期量,增长率x%已知现期量,相对基期量增加M倍已知现期量,相对基期量的增长量N已知现期量,增长率x%计算公式基期量=基期量=方法与技巧截位直除法,特殊分数法截位直除法备注基期量=现期量-N尾数法,估算法1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法基期量比较比较:基期量=如果现期量差距较大,增长率相差不大,可直接比较现期量现期量计算增长量计算已知基期量,增长率x%已知基期量,相对基期量增加M 倍基期量,增长量N已知基期量,现期量基期量,增长率x%已知现期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,预算法现期量=基期量+基期量×M估算法=基期量×(1+M)现期量=基期量+N增长量=现期量-基期量增长量=基期量×x%增长量=×x%尾数法,估算法尾数法特殊分数法1.非凡分数法,当x%可以被视为时,公式可被简化为:增长量=2.预算法(倍数预算)或分数的近似计算(看大则大,看小则小)增长量比较假如基期量为A,经N期变为B,均匀增长量为x已知现期量,增长率x%x=×x%直除法增长量=1.特殊分数法,当x%可以被视为时,公式可页脚内容欢迎共阅被简化为:增长量=2.公式可变换为:增长量=现期量×,其中增函数,所以现期量大,增长率大的情形下,增长量一定大为增长率计算基期量,增长量已知现期量,基期量求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%求两期混合增长率:如果第一期和第二期增长率划分为r1和r2,那么第三期相对第一期增长率为增长率=增长率=截位直除法,插值法截位直除法代入法,公式法x%=-1B=A(1+X%)当x%较小时可简化为B=A(1+nx%)nr3=r1+r2+r1r2简单记忆口诀:连续增长,终究增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)r3求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%已知现期量与增长量已知现期量与基期量已知部分增长量与整体增长量进献率页脚内容x%=x%=a%+已知总体增长率和其中一个部分的增长率,求另外一部分的增长率夹杂增长率a%介于b%和c%之间混合增长率大小居中增长率比较开展速度增长贡献率比较增长率=替代增相当于分数大小比较长率进行大小比较发展速度==1+增长率增长贡献量=贡献率%截位直除法,插值法截位直除法,插值法贡献率是指有效或有用成果欢迎共阅=数目与资本消耗及占用量之比,即投入量与产出量之比截位直除法,插值法拉动增长比重计算求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%某部分现期量为A,整体现期量为为B某部分基期量为A,增长率a%,整体基期量为B,增长率b%某部分现期量为A,增长率a%,整体现期量为B,增长率b%求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%某部分现期量为A,整体现期量为B基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%x%=现期比重=截位直除法,插值法一般先计算,然后按照a和b的大小判断大小现期比重=基期比重=×普通先计算,然后按照a和b的大小判断大小两期比重差值计算:现期比重-基期比重=-××)=×(1-=1.先按照a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.预算法(近似取整预算)4.直除法相当于分数大小比较,同上述做法比重比较现期比重=基期比重=×指数人次与人数进出口和商业顺逆差指数=直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
(完整版)资料分析公式汇总
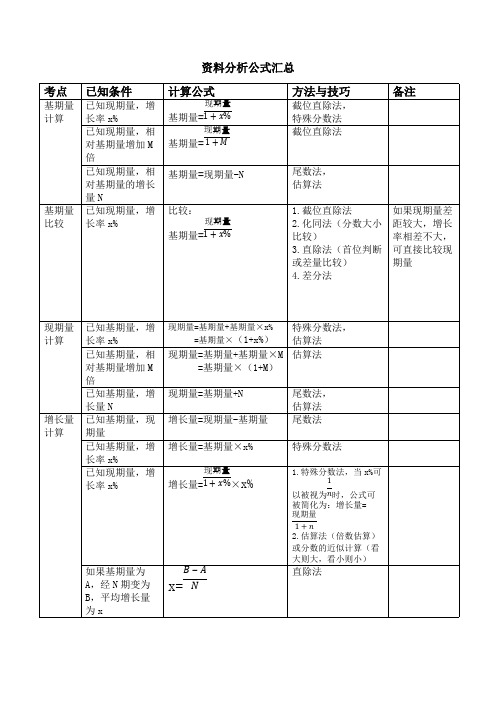
资料分析公式汇总考点已知条件计算公式方法与技巧备注已知现期量,增长率x%基期量=现期量1+x%截位直除法,特殊分数法已知现期量,相对基期量增加M 倍基期量=现期量1+M截位直除法基期量计算已知现期量,相对基期量的增长量N基期量=现期量-N尾数法,估算法基期量比较已知现期量,增长率x%比较:基期量=现期量1+x%1.截位直除法2.化同法(分数大小比较)3.直除法(首位判断或差量比较)4.差分法如果现期量差距较大,增长率相差不大,可直接比较现期量已知基期量,增长率x%现期量=基期量+基期量×x%=基期量×(1+x%)特殊分数法,估算法已知基期量,相对基期量增加M 倍现期量=基期量+基期量×M =基期量×(1+M )估算法现期量计算已知基期量,增长量N现期量=基期量+N 尾数法,估算法已知基期量,现期量增长量=现期量-基期量尾数法已知基期量,增长率x%增长量=基期量×x%特殊分数法已知现期量,增长率x%增长量=×x%现期量1+x% 1.特殊分数法,当x%可以被视为时,公式可1n 被简化为:增长量=现期量1+n2.估算法(倍数估算)或分数的近似计算(看大则大,看小则小)增长量计算如果基期量为A ,经N 期变为B ,平均增长量为xx=B ‒A N直除法增长量比较已知现期量,增长率x%增长量=×x%现期量1+x%1.特殊分数法,当x%可以被视为时,公式可1n被简化为:增长量=现期量1+n2.公式可变换为:增长量=现期量×,其中为x%1+x%x%1+x%增函数,所以现期量大,增长率大的情况下,增长量一定大已知基期量,增长量增长率=增长量基期量截位直除法,插值法已知现期量,基期量增长率=现期量‒基期量基期量截位直除法求平均增长率:如果基期量为A,第n+1期(或经n期)变为B,平均增长率为x%x%=-1nBA代入法,公式法B=A(1+X%)n当x%较小时可简化为B=A(1+nx%)求两期混合增长率:如果第一期和第二期增长率分别为r1和r2,那么第三期相对第一期增长率为r3r3= r1+r2+r1r2简单记忆口诀:连续增长,最终增长大于增长率之和;连续下降,最终下降小于增长率之和(正负号带进公式计算)求总体增长率:整体分为A,B两个部分,分别增长a%与b%,整体增长率x%x%=A×a%+B×b%A+B x%=a%+B(b%-a%)A+B已知总体增长率和其中一个部分的增长率,求另一部分的增长率增长率计算求混合增长率:整体为A,增长率为a%,分为两个部分B,C,增长率为b%和c%混合增长率a%介于b%和c%之间混合增长率大小居中增长率比较已知现期量与增长量比较增长率=代替增现期量基期量长率进行大小比较相当于分数大小比较发展速度已知现期量与基期量发展速度==1+增长率现期量基期量截位直除法,插值法已知部分增长量与整体增长量增长贡献量=部分增长量整体增长量截位直除法,插值法增长贡献率贡献率贡献率%=贡献量(产出量,所得量)投入量(消耗量,占用量)贡献率是指有效或有用成果数量与资源消耗及占用量之比,即投入量与产出量之比拉动增长求B拉动A增长几个百分点:如果B是A的一部分,B拉动A增长x%x%=B的增长量A的基期量截位直除法,插值法某部分现期量为A,整体现期量为为B现期比重=AB截位直除法,插值法某部分基期量为A,增长率a%,整体基期量为B,增长率b%现期比重=AB×1+a%1+b%一般先计算,然后AB根据a和b的大小判断大小某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%一般先计算,然后AB根据a和b的大小判断大小比重计算求基期比重-现期比重:某部分现期量为A增长率a%,整体现期量为B,增长率b%两期比重差值计算:现期比重-基期比重=-×ABAB1+b%1+a%=×(1-)AB1+b%1+a%=×ABa%‒b%1+a%1.先根据a与b的大小判断差值计算结果是正数还是负数;2.答案小于|a-b|3.估算法(近似取整估算)4.直除法某部分现期量为A,整体现期量为B 现期比重=AB相当于分数大小比较,同上述做法比重比较基期比重与现期比重比较:某部分现期量为A,增长率a%,整体现期量为B,增长率b%基期比重=×AB1+b%1+a%直除法,当部分增长率大于整体增长率,则现期比重大于基期比重。
资料分析计算公式

资料分析计算公式在进行资料分析时,掌握一些常用的计算公式是至关重要的。
这些公式能够帮助我们快速、准确地从大量的数据中提取出有价值的信息,为决策提供有力的支持。
接下来,让我们一起深入了解一些常见且重要的资料分析计算公式。
首先是增长率的计算。
增长率反映了某个指标在一定时期内的增长幅度。
其计算公式为:增长率=(本期数值上期数值)÷上期数值 ×100% 。
比如说,某公司去年的销售额为 100 万元,今年的销售额为120 万元,那么今年销售额的增长率就是(120 100)÷ 100 × 100% =20% 。
通过这个公式,我们可以清晰地了解到各项指标的增长情况,从而评估业务的发展趋势。
其次是比重的计算。
比重指的是部分在整体中所占的比例。
计算公式为:比重=部分数值÷整体数值 × 100% 。
例如,一个班级总共有50 名学生,其中男生有 25 名,那么男生在班级中的比重就是 25 ÷ 50× 100% = 50% 。
比重的计算有助于我们了解各个部分在整体中的重要程度和分布情况。
平均数的计算也是经常用到的。
平均数是一组数据的总和除以数据的个数。
公式为:平均数=总和÷个数。
比如,某班级学生的数学考试成绩分别为 80 分、90 分、70 分、85 分、95 分,那么这组成绩的平均数就是(80 + 90 + 70 + 85 + 95)÷ 5 = 84 分。
平均数能够反映出一组数据的一般水平。
在资料分析中,还有一个重要的概念是倍数。
倍数表示两个量之间的相对关系。
计算公式为:倍数=较大值÷较小值。
假设 A 公司的利润为 500 万元,B 公司的利润为 200 万元,那么 A 公司利润是 B 公司的 500 ÷ 200 = 25 倍。
此外,还有一些涉及到基期和现期的计算公式。
基期量的计算公式为:基期量=现期量÷(1 +增长率);现期量的计算公式为:现期量=基期量×(1 +增长率)。
资料分析计算公式整理

资料分析计算公式整理在进行资料分析时,掌握一些常用的计算公式能够帮助我们更高效、准确地处理数据和得出结论。
以下是对一些重要的资料分析计算公式的整理。
一、增长类计算公式1、增长量=现期量基期量例如,2022 年某公司的销售额为 100 万元,2021 年为 80 万元,那么增长量就是 100 80 = 20 万元。
2、增长率=增长量 ÷基期量 × 100%用上例的数据,增长率为(20 ÷ 80)× 100% = 25% 。
3、基期量=现期量 ÷(1 +增长率)假设 2023 年某产品的销量为 120 万件,同比增长 20%,则 2022 年的销量(基期量)为 120 ÷(1 + 20%)= 100 万件。
4、现期量=基期量 ×(1 +增长率)如果已知 2021 年某地区的人口为 50 万人,预计每年以 5%的速度增长,那么 2025 年的人口(现期量)为 50 ×(1 + 5%)^4 万人。
二、比重类计算公式1、比重=部分量 ÷整体量 × 100%比如,某班级男生有 20 人,全班共有 50 人,那么男生所占比重为(20 ÷ 50)× 100% = 40% 。
2、部分量=整体量 ×比重若已知某公司总利润为 1000 万元,其中 A 产品的利润占比为 30%,则 A 产品的利润为 1000 × 30% = 300 万元。
3、整体量=部分量 ÷比重比如某企业中研发部门的人数为 50 人,占总人数的 20%,则该企业总人数为 50 ÷ 20% = 250 人。
三、平均数类计算公式1、平均数=总数 ÷个数例如,某班级5 名学生的数学成绩分别为80、90、85、95、75 分,那么平均成绩为(80 + 90 + 85 + 95 + 75)÷ 5 = 85 分。
资料分析计算公式-资料类

资料分析计算公式-资料类关键信息项:1、计算公式名称2、计算公式表达式3、适用数据类型4、计算目的5、计算结果解读11 计算公式名称本协议所涉及的资料分析计算公式包括但不限于:平均值计算公式、中位数计算公式、众数计算公式、方差计算公式、标准差计算公式、增长率计算公式、比例计算公式等。
111 平均值计算公式平均值=数据总和 ÷数据个数112 中位数计算公式将数据从小到大或从大到小排序,如果数据个数为奇数,则中间的数为中位数;如果数据个数为偶数,则中间两个数的平均值为中位数。
113 众数计算公式众数是一组数据中出现次数最多的数值。
12 方差计算公式方差=(数据 1 平均值)²+(数据 2 平均值)²+… +(数据 n平均值)² ÷ n121 标准差计算公式标准差=方差的平方根122 增长率计算公式增长率=(本期数据上期数据)÷上期数据 × 100%123 比例计算公式比例=部分数据量 ÷总体数据量2、适用数据类型21 平均值、中位数、众数计算公式适用于各种数值型数据,如整数、小数等。
22 方差和标准差计算公式主要用于衡量数据的离散程度,适用于具有一定分布特征的数据。
23 增长率计算公式适用于对比不同时期的数据增长情况,常用于经济、统计等领域。
24 比例计算公式适用于表示部分与整体的关系。
3、计算目的31 平均值用于反映数据的集中趋势,提供一个大致的代表值。
32 中位数可避免极端值对数据代表性的影响。
33 众数可用于发现数据中的常见模式。
34 方差和标准差用于衡量数据的分散程度,判断数据的稳定性。
35 增长率用于评估数据的增长速度和趋势。
36 比例用于了解部分在整体中所占的份额。
4、计算结果解读41 平均值的大小反映了数据的总体水平,但可能受到极端值的影响。
42 中位数不受极端值的影响,更能代表数据的中间位置。
43 众数表示数据中最常出现的数值,可用于了解数据的集中模式。
资料分析常用公式

资料分析常用公式1. 平均数公式平均数(Mean)是表示一组数据集中趋势的量数,计算公式为:$$\text{平均数} = \frac{\sum_{i=1}^{n} x_i}{n}$$其中,$ x_i $ 表示第 $ i $ 个数据,$ n $ 表示数据的总数。
平均数适用于描述数据的中心位置,常用于市场调查、产品评价等领域。
2. 中位数公式中位数(Median)是将一组数据从小到大(或从大到小)排列,位于中间位置的数值。
计算公式为:$$\text{中位数} = \begin{cases}x_{\frac{n+1}{2}} & \text{当 } n \text{ 为奇数时} \\\frac{x_{\frac{n}{2}} + x_{\frac{n}{2}+1}}{2} & \text{当 } n \text{ 为偶数时}\end{cases}$$中位数适用于描述数据的中心位置,特别适用于数据分布不均匀或存在异常值的情况。
3. 标准差公式标准差(Standard Deviation)是衡量一组数据离散程度的量数,计算公式为:$$\sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i \mu)^2}{n}}$$其中,$ \sigma $ 表示标准差,$ x_i $ 表示第 $ i $ 个数据,$ \mu $ 表示平均数,$ n $ 表示数据的总数。
标准差越大,表示数据的离散程度越大,反之越小。
4. 相关系数公式相关系数(Correlation Coefficient)用于衡量两个变量之间的线性关系程度,计算公式为:$$r = \frac{n(\sum xy) (\sum x)(\sum y)}{\sqrt{[n\sum x^2 (\sum x)^2][n\sum y^2 (\sum y)^2]}}$$其中,$ r $ 表示相关系数,$ x $ 和 $ y $ 分别表示两个变量,$ n $ 表示数据的总数。
资料分析公式范文

资料分析公式范文以下是一些常用的资料分析公式:1.平均值公式:平均值是一组数据的总和除以数据的个数。
平均值公式可以表示为:平均值=总和/数据个数平均值可以用来描述一组数据的集中程度。
2.方差公式:方差是一组数据与平均值之间差值的平方的平均值。
方差公式可以表示为:方差= (∑(xi-平均值)²) / 数据个数方差可以用来描述一组数据的离散程度。
3.标准差公式:标准差是方差的平方根,用来衡量一组数据的波动程度。
标准差公式可以表示为:标准差=√方差标准差越大,数据的波动程度越大。
4.相关系数公式:相关系数描述两个变量之间的相关程度。
相关系数公式可以表示为:相关系数=协方差/(标准差1*标准差2)相关系数的取值范围为-1到1,当相关系数为正时,表示两个变量正相关;当相关系数为负时,表示两个变量负相关;当相关系数接近0时,表示两个变量不相关。
5.回归分析公式:回归分析用来建立变量之间的数学关系,并用来预测未来的数值。
最简单的线性回归模型可以表示为:y = a + bx其中y是因变量,x是自变量,a和b是回归系数。
通过拟合数据,可以求得最佳的回归系数,进而进行预测。
6.正态分布公式:正态分布是最常见的概率分布之一,用来描述自然界和人类行为中很多现象的分布情况。
正态分布的概率密度函数可以表示为:f(x)=(1/(σ√2π))*e^(-(x-μ)²/2σ²)其中f(x)是x的概率密度值,μ是均值,σ是标准差。
正态分布具有钟形曲线的形状,均值和标准差决定了曲线的位置和形状。
这些公式是资料分析中常用的基本工具,通过运用这些公式,我们可以从数据中提取出有意义的信息,并进行更深入的分析和推断。
同时,还有许多其他的资料分析公式,如卡方检验公式、t检验公式、ANOVA分析公式等等,这些公式可以根据具体的分析需求来选择和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
资料分析
主要测查报考者对各种形式的文字、图表等资料的综合理解与分析加工的能力,针对一段资料一般有1~5个问题,报考者需要根据资料所提供的信息进行分析、比较、推测和计算,从四个备选答案中选出符合题意的答案。
1、统计术语
◆现期与基期
资料题目中,作为对比参照的时期称为基期,而相对于基期的为现期。
描述基期的具体数值我们称之为基期量,描述现期的具体数值我们称之为现期量。
◆同比与环比
同比:与历史同期相比较
如:今年五月与去年五月相比较;今年第一季度与去年第一季度相比较;今年上半年与去年上半年相比较。
环比:环比实际上即指“与紧紧相邻的统计周期相比较”,包括日环比、周环比、月环比、年环比等。
【例1】2009年全年民营工业实现增加值8288.8亿元,增长18.9%,增幅同比提高4.2个百分点。
【例2】2010年上半年,全国原油产量为9848万吨,同比增长5.3%,上年同期为下降1%。
◆增长率
增长率指的是现期与基期的差值与基期之间的比较。
增长率=(现期量-基期量)÷基期量
【特别提示】
增速、增幅:一般情况下,均与增长率相同。
(但在特殊语境下,增幅是指具体数值的增加,例如:某企业9月份的产值和上月相比,有了200万元的增幅,这里增幅就是指具体数值的增加。
)
【判别特征】:
增长率:(现在)……比(过去)……增长(下降)……%
;
【例1】1959年与1958年比较,支援农村生产支出和农林水利气象等部门的事业费?
A. 提高了151.8%
B. 提高了51.8%
C. 提高了251.8%
D. 提高了105%
◆百分数与百分点
增长率之间的计算只能用百分点,不能用百分数。
【例1】与上年同期相比,2010年6月汽车零售同比增幅()
A.回落42.3个百分点
B.加快42.3个百分点
C.回落42.3%
D.加快42.3%
◆减少率(减少幅度、减少速度)
减少率=减少量÷基期量×100%,“减少率”本质是一种未带负号的“增长率”
2006—2011年我国违法用地案件查处情况(一)【例2】与2006年相比,2011年全国收缴土地面积约减少了:
A.52%
B.110%
C.67%
D.205%
◆发展速度(理解)
发展速度是反映某种社会现象发展程度的相对指标,它是现期发展水平与基期发展水平之比。
计算公式为:
发展速度=末期量÷基期量=增长率+100%。
◆拉动增长率(理解)
“拉动增长……百分点”这个概念是部分量的增长对总量增长的一个贡献。
即:
拉动增长率=部分增长量÷总体基期量
◆成数与翻番
成数:几成相当于十分之几。
【例】某单位有300名员工,其中有60人是研究生学历,则研究生学历的员工占总人数的 2 成。
(60÷300=2/10)
翻番:翻一番为原来的2倍;翻两番为原来的4倍;依此类推,翻n番为原来的2n倍。
◆增长量
它说明社会经济现象在一定时期内增长(或减少)的绝对量。
【判别特征】:增长量:(现在)……比(过去)……增长(下降)(具体值)
【基本应用】:
2000~2008年XX省进出口总额
【例1】以2000年为基准,该省2008年的出口总额约增加()。
A.1244亿元
B.2000亿元
C.2890亿元
D.4134亿元
俄罗斯是世界最大的管道天然气出口国,占管道天然气总出口量的27.8%,2009年出口量为1764.8亿立方米,较2008年增长14.3%。
【例2】2009年俄罗斯管道天然气出口较上年增长了多少亿立方米?()【例3】如果增长趋势与上年保持一致,预计2003年末移动电话用户约为()。
A.21000万户
B.23000万户
C.25000万户
D.29000万户
◆平均数
平均数是指在一组数据中所有数据之和再除以数据的个数。
即:
把n个数的总和除以n,所得的商叫做这n个数的平均数
【例1】某地区新千年以来大力发展旅游业,下表显示其2001年以来游客量统计表。
该地区2001年至2006年平均每年游客量约为多少万人次?( )
◆平均增长量
【例1】我国第二产业就业人员2005年为18084万人,2009年增加到21684万人;
则2009年末与2005年末相比,我国第二产业人员年均增加( )。
A. 566.4万人
B. 708万人
C. 720万人
D. 900万人
◆五年计划
【例2】我国“十一五”期间平均每年增加人口
A. 660.75万人
B. 644万人
C. 657.4万人
D. 528.6万人
◆平均增长速度
平均增长速度则是反映现象逐年递增的平均速度。
平均发展速度(水平法)的计算公式如下:
末期值=初期值×(1+年均增长率)n在实际应用时多次幂的计算相对复杂,所以当增长率较小的时候我们可以采用如下公式:
a(1+x)n≈a(1+nx)进行近似计算。
◆顺差、逆差
顺差:在一个时期内,一个国家(或地区)的出口商品额大于进口商品额,叫做对外贸易顺差(又称净出口额、出超)。
逆差:在一个时期内,一个国家(或地区)的出口商品额小于进口商品额,叫做对外贸易逆差(又称净进口额、入超)。
【例】2010年,我国机电产品出口9334.3亿美元,同比增加30.9%; 高新技术产品出口4924.1亿美元,同比增长30.7%。
船舶、汽车零部件出口保持较快增长,其中船舶出口同比增长的44.5%,汽车零部件出口同比增长44.1% .
2010年,机电产品进口额达到6603.1亿美元,同比增长34.4%,高新技术产品进口额达到4126.1亿美元,同比增长33.2%
下列关于2010年我国进出口贸易的表述正确的是:
A.高新技术产品逆差约为800亿美元
B.……
◆比重
比重即部分在整体中所占的比例。
【判别特征】:比重:(个体)……占(整体)……的(比例)%
式子1:给整体,比重,求个体?=
个体整体比重
式子2:给个体,比重,求整体?=个体
整体
比重
式子3:给个体,整体,求比重?=个体
比重
整体
2011年发现违法用地行为7.0万件,涉及土地5.0万公顷(耕地1.8万公顷),同比分别上升5.8%、11.0%(耕地下降2.4),立案查处违法用地案件4.2万件,涉及土地4.4万公顷(耕地1.5万公顷),同比分别上升2.5%、11.4%(耕地下降5.7万公顷)。
【例1】2011年,发现违法但未立案的违法用地行为占发现违法用地行为总数的比重约为多少?
2003年至2011年,我国第一产业年均增长4.6%,第二产业年均增长11.9%,第三产业年均增长11.1%,均保持较快发展态势。
2010年,我国制造业产出占世界的比重为19.8%,超过美国成为全球制造业第一大国。
【例2】如果2010年我国制造业生产总值为135000亿元,那么2010年世界制造业生产总值约为()万亿元。
◆指数(理解)
◆三大产业
第一产业:农、林、牧、渔业(不含农、林、牧、渔服务业)。
第二产业:采矿业(不含开采辅助活动)、制造业(不含金属制品、机械和设备修理业)、电力、热力、燃气及水生产和供应业、建筑业。
第三产业:服务业,是指除第一产业、第二产业以外的其他行业。
◆国内生产总值
GDP是英文(Gross Domestic Product)的缩写,也即国内生产总值。
它是指一个国家(或地区)所有常住单位在一定时期内生产的最终产品和服务价值的总和,常被公认为衡量国家经济状况的最佳指标,国内生产总值由第一产业、第二产业、第三产业增加值构成,一个国家的国内生产总值就是三大产业的增加值之和。
【例1】经初步核算,2009年上半年我国国内生产总值同比增长7.1%,比一季度加快1.0个百分点。
其中,第一产业增加值12025亿元,增长3.8%,第二产业增加值70070亿元,增长6.6%,第三产业增加值57767亿元,增长8.3%。
则2009年上半年,我国国内生产总值为( )
A.139862亿元
B.147953亿元
C.148634亿元
D.151429亿元
【知识点汇总】四个知识点。
