一些重力加速度的数值
g的符号物理

g的符号物理
g 在物理学中有多个含义,可以作为不同的符号使用。
以下是一些常见的用法:
重力加速度:g 通常用来表示重力加速度,它是描述物体在地球表面上自由下落时加速度大小的物理量。
在国际单位制(SI)中,重力加速度的单位是米每秒平方(m/s²)。
在地球表面附近,重力加速度的数值约为 9.8 m/s²,但这个数值随着地理位置和海拔高度的不同而有所变化。
万有引力常数:g 也可以用来表示万有引力常数,它是描述物体之间引力大小的物理量。
万有引力常数的数值约为 6.674 × 10^-11 N·m²/kg²,它表示两个质量分别为 1 千克的物体,相距 1 米时的相互引力大小。
除了以上两种常见的用法,g 在物理学中还可能表示其他物理量,具体取决于上下文和使用的领域。
需要注意的是,在不同的场合和语境下,g 的含义和单位可能会有所不同,因此需要根据具体情况进行理解和应用。
万有引力常数g的数值

万有引力常数g的数值万有引力常数g是描述地球表面上物体受到的重力的物理常数。
它是一个重要的参数,对于解释地球上物体的运动和重力相关问题非常关键。
本文将对万有引力常数g的数值进行详细介绍和解释。
让我们来了解一下万有引力常数g的定义。
万有引力常数g是指在地球表面上的一个物体所受到的重力加速度。
它的数值是9.8米/秒²。
这意味着在地球表面上,每个物体都会受到一个向下的加速度,大小为9.8米/秒²。
这个加速度的方向是向下的,因为地球的重力是向下的。
万有引力常数g的数值是通过实验测量得到的。
科学家使用了一个被称为重力加速度计的仪器来测量地球表面上物体所受到的重力加速度。
通过多次测量和统计分析,科学家确定了万有引力常数g的平均值为9.8米/秒²。
这个数值是一个近似值,可能会因为地理位置的不同而有所变化。
万有引力常数g的数值对于地球上的物体的运动非常重要。
它决定了物体在地球表面上自由下落的速度。
根据物体自由下落的速度,我们可以计算出物体在不同时间内的位置和速度。
这对于解释和预测物体的运动非常有用。
除了地球表面上的物体,万有引力常数g的数值也适用于地球附近的物体。
例如,地球上的人造卫星和航天器在地球附近的运动也受到了相同的重力加速度。
这是因为地球附近的重力场是非常均匀的,所以不同位置的物体受到的重力加速度几乎是相同的。
值得注意的是,地球表面上的物体所受到的重力加速度不仅仅受到地球的引力影响,还受到其他因素的影响。
例如,地球的自转和地球表面的地形会对物体的重力加速度产生一些影响。
因此,实际的万有引力常数g的数值可能会因为这些因素的影响而略有不同。
总结起来,万有引力常数g是描述地球表面上物体受到的重力的物理常数。
它的数值为9.8米/秒²,是通过实验测量得到的。
万有引力常数g的数值对于解释地球上物体的运动和重力相关问题非常重要。
它决定了物体在地球表面上自由下落的速度,并且适用于地球附近的物体的运动。
海陆空涉及的重力加速度知识

竞业协议(实用)(一)竞业协议(实用)(一)一、引言竞业协议作为保护企业利益和商业机密的重要法律工具,在企业合作和员工离职过程中起着关键作用。
本文旨在介绍竞业协议的基本概念和内容,并探讨其实际应用。
二、竞业协议的定义及作用竞业协议,又称非竞争协议,是指企业与员工、合作方或其他与之存在商业关系的个人或组织,在解除合同或就业关系时签订的协议,约定了离职后在一定期限内禁止从事与前雇主或合作方业务相竞争的行为。
竞业协议的主要作用有以下几个方面:1. 保护商业机密:竞业协议可以防止离职员工或合作方将商业机密、商业计划、客户资源等关键信息带走或运用到竞争对手中,从而保护企业的核心竞争力。
2. 维护市场秩序:竞业协议规定了一定期限内的竞争限制,有助于维护市场竞争的公平和秩序。
3. 保护企业利益:离职员工或合作方直接加入竞争对手,并从中获取利益将对企业造成不小的损失。
竞业协议通过限制离职员工或合作方在一定期限内进行竞争,保护了企业的经济利益。
4. 刺激创新发展:通过限制员工或合作方在离职后的一定期限内从事竞争性活动,可以鼓励企业的内部创新和自主研发。
三、竞业协议的要素竞业协议通常包含以下要素:1. 协议双方:明确协议签署方的身份,并确定双方的权利和义务。
2. 竞争限制范围:约定离职员工或合作方在何种地域范围、何种行业范围内禁止从事竞争性活动,并对禁止行为进行具体描述。
3. 限制期限:约定竞业协议的有效期限,一般不得超过两年。
4. 补偿措施:针对竞业协议的违约行为,约定相应的违约金或赔偿金额。
5. 异议解决:约定双方因竞业协议引发的争议或纠纷如何解决,可以选择仲裁、诉讼等方式。
四、竞业协议的实际应用竞业协议的实际应用中,需要注意以下几点:1. 合法合规:竞业协议必须依法合规,符合相关法律法规的规定。
在签订协议前,应事先对相关法律法规进行了解,确保协议内容的合法性和有效性。
2. 协议灵活性:根据不同行业、不同岗位和不同离职人员的实际情况,灵活制定竞业协议的具体条款,务必合理明确,以避免纠纷的发生。
水的重力加速度

水的重力加速度
水的重力加速度是指水在地球引力作用下所受的加速度,一般用 g 表示,单位是 m/s²。
以下是关于水的重力加速度的一些相关信息:
1. 定义和计算公式
水的重力加速度是指水在重力场中自由落体时所受的恒定加速度。
计算公式为:g = G*M/r²,其中 G 为万有引力常数,M 为地球质量,r 为地球半径。
2. 实验测量值
根据实验数据,水的重力加速度的平均值为 9.8 m/s²,但是实际上它的值会受到许多因素的影响,比如在高海拔地区、沉积物含量高的水域等情况下,其值会稍微有所变化。
3. 影响因素
水的重力加速度会受到多种因素的影响,比如地球自转、地球形状、海拔高度、地质构造等,其中地球自转对其影响最大,对于静止不动的物体,水的重力加速度稍微会有一点降低。
4. 应用
水的重力加速度是物理学中的一个重要概念,广泛应用于流体力学、水力学、气象学等领域中。
对于人们日常生活中的一些实际问题,比如水龙头的水流速度、水底下的物体运动速度等,都需要使用到水的重力加速度的知识。
5. 与其他物质的比较
相对于空气而言,水的密度较大,因此在地球引力的作用下,水的重力加速度也要比空气大得多,空气的重力加速度大约只有地球重力加速度的1/800。
6. 参考值
根据国际标准,水的重力加速度的标准值为 9.80665 m/s²,可以作为试验中的标准值进行参考。
重力和重量的换算公式

重力和重量的换算公式
重力和重量是物理学中常见的概念,重力是指物体受到地球引力的作用力,重量是指物体受到重力作用下所承受的力。
在不同的情况下,我们需要进行重力和重量的换算,下面是相关的换算公式:
1.重力的大小可以用重力加速度g来表示,直接向下的重力大小为mg,其中m为物体的质量,g的数值约等于9.8m/s,公式为G=mg。
2.重力和重量的换算公式为W=mg,其中W为物体的重量,单位是牛顿(N),m为物体的质量,单位是千克(kg),g的数值同上。
3.在不同的重力场中,重量会发生变化,比如在月球表面,重力加速度约为1.6m/s,所以同样质量的物体在月球上的重量只有地球上的约1/6。
4.在一些工程应用中,需要将重量转换为质量来计算,公式为m=W/g。
总之,重力和重量的换算公式对于物理学、工程学等领域有着重要的应用价值,需要掌握和理解。
- 1 -。
重力加速度与纬度的关系

重⼒加速度与纬度的关系 标准重⼒加速度9.80665 m/s²1、重⼒加速度和纬度 把地球当作椭球,公式为:g=9.780327(1+0.0053024sin²Φ-0.0000058sin²2Φ) m/s²(1979修订公式)。
式中Φ为物体所在处的地理纬度。
例如,在⾚道=0,g=9.7803m/s²,在两极=90°,g=9.83m/s²。
带⼊Φ=45度,g=9.780327*(1+0.0053/2)=9.8062 m/s² 带⼊Φ=45.5度,g=9.80665 带⼊Φ=45.542度,g=9.806692、重⼒加速度和向⼼⼒ 由余弦定理,mg=sqrt(Fw^2+F^2-2Fw*F*cost),其中Fw为向⼼⼒ 近似为,mg=F(1-Fw/Fcost)=F(1-3.45*10^(-3)*cost)其中:Fw=mrw^2*cost,F=GmM/r^2,Fw/F=r^3*w^2/GM*cost a≈g(1-3.45*10^(-3)*cost) ⾃转的平均⾓速度为7.292×10^(-5) rad/s 假设R=6371km,g=GM/R^2=3.986*10^14/6371000^2=9.820m/s^2,RW^2=6371000*7.292^2*10^(-10)=0.0339 m/s^2 系数=r^3*w^2/GM=6371000^3*7.292^2*10^(-10)/(3.986*10^14)=0.003453、考虑地球是椭圆 任意纬度半径,R=a*sqrt(1-0.006694*sint^2),a=6378.137km t=45.0度,R=6367.45km t=45.5度,R=6367.27km 带⼊参数:R=6367.27km,g=9.83175*(1-3.45*10^(-3)*cos45.5)=9.808 m/s^2(偏⼤0.0013)4、分析 ⾚道,g=GM/R^2-w^2*R,其中w=2*pi/T 两极,g=GM/R^2,加速度9.8322000国家⼤地坐标系采⽤的地球椭球参数的数值为 长半轴:a=6 378 137m 扁率:f=1/298.257 222 101 地⼼引⼒常数:GM=3.986 004 418×10^14 m^3/s^2 ⾃转⾓速度:ω=7.292 115×10-5rad/s参考数据:a=6378.137km,b=6356.752km,GM=3.986*10^14 m 带⼊参数:R=6356.752km,g=9.864 m/s^2(偏⼤0.032) 带⼊参数:R=6378.137km,g=9.7983*(1-3.46*10^(-3))=9.7644 m/s^2(偏⼩0.016) 带⼊参数:⾚道,g=9.7983-R*w^2=9.7983-0.0339=9.7644 m/s^2。
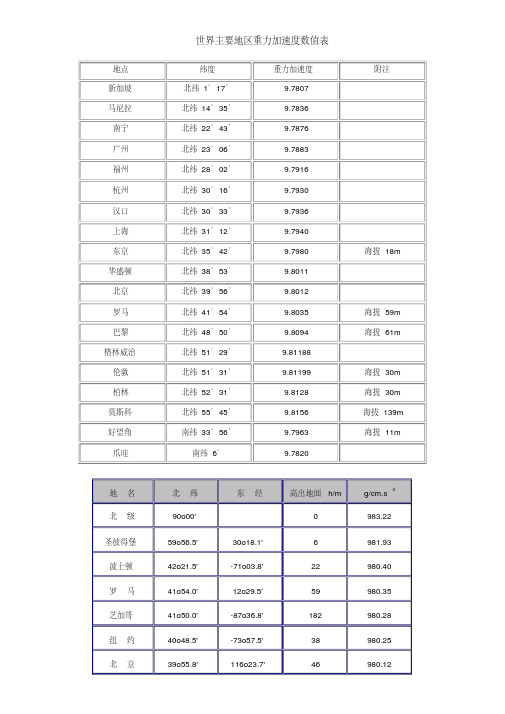
重力加速度数值(世界)

重力加速度数值(世界)————————————————————————————————作者:————————————————————————————————日期:世界主要地区重力加速度数值表地点纬度重力加速度附注新加坡北纬1°17′9.7807马尼拉北纬14°35′9.7836南宁北纬22°43′9.7876广州北纬23°06′9.7883福州北纬28°02′9.7916杭州北纬30°16′9.7930汉口北纬30°33′9.7936上海北纬31°12′9.7940东京北纬35°42′9.7980 海拔18m 华盛顿北纬38°53′9.8011北京北纬39°56′9.8012罗马北纬41°54′9.8035 海拔59m 巴黎北纬48°50′9.8094 海拔61m 格林威治北纬51°29′9.81188伦敦北纬51°31′9.81199 海拔30m 柏林北纬52°31′9.8128 海拔30m 莫斯科北纬55°45′9.8156 海拔139m 好望角南纬33°56′9.7963 海拔11m 爪哇南纬6°9.7820地名北纬东经高出地面h/m g/cm.s-2北级90o00' 0 983.22 圣彼得堡59o56.5' 30o18.1' 6 981.93 波士顿42o21.5' -71o03.8' 22 980.40 罗马41o54.0' 12o29.5' 59 980.35 芝加哥41o50.0' -87o36.8' 182 980.28纽约40o48.5' -73o57.5' 38 980.25 北京39o55.8' 116o23.7' 46 980.12 旧金山37o47.5' -112o25.7' 114 979.96 南京32o03.6' 118o45' 270 979.44 首尔97994 赤道00o00' .... 0 978.04 墨尔本-37o49.9' 144o58.5' 26 979.99 南极-90o00' .... 0 983.22COUNTRY国家CITY城市G(m/sec2)加速度COUNTRY国家CITY城市G(m/sec2)加速度GReece Athens9.800Scotland Glasgow9.816 SouthAfricaCape town9.796Spain Madrid9.800 Netherlands Amsterdam9.813Singapore Singapore9.781 Norway Oslo9.815Argentina Buenos Aires9.797 NewZealandAuckland,NZ9.799UnitedKingdom London,Greenwich9.812 NewZealandWellington,NZ9.801Australia Melbourne9.800 Taiwan Taichung9.789Australia Sydney9.797 Taiwan Taiwan9.788Italy Milano9.806 Taiwan Taipei9.790Italy Rome9.803 Denmark Copenhagen9.815India Calcutta9.788 Germany Fankfurt9.810Japan Tokyo9.798 Mexico Mexico City9.779Canada Ottawa9.806 U.S.A Birmingham9.813Canada Vancouver,BC9.809 U.S.A Chicago9.803Cuba Havana9.788 U.S.A Los Angles9.796Kuwait Kuwait9.795 U.S.A New York9.802Cyprus Nicosia9.797 U.S.A San Francisco9.800Thailand Bangkok9.783 U.S.A Washington,DC9.784Portugal Lisbon9.801Belgium Brussels9.811France Paris9.809 Brazil Rio de Janeiro9.786Finland Helsinki9.819 Sweden Stockholm9.818Philippines Manila9.784 Switzerland Zurich9.807。
重力加速度数值表(世界)
Nicosia
9.797
U.S.A
San Francisco 9.800 Thailand
Bangkok
9.783
U.S.A
Washington,DC 9.784 Portugal
Lisbon
9.801
Belgium Brussels
9.811 France
Paris
9.809
Brazil
Rio de Janeiro 9.786 Finland
1ห้องสมุดไป่ตู้2 38 46
g/cm.s -2 983.22 981.93 980.40 980.35 980.28 980.25 980.12
旧金山
37o47.5'
-112o25.7'
114
南京
32o03.6'
118o45'
270
首尔
赤道
00o00'
....
0
墨尔本
-37o49.9'
144o58.5'
26
Helsinki
9.819
Sweden Stockholm
9.818 Philippines
Manila
9.784
Switzerland Zurich
9.807
南极
-90o00'
....
0
979.96 979.44 97994 978.04 979.99 983.22
COUNTRY 国家
CITY 城市
G(m/sec 2) COUNTRY
加速度
国家
CITY 城市
G(m/sec 2) 加速度
重力加速度

感谢观看
汇报人:XX
重力加速度随纬度的变化规律
重力加速度随纬度的增加而减小 赤道附近的重力加速度最小 两极附近的重力加速度最大 重力加速度的变化规律与地球的形状和自转有关
重力加速度随高度的变化规律
重力加速度随高 度增加而减小
在地球表面附近, 重力加速度约为 9.8m/s²
在高海拔地区, 重力加速度值较 小
重力加速度的分 布规律受到地球 内部质量分布的 影响
物体落地时间计算 卫星轨道稳定 地球质量估算 潮汐现象研究
重力加速度在航天领域的应用
卫星轨道计算
火箭发射速度控 制
宇航员在太空中 的运动研究
航天器返回地球 时的着陆速度计 算
重力加速度在地球物理学中的应用
测量地球的重力加速度 计算地球的质量和赤道半径 研究地球的自转和地球的构造 预测地震和海啸等自然灾害
03
重力加速度的应用
重力加速度在生活中的应用
自由落体运动:利用重力加速度 计算高度、时间等
汽车安全气囊:利用重力加速度 检测碰撞,触发安全气囊保护乘 客
添加标题
添加标题
添加标题
添加标题
投掷运动:利用重力加速度提高 投掷物的速度和距离
地震预警:利用重力加速度检测 地震波,提前预警地震发生
重力加速度在科学研究中的应用
常用单位是厘米每秒平方 ( c m / s ²)
符号表示为g或g''
重力加速度的大小与地球上的 位置有关,赤道最小,两极最 大
02
重力加速度的影响 因素
纬度对重力加速度的影响
纬度越高,重力加速度越大
地球自转产生的离心力随纬度 增加而减小
地球半径随纬度增加而减小, 导致重力加速度增大
世界各地的重力加速度分别是多少

福州
北纬28°02′
9.7916
杭州
北纬30°16′
9.7930
武汉
北纬30°33′
9.7936
上海
北纬31°12′
9.7940
东京
北纬35°42′
9.7980
海拔18m
华盛顿
北纬38°53′
9.8011
9.81199
海拔30m
柏林
北纬52°31′
9.8128
海拔30m
莫斯科
北纬55°45′
9.8156
海拔139m
好望角
南纬33°56′
9.7963
海拔11m
爪哇
南纬6°
9.7820
北极
90
9.832
由于g随纬度变化不大,因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米/秒^2作为重力加速度的标准值。在解决地球表面附近的问题中,通常将g作为常数,在一般计算中可以取g=9.80米/秒^2。理论分析及精确实验都表明,随纬度的提高,重力加速度g的数值略有增大,如赤道附近g=9.780米/秒^2,北极地区g=9.832米/秒^2。
海拔30m
莫斯科
北纬55°45′
9.8156
海拔139m
好望角
南纬33°56′
9.7963
海拔11m
爪哇
南纬6°
9.7820
北极
90
9.832
由于g随纬度变化不大,因此国际上将在纬度45°的海平面精确测得物体的重力加速度g=9.80665米/秒^2作为重力加速度的标准值。在解决地球表面附近的问题中,通常将g作为常数,在一般计算中可以取g=9.80米/秒^2。理论分析及精确实验都表明,随纬度的提高,重力加速度g的数值略有增大,如赤道附近g=9.780米/秒^2,北极地区g=9.832米/秒^2。
国际上以北纬 45 °海平面重力加速度值为标准值:

国际上以北纬45 °海平面重力加速度值为标准值:国际上以北纬45 °海平面重力加速度值为标准值1. 介绍在物理学领域中,重力加速度是一个非常重要的概念。
在地球上,重力加速度并不是一个恒定的数值,它受到地球自转、地壳的板块构造以及地球形状等多种因素的影响而有所不同。
然而,在国际上,为了便于科学研究和标准化计算,人们通常以北纬45 °海平面重力加速度值作为标准值,约为9.80665 m/s²。
本文将深入探讨国际上以北纬45 °海平面重力加速度值为标准值的重要性和影响。
2. 重力加速度的定义与变化重力加速度是指物体在重力作用下每秒钟速度的增加量,通常用字母g 表示。
在地球上,重力加速度的大小并不是恒定的,它受到地点、海拔高度、地壳构造和地球自转等因素的影响而有所变化。
一般来说,重力加速度的数值会随着海拔的增加而减小,随着纬度的增加而增大。
然而,为了便于科学研究和标准化计算,国际上采用了以北纬45 °海平面重力加速度值作为标准值。
3. 以北纬45 °海平面重力加速度值的重要性北纬45 °海平面重力加速度值作为标准值的选择并非偶然,而是基于科学实验和全球数据的分析得出的。
这一数值的选择既能较好地代表地球大部分地区的真实情况,又能够简化科研计算和工程设计中的复杂性。
北纬45 °海平面重力加速度值的标准化应用对于地球物理研究、工程建设和航天科技等领域具有重要意义。
4. 重力加速度值在不同领域的应用北纬45 °海平面重力加速度值作为标准值在科学研究和工程设计中有着广泛的应用。
在地球物理领域,重力场调查是勘探地下资源和研究地球内部结构的重要手段,而以标准值为基准进行数据处理和解释是保证调查结果准确性的重要前提。
在工程领域,建筑物、桥梁和道路等结构的设计需要考虑地面重力加速度值的影响,而标准值的应用可以简化设计计算,并提高工程的稳定性和安全性。
全球各地重力加速度数值

全球各地重力加速度数值
嘿!地球的重力加速度好像在不同地方都不一样哦。
听说南极洲的重力加速度是9.83米每秒平方,可是墨西哥城却只有9.779米每秒平方。
这差距也太大了吧!
东京的重力加速度大约是9.798米每秒平方,但悉尼好像只有9.796米每秒平方。
哇,为什么会有这么微小的差别呢?
在巴黎,重力加速度大约是9.81米每秒平方,而开罗却只有9.79米每秒平方。
这些数字真是让人摸不着头脑啊!
纽约的重力加速度大约是9.81米每秒平方,但科威特城却只有9.78米每秒平方。
噢,地球的重力加速度到底是怎么回事啊?
在里约热内卢,重力加速度大约是9.78米每秒平方,但开普敦却有9.81米每秒平方。
地球各地的重力加速度都不一样,真是太神奇了!。
什么是重力加速度的单位

什么是重力加速度的单位重力加速度是描述物体在地球表面受到重力作用下的加速度的物理量。
它是指物体自由下落时,每秒钟速度增加的大小。
在国际单位制中,重力加速度的单位被称为“米每平方秒”(m/s²)。
重力是物体受到的地球引力作用。
地球具有质量,因此会对周围的物体产生一个向地心的引力。
根据万有引力定律,物体的重力与其质量成正比,与地球质量成反比。
重力加速度是由地球的质量和半径决定的。
在地球表面,重力加速度的近似值为9.8米每平方秒。
这个数值是通过实验测定得出的,代表了物体在自由下落时每秒钟速度增加的大小。
也就是说,如果没有其他因素的干扰,一个物体从静止开始自由下落,它的速度每秒钟会增加9.8米。
重力加速度的单位“米每平方秒”可以理解为每秒钟速度增加9.8米。
这个单位告诉我们,如果一个物体受到的重力加速度为9.8米每平方秒,那么它在自由下落时速度每秒钟增加9.8米。
比如,一个物体从静止开始自由下落1秒钟后,速度将增加到9.8米每秒;2秒钟后,速度增加到19.6米每秒,依此类推。
重力加速度的单位“米每平方秒”可以用来描述物体在垂直自由下落时的加速度。
但需要注意的是,在其他情况下,重力加速度的值可能会有所变化。
例如,在地球其他位置的高度较高或者质量较大的星球上,重力加速度的值会有所不同。
总结起来,重力加速度是描述物体在地球表面受到重力作用下的加速度的物理量。
它的单位为“米每平方秒”(m/s²),表示物体在自由下落时每秒钟速度增加的大小。
重力加速度在地球表面的近似值为9.8米每平方秒。
通过了解重力加速度的定义和单位,我们能够更好地理解物体的自由下落和受力情况。
月球上的重力加速度精确数字

月球上的重力加速度精确数字
月球是地球的唯一卫星,它的引力对地球和人类的生活都有着重要的影响。
在
探索太空的过程中,科学家们也对月球上的重力加速度进行了精确的测量。
根据最新的研究和数据,月球上的重力加速度约为1.625米/秒²。
重力加速度是指地球或其他天体的引力对物体施加的加速度。
在地球上,重力
加速度约为9.8米/秒²,这意味着在没有空气阻力的情况下,任何物体在自由下落
的过程中每秒速度增加9.8米。
而月球的重力加速度约为地球的六分之一,因此在
月球表面上,物体的重量也会相应减小。
科学家通过各种仪器和测量方法,精确测量了月球上的重力加速度。
这些数据
不仅有助于我们更深入地了解月球的物理特性,还对未来的太空探索和人类登月计划有着重要的指导意义。
精确的重力加速度数据还对建造和操作月球基地、月球车等设施提供了重要参考。
除了重力加速度,月球上的引力还受到其他因素的影响,比如月球的形状、密
度分布等。
这些因素也会对重力加速度的精确数值产生一定的影响。
因此,科学家们在进行重力加速度测量时需要综合考虑各种因素,以确保数据的准确性和可靠性。
总的来说,月球上的重力加速度约为1.625米/秒²,这一数据对于太空探索和
未来的月球基地建设都具有重要的意义。
科学家们将继续深入研究月球的物理特性,为人类的探索之路铺平道路。
愿我们能够更加深入地了解月球的奥秘,探索宇宙的未知领域。
重力加速度计算公式

重力加速度计算公式
重力加速度是指物体在重力作用下的加速度,通常用g表示,
是一个重要的物理参数。
计算重力加速度的公式如下:
$$g = \frac{G \cdot M}{R^2}$$
其中,g表示重力加速度,G表示万有引力常数,M表示物体
的质量,R表示距离物体质心的距离。
重力加速度的计算可以通过测量物体的质量以及距离物体质心
的距离来实现。
将这些数值代入上述公式即可得到重力加速度的值。
需要注意的是,上述公式仅适用于球形物体。
对于其他形状的
物体,重力加速度的计算可能稍有区别,需要考虑物体的几何形状。
重力加速度的单位通常为米/秒²。
在地球上,重力加速度的平
均值约为9.8米/秒²。
然而,地球上不同地区重力加速度的值可能
存在细微差异,由于地球的不规则形状和密度分布。
通过计算重力加速度,我们可以了解物体在受到重力作用时的加速度情况,进而推导出物体在自由下落、运动等场景中的运动规律。
在科学研究、工程设计和日常生活中,重力加速度的计算具有重要的意义。
因此,了解和掌握重力加速度的计算公式是物理学和工程学研究中的基础知识,也是解决与重力有关的问题的关键步骤。
以上是关于重力加速度计算公式的简要介绍,希望对您有所帮助。
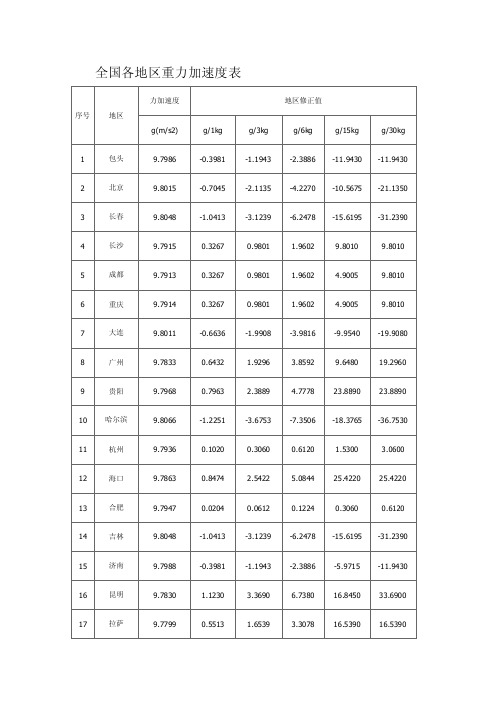
地球各点重力加速度近似计算公式

地球各点重力加速度近似计算公式: 我国主要城市的重力加速度:
北京:9.80151
天津:9.80106
唐山:9.80164
石家庄:9.79973
昆明:9.78363
南宁:9.78769
柳州:9.78850
乌鲁木齐:9.80146
武汉:9.79361
呼和浩特:9.79864
吉林:9.80480
长春:9.80476
西安:9.79136
成都:9.79134
哈尔滨:9.80665
开封:9.79660
南昌:9.79196
广州:9.78833
青岛:9.79849
南京:9.79494
上海:9.79460
福州:9.78910
杭州:9.79362
F=mg-V(&k)g=mg-(m/&f)g(&k)
m:物体的质量
g:物体所在地的重力加速度
&k:空气密度(一般取1.2kg/立方厘米)
&f:物体材料密度
地球各点重力加速度近似计算公式:
g=g0(1-0.00265cos&)/1+(2h/R)
g0:地球标准重力加速度9.80665(m/平方秒)
&:测量点的地球纬度
h:测量点的海拔高度
R:地球的平均半径(R=6370km)
s:时间
根据IEC标准,重力加速度计算公式为:
g=9.80617(1-2.64×10-3cos2ψ+7×10-6cos22ψ)-3.086×10-6Z;式中,ψ为纬度值,Z为海拔高度值。
全国各地区重力加速度表
B 添加义项?文案,原指放书的桌子,后来指在桌子上写字的人。
现在指的是公司或企业中从事文字工作的职位,就是以文字来表现已经制定的创意策略。
文案它不同于设计师用画面或其他手段的表现手法,它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程,多存在于广告公司,企业宣传,新闻策划等。
基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代,文案的称呼主要用在商业领域,其意义与中国古代所说的文案是有区别的。
在中国古代,文案亦作" 文按"。
公文案卷。
《北堂书钞》卷六八引《汉杂事》:"先是公府掾多不视事,但以文案为务。
"《晋书·桓温传》:"机务不可停废,常行文按宜为限日。
" 唐戴叔伦《答崔载华》诗:"文案日成堆,愁眉拽不开。
"《资治通鉴·晋孝武帝太元十四年》:"诸曹皆得良吏以掌文按。
"《花月痕》第五一回:" 荷生觉得自己是替他掌文案。
"旧时衙门里草拟文牍、掌管档案的幕僚,其地位比一般属吏高。
《老残游记》第四回:"像你老这样抚台央出文案老爷来请进去谈谈,这面子有多大!"夏衍《秋瑾传》序幕:"将这阮财富带回衙门去,要文案给他补一份状子。
"文案音译文案英文:copywriter、copy、copywriting文案拼音:wén àn现代文案的概念:文案来源于广告行业,是"广告文案"的简称,由copy writer翻译而来。
多指以语辞进行广告信息内容表现的形式,有广义和狭义之分,广义的广告文案包括标题、正文、口号的撰写和对广告形象的选择搭配;狭义的广告文案包括标题、正文、口号的撰写。
月球上的重力加速度精确数字

月球上的重力加速度精确数字月球是一个天体,它的重力场对于在其表面上的物体产生了影响。
月球上的重力加速度是指物体在月球表面上下落时受到加速度的大小。
对于许多应用而言,精确了解月球上的重力加速度是至关重要的。
在本文中,我们将探讨月球上的重力加速度的精确数字以及如何计算。
首先,让我们理解重力加速度的概念。
重力加速度是指物体在受到地球引力作用下的加速度大小,通常用g表示,其中g的值等于9.8米/秒平方。
在月球上,由于其质量比地球小得多,因此重力加速度较地球要小。
月球上的重力加速度是地球上的约六分之一。
月球上的重力加速度是一个复杂的问题,它受到月球的质量、大小、形状、密度和自转速度等因素的影响。
月球的尺寸是很容易确定的,其半径为1738千米。
而月球的质量约为地球质量的1/81,这意味着月球的引力只有地球引力的约1/6。
月球的形状是椭圆形的,因此在其表面的不同点上,重力加速度的大小也不同。
考虑月球的密度,人们可以从探测器的观察获得这一信息。
月球的密度约为每立方米约3340千克,低于地球的平均密度(5515千克/立方米)。
因此,月球上的重力加速度比地球小。
计算月球上的重力加速度需要使用牛顿万有引力公式。
在地球上,该公式用于计算物体之间的引力大小。
在月球上,该公式用于计算物体与月球之间的引力大小。
该公式如下:F =G × M × m / r²其中,F是物体和月球之间的引力大小,G是万有引力常数,M是月球的质量,m是物体的质量,r是物体和月球之间的距离。
通过使用该公式,可以计算出月球表面上物体的重力加速度。
在月球表面附近,重力加速度的精确大小约为 1.62米/秒平方。
此数值是由NASA的阿波罗任务测定的。
该值是对月球表面上的典型地点(海级)进行平均而得出的。
然而,由于月球表面的地形和地质结构的差异,该数值并不在所有地方都相同。
总之,月球上的重力加速度是一个复杂的问题,它受到月球的多个因素的影响。
地球两极的重力加速度

地球两极的重力加速度地球是我们生活的家园,我们所处的位置也会受到地球的重力影响。
重力是地球各个地方都存在的力量,但是地球不是一个完全均匀的球体,所以地球的不同地方所受到的重力加速度也是有所差异的。
在地球上,重力加速度指的是一个物体受到地球引力作用下的加速度大小,通常用 g 表示。
在地球上任何一个地方,重力加速度的大小都是相同的,约为9.8米/秒²。
但是,由于地球不是一个完全规则的球体,地球的自转和地球的形状使得地球两极地区的重力加速度稍微有所不同。
我们来看一下地球的自转。
地球自转一周大约需要24小时,自转速度大约为1670千米/小时。
由于地球自转速度的存在,地球两极地区相对于地球中心的离心力会稍微大一些,所以在两极地区的重力加速度会稍微小一些。
地球的形状也对重力加速度产生了影响。
由于地球是一个略微扁球体,地球两极地区离地球中心的距离要比赤道地区稍微近一些。
根据万有引力定律,两个物体之间的引力与它们之间的距离有关,距离越近,引力越大。
由于两极地区离地球中心的距离较近,所以两极地区的重力加速度会稍微大一些。
综合以上两个因素,我们可以得出结论,在地球两极地区的重力加速度会稍微小于9.8米/秒²。
具体数值可以通过测量得到,通常为9.78米/秒²左右。
虽然与赤道地区相比,差异并不是很大,但是这种微小的差异也是可以被科学测量出来的。
地球两极地区的重力加速度的微小差异可能对日常生活没有太大影响,但是对于科学研究和测量工作来说却是非常重要的。
在测量重力场强度、地壳运动、地震活动等方面,都需要考虑到地球两极地区的重力加速度差异。
总结一下,地球两极地区的重力加速度会稍微小于赤道地区的9.8米/秒²。
这是由于地球自转速度和地球形状的影响所导致的。
尽管差异并不是很大,但是对于科学研究和测量工作来说,这种微小的差异也是非常重要的。
通过对地球两极地区的重力加速度的研究,我们可以更好地了解地球的物理特性,推动科学的发展和进步。
月球上的重力加速度精确数字

月球上的重力加速度精确数字月球是地球的自然卫星,重力加速度是描述物体在其表面上受到引力加速度的物理量。
在月球上,重力加速度是地球上的约六分之一,因此和地球上相比,月球上的物体在其表面上受到的重力相对较小。
然而,为了更准确地描述月球表面的物理特性,我们需要知道月球上的重力加速度的精确数字。
本文将介绍月球上的重力加速度的精确数字及其相关参考内容。
月球上的重力加速度月球上的重力加速度取决于月球的质量和半径,它是物体在其表面上受到引力加速度的量度。
根据NASA的数据,月球的质量为7.34 × 10²²千克,半径约为1737.1千米。
因此,月球上的重力加速度可通过简单的数学公式计算出来。
重力加速度(g)= G × M / R²其中,G是引力常数(6.674×10^-11 m^3/kg·s^2),M是月球的质量,R是月球的半径。
因此,月球表面上的重力加速度是:重力加速度(g)= 6.674×10^-11 × 7.34 × 10²² / (1737.1×10³)^2= 1.62 m/s²这意味着在月球表面上的物体受到的重力加速度只有地球表面上的约六分之一。
这是因为月球的质量和半径较小,所以其引力相对弱一些。
相关参考内容为了更好地理解这个概念,我们来看看其他一些有用的参考内容:1. 月球测量:NASA的一篇文章介绍了月球的基本特征,包括重力加速度。
2. 月球重力测量:NASA的一个项目,旨在测量月球表面的重力场。
3. 月球文献:一些精选的科学文献,包括重力加速度的研究。
这些参考内容可以向我们展示更多关于月球的物理特性和重力加速度的细节,让我们更好地了解该为什么月球上的物体在其表面上受到的引力相对较小。
结语月球上的重力加速度是一个基本的物理概念,它描述了在其表面上物体受到的引力加速度的量度。
