最优化方法 第三章第四讲 Newton法
AAA最优化理论与方法课件(第3章,马昌凤版)

0.78
H
0.02
0.12
0.14
0.02 0.86
0.04 0.06
0.12 0.04
0.72 0.08
0.14
0.06
0.08
0.74
c 0.76, 0.08,1.12, 0.68T
其最小特征值n 0.52,最大特征值1 0.94
1 1
Байду номын сангаас
n n
2
0.081
方法分类:
1、间接法:对简单问题,求解必要条件或充分条件;
零阶法:只需计算函数值 f(x)
2、迭代算法: 一阶法:需计算 ▽f(x)
二阶法:需计算 ▽2f(x)
直接法 梯度法
从梯度下降到拟牛顿法
训练神经网络的五大学习算法
1、梯度下降法,又称为最速下降法
2、牛顿法
3、共轭梯度法(Conjugate gradient)
最优化理论与方法
Chapter 3 最速下降法和牛顿法
经典是永恒的
3.1 最速下降法及其Matlab实现 3.2 牛顿法及其Matlab实现 3.3 修正牛顿法及其Matlab实现
学习的重要性:
1、直接用于无约束的实际问题; 2、其基本思想和逻辑结构可以推广到约束问题;
3、约束问题可以转化成无约束问题求解。
min f (x) x12 x22 .
xR 2
a2 b2
显然该问题有精确解x* (0,0)T , f (x*) 0. 分析a与b 取不同值时迭代次数的变化规律。初始点都取为
(1,1)T,精度取1e-5。
a
b
离心率
迭代次数 最后目标值
d (1) 4 5 1 / 10 9
最优化方法第三章(3)

其中
0(一般取 1 或用直线搜索技术来确定),
以获得新的参考点(新的迭代点)。然后再开始探测搜索, 模式移动,……。交替进行的“探测搜索”和“模式移动” 将使得迭代点逐渐地向极小点靠近。
T 参考点 r r1 , r2 , , rn 。
2. 算法 算法3.11a(探测搜索) T 已知:目标函数 f (x ) ,步长向量 s s1 , s2 , , sn ,
T yk H k y k T 1 T T H k 1 H k T (1 T ) sk sk H k yk sk sk yk H k sk yk sk yk
(3.87)
只要把DFP算法中涉及DFP校正公式的部分改为 BFGS校正公式便得到BFGS算法。BFGS算法具有与DFP 算法完全相同的性质,但是因为它的 H k 不易变为奇异,
.
可以保证该式成立。
第二,为易于计算,要求 H k 到 H k 1 之间具有简单 的迭代形式。 (3.70) Ek 称为校正矩阵,(3.70)称为校正公式。 最简单的迭代关系为 H k 1 H k Ek
H k 确实近似 Gk1 第三,为使 ,要求每一个 H k 必须 满足逆Newton条件。 H和 设迭代已进行到第 k 1 步, k xk 1均已求出,现在 推导 H k 1 所必须满足的条件。 将 f ( x ) 在点 xk 1 处作Taylor级数展开,
。
r x0 , b0 x0 , c 1, w 0.5(或0.1) .
. ②置 s cs0
③在点 搜索得 b . f (b ) f (r ) ,则转⑤;否则,转⑧. ④若 ⑤做模式移动 r b b0 ,并置 b0 b , f 0 f b . 2 ⑥在点 r 处,以 s 为步长向量按算法3.11a做探测 搜索得b .
最优化牛顿法

Step 1. 给定初始点x0 ,正定矩阵H0 ,精度 0,k : 0
Step 2. 计算搜索方向d k H kf ( x k );
step 3. 令 x k1 x k tk d k , 其中 tk : f ( x k tk d k ) min f ( x k t d k )。
(sk Hk yk
Hk )T yk
yk
)T
SR1校正:H k1
Hk
(sk
H k yk )(sk H k (sk H k yk )T yk
yk )T
SR1校正具有二次终止性, 即对于二次函数,它不 需要线搜索,
而具有n步终止性质 H n G 1 .
定理
设s0 , s1 ,
,
s
n
线性无关,那么对二次
满足上述方程的解很多 ,我们可以如下确定一 组解:
k uk ukT yk sk kvkvkT yk Hk yk
这样,我们可以取:
uk sk ,
k ukT y k 1,
vk H k y k , k vkT y k 1。
即:
uk sk , vk Hk yk ,
k
1 skT y k
x k1 x k t k H k f ( x k )
xk1 xk tk Hkf ( xk )
H k I时 梯度法 最速下降方向 d k f ( x k ) , 度量为 x xT I x
H k Gk1时 Newton法 Newton方向 d k Gk1f (xk ), 度量为 x xT Gk x
当Gk 0 时,有 f ( xk )T d k f ( xk )T Gk1gk gkT Gk1gk 0 ,
牛顿法与修正牛顿法ppt课件

1 3
2 1
1 10
2
4
1 3
24
18
8 6
(3)极小值
x1
x(0)
s (0) (0)
0 0
8 1* 6
8 6
min f (x) 8
11
4、优缺点
▪ 数学分析表明,牛顿法具有很好的局部收敛性质,对
二次函数来说,仅一步就达到优化点,
▪ 但对一般函数来说,在一定条件下,当初始点的选取
充分接近目标函数的极小点时,有很快的收敛速度,但若 初始点选取离最小点比较远,就难保证收敛;
17
x(k1) x(k ) s(k )
五 收敛判断:
▪ 若 f (x(k1) ) ,则 x(k1) 为近似最优点,迭代停止,
输出最优解 xmin x(k 1)和 f (xmin) f (x(k1) ) 终止计算。
▪ 若不满足,令k=k+1,转第二步继续迭代。
9
例:
用牛顿法求函数 f (x) x12 x22 x1x2 10 x1 4x2 60 的极小值。
▪ 牛顿法必须求一阶、二阶导数及求逆阵,这对较复杂
的目标函数来说,是较困难的。
12
5、修正牛顿法
当目标函数为非二次函数时,目标函数在 xk
点展开所得的二次函数是该点附近的一种近似表 达式,所求的极小点,当然也是近似的,需要继
续迭代。但是当目标函数严重非线性时,用式[2]
进行迭代则不能保证一定收敛,即在迭代中可能 会出现 f (x(k1) ) f (x(k ) ) ,所得到的下一点不 如原来的好。这和初始点的选择是否恰当有很大 的关系。
其中 S (k) 称为牛顿方向。
7
3、迭代步骤
最优化方法-拟Newton法

0
1 4
0.25
2 X1 0.5,
f ( X1) 5.5
1 f ( X1) 2
(4)判 断 || f ( X 1 ) |,|转(5)
(5)第二次迭代采用DFP变尺度法,构造 E 0
1 0
G0 0
1
1 S0 X1 - X 0 - 0.5
min
f
(X
)
x2 1
2
x2 2
2 x1 x2
4x1
已知 X 0 [1,1]T , 0.1
解:(1)第一次迭代,实际上是沿负梯度方向进行一维搜索。
(2)
f
(
X
)
2x1 2
x1
2x2 4x2
4 ,
4
f ( X0) 2
,G0 I
➢ 5、DFP算法的收敛速度是超线性的。
Relax 做个题,轻松一下
例:用DFP变尺度算法求解无约束最优化问题
min
f
(X
)
x2 1
2
x2 2
2 x1 x2
4x1
已知 X 0 [1,1]T , 0.1
参照:拟Newton法的基本格式做题:
例:用DFP变尺度算法求解无约束最优化问题
三、对称秩1算法 2、对称秩1算法的性质
四、DFP算法(Davidon-Flether-P0well)
四、DFP算法
在DFP算法中,校正矩阵的构造公式为:
Ek
S
k
S
T k
S kTYk
04工程优化 第3章-2常用一维搜索牛顿法

解: f '( x) 4 x3 12 x 2 12 x 16, f ''( x) 12 x 2 24 x 12,
f '( x0 ) f '(6) 89 x1 x0 6 6 4.75 f ''( x0 ) f ''(6) 69
f '( x1 ) f '(4.75) 84.94 102 , 继续迭代; f '( x1 ) x2 x1 f ''( x1 ) f '(4.75) 84.94 4.75 =4.75 =4.163 f ''(4.75) 144.75 f '( x2 ) f '(4.163) 14.666 102 , 继续迭代;
3.若 x2 x ,则迭代结束,取 x* x ,否则在点
x1 , x2 , x3 , x 中,选取使f (x) 最小的点作为新的x2,并使新的
x 1 , x3各是新的x2近旁的左右两点,继续进行迭代,直到满 足终止准则。
例
用二次插值法求函数f(x)=3x3-4x+2的极小点, 给定 x0=0, h=1, ε=0.2。
应继续迭代。
(2) 在新区间,相邻三点及其函数值: x1=0, x2=0.555, x3=1;
根据公式计算差值多项式的极小点 f1=2, f2=0.292, f3=1.
1 c1 x a1 / 2a2 ( x1 x3 ), f1 f 2 2 c2 c1 f1 f 3 x1 x2 c1 , c2 x1 x3 x2 x3
Newton法----算例
f '( x2 ) x3 x2 f ''( x2 )
牛顿法

牛顿法牛顿迭代法牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。
牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。
设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0) f'(x0)(x-x0),求出L与x轴交点的横坐标x1 = x0-f(x0)/f'(x0),称x1为r的一次近似值。
过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴的横坐标x2 = x1-f(x1)/f'(x1),称x2为r的二次近似值。
重复以上过程,得r的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r 的n+1次近似值,上式称为牛顿迭代公式。
解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。
把f(x)在x0点附近展开成泰勒级数f(x) = f(x0)+(x-x0)f'(x0)+(x-x0)^2*f''(x0)/2! +…取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x-x0)=f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。
牛顿法和拟牛顿法是求解无约束最优化的常用方法,有收敛速度快的优点. 牛顿法属于迭代算法,每一步需要求解目标函数的海赛矩阵的逆矩阵,计算复杂. 拟牛顿法通过正定矩阵近似海赛矩阵的逆矩阵,简化了这个过程。
第四讲 多维无约束最优化Newton法、最速下降法

最速下降法流程图
x(1), ε >0, k=1
k=k+1 || ▽f(x(k) ) ||< ε? No
Yes
stop. x(k) –解
d(k)= -▽f(x(k) )
解 min f(x(k)+λ d(k)) s.t. λ >0 得 x(k+1)=x(k)+λkd(k)
Goldste ε >0 d(1)=-▽ f(x(1)),k=1
k=k+1 ||▽ f(x(k))||< ε? k=1
y
Stop.x(k)—解
N
解 min f(x(k)+λ d(k)) s.t. λ >0
得 λk x(k+1)=x(k)+λk d(k) 求β k d(k+1)= -▽ f(x(k+1))+β kd(k)
共轭梯度法的特点
全局收敛(下降算法);线性收敛; 每步迭代只需存储若干向量(适用于大 规模问题); 有二次终结性(对于正定二次函数,至 多n次迭代可达opt.) 对不同的βk 公式,对于正定二次函数是 相等的,对非正定二次函数,有不同的 效果,经验上PRP效果较好。
例子
例1
3 1 2 2 f ( x) ( x1 ) ( x2 ) x1 x2 2 x1 2 2
重新开始
N k=n?
y
x(1)=x(n+1) d(1)=-▽ f(x(1)),k=1
共轭梯度法的几种形式
k有下列三种等价形式:
f ( x ( k 1) )T f ( x ( k 1) ) k f ( x ( k ) )T f ( x ( k ) ) f ( x ( k 1) )T [f ( x ( k 1) ) f ( x ( k ) )] k f ( x ( k ) )T f ( x ( k ) ) f ( x ( k 1) )T f ( x ( k 1) ) k f ( x ( k ) )T d ( k ) (q1) FR法 (q 2) PRP法 (q3) 共轭下降法
东北大学最优化方法2010年第三章

第一次迭代( k 0 ,即从 xv0 到 xv1 的迭代)时,(t)
的初始步长可取为1,或根据问题中出现的数据的数量级
估计选定。而以后各次迭代的初始步长可按公式(3.5)
计算,
其中 0
般比从
xk
1 到
1hx。k的这距x是k离因pkx为xkk1从(xxkk3到.15小)xvk 或1 的接距近离,所xk以1 把xk按一
上述过程开始时,必须选定初试点 t0 和步长 h。对于
任意给定的 (t),一般来说,无固定选取模式。
但对于在下降算法模式中所引入的 (t) f (xk tpk )
而言,可选取 t0 等于0(理论上)或接近0(实际计算中)。
而对于 h ,如果选得过小,那么需要迭代许多次才能找到
一个搜索区间;如果选得太大,虽然很少几步就可能把极 小点包括进来,但是这又会给下一步搜索极小点的过程增
黄金分割法的思想是:在每次迭代中,合理地设置两
个插入点的位置,以使得在计算函数值次数同样多的条件 下,将区间缩小得最快。
设区间 [a,b] 的长为1。在距点 a 分
别为 和
为了确定
的地方插入 t1和 t2。
和 ,提出以下条
件:
第一,希望 t1 和 t2在 [a,b]中的位置是对称的。按这
一条件,有
1. 搜索区间的确定
在以下讨论中,总假定一元函数 (t) 是单谷函数。
定义3.1 设 : L R1 R1 ,t* 是 (t) 在L上的全局
极小点。如果对于L上任意的两点 t1,t2 t1 t2 ,当 t2 t *
时,(t1 ) (t2 ) ;当 t1 t * 时,(t1 ) (t2 ) ,那么称(t)
牛顿法步骤

牛顿法步骤一、引言牛顿法(Newton's Method)是一种求解方程的迭代方法,由英国物理学家牛顿(Isaac Newton)首次提出。
它通过不断逼近方程的根,使得函数值逐渐趋近于零,从而求得方程的解。
本文将介绍牛顿法的具体步骤。
二、牛顿法的基本思想牛顿法的基本思想是通过构造切线来逼近方程的根。
具体来说,首先选择一个初始点,然后在该点处求取切线,切线与x轴的交点即为下一个近似解。
通过反复迭代,可以逐步逼近方程的根。
三、牛顿法的步骤1. 选择初始点在使用牛顿法求解方程时,首先需要选择一个初始点。
初始点的选择会影响到迭代的结果,通常需要根据问题的特点和经验来确定合适的初始点。
2. 求取切线在初始点处,求取方程曲线的切线。
切线的斜率等于函数在该点的导数值,切线的方程可以表示为:y = f(x0) + f'(x0)(x - x0),其中f(x0)为函数在初始点处的函数值,f'(x0)为函数在初始点处的导数值。
3. 求取切线与x轴的交点求取切线与x轴的交点,即求解方程f(x0) + f'(x0)(x - x0) = 0。
解方程可以得到下一个近似解x1。
4. 迭代求解将x1作为新的初始点,重复步骤2和步骤3,求取下一个近似解x2。
如此反复迭代,直到满足迭代终止条件。
5. 判断迭代终止条件通常情况下,牛顿法的迭代终止条件有两种:一种是迭代次数达到了预设值;另一种是两次迭代之间的近似解之差小于预设的容差值。
根据具体问题的要求和实际情况,选择合适的迭代终止条件。
6. 输出结果当满足迭代终止条件时,输出最终的近似解作为方程的解。
如果迭代未能收敛,需要重新选择初始点或修改迭代终止条件,并进行调整。
四、牛顿法的优缺点牛顿法具有收敛速度快的优点,尤其适用于多项式和光滑函数等具有良好性质的方程。
然而,牛顿法也存在一些缺点,比如对初始点的选择敏感,可能导致迭代发散;另外,对于某些特殊的方程,牛顿法可能无法收敛或收敛很慢。
最优化算法(牛顿、拟牛顿、梯度下降)
最优化算法(⽜顿、拟⽜顿、梯度下降)1、⽜顿法 ⽜顿法是⼀种在实数域和复数域上近似求解⽅程的⽅法。
⽅法使⽤函数f (x)的泰勒级数的前⾯⼏项来寻找⽅程f (x) = 0的根。
⽜顿法最⼤的特点就在于它的收敛速度很快。
具体步骤: ⾸先,选择⼀个接近函数f (x)零点的x0,计算相应的f (x0) 和切线斜率f ' (x0)(这⾥f ' 表⽰函数f 的导数)。
然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和x 轴的交点的x坐标,也就是求如下⽅程的解: 我们将新求得的点的x 坐标命名为x1,通常x1会⽐x0更接近⽅程f (x) = 0的解。
因此我们现在可以利⽤x1开始下⼀轮迭代。
迭代公式可化简为如下所⽰: 已经证明,如果f ' 是连续的,并且待求的零点x是孤⽴的,那么在零点x周围存在⼀个区域,只要初始值x0位于这个邻近区域内,那么⽜顿法必定收敛。
并且,如果f ' (x)不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说,这意味着每迭代⼀次,⽜顿法结果的有效数字将增加⼀倍。
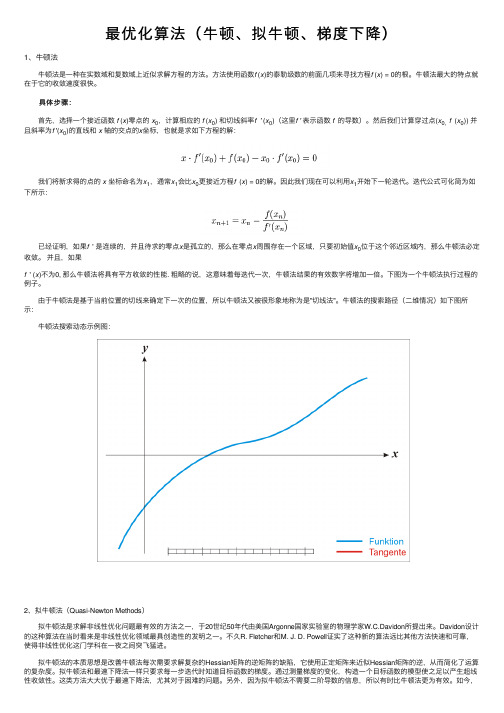
下图为⼀个⽜顿法执⾏过程的例⼦。
由于⽜顿法是基于当前位置的切线来确定下⼀次的位置,所以⽜顿法⼜被很形象地称为是"切线法"。
⽜顿法的搜索路径(⼆维情况)如下图所⽰: ⽜顿法搜索动态⽰例图:2、拟⽜顿法(Quasi-Newton Methods) 拟⽜顿法是求解⾮线性优化问题最有效的⽅法之⼀,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。
Davidon设计的这种算法在当时看来是⾮线性优化领域最具创造性的发明之⼀。
不久R. Fletcher和M. J. D. Powell证实了这种新的算法远⽐其他⽅法快速和可靠,使得⾮线性优化这门学科在⼀夜之间突飞猛进。
拟⽜顿法的本质思想是改善⽜顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使⽤正定矩阵来近似Hessian矩阵的逆,从⽽简化了运算的复杂度。
最优化方法课件

Custom
20
12
400
6
2. 数学模型 (定量优化计算:不增加投入而 增加产出的手段) 第一,无约束极值问题(例1.3)
min f x, y x 2 y 1
2
2
图解法的步骤: 2 2 ①令 f x, y x 2 y 1 c ,显然 ③确定极值点位置,并用以往所学方法求之。
c0 ;
②取 c 0,1, 4,9,并画出相应的曲线(称之为等值线).
。由此
min f x s.t. h x 0
(2)
以向量为变量的实向量值函数最优化问题的一般形式
min f x1 , x2 ,, xn s.t. hi x1 , x2 ,, xn 0, i 1, 2,, l (l n) s j x1 , x2 , , xn 0, j 1, 2,, m
1
,
arccos
向量的夹角 , , 向量的正交 , 1.可微
,
0 ,
2
, 0 (正交性)
设 .如果存在 n 维向量 l , 对于可任意小的 n 维非零向量 p ,总有
f : D R R , x0 D
Example Suppose that a manufacturer of kitchen cabinets is trying to maximize the weekly revenue of a factory. Various orders have come in that the company could accept. They include bookcases with open shelves(开架书橱), cabinets with doors(带门橱柜), cabinets with drawers(带抽屉橱柜) , and custom-designed ( 定 制 的 ) cabinets. The following Table indicates the quantities of materials ( 原 材 料 ) and labor required to assemble the four types of cabinets, as well as the revenue earned. Suppose that 5000 units of wood and 1500 units of labor are available.
最优化方法3.6 拟Newton法

1. DFP 修正公式
考虑如下形式的修正矩阵
Ek uuT vvT
其中 u,v 为 n 维待定向量。
Hk1 yk sk Hk1 Hk Ek
由拟 Newton 方程有
sk Hk yk uuT yk vvT yk
一个取法是令u sk 和 v Hk yk ,而 和 的值 由uT yk 1 及 vT yk 1 确定。
Hk1
Hk
Hk yk ykT Hk ykT Hk yk
sk skT ykT sk
称此为 DFP 修正公式。
算法 3.6.1 DFP 算法
给定控制误差 Step1,给定初始点 x0,初始矩阵 H0,计算 g0,令 k=0。
3.6 拟Newton法
3.6.1 拟 Newton 法的基本思想
最速下降法和阻尼 Newton 法的迭代公式可以表示 为
xk1 xk k Hk gk 其中k 为步长, gk f ( xk ), Hk 为 n 阶对称矩阵。
若令 Hk I ,则是最速下降法;若令 Hk Gk1,就 是阻尼 Newton 法。
k
xk
0
(3, 3)T
f (xk )
|| gk ||
284 406.388976
1 (1.506276, 3.162682)T
55.9680 22.735062
2 (1.042197, 0.364760)T 21.667551 34.655755 3 (0.201121, 0.579099)T 10.326398 15.195930 4 (0.038214, 0.259246)T 5.281025 8.866415 5 (0.545613, 0.128564)T 1.902223 4.373892 6 (0.949383, 0.653520)T 0.524880 6.171830 7 (0.929224, 0.886719)T 0.037381 0.916882 8 (1.000007, 0.998270)T 0.00002 0.045484 9 (0.999915, 0.999862)T 1.0 108 0.001193
Newton-Raphson算法

Newton-Raphson算法简介⽜顿法⼜叫做⽜顿-拉裴森(Newton-Raphson)⽅法,是⼀维求根⽅法中最著名的⼀种。
其特点是在计算时需要同时计算函数值与其⼀阶导数值,从⼏何上解释,⽜顿法是将当前点处的切线延长,使之与横轴相交,然后把交点处值作为下⼀估值点。
图1从数学上解释,⽜顿法可以从函数的泰勒展开得到。
f(x)的泰勒展开可以表⽰为:f(x+\delta)=f(x)+f’(x)\delta+\frac{f’’(x)}{2}\delta^2+O(\delta^3)对于⾜够⼩的\delta,可以将只保留上式右端关于的⼀阶项,得到:\delta=-\frac{f(x)}{f’(x)}于是得到由到的递推公式:x_{i+1}=x_{i}+\delta=x_i-\frac{f(x_i)}{f’(x_i)}可见⽜顿法是让x沿着f(x)梯度的⽅向下降,类似于最优化⽅法中的梯度下降法。
⽜顿法也可以作为最优化算法,只不过那时需要求函数的⼆阶导数。
⽜顿法相⽐⼆分法、截弦法的优点是收敛速度可以达到⼆阶,在根附近没迭代⼀次,结果的有效数字⼏乎可以翻倍。
当然⽜顿法也可能可能失败,⽐如收敛到⼀个局部极值,其切线⽅向与横轴⽔平,从⽽⽆法计算下⼀个迭代值。
另外,⽜顿法的实现需要⽤户提供⼀个函数⽤于计算函数值f(x)与其⼀阶导数值f'(x),因此⽐较适合函数的导数可以解析求出的情况,如果需要求数值导数,则⽜顿法的收敛速度和精度都会受影响。
我们可以将⽜顿法和⼆分法综合起来形成⼀个混合算法,⼀旦⽜顿法在运⾏过程中出现解跳出给定区间或者猜测值远离实际根导致收敛速度较慢时,就采取⼀步⼆分法。
实现⼀:利⽤预先求出的⼀阶导函数import numpy as npimport matplotlib.pyplot as pltdef f(FV, PMT, r, n):return PMT * (1 + r) * (((1 + r)**n - 1)) / r + FVdef df(FV, PMT, r, n):r_plus_1_power_n = (1 + r)**np1 = N * PMT * r_plus_1_power_n / rp2 = -PMT * (r + 1) * (r_plus_1_power_n - 1) / r / rp3 = PMT * (r_plus_1_power_n - 1) / rreturn p1 + p2 + p3def newtonRaphson2(FV,PMT,n,f,df,xmin,xmax,maxit,shift=0.0001,tol=1.0e-9):'''函数作⽤说明:计算组合收益率FV:⽬标⾦额PMT:每期投资⾦额n:定投期数f:函数值(根据要求的⽅程⾃定义)df:导数值(根据要求的⽅程⾃定义)xmin:根的下限xmax:根的上限maxit:最⼤迭代次数tol:计算精度'''import mathfxmin = f(FV, PMT, xmin, n)if fxmin == 0.0:return xminfxmax = f(FV, PMT, xmax, n)if fxmax == 0.0:return xmaxif fxmin * fxmax > 0.0:print('Root is not bracketed') # 在[xmin, xmax]内函数不变号(没根),或者是变了偶数次号(多个根)return 1if fxmin < 0.0: # 确定搜索⽅向使f(xl)<0xl = xminxh = xmaxelse:xl = xmaxxh = xminx = 0.5 * (xmin + xmax) # 根的预测值if x == 0:x += shiftfx, dfx = f(FV, PMT, x, n), df(FV, PMT, x, n) # 求f(x)和其⼀阶导数dxold = math.fabs(xmax - xmin) # 储存步长dx = dxoldfor ii in range(maxit):# ⽜顿法的解跳出解区间或者收敛速度太慢,则下⼀步改⽤⼆分法if ((x - xh) * dfx - fx) * ((x - xl) * dfx - fx) > 0.0 or (math.fabs(2 * fx) > math.fabs(dxold * dfx)):# ⼆分法dxold = dxdx = 0.5 * (xh - xl)x = xl + dxelse:# ⽜顿法dxold = dxdx = fx / dfxtemp = xx -= dxif temp == x:print("total iterate time:%s " % ii)return xif math.fabs(dx) < tol: # 达到要求精度,返回找到的根print("total iterate time:%s " % ii)return xif x == 0:x += shiftfx, dfx = f(FV, PMT, x, n), df(FV, PMT, x, n) # 否则继续迭代,求f(x)和其⼀阶导数if fx < 0.0: # 使根保持在解区间内xl = xelse:xh = xprint('Maximum number of iterations exceeded')return 1### 测试⽤例:⾸先给定PMT,n,r_analytical,计算FV,然后利⽤PMT,n,FV计算r_numerical,两者应该相等##给定r_analytical计算FVR=0.1r_analytical = R / 12PMT = -4e3N = 30n = N * 12FV = -PMT * (1 + r_analytical) * (((1 + r_analytical)**n - 1)) / r_analytical##给定FV反解r_numericalr_numerical = newtonRaphson2(FV, PMT, n, f, df, -1, 1, 100, tol=1.0e-8)print('\nr_analytical=%s,\nr_numerical=%s\n' % (r_analytical, r_numerical))实现⼆:利⽤TensorFlow提供的⾃动微分计算导函数import numpy as npimport mathimport pandas as pdimport tensorflow as tfimport matplotlib.pyplot as plt##⼀个利⽤tensorflow的⾃动微分功能实现⽜顿法解⽅程的⼩程序class NewtonRaphson:def__init__(self, y, x, session):self.y = yself.x = xself.grad = tf.gradients(y, x)self.sess = sessionsess.run(tf.global_variables_initializer())def _fx(self, x_value):# 尽量避免出现f(x)不能计算的情况,⽐如函数试图计算a/0,log(0)等,如果计算结果为inf则x+0.0001再进⾏计算 temp = self.sess.run(y, feed_dict={x: [x_value]})[0]if np.isinf(temp):return self.sess.run(y, feed_dict={x: [x_value + 0.0001]})[0]else:return tempdef _dfx(self, x_value):return self.sess.run(self.grad, feed_dict={x: [x_value]})[0][0]def solve(self, xmin, xmax, maxiter, tol):fmin = self._fx(xmin)fmax = self._fx(xmax)if fmin == 0:return xminif fmax == 0:return xmaxif fmin * fmax > 0.0:raise ValueError('Root is not brackted!!')if fmin < 0:xl = xminxh = xmaxelse:xl = xmaxxh = xminx = (xmin + xmax) / 2fx, dfx = self._fx(x), self._dfx(x)dxold = math.fabs(xmax - xmin)dx = dxoldfor ii in range(maxiter):if ((x - xh) * dfx - fx) * ((x - xl) * dfx - fx) > 0.0 or (math.fabs(2 * fx) > math.fabs(dxold * dfx)):dxold = dxdx = 0.5 * (xh - xl)x = xl + dxelse:dxold = dxdx = fx / dfxtemp = xx -= dx# newtonif temp == x:print("total iterate time:%s " % ii)return xfx, dfx = self._fx(x), self._dfx(x)if fx < 0.0:xl = xelse:xh = xprint('Maximum number of iterations exceeded')return 1PV = 1e4FV = 3e6N = 20cpi = 0.018RATE = 0.15r = RATE / 12PMT = 10000x = tf.placeholder(shape=[1], dtype=tf.float32)y=r * (FV * (1 + cpi)**(N) - PV * (r + 1)**x) / ((r + 1)**x - 1 - r) - PMT sess = tf.InteractiveSession()solver=NewtonRaphson(y,x,sess)nmin = 2nmax = 300solver.solve(nmin,nmax,100,1e-9)Processing math: 0%。
牛顿法

又因
(x*) f (x*) ,
f (x*)
k x*)2
f (x*) . 2 f (x*)
例7 用牛顿法解方程
xex 1 0.
解 这里牛顿公式为
xk 1
xk
xk e xk 1 xk
,
取迭代初值 x0 ,0.迭5 代结果列于表7-5中.
解 先求出三种方法的迭代公式:
(1) 牛顿法
xk 1
xk
xk2 2 . 4 xk
18
(2) 用(4.13)式
xk 1
xk
xk2 2 . 2 xk
(3) 用(4.14)式
xk 1
xk
xk
( xk2 2) xk2 2
.
取初值 x0 ,1.5计算结果如表7-7.
表7 7 三种方法数值结果
k xk
0
0.5
开始值,用弦截法求得的结果见表7-8,
比较例7牛顿法的计算结果可以看出, 1
0.6
弦截法的收敛速度也是相当快的.
2
0.56532
7
以上两式相除得
xk 1 xk 1
C C
xk xk
2
C C
.
据此反复递推有
xk 1 xk 1
C C
x0 x0
2k
C C
.
记
q x0 C , x0 C
整理(4.6)式,得
(4.6)
8
q 2k xk C 2 C 1 q2k .
对任意 x0,总0有 ,q故由1上式推知,当 时 xk ,C即迭代过程恒收敛.
x即4 为 的x *近似. 一般情况只要能使条件(4.10)成立,
则可得到
lim
Newton方法

Newton方法张立卫大连理工大学数学科学学院报告提纲•经典Newton法•带线搜索Newton法•自协调函数的牛顿法内容牛顿方法是求解无约束最优化问题的著名方法,它基于目标函数在迭代点处的二阶Taylor展式计算搜索方向.这一讲讨论经典Newton方法的局部收敛性及带步长的牛顿方法的全局收敛性,并列出阻尼牛顿方法求解自协调(self-concordant)凸函数极小化问题的若干理论结果。
1经典牛顿法经典牛顿法的迭代格式设f在x k附近是二次连续可微的,它在x k处的二阶Taylor展式为q(x k,x)=f(x k)+∇f(x k)T(x−x k)+12(x−x k)T∇2f(x k)(x−x k),设∇2f(x k)是正定矩阵,则q(x k,x)有唯一最小点,记为x k+1,x k+1=x k−[∇2f(x k)]−1∇f(x k),这一迭代格式即经典牛顿法的迭代格式,其中d k=−[∇2f(x k)]−1∇f(x k)是f在x k处的牛顿方向.理解经典迭代显然经典牛顿法产生的x k+1即是f在x k处二阶Taylor展式的稳定点,当∇2f(x k)正定时,还是二阶展式的最优解:x k+1亦可视为沿d k方向,步长αk≡1的迭代点.收敛速度下面给出经典牛顿法的局部收敛定理,见Nocedal,Wright (1999).定理1设f是ℜn上的二阶连续可微函数,∇2f在点x∗的一邻域内满足Lipschitz条件(其常数是L)且∇2f(x∗)正定,其中x∗是满足二阶充分条件的局部极小点,设{x k}由经典牛顿法生成,则(i)当初始点x1充分接近x∗时,序列{x k}有定义且收敛到x∗; (ii){x k}二次收敛到x∗;(iii){∥∇f(x k)∥}二阶收敛到0.证明由于∇2f在点x∗的一领域内满足Lipschitz条件,∇2f(x∗)正定,由关于扰动矩阵之逆的von Neumann引理,存在δ1,∇2f在B(x∗,δ1)上是可逆的,而且∥∇2f(x)−1∥≤2∥∇2f(x∗)−1∥,∀x∈B(x∗,δ1).取δ=min{δ1,1/(2L∥∇2f(x∗)−1∥)}.注意到,若x k ∈B (x ∗,δ1),∥∇2f (x k )(x k −x ∗)−∇f (x k )+∇f (x ∗)∥= ∫10[∇2f (x k )−∇2f (x ∗+t (x k −x ∗))](x k −x ∗)dt ≤L ∥x k −x ∗∥2∫10(1−t )dt=12∥x k −x ∗∥2,得到∥x k +1−x ∗∥=∥x k −∇2f (x k )−1∇f (x k )−x ∗∥=∥∇2f (x k )−1(∇2f (x k )(x −x ∗)−∇f (x k )+∇f (x ∗))∥≤L ∥∇2f (x ∗)−1∥∥x k −x ∗∥2,(1)显然,当x k∈B(x∗,δ)时∥x k+1−x∗∥≤L∥∇2f(x∗)−1∥δ∥x k−x∗∥≤δ/2,即x k+1∈B(x∗,δ).这表明,只要x1∈B(x∗,δ),牛顿方法生成的{x k}就是有定义的,而且∥x k+1−x∗∥≤(1/2)kδ,即x k→x∗,k→∞,即(i)成立.由估计式(1)直接可得到(ii).结论(iii)由下面的推导得到∥∇f (x k +1)∥=∥∇f (x k +1)−∇f (x k )−∇2f (x k )(x k +1−x k )∥= ∫10∇2f (x k +t (x k +1−x k ))−∇2f (x k )]dt (x k +1−x ∗) ≤∫10Lt ∥x k +1−x k ∥2dt=L 2∥∇2f (x k )−1∇f (x k )∥2≤2L ∥∇2f (x ∗)−1∥∥∇f (x k )∥2.局部收敛性由定理1可知,牛顿方法局部收敛速度快,但初始点x1需距离x∗很近时方法才有意义.2带线搜索的牛顿法线搜索将d k=−[∇2f(x k)]−1∇f(x k)作为搜索方向,迭代格式采用x k+1=x k+αk d k,可导致带线搜索的牛顿方法,步长αk可按精确线搜索或非精确线搜索原则来计算.收敛定理定理2设f是二次连续可微凸函数,∇2f(x)于每一x∈ℜn均是正定的.设x1∈ℜn满足水平集{x|f(x)≤f(x1)}是有界的,{x k}由下述带线搜索的牛顿方法生成x k+1=x k−αk[∇2f(x k)]−1∇f(x k),其中步长αk采用精确线搜索,Armijo线搜索与Goldstein线搜索中的任何一种线搜索计算,则{x k}收敛到f的全局最小点x∗.证明容易验证d k=−[∇2f(x k)]−1∇f(x k)是梯度相关的方向,由定理A1a得{x k}的任何聚点均是f的稳定点.由于f的稳定点即f的全局最小点x∗是唯一的,因此序列{x k}必收敛到x∗.a定理A1设f是连续可微函数,f是下有界的,方向序列{d k}与{x k}是梯度相关联的.若{αk}由精确线搜索,Armijo非精确线搜索原则和Goldstein原则中的任一线的搜索原则生成,则{x k}的每一聚点均是f的稳定点.3自协调函数的牛顿法自协调函数定义1若f:Q→ℜ是三次连续可微凸函数,其中Q⊂ℜn是一开凸集,满足下列性质:d3 dt3t=0f(x+th)≤2(d2dt2t=0f(x+th))3/2,∀h,则称f是一自协调函数.若还满足,对任意{x i∈Q},x i→x∈brdy Q(bdry Q即Q的边界),必有f(x i)→∞,称f是强自协调函数.自协调函数的阻尼Newton 法定理3设f 是强自协调的,∇2f 在点x 1∈Q 处是正定的.则(i)对每一x ∈Q ,∇2f (x )是正定的;(ii)若f 是下有界的,则f 在Q 上取得极小值点,极小值点是唯一的;(iii)初始点为x 1∈Q ,按迭代x k +1=x k −αk [∇2f (x k )]−1∇f (x k ),αk =[1+λ(f,x k )]−1,λ(f,x k )=√∇f (x k )T [∇2f (x k )]−1∇f (x k )生成的序列具有下述性质:(iii-1){x k }⊂Q ;(iii-2)若f 在Q 上是下有界的,则{x k }收敛到f 的唯一极小点x ∗;(iii-3)若λ(f,x k )≥1/4,则f (x k )−f (x k +1)≥λ(f,x k )−log(1+λ(f,x k ))≥1/4−log(5/4)=0.026856...;(iii-4)对每一k ,λ(f,x k )≤1/4=⇒f (x k )−f (x ∗)≤−log(1−λ(f,x k ))−λ(f,x k )≤λ(f,x k )22(1−λ(f,x k ))≤2λ(f,x k )23,且λ(f,x k +1)≤2λ2(f,x k )≤12λ(f,x k ).注记基于上述定理,可将迭代分为两个阶段:第一阶段从初始点到第一次满足λ(f,x k )≤1/4的迭代点x k ,第二阶段是从x k 出发的迭代过程.在第一阶段的每一次迭代中目标函数至少下降κ=1/4−log(5/4)>0,因此,这一阶段的迭代次数至多为N 1=[f (x 1)−inf Q f ]/κ.在第二阶段,λ(f,x k )二次收敛到0,f (x k )−inf Q f 也是二次收敛到0的.于是阻尼牛顿方法用于求解强自协调函数极小化问题的迭代次数是N (ϵ)=O (1)[(f (x 1)−inf Q f )+log log 1ϵ].References[1]张立卫,单锋,最优化方法,科学出版社,2010.。
数值最优化李董辉第三章最速下降法和Newton法

Newton法 的优点:收敛快 缺点:对初始点要求很高,而且计算量大
从Newton法出发进行修改 ,利用其优点,克服 其缺点,产生很多效果非常好的其他新算法
第三章 无约束问题算法(I)—— 最速下降法、 Newton法
第一节 最速下降法 第二节 Newton法及其修正形式
第一节 最速下降法
1、 思想 :每次沿最速下降方向进行搜索
2、 算法步骤
3、 最速下降法的收敛性
全局收敛性
收敛速度估计
从上图可以看出,最速下降法 具有锯齿现象
由上面的分析可知,最速下降法的收敛速度 比较慢,通常将其用在某些算法的初始阶段 求较好的初始点
第二节 Newton法及其修正形式
1、思想:用近似二次函数的极小点作为原问题的新的近似解
2、 Newton法的算法步骤
(3.3)
3、Newton的 收敛性
4、 局部二次收敛性
5、 n法的修正形式
上面的Newton法的两种修正形式,在较弱的条件下 具有超线性收敛性或二次收敛性
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 3.4.4 用 Newton 法求解问题
2 min f ( x) 4 x12+x2 -x12 x2 取初始点为 xA (1,1)T , xB (3, 4)T , xC (2,0)T 。
2 min f ( x) 4 x12+x2 -x12 x2
xk 1 xk pk , 令 其中 pk 应满足 Gk pk g k 。
方程组 Gk pk g k 称为 Newton 方程, 公式 xk 1 xk Gk1 g k 称为 Newton 迭代公式。
算法 3.4.1 Newton 法 给定控制误差 0 。
Step1
取初始点 x0 ,令Байду номын сангаасk 0 。
Step2
Step3
计算 g k 。
若 gk ,则 x* xk ,停;否则计算
Gk ,并由 Gk pk g k 解出 pk 。
Step4
令 xk 1 xk pk ,k k 1, 转 Step2。
Newton法
x(1), ε >0, k=1 k=k+1
定理 3.4.1 设 f ( x) 是某一开域内的三阶连续可微函数, 且它在该 开域内有极小点 x*,设 G* G( x* ) 正定,则当 x0 与 x*充分 接近时,对一切 k ,Newton 法有定义,且当xk 为无穷 点列时,xk 二阶收敛于 x*,即 hk 0 且
hk 1 O( hk )
例 3.4.2 用 Newton 法求解 2 , min f ( x) x1 x2 2 x12 2 x1 x2 x2 初始点设为 (0,0)T 。 4 x1 2 x2 1 4 2 G ( x) 解: g ( x) , 2 2 2 x1 2 x2 1 k 0:
8 0 G (0,0) 0 2
8-2x2 -2x1 G ( x) 2 -2x1
解: (2)用 Newton 法得到得迭代点如表所示:
k
0 1 2
xk
(3, 4)T
(2.8333,4.0000)T
f ( xk )
|| g k ||
16.0 16.0 16.0
3.4.3
Newton 法的优缺点
优点 ⑴如果G *正定且初始点合适,算法是二阶收敛的。 ⑵对正定二次函数,迭代一次就可得到极小点。
缺点 ⑴对多数问题算法不是整体收敛的。 ⑵在每次迭代中需要计算 Gk 。 ⑶每次迭代需要求解线性方程组,Gk p g k ,该方 程组有可能是奇异或病态的(有时 Gk 非正定) , pk 可 能不是下降方向。 ⑷收敛于鞍点或极大点的可能性并不小。
由 于 G * 正 定 且 G( x) 连 续 , 所 以 存 在 x* 的 一 个 邻 域
N ( x* ) x / x x* ,使x N ( x* ) ,G( x) 正定且G ( x) 1
有上界。 于是, 若 xk N ( x* ) , 对上式两边乘以Gk1 , 再由 hk 1 的定义有
0 pk hk O( hk ) hk 1 O( hk )
2 2
因此由O()的定义,存在常数 使得
hk 1 hk
2
成立。 若取 充分小使之满足 1,则有
hk 1 hk
2
hk hk 。
因此, xk 1 N ( x* )。 由归纳法,如果 x0 N ( x* ) ,则对所有的 k ,Newton 法有定义,且 hk ( )k h0 0 (k ) 于是定理得证。
例 3.4.3 用 Newton 法求解问题
2 min f ( x) ( x1 2)4 ( x1 2)2 x2 ( x2 1)2 问题极小点为 (2, 1)T , 取初始点为 (1,1)T 。
解: 用 Newton 法得到得迭代点如表所示:
k
0 1 2 3 4 5 6
xk
2
其中 hk xk x* 。
证明:因 f ( x) 是三阶连续可微函数的,故由 Taylor 公 式有 g ( xk h) gk Gk h O( h 2 ) , 取 h hk ,即 xk h x*,得到 0 g * g k Gk hk O( hk 2 ) ,
xC ( 2,0)
8-2x2 -2x1 G ( x) 2 -2x1
8 x1-2x1 x2 g ( x) 2 2 x2-x1
8 4 G ( 2,0) 4 2
Hesse 阵奇异,无法继续计算。
3.4.2
收敛性
1 Gk pk g k g 0 , g0 2 , 1 1 1 G0 p0 g 0 , p0 3 1 2 1 0 x1 x0 p0 3 , g1 , x1 为极小点。 0 2
(1,1)T
(1, 0.5)T
f ( xk )
6.0 1.5
(1.3913043, 0.69565217)T 4.09 101 (1.7459441, 0.94879809)T 6.49 10 2
(1.9862783, 1.0482081)T 2.53 103 (1.9987342, 1.0001700)T 1.63 106
1 0 解: g ( x) ( x1 ,9 x2 ) ,G ( x) 0 9
T
例 3.4.1
k0
1 0 0
xk 1 xk Gk1 g k
1
9 1 0 9 0 * x1 x0 G g x 。 1 0 9 9 0
|| g k ||
4.0 4.5156
0.1273
0.0003
6.0828 8.4495 1.3388 0.0511 0.0001
(0.1550, 0.1650)T
(0.0057, 0.0111)T (0.0000, 0.0000)T
0.0000
xk (0,0)
严格局部极小点
8 x1-2x1 x2 g ( x) 2 2 x2-x1
实用中,判断 若▽2f(x(k)) 非正定时
进行相应处理 ▽2f(x(k)) p= -▽f(x(k)) 得p(k) , x(k+1)=x(k)+p(k)
No || ▽f(x(k)) ||< ε?
Yes
STOP.x(k+1)—l.opt
用 Newton 法求解 1 2 9 2 min f ( x) x1 x2 , 2 2 设初始点 x0 (9,1)T 。
8 x1-2x1 x2 g ( x) 2 2 x2-x1
8-2x2 -2x1 G ( x) -2 x 2 1
解: (1)用 Newton 法得到得迭代点如表所示:
k
0 1 2 3 4
xk
(1,1)T
(0.75, 1.25)T
f ( xk )
1.0000 0.0278 0.0000
(2.8284,4.0000)T
xk ( 2 2,4),
鞍点
8 x1-2x1 x2 g ( x) 2 2 x2-x1
8-2x2 -2x1 G ( x) 2 -2x1
4 2 0 G ( 2 2 ,4 ) 4 2 2
1 T f ( x) qk ( x) f k g k ( x xk ) ( x xk )T Gk ( x xk ) 2
由一阶必要条件知, xk 1应满足qk ( x) 0 , Gk ( x xk ) g k 0。 即
x xk Gk1gk
xk 1 xk Gk1 g k
