matlab遗传算法求函数最小值
matlab遗传算法学习和全局化算法

1 遗传算法步骤1 根据具体问题选择编码方式,随机产生初始种群,个体数目一定,每个个体表现为染色体的基因编码2 选择合适的适应度函数,计算并评价群体中各个体的适应。
3 选择(selection)。
根据各个个体的适应度,按照一定的规则或方法,从当前群体中选择出一些优良的个体遗传到下一代群体4 交叉(crossover)。
将选择过后的群体内的各个个体随机搭配成对,对每一对个体,以一定概率(交叉概率)交换它们中的部分基因。
5 变异(mutation)。
对交叉过后的群体中的每一个个体,以某个概率(称为变异概率)改n 变某一个或某一些基因位上的基因值为其他的等位基因6 终止条件判断。
若满足终止条件,则以进化过程中得到的具有最大适应度的个体作为最优解输出,终止运算。
否则,迭代执行Step2 至Step5。
适应度是评价群体中染色体个体好坏的标准,是算法进化的驱动力,是自然选择的唯一依据,改变种群结构的操作皆通过适应度函数来控制。
在遗传算法中,以个体适应度的大小来确定该个体被遗传到下一代群体中的概率。
个体的适应度越大,被遗传到下一代的概率就越大,相反,被遗传到下一代的概率就越小。
1 [a,b,c]=gaopt(bound,fun)其中,bound=[xm,xM]为求解区间上届和下届构成的矩阵。
Fun 为用户编写的函数。
a为搜索的结果向量,由搜索的出的最优x向量与目标函数构成,b为最终搜索种群,c为中间搜索过程变参数,其第一列为代数,后边列分别为该代最好的的个体与目标函数的值,可以认为寻优的中间结果。
2 ga函数。
[X,F, FLAG,OUTPUT] = GA(fun, n,opts).n为自变量个数,opts为遗传算法控制选项,用gaoptimset()函数设置各种选项,InitialPopulation可以设置初始种群,用PopulationSize 可以设置种群规模,SelectionFcn可以定义选择函数,3 gatool 函数用于打开,GATOOL is now included in OPTIMTOOL。
matlab遗传算法求函数最小值

题目:使用Matlab遗传算法求解函数最小值的步骤及实例分析目录一、概述二、Matlab遗传算法概述1. 遗传算法原理2. Matlab中的遗传算法工具箱介绍三、使用Matlab遗传算法求解函数最小值的步骤1. 初始化种裙2. 适应度函数的定义3. 轮盘赌选择4. 交叉与变异5. 更新种裙6. 终止条件的设置四、实例分析1. 实例背景2. 实例分析步骤五、总结一、概述在实际工程和科学研究中,经常需要求解函数的最小值,这涉及到优化问题。
遗传算法是一种基于自然选择和遗传机制的全局优化算法,在求解函数最小值问题上具有一定的优势。
Matlab作为一款强大的科学计算软件,具备丰富的数值计算工具和优化算法库,其中也包括遗传算法工具箱。
本文将介绍如何使用Matlab中的遗传算法工具箱求解函数最小值的步骤,并通过一个实例进行分析。
二、Matlab遗传算法概述1. 遗传算法原理遗传算法是一种通过模拟自然界生物进化过程进行优化的算法。
其基本思想是将待优化问题映射成遗传个体的表示形式,并通过种裙的进化过程求解最优解。
遗传算法包括选择、交叉和变异等操作,通过这些操作不断迭代种裙,最终得到最优解。
2. Matlab中的遗传算法工具箱介绍Matlab中提供了用于实现遗传算法的专门工具箱,包括遗传算法函数和用于可视化和评估遗传算法的函数。
使用Matlab的遗传算法工具箱,可以方便地实现遗传算法对函数的全局优化。
三、使用Matlab遗传算法求解函数最小值的步骤1. 初始化种裙在使用Matlab遗传算法工具箱时,需要首先对种裙进行初始化。
可以选择随机生成初始种裙,也可以根据问题的特点进行指定初始种裙。
2. 适应度函数的定义适应度函数是遗传算法中用于评价个体优劣的函数,它的设计直接影响遗传算法的求解效果。
在使用Matlab遗传算法工具箱时,需要根据实际的优化问题设计适应度函数。
3. 轮盘赌选择在遗传算法中,选择操作决定了哪些个体会被选择进行繁殖,而轮盘赌选择是一种常用的选择策略。
matlab遗传算法 算例

下面是一个使用MATLAB实现的基本遗传算法算例。
本例用于解决简单的优化问题:寻找函数f(x) = x^2在[-10,10]范围内的最小值。
```matlab定义问题参数PopSize = 100; 种群数量Genes = -10:0.1:10; 基因范围FitnessFunc = @(x) -x.^2; 适应度函数(这里为了方便,使用了-x^2,即求最大值,实际应用中应改为-f(x))MaxGen = 50; 最大迭代次数初始化种群Pop = zeros(PopSize, length(Genes));for i = 1:PopSizePop(i,:) = rand(1,length(Genes))*2*Genes - Genes; 随机产生初始种群end开始迭代for gen = 1:MaxGen计算当前种群适应度Fitness = FitnessFunc(Pop);[BestFit, Index] = max(Fitness); 找到最佳适应度BestFitPos = Pop(Index,:); 找到最佳适应度对应的基因选择(轮盘赌选择)NewPop = zeros(PopSize, length(Genes));SumFitness = sum(Fitness);RandomFitness = rand(PopSize,1)*SumFitness; 随机生成每个个体的"随机适应度"for i = 1:PopSize[~, Index] = min(RandomFitness); 用随机适应度进行选择(越小被选中概率越大)NewPop(i,:) = Pop(Index,:); 将选择出的个体放入新种群RandomFitness(Index) = SumFitness; 将已选择的个体的随机适应度设为最大值,避免重复选择end交叉(杂交)for i = 1:PopSize/2随机选择两个父代个体Parent1 = NewPop(randi([1 PopSize]),:);Parent2 = NewPop(randi([1 PopSize]),:);生成新个体Child1 = (Parent1 + Parent2)/2; 中间值交叉Child2 = Parent1 + (Parent2 - Parent1)*rand; 一点交叉将新个体加入新种群NewPop((i-1)*2+1,:) = Child1;NewPop((i-1)*2+2,:) = Child2;end变异for i = 1:PopSizeif rand < 0.01 变异概率为0.01随机选择一个基因进行变异(取反)GeneIdx = randi(length(Genes));NewPop(i,GeneIdx) = ~NewPop(i,GeneIdx);endend更新种群Pop = NewPop;end输出结果BestFit = FitnessFunc(BestFitPos);fprintf('Best fitness: f\n', BestFit);fprintf('Best position: s\n', num2str(BestFitPos));```这个例子比较简单,只用了基本的遗传算法操作:选择、交叉和变异。
MATLAB实验报告,遗传算法解最短路径以及函数最小值问题讲解

硕士生考查课程考试试卷考试科目:MATLAB教程考生姓名:考生学号:学院:专业:考生成绩:任课老师(签名)考试日期:20 年月日午时至时《MATLAB 教程》试题:A 、利用MATLAB 设计遗传算法程序,寻找下图11个端点的最短路径,其中没有连接的端点表示没有路径。
要求设计遗传算法对该问题求解。
ad ehkB 、设计遗传算法求解f (x)极小值,具体表达式如下:321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。
C 、利用MATLAB 编程实现:三名商人各带一个随从乘船渡河,一只小船只能容纳二人,由他们自己划行,随从们密约,在河的任一岸,一旦随从的人数比商人多,就杀人越货,但是如何乘船渡河的大权掌握在商人手中,商人们怎样才能安全渡河?D 、结合自己的研究方向选择合适的问题,利用MATLAB 进行实验。
以上四题任选一题进行实验,并写出实验报告。
选择题目: A 一、问题分析(10分)141011如图如示,将节点编号,依次为 1.2.3.4.5.6.7.8.9.10.11,由图论知识,则可写出其带权邻接矩阵为:0 2 8 1 500 500 500 500 500 500 500 2 0 6 500 1 500 500 500 500 500 500 8 6 0 7 500 1 500 500 500 500 500 1 500 7 0 500 500 9 500 500 500 500 500 1 500 500 0 3 500 2 500 500 500 500 500 1 500 3 0 4 500 6 500 500 500 500 500 9 500 4 0 500 500 1 500 500 500 500 500 2 500 500 0 7 500 9 500 500 500 500 500 6 500 7 0 1 2 500 500 500 500 500 500 1 500 1 0 4 500 500 500 500 500 500 500 9 2 4 0 注:为避免计算时无穷大数吃掉小数,此处为令inf=500。
matlab遗传算法计算函数区间最大值和最小值

matlab遗传算法计算函数区间最大值和最小值下面是用matlab实现遗传算法计算函数区间最大值和最小值的示例代码:首先定义函数(此处以f(x)=x*sin(10*pi*x)+1为例):matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;end然后设置遗传算法参数:matlaboptions = gaoptimset('Generations', 1000, 'PopulationSize', 50,'StallGenLimit', 200, 'TolCon', 1e-10);其中,Generations表示遗传算法的迭代次数,PopulationSize表示种群大小,StallGenLimit表示在连续多少代没有改变时停止迭代,TolCon表示收敛精度。
接着,编写遗传算法主函数:matlab[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);其中,第一个参数为要优化的函数,第二个参数为变量维度,后面的参数为变量的取值范围。
最后,输出结果:matlabfprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);其中,-fval表示函数最大值,fval表示函数最小值。
完整代码如下:matlabfunction y = myfun(x)y = x*sin(10*pi*x)+1;endoptions = gaoptimset('Generations', 1000, 'PopulationSize', 50, 'StallGenLimit', 200, 'TolCon', 1e-10);[x, fval] = ga(@myfun, 1, [], [], [], [], -1, 2, [], [], options);fprintf('Function maximum is %f\n',-fval);fprintf('Function minimum is %f\n',fval);参考资料:[1][2]。
实验目的和意义

一、实验目的和意义用遗传算法解决下面函数的极小值问题:遗传算法的具体实施策略不限,最好用MATLAB,上交内容包括源程序和运行结果二、实验原理目标函数是一个含有30维变量的复杂型超越函数,决定使用MA TLAB下的遗传函数工具箱来寻找函数最小值。
三、详细设计步骤1、函数编辑在m文件下编辑目标函数:function y =fun(x);y = zeros(size(x,1),1); %产生一个列向量,(种群数)*1,作为预留解空间[xSize, Dim] = size(x); %xSize:种群数; Dim:变量x的维数indices = repmat(1:Dim, xSize, 1); %生成函数中i的空间矩阵,(种群数)*(变量维数)y = sum(((x.^2) / 4000)')' - prod(cos(x ./sqrt(indices))')' + 1; %函数表达式,此处均采用矩阵点乘的形式2、遗传算法参数设置通过gatool(遗传算法工具箱)设置参数,运行程序,选择合适参数。
Number of variables(变量维数):30Population size:100Initial range:[-600;600]Selection function (选择函数): tournament(锦标赛); tournament size:2Mutation function (变异函数): Uniform(); Rate:0.05Crossover function: Intermediate; Ratio: 0.05Generrations: 5000; Stall generations: Inf; Stall time limite: InfFitness function is vectorized: on其余均为工具箱默认参数。
3、运行程序将设置好参数的算法程序运行30次运行,最佳运行结果为:3.4937e-010x1~x30取值:1.0e-004 *-0.0097 0.0017 0.0587 -0.0250 0.0765 0.0391 -0.0824 0.0653-0.0539 -0.3470 -0.1078 0.4388 0.0223 0.0363 0.0003 0.0228-0.0481 -0.4491 -0.5006 -0.2514 0.0608 -0.1022 0.3454 0.11460.0768 -0.0203 0.0910 -0.0571 0.0065 -0.13844、保存遗传算法程序将在工具箱中编辑好的算法导出为m函数并保存:function [X,FVAL,REASON,OUTPUT,POPULATION,SCORES] = untitled%% This is an auto generated M file to do optimization with the Genetic Algorithm and % Direct Search Toolbox. Use GAOPTIMSET for default GA options structure.%%Fitness functionfitnessFunction = @fun;%%Number of Variablesnvars = 30;%Start with default optionsoptions = gaoptimset;%%Modify some parametersoptions = gaoptimset(options,'PopInitRange' ,[-600 ; 600 ]);options = gaoptimset(options,'PopulationSize' ,100);options = gaoptimset(options,'Generations' ,5000);options = gaoptimset(options,'StallGenLimit' ,Inf);options = gaoptimset(options,'StallTimeLimit' ,Inf);options = gaoptimset(options,'PlotInterval' ,30);options = gaoptimset(options,'SelectionFcn' ,{ @selectiontournament 2 });options = gaoptimset(options,'CrossoverFcn' ,{ @crossoverintermediate 0.05 });options = gaoptimset(options,'MutationFcn' ,{ @mutationuniform 0.05 });options = gaoptimset(options,'Display' ,'off');options = gaoptimset(options,'PlotFcns' ,{ @gaplotbestf });options = gaoptimset(options,'Vectorized' ,'on');%%Run GA[X,FVAL,REASON,OUTPUT,POPULATION,SCORES] = ga(fitnessFunction,nvars,options);以上结果亦可在m文件中直接运行获得。
Matlab中求函数的最小值

MATLAB优化应用§1 线性规划模型一、线性规划课题:实例1:生产计划问题假设某厂计划生产甲、乙两种产品,现库存主要材料有A类3600公斤,B类2000公斤,C类3000公斤。
每件甲产品需用材料A类9公斤,B类4公斤,C类3公斤。
每件乙产品,需用材料A类4公斤,B类5公斤,C类10公斤。
甲单位产品的利润70元,乙单位产品的利润120元。
问如何安排生产,才能使该厂所获的利润最大。
建立数学模型:设x1、x2分别为生产甲、乙产品的件数。
f为该厂所获总润。
max f=70x1+120x2s.t 9x1+4x2≤36004x1+5x2≤20003x1+10x2≤3000x1,x2≥0实例2:投资问题某公司有一批资金用于4个工程项目的投资,其投资各项目时所得的净收益(投入资金锪百分比)如下表:B和C的投资要大于项目D的投资。
试确定全文该公司收益最大的投资分配方案。
建立数学模型:设x1、x2 、x3 、x4分别代表用于项目A、B、C、D的投资百分数。
max f=0.15x1+0.1x2+0.08 x3+0.12 x4s.t x1-x2- x3- x4≤0x2+ x3- x4≥0x1+x2+x3+ x4=1x j≥0 j=1,2,3,4实例3:运输问题有A、B、C三个食品加工厂,负责供给甲、乙、丙、丁四个市场。
三个厂每天生产食品箱数上限如下表:四个市场每天的需求量如下表:求在基本满足供需平衡的约束条件下使总运输费用最小。
建立数学模型:设a i j 为由工厂i 运到市场j 的费用,x i j 是由工厂i 运到市场j 的箱数。
b i 是工厂i 的产量,d j 是市场j 的需求量。
b= ( 60 40 50 ) d= ( 20 35 33 34 )s.tx i j ≥0当我们用MATLAB 软件作优化问题时,所有求maxf 的问题化为求min(-f )来作。
约束g i (x)≥0,化为 –g i ≤0来作。
用Matlab实现遗传算法

用GA找到函数最小值x = ga(fitnessfcn,nvars)局部无约束最小值,x是目标函数的适应度函数,nvars是适应度函数的尺寸(设计变量的数量)。
目标函数和适应度函数接受了1×N大小的x矢量,在x返回一个标量的计算值。
x = ga(fitnessfcn,nvars,A,b)在线性不等式约束下,适应度函数的局部最小值。
如果这个问题有m个线性不等式和n个变量,则A是m×n矩阵,b是m×1矩阵。
注意:当人口类型选项设置为“位串”或者“自定义”,线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq)存在线性等式约束下,适应度函数的局部最小值。
如果没有不等式存在,设置A=[] 和 b=[]。
如果问题存在r个线性等式约束和n个变量,那么Aeq 是r ×n矩阵的大小,beq是r大小的矢量。
注意:当人口类型选项设置为“位串”或者“自定义”,线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)定义了一系列设计变量x的最小和最大边界。
以至于在范围内找到一个解。
如果没有边界存在,LB 和 UB设置为空矩阵。
如果x(i)无下界,设置LB(i) = -Inf;如果x(i)无上界,设置UB(i) = Inf。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon)服从在非线性约束条件下的最小值,非线性函数接收x,返回C和Ceq向量,分别代表非线性的不等式和等式。
GA最小化适应度函数,在C(x)≤0和Ceq(x)=0的条件下。
如果无边界存在,设置 LB=[] 和 UB=[]。
注意:当人口类型选项设置为“位串”或者“自定义”,非线性约束不满足。
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)用在结构选项中的值代替默认的优化参数来进行最小化,它也可以用gaoptimset函数来创建,具体参考gaoptimset的用法。
matlab遗传算法实例

matlab遗传算法实例Matlab遗传算法实例引言:遗传算法是一种模拟自然界生物遗传与进化过程的算法,它通过模拟自然选择、交叉、变异等操作来搜索最优解。
Matlab作为一种强大的数值计算软件,提供了丰富的工具箱来实现遗传算法。
本文将介绍一个基于Matlab的遗传算法实例,以帮助读者更好地理解遗传算法的原理和应用。
一、遗传算法基本原理遗传算法主要包括个体编码、适应度评价、选择、交叉和变异等基本操作。
个体编码是将问题的解表示为染色体,通常使用二进制编码。
适应度评价是根据问题的目标函数对个体进行评估,以确定其适应度值。
选择操作通过一定的策略选择适应度较高的个体作为下一代的父代。
交叉操作将选定的父代个体通过染色体交叉产生新的子代个体。
变异操作以一定的概率对个体的染色体进行变异,以增加种群的多样性。
通过迭代上述操作,逐步优化种群,最终找到问题的最优解。
二、遗传算法实例假设我们要解决一个简单的函数优化问题,即求解函数f(x) = x^2 + 8x + 16的最小值。
我们可以使用遗传算法来搜索函数的最优解。
1. 初始化种群我们需要初始化一个包含N个个体的种群。
每个个体都表示问题的一个解,即一个实数x。
这里,我们将种群大小设置为50,取值范围为[-10, 10]之间的随机数。
2. 适应度评价对于每个个体,我们计算其适应度值,即函数f(x)的值。
根据函数的性质,我们知道函数的最小值为-4,在x=-4时取得。
因此,我们可以将适应度值定义为f(x)与-4之间的差的倒数。
3. 选择操作选择操作决定了哪些个体将成为下一代的父代。
通常采用轮盘赌选择算法,即根据个体的适应度值来确定其被选中的概率。
适应度值较高的个体被选中的概率较大。
4. 交叉操作在选择出的父代个体中,通过染色体交叉操作来产生新的子代个体。
我们可以选择单点交叉或多点交叉。
例如,我们可以随机选择两个个体,将它们的染色体在一个随机位置进行交叉,得到两个新的子代个体。
遗传算法求函数最小值

遗传算法求函数最⼩值利⽤遗传算法寻找函数f(x)=sin(10πx)/x x=[1,2]解题思路将⾃变量在给定范围进⾏编码,得到种群编码,按照所选择的适应度函数并通过遗传算法中的选择,交叉和变异对个体进⾏筛选和进化,使适应度值⼤的个体被保留,⼩的个体被淘汰,新的种群继承上⼀代的信息,⼜优于下⼀代,这样反复循环,最后得出最终结果注:程序参考<<MATLAB智能智能算法30个案例>>, 依照matlab程序,⽤python进⾏了重写# -*- coding: utf-8 -*-import matplotlib.pyplot as pltimport numpy as npfrom pylab import *import randomimport mathmpl.rcParams['font.sans-serif'] = ['SimHei']mpl.rcParams['axes.unicode_minus'] = False#定义遗传算法参数pop_size=40generation=20length=30pc=0.65pm=0.01#编码def genEncoding(pop_size,length):pop=[[]]for i in range(pop_size):temp=[]for j in range(length):temp.append(random.randint(0,1))pop.append(temp)return pop[1:]#解码def genDecoding(pop,length):temp=[]for i in range(len(pop)):t=0for j in range(length):t+=pop[i][j]*math.pow(2,j)temp.append(t)return temp#计算⽬标值def calobjValue(pop,length,lb,ub):temp1=[]obj_value=[]x_value=[]temp1=genDecoding(pop,length)for i in range(len(temp1)):x=lb+(ub-lb)*temp1[i]/((math.pow(2,length))-1)x_value.append(x)obj_value.append(np.sin(10*pi*x)/x)return obj_value#计算适应度def fitness(pop,length,lb,ub):obj_value=[]fitness_value=[]obj_value=calobjValue(pop,length,lb,ub)for i in range(len(obj_value)):fitness_value.append(obj_value[i]-1)fitness_value=list(map(abs,fitness_value))return fitness_value#累积适应度def cumsum(newfitness_value):accumulation_value=[]t=0for i in range(len(newfitness_value)):t+=newfitness_value[i]accumulation_value.append(t)return accumulation_value#选择函数def selection(pop,fitness_value):newfitness_value=[]accumulation_value=[]total_fit=np.sum(fitness_value)for i in range(len(fitness_value)):newfitness_value.append(fitness_value[i]/total_fit) accumulation_value=cumsum(newfitness_value)ms=[]for i in range(len(pop)):ms.append(random.random())newin=0newpop=[]for i in range(len(ms)):j=0for j in range(len(accumulation_value)):if ms[i]<accumulation_value[j]:t=pop[j]newpop.append(t)breakreturn newpop#交叉函数def crossover(pop,fitness_value,pc):newpop=[]newpop=selection(pop,fitness_value)for i in range(len(newpop)-1):if random.random()<pc:temp1=[]temp2=[]temp1=newpop[i][3:15]temp2=newpop[i+1][3:15]newpop[i][3:15]=temp2newpop[i+1][3:15]=temp1return newpopdef mutation(pop,fitness_value,pc,pm,length):newpop=[]newpop=crossover(pop,fitness_value,pc)for i in range(len(newpop)):if random.random()<pm:m1=random.randint(0,length-1)m2=random.randint(0,length-1)m3=random.randint(0,length-1)if newpop[i][m1]==1:newpop[i][m1]=0else:newpop[i][m1]=1if newpop[i][m2]==1:newpop[i][m2]=0else:newpop[i][m2]=1if newpop[i][m3]==1:newpop[i][m3]=0else:newpop[i][m3]=1i=0return newpopif __name__ =='__main__':#画出函数图plt.figure(1)lb=1ub=2x=np.arange(lb,ub,0.01)y=sin(10*pi*x)/xplt.plot(x,y)plt.xlabel("⾃变量x")plt.ylabel("⾃变量y")plt.title('sin(10*pi*x)/x')pop=genEncoding(pop_size,length)obj_value=calobjValue(pop,length,lb,ub)fitness_value=fitness(pop,length,lb,ub)gen=0x_value=[]best_x=[]best_individual=[]Generation=[]while gen<generation:newpop=mutation(pop,fitness_value,pc,pm,length) temp=genDecoding(newpop,length)for i in range(len(temp)):x=lb+(ub-lb)*temp[i]/((math.pow(2,length))-1)x_value.append(x)obj_value=calobjValue(newpop,length,lb,ub)k=0j=0for i in range(len(obj_value)):if k>obj_value[i]:k=obj_value[i]j=ibest_individual.append(k)best_x.append(x_value[j])fitness_value=fitness(newpop,length,lb,ub)Generation.append(gen)gen=gen+1k=0j=0for i in range(len(best_individual)):if k>best_individual[i]:k=best_individual[i]j=iprint(best_individual[j])print(best_x[j])best_individual.sort(reverse=True)plt.figure(2)plt.plot(Generation,best_individual)plt.xlabel("遗传代数")plt.ylabel("解的变化") plt.title("进化过程") plt.show()。
遗传算法matlab程序代码

遗传算法matlab程序代码遗传算法是一种优化算法,用于在给定的搜索空间中寻找最优解。
在Matlab中,可以通过以下代码编写一个基本的遗传算法:% 初始种群大小Npop = 100;% 搜索空间维度ndim = 2;% 最大迭代次数imax = 100;% 初始化种群pop = rand(Npop, ndim);% 最小化目标函数fun = @(x) sum(x.^2);for i = 1:imax% 计算适应度函数fit = 1./fun(pop);% 选择操作[fitSort, fitIndex] = sort(fit, 'descend');pop = pop(fitIndex(1:Npop), :);% 染色体交叉操作popNew = zeros(Npop, ndim);for j = 1:Npopparent1Index = randi([1, Npop]);parent2Index = randi([1, Npop]);parent1 = pop(parent1Index, :);parent2 = pop(parent2Index, :);crossIndex = randi([1, ndim-1]);popNew(j,:) = [parent1(1:crossIndex),parent2(crossIndex+1:end)];end% 染色体突变操作for j = 1:NpopmutIndex = randi([1, ndim]);mutScale = randn();popNew(j, mutIndex) = popNew(j, mutIndex) + mutScale;end% 更新种群pop = [pop; popNew];end% 返回最优解[resultFit, resultIndex] = max(fit);result = pop(resultIndex, :);以上代码实现了一个简单的遗传算法,用于最小化目标函数x1^2 + x2^2。
matlab计算函数最大值及最小值

matlab计算函数最大值及最小值在MATLAB中,有几种方法可以计算一个函数的最大值和最小值。
下面将介绍几种常用的方法。
1.通过绘制函数图像找到最大值和最小值:首先,可以通过绘制函数图像来观察函数的最大值和最小值所在的位置。
可以使用plot函数来绘制函数的图像。
例如,我们想计算函数y=x^3-2x的最大值和最小值:```x=-10:0.1:10;y=x.^3-2*x;plot(x, y)```通过观察图像,可以确定函数的最大值和最小值的位置。
2. 使用fminbnd函数找到函数的最小值:MATLAB中的fminbnd函数可以用于寻找函数的最小值。
该函数使用了黄金分割算法。
例如,我们想计算函数y=x^3-2x的最小值:```[x, y] = fminbnd(f, -10, 10);```这段代码将返回函数的最小值y以及对应的x值。
3. 使用fmincon函数找到函数的最小值(约束最优化):如果函数有特定的约束条件,可以使用fmincon函数来计算函数的最小值。
fmincon函数基于无约束的最优化算法,并添加了约束条件。
例如,我们想计算函数y=x^2的最小值,但限制x的范围在0到1之间:```x0=0.5;%初始解A=[];b=[];Aeq = [];beq = [];lb = 0; % x的下限ub = 1; % x的上限[x, y] = fmincon(f, x0, A, b, Aeq, beq, lb, ub);```这段代码将返回函数的最小值y以及对应的x值。
4. 使用max和min函数找到向量或矩阵的最大值和最小值:如果需要计算向量或矩阵的最大值和最小值,可以使用MATLAB中的max和min函数。
例如,计算向量x=[1,2,3,4,5]的最大值和最小值:```x=[1,2,3,4,5];max_value = max(x);min_value = min(x);```这段代码将返回向量x的最大值和最小值。
(完整版)遗传算法matlab实现源程序
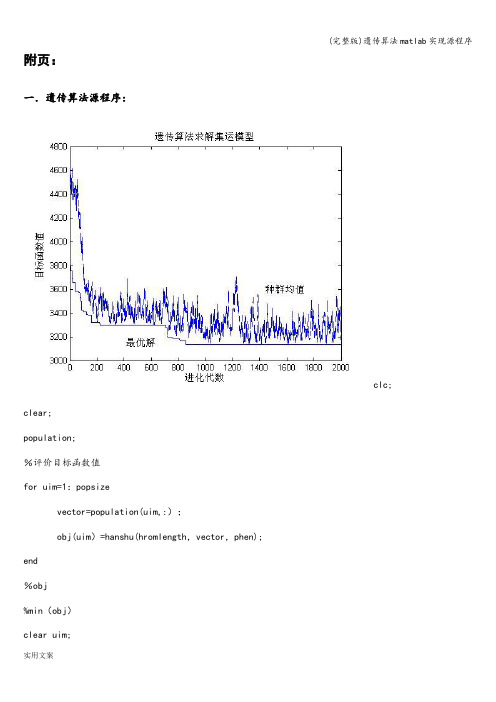
附页:一.遗传算法源程序:clc; clear;population;%评价目标函数值for uim=1:popsizevector=population(uim,:);obj(uim)=hanshu(hromlength,vector,phen);end%obj%min(obj)clear uim;objmin=min(obj);for sequ=1:popsizeif obj(sequ)==objminopti=population(sequ,:);endendclear sequ;fmax=22000;%==for gen=1:maxgen%选择操作%将求最小值的函数转化为适应度函数for indivi=1:popsizeobj1(indivi)=1/obj(indivi);endclear indivi;%适应度函数累加总合total=0;for indivi=1:popsizetotal=total+obj1(indivi);endclear indivi;%每条染色体被选中的几率for indivi=1:popsizefitness1(indivi)=obj1(indivi)/total;endclear indivi;%各条染色体被选中的范围for indivi=1:popsizefitness(indivi)=0;for j=1:indivifitness(indivi)=fitness(indivi)+fitness1(j);endendclear j;fitness;%选择适应度高的个体for ranseti=1:popsizeran=rand;while (ran>1||ran<0)ran=rand;endran;if ran〈=fitness(1)newpopulation(ranseti,:)=population(1,:);elsefor fet=2:popsizeif (ran〉fitness(fet—1))&&(ran<=fitness(fet))newpopulation(ranseti,:)=population(fet,:);endendendendclear ran;newpopulation;%交叉for int=1:2:popsize-1popmoth=newpopulation(int,:);popfath=newpopulation(int+1,:);popcross(int,:)=popmoth;popcross(int+1,:)=popfath;randnum=rand;if(randnum〈 P>cpoint1=round(rand*hromlength);cpoint2=round(rand*hromlength);while (cpoint2==cpoint1)cpoint2=round(rand*hromlength);endif cpoint1>cpoint2tem=cpoint1;cpoint1=cpoint2;cpoint2=tem;endcpoint1;cpoint2;for term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int,ss)==popfath(term)tem1=popcross(int,ss);popcross(int,ss)=popcross(int,term);popcross(int,term)=tem1;endendclear tem1;endfor term=cpoint1+1:cpoint2for ss=1:hromlengthif popcross(int+1,ss)==popmoth(term)tem1=popcross(int+1,ss);popcross(int+1,ss)=popcross(int+1,term);popcross(int+1,term)=tem1;endendclear tem1;endendclear term;endclear randnum;popcross;%变异操作newpop=popcross;for int=1:popsizerandnum=rand;if randnumcpoint12=round(rand*hromlength);cpoint22=round(rand*hromlength);if (cpoint12==0)cpoint12=1;endif (cpoint22==0)cpoint22=1;endwhile (cpoint22==cpoint12)cpoint22=round(rand*hromlength);if cpoint22==0;cpoint22=1;endendtemp=newpop(int,cpoint12);newpop(int,cpoint12)=newpop(int,cpoint22);newpop(int,cpoint22)=temp;。
Matlab实现遗传算法的示例详解

Matlab实现遗传算法的⽰例详解⽬录1算法讲解1.1何为遗传算法1.2遗传算法流程描述1.3关于为什么要⽤⼆进制码表⽰个体信息1.4⽬标函数值与适应值区别1.5关于如何将⼆进制码转化为变量数值1.6关于代码改进2MATLAB⾃带ga函数2.1问题描述2.2⾃带函数使⽤3⾃编遗传算法各部分代码及使⽤3.1代码使⽤3.2Genetic1--主函数3.3PI(PopulationInitialize)--产⽣初始种群3.4Fitness--计算⽬标函数值3.5FitnessF--计算适应值3.6Translate--将⼆进制码转换3.7Probability--染⾊体⼊选概率3.8Select--个体选择3.9Crossing--交叉互换3.10Mutation--基因突变3.11Elitist--最优个体记录与最劣个体淘汰3.12完整代码这篇⽂章⽤了⼤量篇幅讲解了如何从零开始⾃⼰写⼀个遗传算法函数,主要是为了应对学⽣作业等情况,或者让⼤家对遗传算法有更充分的理解,如果要⽤于学术研究,最好还是使⽤⾃带遗传算法,之后可能会推出更多⾃带遗传算法⼯具箱的使⽤。
1 算法讲解1.1 何为遗传算法遗传、突变、⾃然选择、杂交,遗传算法是⼀种借鉴了进化⽣物学各类现象的进化算法。
看到⼀个很形象的⽐喻来描述各类进化算法的区别:爬⼭算法:⼀只袋⿏朝着⽐现在⾼的地⽅跳去。
它找到了不远处的最⾼的⼭峰。
但是这座⼭不⼀定是最⾼峰。
这就是爬⼭算法,它不能保证局部最优值就是全局最优值。
模拟退⽕:袋⿏喝醉了。
它随机地跳了很长时间。
这期间,它可能⾛向⾼处,也可能踏⼊平地。
但是,它渐渐清醒了并朝最⾼峰跳去。
这就是模拟退⽕算法。
遗传算法:有很多袋⿏,它们降落到喜玛拉雅⼭脉的任意地⽅。
这些袋⿏并不知道它们的任务是寻找珠穆朗玛峰。
但每过⼏年,就在⼀些海拔⾼度较低的地⽅射杀⼀些袋⿏。
于是,不断有袋⿏死于海拔较低的地⽅,⽽越是在海拔⾼的袋⿏越是能活得更久,也越有机会⽣⼉育⼥。
matlab计算函数最大值及最小值

matlab计算函数最大值及最小值MATLAB是一种集成开发环境(IDE),用于计算、数据分析、数据可视化和数学模型。
它是专为工程和科学计算而设计的,可以帮助用户轻松地进行复杂数学计算和可视化。
在MATLAB中,计算函数的最大值和最小值是一个非常基本的操作,本文将详细介绍如何在MATLAB中计算函数的最大值和最小值。
步骤一:打开MATLAB首先,打开MATLAB工作环境。
这可以通过在计算机的搜索栏中输入“MATLAB”并单击“打开”按钮来完成。
如果计算机上没有安装MATLAB,则需要从Mathworks网站下载和安装MATLAB。
步骤二:选择并输入要计算的函数在MATLAB中,可以通过符号表达式或函数句柄来表示一个函数。
例如,我们要计算函数y = 2x^2 - 3x + 4在取值范围为[-2,2]时的最大值和最小值。
为了实现这个目标,可以使用MATLAB自带的fplot 函数。
输入以下命令:fplot(@(x)2*x^2-3*x+4,[-2,2])命令中的“@”符号用于定义一个匿名函数,也可以使用符号表达式或函数句柄表示要计算的函数。
[-2,2]则是要计算函数的取值范围。
运行这个命令,MATLAB会生成y值随x变化的图表。
步骤三:计算函数的最大值和最小值在MATLAB中,可以使用max和min函数来计算函数的最大值和最小值。
例如,我们可以使用以下命令计算函数y = 2x^2 - 3x + 4在取值范围为[-2,2]时的最大值和最小值:syms x y(x)y(x)=2*x^2-3*x+4;xmax=fminbnd(-y,-2,2); #最大值xmin=fminbnd(y,-2,2); #最小值运行这些命令,MATLAB会输出函数的最大值和最小值。
至此,我们完成了计算函数的最大值和最小值的过程。
以上步骤也可以通过matlab自带的3D画图工具箱实现更快捷的展示方式。
这只是MATLAB功能的一部分,MATLAB的强大功能可以帮助用户在数学计算、数据分析和数据可视化方面取得更好的成果。
遗传算法求解函数最大值最小值

遗传算法是一种模拟自然选择和遗传机制的优化搜索算法,它能够通过模拟生物进化的过程来寻找最优解。
在数学和计算领域,遗传算法被广泛应用于求解函数的最大值和最小值问题。
1. 遗传算法的基本原理遗传算法是一种基于裙体的优化算法,它模拟了自然界中的优胜劣汰和随机性变异的过程。
其基本原理包括遗传、变异、选择和适应度评价。
1.1 遗传:遗传算法通过模拟生物的交配过程来产生新的个体,其中将两个个体的染色体交叉并产生新的后代。
1.2 变异:遗传算法引入随机性的变异操作,以增加搜索空间的多样性,使算法不至于陷入局部最优解。
1.3 选择:个体的适应度评价后,根据一定的选择策略选择出部分个体作为下一代的种裙,通常适应度高的个体有更大的概率被选择。
1.4 适应度评价:遗传算法通过适应度函数对个体进行评价,以确定个体在种裙中的适应度。
适应度函数通常是需要优化的函数。
2. 遗传算法在求解函数最大值和最小值问题中的应用遗传算法作为一种全局搜索算法,具有寻找函数最大值和最小值的能力。
对于一个给定的函数,遗传算法能够在较短的时间内找到该函数的全局最优解。
2.1 函数最大值求解:对于函数的最大值求解问题,可以将函数的负值作为适应度函数,通过遗传算法来求解负值最小化的问题,从而达到求解函数最大值的目的。
2.2 函数最小值求解:对于函数的最小值求解问题,则可以直接将函数的值作为适应度函数,通过遗传算法来求解函数最小值问题。
3. 遗传算法在实际应用中的优势遗传算法作为一种全局搜索算法,在求解函数最大值和最小值问题中具有以下优势:3.1 并行性:遗传算法能够并行处理多个个体,从而加速搜索过程,尤其适合于复杂的高维优化问题。
3.2 全局搜索能力:遗传算法不容易陷入局部最优解,能够在较短的时间内找到函数的全局最优解。
3.3 适应性强:遗传算法能够适应不同类型的函数和问题,具有较强的通用性。
4. 遗传算法在求解函数最大值和最小值问题中的应用实例以下是一些实际应用中遗传算法在求解函数最大值和最小值问题中的应用实例:4.1 Rosenbrock函数最小值求解:Rosenbrock函数是一个经典的优化测试函数,遗传算法在求解Rosenbrock函数的最小值时具有良好的表现。
遗传算法的Matlab实现讲解

Matlab函数调用实现GA
• Matlab的GA函数
[x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[], options);
fitnessfcn — Fitness function nvars — Number of variables for the problem Aineq — Matrix for inequality constraints Bineq — Vector for inequality constraints Aeq — Matrix for equality constraints Beq — Vector for equality constraints LB — Lower bound on x UB — Upper bound on x nonlcon — Nonlinear constraint Function options — Options structure
global Cmin;
Cmin=-10^6; popsize=50; %群体大小 Gene=20; chromlength=20; %字符串长 度(个体长度) pc=0.8; %交叉概率 pm=0.01; %变异概率 Xmax=10; Xmin=0;
[bestindividual,bestfit]=best(pop,fitvalue); %求出群体中适应值最大的 个体及其适应值
Matlab函数调用实现GA
• GA函数调用步骤
第一步:编写适应度函数; 第二步:对GA参数进行设置; options = gaoptimset(‘参数名’, 参数值, …, ‘参数名’, 参数值) 例:options = gaoptimset('PopulationSize', 100) 第三步:调用GA函数; [x fval] = ga(@fitnessfun, nvars) [x fval exitflag output population scores] = ga(@fitnessfcn, nvars) [x fval] = ga(@fitnessfun, nvars, [],[],[],[],[],[],[],options);
matlab遗传算法工具箱函数及实例讲解

matlab遗传算法工具箱函数及实例讲解最近研究了一下遗传算法,因为要用遗传算法来求解多元非线性模型。
还好用遗传算法的工具箱予以实现了,期间也遇到了许多问题。
首先,我们要熟悉遗传算法的基本原理与运算流程。
基本原理:遗传算法是一种典型的启发式算法,属于非数值算法范畴。
它是模拟达尔文的自然选择学说和自然界的生物进化过程的一种计算模型。
它是采用简单的编码技术来表示各种复杂的结构,并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。
遗传算法的操作对象是一群二进制串(称为染色体、个体),即种群,每一个染色体都对应问题的一个解。
从初始种群出发,采用基于适应度函数的选择策略在当前种群中选择个体,使用杂交和变异来产生下一代种群。
如此模仿生命的进化进行不断演化,直到满足期望的终止条件。
运算流程:Step 1:对遗传算法的运行参数进行赋值。
参数包括种群规模、变量个数、交叉概率、变异概率以及遗传运算的终止进化代数。
Step 2:建立区域描述器。
根据轨道交通与常规公交运营协调模型的求解变量的约束条件,设置变量的取值范围。
Step 3:在Step 2的变量取值范围内,随机产生初始群体,代入适应度函数计算其适应度值。
Step 4:执行比例选择算子进行选择操作。
Step 5:按交叉概率对交叉算子执行交叉操作。
Step 6:按变异概率执行离散变异操作。
Step 7:计算Step 6得到局部最优解中每个个体的适应值,并执行最优个体保存策略。
Step 8:判断是否满足遗传运算的终止进化代数,不满足则返回Step 4,满足则输出运算结果。
其次,运用遗传算法工具箱。
运用基于Matlab的遗传算法工具箱非常方便,遗传算法工具箱里包括了我们需要的各种函数库。
目前,基于Matlab的遗传算法工具箱也很多,比较流行的有英国设菲尔德大学开发的遗传算法工具箱GATBX、GAOT以及Math Works公司推出的GADS。
遗传算法Matlab代码

遗传算法优缺点遗传算法的优点:1. 与问题领域无关切快速随机的搜索能力。
2. 搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较,robust.3. 搜索使用评价函数启发,过程简单4. 使用概率机制进行迭代,具有随机性。
5. 具有可扩展性,容易与其他算法结合。
缺点是:1。
没有能够及时利用网络的反馈信息,故算法的搜索速度比较慢,要得要较精确的解需要较多的训练时间。
2。
算法对初始种群的选择有一定的依赖性,能够结合一些启发算法进行改进。
3。
算法的并行机制的潜在能力没有得到充分的利用,这也是当前遗传算法的一个研究热点方向。
核心函数:(1)function [pop]=initializega(num,bounds,eevalFN,eevalOps,options)--初始种群的生成函数【输出参数】pop--生成的初始种群【输入参数】num--种群中的个体数目bounds--代表变量的上下界的矩阵eevalFN--适应度函数eevalOps--传递给适应度函数的参数options--选择编码形式(浮点编码或是二进制编码)[precision F_or_B],如precision--变量进行二进制编码时指定的精度F_or_B--为1时选择浮点编码,否则为二进制编码,由precision指定精度)(2)function [x,endPop,bPop,traceInfo] = ga(bounds,evalFN,evalOps,startPop,opts,...termFN,termOps,selectFN,selectOps,xOverFNs,xOverOps,mutFNs,mutOps)--遗传算法函数【输出参数】x--求得的最优解endPop--最终得到的种群bPop--最优种群的一个搜索轨迹【输入参数】bounds--代表变量上下界的矩阵evalFN--适应度函数evalOps--传递给适应度函数的参数startPop-初始种群opts[epsilon prob_ops display]--opts(1:2)等同于initializega的options参数,第三个参数控制是否输出,一般为0。
利用遗传算法求函数的极小值

1、利用遗传算法求出下面函数的极小值:z=2-exp[-(x2+y2)], x,y∈[-5,+5]对于此函数,求某一极值、或说最值时,由于x、y定义域与系数相同,x与y相对于z 来说是地位等同的,因此可以转换成求该函数极值:;继而转换成了一种单变量函数。
函数的实现:(1)ga_main脚本文件% GA main program% Edited by Bian Xuezi% n ---- 种群规模% ger ---- 迭代次数% pc ---- 交叉概率% pm ---- 变异概率% v ---- 初始种群(规模为n)% f ---- 目标函数值% fit ---- 适应度向量% vx ---- 最优适应度值向量% vmfit ---- 平均适应度值向量clear all;close all;clc;tic;n=20;ger=100;pc=0.70;pm=0.009;% 生成初始种群v=init_population(n,20);[N,L]=size(v);disp(sprintf('Number of generations:%d',ger)); disp(sprintf('Population size:%d',N));disp(sprintf('Crossover probability:%.3f',pc)); disp(sprintf('Mutation probability:%.3f',pm)); % 待优化问题xmin=-5;ymin=-5;xmax=5;ymax=5;f='-2+exp(-x.^2-y.^2)';%初始化sol=0.1;vmfit=[];it=1;vx=[];%C=[];% 计算适应度,并画出图形x=decode(v(:,1:10),xmin,xmax);y=decode(v(:,11:20),ymin,ymax);fit=eval(f);figure(1);[X,Y]=meshgrid(-5:0.1:5,-5:0.1:5);Z=-2+exp(-X.^2-Y.^2);mesh(X,Y,Z);grid on;hold on;plot3(x,y,fit,'k*');title('染色体的初始位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 开始进化while it<=ger%Reproduction(Bi-classist Selection) vtemp=roulette(v,fit);%Crossoverv=crossover(vtemp,pc);%MutationM=rand(N,L)<=pm;%M(1,:)=zeros(1,L);v=v-2.*(v.*M)+M;%Resultsx=decode(v(:,1:10),xmin,xmax);y=decode(v(:,11:20),ymin,ymax);fit=eval(f);[sol,indb]=max(fit);v(1,:)=v(indb,:);media=mean(fit);vx=[vx sol];vmfit=[vmfit media];it=it+1;end%%%% 最后的结果disp(sprintf('\n')); %空一行% 显示最优解及最优值disp(sprintf('Maximum found[x,f(x)]:[%.4f,%.4f,%.4f]',x(indb),y(indb),sol)); % 图形显示最优结果figure(2);[X,Y]=meshgrid(-5:0.1:5,-5:0.1:5);Z=-2+exp(-X.^2-Y.^2);mesh(X,Y,Z);grid on;hold on;plot3(x,y,fit,'k*');title('染色体的最终位置');xlabel('x');ylabel('y');zlabel('f(x,y)');% 图形显示最优及平均函数值变化趋势figure(3);plot(vx);%title('最优,平均函数值变化趋势'); xlabel('Generations');ylabel('f(x,y)');hold on;plot(vmfit,'r');hold off;runtime=toc(2)Crossover函数%Crossoverfunction v=crossover(vtemp,pc) [N,L]=size(vtemp);C(:,1)=rand(N,1)<=pc;I=find(C(:,1)==1);I';j=1;for i=1:2:size(I)if i>=size(I)break;endsite=fix(1+L*rand(1));temp=vtemp(I(i,1),:);vtemp(I(i,1),site:end)=vtemp(I(i+1,1),site:end); vtemp(I(i+1,1),site:end)=temp(:,site:end);%j=j+2;endv=vtemp;(3)decode函数%Decodify bitstringsfunction x=decode(v,min,max)% x ----真实值% v ----待解码的已编码的0-1串v=fliplr(v);[s,c]=size(v);aux=0:1:c-1 ;%21;aux=ones(s(1),1)*aux;x1=sum((v.*2.^aux)');x=min+(max-min)*x1./(2^c-1); % ; (4)init_population函数function v=init_population(n1,s1)v=round(rand(n1,s1));(5)roulette函数function vtemp=roulette(v,fit)N=size(v);fitmin=abs(min(fit));fit=fitmin+fit;%fitS=sum(fit);for i=1:NSI=S*rand(1);for j=1:Nif SI<=sum(fit(1:j))vtemp(i,:)=v(j,:);breakendendend。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
end
function mutchrom=exmut(chrom,pm)
[m,n]=size(chrom);
s=rand(m,n)<=pm;
domut=find(sum(s')>0);
mutchrom=zeros(length(domut),n);
newchrom(find(~docross),:)=chrom(find(~docross),:);
%适应度计算
function fitv=fel(x)
ob=512^2*20-fun(x);
fitv=ob/sum(ob);
%目标函数
function y=fun(x)
[nind,lind]=size(x);
y=zeros(nind,1);
for i=1:lind
y=x(:,i).^2+y;
end
%基本位变异操作
function newchrom=mut(chrom,pm)
[m,n]=size(chrom);
%基于适应度的轮盘选择
chrom=exrws(chrom,fitv,Nesl);
while gen<maxgen
%单点交叉后得到大小为popsize子代新种群,与原来的父代种群合并为大小为2*popsize的新种群
newchrom=[chrom;exxov(chrom,px)];
for i=1:dim
exchrom=chrom(:,li(i):lf(i));
for j=1:bits
phen(:,i)=exchrom(:,j).*2^(bits-j)+phen(:,i);
end
gen=0; %代计数器
x=bs(chrom,lb,ub,dim,bits);
obj=fun(x);
figure(1)
plot(obj,'-xr');grid;
title('初始种群中个体的分布图')
xlabel('个体');
ylabel('目标函数值');
obj=min(obj);
figure(5)
plot(trace(:,1));
title('经过500次遗传迭代后种群最优解的变化')
xlabel('迭代次数');
ylabel('目标函数值');
figure(7)
plot(trace(:,2));
dot=ceil(rand(1).*lind);
mask=[zeros(1,dot) ones(1,lind-dot)];
newtemp(odd(i),:)=(temp(odd(i),:).*mask)+(temp(even(i),:).*(~mask));
newchrom=[newchrom(I,:);exrws(newchrom,fitv,Nesl-1)];
%变异概率为pm的基本位变异,假设有N个染色体发生了变异,将这N个染色体插入原来的种群中,得到大小为popsize+N的新种群
chrom=[newchrom;exmut(newchrom,pm)];
%十进制转换
function phen=bs(chrom,lb,ub,dim,bits)
[m,n]=size(chrom);
li=[1:bits:n-bits+1];
lf=[bits:bits:n];
phen=zeros(m,dim);
j=1:n;
mutchrom=(~chrom(domut,j)).*s(domut,j)+chrom(domut,j).*(~s(domut,j));
%基于适应度的轮盘选择
function newchrom=exrws(chrom,fitv,Nsel);
[Nind,ans]=size(fitv);
newtemp(even(i),:)=(temp(even(i),:).*mask)+(temp(odd(i),:).*(~mask));
end
if rem(m,2),
newtemp(m,:)=temp(m,:);
Байду номын сангаас end
newchrom(find(docross),:)=newtemp;
%最优个体保护策略 (先提出种群中的最优个体,然后用轮盘选择出Nesl-1个个体
%构建成新的种群,再将最优个体插入新种群的第一行)
x=bs(newchrom,lb,ub,dim,bits);
fitv=fel(x);
[Y,I]=max(fitv);
cumfit=cumsum(fitv);
decumfit=[0;cumfit(1:Nind-1)];
for i=1:Nsel
ch=rand(1)*cumfit(Nind);
for j=1:Nind
if (ch<=cumfit(j))&(ch>decumfit(j)),
function obj=yichuan(lb,ub,px,pm)
%lb,ub为自变量的下界与上界,px为杂交概率,pm为变异概率
popsize=40; %设定种群大小为40
maxgen=500; %设定最大遗传代数为500代
plot(obj,'-xr');grid;
title('经过100次遗传迭代后种群中个体的分布图')
xlabel('个体');
ylabel('目标函数值');
end
if gen==250
figure(4)
trace(gen,2)=sum(obj)/length(obj);
aver=zeros(length(fitv),1);
aver(:,1)=sum(fitv)/length(fitv);
aver=(fitv-aver).^2;
trace(gen,3)=sum(aver)/length(fitv);
xlabel('个体');
ylabel('目标函数值');
Nesl=popsize; %轮盘选择个数,设定为与种群大小相等
gen=0; %遗传代数计数器,设定初始值为0
obj=fun(x);
fitv=fel(x);
title('经过500次遗传迭代后种群平均值的变化')
xlabel('迭代次数');
ylabel('目标函数值');
figure(8)
plot(trace(:,3));
xlabel('迭代次数');
ylabel('种群的方差');
title('500次迭代过程中种群方差的变化');
%最优个体保护策略 (先提出种群中的最优个体,然后用轮盘选择出Nesl-1个个体
%构建成新的种群,再将最优个体插入新种群的第一行)
x=bs(chrom,lb,ub,dim,bits);
fitv=fel(x);
[Y,I]=max(fitv);
s=rand(m,n)<=pm;
i=1:m;
j=1:n;
newchrom(i,j)=(~chrom(i,j)).*s(i,j)+chrom(i,j).*(~s(i,j));
%trace(gen,4)=shang(fitv);
% trace(gen,5)=cshang(chrom,duan);
end
figure(5)
plot(obj,'-xr');grid;
title('经过500次遗传迭代后种群中个体的分布图')
figure(2)
plot(obj,'-xr');grid;
title('经过20次遗传迭代后种群中个体的分布图')
xlabel('个体');
ylabel('目标函数值');
end
if gen==100
figure(3)
docross=rand(nind,1)<px;
temp=chrom(find(docross),:);
[m,n]=size(temp);
xops=floor(m/2);
odd=1:2:m-1;
even=2:2:m;
for i=1:xops
dim=20; %定义变量的维数为20
bits=20; %设定变量的二进制位数为20
duan=20;
trace=zeros(maxgen,2); %遗传算法性能跟踪
chrom=crt(popsize,dim*bits); %创建初始种群
end
phen=lb+phen.*(ub-lb)/(2^bits-1);
%创建种群
function [chrom]=crt(popsize,bits)
chrom=zeros(popsize,bits);
for i=1:popsize
pop=round(rand(1,bits));
newcode(i)=j;
end
end
end
newchrom=chrom(newcode,:);
