(精选)数值计算方法上机实习题
数值计算方法I上机实验考试题

数值计算方法I 上机实验考试题(两题任选一题)
1.小型火箭初始质量为900千克,其中包括600千克燃料。
火箭竖直向上发射时燃料以15千克/秒的速率燃烧掉,由此产生30000牛顿的恒定推力.当燃料用尽时引擎关闭。
设火箭上升的整个过程中,空气阻力与速度平方成正比,比例系数为0.4(千克/米).重力加速度取9.8米/秒2.
A. 建立火箭升空过程的数学模型(微分方程);
B. 求引擎关闭瞬间火箭的高度、速度、加速度,及火箭到达最高点的时间和高度.
2.小型火箭初始质量为1200千克,其中包括900千克燃料。
火箭竖直向上发射时燃料以15千克/秒的速率燃烧掉,由此产生40000牛顿的恒定推力.当燃料用尽时引擎关闭。
设火箭上升的整个过程中,空气阻力与速度平方成正比,比例系数记作k ,火箭升空过程的数学模型为
0)0(,0,01222==≤≤-+⎪⎭
⎫ ⎝⎛-==t dt dx x t t mg T dt dx k dt x d m 其中)(t x 为火箭在时刻t 的高度,m =1200-15t 为火箭在时刻t 的质量,T (=30000牛顿)为推力,g (=9.8米/秒2)为重力加速度, t 1 (=900/15=60秒)为引擎关闭时刻.
今测得一组数据如下(t ~时间(秒),x ~高度(米),v ~速度(米/秒)):
现有两种估计比例系数k 的方法:
1.用每一个数据(t,x,v )计算一个k 的估计值(共11个),再用它们来估计k 。
2.用这组数据拟合一个k .
请你分别用这两种方法给出k 的估计值,对方法进行评价,并且回答,能否认为空气阻力系数k=0.5(说明理由).。
(完整版)数值计算方法上机实习题答案

(完整版)数值计算⽅法上机实习题答案1.设?+=105dx xx I nn ,(1)由递推公式nI I n n 151+-=-,从0I 的⼏个近似值出发,计算20I ;解:易得:0I =ln6-ln5=0.1823, 程序为:I=0.182; for n=1:20I=(-5)*I+1/n; end I输出结果为:20I = -3.0666e+010 (2)粗糙估计20I ,⽤nI I n n 515111+-=--,计算0I ;因为 0095.056 0079.01020201020≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2120=+=I 程序为:I=0.0087; for n=1:20I=(-1/5)*I+1/(5*n); end I0I = 0.0083(3)分析结果的可靠性及产⽣此现象的原因(重点分析原因)。
⾸先分析两种递推式的误差;设第⼀递推式中开始时的误差为000I I E '-=,递推过程的舍⼊误差不计。
并记nn n I I E '-=,则有01)5(5E E E n n n -==-=-Λ。
因为=20E 20020)5(I E >>-,所此递推式不可靠。
⽽在第⼆种递推式中n n E E E )51(5110-==-=Λ,误差在缩⼩,所以此递推式是可靠的。
出现以上运⾏结果的主要原因是在构造递推式过程中,考虑误差是否得到控制,即算法是否数值稳定。
2.求⽅程0210=-+x e x的近似根,要求41105-+?<-k k x x ,并⽐较计算量。
(1)在[0,1]上⽤⼆分法;程序:a=0;b=1.0;while abs(b-a)>5*1e-4 c=(b+a)/2;if exp(c)+10*c-2>0 b=c; else a=c; end end c结果:c =0.0903(2)取初值00=x ,并⽤迭代1021x k e x -=+;程序:x=0; a=1;while abs(x-a)>5*1e-4 a=x;x=(2-exp(x))/10; end x结果:x =0.0905(3)加速迭代的结果;程序:x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;y=exp(x)+10*x-2; z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x); b=x; end x结果:x =0.0995(4)取初值00=x ,并⽤⽜顿迭代法;程序:x=0; a=0;b=1;while abs(b-a)>5*1e-4 a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x; end x结果: x =0.0905(5)分析绝对误差。
上机数值计算练习题及答案.docx

习题31、在MATLAB 中,先运行指令A=magic(3), B=[l,2,l;3,4,3;5,6,7], C=reshape(l:6,3,2)生成阵列A 珂,B3X2,C3X2 ,然后根据运行结果回答以下问题:(1)计算A*B,B*A,这两个乘积相同吗?(2)计算A\B, B/A,左除、右除结果相同吗?(3)计算B(:,[1,2]).*C和C.*B(:, [1,2]),这两个乘积相同吗?(4)计算A\A和AAA,这两个计算结果相同吗?(5)计算A\eye(3)和inv(A),这两个计算结果相同吗?(提示:根据对计算结果的目测回答问题)解答如下:运行指令:A=magic(3), B=[l,2,l;3,4,3;5,6,7], C=reshape(l:6,3,2)得到结果:8 1 63 5 74 9 2B =1 2 13 4 35 6 7C =1 42 53 6(1)计算A*B,并得到结果如下:» A*Bans =41 56 5353 68 6741 56 45计算B*A, 并得到结果如下:»B*Aans =18 20 2248 50 5286 98 86从以上计算结果可以得出结论:A*BJ (2)计算A\B ,并得到结果如下:» A\Bans =0.0333 0.1000 0.16110.5333 0.6000 0.74440.0333 0.1000 -0.1722计算B/A, 并得到结果如下:B/Aans =0.0056 0.0889 0.17220.1389 0.2222 0.30560.2333 0.7333 0.2333 与B*A这两个乘积不同。
从以上计算结杲可以得出结论:左除、右除结杲不同。
(3)计算B(:,[1,2]).弋,并得到结果如下:A =» B(:,[1,2]).*C ans =1 8 6 20 15 36计算C.*B(:, [1,2]),并得到结果如下: » CFB(:, [1,2]) ans =1 6 20 15 36从以上计算结果可以得出结论:B(: J1,2]).*C 和C ・*B(:, [1,2])的两个乘积相同。
数值计算方法上机实习题考证

数值计算⽅法上机实习题考证--------------------------------------------------- 此⽂档包含我们计算⽅法的经典算法包含(数值计算⽅法上机实习题)1.设?+=105dx xx I nn ,(1)由递推公式n I I n n 151+-=-,从0I 的⼏个近似值出发,计算20I ;(2)粗糙估计20I ,⽤nI I n n 51511+-=-,计算0I ;(3)分析结果的可靠性及产⽣此现象的原因(重点分析原因)。
(1) 解答:n=0,0.1823)05ln()15ln()5(51515101010=+-+=++=+=+=x d xdx x dx x x I nn这⾥可以⽤for 循环,while 循环,根据个⼈喜好与习惯:for 循环程序: While 循环程序: I=0.1823; I=0.1823; for n=1:20 i=1;I=(-5)*I+1/n; while i<21 End I=(-5)*I+1/i; I i=i+1; fprintf('I20=%f',I) end I = -2.0558e+009 >> II20=-2055816073.851284>> I = -2.0558e+009 (2) 粗略估计I 20: Mathcad 计算结果: for 循环程序: While 循环程序: >> I=0.007998; I=0.007998; >> for n=1:20 n=1;I=(-0.2)*I+1/(5*n); while n<21End I=(-0.2)*I+1/(5*n); >> I n=n+1; I =0.0083 end >> II =0.0083(3) 算法误差分析:计算在递推过程中传递截断误差和舍⼊误差第⼀种算法:(从1——>20)1x x 205x +d 7.998103-?=*000e I I =-*115(5)5()555n n n n n n n n n n e I I I I I I e e e n n------=-=-+--+=-===误差放⼤了5n倍,算法稳定性很不好;第⼆种算法:(从20——>1)*n n ne I I =-***111111111()()555555n n n n n n nn e I I I I I I e n n ---=-=-+--+=-=0111...()55n ne e e ===误差在逐步缩⼩,算法趋近稳定,收敛。
数值计算方法上机题目资料

2. 程序输入、输出用文件形式。 3. 编程语言要求用C, 编程环境TC或VC 4. 程序要求调试通过。 5. 每个方法要求给出一个具体的算例(可选
作业题)来验证。
五、上机报告要求
1.报告内容包括:
每种方法的算法原理及程序框图。 程序使用说明 具体算例及结果
上机调试体会及收获。
2.报告要手写。
六、上机报告及源程序提交时间
1.上机报告在考试当天提交。 2.源程序在考试前提交。
提交格式:文件夹(班级+姓名)
输入文件 程序文件夹 输出文件
不要拷贝其它文件!!! 源程序
六、上机报告及源程序提交时间
源程序提交: 把以上文件压缩后,发送到以下邮箱:
haoyq@
七、考核方式
1.算法手算笔试(80%)+上机内容笔试 (10%)+上机报告(10%)
2.上机内容笔试可能形式:
编一段算法程序 给出一段算法程序,说明算法的名称。 程序填空 程序改错(包括算法和语法的错误)
数值计算方法上机练习
一、上机练习目的
复习和巩固数值计算方法的基本数学模型, 全面掌握运用计算机进行数值计算的具体 过程及相关问题。
利用计算机语言独立编写、调试数值计算 方法程序,培养学生利用计算机和所学理 论知识分析解决实际问题的能力。
二、上机练习任务
• 利用计算机基本C语言编写并调试一系列 数值方法计算通用程序,并能正确计算给 定题目,掌握调试技能。
• 掌握文件使用编程技能,如文件的各类操 作,数据格式设计、通用程序运行过程中 文件输入输出运行方式设计等。
• 写出上机练习报告。
三、数值计算方法上机题目
计算方法上机实习题大作业(实验报告)

计算方法实验报告班级: 学号: 姓名: 成绩:1 舍入误差及稳定性一、实验目的(1)通过上机编程,复习巩固以前所学程序设计语言及上机操作指令;(2)通过上机计算,了解舍入误差所引起的数值不稳定性二、实验内容1、用两种不同的顺序计算1000021n n -=∑,分析其误差的变化 2、已知连分数()101223//(.../)n n a f b b a b a a b =++++,利用下面的算法计算f : 11,i n n i i i a d b d b d ++==+ (1,2,...,0)i n n =-- 0f d = 写一程序,读入011,,,...,,,...,,n n n b b b a a 计算并打印f3、给出一个有效的算法和一个无效的算法计算积分1041nn x y dx x =+⎰ (0,1,...,10)n = 4、设2211N N j S j ==-∑,已知其精确值为1311221N N ⎛⎫-- ⎪+⎝⎭(1)编制按从大到小的顺序计算N S 的程序(2)编制按从小到大的顺序计算N S 的程序(3)按两种顺序分别计算10001000030000,,,S S S 并指出有效位数三、实验步骤、程序设计、实验结果及分析1、用两种不同的顺序计算1000021n n -=∑,分析其误差的变化 (1)实验步骤:分别从1~10000和从10000~1两种顺序进行计算,应包含的头文件有stdio.h 和math.h(2)程序设计:a.顺序计算#include<stdio.h>#include<math.h>void main(){double sum=0;int n=1;while(1){sum=sum+(1/pow(n,2)); if(n%1000==0)printf("sun[%d]=%-30f",n,sum);if(n>=10000)break;n++;}printf("sum[%d]=%f\n",n,sum); }b.逆序计算#include<stdio.h>#include<math.h>void main(){double sum=0;int n=10000;while(1){sum=sum+(1/pow(n,2));if(n%1000==0)printf("sum[%d]=%-30f",n,sum);if(n<=1)break;n--;}printf("sum[%d]=%f\n",n,sum);}(3)实验结果及分析:程序运行结果:a.顺序计算b.逆序计算结果分析:两种不同顺序计算结果是一样的,顺序计算误差从一开始就很小,而逆序计算误差最开始十分大,后来结果正确。
计算方法上机实习题

数值计算方法上机实习题1. 设⎰+=105dx xx I nn , (1) 由递推公式nI I n n 151+-=-,从0=0.1822I , 0=0.1823I 出发,计算20I ; (2) 20=0I ,20=10000I , 用nI I n n 51511+-=-,计算0I ;(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
解:(1)程序如下: clear all clc I=0.1822; %题中的已知数据 for n=1:20; I=(-5)*I+1/n; %由递推公式所得 end fprintf('I20=%f\n',I) M=0.1823; %与I 的计算结果形成对比for i=1:20; M=(-5)*M+1/i; %由递推公式所得 end fprintf('M20=%f\n',M) 输出结果为: I20=-11592559237.912731 M20=-2055816073.851284 (2)程序如下: clear all clc I=0; %赋予I20的初始值 for n=0:19; I=(-1/5)*I+1/(5*(20-n)); %有递推公式得 end fprintf('I0=%f\n',I)M=10000; for i=0:19; M=(-1/5)*M+1/(5*(20-i));%有递推公式得 end fprintf('M0=%f\n',M) 输出结果为: I0=0.182322 M0=0.182322(3)由输出结果可看出第一种算法为不稳定算法,第二中算法为稳定算法。
由于误差*000***21111120115(5)5()555nn n n n n n n n n e I I e I I I I I I e e e n n------=-=-=-+--+=-===第一种算法为正向迭代算法,每计算一步误差增长5倍,虽然所给的初始值很接近,随着n 的增大,误差也越来越大。
计算方法上机实习作业
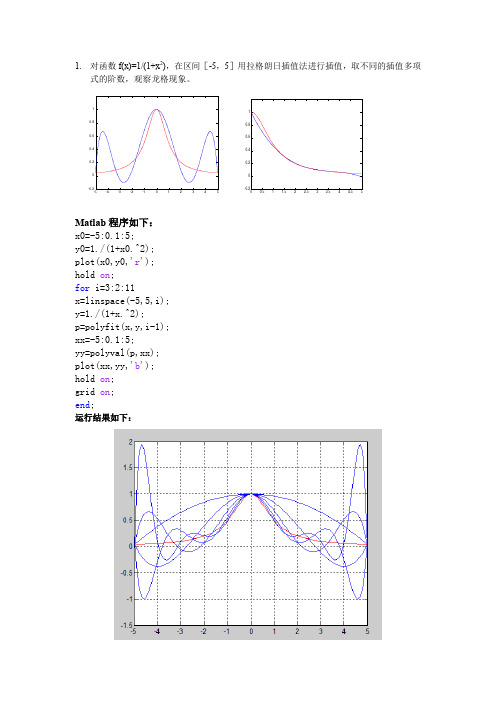
如图所示,在两端出现龙格现象,并且阶数越高龙格现象越明显。 若在区间[0,5]进行插值,是否还存在龙格现象?
Matlab 程序如下: x0=0:0.1:5; y0=1./(1+x0.^2); plot(x0,y0,'r'); hold on; for i=3:2:11 x=linspace(-0,5,i); y=1./(1+x.^2); p=polyfit(x,y,i-1); xx=0:0.1:5; yy=polyval(p,xx); plot(xx,yy,'b'); hold on; grid on; end;
0
1
2
3
4
Matlab 程序如下: clear;clc; x=0:0.1:2.5; y=sin(x); y1=x; y2=x-x.^3/6; y3=x-x.^3/6+x.^5/120; plot(x,y,'b',x,y1,'g',x,y2,'r',x,y3,'k')
输出结果如图:
1.500000000000000 1.414213562374690 1.414213562373095
1.416666666666667 1.414213562373095
2.000000000000000 1.732050810014727 1.732050807568877
1.750000000000000 1.732050807568877
x 2 n 1 ,编写程序实 ( 2n 1)! k 1 现如下功能:对 n=1,2,3,绘制出区间[0,2.5 ]上的近似函数的图形以及 sin x 本身的图
4.由正弦函数的 Tylor 展开式取前 n 项,得 sin x ( 1) n1
数值计算方法第一次上机实习报告

数值计算方法第一次实习报告一、 实习题目。
1. 分别用高斯-赛德尔迭代法、雅克比迭代法、列主元消去法解下列方程组。
⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++=+++ 1.84711.2671x 0.2568x 0.2471x 0.2368x1.74710.2271x 1.2168x 0.2071x 0.1968x 1.64710.1871x 0.1768x 1.1675x 0.1582x 1.54710.1490x 0.1397x 0.1254x 1.1161x4321432143214321 2. 用迭代法求x 5-x-0.2=0的正根,要求精确到小数点后第五位。
二、算法原理。
1、雅可比迭代法基本原理 将矩阵分解为,其中则式可记为,变形可得,可逆时,有于是得到迭代的过程为式中,,即2、高斯-赛德尔迭代法基本原理赛德尔迭代法是对雅可比迭代法的一种改进,雅可比迭代法是在每一步计算的各个分量时均只用到中的分量。
实际上,在计算时,分量都已经计算出来而没有被直接利用,因此可以考虑以来代替计算。
即121311121232222121-1,212121000, ,0000n n n n nn a a a a a a a a D L U aa a a a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦=Ax b ()=D L U x b--()=+Dx L U x b+D ()11220nn a a a ≠ ()11=D +x L U x D b --+=+x Bx f ()11D,=D B L U f b --=+()=11=+=1,2,,n i i ij j j ii j i x b a x i n a ≠⎛⎫ ⎪ ⎪ ⎪⎝⎭∑ ()+1k x ()k x ()+1k i x ()()+1+1-1,,k k i i x x ()()+1+1-1,,k k i i x x ()()1-1,,kki x x矩阵形式为,可得,于是赛德尔迭代法的矩阵形式为式中,。
(完整word版)数值分析上机作业1-1解析

考虑一个高次的代数多项式
(E1-1)
显然该多项式的全部根为l,2,…,20,共计20个,且每个根都是单重的(也称为简单的)。现考虑该多项式方程的一个扰动
(E1-2)
其中 是一个非常小的数。这相当于是对(E1-1)中 的系数作一个小的扰动。我们希望比较(E1-1)和(E1-2)根的差别,从而分析方程(E1-1)的解对扰动的敏感性。
ve=zeros(1,21);
ve(21-Numb)=ess;
root=roots(poly(1:20)+ve);
x0=real(root); y0=imag(root);
plot(x0',y0','*');
disp(['对扰动项 ',num2str(Numb),'加扰动',num2str(ess),'得到的全部根为:']);
ess分别为1e-6,1e-8.1e-10,1e-12的图像如下:
从实验的图形中可以看出,当ess充分小时,方程E.1.1和方程E.1.2的解相差很小,当ess逐渐增大时,方程的解就出现了病态解,这些解都呈现复共轭性质。
(2)将扰动项加到x18上后,ess=1e-009时方程的解都比较准确,没有出现复共轭现象。ess=1e-008时误差与x19(ess=1e-009)时相当,即扰动加到x18上比加到x19小一个数量级。对x8的扰动ess=1000时没有出现复共轭,误差很小;对x的扰动ess=10e10时没有出现复共轭,误差很小。因此,扰动作用到xn上时,n越小,扰动引起的误差越小。
if((Numb>20)|(Numb<0))errordlg('请输入正确的扰动项:[0 20]之间的整数!');return;end
数值分析上机实习题

数值分析上机实习题第2章插值法1. 已知函数在下列各点的值为试⽤四次⽜顿插值多项式)(x p 4及三次样条韩式)(S x (⾃然边界条件)对数据进⾏插值。
⽤图给出(){}10,11,1,0,08.02.0,,x i =+=i x y i i ,)(x p 4及)(x S Python 代码import numpy as npimport matplotlib.pyplot as pltfrom matplotlib.font_manager import FontPropertiesfont_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc",size=12) #求⽜顿n 次均差 def qiujuncha(x,f,n): for i in range(1,n): for j in range(4,i-1,-1):f[j]= (f[j] - f[j-1])/(x[j]-x[j-i]) #根据⽜顿多项式求值 def niudun(x,f,x1): sum = f[0]; tmp = 1;for i in range(1,5): tmp *= (x1-x[i-1]) sum = sum + f[i]*tmp return sum#⽜顿插值画图 def drawPic(x,f):x1 = np.linspace(0.2, 1, 100) plt.plot(x1, niudun(x,f,x1))plt.title(u"⽜顿四次插值",fontproperties=font_set) plt.xlabel(u"x 轴",fontproperties=font_set) plt.ylabel(u"y 轴", fontproperties=font_set) plt.show() def qiu_h(x,h): n = len(x) -1 for i in range(n): print(i)h[i] = x[i+1]-x[i]#⾃然边界条件下的三次样条插值求Mdef qiu_m(h,f,o,u,d):n = len(h)o[0] = 0u[n] = 0d[n] = d[0] = 0a = []for i in range(1,n):u[i] = h[i-1]/(h[i-1]+h[i])for i in range(1,n):o[i] = h[i]/(h[i-1]+h[i])for i in range(1,n-1):d[i] = 6*(f[i+1]-f[i])/(h[i-1]+h[i])t = [0 for i in range(5)]t[0] =2t[1] = o[0]a.append(t)for i in range(1,n):t = [0 for i in range(5)]t[i - 1] = u [i + 1]t[i] = 2t[i + 1] = o [i + 1]a.append(t)t = [0 for i in range(5)]t[n - 1] = u[n]t[n] = 2a.append(t)tmp = np.linalg.solve(np.array(a),np.array(d))m = []for i in range(5):m.append(tmp[i])return m#根据三次条插值函数求值def yangtiao(x1,m,x,y,h,j):returnm[j]*(x[j+1]-x1)**3/(6*h[j])+m[j+1]*(x1-x[j])**3/(6*h[j])+(y[j]-m[j]*h[j]**2/6)*(x[j+1]-x1)/h[j] +(y[j+1]-m[j+1]*h[j]**2/6)*(x1-x[j])/h[j] def main():x = [0.2, 0.4, 0.6, 0.8, 1.0]y = [0.98, 0.92, 0.81, 0.64, 0.38]f = y[:]f1 = y[:]h = [0.2,0.2,0.2,0.2]u = [0 for n in range(5)]d = [0 for n in range(5)]o = [0 for n in range(5)] qiujuncha(x,f,4) qiujuncha(x,f1,2)m = qiu_m(h,f1,o,u,d) x1 = np.linspace(0.2, 0.4, 10)p1= plt.plot(x1, yangtiao(x1,m,x,y,h,0),color='red') x1 = np.linspace(0.4, 0.6, 10)plt.plot(x1, yangtiao(x1, m, x, y, h, 1),color='red') x1 = np.linspace(0.6, 0.8, 10)plt.plot(x1, yangtiao(x1, m, x, y, h, 2),color='red') x1 = np.linspace(0.8, 1.0, 10)plt.plot(x1, yangtiao(x1, m, x, y, h, 3),color='red') x1 = np.linspace(0.2, 1.0, 40)p2 = plt.plot(x1,niudun(x,f,x1),color='green') plt.xlabel(u"x 轴", fontproperties=font_set) plt.ylabel(u"y 轴",fontproperties=font_set) plt.title("三次样条插值和⽜顿插值")plt.legend(labels=[u'三次样条插值',u'⽜顿插值'],prop=font_set,loc="best") plt.show() main()实验结果运⾏结果可得插值函数图(如图1-1),4次⽜顿插值函数)(x p 4和三次样条插值函数)(x S 如下:)6.0(*)4.0(*)2.0(625.0)4.0(*)2.0(*3.098.0)(4-------=x x x x x x x P 98.0)8.0(*)6.0(*)4.0(*)2.0(*20833.0+-----x x x x]4.0,2.0[),2.0(467.4)4.0(9.4)2.0(167.1)(S 3∈-+-+-=x x x x x]6.0,4.0[),4.0(113.4)6.0(6467.4)4.0(575.1)6.0(167.1)(S 33∈-+-+----=x x x x x x ]8.0,6.0[),6.0(2.3)8.0(113.4)6.0(575.1)(S 3∈-+-+--=x x x x x]0.1,8.0[),8.0(9.1)0.1(2.3)(S ∈-+-=x x x x图1-1三次样条插值和⽜顿插值图2.在区间[-1,1]上分别取n = 10,20⽤两组等距节点对龙格函数做多项式插值三次样条插值,对每个n值画出插值函数及图形。
数值计算方法上机实习题

数值计算方法上机实习题(总13页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--数值计算方法上机实习题1.设⎰+=105dx xx I nn , (1) 由递推公式nI I n n 151+-=-,从I 0=0.1824, 0=0.1823I 出发,计算20I ; (2) 20=0I ,20=10000I , 用nI I n n 515111+-=--,计算0I ;(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
答:第一个算法可得出e 0=|I 0−I 0∗| e n =|I n −I n ∗|=5n |e 0|易知第一个算法每一步计算都把误差放大了5倍,n 次计算后更是放大了5n 倍,可靠性低。
第二个算法可得出e n =|I n −I n ∗| e 0=(1)n|e n |可以看出第二个算法每一步计算就把误差缩小5倍,n 次后缩小了5n 倍,可靠性高。
2.求方程0210=-+x e x 的近似根,要求41105-+⨯<-k k x x ,并比较计算量。
(1) 在[0,1]上用二分法; (1) [0,1]上的二分法二分法子程序:function [root,n]=EFF3(f,x1,x2) %第二题(1)二分法f1=subs(f,symvar(f),x1);%函数在x=x1的值 f2=subs(f,symvar(f),x2);%x=x2 n=0;%步数er=5*10^-4;%误差 if(f1==0) root=x1; return; elseif(f2==0) root=x2; return;elseif(f1*f2>0)disp('两端点函数值乘积大于0!'); return; elsewhile(abs(x1-x2)>er)%循环 x3=(x1+x2)/2;f3=subs(f,symvar(f),x3); n=n+1; if(f3==0) root=x3; break;elseif(f1*f3>0) x1=x3; elsex2=x3; end endroot=(x1+x2)/2;%while 循环少一步需加上 end计算根与步数程序:fplot(@(x) exp(x)+10*x-2,[0,1]); grid on; syms x;f=exp(x)+10*x-2; [root,n]=EFF3(f,0,1);fprintf('root=% ,n=%d \n',root,n);计算结果显示:root= ,n=11(2) 取初值00=x ,并用迭代1021x k e x -=+;(2) 初值x 0=0迭代 迭代法子程序:function [root,n]=DDF(g,x0,err,max) (接下页) %root 根,n+1步数,g 函数,x0初值,err 误差,max 最大迭代次数 X(1)=x0; for n=2:maxX(n)=subs(g,symvar(g),X(n-1)); c=abs(X(n)-X(n-1)); root=X(n); if(c<err)计算根与步数程序:syms x;f=(2-exp(x))/10; (接下页) x0=0;err=5*10^(-4); max=100;[root,n]=DDF(f,x0,err,max); fprintf('root=% ,n=%d \n',root,n);计算结果显示: root= ,n=4(3) 加速迭代的结果;(4) 取初值00 x ,并用牛顿迭代法;(5) 分析绝对误差。
数值计算方法上机实习题答案.doc

1.设I n 1 x ndx ,0 5 x( 1)由递推公式 I n 5I n 11,从 I 0的几个近似值出发,计算I 20;n解:易得: I 0 ln6-ln5=0.1823, 程序为:I=0.182;for n=1:20I=(-5)*I+1/n;endI输出结果为: I 20= -3.0666e+010( 2)粗糙估计 I 20,用 I n 1 1I n 1 1 ,计算 I 0;5 5n0.0079 1 x 20 1 x 200.0095因为dx I 20dx 6 5所以取 I 20 1(0.0079 0.0095) 0.0087 2程序为: I=0.0087;for n=1:20I=(-1/5)*I+1/(5*n);endII 0= 0.0083( 3)分析结果的可靠性及产生此现象的原因(重点分析原因 )。
首先分析两种递推式的误差;设第一递推式中开始时的误差为E0 I 0 I 0,递推过程的舍入误差不计。
并记 E n I n I n,则有 E n 5E n 1 ( 5) n E0。
因为 E20( 5) 20 E0 I 20,所此递推式不可靠。
而在第二种递推式中E0 1E1 (1)n E n,误差在缩小,5 5所以此递推式是可靠的。
出现以上运行结果的主要原因是在构造递推式过程中,考虑误差是否得到控制,即算法是否数值稳定。
2.求方程e x10x 2 0 的近似根,要求x k 1x k 5 10 4,并比较计算量。
(1)在 [0, 1]上用二分法;程序: a=0;b=1.0;while abs(b-a)>5*1e-4c=(b+a)/2;if exp(c)+10*c-2>0b=c;else a=c;endendc结果: c =0.0903( 2)取初值x0 0,并用迭代 x k 1 2 e x ;10程序: x=0;a=1;while abs(x-a)>5*1e-4a=x;x=(2-exp(x))/10;endx结果: x =0.0905(3)加速迭代的结果;程序: x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;y=exp(x)+10*x-2;z=exp(y)+10*y-2;x=x-(y-x)^2/(z-2*y+x);b=x;endx结果: x =0.0995( 4)取初值x00 ,并用牛顿迭代法;程序: x=0;a=0;b=1;while abs(b-a)>5*1e-4a=x;x=x-(exp(x)+10*x-2)/(exp(x)+10); b=x;end x 结果: x =0.0905( 5) 分析绝对误差。
数值分析计算实习题目一
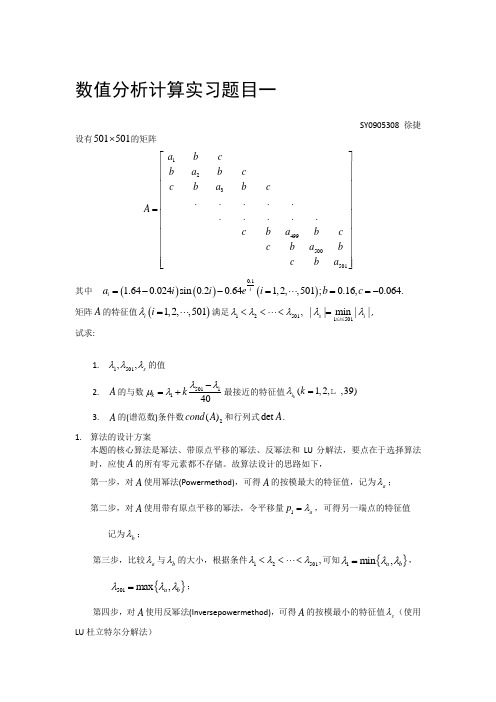
数值分析计算实习题目一SY0905308 徐捷设有501501⨯的矩阵123499500501..........a b c b a b c c b a b c A cb a bc cb a b cba ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦其中()()()0.11.640.024sin 0.20.641,2,,501;0.16,0.064.ii a i i ei b c =--=⋅⋅⋅==-矩阵A 的特征值()1,2,,501i i λ=⋅⋅⋅满足12501,λλλ<<⋅⋅⋅<1501||min ||s i i λλ≤≤=, 试求:1.1501,,s λλλ的值2. A 的与数5011140k kλλμλ-=+最接近的特征值(1,2,,39)k i k λ=3. A 的(谱范数)条件数2()cond A 和行列式det A .1. 算法的设计方案本题的核心算法是幂法、带原点平移的幂法、反幂法和LU 分解法,要点在于选择算法时,应使A 的所有零元素都不存储。
故算法设计的思路如下,第一步,对A 使用幂法(Powermethod),可得A 的按模最大的特征值,记为a λ; 第二步,对A 使用带有原点平移的幂法,令平移量1a p λ=,可得另一端点的特征值记为b λ;第三步,比较a λ与b λ的大小,根据条件12501,λλλ<<⋅⋅⋅<可知{}1min ,a b λλλ=,{}501max ,a b λλλ=;第四步,对A 使用反幂法(Inversepowermethod),可得A 的按模最小的特征值s λ(使用LU 杜立特尔分解法)第五步,根据5011140k kλλμλ-=+计算出k μ,然后利用带有原点平移的反幂法求得k i λ,其中平移量k k p μ=,反幂法运算39次,可得2239,,,i i i λλλ ;第六步, 根据定义,非奇异的实对称矩阵A 的谱范数条件数()12||ncond A λλ=,其中1n λλ和分别是矩阵A 的模为最大和模为最小的特征值,对于本题,则有{}15012|max ||,|||()||s cond A λλλ=;第七步,由LU 分解可知,A LU =,可得5011det det()det()det()(1501)n iii A LU L U u i ====⋅=≤≤∏。
数值计算方法上机实习题NEW

数值计算方法上机实习题1. 设,(1) 由递推公式,从 , 出发,计算 ; 程序如下:function I=myhs(I0,n) if n>=1I=myhs(I0,n-1)*(-5)+1/n; elseif n==0 I=I0; end命令行窗口输入: I0=0.1822;I1=myhs(I0,20); I0=0.1823;I2=myhs(I0,20);运行结果:当I0=0.1822时,I20=-1.1593e+10。
当I0=0.1823时,I20= -2.0558e+9。
(2) ,20=10000I , 用,计算0I ; 程序如下:function I=myhs2(I20,n) if (n<20)I=myhs2(I20,n+1)*(-1)/5+1/(5*(n+1)); elseif n==20 I=I20; end命令行窗口输入:I20=0;I1=myhs2(I20,20); I20=10000;I2=myhs2(I20,20);运行结果:当I 20=0时,I 0=0.182321556793955。
当I 20=10000时,I 0= 0.182321556898812。
(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
根据上式,假设I n 的真值为I*,误差为e n ,即e=I*-I n 。
综合递推式,有e n =-5*e n-1,这意味着哪怕开始只有一点点误差,只要n 足够大,按照这种计算一步误差增长5倍的方式,所得的结果总是不可信的,因此整个算法是不稳定的。
根据上式,假设I n 的真值为I*,误差为e n ,即e=I*-I n 。
综合递推式,有e n-1. =(-1/5)*e n ,按照这种计算误差会以每步缩小到1/5的方式进行,根据(2)得到的结果而言,该算法是相对稳定的。
2. 求方程0210=-+x e x 的近似根,要求41105-+⨯<-k k x x ,并比较计算量。
数值方法计算实习题1

信计091 龚立丽200900901004数值方法计算实习题要求:1、用Matlab语言或你熟悉的其他算法语言编写程序,使之尽可能具有通用性;2、根据上机计算实践,对所使用的数值方法的特点、性质、有效性、误差和收敛性等方面进行必要的讨论和分析;3、完成计算后写出实验报告,内容包括:课题名称、解决的问题、采用的数值方法、算法程序、数值结果、对实验结果的讨论和分析等;4、特别说明:严禁抄袭,否则一经发现,所有雷同实验报告最多评为及格。
一、下表给出了飞行中鸭子的上部形状的节点数据,试用三次样条插值函数(自然边界条件)和20次Lagrange插值多项式对数据进行插值。
用图示出给定的数据,以及()s x和20()L x。
x0.9 1.3 1.9 2.1 2.6 3.0 3.9 4.4 4.7 5.0 6.0y 1.3 1.5 1.85 2.1 2.6 2.7 2.4 2.15 2.05 2.1 2.25x7.0 8.0 9.2 10.5 11.3 11.6 12 12.6 13.0 13.3y 2.3 2.25 1.95 1.4 0.9 0.7 0.6 0.5 0.4 0.25解:>> x=[0.9 1.3 1.9 2.1 2.6 3.0 3.9 4.4 4.7 5.0 6.0 7.0 8.0 9.2 10.5 11.3 11.6 12 12.6 13.0 13.3];>> y=[1.3 1.5 1.85 2.1 2.6 2.7 2.4 2.15 2.05 2.1 2.25 2.3 2.25 1.95 1.4 0.9 0.7 0.6 0.5 0.4 0.25];(1)三次样条插值法在MATLAB中编写m文件function[f,f0]=scyt(x,y,y2_1,y2_N,x0)%y2_1和y2_N分别为自然边界条件%插值点x的坐标:x0syms t;f=0.0;f0=0.0;if(length(x)==length(y))n=length(x);elsedisp('x和y的维数不相等');return;endfor i=1:nif(x(i)<=x0)&&(x(i+1)>=x0)index=i;break;endendA=diag(2*ones(1,n));A(1,2)=1;A(n,n-1)=1;u=zeros(n-2,1);lamda=zeros(n-1,1);c=zeros(n,1);for i=2:n-1u(i-1)=(x(i)-x(i-1))/(x(i+1)-x(i-1));lamda(i)=(x(i+1)-x(i))/(x(i+1)-x(i-1));c(i)=3*lamda(i)*(y(i)-y(i-1))/(x(i)-x(i-1))+3*u(i-1)*(y(i+1)-y(i))/(x(i+1)-x(i) );A(i,i+1)=u(i-1);A(i,i-1)=lamda(i);endc(1)=3*(y(2)-y(1))/(x(2)-x(1))-(x(2)-x(1))*y2_1/2;c(n)=3*(y(n)-y(n-1))/(x(n)-x(n-1))-(x(n)-x(n-1))*y2_N/2;m=zgf(A,c);h=x(index+1)-x(index);f=y(index)*(2*(t-x(index))+h)*(t-x(index+1))^2/h/h/h+y(index+1)*(2*(x(index+1)-t)+h)*(t-x(index))^2/h/h/h+m(index)*(t-x(index))*(x(index+1)-t)^2/h/h-m(index+1 )*(x(index+1)-t)*(t-x(index))^2/h/h;f0=subs(f,'t',x0);其中的zgf函数为追赶法,其程序为function x=zgf(A,b)n = rank(A);for(i=1:n)if(A(i,i)==0)disp('Error: 对角有元素为0!');return;endend;d = ones(n,1);a = ones(n-1,1);c = ones(n-1);for(i=1:n-1)a(i,1)=A(i+1,i);c(i,1)=A(i,i+1);d(i,1)=A(i,i);endd(n,1) = A(n,n);for(i=2:n)d(i,1)=d(i,1) - (a(i-1,1)/d(i-1,1))*c(i-1,1);b(i,1)=b(i,1) - (a(i-1,1)/d(i-1,1))*b(i-1,1);endx(n,1) = b(n,1)/d(n,1);for(i=(n-1):-1:1)x(i,1) = (b(i,1)-c(i,1)*x(i+1,1))/d(i,1); end在MATLAB 中输入指令 >> [f,f0]=scyt(x,y,0,0) f =1000/729*(27/5*t-1377/100)*(t-39/10)^2+1000/729*(522/25-24/5*t)*(t-3)^2+100/81*(-6396162352027119/288230376151711744*t+19188487056081357/288230376151711744)*(39/10-t)^2-100/81*(-176836856862157557/90071992547409920+4534278381080963/9007199254740992*t)*(t-3)^2 f0 =2.5851 得三次样条插值函数 S(x)=1000/729*(27/5*x-1377/100)*(x-39/10)^2+1000/729*(522/25-24/5*x)*(x-3)^2+100/81*(-6396162352027119/288230376151711744*x+19188487056081357/288230376151711744)*(39/10-x)^2-100/81*(-176836856862157557/90071992547409920+4534278381080963/9007199254740992*x)*(x-3)^2>> xi=0.9:0.01:13.3;yi=interp1(x,y,xi,'spline'); >> title('试验一--三次样条插值图示')024********0.511.522.53试验一--三次样条插值图示(2)用拉格朗日法插值 %定义Lagrange 程序function f=Language(x,y,x0) syms t ;if (length(x)==length(y)) n=length(x);elsedisp('x 和y 的维数不相等'); return ; end f=0.0; for (i=1:n) l=y(i); for (j=1:i-1)l=l*(t-x(j))/(x(i)-x(j)); end ;for (j=i+1:n)l=l*(t-x(j))/(x(i)-x(j)); end ; f=f+l; simplify(f); if (i==n)if (nargin==3) f=subs(f,'t',x0); elsef=collect(f); f=vpa(f,6); end end end>> Language(x,y) ans =52462.6*t+189995.*t^3-189851.*t^4+136778.*t^5-11.3161*t^12-.277283e-6*t^18+1.18284*t^13-73866.6*t^6+.111076e-4*t^17-.976904e-1*t^14+.427949e-8*t^19-.307453e-10*t^20+30677.6*t^7+2564.20*t^9-9968.98*t^8+.628590e-2*t^15-525.813*t^10-9652.78-.308159e-3*t^16+86.2514*t^11-128683.*t^2二、已知Wilson 矩阵1078775658610975910A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,且向量32233331b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,则方程组A x b =有准确解[]1111Tx =。
数值计算方法上机实验题

数值计算方法上机实验实验内容:1.要求:分别用复化梯形法,复化Simpson 法和 Romberg 公式计算.2.给定积分dx e x⎰31和dx x ⎰311 ,分别用下列方法计算积分值要求准确到510- ,并比较分析计算时间. 1)变步长梯形法; 2)变步长 Simpson 法; 3) Romberg 方法.算法描述:1、复合梯形法:⎰=tdt t a t V 0)()( ))()(2)((211∑-=++=n k k n b f x f a f hT输入 被积函数数据点t,a. 输出 积分值.n T复合Simpson 法:⎰=tdt t a t V 0)()( ))()(2)(4)((6101121∑∑---=++++=n k n k k k n b f x f x f a f hS输入 被积函数f(x),积分区间[a,b]和n 输出 复合Simpson 积分值n S步1 .);()(;a x b f a f S nab h n ⇐-⇐-⇐ 步2 对n k ,,2,1 =执行).(2;2);(4;2x f S S hx x x f S S h x x n n n n +⇐+⇐+⇐+⇐步3 n n S hS ⨯⇐6步4 输出n SRomberg 积分法:根据已知数据对其进行多项式拟合得出p(x);f(x)⇐p(x); 输入 被积函数f(x),积分区间端点a,b,允许误差ε 输出 Romberg 积分值n R 2 步1 .0;0;0;0));()((2;1111⇐===+⇐-⇐k R C S b f a f hT a b h 步2 反复执行步3→步9. 步3 .2;0h a x S +⇐⇐ 步4 反复执行步5→步6. 步5 ;);(h x x x f S S +⇐+⇐步6 若x ≥b,则退出本层循环. 步7 执行.6316364;1511516;3134;2212212212212C C R S S C T T S S h T T -⇐-⇐-⇐+⇐步8 执行.1;;;;;2;2121212112+⇐⇐⇐⇐⇐⇐-⇐k k R R C C S S T T hh R R e 步9 若e ≤ε且k ≥5,则退出循环. 步10 .22R R n ⇐ 步11 输出.2n R2、变步长梯形算法:功能 求积分⎰ba)(dx x f ,允许误差为ε。
数值计算方法上机实习题考证

---------------------------------------------------此文档包含我们计算方法的经典算法包含(数值计算方法上机实习题)1. 设⎰+=105dx x x I nn , (1) 由递推公式nI I n n 151+-=-,从0I 的几个近似值出发,计算20I ; (2) 粗糙估计20I ,用n I I n n 51511+-=-,计算0I ; (3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
(1) 解答:n=0,0.1823)05ln()15ln()5(51515101010=+-+=++=+=+=⎰⎰⎰x d x dx x dx x x I nn 这里可以用for 循环,while 循环,根据个人喜好与习惯:for 循环程序: While 循环程序:I=0.1823; I=0.1823;for n=1:20 i=1;I=(-5)*I+1/n; while i<21End I=(-5)*I+1/i;I i=i+1;fprintf('I20=%f',I) endI = -2.0558e+009 >> II20=-2055816073.851284>> I = -2.0558e+009(2) 粗略估计I 20: Mathcad 计算结果: for 循环程序: While 循环程序: >> I=0.007998; I=0.007998;>> for n=1:20 n=1;I=(-0.2)*I+1/(5*n); while n<21End I=(-0.2)*I+1/(5*n);>> I n=n+1;I =0.0083 end>> II =0.0083(3) 算法误差分析:计算在递推过程中传递截断误差和舍入误差第一种算法:(从1——>20)01x x 205x +⎛⎜⎜⎜⎠d 7.998103-⨯=*000e I I =-***21111120115(5)5()555n n n n n n n n n n e I I I I I I e e e n n------=-=-+--+=-===误差放大了5n 倍,算法稳定性很不好;第二种算法:(从20——>1)*n n ne I I =- ***111111111()()555555n n n n n n n n e I I I I I I e n n ---=-=-+--+=-=0111...()55n n e e e === 误差在逐步缩小,算法趋近稳定,收敛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值计算方法上机实习题
1. 设⎰+=1
05dx x
x I n
n , (1) 由递推公式n
I
I
n n 1
51+
-=-,从, 0=0.1823I 出发,计算20I ;
(2) 20=0I ,20=10000I , 用n
I I n n 51
5111+-
=--,计算0I ; (1)由I 0计算I 20
递推子程序:
function f=fib(n,i) if n>=1
f=fib(n-1,i)*(-5)+(1/(n)); elseif n==0 f=i; end
计算和显示程序:
I=0.1824; I1=0.1823; fib1=fib(20,I); fib2=fib(20,I1);
fprintf('I_0=0.1824时,I_20=%d\n',fib1); fprintf('I_0=0.1823时,I_20=%d\n',fib2);
计算结果显示:
I_0=0.1824时,I_20=7.480927e+09 I_0=0.1823时,I_20=-2.055816e+09
(2)由I 20计算I 0
程序:
n=21; i1=0; i2=10000; f1=i1; f2=i2; while n~=0;
f1=f1*(-1/5)+(1/(5*n)); f2=f2*(-1/5)+(1/(5*n)); n=n-1; end
fprintf('I_20=0 时,I_0=%4.8f\n',f1); fprintf('I_20=10000时,I_0=%4.8f\n',f2);
计算结果显示:
I_20=0 时,I_0=0.18232156 I_20=10000时,I_0=0.18232156
(3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。
答:第一个算法可得出
易知第一个算法每一步计算都把误差放大了5倍,n 次计算后更是放大了5n
倍,可靠性低。
第二个算法可得出
可以看出第二个算法每一步计算就把误差缩小5倍,n 次后缩小了5n
倍,可靠性高。
2. 求方程0210=-+x e x
的近似根,要求41105-+⨯<-k k x x ,并比较计算量。
(1) 在[0,1]上用二分法; (1) [0,1]上的二分法
二分法子程序:
function [root,n]=EFF3(f,x1,x2) %第二题(1)二分法
f1=subs(f,symvar(f),x1);%函数在x=x1的值 f2=subs(f,symvar(f),x2);%x=x2 n=0;%步数 er=5*10^-4;%误差 if(f1==0) root=x1; return; elseif(f2==0) root=x2; return; elseif(f1*f2>0)
disp('两端点函数值乘积大于0!'); return; else
while(abs(x1-x2)>er)%循环 x3=(x1+x2)/2;
f3=subs(f,symvar(f),x3); n=n+1; if(f3==0) root=x3; break; elseif(f1*f3>0) x1=x3; else x2=x3; end end
root=(x1+x2)/2;%while 循环少一步需加上 end
计算根与步数程序:
fplot(@(x) exp(x)+10*x-2,[0,1]); grid on; syms x;
f=exp(x)+10*x-2; [root,n]=EFF3(f,0,1);
fprintf('root=%6.8f ,n=%d \n',root,n);
计算结果显示:
root=0.09057617 ,n=11
(2) 取初值00=x ,并用迭代10
21
x k e x -=+;
(4) 取初值00 x ,并用牛顿迭代法;
(5) 分析绝对误差。
答:可以看到,在同一精度下,二分法运算了11次,题设迭代算式下运算了4次,加速迭代下运算了2次,牛顿迭代下运算了2次。
因不动点迭代法和二分法都是线性收敛的,但二分法压缩系数比题设迭代方法大,收敛速度较慢。
加速迭代速度是超线性收敛,牛顿法是二阶,收敛速度快。
3.钢水包使用次数多以后,钢包的容积增大,数据如下:
试从中找出使用次数和容积之间的关系,计算均方差。
(用ax b
y c x
+=
+拟合)
xlabel('次数
','FontSize',14,'FontWeight','Bold'); ylabel('容积
','FontSize',14,'FontWeight','Bold'); set(gxt,'LineWidth',1.5);
grid on;
%计算均方差
for i=1:15
y2(i)=(f(1).*x(i)+f(2))./(f(3)+x(i)); (接下页)
end
j=0;
for i=1:15
j=j+(y(i)-y2(i))^2;
end
jfc=sqrt(j/15);
fprintf('拟合出的方程
为:(x+%4.4f)y=%4.4fx+%4.4f \n均方差为:%4.8f \n',f(3),f(1),f(2),jfc);指标选择,因题设方程为非线性的,要转化为线性方程故需提指标为:
其驻点方程为:
计算结果显示:
4.设⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫
⎝⎛----------------=410100141010014101101410010141001014A ,⎪⎪⎪⎪⎪⎪
⎪⎪⎭
⎫
⎝⎛--=625250b ,b x =A
分析下列迭代法的收敛性,并求42
110-+≤-k k x x 的近似解及相应的迭代次数。
(1) Jacobi 迭代
Jacobi 迭代子程序:
function [x,k]=Jacobifl2(A,b,x0,eps,max1) %jacobi 按矩阵的分量算法
%x0初值,eps 误差,max1最大迭代次数 n=length(x0);
Jacobi 迭代计算程序:
A=[4 -1 0 -1 0 0;-1 4 -1 0 -1 0;0 -1 4 -1 0 -1; -1 0 -1 4 -1 0; 0 -1 0 -1 4 -1;0 0 -1 0 -1 4;];
b=[0 5 -2 5 -2 6]'; x0=[0 0 0 0 0 0]';
(3)SOR迭代(取
,找到迭代步数最少的)。
5.用逆幂迭代法求⎪⎪⎪⎭
⎫ ⎝⎛=111123136A 最接近于11的特征值和特征向量,准确到3
10-。
6.用经典R-K 方法求解初值问题
(1)⎩⎨⎧-+-='++-='x x y y y x y y y sin 2cos 22sin 22212211,]10,0[∈x , ⎩⎨⎧==3)0(2
)0(2
1y y ;
(2)⎩⎨⎧-+-='++-='x x y y y x y y y sin 999cos 999999998sin 22212
211,]10,0[∈x , ⎩⎨⎧==3)0(2
)0(21y y。
和精确解⎩⎨⎧+=+=--x e x y x
e x y x
x cos 2)(sin 2)(2
1比较,进行误差分析得到结论,图形显示精确解和数值解。
计算结果显示:
(1)Ode 23的题1
(2)Ode 3的题2
(3)Ode 45的题1
7.用有限差分法求解边值问题(h=0.1),并图形显示。
⎩⎨
⎧==-=+-''1
)1()1(0
)1(2y y y x y .
b=b';% n-1
u(1)=b(1)/B(1);
v(1)=C(1)/B(1);
for k=2:n-2;
u(k)=(b(k)-u(k-1)*C(k-1))/(B(k)-v(k-1)*C(k-1)); v(k)=C(k)/(B(k)-v(k-1)*C(k-1));
end
u(n-1)=(b(n-1)-u(n-2)*C(n-2))/(B(n-1)-v(n-2)*C(n-2)) ;
V(n-1)=u(n-1);
for k=n-2:-1:1
V(k)=u(k)-v(k)*V(k+1);
end
y=[1,V,1];总结:
对比两个步长下,求边值问题,步长小,越精确。
(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
