线性规划求最优解
求线性规划问题的最优整数解的方法

求线性规划问题的最优整数解的方法作者:陈树礼来源:《中学教学参考·理科版》2010年第01期线性规划是新教材新增内容,在近几年高考中都以较易题目出现,要学好本节内容,应注意以下三点.一、判定最优解求线性目标函数z=ax+by(a≠0、b≠0)在线性约束条件下的最优解问题,可转化为求直线y=-abx+zb在y轴上的截距的最大值和最小值.易知在b>0时,当zb最大时,z取得最大值,当zb最小时,z取得最小值;在b二、求出最优解依据边界直线的斜率(或倾斜角)计算出最优解.三、修正最优解,得到最优整数解现改编人教版高二(上例3的问题,以求达到抛砖引玉的目的.【例】某工厂生产甲、乙两种产品.已恬生产甲种产品1t需耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1t需耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品的利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t、B种矿石不超过200t、煤不超过360t.求:(1)甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(2)若甲种产品每吨利润600元,乙产品每吨利润200元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(3)若甲种产品每吨利润400元,乙产品每吨利润200元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(4)若甲种产品每吨利润200元,乙产品每吨利润600元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?(5)若甲种产品每吨利润1000元,乙产品每吨利润800元.甲、乙两种产品各生产多少吨(精确到1吨)才能使利润最大?解:(1)设生产甲、乙两种产品分别为x吨,y吨.利润为z元.则10x+4y≤300,5x+4y≤200,4x+9y≤360,x≥0,y≥0,z=600x+1000y.作出以上不等式组表示的平面区域,即可行域.作直线:600x+1000y=0,即直线:3x+5y=0,则z=200(3x+5y).设u=3x+5y,则当u最大时,z最大.易知直线NQ、MN、PM的斜率分别为-52,-54,-49,直线l的斜率为-53.平移直线∵M点为最优解点.由方程组5x+4y=200,4x+9y=360得M点的坐标为(36029,100029).∵x,y都是正整数,∴u=3x+5y=608029也应为正整数.∴u=3x+5y≤209.于是整点(11,35)为所求.当生产甲产品11吨,乙产品35吨时,能使利润总额最大.(2)此时目标函数为z=600x+200y.作直线平移直线∵直线经过点Q(30,0)时,z取得最大值.即只生产甲产品30吨时,获得利润最大.(3)此时目标函数为z=400x+200y.作直线平移直线∵-类似(1)可求解.(4)此时目标函数为z=200x+600y.作直线平移直线∵--49.∴当直线经过点P(0,40)时,5x+4y=0,即只生产乙产品40吨时,获得利润最大.(5)此时目标函数为z=1000x+800y.作直线平移直线∵-∴当直线与直线5x+4y=0重合时,z取得最大值.∴当点位于线段MN上任意一点时,都能使z取得最大值.总之,在本部分内容的学习中,要做到“一定、二算、三修正”.(责任编辑金铃)。
线性规划的定义及解题方法

线性规划的定义及解题方法线性规划是一种数学建模技术,旨在解决在约束条件下,寻求最优解的问题。
它的实际应用十分广泛,例如管理学、经济学、物流学等领域。
线性规划可以分为单目标和多目标两种,但其中比较常见的是单目标线性规划。
本文将从线性规划的定义、模型建立、求解方法等方面阐述其原理与应用。
一、线性规划的定义线性规划的定义是:在有限约束条件下,目标函数为线性的最优化问题。
它通过数学模型的建立,将涉及到的变量、约束条件与目标函数转化为线性等式或不等式的形式,从而寻找最优解。
通常,线性规划的目标是最大化或最小化某个变量,可以用以下的形式去表示:$$Z=C_1X_1+C_2X_2+……+C_nX_n $$其中,$Z$为目标函数值,$X_1, X_2,……,X_n$为待求变量,$C_1, C_2,……,C_n$为相应的系数。
在线性规划中,会涉及到许多变量,这些变量需要受到一些限制。
这些限制可以用不等式或等式来表示,这些方程式被称为约束条件。
例如:$$A_1X_1+A_2X_2+……+A_nX_n≤B$$$$X_i≥0, i=1,2,……, n $$这两个方程就代表了一些约束条件,例如目标函数系数的和不能超过某个值,若$X_i$为生产的产品数量,则需保证产量不能小于零等。
这些约束条件用于限制变量的取值范围,而目标函数则用于求解最优解。
二、线性规划的模型建立在建立线性规划模型时,需要考虑几个要素:1. 决策变量:它是模型求解的关键。
决策变量是指在模型中未知的数量,也就是需要我们寻找最优解的那些变量。
2. 目标函数:确定目标函数,既要知道最大化还是最小化,还要知道哪些变量是影响目标函数的。
3. 约束条件:约束条件通常是一组等式或不等式,代表问题的限制。
例如在一个工厂中最大的生产量、原材料的数量限制、人工的数量等等,这些都是约束条件。
4. 模型的参数:模型参数是指约束条件的系数和模型中的常数。
它们是从现实问题中提取出来的,由于模型的解法通常是数学的,因此需要具体的数值。
线性规划题及答案

线性规划题及答案引言概述:线性规划是运筹学中的一种数学方法,用于寻觅最优解决方案。
在实际生活和工作中,线性规划问题时常浮现,通过对问题进行建模和求解,可以得到最优的决策方案。
本文将介绍一些常见的线性规划题目,并给出详细的答案解析。
一、生产规划问题1.1 生产规划问题描述:某工厂生产两种产品A和B,产品A每单位利润为100元,产品B每单位利润为150元。
每天工厂有8小时的生产时间,产品A每单位需要2小时,产品B每单位需要3小时。
问工厂每天应该生产多少单位的产品A 和产品B,才干使利润最大化?1.2 生产规划问题答案:设产品A的生产单位为x,产品B的生产单位为y,则目标函数为Max Z=100x+150y,约束条件为2x+3y≤8,x≥0,y≥0。
通过线性规划方法求解,得出最优解为x=2,y=2,最大利润为400元。
二、资源分配问题2.1 资源分配问题描述:某公司有两个项目需要投资,项目A每万元投资可获得利润2万元,项目B每万元投资可获得利润3万元。
公司总共有100万元的投资额度,问如何分配投资额度才干使利润最大化?2.2 资源分配问题答案:设投资项目A的金额为x万元,投资项目B的金额为y万元,则目标函数为Max Z=2x+3y,约束条件为x+y≤100,x≥0,y≥0。
通过线性规划方法求解,得出最优解为x=40,y=60,最大利润为240万元。
三、运输问题3.1 运输问题描述:某公司有两个仓库和三个销售点,每一个销售点的需求量分别为100、150、200,每一个仓库的库存量分别为80、120。
仓库到销售点的运输成本如下表所示,问如何安排运输方案使得总成本最小?3.2 运输问题答案:设从仓库i到销售点j的运输量为xij,则目标函数为Min Z=∑(i,j) cij*xij,约束条件为每一个销售点的需求量得到满足,每一个仓库的库存量不超出。
通过线性规划方法求解,得出最优的运输方案,使得总成本最小。
四、投资组合问题4.1 投资组合问题描述:某投资者有三种投资标的可选择,预期收益率和风险如下表所示。
线性目标函数最优解的求解方法
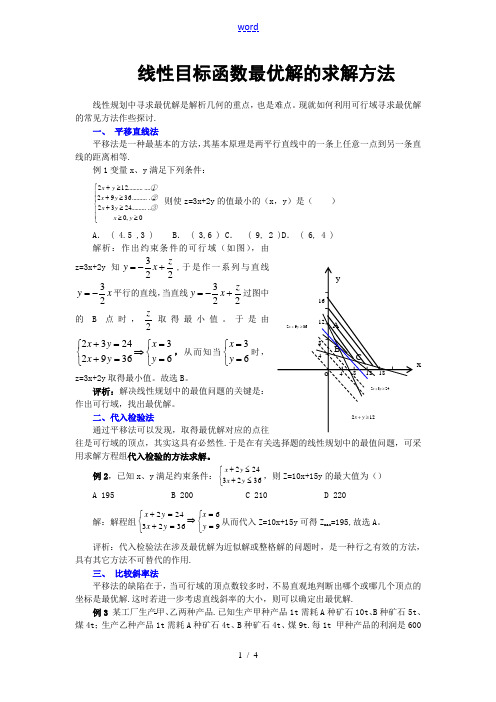
线性目标函数最优解的求解方法线性规划中寻求最优解是解析几何的重点,也是难点。
现就如何利用可行域寻求最优解的常见方法作些探讨.一、 平移直线法平移法是一种最基本的方法,其基本原理是两平行直线中的一条上任意一点到另一条直线的距离相等.例1变量x 、y 满足下列条件:⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+≥+0,0............2432...........3692..............122y x ③y x ②y x ①y x 则使z=3x+2y 的值最小的(x ,y )是( )A . ( 4.5 ,3 )B . ( 3,6 )C . ( 9, 2 )D . ( 6, 4 ) 解析:作出约束条件的可行域(如图),由z=3x+2y 知223zx y +-=,于是作一系列与直线x y 23-=平行的直线,当直线223zx y +-=过图中的B 点时,2z取得最小值。
于是由⎩⎨⎧==⇒⎩⎨⎧=+=+6336922432y x y x y x ,从而知当⎩⎨⎧==63y x 时,z=3x+2y 取得最小值。
故选B 。
评析:解决线性规划中的最值问题的关键是:作出可行域,找出最优解。
二、代入检验法通过平移法可以发现,取得最优解对应的点往往是可行域的顶点,其实这具有必然性.于是在有关选择题的线性规划中的最值问题,可采用求解方程组代入检验的方法求解。
例2,已知x 、y 满足约束条件:⎩⎨⎧≤+≤+3623242y x y x ,则Z=10x+15y 的最大值为()A 195B 200C 210D 220解:解程组⎩⎨⎧==⇒⎩⎨⎧=+=+963623242y x y x y x 从而代入Z=10x+15y 可得Z max =195,故选A 。
评析:代入检验法在涉及最优解为近似解或整格解的问题时,是一种行之有效的方法,具有其它方法不可替代的作用.三、 比较斜率法 平移法的缺陷在于,当可行域的顶点数较多时,不易直观地判断出哪个或哪几个顶点的坐标是最优解.这时若进一步考虑直线斜率的大小,则可以确定出最优解.例3 某工厂生产甲、乙两种产品.已知生产甲种产品1t 需耗A 种矿石10t 、B 种矿石5t 、煤4t ;生产乙种产品1t 需耗A 种矿石4t 、B 种矿石4t 、煤9t.每1t 甲种产品的利润是600元,每1t 乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A 种矿石不超过300t 、B 种矿石不超过200t 、煤不超过360t .甲、乙两种产品应各生产多少(精确到0.1t ),能使利润总额达到最大?解:设生产甲、乙两种产品分别为xt 、yt ,利润总额为z 元,那么⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+≤+0,0360942004515025y x y x y x y x 且Z=600x+1000y 作出约束条件所表示的平面区域(如左图),即可行域. 作直线l :600x+1000y=0,即直线l :3x+5y=0.因为94534525-<-<-<-,即k EN <k MN <k l <k FN ,所以把直线l 向上方移至m 的位置,直线经过可行域上的点M ,此时Z=600x+1000y 取最大值.解方程组⎩⎨⎧=+=+3609420045x x y x 得M 的坐标x=29360=12.3,y=291000=34.5,代入计算得Z max =291216000. 答:应生产甲产品约12.3t,乙产品34.5t ,能使利润总额达到最大.评析:这是高中新教材第二册上册第七章,“简单的线性规划”一节中的例3(P62~63),确定了直线斜率的大小,实质是确定了直线在向上平移的过程中,在经过可行域X 围内时,即可确定最优解。
线性规划的图解法

生产每吨产品所需资源 所需工时占总工时比例 所需原材料(吨)
产 A 1/3 1/3
品 B 1/3 4/3
C 1/3 7/3
设三种产品的产量分别是x1、x2、 x3吨,由于有三个决策变量,用图解 法求解下面的线性规划时,必须首先 建立空间直角坐标系。 M ax Z = 2 x1 +3 x2 +x3
1/ 3x1 +1/ 3x 2 +1/ 3x 3 1 s.t 1/ 3x1 + 4 / 3x 2 + 7 / 3x 3 3 x ,x ,x 0 1 2 3
x2
14 —
12 — 10 —
2x1 + x2 16 B C 2x1 + 2x2 18
4x1+ 6x2=48 2x1+ 2x2 =18
(0,6.8) 8 —
6—
最优解 (3,6)
4x1 + 6x2 48
4—
2— | 2 | 4 | 6
D
| 8 | 10 | 12 | 14 | 16 | 18
4x 1 2x 1 s. . t 2x 1 x ,x 2 1 6x 2 48 2x 2 18
x 2 16
0
按小组分工完成(1)画约束条件1;(2)画约束条 件2; (3)画约束条件3; (4)标明可行域; (5) 目标函数等值线; (6)说明如何得到最优解,算出相 应的目标函数最优值。 其他几 个小组对应讲评。
(案例1)某工厂生产A、B、C三种产品, 每吨的利润分别为2000元、3000元、1000元, 生产单位产品所需的工时及原材料如表1-2所 示。若供应的原材料每天不超过3吨,所能利 用的劳动力总工时是固定的,应如何制定日生 产计划,使三种产品的总利润最大?
目标规划和线性规划的区别]
![目标规划和线性规划的区别]](https://img.taocdn.com/s3/m/aa35d46ad5bbfd0a78567399.png)
(Goal programming)
目标规划概述 目标规划的数学模型
目标规划的图解法 目标规划的单纯形法
一、目标规划概述
目标规划是在线性规划的基础上,为适应经济管理 中多目标决策的需要而逐步发展起来的一个分支。
(一)、目标规划与线性规划的比较
1、线性规划只讨论一个线性目标函数在一组线性约束 条件下的极值问题;而目标规划是多个目标决策,可求 得更切合实际的解。
(二)、目标规划的基本概念
例题4—1
线性规划模型为:
maxZ = 8x1 + 10 x2 2x1 + x2 ≤11 ①
x1 +2x2 ≤10 ②
x1, x2≥0 X*=(4,3)T Z*=62
目标函数的地位突出,约束条件是必须严 格满足的等式或不等式,是绝对化的“硬约 束”,此种问题若要求太多时,很容易相互矛 盾,得不到可行解。如根据市场情况再加以下 要求:
目标值之间的差异,记为 d 。 正偏差变量:表示实现值超过目标值的部分,记为 d
+。 负偏差变量:表示实现值未达到目标值的部分,记为
d-。
在一次决策中,实现值不可能既超过目标值又未达到 目标值,故有 d+× d- =0,并规定d+≥0, d-≥0
当完成或超额完成规定的指标则表示:d+≥0, d-=0 当未完成规定的指标则表示: d+=0, d-≥0 当恰好完成指标时则表示: d+=0, d-=0 ∴ d+× d- =0 成立。
后面乘任意大的数还是小。必须“满足”第一级才能 “满足”第二级,依次类推。
权系数ωlk :区别具有相同优先因子的两个目标的 重要性差别,决策者可视具体情况而定。 (优先因子和权系数的大小具有主观性和模糊性,它 不是运筹学本身的问题,主要是决策人自身的经验, 可用专家评定法给以量化。)
最优化计算方法-第5章(线性规划)

第五章线性规划线性规划(Linear Programming,简记为LP)是数学规划的一个重要的分支,其应用极其广泛.1939年,前苏联数学家康托洛维奇(Л.B.Kah )在《生产组织与计划中的数学方法》一书中,最早提出和研究了线性规划问题.1947年美国数学家丹泽格(G. B. Dantzig)提出了一般线性规划的数学模型及求解线性规划的通用方法─单纯形方法,为这门科学奠定了基础.此后30年,线性规划的理论和算法逐步丰富和发展.1979年前苏联数学家哈奇扬提出了利用求解线性不等式组的椭球法求解线性规划问题,这一工作有重要的理论意义,但实用价值不高.1984年在美国工作的印度数学家卡玛卡(N. Karmarkar)提出了求解线性规划的一个新的内点法,这是一个有实用价值的多项式时间算法.这些为线性规划更好地应用于实际提供了完善的理论基础和算法.第一节线性规划问题及其数学模型一、问题的提出例1 某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品,已知条件如表所示。
问应如何安排计划使该工厂获利最多?ⅠⅡ现有资源设备原材料A 原材料B 14248台时16kg12kg每件利润23ⅠⅡ现有资源设备原材料A 原材料B 1402048台时16kg12kg每件利润23解: 设x 1、x 2 分别表示在计划期内产品Ⅰ、Ⅱ的产量。
12max 23z x x =+..s t 1228x x +≤1416x ≤2412x ≤12,0x x ≥二、线性规划问题的标准型112211112211211222221122123max ..,,0n nn n n n m m m mn n mn z c x c x c x s t a x a x a x b a x a x a x b a x a x a x b x x x x =+++⎧⎪+++=⎪⎪+++=⎨⎪⎪+++=⎪≥⎩,,其中1,,0m b b ≥11max ..,1,2,,0,1,2,,nj jj nij j i j j z c x s t a x b i mx j n=====≥=∑∑ 12(,,,)T n c c c =c 12(,,,)Tn x x x =x 12(,,,)Tm b b b =b 111212122212n nm m mn a a a a a a a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A 12[,,,]n = p p pmax ..()Tz s t ⎧=⎪=≥⎨⎪≥⎩c x Ax b b x 001max ..()Tnj j j z s tx =⎧=⎪⎪=≥⎨⎪⎪≥⎩∑c xp bb x 00对于不是标准形式的线性规划问题,可以通过下列方法将线性规划的数学模型化为标准形式:(1)目标函数的转换对min z 可以化max()z -(2)右端项的转换对0i b <,给方程两边同时乘以1-(3)约束条件的转换约束条件为≤方程左边加上一个变量,称为松弛变量约束条件为≥方程左边减上一个变量,称为剩余变量(4)变量的非负约束变量j x 无限制时,令,,0j j j j j x x x x x ''''''=-≥变量0j x ≤时,令j jx x '=-例将下列线性规划模型转化为标准形式12312312312312min 23..7232500x x x s t x x x x x x x x x x x -+-⎧⎪++≤⎪⎪-+≥⎨⎪--=-⎪≥≥⎪⎩,解(1)变量的非负约束令345x x x =-1245max 233x x x x -+-..s t 612457x x x x x ++-+=712452x x x x x -+--=12453225x x x x -++-=§2 两变量线性规划问题的图解法例1 求下列线性规划的解12121212max ..284300z x x s t x x x x x x =+⎧⎪+≤⎪⎪≤⎨⎪≤⎪≥≥⎪⎩,解(1)画可行域c A B D C 2x 1x O (2)画出目标函数的梯度向量:(3)作目标函数的一条等值线,120x x z +=将等值线沿梯度方向移动当等值线即将离开可行例2 求下列线性规划的解12121212max 2..284300z x x s t x x x x x x =+⎧⎪+≤⎪⎪≤⎨⎪≤⎪≥≥⎪⎩,解(1)画可行域c A B D C 2x 1x O (2)画出目标函数的梯度向量:(3)作目标函数的一条等值线,1202x x z +=将等值线沿梯度方向移动当等值线即将离开可行域时与可行域“最后的交点点为问题的最优解例3 求下列线性规划的解12121212max ..2200z x x s t x x x x x x =+⎧⎪-≤⎪⎨-≥-⎪⎪≥≥⎩,c2x 1x O无解例4 求下列线性规划的解12121212min 3..123600z x x s t x x x x x x =-⎧⎪≤⎪⎨≥⎪⎪≥≥⎩++,2x 1x O线性规划问题的性质:(1)线性规划的可行域为凸集,顶点个数有限.若可行域非空有界,则可行域为凸多边形.(2)线性规划可能有唯一最优解,可能有无数多个最优解,也可能无解最优解.无最优解可能是目标函数在可行域上无界,也可能可行域为空集.(3)若线性规划有最优解,则最优解必可在可行域的某个顶点达到.若两个顶点都为最优解,那么这两点连线上的所有点都是线性规划的最优解.§3 线性规划解的概念及其性质1 线性规划解的概念考虑线性规划问题max ..()Tz s t ⎧=⎪=≥⎨⎪≥⎩c x Ax b b x 00定义.1 矩阵A 中任何一组m 个线性无关的列向量构成的可逆矩阵B 称为线性规划的一个基矩阵与这些列向量对应的变量称为基变量(basis variable )其余变量称为基对应的非基变量(nonbasis variable )B 若设一个基为12(,,)m B p p p = ,12,,,m x x x ——为基B 对应的基变量1,,m n x x + ——为基B 对应的非基变量1B m x x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1m N n x x x +⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦12(,,,)m m n ++= N p p p (,)=A B N 从而令=Ax b 则(,)N x ⎡⎤=⎢⎥⎣⎦B x B N b11B Nx B b B Nx --=-B N Bx Nx b+=令0N x =则1B x B b-=10B b -⎡⎤⎢⎥⎣⎦——基本解(basis solution )满足10B b -⎡⎤≥⎢⎥⎣⎦,=≥0Ax b x 的基本解——基本可行解(basis feasible solution )对应的基称为可行基(feasible basis ).B 可以写成即:定义4 若基本可行解中所有基变量都为正,这样的基本可行解称为非退化解(non-degenerate solution).若基本可行解中某基变量为零,这样的基本可行解称为退化解(degenerate solution).例1212112max ..28400z x x s t x x x x x =-⎧⎪+≤⎪⎨≤⎪⎪≥≥⎩,标准化得:12123141234max ..28400,00z x x s t x x x x x x x x x =-⎧⎪++=⎪⎨+=⎪⎪≥≥≥≥⎩,,12341210(,,,)1001⎡⎤==⎢⎥⎣⎦A p p p p 子阵是否为基基变量非基变量基本解目标函数值134(,)=B p p 34,x x 12,x x (0,0,8,4)是231(,)=B p p 31,x x 24,x x (4,0,4,0)312(,)=B p p 12,x x 34,x x (4,2,0,0)424(,)=B p p 24,x x 13,x x (0,4,0,4)-4514(,)=B p p 14,x x 23,x x (8,0,0,4)-是是是是042基本可行解1x O(4,0)(4,2)(0,4)(8,0)2x 顶点2 解的判别定理定理1 最优解的判别准则设B 为线性规划LP 的一个基,1(1)0-≥B b 1(2)T T--≥0Bc B A c 则基对应的基本可行解1-⎡⎤⎢⎥⎣⎦0B b 是LP 的最优解.1(1,2,,)σ--== TBj j j c B p c j n 为变量对应的检验数j x 112[0,,0,,,]σσσ-++-= ,T TBm m n c B A c 显然基变量对应得检验数为零.定理2 无穷多个最优解的判别定理在线性规划的最优解中,某个非基变量对应的检验数为零,则线性规划有无数多最优解.定理3 无界解的判别定理设B 为线性规划的一个可行基,若基本可行解中s x 对应的检验数0σ<s ,且1-≤0s B p 则线性规划具有无界解(或称无解).某非基变量§3.4 单纯形表设B 为线性规划的一个基,x 为对应的可行解,则=Ax b两边同乘得1-B 11--=B Ax B b两边同乘得T Bc 11T T --=BBc B Ax c B b T z =c xTz -=c x 11T T --+-=TBBz c B Ax c x c B b 11(T T --+-=)TBBz c B A c x c B b1111()T TT z ----⎧+-=⎨=⎩BBc B A c x c B b B Ax B b 11111T T Tz ----⎡⎤⎡⎤-⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦0BBc B b c B A c x B A B b 定义矩阵1111TT----⎡⎤-⎢⎥⎣⎦T BBc B b c B A c B bB A 为基B 对应的单纯形表(table of simplex ),记为()T B1111()T T----⎡⎤-=⎢⎥⎣⎦T BBc B b c B A c T B B bB A 检验数函数值基变量的值各变量的系数100T b -=Bc B b 101020(,,,)--= T TBn c B A c b b b 10201-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥ b b B b则单纯形表可写成000101011102()⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦B n n m m mn b b b b b b T b b b 1112121222111112(,,)---⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦n n n m m mn b b b b b b B A B p B p bb b上例中1212112max ..28400z x x s t x x x x x =-⎧⎪+≤⎪⎨≤⎪⎪≥≥⎩,标准化得:121231412max ..28400z x x s t x x x x x x x =-⎧⎪++=⎪⎨+=⎪⎪≥≥⎩,12341210(,,,)1001⎡⎤==⎢⎥⎣⎦A p p p p 子阵是否为基基变量非基变量基本解目标函数值134(,)=B p p 34,x x 12,x x (0,0,8,4)是231(,)=B p p 31,x x 24,x x (4,0,4,0)312(,)=B p p 12,x x 34,x x (4,2,0,0)424(,)=B p p 24,x x 13,x x (0,4,0,4)-4514(,)=B p p 14,x x 23,x x (8,0,0,4)-是是是是042基本可行解1x O(4,0)(4,2)(0,4)(8,0)2x 顶点13410(,)01⎡⎤==⎢⎥⎣⎦B p p 231(,)=B p p 12341210(,,,)1001⎡⎤==⎢⎥⎣⎦A p p p p T(0,0)=B C 10()T⎡⎤-=⎢⎥⎣⎦c T B b A 34011008121041001z x x -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦23140101()4021141001x x ⎡⎤⎢⎥=-⎢⎥⎢⎥z T B 121101--⎡⎤=⎢⎥⎣⎦B 31401014021141001z x x ⎡⎤⎢⎥−−→-⎢⎥⎢⎥⎣⎦T(0,1)=B C单纯形表的特点:1、基变量对应的检验数为零2、基变量的系数构成单位阵§5旋转变换(基变换)设已知12(,,,,,)= r m j j j j B p p p p T()=B 1 r m j j j z x x x 1sn x x x 0001001011110102⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦sn s n r r rs rn m m ms mn b b b b b b b b b b b b b b b b为了将s x 变为基变量,而将r j x 变为非基变量,必须使表中的第s 列向量变为单位向量,变换按下列步骤进行:(1)将()T B 中第r 行,第s 列的元素化为1.01(,,,,,1,,) rj r rnr rs rs rs rsb b b b b b b b (2)将()T B 中第s 列的的其余元素化为0.0101(,,,,,0,,)---- is rn is rj is r is r i i ij in rs rs rs rsb b b b b b b b b b b b b b b b由此得出变换后矩阵中各元素的变换关系式如下,其中,01== ,,,rjrj rsb b j nb ,,01,01=-≠== ,,,,,,is rjij ij rsb b b b i r i m j nb 变换式称为旋转变换rs b 称为旋转元,r称为旋转行称为旋转列,s s x 称为入基变量,称为出基变量,r j x {,}r s定理3.5.1,01== ,,,rj rj rsb b j n b ,,0,01=-≠== ,,,,,is rj ij ij rsb b b b i r i m j n b 在变换之下,将基12(,,,,,)= r m j j j j B p p p p 的单纯形表变为基12(,,,,,)= m j s j j B p p p p 的单纯形表第6节单纯形法基本思路是:线性规划(通常是求最小值的形式)若有最优解,其必定在可行域(在相应几何空间中是一个凸多面体)的顶点达到,故从某一个顶点出发,沿着凸多面体的棱向另一顶点迭代,使得目标函数的值增加,经过有限次迭代,将达到最优解点.1.入基变量及出基变量的确定入基变量的确定由上面可知,目标函数用非基变量表示的形式为01n j jj m z z x σ=+=-∑若某检验数0j σ<则j x 的系数大于零,将j x 由零变为非零,目标函数值增大.所以,为了使的取值目标函数值增加,可以将某检验数0j σ<对应的非基变量j x 中的某个变为基变量.{}min 0j s j σ=<则s x 可选作为入基变量.即:在负检验数中,列标最小的检验数对应的非基变量入基.2.出基变量的确定在确定出基变量时应满足两个原则:(1)目标函数值不减;(2)保证新的基本解为基本可行解.0min 0,0i is is b b i m b θ⎧⎫=>≤≤⎨⎬⎩⎭min ,00i is is b r i b i m b θ⎧⎫==>≤≤⎨⎬⎩⎭,2 单纯形法设已知一个初始可行基及B T()B 基变量指标集合为{}1,,B m J j j = 非基变量的指标集合为{}1,2,,\N BJ n J =单纯形法若所有()00j N b j J ≥∈,则停止,最优解为0,1,,0,ij i j N x b i m x j J **⎧==⎪⎨=∈⎪⎩否则转(2).(1)最优性检验(2)选入基变量{}0min 0,j N s j b j J =<∈若()01~is b i m ≤=,则停止,(LP)无最优解,否则转(3)(3)选出基变量0min 0,0i is is b b i m b θ⎧⎫=>≤≤⎨⎬⎩⎭0min ,00i is is b r i b i m b θ⎧⎫==>≤≤⎨⎬⎩⎭,(4)作{},r s 旋转运算,01rj rj rsb b j n b == ,,,,,01,01is rj ij ij rsb b b b i r i m j n b =-≠== ,,,,,,得B 的单纯形表()()ijT B b =,以ij b 代替ij b ,转(1)例1 求线性规划问题的解解标准型为:121231425max 2328416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥12121212max 2328416.412,0z x x x x x s t x x x =++≤⎧⎪≤⎪⎨≤⎪⎪≥⎩12123142512345max 2328416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥⎩-20-381612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢0T()B =0345[,,]B p p p =00T()T c B bA ⎡⎤-=⎢⎥⎣⎦-20-381612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣0T()B =8/116/408-3441202101001/400400135z x x 12345x x x x x 01/20⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢1/4-41x08-3441202101001/400400135z x x 12345x x x x x 01/20⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/4-1x 4/212/40140244011/201001/40002-15z x 12345x x x x x 3/21/80⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/8-1x 32x 1/2例2求线性规划问题的解解标准型为:121231425max 228416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥12121212max 228416.412,0z x x x x x s t x x x =++≤⎧⎪≤⎪⎨≤⎪⎪≥⎩12123142512345max 228416.412,,,,0z x x x x x x x s t x x x x x x x =+++=⎧⎪+=⎪⎨+=⎪⎪≥⎩-10-281612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢0T()B =0345[,,]B p p p =00T()T c B bA ⎡⎤-=⎢⎥⎣⎦-10-281612121004001004001345z x x x 12345x x x x x 000⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣0T()B =8/116/404-2441202101001/400400135z x x 12345x x x x x 01/40⎤⎥⎥⎥⎥⎥⎥⎡⎢⎢⎢⎢⎢⎢1/4-41x0-2441202101001/400400135z x x 12345x x x x x 00⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/4-1x 4/212/4080244011/201001/400015z x 12345x x x x x 100⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/8-1x 32x 41/42-1/2080244011/201001/400015z x 12345x x x x x 100⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣1/8-1x 2x 2T 0803280101/410101/2-004-12z 12345x x x x x 00⎤⎥⎥⎥⎥⎥⎥⎦⎡⎢⎢⎢⎢⎢⎢⎣01x 2x 42-1/25x 11212x k x k x =+12120,1,1k k k k ≤≤+=全部最优解为§7 两阶段法第二阶段从初始可行基开始,用单纯形法求解原问题.(LP )max ..(0)0T z c x s t Ax b b x ⎧=⎪=≥⎨⎪≥⎩(ALP )max ..0()T w s t z ⎧=-⎪-=⎪⎨+≥⎪⎪≥⎩00T e y c x A =b b x y x 第一阶段引入人工变量,构造辅助问题,求辅助问题的最优解,得出原问题的初始可行基及对应的基本可行解.(ALP)12112211112211121122222211212312max..0 ,,,,0mn nn nn nm m mn n m mn mw y y ys t z c x c x c xa x a x a x y ba x a x a x y ba x a x a x y bx x x x y y y=----⎧⎪----=⎪⎪++++=⎪++++=⎨⎪⎪++++=⎪⎪≥⎩,,,,,121111211112122122212000000100()010001m m m m i i i in i=1i i i n n n m m m mn b a a a c c c b a a a T B b a a a b a a a ===⎡⎤----⎢⎥⎢⎥---⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦∑∑∑∑。
线性规划中的最优解求解

线性规划中的最优解求解线性规划是一种在运筹学和数学中广泛应用的数学建模技术,通过确定一组线性约束条件下的最优解,以实现目标最大化或最小化。
最优解是指在满足给定约束条件的前提下,能使目标函数达到最优值的解。
在线性规划问题中,最优解的求解有多种方法。
本文将介绍线性规划中的两种主要方法:图解法和单纯形法。
一、图解法图解法是一种简单直观的方法,适用于只有两个变量的问题。
它通过在平面坐标系上画出约束条件的图形,找到可行域(满足所有约束条件的解集),并在可行域内寻找使目标函数达到最优值的点。
具体步骤如下:1. 绘制坐标系,并画出约束条件的直线或曲线。
每个约束条件都会限制变量的取值范围,在平面上形成一条直线或曲线。
2. 标出可行域。
根据所有约束条件的交集,确定满足所有约束条件的解的集合,即可行域。
可行域通常是一个多边形区域。
3. 确定目标函数。
根据问题的要求确定目标函数,并将其表示为直线或曲线。
4. 在可行域内寻找最优解。
通过平行于目标函数的线,将其移动至与可行域相切,并找到使目标函数取得最优值的点。
图解法的优点是简单易懂,能够提供初步的解决方案。
然而,对于复杂问题和具有多个变量的大规模问题,图解法可能不适用。
二、单纯形法单纯形法是一种基于矩阵运算的高效方法,适用于多变量和大规模问题。
它通过不断进行迭代计算,寻找最优解。
具体步骤如下:1. 将线性规划问题转化为标准形式。
标准形式要求目标函数为最小化问题,并且所有约束条件均为等式形式。
如果原问题不符合标准形式,可以进行线性变换进行转化。
2. 构建初始单纯形表。
将原问题的线性规划模型表示为矩阵形式,并构建单纯形表,包括目标函数系数、基变量和非基变量等信息。
3. 迭代计算。
根据单纯形表中的信息,进行迭代计算,通过选择合适的主元(即最大系数法则)和更新各个单元的值,逐步接近最优解。
4. 判断终止条件。
在每一次迭代计算后,判断是否满足终止条件,即目标函数是否达到最优解。
第三章 线性规划的灵敏度分析和最优解的解释

3.1 灵敏度分析简介
灵敏度分析是研究线性规划的参数(非可控输入)发生 变化对最优解的影响程度
线性规划的参数包括:
• 目标函数系数 • 约束条件右侧值 • 约束条件系数矩阵
最优解中包含的信息:
• 目标函数值 • 决策变量值 • 递减成本(reduced cost) • 松弛/剩余变量
4
3.1 灵敏度分析简介
利用Lingo 软件做灵敏度分析
16
17
利用Excel做灵敏度分析
Microsoft Excel 16.0 敏感性报告 工作表: [数据模型与决策第3章例题.xlsx]第三章例题1 报告的建立: 2021/5/29 10:48:56
可变单元格
单元格 $B$15 $C$15
名称 决策变量值 x1 决策变量值 x2
作者
John Loucks
St. Edward’s University
1
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介 3.2 目标函数系数变化的分析 3.3 约束条件右端值变化的分析 3.4 传统灵敏度分析的局限性
2
第三章 线性规划的灵敏度分析和最优解的解释
3.1 灵敏度分析简介 3.2 目标函数系数变化的分析 3.3 约束条件右端值变化的分析 3.4 传统灵敏度分析的局限性
6
x1 < 6
2x1 + 3x2 < 19 x1 + x2 < 8
x1, x2 > 0
固定x2的系数7,改变x1 的系数
5
最优解:
Max 14/3x1 + 7x2
4
x1 = 5, x2 = 3
3
Max 7x1 + 7x2
简单的线性规划整点最优解
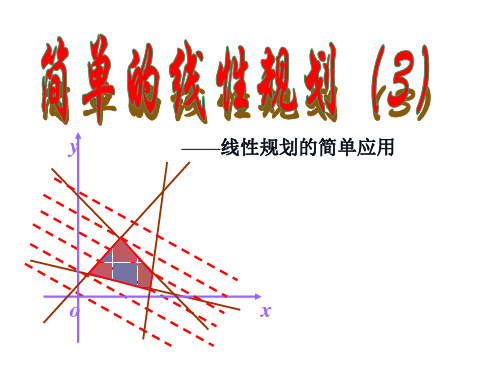
0
使z=2x+y取得最大值的可行解为 (2,-1) ,
1
且最大值为 3 ;
y=-1
(-1,-1)
2x+y=0
使z=2x+y取得最小值的可行解 (-1,-1) ,
x
(2,-1)
且最小值为 -3 ;
这两个最值都叫做问题的 最优解。
返回
例题分析
例1:某工厂生产甲、乙两种产品.已知生产甲种产品1t需消
耗A种矿石10t、B种矿石5t、煤4t;生产乙种产品1吨需消 耗A种矿石4t、B种矿石4t、煤9t.每1t甲种产品的利润是600 元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的 计划中要求消耗A种矿石不超过300t、消耗B种矿石不超过 200t、消耗煤不超过360t.甲、乙两种产品应各生产多少(精 确到0.1t),能使利润总额达到最大?
3.在可行域内找整数解,一般采用平移找解法,即打网 络、找整点、平移直线、找出整数最优解
解线性规划应用问题的一般步骤:
1)理清题意,列出表格: 2)设好变元并列出不等式组和目标函数 3)由二元一次不等式表示的平面区域做出可行域; 4)在可行域内求目标函数的最优解 5)还原成实际问题 (准确作图,准确计算)
甲产品 xt
(1t)
10 5 4
600
乙产品 yt 资源限额
(1t)
(t)
4
300
4
200
9
360
1000
设生产甲、乙两种产品.分别为x t、yt,利润总额为z元
把题中限制条件进行转化:
10x+4y≤300
5x+4y≤200 4x+9y≤360
x≥0
y ≥0
线性规划求最值(详细)

其中P( x, y), M (1,0) 2 2 由图知 PM 1的最小值 AM 1
解:z (x 1) y 1 PM 1
2
2
补:x y OP
2 2
2
zmin 2 1 1
2
A P( x, y)
O
其中P( x, y)
2
B
由图知 OP 的最小值 d
z=2x+y
可行解: 满足约束条件的解(x,y) 即不等式组的解 可行域: 可行解组成的集合 (阴影部分) A(5,2),B(1,1) 最优解: 使目标函数取得最值的可行解 y x=1 2x+y=z 线性规划问题: 可行域 线性目标函数在线性约 最优解 束条件下的最值 的问题
o
1 x-4y+3=0
A(5,2)
(1)求z x y 10y 25最小值
x y20 (2) x,y满足 x y 4 0 2x y 5 0 2 2
2 2
2 y 1 ( 2)求 的范围 x 1
x y20 C
M
(1)解:z x (y - 5) PM
其中P( x, y), M (0,5)
(1)画区域
(2)z 2 x 3 y化为y x 3 2 z 3 表示斜率为 ,纵截距为 的一组平行线 3 3
x 2 y 8 (4)解方程组 得点A(4,2) 4 x 16
(3)直线过点 A 时纵截距最大,此时z最大,过点 O 时z最小
zmax 2 4 3 6 14 Zmin 0 注:斜率越大, 倾斜角越大
2
由图知 PM 最小值 d 2
2
A
N
运筹学学习与考试指导

运筹学学习与考试指导模拟考试试题(一)一、单项选择题(从下列各题四个备选答案中选出一个正确答案,答案选错或未选者,该题不得分.每小题2分,共10分)B 2.C 3.A 4。
D 5。
B1.线性规划具有唯一最优解是指( )。
A 。
不加入人工变量就可进行单纯形法计算 B 。
最优表中非基变量检验数全部非零 C.最优表中存在非基变量的检验数为零 D 。
可行解集合有界 2.设线性规划的约束条件为⎪⎩⎪⎨⎧≥=++=++0,,,4223421421321x x x x x x x x x 则基本可行解为( )。
A 。
(0,0,4,3) B.(3,4,0,0) C.(2,0,1,0) D.(3,0,4,0) 3.min Z =3x 1+4x 2, x 1+x 2≥4, 2x 1+x 2≤2, x 1、x 2≥0,则( ). A.无可行解B.有唯一最优解C.有多重最优解D.有无界解4.互为对偶的两个线性规划问题的解存在关系( d )。
A.原问题无可行解,对偶问题也无可行解 B.对偶问题有可行解,原问题也有可行解 C 。
若最优解存在,则最优解相同D.一个问题有无界解,则另一个问题无可行解5.有6个产地4个销地的平衡运输问题模型具有特征( b )。
A.有10个变量24个约束 B.有24个变量10个约束 C.有24个变量9约束 D.有9个基变量10个非基变量二、判断题(你认为下列命题是否正确,对正确的打“√”;错误的打“×”。
每小题2分,共20分)1.若线性规划无最优解则其可行域无界。
( ) 2.凡基本解一定是可行解。
( )3.线性规划的最优解一定是基本最优解。
( )4.可行解集非空时,则在极点上至少有一点达到最优值.( ) 5.原问题具有无界解,则对偶问题不可行。
( )6.互为对偶问题,或者同时都有最优解,或者同时都无最优解。
( ) 7.加边法就是避圈法。
( )8.一对正负偏差变量至少一个大于零。
( ) 9.要求不超过目标值的目标函数是minZ=d+。
线性规划和最优解

线性规划和最优解线性规划是一种在数学和运筹学领域常见的问题求解方法,可以应用于各种现实生活中的决策问题。
它是通过一系列线性等式和不等式来建模,并在满足特定约束条件下求解使目标函数取得最优值的变量值。
线性规划的最优解能够帮助我们做出高效的决策,下面将详细介绍线性规划的原理和求解方法。
一、线性规划的基本概念线性规划中,我们首先需要明确问题的目标,并将其表示为一个线性函数,也被称为目标函数。
目标函数可以是最大化或最小化的,具体取决于问题的需求。
其次,我们需要确定一组变量,这些变量的取值将会对目标函数产生影响。
接下来,我们还需要列举出一系列约束条件,这些约束条件通常来自于问题的实际情况,例如资源限制、技术要求等。
最后,我们需要确定这些变量的取值范围,这也是约束条件的一部分。
二、线性规划的数学建模在线性规划中,我们可以通过以下步骤进行数学建模:1. 确定目标函数:根据问题的要求,我们可以定义一个线性函数作为目标函数。
例如,如果我们要最大化某个产品的利润,那么利润就可以是目标函数。
2. 列举约束条件:根据问题的实际情况,我们需要列举出一系列约束条件。
这些约束条件可以是线性等式或不等式,并且通常包含了变量的取值范围。
3. 确定变量的取值范围:根据问题的实际情况,我们需要确定变量的取值范围。
例如,如果某个变量代表一个产品的产量,那么它的取值范围可能是非负数。
4. 构建数学模型:根据目标函数、约束条件和变量的取值范围,我们可以构建一个数学模型,将问题转化为线性规划模型。
三、线性规划的最优解求解方法线性规划的最优解可以通过以下方法求解:1. 图形法:对于只有两个变量的简单线性规划问题,我们可以通过绘制变量的可行域图形,并计算目标函数在图形上的最优解点来求解问题。
2. 单纯形法:单纯形法是一种常用的求解线性规划问题的算法。
它通过逐步迭代改进解向量,从而逼近最优解。
这个方法通常适用于复杂的线性规划问题,可以在较短的时间内得到比较好的结果。
1.2线性规划的解

. ..
x2 .3 .
. x1 2x2 2 . . . . .
0
x1
解: (1)在直角坐标系上画出可行域
x1 4
x1 2x2 8
(2)做目标函数的等值线 x1 2x2 2
(3)最优值z* 8
求交点:
x1 x2
2x2 3
8
x1 x1
2x2 4
8
(x1, x2 ) (2,3)
(x1, x2 ) (4,2)
max z 7x1 x2
x1 2x2 6
s.t
x1 x2 1 x1 2
x1 , x2 0
其标准型为
max z 7x1 x2
x1 2x2 x3 6
s.t
x1 x2 x4 1 x1 x5 2
x1, x2 , x3 , x4 , x5 0
1 2 1 0 0
系数矩阵A
2x1 x2 3
可行域为空集
无可行解
该问题无最优解
图解法的基本步骤:
1、在直角坐标系x1ox2上做出可行域S的图形
(一般是一个凸多边形)
2、令目标函数值取一个给定的常数k,
做等值线Z c1x1 c2 x2 k 3、对max 问题,令目标函数值k由小变大, 即让等值线向上平移,
若它与可行域S最后交于一个点(一般是S的一个顶点), 则该点就是所求的最优点, 若与S的一条边界重合,此时边界线上的点均是最优点
退化基本可行解:基本可行解中,存在取0值的基变量
对应的基称为退化基
非退化基本可行解:基本可行解中,基变量的取值均>0
对应的基称为非退化基
线性规划问题
退化的线性规划问题:存在退化基 非退化的线性规划问:题 所有基均非退化
线性规划求最优解

x1
am2 x2
L
amn xn (, )bm
(2)
x j 0 j 1, 2,L , n
(3)
(1)式称为目标函数(2)式中等式或不等式称为约束条件 (3)式是非负约束条件
x1 , x2, …,xn称为决策变量,简称变量。
满足约束条件的一组变量的值 x1 x10 , x2 x20 ,L , xn xn0
x1 x2 ( x7 x6 ) x4 7 x1 x2 ( x7 x6 ) x5 2 3x1 x2 2( x7 x6 ) 5
最后,令F=-f,则可将求f的最小值问题转化成求F的最大值问题。标准型为:
max F x1 2x2 0x4 0x5 3x6 3x7
(1)
1 3
x1
4 3
x2
7 3
x3
x5
3
x1 0, x2 0, x3 0, x4 0, x5 0
线性规划问题的数学模型的一般形式
max(或 min) f c1x1 c2 x2 L cn xn
(1)
a11x1 a12 x2 L a1n xn (, )b1
a21x1
a22 x2 L LL
a2n xn L
L
(, )b2 L
am1
(1)
a11x1 a12 x2 L a1n xn b1
a21x1 L
a22 x2 L
L L
a2n xn b2 LL
(2)
am1x1 am2 x2 L amn xn bm
【精选】线性规划问题的求解步骤

【例4】
某厂拟生产甲、乙两种适销产品,每件销售 收入分别为3000元、2000元,甲、乙产品都需要 在A、B两种设备上加工, 在每台A、B设备上加工 1件甲设备所需工时分别为1h, 2h, 加工1件乙设备 所需工时分别为2h, 1h, A、B两种设备每月有效使 用台时数分别为400h和500h, 如何安排生产可使 收入最大?
解决线性规划问题的方法
图解法解决线性规划问题时,根据约束条件 画出可行域是关键的一步,一般地,可行域可以 是封闭的多边形,也可以是一侧开放的非封闭平 面区域. 第二是画好线性目标函数对应的平行直 线系,特别是其斜率与可行域边界直线斜率的大 小关系要判断准确. 通常最优解在可行域的顶点 (即边界线的交点)处取得,但最优整数解不一定 是顶点坐标的近似值,它应是目标函数所对应的 直线平移进入可行域最先或最后经过的那一整点 的坐标.
【例2】
要将两种大小不同的钢板截成A、B、C
三种规格,每张钢板可同时截得三种规格的
小钢板的块数如下表所示:
规格类型
钢板类型
A规格
B规格
C规格
第一种钢板
2
1
1
第二种钢板
1
2
3
各截这两种板张数最少?
【例3】
一个化肥厂生产甲、乙两种混合肥料, 生产 1车皮甲种肥料的主要原料是磷酸盐4t, 硝酸盐 18t;生产1车皮乙种肥料需要的主要原料是磷 酸盐1t, 硝酸盐15t. 现库存磷酸盐10t, 硝酸盐66t. 若生产1车皮甲种肥料, 产生的利润为10000元, 生产1车皮乙种肥料, 产生的利润为5000元, 那么 分别生产甲、乙两种肥料各多少车皮, 能够产生 最大的利润?
必修五《考一本》第27课时
线性规划问题的求解步骤:
运筹学--线性规划问题最优解的确定与改进

线性规划问题最优解确实定与改良线性规划是运筹学的一个重要分支。
自1947年丹捷格〔G.B.Dantzig 〕提出了一般线性规划问题求解的方法——单纯形法之后,线性规划在理论上趋向成熟,在实用中日益广泛与深入。
线性规划最优解求解问题,在《运筹学》本科版给出了图解法和单纯形法。
一般线性规划问题的标准型为:1max (14)nj ji z c x ==-∑1,1,2(15)0,1,2,(16)ni j j i j j a x b i m x j n ===-≥=-⎧∑⎪⎨⎪⎩满足约束条件〔1-5〕式、〔1-6〕式的解12(,,,)T n X x x x =,称为线性规划问题的可行解,其中使目标函数到达最大值的可行解称为最优解。
2009年中国科教创新导刊,第三十期李高秀写的《线性规划中最优解的准确确定》中详细介绍了图解法的过程,图解法适合于二元线性规划问题,对于多元线性规划问题图解法相对较难。
图解法过程:1 线性目标函数最值的分析对于线性目标函数Z=ax+by ,假设b ≠0时,目标函数可变为a zy x b b=-+,则是直线a zy x b b=-+在y 轴上的截距。
(1)b>0时,随着直线a zy x b b=-+的平移,直线在与可行域有公共点的条件下,它在y 轴上的截距z b 最大时z 最大;当zb最小时z 最小。
(2)b<0时,随着直线a zy x b b=-+的平移,直线在与可行域有公共点的条件下,它在y 轴上的截距z b 最大时z 最小;当zb最小时z 最大。
由以上两点可知,要求线性目标函数z=ax+by 的最大最小值要注意y 的系数b 的正负和平移直线在y 轴上的截距。
2 在图上分别作出约束函数和目标函数,平移目标函数线到可行域的交点时,要把目标函数的斜率与相交于这一点的直线的斜率进行比较上述的最值分析是确定平移目标函数的大概方向,而这次是确定最优解确实凿位置。
斜率比较大小的目的是直观形象的比较两直线的方向和倾斜程度。
《线性规划》034第二章2.2最优基可行解=续=第六次课

④ x 2 2 x 3 x4 2 ② x 2 x 3 x5 5 ③
2
故s=2,js=4,则取x4为离基变量。
所以得到新基为B1=( p1,p2,p5 )
1 0 2 0 1 0 0 1 1
1 0 2 B1 0 1 0 1 0 0 1 1
2.2 最优基可行解的求法
(2)对于基B2=( p3,p4,p5 )
基B2对应的典式为: 把非基变量转换为基变量,称为进基。 min f 6 3 x1 3 x2 此处x1作为进基变量
s.t. 3 x1 2 x2 x3 8 x1 3 x2 x1 5 x2 1 x4 4 x5 3
注:(3)、从原基解的典式导出新基解的典式的方法(P34)
①、若使用计算机编程求解LP,可按照(2.33)~~(2.37)的 公式编制程序,以实现旧典式向新典式的转换;
√
②、对简单问题用手工计算时,可以直接对原典式使用 消去法获得新典式。
2.2 最优基可行解的求法
例4(P35) 求解下列线性规划问题: 解题步骤:
2.2 最优基可行解的求法
二、最优基可行解的判别法则
若基可行解 x(0)对应的典式中,有某个检验数r 0 , 情形二: T 而 (b1r , b2r ,, bmr ) 中至少有一个大于零,并且 bi 0 0 定理2.6 (i 1,2,, m) ,则必存在另一基可行解,其对应的目标 (P31) 函数值比 f ( x (0) )小。
2.2 最优基可行解的求法
二、最优基可行解的判别法则
若基可行解 x(0)对应的典式中,有某个检验数r 0 , 情形二: T 而 (b1r , b2r ,, bmr ) 中至少有一个大于零,并且 bi 0 0 定理2.6 (i 1,2,, m) ,则必存在另一基可行解,其对应的目标 (P31) 函数值比 f ( x (0) )小。 T b10 , b20 , , bm 0 B 1b 对应基解中基变量值部分。 定义(P32):对于LP的一个基可行解,如果其基分量值都是正 的,就称它是一个非退化的基可行解;否则(即基分量值有等 于零的),就称它为退化的基可行解。
线性规划的最优解

线性规划的最优解线性规划是一种数学模型,用于解决在一定约束条件下,求解一种或多种线性目标使其最大化或最小化的问题。
线性规划的最优解是指在给定约束条件下能够使目标函数取得最优值的变量取值。
线性规划的最优解求解过程通常包括以下几个步骤:1.确定决策变量:首先需要明确问题中的决策变量,即可以通过调整的变量。
例如,生产中可以根据需要确定产品的生产数量、仓库的存货量等。
2.建立目标函数:根据问题的要求,建立目标函数,即将问题的目标转化为数学表达式。
目标函数可以是最大化或最小化的形式,根据问题的具体需求确定。
通常目标函数是一个线性函数,即由决策变量线性组合而成。
3.确定约束条件:根据问题的限制条件,确定约束条件。
约束条件可以是等式约束或不等式约束。
等式约束限制了决策变量之间的关系,不等式约束则限制了决策变量的取值范围。
4.确定可行域:根据约束条件确定可行域,即决策变量的取值范围。
可行域是决策变量满足所有约束条件的取值范围。
5.求解最优解:通过线性规划求解算法对可行域进行搜索,找到使目标函数最优化的决策变量取值。
通常使用单纯形法、内点法等算法进行求解。
最优解即是能够使目标函数取得最优值的决策变量取值。
线性规划的最优解具有如下特点:1.最优解是唯一的:在满足约束条件的前提下,只存在一个使目标函数取得最优值的决策变量取值。
2.最优解存在:若问题满足有限性条件和可行性条件,则一定存在最优解。
3.最优解在可行域的边界上:最优解必须在可行域的边界上取得,即通过最优解的决策变量取值,能够满足所有约束条件。
4.最优解的存在条件:最优解存在的条件是目标函数是线性函数,并且可行域是一个有界区域。
通过线性规划求解最优解可以帮助决策者提供具有最佳效益的决策方案,同时也能够帮助优化资源分配和提高生产效率。
因此,线性规划的最优解在实际应用中具有重要的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B1 B2 B3 B4 B5 4 7 6 6 6 8 9 9 7 9 7 15 12 17 14 10 12 8 7 14 6 10 12 10 6
A1 A2 A3 A4 A5
ci
j
6
问应如何分配,使这五人分别完成这五项任 务的总时间最小?
匈牙利算法基本思想
• 匈牙利算法适用于极小化且成本矩阵的所有元 素都非负的分配问题 • 如果成本矩阵的所有元素都非负,并且存在 一 组位于不同行不同列的0元素, 则只要令对应于 这些0元素位置的xij=1, 其余的xij=0, 即为所 求的最优解. 因为此时必有z=0就是问题的最优 值 • 匈牙利算法的关键: 如何产生并寻找一组位于 不同行不同列的0元素
14
0 3 ( 0 ) 0 ) 1 7 ( 0 2 3 ( ) 0 0 5 0 2 3
-1 0 0
11 8 0 7 3 1 2 1 1 0 4 0 ) 1 4 ( 0
0 -1
1 3 ( 0 ) 0 ( 0 ) 6 (0 ) 1 2 1 0 5 0 1 2
7
分配问题的性质—匈牙利算法的依据
定理1:对于分配问题,成本矩阵的 任一行(或列)减去(或加上)一个相同 的数得到的新指派问题与原问题同解
作用: 如何在效率矩阵中产生零元素
8
证明:
z = cij x ij (c kj s)x kj
i 1 j1 ik n j1 n n n
4 7 6 6 6 8 7 9 17 9 12 7 14 9 12 15 12 14 10 8 7 6 10 10 6 11 8 7 3 2 1 0 4 4 ( 0 )
4 7 6 6 6
1 3
0 0 0 0 0 0 0 0 0 0
11
覆盖原则
• 1、从第一行开始,若该行只有一个0元素,就对这 个0打上(),对打()的0元素所在列画一条直线; 若该行没有或有两个以上0(已划去的不计在内), 则转下一行,依次进行到最后一行; • 2、从第一列开始,与行做法类似,依次进行到最 后一列; • 3、重复以上两个步骤。若还有未被划去的0, 且未 被划去的0之间存在闭回路。这时可沿着闭回路的 走向,对每个间隔的0打(),然后对打()的0, 或所在的行,或所在的列,画一条直线。
12
变换原则
1、从矩阵未被直线覆盖的数字中找出一个最小 的数k; 2、对矩阵的每行,当该行有直线覆盖时,令 ui=0,无直线覆盖的令ui=k ; 3、对矩阵有直线覆盖的列,令vj=-k ,对无直 线覆盖的令vj=0 ; 4、从原矩阵的每个元素cij中分别减去ui和vj , 得到一个新矩阵。
13
例题求解
11 8 2 10 7 3 3 6 2 1 1 8 0 4 3 6 4 0 4 3 3 0 11 8 1 7 7 3 2 3 2 1 0 5 0 4 2 3 4 0
0 3 ( 0 ) (0 ) 1 7 0 2 3 0 ( 0 ) 5 0 2 3
人完成。求最佳分配方案。
两个基本类型
若完成任务的成本表现为资源的消耗, 则考虑 的是如何分配任务, 使目标极小化; 若完成任务的成本表现为生产效率的高低, 则 要考虑如何分配, 使目标极大化。
3
分配问题的数学模型
设决策变量为:
1 xij 0 第i员工分配做第j项工作 否则
n n
min(or max) z = c ij xij
• 作用: 如何寻找位于不同行不同列的零元 素.
10
分配问题的求解-匈牙利方法步骤
第一步:成本矩阵的每一行及每一列减去该行或列的最小
数,使每行每列至少有一个0;
第二步:画直线覆盖全部0元素。覆盖原则
如果直线条数= n (此时矩阵每行都有一个打()的 0,并且所有打()的0必在不同行不同列),只要令对应 打()0元素的xij=1即为最优解,算法结束。 如果直线条数< n(此时打()的0个数<n),转下一 步; 第三步:进行成本矩阵变换。变换原则 得到一个新的成本矩阵,转第二步。 直到矩阵的每一行都有一个打()的0元素为止
c ij x ij c kj x kj (s) x kj
i 1 j1 ik n n j1 n j1
n
n
n
c ij x ij c kj x kj (s)
i 1 j1 ik j1
z (s)
9
指派问题的性质(续)
•定理2: 若成本矩阵C的元素可分成0 与非0两部分, 则覆盖0元素的最少直 线数等于不同行不同列的0元素的最 大个数.
期中考试:4月18日8:00-9:30 4106
1
4月23日(周六)调课
春假后 5月6日(周五)8:00 – 9:30
2
第二节 经典分配(指派)问题与匈牙利法
n个员工分配作n项工作,已知第i个员工做第 j项工作的成本为cij,i=1,…,n; j=1,…,n。
规定:每人完成其中一项,每项只交给一个
s.t.
x
n
i 1 j1
x
i 1
j1 n
ij
1
i = 1,2, , n
பைடு நூலகம்
ij
1
j = 1,2, , n
i = 1,2, , n; j = 1, , n
4
x ij 0或1,
分配问题成本(效率)矩阵
c11 c12 c c 21 22 C c31 c32 cn1 cn 2 c13 c1n c23 c2 n c33 c3n cn 3 cnn
•分配问题(基)可行解的结构: 在n2个分量中只有n 个分量为1,其余的全部为0; 并且这些为1的分量的 位置应位于成本矩阵的不同行不同列上. 即
分配问题的解应对应于成本矩阵的不同行与 不同列(为什么?)
5
例:已知分配A1、A2、A3、A4、A5五人分别完 成五项任务, 他们分别完成各任务的时间如下
