基于MATLAB的控制系统频域设计
MATLAB在控制系统设计中的应用

MATLAB在控制系统设计中的应用控制系统是现代工业中不可或缺的一部分,它被广泛应用于各种工业自动化过程中。
而在控制系统的设计和优化过程中,MATLAB(Matrix Laboratory)无疑是一个强大且高效的工具。
本文将探讨MATLAB在控制系统设计中的应用,并且着重介绍其在模型建立、系统分析和控制器设计等方面的功能。
一、模型建立在控制系统设计的初期阶段,模型建立是一个非常关键的步骤。
传统的方法往往需要依靠复杂的数学计算和推导,而MATLAB则提供了一种简单、直观的处理方式。
通过利用MATLAB的建模工具箱,用户可以轻松地构建线性和非线性模型,包括连续和离散模型。
用户只需通过输入系统的数学公式或离散数据,MATLAB即可自动生成系统的状态空间、传递函数或差分方程等表示形式。
此外,MATLAB还提供了参数估计和系统辨识等功能,可以根据实验数据自动拟合出合适的模型。
这些功能不仅节省了建模的时间和精力,还大大降低了建模的难度。
二、系统分析在控制系统设计的过程中,系统分析是确保系统性能和稳定性的重要步骤。
MATLAB提供了一系列的工具和函数,可以方便地对系统进行频域和时域的分析。
例如,通过调用MATLAB的频域分析工具箱,用户可以绘制系统的频率响应曲线,了解系统在不同频率下的增益和相位变化情况。
这对于稳定性分析和滤波器设计非常有帮助。
此外,MATLAB还提供了时域分析工具箱,可以对系统的过渡过程、稳态误差和阶跃响应等进行详细分析。
这些分析结果可以帮助用户了解系统的动态特性,并且为控制器的设计提供指导。
三、控制器设计在控制系统设计的最后阶段,控制器的设计是至关重要的环节。
MATLAB提供了多种控制器设计方法和算法,可以根据用户的需求和系统的特性进行选择。
例如,MATLAB中的PID Toolbox提供了经典的比例积分微分(PID)控制器设计方法,用户只需输入系统的传递函数和控制目标,即可自动计算出合适的PID参数。
MATLAB进行控制系统频域分析报告

一、基于MATLAB 的线性系统的频域分析基本知识(1)频率特性函数)(ωj G 。
设线性系统传递函数为:nn n n m m m m a s a s a s a b s b s b s b s G ++⋅⋅⋅++++⋅⋅⋅++=---1101110)( 则频率特性函数为:nn n n m m m m a j a j a j a b j b j b j b jw G ++⋅⋅⋅++++⋅⋅⋅++=---)()()()()()()(1101110ωωωωωω 由下面的MATLAB 语句可直接求出G(jw)。
i=sqrt(-1) % 求取-1的平方根GW=polyval(num ,i*w)./polyval(den ,i*w)其中(num ,den )为系统的传递函数模型。
而w 为频率点构成的向量,点右除(./)运算符表示操作元素点对点的运算。
从数值运算的角度来看,上述算法在系统的极点附近精度不会很理想,甚至出现无穷大值,运算结果是一系列复数返回到变量GW 中。
(2)用MATLAB 作奈魁斯特图。
控制系统工具箱中提供了一个MATLAB 函数nyquist( ),该函数可以用来直接求解Nyquist 阵列或绘制奈氏图。
当命令中不包含左端返回变量时,nyquist ()函数仅在屏幕上产生奈氏图,命令调用格式为:nyquist(num,den)nyquist(num,den,w)或者nyquist(G) nyquist(G,w)该命令将画出下列开环系统传递函数的奈氏曲线: )()()(s den s num s G = 如果用户给出频率向量w,则w 包含了要分析的以弧度/秒表示的诸频率点。
在这些频率点上,将对系统的频率响应进行计算,若没有指定的w 向量,则该函数自动选择频率向量进行计算。
w 包含了用户要分析的以弧度/秒表示的诸频率点,MATLAB 会自动计算这些点的频率响应。
当命令中包含了左端的返回变量时,即:[re,im,w]=nyquist(G)或[re,im,w]=nyquist(G,w)函数运行后不在屏幕上产生图形,而是将计算结果返回到矩阵re 、im 和w 中。
自动控制原理 matlab实验报告

自动控制原理实验(二)一、实验名称:基于MATLAB的控制系统频域及根轨迹分析二、实验目的:(1)、了解频率特性的测试原理及方法;(2)、理解如何用MATLAB对根轨迹和频率特性进行仿真和分析;(3)、掌握控制系统的根轨迹和频率特性两大分析和设计方法。
三、实验要求:(1)、观察给定传递函数的根轨迹图和频率特性曲线;(2)、分析同一传递函数形式,当K值不同时,系统闭环极点和单位阶跃响应的变化情况;(3)、K值的大小对系统的稳定性和稳态误差的影响;(4)、分析增加系统开环零点或极点对系统的根轨迹和性能的影响。
四、实验内容及步骤(1)、实验指导书:实验四(1)、“rlocus”命令来计算及绘制根轨迹。
会出根轨迹后,可以交互地使用“rlocfind”命令来确定点击鼠标所选择的根轨迹上任意点所对应的K值,K值所对应的所有闭环极点值也可以使用形如“[K, PCL] = rlocfind(G1)”命令来显示。
(2)、波特图:bode(G1, omga)另外,bode图还可以通过下列指令得出相位和裕角:[mag,phase,w] = bode(sys)(3)、奈奎斯特图:nuquist(G, omega)(2)课本:例4-1、4-2、4-7五实验报告要求(1)、实验指导书:实验四思考题请绘制下述传递函数的bode图和nyquist图。
1. 根据实验所测数据分别作出相应的幅频和相频特性曲线;2. 将思考题的解题过程(含源程序)写在实验报告中。
幅频特性曲线相频特性曲线Gs = zpk([10], [-5; -16; 9], 200)subplot(1, 2, 1)bode(Gs)gridsubplot(1, 2, 2)nyquist(Gs)grid(2)课本:例4-1、4-2、4-7图像结果:程序:Gs = zpk([-1], [0; -2; -3],1) rlocus(Gs)图像结果:程序:Gs = zpk([-2], [-1-j; -1+j],1) rlocus(Gs)程序:K=[0.5 1 2]for i=1:1:3num=[1,1,0,0]; den=[1,1,K(i)]; sys=tf(num,den); rlocus(sys); hold ongrid onend图像结果:目标:改变增益K和转折频率依次调节源程序:k1=[4.44,10,20];num=[1,2];den=conv([1,1],[1,2,4]);%一阶转折频率 1/T(wn1=2,wn2=1)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 num1=[1,1];den1=conv([1,2],[1,2,4]);%一阶转折频率 1/T(wn1=1,wn2=2)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 t=[0:0.1:7]; %for i=1:3g0=tf(k1(i)*num,den);g=feedback(g0,1);[y,x]=step(g,t);c(:,i)=y;g1=tf(k1(i)*num1,den1);g(1)=feedback(g1,1);[y1,x]=step(g(1),t);c1(:,i)=y1;endplot(t,c(:,1),'-',t,c(:,2),'-',t,c(:,3),'-',t,c1(:,1),'-',t,c1(:,2), '-',t,c1(:,3),'-');gridxlabel('Time/sec'),ylabel('out')结果分析:在本题中(1)改变k值:k值越大,超调量越大,调节时间越长,峰值时间越短,稳态误差越小(2)改变转折频率:超调量,调节时间,峰值时间,稳态误差同样有相应的变化。
基于matlab gui的控制系统界面设计毕业设计论文

基于MATLAB GUI的控制系统界面设计摘要:MATLAB语言是一种十分有效的工具,能容易地解决在系统仿真及控制系统设计领域的教学与研究中遇到的问题,它可以将使用者从频繁的底层编程中解放出来,把有限的宝贵时间更多地华仔解决科学问题上。
MATLABA GUI是MATLAB人际交互界面。
由于GUI本身提供了windows基本控件的支持,并且具有良好的时间驱动机制,同时提供了MATLAB数学库的接口,所以GUI对于控制系统仿真的平台设计显得十分合适。
GUI对于每个用户窗口生成.fig和.m 文件。
前者负责界面的设计信息,后者负责后台代码的设计。
本文界面设计主要基于MATLAB GUI平台,结合控制系统基础理论和MATLAB控制系统工具箱,实现了用于控制系统界面的设计。
主要包括:进行常规控制环节(比如PID)的图形界面设计,能够在已知传输函数的情况下,输出常用响应曲线。
关键词:控制系统;MATLAB GUI;计算机设计Control system based on MATLAB GUI interface designAbstract: MATLAB language is a very effective tool,and can be easily resolved in the system simulation and control system of teaching in the field of computer-aided design and research problems,it could be the bottom of the user from tedious programming liberate the limted spend more valuable time to solve scientific problems. The MATLAB GUI is the interative interface.As the GUI itself provides the basic control windows support,and has a good mechanism for event-driven,while providing the MATLAB Math Library interface,the GUI for control system simulation platform for the design of it is suitable. GUI window generated for each user.Figand .M file. The former is responsible for the design of the interfaceinformation,which is responsible for the design of the background code.Research done in this article is mainly based on MATLAB GUI platform,the basis of combination of control syetem theory and MATLAB Control System Toolbox,the realization of control systems for computer-aided analysis and design software.Mainly includes:routine control links,such as PID,graphical interface design,can in the known transfer function of the case,the output respnonse curve is commonly used.Key words: Control System;MATLAB GUI;Computer design目录1 概述 (1)1.1 本文研究的目的以及意义 (1)1.2 已了解的本课题国内外研究现状 (1)1.3 本课题研究内容 (3)2 控制系统与MATLAB语言 (3)2.1 控制系统理论基础 (3)2.1.1 控制系统的古典理论与现代理论 (3)2.1.2 控制系统理论的基本内容 (4)2.2 MATLAB语言与控制系统工具箱 (4)2.2.1 MATLAB软件介绍 (5)2.2.2 控制系统工具箱介绍 (7)3 MATLAB简介及应用 (9)3.1 MATLAB GUI (9)3.2 图形用户界面设计工具的启动 (10)3.2.1图形用户界面设计工具的启动方式 (10)3.2.2 菜单方式 (10)3.2.3 图形用户界面设计窗口 (13)3.3 图形用户界面开发环境(GUIDE) (14)3.4 控件对象及属性 (16)3.5 菜单设计 (18)3.5.1 建立用户菜单 (18)3.5.2 菜单对象常用属性 (18)3.5.3 快捷菜单 (18)3.5.4 对话框设计 (19)3.5.5 公共对话框 (19)3.6 GUI程序设计 (19)4 GUI控制系统界面 (20)4.1 GUI控制系统界面设计 (20)4.1.1 具体设计步骤 (20)4.2 具体实现过程 (23)4.2.1 运行效果 (23)4.2.2 实现代码 (24)[参考文献] (25)附录 (26)谢辞 (29)1 概述1.1 本文研究的目的以及意义自动控制原理是自动控制专业和自动化专业的主要课程之一[3],是研究自动控制技术的基础理论课,是必修的专业基础课程。
实验三利用MATLAB进行系统频域分析

实验三利用MATLAB进行系统频域分析系统频域分析是指通过对系统的输入输出信号进行频域分析,从而分析系统的频率响应特性和频率域特征。
利用MATLAB进行系统频域分析可以方便地实现信号的频谱分析、滤波器设计等功能。
下面将介绍如何利用MATLAB进行系统频域分析的基本步骤。
一、信号频谱分析1. 将信号导入MATLAB环境:可以使用`load`函数导入数据文件,或者使用`audioread`函数读取音频文件。
2. 绘制信号的时域波形图:使用`plot`函数绘制信号的时域波形图,以便对信号的整体特征有一个直观的了解。
3. 计算信号的频谱:使用快速傅里叶变换(FFT)算法对信号进行频谱分析。
使用`fft`函数对信号进行频域变换,并使用`abs`函数计算频谱的幅度。
4. 绘制信号的频谱图:使用`plot`函数绘制信号的频谱图,以便对信号的频率特征有一个直观的了解。
二、滤波器设计1.确定滤波器类型和要求:根据系统的要求和信号的特性,确定滤波器的类型(如低通滤波器、高通滤波器、带通滤波器等)和相应的频率响应要求。
2. 设计滤波器:使用MATLAB中的滤波器设计函数(如`fir1`、`butter`、`cheby1`等)来设计滤波器。
这些函数可以根据指定的滤波器类型、阶数和频率响应要求等参数来生成相应的滤波器系数。
3. 应用滤波器:使用`filter`函数将滤波器系数应用到信号上,得到滤波后的信号。
三、系统频率响应分析1. 生成输入信号:根据系统的要求和实际情况,生成相应的输入信号。
可以使用MATLAB中的信号生成函数(如`square`、`sine`、`sawtooth`等)来生成基本的周期信号,或者使用`randn`函数生成高斯白噪声信号。
2.绘制输入信号的频谱图:使用前面提到的信号频谱分析方法,绘制输入信号的频谱图。
3. 输入信号与输出信号的频域分析:使用`fft`函数对输入信号和输出信号进行频谱分析,并使用`abs`函数计算频谱的幅度。
基于Matlab的控制系统频域分析

基于Matlab的控制系统频域分析為解决经典控制理论频域分析中计算和绘图复杂的问题,引入了基于Matlab 的分析方法。
利用Matlab对具体实例进行了Nyquist图和Bode图的绘制及性能指标的计算,说明了Matlab在控制理论应用中能节省大量的计算量,提高工作效率。
标签:控制系统分析;频率特性;Matlab仿真稳定性、准确性、快速平稳性是控制系统的主要性能指标,经典控制理论的主要内容是通过时域法、复域法和频域法三大方法研究分析线性系统的性能指标。
绘制根轨迹、Nyquist图、Bode图等是控制类工程技术人员的必备技能之一,但是手工绘图效率低,容易出现较大误差,给工程设计和系统分析带来不便。
随着计算机技术的发展,Matlab等仿真软件在控制工程领域得到了广泛应用。
1 频域法简介频域法又称频率特性法,频率特性是指线性系统输入r(t)为正弦信号时,其稳态输出与输入的幅值比、相角差随频率变化的规律,其中:为稳态输出和输入的幅值比,称为幅频特性;为稳态输出和输入的相角差,称为相频特性。
一般对线性定常系统而言,频率特性,系统传递函数中令,即得系统频率特性,其物理意义明确,许多元部件此特性都可用实验法确定,所以工程上应用广泛。
2 Matlab相关函数Matlab是一种广泛应用于工程计算及数值分析领域的新型高级语言。
Matlab 功能强大、简单易学、编程效率高,深受广大科技工作者的欢迎。
自动控制是Matlab最重要的应用领域之一,Matlab支持控制系统设计过程的每个环节:系统建模、分析、仿真到控制器设计和实现,并可以用于不同领域的系统设计。
本文进行频域分析所涉及的相关函数简单介绍如下:bode(num,den):给定传递函数(num,den)作波特图;margin(num,den):作波特图,计算波特图上的稳定裕量,并将计算结果表示在图的上方;nyquist(num,den):给定传递函数(num,den)作Nyquist图。
MATLAB用于控制系统频域分析

例5-9-1超前校正 超前校正
K 20 = G0 ( s ) = s (0.5s + 1) 0.5s 2 + s 20(0.25s + 1) 5s + 20 =Байду номын сангаасGe ( s ) = Gc ( s )G0 ( s ) = s (0.5s + 1)(0.04 s + 1) 0.02 s 3 + 0.54 s 2 + s
>> bode(20,[0.5,1,0]); >> hold on; >> bode([5,20],[0.02,0.54,1,0]);grid; >>
K 5 = G0 ( s ) = s ( s + 1)(0.5s + 1) 0.5s 3 + 1.5s 2 + s 5(12.5s + 1) 62.5s + 5 = Ge ( s ) = Gc ( s )G0 ( s ) = s ( s + 1)(0.5s + 1)(125s + 1) 62.5s 4 + 188s 3 + 126.5s 2 + s
MATLAB用于控制系统频域分析 用于控制系统频域分析
《自动控制原理》课件系列
哈尔滨工业大学航天学院控制科学与工程系 王彤
0型系统Nyquist图的绘制 图的绘制
5 5 G ( s) = = 3 (2s + 1)( s + 1)(0.5s + 1) s + 3.5s 2 + 3.5s + 1
基于MATLAB的控制系统设计与仿真实践

基于MATLAB的控制系统设计与仿真实践控制系统设计是现代工程领域中至关重要的一部分,它涉及到对系统动态特性的分析、建模、控制器设计以及性能评估等方面。
MATLAB作为一种强大的工程计算软件,在控制系统设计与仿真方面有着广泛的应用。
本文将介绍基于MATLAB的控制系统设计与仿真实践,包括系统建模、控制器设计、性能评估等内容。
1. 控制系统设计概述控制系统是通过对被控对象施加某种影响,使其按照既定要求或规律运动的系统。
在控制系统设计中,首先需要对被控对象进行建模,以便进行后续的分析和设计。
MATLAB提供了丰富的工具和函数,可以帮助工程师快速准确地建立系统模型。
2. 系统建模与仿真在MATLAB中,可以利用Simulink工具进行系统建模和仿真。
Simulink是MATLAB中用于多域仿真和建模的工具,用户可以通过拖拽图形化组件来搭建整个系统模型。
同时,Simulink还提供了各种信号源、传感器、执行器等组件,方便用户快速搭建复杂的控制系统模型。
3. 控制器设计控制器是控制系统中至关重要的一部分,它根据系统反馈信息对输出信号进行调节,以使系统输出达到期望值。
在MATLAB中,可以利用Control System Toolbox进行各种类型的控制器设计,包括PID控制器、根轨迹设计、频域设计等。
工程师可以根据系统需求选择合适的控制器类型,并通过MATLAB进行参数调节和性能优化。
4. 性能评估与优化在控制系统设计过程中,性能评估是必不可少的一环。
MATLAB提供了丰富的工具和函数,可以帮助工程师对系统进行性能评估,并进行优化改进。
通过仿真实验和数据分析,工程师可以评估系统的稳定性、鲁棒性、响应速度等指标,并针对性地进行调整和改进。
5. 实例演示为了更好地说明基于MATLAB的控制系统设计与仿真实践,我们将以一个简单的直流电机速度控制系统为例进行演示。
首先我们将建立电机数学模型,并设计PID速度控制器;然后利用Simulink搭建整个闭环控制系统,并进行仿真实验;最后通过MATLAB对系统性能进行评估和优化。
《自动控制原理》Matlab求解控制系统频域分析实验

《自动控制原理》Matlab求解控制系统频域分析实验
一、实验目的
1、加深了解系统频率特性的概念。
2、学习使用Matlab软件绘制Nyquist图、Bode图的基本方法。
3、掌握典型环节的频率特性。
二、实验仪器
Matlab2014b版
三、实验原理
1.奈奎斯特图(幅相频率特性图)
MATLAB为用户提供了专门用于绘制奈奎斯特图的函数nyquist
axis([-2,0.4,-1.5,1.5]);
k=500;
num=[1,10];
den=conv([1,0],conv([1,1],conv([1,20],[h,50])));
w=logspace(-1,3,200)
bode(k*num,den,w);
grid;
五、实验原始数据记录与数据处理
六、实验结果与分析讨论
范围是自动确定的。当需要指定幅值范围和相角范围时,则需用下面的功能指令:
[mag,phase,w]=bode(num,den,w)
四、实验内容及步骤
z=[]:
p=[0,-1,-2]:
k=5;
g=zpk(z,p,k):
nyquist(g);
w=0.5:0.1:10:
figure(2):
nyquist(g:w);
基于MATLAB自动控制系统时域频域分析与仿真

基于MATLAB自动控制系统时域频域分析与仿真MATLAB是一款强大的数学软件,也是自动控制系统设计的常用工具。
它不仅可以进行时域分析和频域分析,还可以进行相关仿真实验。
本文将详细介绍MATLAB如何进行自动控制系统的时域和频域分析,以及如何进行仿真实验。
一、时域分析时域分析是指对系统的输入信号和输出信号进行时域上的观察和分析,以了解系统的动态特性和稳定性。
MATLAB提供了一系列的时域分析工具,如时域响应分析、稳态分析和步骤响应分析等。
1.时域响应分析通过时域响应分析,可以观察系统对于不同的输入信号的响应情况。
在MATLAB中,可以使用`lsim`函数进行系统的时域仿真。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
-定义输入信号。
- 使用`lsim`函数进行时域仿真,并绘制系统输出信号。
例如,假设我们有一个二阶传递函数模型,并且输入信号为一个单位阶跃函数,可以通过以下代码进行时域仿真:```num = [1];den = [1, 1, 1];sys = tf(num, den);t=0:0.1:10;u = ones(size(t));[y, t, x] = lsim(sys, u, t);plot(t, y)```上述代码中,`num`和`den`分别表示系统的分子和分母多项式系数,`sys`表示系统模型,`t`表示时间序列,`u`表示输入信号,`y`表示输出信号。
通过绘制输出信号与时间的关系,可以观察到系统的响应情况。
2.稳态分析稳态分析用于研究系统在稳态下的性能指标,如稳态误差和稳态标准差。
在MATLAB中,可以使用`step`函数进行稳态分析。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
- 使用`step`函数进行稳态分析,并绘制系统的阶跃响应曲线。
例如,假设我们有一个一阶传递函数模型,可以通过以下代码进行稳态分析:```num = [1];den = [1, 1];sys = tf(num, den);step(sys)```通过绘制系统的阶跃响应曲线,我们可以观察到系统的稳态特性。
基于MATLAB的控制系统数学建模

频率响应与传递函数
系统的频率响应反映了系统对不同频率输入信号的响应能力,传 递函数描述了系统输入输出之间的数学关系。
频域性能指标
包括幅值裕度、相位裕度、谐振频率等,用于评价系统的稳定性 和性能。
利用MATLAB进行频域分析
01
MATLAB频域分析 工具箱
习等功能,提高系统的性能和稳定性。
绿色环保
未来控制系统将更加注重绿色环保,采用 更加高效、节能的技术和设备,减少对环
境的影响。
多领域融合
控制系统将与其他领域进行更多的交叉融 合,如计算机科学、机械工程、电子工程 等,形成更加综合的学科体系。
远程控制和自动化
随着互联网和物联网技术的普及,远程控 制和自动化将成为控制系统的重要发展方 向,提高生产效率和便利性。
实例分析:典型环节传递函数建模
一阶惯性环节
传递函数为`1/(T*s+1)`,其中`T`为时间常数,`s`为复频率。 在MATLAB中可表示为`sys = tf([1], [T, 1])`。
二阶振荡环节
传递函数为`1/(s^2/ωn^2+2ζs/ωn+1)`,其中`ωn`为自然频率,`ζ`为阻 尼比。在MATLAB中可表示为`sys = tf([1], [1/ωn^2, 2ζ/ωn, 1])`。
数学模型描述方法
微分方程法
通过列写系统或元件的微分方程来描述系统的动态特性,适用于线 性定常系统、非线性系统以及时变系统。
传递函数法
在零初始条件下,系统输出量的拉普拉斯变换与输入量的拉普拉斯 变换之比,适用于线性定常系统。
状态空间法
以系统的状态变量为基础,通过状态方程和输出方程来描述系统的动 态特性,适用于多输入多输出系统、非线性系统以及时变系统。
MATLAB与控制系统的频域分析

、
对数 频率特 性 图 ( 德 图 ) 伯
B d (u d nw) o en m,e, 函数 可利用 指 定 的角 频率 矢量绘 制 出系 统 的伯德 图。一 典型 二阶系 统 开环传 递 函数
G 南 (
要改参 制统雌 并析 对绕 影。TB 求变数 系 分参 / 响 A 系 ML A
应用。
关键 词:MA L T AB;伯 德 图;奈 奎斯特 图;频率 特性
中图分类号 :T 2 4 P 7 文献标 识码 :A 文章 编号 : 1 0- 6 2 ( 0 )O 0 5 . 4 0 8- 1 9 2 1 1 l 8- 0
工程 上 ,控 制系 统性 能分 析 目前 广泛应 用 的有 两种 方法 :一种 是频 率特 性法 :另一种 是 根轨 迹法 。 这些方 法 的使 用 需要绘 制 时间 响应 曲线 、 轨迹 图及频 率特 性 中 的 B d 、 q i 图和 Ni os曲线 等 。 根 o e图 Ny us t c l h 这些 曲线 的绘制 过去 通 常是 由手 工完 成 的 ,其 误差较 大 、效率 低 ,对 于 某 些较 复杂 的高 阶系 统 ,很难 用
特 性 的幅值和 角度值 ,当该函 数不 带返 回参数 时 ,将直 接在 屏幕 上绘 制 出系统 的伯 德 图 。取 wn1,,取 =0 亏 [.:06 ] O 2 .:1时的二 阶系 统 的伯 德 图可直 接 由 b d 0" 得  ̄ . 行 下面 的 M 文件 ,运行 后得 到 的伯德 oe i  ̄数 J l o执
f ri=ko a o i si
sb lt ,,) u po( 1 2 1
gi n rdo
tl ‘ o e arm’ ie B d ga ) t( Di ; xa l ‘rq e c (a /e ) ; l e Fe u ny rd sc’ b( ) ya l ‘ g i d (B ’ l e Ma nt e ) ; b( u d )
实验3-基于matlab的控制系统频域分析

利用MATLAB绘制系统的频率特性曲线举例
MATLAB中提供了简单的命令,可用于绘制系统的 频率特性曲线。 例:已知
Go (s) 1 s s 1
2
试绘制系统的频率特性曲线。 解:在MATLAB Command Window下键入下列语句: num=[0 0 1]; den=[1 1 1] ; w=logspace(-1,2); Bode(num,den.w)
5.求系统模值裕度与相位裕度的函数
margin( )
函数命令调用格式: [Gm,Pm,Wcp,Wcg]=margin(sys) [Gm,Pm,Wcp,Wcg]=margin(mag,phase,w)
Margin(sys)
margin(mag,phase, w)
函数命令使用说明: margin( )函数可以从频率响应数据中计算出模值 稳定裕度、相位稳定裕度及其对应的角频率。输入参 量sys一般是用系统的开环传递函数描述的系统模型, 对于开环SISO系统,既可以是连续时间系统也可以是 离散时间系统。当不带输出变量引用函数时, margin( )函数可在当前图形窗口中绘制出带有稳定裕 度的Bode图。 margin(mag,phase,w)函数可以在当前窗口中绘制 出带有系统的模值裕度与相位裕度Bode图,其中, mag,phase及w分别为由bode或dbode求出的模值裕度、 相位裕度及其对应的角频率。
可以得到如图所示的波德图。
键入语句: nyquist(num,den,{1/57.3,100/57.3}) grid 可以得到系统的极坐标图。
求系统的幅值和相位稳定裕度 得到频率特性后,还可以利用命令: [g,p,wc,wp]=margin(num,den) 本例结果如下: g= Inf p= 90.0000 wg= NaN wp= 1.0000 该系统幅值稳定裕度为无穷大,不存在穿越-1800的频率 点,在ω=1处,幅值为1,相位稳定裕度为900。
使用Matlab进行控制系统设计的基本步骤

使用Matlab进行控制系统设计的基本步骤控制系统设计是一项重要的工程任务,它涉及到系统建模、控制器设计和系统分析等方面。
而Matlab作为一款强大的数学工具软件,提供了丰富的功能和工具,可以帮助工程师实现控制系统设计的各个环节。
本文将介绍使用Matlab进行控制系统设计的基本步骤。
一、系统建模控制系统设计的第一个关键步骤是系统建模。
系统建模是将实际的物理系统或过程转化为数学方程的过程。
Matlab提供了多种建模方法,可以根据实际需求选择适合的方法。
1.1 时域建模时域建模是一种基于微分方程和代数方程的建模方法,适合描述连续系统的动态特性。
可以使用Matlab的Simulink工具箱进行时域建模,通过拖拽模块和连接线的方式,构建系统模型。
1.2 频域建模频域建模是一种基于频率响应的建模方法,适合描述系统的幅频、相频特性。
可以使用Matlab的控制系统工具箱进行频域建模,通过输入系统的传递函数或状态空间矩阵,得到系统的频域特性。
1.3 时频域建模时频域建模是一种综合了时域和频域特性的建模方法,适合描述非线性和时变系统。
可以使用Matlab的Wavelet工具箱进行时频域建模,通过连续小波变换或离散小波变换,得到系统的时频域特性。
二、控制器设计在系统建模完成后,接下来是设计控制器。
控制器设计的目标是使得系统具有所需的稳定性、响应速度和鲁棒性等性能。
2.1 经典控制器设计Matlab提供了经典控制器的设计函数,如比例控制器(P控制器)、比例积分控制器(PI控制器)和比例积分微分控制器(PID控制器)等。
可以根据系统的特性和性能要求,选择合适的控制器类型和调节参数。
2.2 线性二次调节器设计线性二次调节(LQR)是一种优化控制方法,可以同时优化系统的稳态误差和控制能量消耗。
在Matlab中,可以使用lqr函数进行LQR控制器的设计,通过调整权重矩阵来获得不同的控制性能。
2.3 非线性控制器设计对于非线性系统,经典控制器往往无法满足要求。
实验八 基于MATLAB控制系统的频率法串联超前校正设计

实验八基于MATLAB控制系统的频率法串联超前校正设计一、实验目的1、对给定系统设计满足频域性能指标的串联校正装置。
2、掌握频率法串联有源和无源超前校正网络的设计方法。
3、掌握串联校正环节对系统稳定性及过渡过程的影响。
二、实验原理用频率法对系统进行超前校正的基本原理,是利用超前校正网络的相位超前特性来增大系统的相位裕量,以达到改善系统瞬态响应的目标。
为此,要求校正网络最大的相位超前角出现在系统的截止频率(剪切频率)处。
串联超前校正的特点:主要对未校正系统中频段进行校正,使校正后中频段幅值的斜率为-20dB/dec,且有足够大的相位裕度;超前校正会使系统瞬态响应的速度变快,校正后系统的截止频率增大。
这表明校正后,系统的频带变宽,瞬态响应速度变快,相当于微分效应;但系统抗高频噪声的能力变差。
1、用频率法对系统进行串联超前校正的一般步骤为:1)根据稳态误差的要求,确定开环增益K。
2)根据所确定的开环增益K,画出未校正系统的波特图,计算未校正系统的相位裕度。
3)计算超前网络参数a和T。
4)确定校正网络的转折频率。
5)画出校正后系统的波特图,验证已校正系统的相位裕度。
6)将原有开环增益增加倍,补偿超前网络产生的幅值衰减,确定校正网络组件的参数。
三、实验内容1、频率法有源超前校正装置设计例1、已知单位负反馈系统被控制对象的传递函数为:试用频率法设计串联有源超前校正装置,使系统的相位裕度 ,静态速度误差系数 。
clc; clear;delta=2; s=tf('s');G=1000/(s*(0.1*s+1)*(0.001*s+1));margin(G) 原系统bode 图[gm,pm]=margin(G) phim1=50;phim=phim1-pm+delta; phim=phim*pi/180;alfa=(1+sin(phim))/(1-sin(phim)); a=10*log10(alfa); [mag,phase,w]=bode(G); adB=20*log10(mag); Wm=spline(adB,w,-a); t=1/(Wm*sqrt(alfa)); Gc=(1+alfa*t*s)/(1+t*s); [gmc,pmc]=margin(G*Gc) figure;margin(G*Gc) 矫正后bode figure(1);step(feedback(G,1)) 矫正后01 figure(2);step(feedback(G*Gc,1)) 矫正后02结果显示: gm = 1.0100 pm =0()(0.11)(0.0011)K G s s s s =++045γ≥11000v K s -=0.0584gmc =7.3983pmc =45.7404分析:根据校正前后阶跃响应的曲线可知:校正后的系统满足动态性能指标以及频域性能指标。
利用Matlab进行控制系统设计和分析

利用Matlab进行控制系统设计和分析控制系统是各个工程领域中不可或缺的一部分。
它可以用来控制机器人、飞行器、电机以及其他众多的实际工程应用。
Matlab作为一种功能强大的数值计算软件,提供了丰富的工具和函数来进行控制系统设计和分析。
本文将介绍如何利用Matlab来进行控制系统的设计和分析。
一、控制系统基本概念在开始之前,我们先来了解一些控制系统的基本概念。
控制系统由三个基本组成部分构成:输入、输出和反馈。
输入是指信号或者指令,输出则是系统对指令的响应,而反馈则是输出信号对系统输入的影响。
二、Matlab中的控制系统工具箱Matlab提供了专门用于控制系统设计和分析的工具箱。
其中最重要的是Control System Toolbox。
该工具箱中包含了一系列用于控制系统设计和分析的函数和工具。
使用Control System Toolbox,我们可以很方便地进行控制系统的建模、设计和分析。
三、控制系统的建模控制系统的建模是指将实际系统抽象为数学模型。
在Matlab中,我们可以使用State Space模型、Transfer Function模型以及Zero-Pole-Gain模型来描述控制系统。
1. 状态空间模型状态空间模型是一种常用的描述系统动态响应的方法。
在Matlab中,我们可以使用stateSpace函数来创建状态空间模型。
例如,我们可以通过以下方式创建一个简单的二阶状态空间模型:A = [0 1; -1 -1];B = [0; 1];C = [1 0];D = 0;sys = ss(A, B, C, D);2. 传递函数模型传递函数模型是另一种常用的描述系统动态响应的方法。
在Matlab中,我们可以使用tf函数来创建传递函数模型。
例如,我们可以通过以下方式创建一个简单的一阶传递函数模型:num = 1;den = [1 2];sys = tf(num, den);3. 零极点增益模型零极点增益模型是用来描述系统频域特性的一种方法。
基于MATLAB的控制系统频域设计

基于MATLAB的控制系统频域设计姓名:学院:专业:班级:学号:基于MATLAB的控制系统频域设计一实验目的1. 利用计算机作出开环系统的波特图2. 观察记录控制系统的开环频率特性3. 控制系统的开环频率特性分析二预习要点1.预习Bode图和Nyquist图的画法;2.Nyquist稳定性判据内容。
三实验方法1、奈奎斯特图(幅相频率特性图)对于频率特性函数G(jw),给出w从负无穷到正无穷的一系列数值,分别求出Im(G(jw))和Re(G(jw))。
以Re(G(jw)) 为横坐标, Im(G(jw)) 为纵坐标绘制成为极坐标频率特性图。
MATLAB提供了函数nyquist()来绘制系统的极坐标图,其用法如下:nyquist(a,b,c,d):绘制出系统的一组Nyquist曲线,每条曲线相应于连续状态空间系统[a,b,c,d]的输入/输出组合对。
其中频率范围由函数自动选取,而且在响应快速变化的位置会自动采用更多取样点。
nyquist(a,b,c,d,iu):可得到从系统第iu个输入到所有输出的极坐标图。
nyquist(num,den):可绘制出以连续时间多项式传递函数表示的系统的极坐标图。
nyquist(a,b,c,d,iu,w)或nyquist(num,den,w):可利用指定的角频率矢量绘制出系统的极坐标图。
当不带返回参数时,直接在屏幕上绘制出系统的极坐标图(图上用箭头表示w的变化方向,负无穷到正无穷)。
当带输出变量[re,im,w]引用函数时,可得到系统频率特性函数的实部re和虚部im及角频率点w矢量(为正的部分)。
可以用plot(re,im)绘制出对应w从负无穷到零变化的部分。
2、对数频率特性图(波特图)对数频率特性图包括了对数幅频特性图和对数相频特性图。
横坐标为频率w,采用对数分度,单位为弧度/秒;纵坐标均匀分度,分别为幅值函数20lgA(w),以dB表示;相角,以度表示。
MATLAB提供了函数bode()来绘制系统的波特图,其用法如下:bode(a,b,c,d,iu):可得到从系统第iu个输入到所有输出的波特图。
应用MATLAB实现自动控制系统的频域法校正
2 0 1 4年第 3期
J o u na r l o f Gu a n g d o n g P o l y t e c h n i c No r ma l Un i v e r s i t y
应 用 MA T L AB实 现 自动 控 制 系 统 的频 域 法 校 正
如下 :
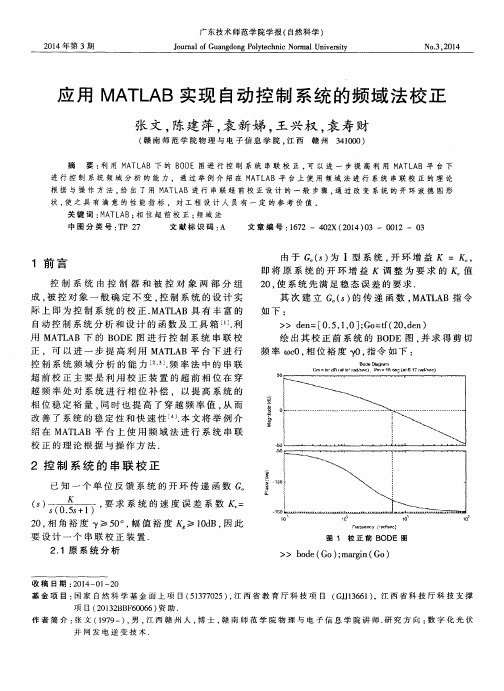
> >d e n =[ 0 . 5 , 1 , 0] ; G o = f( i 2 0 , d e n ) 绘出其校正前系统 的 B O DE 图 . 并 求 得 剪 切
频率 ( 1 ) c O, 相 位 裕 度 0, 指令 如下 :
B u ∞ D b ”
正 , 可 以 进 一 步 提 高 利 用 MA T L A B 平 台 下 进 行 控制系统频域 分析 的能 力【 ’ , . 频 率 法 中 的 串 联
1 前 言
控 制 系 统 由 控 制 器 和 被 控 对 象 两 部 分 组
由于 G 。 ( S ) 为 I型 系 统 , 开 环 增 益 K =K ,
占2 p n 0 m 求 的 即将原 系统 的开 环增 益 K调 整 为 要
值
2 0, 使 系 统 先 满 足 稳 态误 差 的 要 求 .
项 目( 2 0 1 3 2 B B F 6 0 0 6 6) 资 助.
作者 简 介 : 张文 ( 1 9 7 9 一), 男 , 江 西赣 州 人 , 博士 , 赣 南 师 范学 院 物 理 与 电子信 息 学 院讲 师 . 研究方向 : 数 字 化 光 伏
并 网发 电逆 变技术 .
p 】
2. 2 相 位 超 前 校 正 装 置 设 计
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB的控制系统频域设计姓名:学院:专业:班级:学号:基于MATLAB的控制系统频域设计一实验目的1. 利用计算机作出开环系统的波特图2. 观察记录控制系统的开环频率特性3. 控制系统的开环频率特性分析二预习要点1.预习Bode图和Nyquist图的画法;2.Nyquist稳定性判据内容。
三实验方法1、奈奎斯特图(幅相频率特性图)对于频率特性函数G(jw),给出w从负无穷到正无穷的一系列数值,分别求出Im(G(jw))和Re(G(jw))。
以Re(G(jw)) 为横坐标, Im(G(jw)) 为纵坐标绘制成为极坐标频率特性图。
MATLAB提供了函数nyquist()来绘制系统的极坐标图,其用法如下:nyquist(a,b,c,d):绘制出系统的一组Nyquist曲线,每条曲线相应于连续状态空间系统[a,b,c,d]的输入/输出组合对。
其中频率范围由函数自动选取,而且在响应快速变化的位置会自动采用更多取样点。
nyquist(a,b,c,d,iu):可得到从系统第iu个输入到所有输出的极坐标图。
nyquist(num,den):可绘制出以连续时间多项式传递函数表示的系统的极坐标图。
nyquist(a,b,c,d,iu,w)或nyquist(num,den,w):可利用指定的角频率矢量绘制出系统的极坐标图。
当不带返回参数时,直接在屏幕上绘制出系统的极坐标图(图上用箭头表示w的变化方向,负无穷到正无穷)。
当带输出变量[re,im,w]引用函数时,可得到系统频率特性函数的实部re和虚部im及角频率点w矢量(为正的部分)。
可以用plot(re,im)绘制出对应w从负无穷到零变化的部分。
2、对数频率特性图(波特图)对数频率特性图包括了对数幅频特性图和对数相频特性图。
横坐标为频率w,采用对数分度,单位为弧度/秒;纵坐标均匀分度,分别为幅值函数20lgA(w),以dB表示;相角,以度表示。
MATLAB提供了函数bode()来绘制系统的波特图,其用法如下:bode(a,b,c,d,iu):可得到从系统第iu个输入到所有输出的波特图。
bode(a,求取系统对数频率特性图(波特图):bode()求取系统奈奎斯特图(幅相曲线图或极坐标图):nyquist() b,c,d):自动绘制出系统的一组Bode图,它们是针对连续状态空间系统[a,b,c,d]的每个输入的Bode图。
其中频率范围由函数自动选取,而且在响应快速变化的位置会自动采用更多取样点。
bode(num,den):可绘制出以连续时间多项式传递函数表示的系统的波特图。
bode(a,b,c,d,iu,w)或bode(num,den,w):可利用指定的角频率矢量绘制出系统的波特图。
当带输出变量[mag,pha,w]或[mag,pha]引用函数时,可得到系统波特图相应的幅值mag 、相角pha 及角频率点w 矢量或只是返回幅值与相角。
相角以度为单位,幅值可转换为分贝单位:magdb=20×log10(mag) 四 实验内容下面举例说明用MATLAB 对控制系统频域设计1.用Matlab 作Bode 图.画出对应Bode 图 , 并加标题. (1)25425)(2++=s s s G num=25;den=[1 4 25]; G=tf(num,den); figure(1) margin(G); figure(2) nichols(G);axis([-207 0 -40 40]);ngrid figure(3) nyquist(G); axis equalBode DiagramGm = Inf dB (at Inf rad/sec) , P m = 68.9 deg (at 5.83 rad/sec)Frequency (rad/sec)10101010-180-135-90-450P h a s e (d e g)-60-40-2020M a g n i t u d e (d B )(2))92.1()12.0(9)(22++++=s s s s s s G num=conv([0 1],[1 0.2 1]);den=conv([1 0],[1 1.2 9]); G=tf(num,den); figure(1) margin(G);figure(2) nichols(G);axis([-207 0 -40 40]);ngrid figure(3) nyquist(G); axis equal-40-30-20-10010M a g n i t u d e (d B )10101010-90-4504590P h a s e (d e g )Bode DiagramGm = Inf , P m = 90.4 deg (at 0.11 rad/sec)Frequency (rad/sec)2.用Matlab 作 Nyquist 图.画对应Nyquist 图,并加网格标题.18.01)(2++=s s s G num=1;den=[1 0.8 1]; G=tf(num,den); figure(1) margin(G); figure(2) nichols(G);axis([-207 0 -40 40]);ngrid figure(3) nyquist(G); axis equal-1.5-1-0.50.511.5Nyquist DiagramReal AxisI m a g i n a r y A x i s3.典型二阶系统2222)(nn n s s s G ϖξϖϖ++=,试绘制ξ取不同值时的Bode 图。
取]0.1:1.0:1.0[,6==ξϖn 。
当w=6, ζ=0.1时num=36;den=[1 1.2 36]; G=tf(num,den); figure(1)margin(G);-60-40-2020M a g n i t u d e (d B)P h a s e (d e g )Bode D iagramGm = I nf dB (at I nf rad/sec) , P m = 16.3 deg (at 8.4 rad/sec)当w=6, ζ=1.0时num=36;den=[1 12 36]; G=tf(num,den); figure(1) margin(G);-50-40-30-20-100M a g n i t u d e (d B )10-110101102-180-135-90-450P h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/sec) , P m = -180 deg (at 0 rad/sec)Frequency (rad/sec)num=50;den=conv([1 5],[1 -2]); G=tf(num,den); figure(1) margin(G); figure(2) nichols(G);axis([-207 0 -40 40]);ngrid figure(3) nyquist(G); axis equal hold on impulse(G)4.某开环传函为:)2)(5(50)(-+=s s s G ,试绘制系统的Nyquist 曲线,并判断闭环系统稳定性,最后求出闭环系统的单位脉冲响应。
num=50;den=conv([1 5],[1 -2]); G=tf(num,den); figure(1) margin(G);figure(2) nichols(G);axis([-207 0 -40 40]);ngrid figure(3) nyquist(G); axis equal-1.5-1-0.50.511.5Nyquist DiagramReal AxisI m ag i n a r y A x i s有奈奎斯特图可知它有左半平面的开环极点,也可看出他包围了(-1,j0),所以系统不稳定。
01234567812345677单位脉冲响应Tim e (sec)A m p l i t u d e5.()⎩⎨⎧==++=1.0,5.0,1,21.0,12122ζζT Ts s T s G当T=0.1,ζ=2时 num=1;den=[0.01 0.4 1]; G=tf(num,den); figure(1) margin(G); figure(2) nichols(G);axis([-207 0 -40 40]);ngrid figure(3) nyquist(G); axis equal title('波特图')-0.8-0.6-0.4-0.20.20.40.60.8波特图Real AxisI m a g i n a r y A x i s当T=0.1,ζ=1时-0.8-0.6-0.4-0.20.20.40.60.8波特图R eal AxisI m a g i n a r y A x i s当T=0.1,ζ=0.5时-1.5-1-0.50.511.5波特图R eal AxisI m a g i n a r y A x i s当T=0.1,ζ=0.1时; num=1;den=[0.01 0.02 1]; G=tf(num,den); figure(1) margin(G); figure(2) nichols(G);axis([-207 0 -40 40]);ngrid figure(3) nyquist(G); axis equal title('波特图')-6-4-20246-6-4-2246波特图R eal AxisI m a g i n a r y A x i s6.()()()11.0101.06.31++=s s s s G要求:(a) 作波特图num=31.6;den=conv([1 0],[0.01 1]); den=conv(den,[0.1 1]); G=tf(num,den); figure(1) margin(G);-150-100-50050100M a g n i t u d e (d B )10-110101102103104P h a s e (d e g )Bode DiagramGm = 10.8 dB (at 31.6 rad/sec) , P m = 22.3 deg (at 16.3 rad/sec)Frequency (rad/sec)(b) 由稳定裕度命令计算系统的稳定裕度g L 和c ,并确定系统的稳定性 K=1/0.1;G0=zpk([],[0 -100 -10],K); [lg, γc,wx,wc]=margin(G0) lg =1.1000e+004 γc= 89.9370 wx = 31.6228 wc = 0.0100-50-40-30-20-1001020304050N yquist D iagramR eal AxisI m a g in a r y A x is有奈奎斯特图可知它有左半平面的开环极点,也可看出他包围了(-1,j0),所以系统不稳定。
