《振动力学》课程作业
《振动力学》习题集(含答案)【精选】精心总结

令 引起的静变形为 ,则有:
,即
令 + 引起的静变形为 ,同理有:
得:
则系统的自由振动可表示为:
其中系统的固有频率为:
注意到 与 方向相反,得系统的自由振动为:
1.9质量为m、长为l的均质杆和弹簧k及阻尼器c构成振动系统,如图E1.9所示。以杆偏角 为广义坐标,建立系统的动力学方程,给出存在自由振动的条件。若在弹簧原长处立即释手,问杆的最大振幅是多少?发生在何时?最大角速度是多少?发生在何时?是否在过静平衡位置时?
解:
(1)保持水平位置:
(2)微幅转动:
故:
2.10求图T 2-10所示系统的固有频率,刚性杆的质量忽略不计。
图T 2-10答案图T 2-10
解:
m的位置:
, ,
,
,
2.11图T 2-11所示是一个倒置的摆。摆球质量为m,刚杆质量可忽略,每个弹簧的刚度为 。
(1)求倒摆作微幅振动时的固有频率;
(2)摆球质量m为0.9 kg时,测得频率 为1.5 Hz,m为1.8 kg时,测得频率为0.75 Hz,问摆球质量为多少千克时恰使系统处于不稳定平衡状态?
图E1.2
解:
如图,令 为柱体的转角,则系统的动能和势能分别为:
利用 和 可得:
1.3转动惯量为J的圆盘由三段抗扭刚度分别为 , 和 的轴约束,如图E1.3所示。求系统的固有频率。
图E1.3
解:
系统的动能为:
和 相当于串联,则有:
以上两式联立可得:
系统的势能为:
利用 和 可得:
1.4在图E1.4所示的系统中,已知 ,横杆质量不计。求固有频率。
图E1.4答案图E1.4
解:
对m进行受力分析可得:
北航高等结构动力学(振动力学)大作业

《高等结构动力学》课程Case Study斜坡缓冲车辆的运动学模型与缓冲距离影响因素分析姓名: 班号: 学号:摘要: 为了计算无动力车辆在斜坡上的最小缓冲距离,本文建立了斜坡行驶车辆的半车模型的运动学方程,采用龙格库达法对微分方程求解,得到初始速度与斜坡角度对缓冲距离的影响规律。
1.引言为防止制动失灵的车辆冲下山谷, 盘山公路的下行方向每隔一定距离需要设置一个缓冲区,如图1所示。
缓冲区一般由一段具有上升坡度的渣土路面形成。
制动失灵的车辆驶入缓冲区后,其动能一部分转换成势能,一部分由车轮与路面的摩擦耗散。
图2所示为一车辆简化模型,车体高h=1.8m, 长b=5m 。
已知前轮刚度K 1=5.5*105N/m, 前轮阻尼系数C 1=8*104N •s/m, 后轮刚度K 2=8.5*105N/m, 后轮阻尼系数C 2=C 1; 车体按匀质记,总重10吨,质心距地面高度H=1.5m 。
摩擦力按下式计算:()()i i f t N t μ=⋅ i=1, 2 μ—摩擦系数,μ=0.3N i -- 车轮所受地面的正压力。
图1 盘山公路缓冲区示意图 图2 车辆简化模型假设: ① 车辆行驶过程中的车体变形很小,可忽略不计。
② 车轮质量与车身质量相比很小,可忽略不计。
分别给出缓冲区坡度为300和450时的车辆驶入速度与缓冲区长度的关系曲线以及车速为70Km/小时时缓冲区的最小长度。
2 斜坡行驶车辆的动力学模型斜坡行驶车辆的物理模型与力学模型分别如图3和图4所示。
图3 斜坡行驶车辆物理模型图4 斜坡行驶车辆力学模型2).图5 斜坡行驶车辆模型受力分析建立如图5所示的斜坡行驶车辆的力学模型,以质心C 点垂直方向坐标cy 和转角c θ为广义坐标,1y 和2y 分别为弹簧位置垂直方向坐标(均取在弹簧原长的位置处),采用达朗贝尔原理建立车辆运动的微分方程如下。
以C 点垂直斜面方向的力平衡方程:111222()()cos 0c my k y cy k y cy mg α++++-=(1)以C 点沿斜面方向的力平衡方程:111222()sin 0c mx k y cy k y cy mg μα+++++=(2)以质心C 点取矩的力矩平衡方程:111222111222()()()()()()022cc c L LJ cy k y cy k y H y k y cy H y k y cy θμμ-+-++-++-+=+(3)式中,车辆转动惯量22()12m J b h =+;A 点坐标12c c Ly y θ=-,B 点坐标12c c Ly y θ=+,坐标几何关系如图6所示。
《振动力学》习题集(含答案)
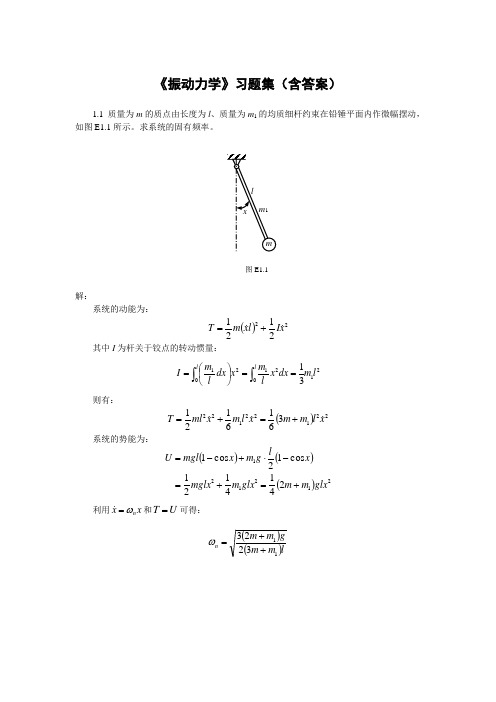
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
振动习题答案

《振动力学》——习题第二章 单自由度系统的自由振动2-1 如图2-1 所示,重物1W 悬挂在刚度为k 的弹簧上并处于静止平衡位置,另一重物2W 从高度为h 处自由下落到1W 上且无弹跳。
试求2W 下降的最大距离和两物体碰撞后的运动规律。
解:222221v gW h W =,gh v 22=动量守恒:122122v gW W v g W +=,gh W W W v 221212+=平衡位置:11kx W =,kW x 11=1221kx W W =+,kW W x 2112+=故:kW x x x 21120=-= ()2121W W kgg W W k n +=+=ω故:tv t x tx t x x n nn n nn ωωωωωωsin cos sin cos 12000+-=+-=&xx 0x 1x 12平衡位置2-2 一均质等直杆,长为l ,重量为w ,用两根长h 的相同的铅垂线悬挂成水平位置,如图2-2所示。
试写出此杆绕通过重心的铅垂轴做微摆动的振动微分方程,并求出振动固有周期。
解:给杆一个微转角θ2aθ=h α2F =mg由动量矩定理:ah a mg a mg Fa M ml I MI 822cos sin 12122-=-≈⋅-====αθαθ&&其中12cossin ≈≈θααh l ga p ha mg ml n 22222304121==⋅+θθ&& g h a l ga h l p T n 3π23π2π222===2-3 一半圆薄壁筒,平均半径为R , 置于粗糙平面上做微幅摆动,如图2-3所示。
试求其摆动的固有频率。
图2-3 图2-42-4 如图2-4 所示,一质量m连接在一刚性杆上,杆的质量忽略不计,试求下列情况系统作垂直振动的固有频率:(1)振动过程中杆被约束保持水平位置;(2)杆可以在铅垂平面内微幅转动;(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
振动力学习题集含答案

解:
,
动量守恒:
,
平衡位置:
,
,
故:
故:
2.4在图E2.4所示系统中,已知m, , , 和 ,初始时物块静止且两弹簧均为原长。求物块运动规律。
图E2.4答案图E2.4
解:
取坐标轴 和 ,对连接点A列平衡方程:
即:
(1)
对m列运动微分方程:
即:
(2)
由(1),(2)消去 得:
图E2.7
解:
,
s=1时共振,振幅为:
(1)
远离共振点时,振幅为:
(2)
由(2)
由(1)
, ,
故:
2.7求图T 2-7中系统的固有频率,悬臂梁端点的刚度分别是 及 ,悬臂梁的质量忽略不计。
图T 2-7答案图T 2-7
解:
和 为串联,等效刚度为: 。(因为总变形为求和)
和 为并联(因为 的变形等于 的变形),则:
图E1.9答案图E1.9
解:
利用动量矩定理得:
,
,
,
,
1.12面积为S、质量为m的薄板连接于弹簧下端,在粘性流体中振动,如图E1.12所示。作用于薄板的阻尼力为 ,2S为薄板总面积,v为速度。若测得薄板无阻尼自由振动的周期为 ,在粘性流体中自由振动的周期为 。求系数 。
图E1.12
解:
平面在液体中上下振动时:
和 为串联(因为总变形为求和),故:
故:
2.9如图T 2-9所示,一质量m连接在一刚性杆上,杆的质量忽略不计,求下列情况系统作垂直振动的固有频率:
(1)振动过程中杆被约束保持水平位置;
(2)杆可以在铅锤平面内微幅转动;
(3)比较上述两种情况中哪种的固有频率较高,并说明理由。
振动力学习题集含答案

解:
利用动量矩定理得:
,
,
,
,
面积为S、质量为m的薄板连接于弹簧下端,在粘性流体中振动,如图所示。作用于薄板的阻尼力为 ,2S为薄板总面积,v为速度。若测得薄板无阻尼自由振动的周期为 ,在粘性流体中自由振动的周期为 。求系数 。
图
解:
平面在液体中上下振动时:
,
,
图所示系统中,已知m,c, , , 和 。求系统动力学方程和稳态响应。
(2)
若取下面为平衡位置,求解如下:
,
图T 2-17所示的系统中,四个弹簧均未受力,k1=k2=k3=k4=k,试问:
(1)若将支承缓慢撤去,质量块将下落多少距离?
(2)若将支承突然撤去,质量块又将下落多少距离?
图T 2-17
解:
(1) ,
(2) ,
如图T 2-19所示,质量为m2的均质圆盘在水平面上可作无滑动的滚动,鼓轮绕轴的转动惯量为I,忽略绳子的弹性、质量及各轴承间的摩擦力,求此系统的固有频率。
因此有:
图所示阶梯杆系统中已知m,ρ,S,E和k。求纵向振动的频率方程。
图
解:
模态函数的一般形式为:
题设边界条件为:
,
边界条件可化作:
,
导出C2= 0及频率方程:
,其中
长为l、密度为ρ、抗扭刚度为GIp的的等直圆轴一端有转动惯量为J的圆盘,另一端连接抗扭刚度为k的弹簧,如图所示。求系统扭振的频率方程。
《振动力学》习题集(含答案)
质量为m的质点由长度为l、质量为m1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。求系统的固有频率。
图
解:
系统的动能为:
其中I为杆关于铰点的转动惯量:
《振动力学》作业资料(含答案解析)

《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得:()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得:()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含答案)

《振动力学》习题集(含答案)质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。
求系统的固有频率。
图-解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l⎰⎰==⎪⎭⎫ ⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: [()()lm m g m m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
图解::如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω:转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。
求系统的固有频率。
,图解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:]()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω:在图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
大工18秋《振动力学(二)》在线作业3

大工18秋《振动力学(二)》在线作业3
问题1
请解释简谐振动的定义和基本特点。
简谐振动是指系统在无阻尼、无外力的情况下,只受到弹性恢
复力作用下的振动。
简谐振动具有以下基本特点:
1. 振动质点的振幅保持不变;
2. 振动质点的加速度与质点的位移成正比,且方向相反;
3. 振动是周期性的,即振动质点在一定时间内重复相同的运动;
4. 简谐振动具有固有频率,即振动频率只取决于系统的质量和
弹性系数。
问题2
请列举简谐振动的几个典型例子。
简谐振动的典型例子包括:
1. 弹簧振子:弹簧与质点组成的系统在无阻尼、无外力的情况
下的振动;
2. 转子振动:旋转机械中转子的振动;
3. 电磁振荡:电磁场中电荷的振动;
4. 摆振:摆的振动,如单摆、复摆等。
问题3
简述简谐振动与非简谐振动的区别。
简谐振动与非简谐振动的区别主要在于振动系统的特性:
1. 简谐振动是在无阻尼、无外力的情况下,只受到弹性恢复力
作用的振动;而非简谐振动可能会受到其他因素的影响,如摩擦力、外部驱动力等;
2. 简谐振动的振幅保持不变,而非简谐振动的振幅可能会随时
间变化;
3. 简谐振动具有固有频率,而非简谐振动的频率可能受到外部
因素的干扰而发生改变。
振动力学习题集

2振动力学》习题集(含答案)质量为 m 的质点由长度为 l 、质量为 m 1 的均质细杆约束在铅锤平面内作微幅摆动,如 图所示。
求系统的固有频率。
解: 系统的动能为:1 2 1 2 T m xl I x22 其中 I 为杆关于铰点的转动惯量:利用xnx 和T U 可得:3 2m m 1 g2 3m m 1 lml 1dxx 2l m 1x 2dxlm 1l31则有:系统的势能为:1 2 2 1 2 2ml x m 1l x 2 611 2 2 3m m 1 l x6U mgl 1 cosxm 1g cosx 1 2mglx14m 1glx1 2m4m 1 glx 2图质量为m、半径为R的均质柱体在水平面上作无滑动的微幅滚动,在两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
CA=a的A 点系有解:如图,令为柱体的转角,则系统的动能和势能分别为:利用1212 1 2 23T I B mR2mR2 2mR2B2241222U2k Ra2 k R a24k R a 23mR2R 3m图U 可得:n J k 2 k 3转动惯量为 J 的圆盘由三段抗扭刚度分别为 k 1 , k 2 和 k 3 的轴约束,如图所示。
求系统的固有频率。
k 2解:系统的动能为:12J 2k 2和 k 3相当于串联,则有:以上两式联立可得:系统的势能为:k 2k 3 k 1 k 2 k 3k 1 3,k 2k 2k 3k 3k 2k 2 k 3利用U 12k 1k 2 2212k 3 k 1 k 2 k 3 k 2k 3 2k 2 k 3n 和T U 可得:在图所示的系统中,已知 k i i 1,2,3 , m, a 和b ,横杆质量不计。
求固有频率。
答案图解:对 m 进行受力分析可得:质量 m 1在倾角为 的光滑斜面上从高 h 处滑下无反弹碰撞质量 m 2 ,如图所示。
确定mg k 3x 3 ,即 x 3mgk 3如图可得:F 1 mgb F 2 x 1, x 2k 1a b k 1k 2mga a b k 2x 0 x 1 x x 1a x 2 x 1ab a 2k 1 2b 2k 2 mga b 2 k 1k 2 x 则等效弹簧刚度为:x 0 x 3a 2k 1b 2 k 2 a b 2k 1k 21mgk 0mg2b k 1k 2k3a 2k 1k 3b 2k 2k 3 a b 2 k 1k 2则固有频率为:nk 1k 2k 3 a b 2 2 2 2 m k 1k 2 a b k 3 k 1a k 2bx 2mg系统由此产生的自由振动。
《振动力学》课程作业
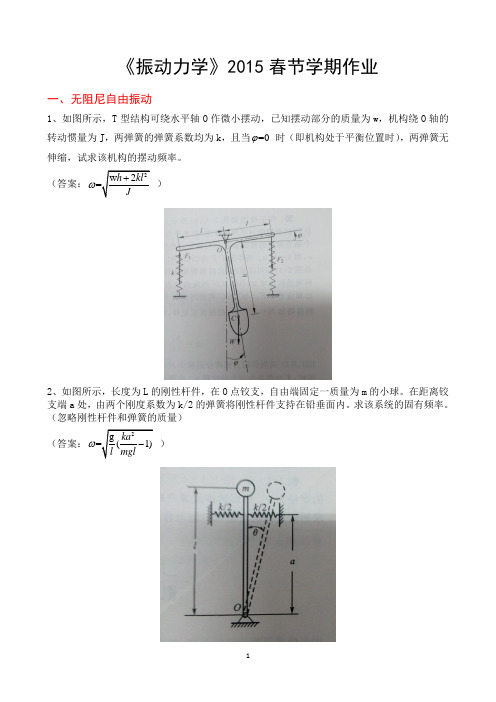
《振动力学》2015春节学期作业一、无阻尼自由振动1、如图所示,T型结构可绕水平轴O作微小摆动,已知摆动部分的质量为w,机构绕O轴的ϕ时(即机构处于平衡位置时),两弹簧无转动惯量为J,两弹簧的弹簧系数均为k,且当=0伸缩,试求该机构的摆动频率。
(答案:ω)2、如图所示,长度为L的刚性杆件,在O点铰支,自由端固定一质量为m的小球。
在距离铰支端a处,由两个刚度系数为k/2的弹簧将刚性杆件支持在铅垂面内。
求该系统的固有频率。
(忽略刚性杆件和弹簧的质量)(答案:ω)3、如图所示,悬臂梁长为L,截面抗弯刚度为EI,梁的自由端有质量为m的质量块,弹簧刚度为k,求系统的固有频率。
(答案:ω=)4、如图所示,半径为R的均质半圆柱体,在水平面内只作滚动而不滑动的微摆动,求其固有角频率。
(答案:ω=)5、如图所示,抗弯刚度为62EI=⨯⋅的梁AB,借弹簧支撑于A,B两点处,弹簧系3010(N m)数均为300(/)=的物W N k N m=。
忽略梁的质量,试求位于B点左边3m处,重量为1000()块自由振动的周期。
(答案:T=0.533s)6、一个重W的水箱,借助四根端点嵌固的竖置管柱支撑着。
每根柱子的长为L,抗弯刚度为EI。
试求该水箱顺水平方向自由振动的周期。
(管柱的质量忽略不计)T=)(答案:27、《结构动力学基础》,第2章课后习题,第1题、第2题、第8题二、有阻尼自由振动1、如图所示,库伦曾用下述方法测定液体的粘性系数'c :在弹簧上悬挂一薄板A ,先测出薄板在空气中的振动周期1T ,然后测出在待测粘性系数的液体中的振动周期2T 。
设液体对薄板的阻力等于2A 'c v ,其中2A 为薄板的表面面积,v 为薄板的速度。
如薄板重W ,试有测得的数据1T 和2T ,求出粘性系数'c 。
空气对薄板的阻力不计。
(答案:'c =)2、物体质量为2kg ,挂在弹簧下端。
弹簧常数k=48.02N/cm,求临界阻尼系数。
《振动力学》习题集(含答案)
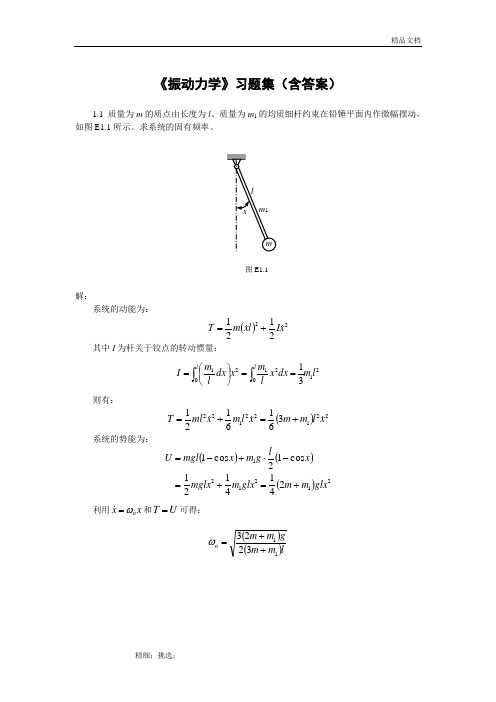
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
振动力学习题集

《振动力学》习题集(含答案)质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图所示。
求系统的固有频率。
图解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图所示。
求系统的固有频率。
图解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn = 和U T =可得:()mkR a R mR a R k n 343422+=+=ω转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图所示。
求系统的固有频率。
图解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn = 和U T =可得:()()3232132k k J k k k k k n +++=ω在图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
课时作业1:第1讲 机械振动

第1讲机械振动1.(多选)关于受迫振动和共振,下列说法正确的是()A.火车过桥时限制速度是为了防止火车发生共振B.若驱动力的频率为5 Hz,则受迫振动稳定后的振动频率一定为5 HzC.当驱动力的频率等于系统的固有频率时,受迫振动的振幅最大D.受迫振动系统的机械能守恒答案BC解析火车过桥时限制速度是为了防止桥发生共振,选项A错误;对于一个受迫振动系统,若驱动力的频率为5 Hz,则振动系统稳定后的振动频率也一定为5 Hz,选项B正确;由共振的定义可知,选项C正确;受迫振动系统,驱动力做功,系统的机械能不守恒,选项D错误.2.(多选)(2019·江苏卷·13B(1))一单摆做简谐运动,在偏角增大的过程中,摆球的() A.位移增大B.速度增大C.回复力增大D.机械能增大答案AC解析摆球做简谐运动,在平衡位置处位移为零,在摆角增大的过程中,摆球的位移增大,速度减小,选项A正确,B错误;在摆角增大的过程中,摆球受到的回复力增大,选项C正确;单摆做简谐运动,机械能守恒,所以在摆角增大的过程中,摆球机械能保持不变,选项D错误.3.如图1所示,弹簧振子在a、b两点间做简谐运动,当振子从平衡位置O向a运动过程中()图1A.加速度和速度均不断减小B.加速度和速度均不断增大C.加速度不断增大,速度不断减小D.加速度不断减小,速度不断增大答案 C解析在振子由O到a的过程中,其位移不断增大,回复力增大,加速度增大,但是由于加速度与速度方向相反,故速度减小,选项C正确.4.(2020·浙江嘉兴市期末)如图2所示,两根完全相同的水平弹簧和一根张紧的水平细线将甲、乙两物块束缚在光滑水平面上,已知甲的质量大于乙的质量.当细线突然断开后,两物块都开始做简谐运动,则在运动过程中( )图2A .甲的振幅大于乙的振幅B .甲的振幅小于乙的振幅C .甲的最大速度小于乙的最大速度D .甲的最大速度大于乙的最大速度 答案 C解析 线断开前,两根弹簧伸长的长度相同,离开平衡位置的最大距离相同,即振幅相同,故A 、B 错误;当线断开的瞬间,弹簧的弹性势能相同,到达各自的平衡位置时,甲、乙的最大动能相同,由于甲的质量大于乙的质量,由E k =12m v 2可知,甲的最大速度小于乙的最大速度,故C 正确,D 错误.5.如图3甲所示,弹簧振子以O 点为平衡位置,在A 、B 两点之间做简谐运动.取向右为正方向,振动物体的位移x 随时间t 的变化如图乙所示,则由图可知( )图3A .t =0.2 s 时,振动物体的加速度方向向左B .t =0.6 s 时,振动物体的速度方向向右C .在t =0.4 s 到t =0.8 s 时间内,振动物体的动能逐渐减小D .在t =0到t =2.4 s 时间内,振动物体通过的路程是80 cm 答案 A解析 由题图乙可知,t =0.2 s 时,振动物体远离平衡位置向右运动,位移增大,根据F =-kx 可知,回复力方向向左,故加速度方向向左,A 正确;t =0.6 s 时,振动物体靠近平衡位置向左运动,故振动物体的速度方向向左,B 错误;在t =0.4 s 到t =0.8 s 时间内,振动物体向平衡位置运动,速度逐渐增大,动能逐渐增大,C 错误;在t =0到t =2.4 s 时间内,振动物体通过的路程是4A ×2.4 s1.6 s=60 cm ,故D 错误.6.(2021·浙江绍兴市新昌县知新中学月考)图4甲是利用沙摆演示简谐运动图象的装置.当盛沙的漏斗下面的薄木板被水平匀速拉出时,做简谐运动的漏斗漏出的沙会在板上显示出沙摆的振动位移随时间变化的关系曲线.已知木板被水平拉动的速度为0.20 m/s ,图乙所示的一段木板的长度为0.60 m ,则这次实验沙摆的摆长大约为(取g =π2 m/s 2)( )图4A .0.56 mB .0.65 mC .1.00 mD .2.25 m答案 A解析 由于木板匀速拉动,据x =v t ,则t =x v =0.600.20 s =3 s ,显然t =2T ,则T =1.5 s ,据T=2πlg,可计算出摆长l 大约为0.56 m ,故A 正确.7.(多选)如图5所示,一轻质弹簧上端固定在天花板上,下端连接一物块,物块沿竖直方向以O 点为平衡位置,在C 、D 两点之间做周期为T 的简谐运动.已知在t 1时刻物块的速度大小为v 、方向向下,动能为E k .下列说法正确的是( )图5A .如果在t 2时刻物块的速度大小也为v ,方向向下,则t 2-t 1的最小值小于T2B .如果在t 2时刻物块的动能也为E k ,则t 2-t 1的最小值为T2C .当物块通过O 点时,其加速度最小D .物块在C 、D 两点的加速度相同 答案 AC解析 如果在t 1时刻物块位于O 点上方且向下运动,t 2时刻物块位于O 点下方且与t 1时刻物块速度相同,则t 2-t 1的最小值小于T2,选项A 正确;如果在t 2时刻物块的动能也为E k ,则t 2时刻物块速度与t 1时刻大小相等,方向可能相同,也可能相反,t 2-t 1的最小值小于T2,选项B 错误;题图中O 点是平衡位置,物块通过O 点时位移最小,根据a =-kxm 知,其加速度最小,选项C 正确;C 、D 两点关于平衡位置对称,加速度等大反向,选项D 错误.8.(多选)如图6所示为同一地点的两单摆甲、乙的振动图象,则下列说法中正确的是( )图6A .甲、乙两单摆的摆长相等B .甲摆的振幅比乙摆大C .甲摆的机械能比乙摆大D .在t =0.5 s 时有正向最大加速度的是乙摆 答案 ABD解析 由题图可以看出,甲摆的振幅比乙摆的大,两单摆的振动周期相同,根据单摆周期公式T =2πlg可得,甲、乙两单摆的摆长相等,故A 、B 正确;两单摆摆球的质量未知,所以两单摆的机械能无法比较,故C 错误;在t =0.5 s 时,乙摆在负向最大位移处,即有正向最大加速度,而甲摆的位移为零,加速度为零,故D 正确.9.(多选)弹簧振子做简谐运动,O 为平衡位置,当它经过点O 时开始计时,经过0.3 s ,第一次到达点M ,再经过0.2 s 第二次到达点M ,则弹簧振子的周期可能为( ) A .0.53 s B .1.4 s C .1.6 s D .2 s答案 AC解析 如图甲所示,设O 为平衡位置,OB (OC )代表振幅,若振子一开始从平衡位置向点C 运动,振子从O →C 所需时间为T4.因为简谐运动具有对称性,所以振子从M →C 所用时间和从C →M 所用时间相等,故T 4=0.3 s +0.22 s =0.4 s ,解得T =1.6 s ;如图乙所示,若振子一开始从平衡位置向点B 运动,设点M ′与点M 关于点O 对称,则振子从点M ′经过点B 到点M ′所用的时间与振子从点M 经过点C 到点M 所需时间相等,即0.2 s .振子从点O 到点M ′、从点M ′到点O 及从点O 到点M 所需时间相等,为0.3 s -0.2 s 3=130s ,故周期为T =0.5 s +130s ≈0.53 s ,故A 、C 正确.10.(2020·山东青岛市西海岸区模拟)两单摆在不同的驱动力作用下其振幅A 随驱动力频率f 变化的图像如图7中甲、乙所示,则下列说法正确的是( )图7A .单摆振动时的频率与固有频率有关,振幅与固有频率无关B .若两单摆放在同一地点,则甲、乙两单摆的摆长之比为4∶1C .若两单摆摆长相同放在不同的地点,则甲、乙两单摆所处两地的重力加速度之比为4∶1D .周期为2 s 的单摆叫作秒摆,在地面附近,秒摆的摆长约为2 m 答案 B解析 做受迫振动的物体的频率等于驱动力的频率,单摆振动时的频率由驱动力的频率决定,与单摆的固有频率无关,当驱动力频率等于单摆的固有频率时,单摆的振幅最大,发生共振,选项A 错误;由题图可知,甲、乙两个单摆的固有频率之比为1∶2,则由T =1f=2πl g可知,l =g4π2f 2,则若两单摆放在同一地点,则甲、乙两单摆的摆长之比为4∶1;若两单摆摆长相同放在不同的地点,则甲、乙两单摆所处两地的重力加速度之比为1∶4,选项B 正确,C 错误;在地面附近,秒摆的摆长为l =gT 24π2≈1 m ,选项D 错误.11.(2019·全国卷Ⅱ·34(1))如图8,长为l 的细绳下方悬挂一小球a ,绳的另一端固定在天花板上O 点处,在O 点正下方34l 的O ′处有一固定细铁钉.将小球向右拉开,使细绳与竖直方向成一小角度(约为2°)后由静止释放,并从释放时开始计时.当小球a 摆至最低位置时,细绳会受到铁钉的阻挡.设小球相对于其平衡位置的水平位移为x ,向右为正.下列图像中,能描述小球在开始一个周期内的x -t 关系的是( )图8答案 A解析 由单摆的周期公式T =2πlg可知,小球在钉子右侧时的振动周期为在钉子左侧时振动周期的2倍,故B 、D 项错误;由机械能守恒定律可知,小球在左、右最大位移处距离最低点的高度相同,但由于摆长不同,所以小球在左、右两侧摆动时相对平衡位置的最大水平位移不同,当小球在钉子右侧摆动时,最大水平位移较大,故A 项正确,C 项错误.12.(多选)(2018·天津卷·8)一振子沿x 轴做简谐运动,平衡位置在坐标原点.t =0时振子的位移为-0.1 m ,t =1 s 时位移为0.1 m ,则( ) A .若振幅为0.1 m ,振子的周期可能为23 sB .若振幅为0.1 m ,振子的周期可能为45 sC .若振幅为0.2 m ,振子的周期可能为4 sD .若振幅为0.2 m ,振子的周期可能为6 s 答案 AD解析 若振幅为0.1 m ,则t =T2+nT (n =0,1,2,…).当n =0时,T =2 s ;n =1时,T =23 s ;n =2时,T =25 s.故选项A 正确,选项B 错误.若振幅为0.2 m ,振动分两种情况讨论:①振子振动如图甲所示,则振子由C 点振动到D 点用时至少为T2,周期最大为2 s.②振子振动如图乙中实线所示.由x =A sin(ωt +φ)知t =0时,-A 2=A sin φ,φ=-π6,即振子由C 点振动到O 点用时至少为T12,由简谐运动的对称性可知,振子由C 点振动到D 点用时至少为T6,则T 最大为6 s ;若由C 点振动到O 点用时1112T ,振子由C 点振动到D 点用时76T ,则T 为67s.若振子振动如图乙中虚线所示,振子由C 点振动到D 点用时至少T2,周期最大为2 s.综上所述,选项C 错误,D 正确.。
振动力学作业题解

第02章 单自由度系统的振动2.1 一根抗弯刚度72=3610Ncm EI ⨯的简支架,两支承间跨度l 1=2m ,一端伸臂l 2=1m ,略去梁的分布质量,试求悬臂端处重为Q =2548 N 的重物的自由振动频率。
【提示:22123()EJ k l l l =+,2212()3st Ql l l EI δ+=,11.77n ω=L 1/s 】 2.2 梁AB 其抗弯刚度72=910Ncm EI ⨯,A 端与B 端由弹簧支承,弹簧刚性系数均为k =52.92 kN/m ,如图所示。
略去梁的分布质量,试求位于B 端点左边1米处,重为Q =4900 N 的物块自由振动的周期。
【解法1:通过计算静变形求解。
A ,B 弹簧受力为3Q 和23Q ,压缩量为3Q k 和23Q k ,则由弹簧引起的静变形为159Qk δ=;利用材料力学挠度公式求出梁变形引起的静变形222212(321)4619Q QEI EIδ⋅⋅--==⋅。
周期为:22 1.08nT πω===s 。
解法2:通过弹簧刚度的串并联计算总等效刚度求解。
A ,B 弹簧相对Q 处的等效刚度为(产生单位变形需要的力,利用解法1中计算的静变形结果)195k k =;利用材料力学挠度公式求出梁相对Q 处的等效刚度294EI k =;总等效刚度为:12111eq k k k =+。
周期为22 1.08nT πω===s 。
】 2.4 一均质刚杆重为P ,长度为L 。
A 处为光滑铰接,在C 处由刚性系数为k 的弹簧使杆在水平位置时平衡。
弹簧质量不计,求杆在竖直面内旋转振动时的周期。
【解:利用定轴转动微分方程:21()32st P l l P k a a g ϕϕδ=--&&,2st lk a P δ=, 得:22103P l k a gϕϕ+=&&,22n T πω===题 2-1 图BAQ题 2-2 图QkkAB 题 2-4 图2.8一个重为98 N的物体,由刚性系数为k=9.8 kN/m的弹簧支承着(简化为标准m-k-c振动系统),在速度为1 cm/s时其阻力为0.98 N。
《振动力学》习题集(含答案解析)
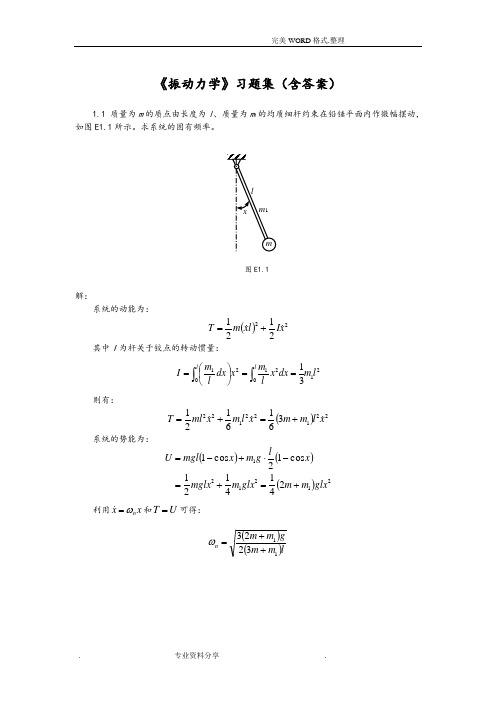
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解:系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解:系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
《振动力学》习题集(含标准答案)

《振动力学》习题集(含答案)————————————————————————————————作者:————————————————————————————————日期:《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得: ()()lm m gm m n 113223++=ωml m 1 x1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得: ()mkR a R mR a R k n 343422+=+=ωkk A Ca R θ1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ&J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得: ()()3232132k k J k k k k k n +++=ωkk 2 kJ1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《振动力学》2015春节学期作业一、无阻尼自由振动1、如图所示,T 型结构可绕水平轴O 作微小摆动,已知摆动部分的质量为w ,机构绕O 轴的转动惯量为J ,两弹簧的弹簧系数均为k ,且当=0ϕ 时(即机构处于平衡位置时),两弹簧无伸缩,试求该机构的摆动频率。
(答案:2w 2=h kl Jω+ )2、如图所示,长度为L 的刚性杆件,在O 点铰支,自由端固定一质量为m 的小球。
在距离铰支端a 处,由两个刚度系数为k/2的弹簧将刚性杆件支持在铅垂面内。
求该系统的固有频率。
(忽略刚性杆件和弹簧的质量)(答案:2g =(1)ka l mglω-)3、如图所示,悬臂梁长为L ,截面抗弯刚度为EI ,梁的自由端有质量为m 的质量块,弹簧刚度为k ,求系统的固有频率。
(答案:333EI kL mL ω+=)4、如图所示,半径为R 的均质半圆柱体,在水平面内只作滚动而不滑动的微摆动,求其固有角频率。
(答案:8(916)g R ωπ=- )5、如图所示,抗弯刚度为623010(N m )EI =⨯⋅ 的梁AB ,借弹簧支撑于A,B 两点处,弹簧系数均为300(/)k N m = 。
忽略梁的质量,试求位于B 点左边3m 处,重量为1000()W N = 的物块自由振动的周期。
(答案:T=0.533s )6、一个重W 的水箱,借助四根端点嵌固的竖置管柱支撑着。
每根柱子的长为L,抗弯刚度为EI 。
试求该水箱顺水平方向自由振动的周期。
(管柱的质量忽略不计)(答案:3248WL T EIgπ= )7、《结构动力学基础》,第2章课后习题,第1题、第2题、第8题二、有阻尼自由振动1、如图所示,库伦曾用下述方法测定液体的粘性系数'c :在弹簧上悬挂一薄板A ,先测出薄板在空气中的振动周期1T ,然后测出在待测粘性系数的液体中的振动周期2T 。
设液体对薄板的阻力等于2A 'c v ,其中2A 为薄板的表面面积,v 为薄板的速度。
如薄板重W ,试有测得的数据1T 和2T ,求出粘性系数'c 。
空气对薄板的阻力不计。
(答案:'2221122Wc T T gAT T π=- )2、物体质量为2kg ,挂在弹簧下端。
弹簧常数k=48.02N/cm,求临界阻尼系数。
(答案:196Ns/m )3、挂在弹簧下端的物体,质量为1.96kg ,弹簧常数k=0.49N/cm,阻尼系数c=0.196Ns/cm 。
设在t=0时刻将物体从平衡位置向下拉5cm ,然后无初速度地释放,求此后的运动。
(答案:55(15t)cm t x e -=+ )4、《结构动力学基础》,第2章课后习题,第12题三、简谐荷载作用下的强迫振动1、如图所示,一无重简支梁,在跨中有重W=20kN 的电机,电机偏心所产生的离心力为(t)10sin F t ω=kN ,若机器每分钟的转数n=500r/min ,梁的截面抗弯刚度为421.00810EI kN m =⨯⋅ 。
在不计阻尼的情况下,试求梁的最大位移和弯矩。
(答案:33max0.00776(m)4848WL FL y EI EI μ=+=;max 58.66(kN m)44WL FL M μ=+=⋅ )2、建立图示系统的动力学平衡方程,并求系统发热稳态响应。
(答案: 222120222222121222222221212122x(t)Asin(t ),(k k ),[k k (k k )](k )k arctan[k k (k k )](k k )(k )c A F m c m c m c m ωθωωωωωθωωω=+++=-++--=-+++- )3、如图所示,系统的刚性棒质量不计,0(t)F sin f t ω= 。
试建立系统的运动方程,并分别求出○10ωω= ;○20/2ωω= 时,质量块的线位移幅值。
(答案:○104c F kA m=;○202649k181A cmk=+)四、周期荷载作用下的强迫振动,一般性荷载作用下的强迫振动 1、在如图(a )所示的系统中,s x 的变化规律如图(b )所示。
试求系统的稳态响应。
(答案:22221sin(n t )1,arctan42(n )[2k m(n )](cn )n n n a ka cn x n k m ωθωθπωωω∞=-=-=--+∑)2、如图所示,无阻尼单自由度系统受到周期力(t)t F 的作用。
应用傅里叶级数求该系统的稳态响应。
(答案:00222102(cos n 1)sin n t 2(t),,(n )n F x n m T πωπωωπωω∞=-=-=-∑为系统自振圆频率)3、如图所示,求无阻尼质量弹簧系统在跃阶力作用下的动态响应。
假设初始条件等于零。
(答案:00200002(1cos t),t T (t)[cos (t T)cos t],t TF m x F m ωωωωω⎧-≤⎪⎪=⎨⎪-->⎪⎩ )4、如图所示,试确定一个自由度系统对图中抛物线施力函数2211(1t /)Q Q t =- 的无阻尼反应。
(答案:○110t t ≤≤时,21222112(1)(1cos t)Q t x m t t ωωω⎡⎤=+--⎢⎥⎣⎦; ○21t t >时,111221122[cos (t t )cos t]sin (t t )cos t Q x m t t ωωωωωωω⎧⎫=-----⎨⎬⎩⎭)五、逐步积分方法1、如图(a )所示,单自由度钢架,受图(b )所示冲击载荷,取0.12t s ∆= ,试用线性加速度的逐步积分法,计算0<t<0.72s 时段内的线性弹性位移响应。
六、单自由度系统的减振与隔振1、简述减振与隔振的常用方法?结合例子说明隔振的基本原理?七、两自由度系统自由振动 1、如图所示,建立系统的运动方程 (答案:121220000000M m ml x c c x k k x mlml mgl θθθ+++⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)2、如图所示的一个圆板,质量为M ,半径为r ,在板的中心装有一个长度为L 的单摆。
摆端有集中质量m ,摆可以自由旋转,板只能滚动而不滑动。
求系统在平衡位置作微幅振动的固有频率。
(答案:1220,(1)3g m L Mωω==+ )3、如图所示,当只研究汽车在铅垂平面的振动时,可将车身简化为支撑在两弹簧上的刚性梁。
若汽车质量m=1500kg ,绕质心c 的转动惯量I=22002kg m ⋅,1235/,38/k kN m k kN m ==,121.4, 1.7L m L m ==,以x 和θ为广义坐标,求其自振频率和振型。
(思考:是否可以用弹簧处的铅垂位移1y 和2y 为广义坐标求解?比较两者的异同点) (答案: 12126.82/,9.12/,(10.205),(13.324)T T rad s rad s ωωφφ===-= ;思考比较:列运动微分方程可知后者选取的自由度坐标不仅位移1y 和2y 耦合,而且加速度1y 和2y 之间也有耦合)八&九、多自由度系统自由振动1、《结构动力学基础》 第三章,第3-1题。
2、如图所示,假设(t)0(i 1,2,3)i f == ,建立系统的运动微分方程。
(答案:111221122122223322233233334333430000000000m x c c c x k k k x m x c c c c x k k k k x m x c c c x k k k x +-+-⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+-+-+-+-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+-+⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ )3、如图所示,三个单摆用弹簧连接,13212,2,m m m m m k k k===== ,以(i 1,2,3)i φ=为广义坐标。
求系统的自振频率和振型,并画出振型图。
(答案:22123222,,gg kh g kh ll ml l ml ωωω==+=+;123[111],[101],[111]T T T φφφ==-=- )4、如图,用逆幂法求解系统的第1阶自振频率和振型,要求21ω 的误差3110ε-< 。
(10.445,(11.802 2.246)T kA mω== )5、如图,已知弹簧质量系统,用综合法求解全部特征对,并画出全部振型图。
(答案:2211222233440.586,(1,2.414,2.414,1);1,(1,2,2,1);2,(1,1,1,1); 3.414,(1,0.414,0..414,1)T T T Tk k A A m mk k A A m mωωωω====--==--==-- )6、如图所示悬臂梁质量不计,梁的弯曲刚度为EI,求系统的固有频率和模态,求作用在梁自由端的静力P突然移去后系统的自由振动响应。
(答案:121233321231120.5838, 3.8843,[13.1205],[10.3205],(2.6605cos0.0062cos)(0.8526cos0.0193cos)T TEI EIml mlPlx t tEIPlx t tEIωωωωωω====-⎧⎫=+⎪⎪⎪⎪⎨⎬⎪⎪=-⎪⎪⎩⎭ϕϕ)十、多自由度系统强迫振动1、如图所示,在第一个质量块个作用有外力sinp t=。
两质量块的质量122m m==,弹簧刚度1231k k k===。
试用振型分解法求系统的稳态响应。
(答案:0sin1t⎡⎤⎢⎥⎣⎦)11、动力减振原理与减振器试简述动力减振器的设计步骤?十二&十三、动力学能量原理1、无质量刚性杆可绕杆端的轴自由转动,另一端附有质量m1,并用弹簧悬挂两质量m2和m3,杆中点支以弹簧使杆呈水平,如图所示。
试写出系统动能和势能表达式并依次写出系统的刚度阵和质量阵。
(答案:233222211212121x m x m x m T ++=)3232122332232212121)(21)421x x k x x k x k x k k x k k U --++++=(十四、瑞利法1、计算重力坝沿水流方向的自振频率时,可以取沿坝轴线方向单位长度的坝体近似地简化为如图所示的变截面悬臂梁。
试用李兹法求如图所示重力坝的第一阶和第二阶自振频率。
(答案:ρωρωEgh bEghb 2221994.4,535.1==)2、取试探振型(1,2 3)T,用瑞利法求解如图所示三自由度系统的基频。
(答案:mk 465.01=ω)3、《结构动力学基础》第五章,第8题。
