有效翼缘宽计算(wyg) - 360文档中心

压型钢板受压翼缘的有效计算宽度

压型钢板受压翼缘的有效计算宽度压型钢板是一种常见的结构材料，广泛应用于建筑、桥梁、汽车、机械等领域。

在设计和计算压型钢板受压翼缘时，需要考虑其有效计算宽度。

有效计算宽度是指在计算抗弯承载力或屈曲承载力时，将受压翼缘视作由若干个平行于受压翼缘的板条构成，并将其转化为等效的简支梁的宽度。

有效计算宽度的计算方法与压型钢板的几何形状和受力状况有关。

下面将分别介绍常见几种压型钢板受压翼缘的有效计算宽度计算方法。

1.U型钢梁的受压翼缘对于U型钢梁的受压翼缘，其内侧边缘是由一系列平行的板条构成的。

根据简化假设，可以将这些板条视为一系列等效的简支梁。

有效计算宽度可以通过以下公式计算：bw = (n-1)×tw + bf其中，bw为有效计算宽度，n为受压翼缘上板条的数量，tw为受压翼缘上板条的厚度，bf为翼缘的宽度。

2.Z型钢梁的受压翼缘对于Z型钢梁的受压翼缘，其计算方法与U型钢梁类似。

不同之处在于，Z型钢梁的翼缘有两个，分别是上翼缘和下翼缘。

有效计算宽度可以通过以下公式计算：bw = (n1-1)×tw1 + bf1 + bf2 + (n2-1)×tw2其中，bw为有效计算宽度，n1和n2分别为上翼缘和下翼缘上板条的数量，tw1和tw2分别为上翼缘和下翼缘上板条的厚度，bf1和bf2分别为上翼缘和下翼缘的宽度。

3.槽钢的受压翼缘对于槽钢的受压翼缘，其计算方法与U型钢梁类似。

槽钢的翼缘上有两个板条，分别是上翼缘和下翼缘。

有效计算宽度可以通过以下公式计算：bw = (n-1)×tw + bf1 + bf2其中，bw为有效计算宽度，n为翼缘上板条的数量，tw为翼缘上板条的厚度，bf1和bf2分别为上翼缘和下翼缘的宽度。

需要注意的是，以上计算方法都是基于一些假设和简化的前提条件，实际情况可能存在一定的差异。

在实际工程中，还需要结合具体的受力情况和设计要求进行合理的计算和选择。

翼缘宽厚比限值计算

翼缘宽厚比限值计算翼缘宽厚比是钢结构设计中一个重要的参数，它是指钢梁或钢柱翼缘厚度与腹板高度的比值。

翼缘宽厚比的大小直接影响到钢结构构件的稳定性和承载能力，因此，在设计钢结构时，需要对翼缘宽厚比进行合理的限值计算。

一、翼缘宽厚比限值的规范要求在钢结构设计中，通常需要遵守国家规范和行业标准的规定。

在中国钢结构设计规范中，对翼缘宽厚比限值做出了以下规定：对于一般用途的钢结构构件，翼缘宽厚比不应小于30；对于重要用途的钢结构构件，翼缘宽厚比不应小于40；对于特殊用途的钢结构构件，如桥梁、高层建筑等，其翼缘宽厚比应根据实际情况进行计算确定。

二、翼缘宽厚比限值的计算方法根据钢结构稳定性理论，翼缘宽厚比的大小与钢结构的稳定承载能力密切相关。

当翼缘宽厚比过小时，钢结构构件容易失稳，导致承载能力急剧下降；当翼缘宽厚比过大时，钢结构构件虽然稳定性较好，但会造成材料浪费和结构重量增加。

（1）计算临界失稳应力临界失稳应力是指钢结构发生失稳时的应力值。

根据钢结构稳定性理论，可以计算出钢结构的临界失稳应力：σcr = π2EI/[(h+tw)2]其中，σcr为临界失稳应力；E为钢结构的弹性模量；I为钢结构的惯性矩；h为钢结构的截面高度；tw为钢结构的翼缘厚度。

（2）确定翼缘宽厚比的限值根据临界失稳应力和实际使用应力的情况，可以确定翼缘宽厚比的限值。

假设实际使用应力为σs，则翼缘宽厚比的限值为：ε = (σs/σcr)1/2 × (h/tw)其中，ε为翼缘宽厚比的限值。

根据上述公式，可以计算出不同使用应力下的翼缘宽厚比的限值。

在实际设计过程中，应根据实际情况选择合适的翼缘宽厚比限值。

根据经验进行确定在实际设计过程中，可以根据经验来确定翼缘宽厚比的限值。

根据国内外相关规范和工程实践经验，一般建议在以下范围内选择翼缘宽厚比的限值：（1）对于一般用途的钢结构构件，翼缘宽厚比不应小于30；（2）对于重要用途的钢结构构件，翼缘宽厚比不应小于40；（3）对于特殊用途的钢结构构件，如桥梁、高层建筑等，其翼缘宽厚比应根据实际情况进行计算确定。

t形截面受压翼缘的有效宽度

t形截面受压翼缘的有效宽度【知识文章】T形截面受压翼缘的有效宽度1. 简介T形截面在工程实践中被广泛应用，其具备较高的强度和刚度。

在设计和分析中，了解T形截面受压翼缘的有效宽度是至关重要的。

本文旨在深入探讨T形截面受压翼缘的有效宽度，为读者提供有价值的知识和理解。

2. T形截面的构造和特性T形截面由一个纵向的翼缘和一个横向的腹板组成。

其特点是翼缘具有较高的抗弯刚度，而腹板则主要承受剪力作用。

由于受力特性的不同，翼缘和腹板在设计和分析中需要分别考虑。

3. T形截面受压翼缘的概念当T形截面受到纵向压力时，翼缘处于压缩状态。

为了准确计算翼缘的受压性能，引入了有效宽度的概念。

有效宽度是指受压翼缘的有效部分，在计算弯曲和稳定性时起到关键作用。

4. 受压翼缘的有效宽度计算方法为了计算受压翼缘的有效宽度，我们可以采用不同的方法。

其中较常用的是弧长法、等效直角支撑法和解析法。

这些方法的原理和适用条件各有不同，根据具体情况可以灵活选择。

5. 弧长法弧长法是一种较为简便的方法，适用于较为简单的T形截面。

该方法基于压力分布的近似计算，将翼缘的净截面面积与等效受压翼缘的宽度联系起来。

通过一系列计算和修正，可以得到较为准确的结果。

6. 等效直角支撑法等效直角支撑法是一种更为精确的计算方法，适用于更复杂的T形截面。

该方法基于对受压翼缘的支撑情况进行模拟，将其等效为一组直角支撑。

通过对这组支撑的性能进行计算和分析，可以得到更准确的有效宽度。

7. 解析法解析法是一种较为精细的计算方法，适用于复杂且要求较高精度的T形截面。

该方法基于对T形截面受压翼缘的边界条件进行数学建模和求解。

通过使用适当的数学方法和工具，可以得到更准确的有效宽度。

8. 对T形截面受压翼缘有效宽度的个人观点和理解对于T形截面受压翼缘的有效宽度计算，个人认为需要综合考虑结构的实际情况和设计要求。

在选择计算方法时，需要根据截面形状、材料性质和受力状态进行合理的判断。

梁翼缘计算宽度

梁翼缘计算宽度
，文章内容有章法，
《梁翼缘计算宽度》
一、引言
梁翼缘计算宽度是构建结构的基础，需要适当的宽度和厚度才能使连接部件具有足够的受力性能。

此外，翼缘有助于减少梁肋连接处的应力集中，从而提高梁的刚度和强度。

因此，计算梁翼缘的宽度是非常重要的。

二、梁翼缘计算宽度原理
梁翼缘计算宽度的主要原理是：在一定的设计载荷和设计原则下，要考虑到影响因素，确定出梁翼缘的宽度，以及梁翼缘内的抗拉和抗推应力场模式，从而使梁翼缘钢更有效、更安全地弯曲。

三、梁翼缘计算宽度过程
(1)确定设计载荷及设计原则；
(2)确定梁翼缘的作用和结构参数，包括有梁的跨度、梁的宽度、梁的厚度；
(3)分析梁翼缘的受力性能，包括有抗拉抗推应力场；
(4)确定材料性能，找出梁翼缘的计算宽度；
(5)对梁翼缘上及其配件进行安装，测试翼缘的强度，确保翼缘的安全使用。

四、结论
梁翼缘计算宽度是非常重要的，需要考虑到多个影响因素，通过相关的计算，把梁翼缘的宽度计算出来，使梁翼缘结构具有更好的性能，有助于更安全、更加有效地使用。

对梁翼缘有效宽度的理解

对梁翼缘有效宽度的理解于淑兰【摘要】阐述了在实际工作中对《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)中关于T梁、箱梁翼缘有效宽度的计算、使用场合的理解.【期刊名称】《北方交通》【年(卷),期】2007(000)010【总页数】3页(P51-53)【关键词】翼缘;有效宽度;承载能力极限状态;正常使用极限状态【作者】于淑兰【作者单位】辽宁省交通勘测设计院,沈阳,110005【正文语种】中文【中图分类】工业技术第 10 期北方交通·51 ．对粱翼缘有效宽度的理解于淑兰（辽宁省交通勘测设计院，沈阳110005 ）摘要阐述了在实际工作中对《公路钢筋混凝土及预应力混凝土桥涵设计规范》(ⅡG D62-2004)中关于 T 梁、箱梁翼缘有效宽度的计算、使用场合的理解。

关键词翼缘有效宽度承载能力极限状态正常使用极限状态《公路钢筋混凝土及预应力混凝土桥涵设计规范》 ( JTGD62-2004)，以下称“ 新桥规” ，对梁的计算有一个很大的补充，就是借鉴着《德国规范( DIN1075)》并加了一点修正，填补了我国规范在计算箱梁翼缘有效宽度方面的空白，而且对有效宽度的使用场合进行了规定，对实际设计起到指导性的作用。

1有效宽度的概念在新桥规的条文说明中明确解释道：当梁受弯时，横桥向翼缘会产生剪力滞效应。

就是近腹板的翼缘的法向应力与腹板法向应力相同，而离腹板越远则法向应力越小（其分布规律主要取决于截面和梁跨径的相对尺寸以及荷载形式）。

这种同一纤维层上沿翼缘宽度变化的法向应力需用高等材料力学的方法才能精确求出。

为了在计算中应用初等材料力学方法求解，引入了“ 有效宽度”的概念。

即令翼缘有效宽度内的法向应力体积等于原翼缘全宽的法向应力体积，并按有效宽度内的翼缘任一纤维层法向应力值与同一纤维层的腹板内的应力值相同，来确定翼缘有效宽度。

这里有两点需注意：(1) 梁处于受弯状态。

当然梁本身就定义为受弯构件。

压型钢板受压翼缘的有效计算宽度

压型钢板受压翼缘的有效计算宽度压型钢板是一种常用的构造材料，广泛应用于桥梁、楼梯、平台等结构中。

在设计过程中，需要对压型钢板的受压翼缘进行计算，以确定其有效计算宽度。

本文将详细介绍压型钢板受压翼缘的有效计算宽度的确定方法。

首先，我们需要了解什么是压型钢板的受压翼缘。

压型钢板是由热轧、冷弯或冷轧工艺制成的具有特定形状的钢板。

它由翼缘、腹板和连接部分组成。

其中，翼缘是板的边缘部分，垂直于腹板，承受受压力。

受压翼缘是指在受压力作用下，压型钢板翼缘内部的一部分。

确定压型钢板受压翼缘的有效计算宽度需要考虑以下几个方面：1.翼缘受压力的分布。

在受压力作用下，压型钢板翼缘的压力分布不均匀。

通常，翼缘的中央部分受力较大，而边缘部分受力较小。

因此，为了准确计算翼缘的有效计算宽度，需要确定受压力作用下翼缘各个位置的压力大小。

2.翼缘板的屈曲计算。

在受压力作用下，压型钢板翼缘会发生屈曲。

屈曲是指材料在受压力作用下发生的弯曲变形。

为了确定翼缘的有效计算宽度，需要计算翼缘板的屈曲载荷和屈曲长度。

屈曲载荷是指使翼缘屈曲的最小载荷，而屈曲长度是指翼缘板屈曲后的长度。

通过计算这些参数，可以确定受压翼缘的有效计算宽度。

3.材料的强度和刚度。

压型钢板的材料具有一定的强度和刚度，它们对翼缘受力性能起到重要影响。

在计算过程中，需要考虑材料的强度和刚度参数，以确定翼缘的有效计算宽度。

4.结构的限制条件。

在实际设计中，还需要考虑结构的限制条件，如构件的连接方式、荷载的大小和分布等。

这些限制条件将影响到翼缘的有效计算宽度。

因此，在确定计算宽度时，需要综合考虑这些限制条件。

综上所述，压型钢板受压翼缘的有效计算宽度需要综合考虑翼缘受压力的分布、翼缘板的屈曲计算、材料的强度和刚度以及结构的限制条件等因素。

只有在对这些因素进行充分考虑的基础上，才能准确确定翼缘的有效计算宽度，从而保证结构的安全性和稳定性。

通过以上的介绍，相信读者对于压型钢板受压翼缘的有效计算宽度有了一定的了解。

混凝土梁有效翼缘宽度取值研究

代入式（４），可解得：［一１ｅｋｘ）＝７ｎｑ
，
对Ｅ．Ｒｅｉｓｓｎｅｒ所用的二次型分布的纵向位移进行修正，得到梁的纵向位移ｕ（ｘ，Ｙ）沿宽度方向的函数表
达式如下：
＋
一
＋
１．２规范中存在的问题
下简称为我国《规范》）在７．２．３条中，对Ｔ形、Ｉ形、倒Ｌ形截面受弯构件位于受压区的有效翼缘宽度ｂ取值，分别从计算跨度ｆ０、梁肋净距ｓ翼缘高度
我国《规范》中对于混凝土梁有效翼缘宽度的
摘
要：指出了我国《混凝土结构设计规范》中混凝土梁有效翼缘宽度取值的问题。采用能量变分法，推导弹性状态下有效翼
缘宽度的计算公式，考虑不同的支座条件下，跨度、梁肋净距、翼缘相对刚度对取值的影响，并验证了公式的准确性。提出了
１问题引出
１．１我国规范的规定ＧＢ５００１０— ２００２｛混凝土结构设计规范》 ¨ （以
剪强度考虑的。这项规定基本上是基于试验得出，该项控制指标一般用于承载能力极限状态下。各国规范关于此项的取值规定相差不大，介于ｂｂ＋１０与ｂｂ＋１６ｈ；之间。
对规范的理解是：在受弯极限承载力状态下，规范对有效翼缘宽度有具体规定，但在弹性状态下无规定。

曲线钢箱梁上翼缘有效宽度分析和实用计算方法研究

不安全．
对于箱梁由剪力滞影响而引起的翼缘宽度的折减，国现行桥梁规范中对于钢筋混凝土直线桥梁已中有明确规定，于钢结构桥梁还缺乏具体规定，于曲线钢箱梁由于其结构更趋复杂，对对由剪力滞影响而引
中圈分类号：ＴＵ３５１７．文献标识码：Ａ文章编号：１０－８９２０）３０６ —６００２３（０６０ —３７０
ＳｕｙｏｔｄｎＡｎａｙｉｆＥｑｕｖｌｎｔＴｏａｅＷｉｈａｎｃｅｅｌｓｓｏｉａｅｐＦｌｎｇｄｔｎｄＣｏｒｔＣａｃｌｔｏｒｕａｆＣｕｖｄＳｅｌＢｏ — ｉｄｒｉｕａｉｎＦｏｍｌｓｏｒｅｔｅｘｇｒｅｓ
ＹＡ０ —ｉ。ＸＵＩｉｌＨｕ，ＣＡＩＧｕ— ｈｎｉｕ。ｃ
（．ｏｌｅｏｒｈｔｃｒｌＥｇｎｅｉｇ，ｎｉｎｉｅｓｙ，ｕｉ１ＣｌｇＡｃｉｔａｎｉｅｒｎＸｉｊｇＵｎｖｒｉＵｒｍｑ，Ｘｉｊｎ３０８ｈｎｌｅｆｅｕａｔｎｉｇ８００，Ｃｉａａ２．ＸｉｊｎｒｈｔｃｒｌＤｓｎＬｍｉｄＣｍａｙ・ｕｉｎｉｎ３００ＣｉａｎｉｇＡｃｉｔａｅｉｉｔｏｐｎＵｒｍｑ・Ｘｉａｇ８００・ｈｎ）ａｅｕｇｅｊ
摘要：采用空间薄板有限元法，析了曲线钢箱梁桥的有效宽度规律ｌ分通过算例分析验证了计算方法的准确性，提出了供工程设计参考的实用箱梁上翼缘有效宽度比计算方法ｆ为完善规范有关钢结构箱梁桥上翼缘有效

带翼缘剪力墙有效翼缘宽度的解析解与简化公式

带翼缘剪力墙有效翼缘宽度的解析解与简化公式王斌;史庆轩;何伟锋【摘要】为了研究高层建筑结构中带翼缘剪力墙有效翼缘宽度的取值,本文基于能量变分原理,推导了剪力墙翼缘截面正应力的解析表达式,并依据应力等效原则计算了弹性阶段有效翼缘宽度的解析解.采用有限元方法对一组T形截面剪力墙进行了参数化分析,描述了有效翼缘宽度随加载过程的变化规律.通过引入无量纲剪滞系数β定量描述了剪滞效应随不同设计参数的变化规律.根据有限元计算结果,拟合出了不同受力阶段剪滞系数的经验计算式,考虑边界条件的约束构造出了描述正应力分布的曲线函数,进而推导出不同受力阶段有效翼缘宽的简化计算公式.通过与有限元计算结果的比对验证了简化公式的准确性,为工程设计提供参考.%To study the effective flange width of flanged shear walls in high-rise buildings, in this study, we derive an analytical expression for normal stress in the flange section of a shear wall using the energy variational method, then we derive an analytical solution for determining the effective flange width in the elastic stage based on the stress equivalent principle.We perform a parametric analysis for T-shaped shear walls using the finite element (FE) method in order to discuss the change laws of effective flange width along with the loading process and quantitatively describe the variation of the shear lag effect for different parameters by introducing the dimensionless shear lag coefficient β.Based on our FE calculation results, we fitted the empirical formulas of the shear lag coefficients and derived the curve function for describing the normal stress distribution by considering the constraint of boundary conditions.We then obtained simplified calculationformulas for the effective flange width at different loading stages.In a comparison with the finite element calculation results, we verified the accuracy of these simplified formulas, which can provide a reference for project design.【期刊名称】《哈尔滨工程大学学报》【年(卷),期】2017(038)003【总页数】8页(P404-411)【关键词】带翼缘剪力墙;剪滞效应;解析解;能量变分原理;有效翼缘宽度;简化计算;剪力墙【作者】王斌;史庆轩;何伟锋【作者单位】西安建筑科技大学土木工程学院,陕西西安 710055;西安建筑科技大学土木工程学院,陕西西安 710055;中色科技股份有限公司苏州分公司,江苏苏州215000【正文语种】中文【中图分类】TU398结构布置时，矩形墙肢通常被组合成了箱形、T形、工字形等带翼缘剪力墙形式。

长悬臂混凝土箱梁翼缘板荷载有效分布宽度计算分析

长悬臂混凝土箱梁翼缘板荷载有效分布宽度计算分析郭晓雷;卜建清【摘要】长悬臂混凝土箱梁由于增加了翼缘板的长度,采用我国规范的荷载有效分布宽度进行翼缘板受力计算将造成配筋与实际不符.以有限元为基础,采用大型有限元ANSYS软件建立不带边梁全箱梁模型以及带边梁全箱梁模型,考虑翼缘板长度、厚度以及荷载作用位置在不同坡度的情况下,进行荷载有效宽度计算对比分析,结论表明,长悬臂翼缘板的边梁效应不容忽略.并根据最小二乘法原理,利用Matlab软件拟合得出不带边梁全箱梁模型和带边梁全箱梁模型翼缘板荷载有效宽度的计算公式,为翼缘板配筋计算提供帮助.%Since the long cantilever concrete box girder increases the length of the flange plate,using the load effective width of flange plate from Chinese code to calculate stress will cause reinforcement not to tally with the actual condition.On the basis of finite element,large finite element software ANSYS is used to establish box girder model without boundary beam and box girder model with boundary beam.With different flange plate length and thickness and with load position at different slope,the load effective widths are calculated to make a comparison and analysis.The conclusion shows that responses of boundary beams of long cantilever flange plate should not be ignored.Based on the principle of least square method,the Matlab software is used to fit the formula of load effective width of flange plate of the box girder model without boundary beam and box girder model with boundary beam,giving help to its reinforcement design.【期刊名称】《石家庄铁道大学学报（自然科学版）》【年(卷),期】2017(030)004【总页数】6页(P1-5,19)【关键词】长悬臂;翼缘板;边梁;最小二乘法;荷载有效分布宽度【作者】郭晓雷;卜建清【作者单位】石家庄铁道大学交通运输学院,河北石家庄050043;石家庄铁道大学土木工程学院,河北石家庄050043【正文语种】中文【中图分类】TU997随着城市空间问题越趋于严重，混凝土箱梁开始采用增加翼缘板长度的长悬臂混凝土箱梁，然而我国规范在进行翼缘板配筋设计时采用的荷载有效分布宽度计算公式只适用于短悬臂板[1]，对于长悬臂翼缘板进行计算分析将造成配筋不足而致使翼缘板开裂。

压型钢板受压翼缘的有效计算宽度

压型钢板受压翼缘的有效计算宽度压型钢板是一种常用的结构材料，在结构设计和计算中十分重要。

在受压情况下，压型钢板的受压翼缘的有效计算宽度是一个关键参数，它影响着受压翼缘的抗弯强度和稳定性。

有效计算宽度的准确确定对于结构设计的准确性和安全性至关重要。

压型钢板的截面形状通常为矩形或梯形，翼缘一般有上翼缘、下翼缘和侧翼缘。

在受压情况下，翼缘会受到弯曲作用，因此需要确定其有效计算宽度。

首先，我们需要明确有效计算宽度的定义。

有效计算宽度是指受压翼缘表面上任意一点到中性轴的距离。

它是起到受压翼缘抵抗弯矩作用的有效宽度，一般用字母$b$表示。

对于矩形截面的压型钢板，可将其有效宽度简化为截面宽度的两个翼缘边缘的距离之和。

即$b_{\text{eff}} = b - 2c$，其中$b$为翼缘截面的宽度，$c$为翼缘的厚度。

这种简化方法适用于无特殊要求和加载情况的压型钢板。

然而，在一些特殊的情况下，如有较大的荷载和弯矩作用，简化计算可能不够准确。

在这种情况下，可以使用更精确的计算方法，如有限元分析或实验测试。

这些方法可以更精确地确定受压翼缘的应力分布和变形情况，进而确定其有效计算宽度。

对于梯形截面的压型钢板，其受压翼缘的有效计算宽度可以通过类似的方法来确定。

首先将梯形截面划分为矩形和直角三角形的组合，然后分别计算矩形和直角三角形部分的有效计算宽度，最后求和得到总的有效计算宽度。

需要注意的是，有效计算宽度的确定应该根据具体的受压情况和要求进行，结合工程实践和经验进行合理选择。

在实际设计中，还需要考虑钢板的材料性能、荷载情况和结构要求等因素，综合权衡确定合适的计算宽度。

总之，压型钢板受压翼缘的有效计算宽度是结构设计和计算中的重要参数，对于保证结构的稳定性和安全性十分关键。

其准确确定需要考虑多种因素，包括截面形状、加载情况、材料性能等。

综合使用理论计算、有限元分析和实验测试等方法，可以得到更准确的有效计算宽度。

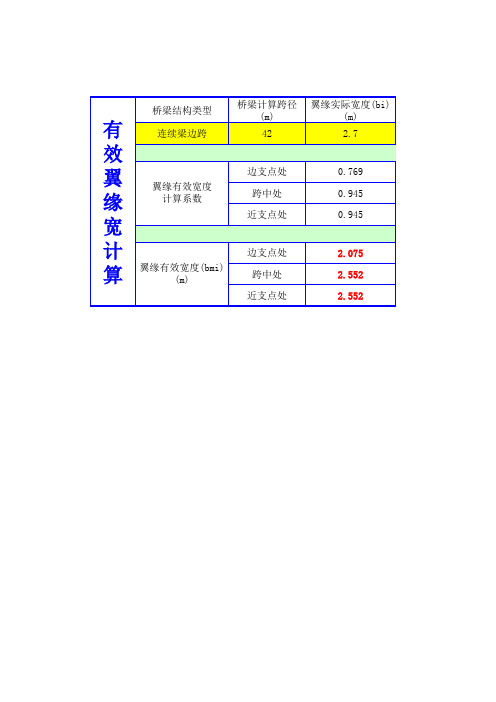
有效翼缘宽计算

ps-y 1.2892444 2.1516444 0.05 0.056 0.057 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.6 0.7
ps-x 1 0.9 0.85 0.7 0.57 0.455 0.39 0.33 0.29 0.25 0.23 0.2 0.17 0.15
注：1.表中黄色区域为数据录入区域. 2.当箱梁的翼缘实际跨度小于或等于0.3 倍的梁高时，根据规范，翼缘的有效宽度应采用翼缘的实际宽度. 3.本表格中的翼缘有效宽度计算系数由规范中ρ s、ρ f曲线分段直线拟合得来. 4.本表格中所计算的bi为一片翼缘的宽度，对于由多片翼缘构成的箱梁，请分别计算求和.
1 0.9 0.85 0.7 0.57 0.455 0.39 0.33 0.29 0.25 0.23 0.2 0.17 0.15
-0.06 -0.02 -0.286667 -0.384615 -0.434783 -0.769231 -0.833333 -1.25 -1.25 -2.5 -1.666667 -3.333333 -5
m值 -0.06 -0.02 -0.286667 -0.384615 -0.434783 -0.769231 -0.833333 -1.25 -1.25 -2.5 -1.666667 -3.333333 -5
0.05 0.056 0.057 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.6 0.7
0.6055556 0.75 0.5 0.65 0.6055556 0.7583333 0.7269231 0.7269231 1.35 1.0666667 1.0666667 1.5333333
名称定义

压型钢板受压翼缘的有效计算宽度

压型钢板受压翼缘的有效计算宽度压型钢板受压翼缘的有效计算宽度是指在受拉应力均匀分布的假定下，根据受压翼缘的几何形状和受压变形特性计算得到的一种等效宽度。

有效计算宽度的确定是为了准确计算受压翼缘的抗弯承载能力，从而确保结构的稳定性和安全性。

一、受压翼缘的几何形状对有效计算宽度的影响受压翼缘常见的形状有平板、角钢、工字钢翼缘等。

不同形状的受压翼缘会对其抗弯承载能力产生不同的影响。

在计算受压翼缘的有效计算宽度时，需要根据其几何形状进行不同的处理。

1.平板翼缘：对于平板翼缘，其有效计算宽度一般可以直接通过几何尺寸进行确定。

如果平板翼缘边缘存在较大的不平整或有较大的切槽时，需要考虑相应的修正。

2.角钢翼缘：对于角钢翼缘，其有效计算宽度可以通过将角钢翼缘的两个翼缘厚度之和加上与翼缘翼角相关的修正值来确定。

修正值一般根据经验公式进行计算。

3.工字钢翼缘：对于工字钢翼缘，其有效计算宽度一般取其翼缘宽度的一半。

如果工字钢翼缘翼角较小，还需要考虑相应的修正。

二、计算方法根据以上受压翼缘的几何形状，可以采用以下计算方法确定其有效计算宽度。

1.平板翼缘：如果平板翼缘较为规则，可以直接通过翼缘的宽度来确定其有效计算宽度。

需要注意的是，在计算有效计算宽度时，要考虑翼缘边缘的不规则性对其承载能力的影响，可以按比例进行修正。

如果平板翼缘存在切槽或切口等的情况，需要根据具体的情况进行修正计算。

2.角钢翼缘：对于角钢翼缘，其有效计算宽度可以通过将两个翼缘厚度之和与翼缘翼角相关的修正值相加来确定。

修正值可以根据经验公式进行计算，一般情况下取修正值为0.6倍翼角。

3.工字钢翼缘：对于工字钢翼缘，其有效计算宽度一般取其翼缘宽度的一半。

需要注意的是，在计算有效计算宽度时，如果工字钢翼缘翼角较小，还需要考虑相应的修正值。

修正值可以根据经验公式计算，一般情况下取修正值为0.6倍翼角。

三、实例应用假设压型钢板受压翼缘为工字钢翼缘，其翼缘宽度为100毫米，翼缘厚度为10毫米，翼缘翼角为45°。

翼缘宽厚比限值计算

翼缘宽厚比限值计算
翼缘宽厚比是指飞机的翼缘的宽度与其厚度之比。

在飞机设计中，翼缘宽厚比的选择对于飞机的性能和安全非常重要。

本文将介绍翼缘
宽厚比的计算方法以及其在飞机设计中的意义。

翼缘宽厚比的计算通常采用以下公式：
翼缘宽厚比 = 翼缘宽度 / 翼缘厚度
其中，翼缘宽度是翼缘顶部到底部的距离，翼缘厚度是翼缘顶部
到底部的距离的一半。

通过计算翼缘宽厚比，可以得到一个反映翼缘
形状的参数。

翼缘宽厚比的选择对飞机的性能和安全具有重要影响。

较小的翼
缘宽厚比通常可以减小飞机的湍流阻力，提高飞行速度和燃油效率。

这是因为较小的翼缘宽厚比可以减小空气在翼缘上的阻力，使得飞机
在空气中滑行的阻力减小。

另一方面，较大的翼缘宽厚比对于飞机的低速性能具有重要意义。

较大的翼缘宽厚比可以增加飞机翼面积，提高升力系数，使飞机在起
飞和降落时更加稳定，减少失速和冲洗现象。

此外，较大的翼缘宽厚
比还可以增加飞机的结构强度，提高其抗风荷载的能力。

在实际的飞机设计中，翼缘宽厚比的选择需要综合考虑飞机的性
能要求、安全要求和结构限制。

一般来说，中等翼缘宽厚比的设计可
以在性能和安全之间取得平衡。

然而，在一些特殊应用中，如超音速飞行器设计中，较小的翼缘宽厚比可能更为适合。

总之，翼缘宽厚比是飞机设计中一个重要的参数，它对飞机的性能和安全具有重要影响。

通过合理选择翼缘宽厚比，可以使飞机在空中飞行更加高效、稳定和安全。

因此，在飞机设计中，应该根据具体情况综合考虑各种因素，确定最适合的翼缘宽厚比。

压型钢板受压翼缘的有效计算宽度

压型钢板受压翼缘的有效计算宽度压型钢板是一种常见的结构材料，广泛应用于建筑、桥梁和机械制造等领域。

在设计和计算压型钢板构件时，了解受压翼缘的有效计算宽度非常重要。

什么是压型钢板受压翼缘的有效计算宽度？一般而言，钢板的有效宽度是指翼缘上的一段区域，可以在计算弯曲和屈服承载能力时起作用。

从截面力学的角度来看，这个宽度被视为受压翼缘的有效工作区域。

在计算有效宽度时，需要考虑以下几个因素：1. 稳定性要求：翼缘的稳定性是指其抵抗局部屈曲的能力。

为了保证结构的整体稳定性，翼缘的有效宽度应满足一定的要求。

根据规范的要求，可以利用受压翼缘平衡原则计算出它的有效宽度。

2. 截面形状：不同类型的压型钢板具有不同的截面形状。

常见的压型钢板可分为槽钢、工字钢、角钢等，它们的受压翼缘形状也不尽相同。

在计算有效宽度时，需要考虑翼缘的几何形状和尺寸。

3. 材料性质：压型钢板的材料特性对其受力性能有着重要影响。

常见的材料参数包括弹性模量、屈服强度等。

在计算有效宽度时，需要考虑翼缘的材料性质，并结合相关的弹性和塑性力学理论进行分析。

4. 边缘效应：压型钢板在受力作用下，其边缘区域往往会发生边缘效应，即应力分布不均匀的现象。

这种效应会使得翼缘的工作宽度发生变化，需要综合考虑边缘效应对有效宽度的影响。

在实际工程中，为了准确计算压型钢板受压翼缘的有效宽度，需要结合工程经验和规范要求进行分析。

可以通过理论计算、试验验证和数值模拟等手段，对压型钢板受压翼缘的有效宽度进行评估和确定。

总之，了解压型钢板受压翼缘的有效计算宽度对于工程设计和结构计算至关重要。

设计人员应仔细研究各种因素的影响，合理确定有效宽度，以保证结构的安全性和可靠性。

只有在全面考虑的基础上，才能设计出高质量的压型钢板构件，满足工程需求。

翼缘宽厚比限值计算

翼缘宽厚比限值计算
翼缘宽厚比是指飞机翼缘截面的宽度与厚度之比。

它是衡量翼缘结构强度和稳定性的一个重要参数，对于飞机的设计和制造具有重要的意义。

在飞机结构设计中，翼缘宽厚比的选择需要考虑多种因素，包括结构强度、飞行稳定性、气动特性等。

下面将介绍翼缘宽厚比限值的计算方法。

翼缘宽厚比的计算可以根据结构强度和振动特性来进行。

对于结构强度的计算，一般采用截面刚度方法。

根据材料强度和约束条件，可以确定翼缘截面的最大应力。

然后，根据翼缘材料的弹性模量，可以计算出翼缘的截面刚度。

结构强度的计算公式如下：
B/t <= C*(E/S)^0.5
其中，B是翼缘的宽度，t是翼缘的厚度，E是翼缘材料的弹性模量，S是翼缘截面的面积，C是一个与材料特性相关的系数。

这个公式可以保证翼缘的弯曲刚度足够大，以满足结构强度的要求。

翼缘宽厚比还需要考虑振动特性。

独立于结构强度的计算，根据气动和动力学的需求，需要保证翼缘的振动频率不会产生共振。

翼缘的共振频率是由翼缘宽度、厚度和材料的弹性模量等参数共同决定的。

具体的计算方法可以通过有限元分析等方法进行。

翼缘宽厚比的计算需要考虑结构强度和振动特性两方面的要求。

通过合理选择翼缘的宽度和厚度，以及合适的材料参数，可以保证飞机翼缘结构的强度和稳定性。

还需要注意根据具体的应用场景和要求进行调整。

这样才能设计出更加优秀和可靠的飞机。

翼缘宽厚比限值计算

翼缘宽厚比限值计算
翼缘宽厚比（flange width-thickness ratio）是指飞机机翼的翼缘（flange）宽度与其厚度之比。

翼缘宽厚比的大小对飞机机翼的结构强度
和稳定性有着重要影响，因此在飞机设计中需要进行限值计算。

首先，翼缘宽厚比的限值计算需要考虑飞机的操作条件，如飞行速度、加速度、载荷等。

一般来说，高速飞行中产生的气动载荷会对机翼产生较
大的压力和弯矩，因此需要较大的翼缘宽厚比。

而低速飞行中产生的气动
载荷较小，翼缘宽厚比可以适当小一些。

其次，翼缘宽厚比的限值计算还需要考虑材料的强度和刚度。

翼缘宽
度较大会增加刚度，降低损伤和疲劳的风险；而翼缘厚度较大会增加结构
的强度。

因此，在限值计算中需要综合考虑这两个因素，找到一个合适的
平衡点。

最后，翼缘宽厚比的限值计算还需要考虑结构的可制造性和可维修性。

翼缘的宽度越大，制造工艺和成本会越高；翼缘的厚度越大，维修和更换
的难度也会增加。

因此，在限值计算中，需要综合考虑这些因素，确保翼
缘宽厚比的限值既满足结构强度和稳定性要求，又具备良好的制造和维修
性能。

综上所述，翼缘宽厚比的限值计算是一项复杂而综合的工作，需要考
虑飞机操作条件、材料特性和结构性能等多个因素。

设计人员需要通过合
理的计算和分析，找到符合要求的翼缘宽厚比值，以确保飞机机翼的安全
和可靠性。