电子科技大学矩阵理论!
关于矩阵奇异值的若干性质

第2"卷第1期2021年1月高等数学研究STUDIES IN COLLEGE MATHEMATICSVol.2",No.1Jan. , 2021doi : 10. 3969/j. issn. 1008-1399. 2021. 01. 017关于矩阵奇异值的若干性质尹小艳,杨丹丹(西安电子科技大学数学与统计学院,陕西西安J10071)摘要探讨矩阵奇异值的性质及其与范数、谱半径、特征值等矩阵“大小”度量的关系,帮助学生建立这些概念之间的内在联系,强化对相关概念的理解和掌握.关键词奇异值;谱半径;范数"条件数中图分类号 O151.2 文献标识码 A文章编号 1008 - 1399(2021)01 - 0056 - 03Properties of Singular Values of MatricesYIN Xiaoyan and YANG Dandan(School of Mathematics and S t a t i s t i c s,Xidian University,Xi’an 710071)Abstract W e gather several properties of singular values and investigate the relations between singular values and some other measures on matrices such as n o r m,spectral radius,eigenvalues and so on.This work m a y lead the students to a deeper comprehension of these concepts.Keywords singular value,spectral radius,n o r m,condition number1引言矩阵的奇异值是矩阵的重要数字特征,在矩阵 计算、误差分析、图像处理、数据挖掘、推荐系统等理 论和实际问题中应用广泛&一2'矩阵作为有限维 线性空间上线性变换的数学模型,除奇异值外,对矩 阵的“大小”,还有着多种不同的度量,比如大家熟知 的矩阵范数、特征值、谱半径等.本文介绍奇异值的一些重要性质,并深人探讨这几个概念之间的有机联系,帮助同学们更好地理解和掌握矩阵的这几种数值'收稿日期! 2020 - 03 - 17 修改日期2020- 07 -05基金项目:西安电子科技大学矩阵分析与计算精品课程建设项目;西 安电子科技大学教学改革项目一研究型教学在矩阵分析与计算课程中的探索与实践,西安电子科技大学高等代数MOOC建设项目.作者简介:尹小艳(1979 —),女,陕西咸阳人,副教授,博士,从事矩阵 理论研究工作.Email:xyyin@.2奇异值的概念定义&]设A)crx",称'")=槡),("*"),4=1,2,…,-为矩阵"的正奇异值,简称奇异值.因为对任意矩阵crx",总有")= -(a),从而矩阵"的正奇异值的个数总是等于"的$.3奇异值的基本性质(1)对任意 A)crx",A=0L'1")=…='r(A)=0.证明设A为任意复矩阵,A=0 l a2a=0L)1 (A2a)=…=A…(A2a)=0L'1(A)=…='(A)=0.第2"卷第1期尹小艳,杨丹丹:关于矩阵奇异值的若干性质57(2) 对任意w阶方阵A,有A非奇异Lff,(A)>0,i=1,2,…,w.(3) 对任意w R复方阵A,有|det(A) |y^A) - ■••f f…(A).这里|det(A) |表示矩阵A的行列式的模.证明设A为任意w阶复方阵,det(A)2 =det(A*A)=Ai(A*A)…A…(A*A)='!(A)…'!(A)(4) 奇异值具有转置、共轭、酉不变性.即对任意A)CTx",i=1,2,…,r,有'(A*)='(A)='(A T)='(A),at(U A V)=at(A),这里A*,A T,A分别表示矩阵A的共轭转置、转置和共轭矩阵,U@分别为适当阶的酉矩阵.证明对任意A)Crx",'2(A *)=)i(AA *)=)i(A *A)=ai(A),'(A T)=A!((A T)* A T)=A,((A*)TA T)=A,((A A*)T)=)i(AA * )=A;(A *A)=ai(A),a!(A T)=a!((A T)* )=(a(A),a i(U A V)=A t(V*A*U*U A V)=At(A*A)=a2(A).(5) 奇异值分解(S T O)定理对任意A)CTx",必存在™•阶酉矩阵U和w阶酉矩阵@,使得0]U*A V=,其中'Y d i a g',•••'),'!,•••,'r 为 A的奇异值.奇异值分解在图像处理、数值计算等方面有着极为重要的应用,关于这一定理的重要意义及其应用后续文章会深人探讨.(6) 奇异值的几何意义先看一个具体的例子•设30' 3 0]* ;1A=U〇1.V=(«! w2)$ 1.其中 “1=(1,“2=(f,>#)'于是对V x Y h V i+h V i,有A v#=3«i ,A v2=m2故!=A# =ZiMi +Z2m2=3〇i M1+02a2.此时,若I I # I I 2=1即〇2Z〇2=i,则对应向量!满足32+/2 = 1.这表明4把财2中的单位圆{•r)N2,|| z || 2=1}变成了椭圆{:V =A:r,|| z || 2=1},而两个奇异值恰好是这一椭圆的两个半轴长,长轴所在直线span+1},短轴所在直线span {m2 },它们分别是spanV h s p a n+z}的像.一般地,设A)C,",记null(A)的正交补空间为W,A B r维子空间W中的单位复球面映成C™中的复椭球面,其中A的奇异值'1,…,〇,即为该椭球面的r个半轴长.3奇异值与矩阵其它度量的关系3.1奇异值与特征值的关系(1) 对任意w阶复方阵A,最大、最小奇异值构 成矩阵特征值的模的上下界•即V A)A(A),有f f m i n(A)"|A I(A)证明设A为任意w阶方阵,对V A)A(A),设#为A的属于特征值A的单位特征向量,A# =A#,I I # I I =1,由Amm (A *A)3"A*A"Am… (A *A)3可知,a?i n(A)=Amin(A*A)"#*A*A#= |A |2#* #=|A |z"Ama X(A*A)=a?ax(A)•(2) 设A为w阶方阵,对;=1,2,••,,,|(A) |模>0,若A正规a,(A)=1 |(A) |绝对值>0,若 A* =AU(A),A>。
矩阵理论第3章习题解答

4设 是 阶的实对称矩阵,并且 你能用几种方法证明
证:(1)设 是矩阵 的一个特征值, 是对应于 的一个非零特征向量,即 所以 即 所以矩阵 的特征值全为零,又 酉相似与对角矩阵 所以
(2)设 则 Βιβλιοθήκη 题设矛盾,所以结论成立。5试证:对于每一个实对称矩阵 ,都存在一个 阶方阵 ,使 。
证:矩阵 是一个对称矩阵,则 酉相似于一个对角矩阵,即
令 ,则
又由 令 则 。
7证明:一个正规矩阵若是三角矩阵,则它一定是对角矩阵.
证明参考课本101页引理3必要性的证明.
8证明:正规矩阵是幂零阵 的充要条件是
证:充分性: 则结论显然。
必要性:若 ,由题设矩阵 是正规矩阵,则 酉相似于一个对角矩阵,即
证:必要性:设 为正定的Hermite矩阵,根据定义有 ,即 ,同时有 所以
充分性:设 ,则 ,则矩阵 是Hermite矩阵。由于矩阵 是正定Hermite矩阵,存在一个正定的Hermite矩阵 ,使得 则有 对矩阵 施行相似变换: 则矩阵 与矩阵 有相同的特征值,且 是Hermite矩阵.
对 可得 即 是正定的Hermite矩阵,所以其所有的特征值为正,从而矩阵 所有的特征值为正,即矩阵 为正定的Hermite矩阵.
矩阵 的特征值为 ;其对应的特征向量构成的矩阵为
则酉变换为
13设矩阵 的最大秩分解为 ,证明:
证:充分性显然。
必要性:(反证法)如果存在向量 使得 ,但 ,令 ,则 。由于 是矩阵 的最大秩分解,则矩阵 的列向量是线性无关的,如果 ,则 ,从而 ,与题设矛盾,所以 。
15设 , 均为正定矩阵的Hermite矩阵,则 为正定的Hermite矩阵的充要条件是 .
杭州电子科技大学2013-2014-1(秋季)研究生开课表

外国语 外国语 外国语 外国语 外国语
英语9班 英语10班 英语11班 英语12班 英语13班 英语14班 英语15班 英语16班 英语17班 自然辩证法概论(秋季) 压力管理与潜能开发(秋季) 英语听说(秋季)1班 英语听说(秋季)2班 英语听说(秋季)3班 英语听说(秋季)4班 英语听说(秋季)5班 日语(秋季) 科技文献检索(秋季)(理工类) 英文科技论文写作(秋季) 企业运营管理(秋季) 世界民族音乐文化(秋季) 羽毛球
副教授 三8-9
马克思 马克思 马克思 马克思 马克思
思想政治教育学原理 马克思主义经典著作选读 社会科学方法论专题研究 教育心理学专题研究 学生事务管理研究
Z1 Z1 Z1 Z2 Z3
32 32 32 32 32
2 2 2 2 2
黄岩 李颖姣 贺武华 吕澜 吕金海、 金一斌
45
副教授 讲师 教授 教授 副教授 、 教授
2
黄岩
副教授 一6-7
113
111
12-201
32 32 32 48 48 48 48 48 48 48 48
2 2 2 3 3 3 3 3 3 3 3
王海稳 李庆真 姜志强 邬静洁 周晓琴 骆汉卫 于莹 邬静洁 周晓琴 骆汉卫 于莹
副教授 一3-4 副教授 一3-4 副教授 一3-4 副教授 二3-5 副教授 二3-5 副教授 二3-5 副教授 二3-5 副教授 二6-8 副教授 二6-8 副教授 二6-8 副教授 二6-8
自动化 自动化 自动化 自动化 外国语 外国语 外国语 外国语 外国语 外国语 外国语 外国语 外国语 外国语
80 20 20 20 9 2 3 14 14 14 14 14 14 14
15 8 8 9 9 3 3 14 14 8 7 12 4 4 7 6 5 3 8 20
工程矩阵理论试题A
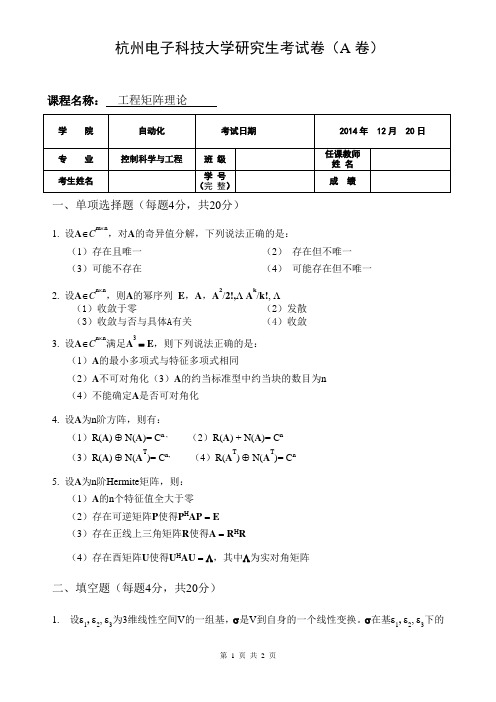
杭州电子科技大学研究生考试卷(A卷)课程名称:工程矩阵理论一、单项选择题(每题4分,共20分)1. 设A∈C m⨯n,对A的奇异值分解,下列说法正确的是:(1)存在且唯一(2)存在但不唯一(3)可能不存在(4)可能存在但不唯一2. 设A∈C n⨯n,则A的幂序列E,A,A2/2!, A k/k!,(1)收敛于零(2)发散(3)收敛与否与具体A有关(4)收敛3. 设A∈C n⨯n满足A3= E,则下列说法正确的是:(1)A的最小多项式与特征多项式相同(2)A不可对角化(3)A的约当标准型中约当块的数目为n(4)不能确定A是否可对角化4. 设A为n阶方阵,则有:(1)R(A) ⊕ N(A)= C n , (2)R(A) + N(A)= C n(3)R(A) ⊕ N(A T)= C n, (4)R(A T) ⊕ N(A T)= C n5. 设A为n阶Hermite矩阵,则:(1)A的n个特征值全大于零(2)存在可逆矩阵P使得P H AP=E(3)存在正线上三角矩阵R使得A=R H R(4)存在酉矩阵U使得U H AU=Λ,其中Λ为实对角矩阵二、填空题(每题4分,共20分)1. 设ε1, ε2, ε3为3维线性空间V的一组基,σ是V到自身的一个线性变换。
σ在基ε1, ε2, ε3下的矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211a a a a a a a a a ,则σ在基ε3, 2ε2, 3ε1下的矩阵为。
2. 设方阵A 满足A 2= 3A, 则sin (3A ) = 。
3.矩阵A = diag 21312,,0203⎛⎫⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,则A 的最小多项式为 。
4. 设X = (x 1, x 2, , x n )T 为变向量,α = (a 1, a 2, , a n )T 为常向量,H = (h ij )n ⨯n 为常矩阵,则:,()=HX X XT D D。
5. 设A ∈C n ⨯n 为Hermite 矩阵,X ∈C n ,A 的n 个特征值为λ1,λ2, ,λn ,满足λ1 ≤ λ2 ≤ ≤ λn ,则: XX AXX H X H 0max ≠ =。
《信息论》(电子科大)第七章_信息率失真理论

电子科技大学
称全部n 称全部n×m个失真度组成的矩阵为失真 矩阵: 矩阵:
d(x1, y1 ) d(x1, y2 ) d(x , y ) d(x , y ) 2 2 2 1 [D] = ... ... d(xn , y1 ) d(xn , y2 ) ... d(x1, ym ) ... d(x2 , ym ) ... ... ... d(xn , ym )
电子科技大学
i = 1,2,L,n, j = 1,2,L,m
µi ln − Sd(xi , yj ) − =0 p(yj ) p(xi ) p(yj / xi ) i = 1,2,L,n, j = 1,2,L,m
µi 令ln λi = p(xi )
ln
p(yj / xi ) p(yj )
电子科技大学
∂ {−S[∑∑p(xk )p(yl / xk )d(xk , yl ) − D]} ∂p(yj / xi ) k =1 l =1
n m
= −Sp(xi )d(xi , yj )
p(yj / xi ) ∂Φi ∴ = p(xi )ln ∂p(yj / xi ) p(yj ) − Sp(xi )d(xi , yj ) − µi = 0
电子科技大学
d(xi , yj ) = (yj − xi )
2
称为平方误差失真度。 称为平方误差失真度。
(2)平均失真度 (2)平均失真度
D = E[d(xi , yj )] = ∑∑p(xi )p(yi / xi )d(xi , yj )
i =1 j=1 n m
电子科技大学
(3)保真度准则 (3)保真度准则 如果给定的允许失真为D 如果给定的允许失真为D 为保真度准则。 则称 p(yj / xi ) = p(yj )
电子科技大学 矩阵理论!ppt课件

( , ) H aibi i 1
则上式定义了一个内积,C n是酉空间.
返回
定义: 设1,L , n是酉空间V一组基,令aij ( i , j ),
则称矩阵A=(aij )为基1,L
,
的度量矩阵
n
,或Gram矩阵
.
定理:
设矩阵A=(aij
)为酉空间V的一组基1,L
,
的
n
度量矩阵,则
(1) AH A;
xi H Bx j ij .
返回
定理 6 设n n矩阵 A AH , B BH,且B正定,与B共扼 向量系x1 , x2 ,L , xn具有以下性质, (1) xi 0 ( i 1, 2,L ,n ) ; (2) x1 , x2 ,L , xn 线性无关 ; (3)i与xi满足方程Axi i Bxi ; (4)若令X ( x1 , x2 ,L , xn ) , X H BX E , X H AX diag( 1 , 2 ,L ,n )
定义 4 ( x, y) 0
向量 x和y正交,记为 x y
勾股定理: x y
|| x y ||2 || x ||2 || y ||2
垂线最短定理:欧氏空间Vn ( R) 中的一个固定向量 和一个子空间中各向量的距离“垂线最短”.
返回
定义5
n维欧氏空间V中向量1 ,2 ,L ,k的Gram行列式 :
b
(f (x), g(x)) a f ( x )g( x )dx
证明: C[a,b]是欧氏空间.
b
f ( x ), g( x ), a f ( x )g( x )dx 是唯一确定实数
返回
1
f
,
g
b
a
矩阵可交换成立的条件与性质

毕业设计(论文)题目矩阵可交换成立的条件与性质学院理学院专业数学与应用数学年级 2008级班级 0814 姓名吴锦娜学号 2008530088 指导教师李伟职称副教授矩阵可交换成立的条件与性质[摘要]矩阵是高等数学中一个重要内容,在数学领域以及其他科学领域有着重大的理论意义.众所周知,矩阵的乘法在一般情况下是不满足交换律的,即在通常情况下,BAAB .但是,在某些特殊情况下,矩阵的乘法也能满足交换律.可交换矩阵有着很多特殊的性质和重要的作用.本文从可交换矩阵和相关知识的定义出发,探讨了矩阵可交换的一些条件和可交换矩阵的部分性质及应用,并且介绍了几类特殊的可交换矩阵.[关键词]矩阵可交换条件性质应用The Conditions for The Commutation of Matrix and Its Some Properties[Abstract] Matrix, a important content in altitude-mathematics, has a great theoretic significance in the aspect of both mathematics and other science field。
As far as we have concerned,the multiplication of matrix could not satisfy the exchange rule under the normal condition, that is to say, normally,AB≠BA。
Whereas, in some certain conditions, the multiplication of matrix could satisfy the exchange rule。
The exchangeable matrix has many special properties and important effection。
西安电子科技大学考研复试科目-离散数学08图论c

西安电子科技大学计算机学院 毛立强
10
lqmao@
路径和回路
最邻近算法 选任意点作为始点,找出一个与始点最近的点,形成一条边 的初始路径,然后用第二步的方法逐步扩充这条路径; 设x表示最新加到这条路径上的点,从不在路径上的所有点 中,选一个与x最邻近的点,把连接x与此点的边加到这条路 径中。重复这一步,直至G中所有顶点包含在路径中。 把始点和最后加入的顶点之间的边放入,就得出一个回路。
A = ∑ A( i )
+ i =1 ∞
而在n个结点的简单有向图中,基本路径长度不超过n-1,基 本回路长度不超过n,因此仅需考察 Bn-1=A+A(2)+ A(3)+···+ A(n-1),i≠j时 Bn=A+A(2)+ A(3)+···+ A(n),i=j时 此时,bij≠0,i≠j时表示从vi到vj是可达的,i=j时表示经过vi 的回路存在;bij=0,i≠j时表示从vi到vj是不可达的,分属于 不同强分图,i=j时表示经过vi的回路不存在。即bij表明了结 点间的可达性。 西安电子科技大学计算机学院 毛立强
西安电子科技大学计算机学院 毛立强
11
lqmao@
路径和回路
a 13 b 12 10 14 6 d e 7 9 8 15 c 11
西安电子科技大学计算机学院 毛立强
12
lqmao@
路径和回路
a 13 b 12 10 14 6 d e 7 9 8 15 c 11
西安电子科技大学计算机学院 毛立强
3
lqmao@
路径和回路
|S|=3,w(G-S)=4,4>3,所以该图不是汉密尔顿图。
西安电子科技大学计算机学院 毛立强
4
lqmao@
路径和回路
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.上三角矩阵R 的逆 R 1 也是上三角矩阵,且对角 元是R 对角元的倒数;
2.两个上三角矩阵 R1、R2 的乘积 R1R2也是上三角
矩阵,且对角元是 R1与R2对角元之积; 3.酉矩阵U 的逆 U 1也是酉矩阵; 4.两个酉矩阵之积 U1U2也是酉矩阵.
返回
返回
返回
返回
(3 )三角 |A | 不 B | ||A ||等 ||B || |式 ,A ,B P m n .
则称映 |||射 |为pmn上的矩阵 . 范数
返回
例 1 设APmn, 则
nm
|| A||m1
| aij |
j1i1
nm
1
|| A||m2(
| aij |2)2
j1i1
|A ||m | m i,j{a a i||j} x 1 i m 1 j n
返回
定义 2 设 |||a | : P m l R ,|||b | : P l n R ,
||||c:Pmn R是 矩 阵 范 数 , 如 果 ||A|c B | ||A |a |||B |b |
则 称 矩 |||a |阵 ,|||b |和 范 |||c |数 相. 容 如果 ||A|B |||A ||||B ||
0 0 0 0 0 0
返回
定理 2 设 A C r m n ,且 A B 1 D 1 B 2 D 2 均 为 A 的最大秩分解,则
(1) 存在 r阶可逆Q, 矩使 阵得 B 1 B 2 Q D 1 Q 1 D 2
( 2 ) D 1 H ( D 1 D 1 H ) 1 ( B 1 H B 1 ) 1 B 1 H D 2 H (D 2 D 2 H ) 1 (B 2 H B 2 ) 1 B 2 H
被称为极大列和范数 .
例 5 从属|于 | x||的算子范数为
n
|| A||max( | aij |) i j1
被称为极大行和范数 .
返回
定义 2 设ACnn,i是A的特征值,
r(A)ma|xi |称为A的谱半径 . i
例 6 设 A Pm n ,则|从 |x|2 |的 属算 于子 范数(又称为谱范数) 为
则称||映 ||为 C 射 n上向 x的 量 范 . 数
向 量 范 数 的 性 质 :
(1)||0||0; (2)x0时|, | 1 x| | 1;
||x|| 返回
(3 )对x 任 C n , 意 | |x 有 | ||x |||;
( 4 ) 对 x ,y 任 C n , ||x || 意 || 有 y ||| | |x | y |.|
例 2 设 x P n ,A P n n , |A ||则 m |2是 |x ||与 2 |
相容的矩阵范数 .
返回
定理 1 设 ||x|a | 是 Pn上的向 ,A 量 Pn 范 n,则 数
|| A||am xa|x|||Ax|x||a|a
(max|| ||u||a1
Au||a)
是 与 向 量||x范 ||a相 数容 的 矩.阵 范 数
例 1 设 x (x 1 ,x 2 ,L ,x n ) C n , 则
n
(1) || x ||1 | xi | i1
n
(2)|| x||2( | xi |2)1/2 i1
1范数 2范数
(3)||x||m 1iax n|xi |
无穷范数
返回
定 理1(Ho ..lder不 等 式 ) 若p,q1,且1pq11,
则 对 C n 任 意 向 量 x (x 1 ,x 2,L ,x n )T ,y (y 1 ,y 2 ,L , y n )T 都 有
n
n
n
|xi||yi|( |xi|p)1/p( |yi|q)1/q
i 1
i 1
i 1
例 2 设 x (x 1 ,x 2 ,L ,x n ) C n , 则
n
||x||p( |xi|p)1/p 1p i1 ..
返回
注 1 . ra (A n ) rka (A n H A )k ra (A n H ) A k
2. Hermite 矩阵的基本性质
( 1 )( A ,) ( ,A ) , , C n
(A ,)(A )HHAH H A
(, A)
返回
(2 ) i R , i (A )
( 3 ) A x i i x i , A x j j x j ,i j ( x i , x j ) 0
定义 1 设||•||a是Pn上的向量||范 ||m数 是, Pnn上的矩阵范数,且
||A|a |x ||A |m |||x|a | 则|称 ||m | 为与向||•量 |a | 相 范容 数的矩 .
返回
例 1 设xPn,APnn,则
nn
|| A||m1
| aij |
j1i1
是与向量 ||•|1范 | 相数 容的矩. 阵范数
返回
定理 3 设APnn,
(1 ) 若 A (a 1 ,a 2 , ,a n )则 ,
n
||A||2 F||A||m 22 ||ai ||2 2
i1
其中 ||ai|2 2 |, aiH ai.
n
(2) ||A |m 2 |2t(rA H A ) i(A H A )
i1
(3) 对任意的 U、 酉 V 矩 Pn阵 n,有
则称A为正规矩阵.
引理 1 设A为正规矩 A与B 阵 酉, 相似, B为正规矩阵
返回
引理 2 (Schu) r设ACnn,则存在酉矩
U,使得
AURUH
其中R, 是一个上三角矩 对阵 角且 线主 上的
元 素 为 A的 特 征.值
引理 3 设A正规矩阵且是三角 ,矩 则A是 阵
对角矩阵 .
返回
定理 5 n阶复矩阵 A是正规矩阵的充要条件 是A与对角矩阵酉相似. 即存在 n阶酉矩U阵 , 使得
||A |2 m |2 ||U H A|V 2 m |2 ||UA H |2 m |V 2
返回
推论 1 设APnn, 对任意的U 酉 、V矩 P阵 nn,
有 |A ||m |2 |U | |m |2 A |A | |m V |2 |U | |A m |2 V
返回
3. 算子范数
一、 算子范数
返回
定义 3 设 x(k)(x1 (k),x2 (k),,xn (k))T C n , 如 k l i m xi(k)ai (i1,2,,n)
则称向 x(k)收 量敛 a序 (a1 于 ,a 列 2,,an).
定义 4 lim x(k) a
k
lim||x(k)a||0
k
定理 4 设|| ||是Cn上 的 任 一 向 量 范 数 , 则
返回
§4 矩阵的最大秩分解
定理 1 设 ACrm n,则 存B 在 Crm 矩 r, 阵 DCrrn, 使 得
ABD
返回
矩阵的最大秩分解步骤:
一、进行行初等变化为 ,行标准形:
i1
i2
ir
0 1 * 0 0 *
0
0
0
1
0
*
~
A
0
0
0
0
1
*
0 0 0 0 0 0
P63页,相容的矩阵范数一定存在与之相容 的向量范数。
返回
定理 3 如果 ||•||m:CnnR是一相容 阵范数,则A 对 C 任 nn一 ,有
|i |||A||m
其中i, 是A的特征 . 值
返回
二、算子范数 的计算:
例 4 从属于向||量 x|1 |的 范算 数子范数
n
|| A||1ma(x |aij|) j i1
A Ud (1 i, a 2, g,n)U H
其中 1,2 , ,,n是 A 的 n个特 . 征值
返回
定理6
返回
§3 Hermite矩阵及其分解
定义1 A C n n ,A H A A 是 H e r m ite 矩 阵 A C n n ,A H A A 是 反 H e r m i t e 矩 阵
是Cn上的向量范数 Hol, de范 称 r 数 .为
返回
定理 2 设 ||||是 Cm 上的A 范 Cn m 数 n,, 则 || A||是Cn上的范数 .
定义 2 设 在 V n(P )上定 ||x|义 a |,|ቤተ መጻሕፍቲ ባይዱx|b |了 两种 量范数,若 C1存 0,C2 在 0, 常使 数得
C 1 ||x ||a ||x ||b C 2 ||x ||a x V n ( P ) 则|称 |x|a |与 ||x|b |等.价 定理 3 Vn(P)上的任意两个向量 均范 等数 价 .
第二章
向量与 矩 阵的范数
返回
1 向量的范数
定义 1 设映射 ||||:CnR满足: (1 )正定 ||x | |0 性 ,当且 x 0 时 仅 ||x |, |当 0 ;
( 2 ) 齐|次 |x | | |||性 x || ,R ,x C n ;
(3 )三角||x 不 y| ||等 |x | |||y 式 || ,x ,y C n .
||A||2 r(AHA)
返回
三、 谱范数的性质
定理 4 设ACnn,则 ( 1 )|A ||2 | |A |H |2 | |A |T |2 | |A ||2 | ( 2 )|A |H A |2 | |A |H A |2 | |A ||2 2 | (3) 对任 n阶 何 酉U 矩 及 V 都 阵有
推论 1 设 ||x|a |是 Pn上 的 向 ,A 、 量 BP 范 nn, 数
||A||a是从属 ||x于 ||a的算子范数,容 则的 它 矩阵范数,即
||A|a B | ||A |a |||B |a |
