苏教版八年级数学下册10.5分式方程公开课优质教案(13)
新版苏科版八年级数学下册教案第十章分式10.5分式方程一 教案
完成检测题
交流问难
口述基础知识.
分组展示板演并讲解学生讲解
试试看.
小组交流合作,指生说说等量关系
小组合作,共同探究
学生 说说自己的收获与不足
板
书
设
计
教学
札记
3、自学检测:
(1)下列各式中,分式方程是()
A、 B、
C、 D、
(2)分式方程 解的情况是()
A、有解, B、有解
C、有解, D、无解
(3)质疑问难,提出学习中存在的问题.
三、交流展示
(一)展示一
分组展示自主先学中的问题,归纳所学知识.
讲清:
1、分式方程的定义.
2、分式方程的解法.
3、检验.
(二)展示二(例题)
教
学
过
程
教
学
过
程
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
一、情境引入1ຫໍສະໝຸດ .甲、乙两人加工同一种服装,乙每天比甲多加工一件,乙加工服装24件所用的时间与甲加工服装20件所用的时间相同.怎样用方程来描述其中数量之间的相等关系?
2.一个两位数的个位数字是4,如果把个位数字与十位数字对调,那么所得的两位数与原两位数的比值是 .怎样用方程来描述其中数量之间的相等关系?
10.5分式方程
教学
目标
1、会用分式方程表示实际问题中的等量关系,体会分式方程的模型作用;
2、理解分式方程的概念;
3、能判断出分式方程,会解可化为一元一次方程的分式方程.
重点
会解可化为一元一次方程的分式方程.
难点
会解可化为一元一次方程的分式方程.
八年级数学苏科版下册 第十单元 《10.5分式方程》教学设计 教案

10.5分式方程一、教学目标:1.能将实际问题中的等量关系用分式方程表示,列出分式方程解决简单的实际问题,并根据实际问题的意义检验所得的结果是否合理。
2.能熟练并准确地解分式方程,能通过分式方程的简单变形,简化运算。
3.发展学生分析问题、解决问题的能力,渗透数学的转化思想,培养学生的应用意识。
二、教学重、难点:重点:根据实际分析问题中的等量关系,列出分式方程难点:把实际问题中的等量关系抽象成数学式子构建方程。
三、教学过程:(一)课前导学:列方程(组)解应用题的一般步骤是什么?关键是什么?(1)审题,找出等量关系(2)根据题意设末知数(一般求什么设什么,也可间接设)(3)根据等量关系,列方程(组);(4)解所列方程(组);(5)检验所列方程(组)的解是否符合题意;(6)写出完整的答案,注意单位.关键:分析题意寻找等量关系,列方程.(二)情景导入:周末小明打算去离家相距19千米的景区游玩,早上他从家出发去景区,先步行7千米,然后改骑自行车,共用2小时到达景区。
已知他骑自行车的速度是步行速度的4倍。
若设他步行的速度为x千米/小时,则骑自行车的速度为______千米/小时,步行时间为_______ 小时,骑车时间为________小时,根据题意可列方程为________________________.(三)合作探究:例4 为迎接区中学生田径运动会,计划由我校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,其余2个小组的每名同学要比原计划多做 4面彩旗才能完成任务。
如果这3个小组的人数相等,那么每个小组有多少名学生?要求:阅读题目,完成下列填空,讨论交流答案。
若设每个小组有x名学生,则3个小组有_____人,2个小组有_______人,原计划每人做____________面彩旗,实际每人做________面彩旗,根据等量关系________________________________________________可得方程______________。
苏科版数学八年级下册 10.5分式方程 教案
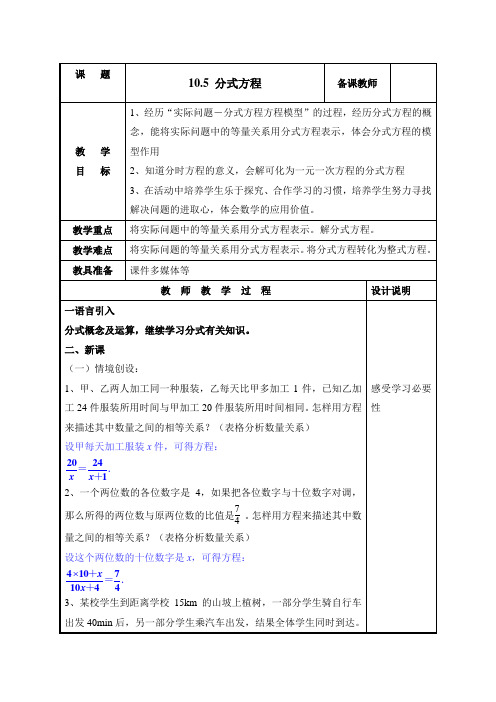
已知汽车的速度是自行车的速度的3倍。
怎样用方程来描述其中数量之间的相等关系?(表格分析数量关系) 设自行车的速度为x km/h ,可得方程:
.151540360
=+x x 也可以设时间为未知数
(二)归纳概念:
1、上面所得到的方程有什么共同特点?
2、这些方程与整式方程有什么区别?
结论:分母中含有未知数的方程叫做分式方程。
类比:数式分类,将方程进行分类。
学生再举例(2个学生)
3、概念辨析:【判断下列方程是否为分式方程】
,,
,
(三)探索解法: 4、四个方程中选择一个解
24x +1 =20x , 41071044+=.+x x .151540
360=+x x 选择解这个一元一次方程
说出选择的理由。
用表格表示数量关系
感受分式方程模型作用 选择理由
体会如何解分式方程
等式 方程
一元一次 二元一次
2
1
1
x 21
1
x 21
1
x
、两个方程中选择一个解,说出选择的理由。
五、归纳梳理。
411x x
9
7
263
x x x x 411x x。
苏科版数学八年级下册10.5《分式方程》教学设计3

苏科版数学八年级下册10.5《分式方程》教学设计3一. 教材分析苏科版数学八年级下册10.5《分式方程》是学生在学习了分式、方程的基础上,进一步深化对分式方程的理解和应用。
本节课通过具体的例子引导学生理解分式方程的定义、特点及解法,培养学生解决实际问题的能力。
教材内容由浅入深,循序渐进,既注重了基础知识的巩固,又提高了学生的思维能力。
二. 学情分析学生在学习本节课之前,已经掌握了分式和方程的基础知识,对于分式方程有一定的认识。
但部分学生对分式方程的理解仍停留在表面,难以把握其本质特征。
此外,学生在解决实际问题时,往往不能灵活运用所学知识,对于分式方程的解法技巧有待提高。
三. 教学目标1.理解分式方程的定义、特点及解法。
2.培养学生解决实际问题的能力。
3.提高学生的数学思维能力和创新意识。
四. 教学重难点1.分式方程的定义和特点。
2.分式方程的解法及应用。
五. 教学方法1.情境教学法:通过生活实例引入分式方程,让学生感受到数学与实际的联系。
2.案例教学法:分析典型例题,引导学生总结解题方法。
3.小组合作学习:鼓励学生相互讨论、交流,提高解决问题的能力。
4.启发式教学法:教师提问,引导学生思考,激发学生的求知欲。
六. 教学准备1.教学课件:制作课件,展示分式方程的相关概念、例题及解法。
2.练习题:准备分式方程的相关练习题,用于巩固所学知识。
3.教学素材:收集与分式方程相关的实际问题,用于引入和拓展。
七. 教学过程1.导入(5分钟)利用生活实例引入分式方程,激发学生的学习兴趣。
例如,讲解一个实际问题:某商品打8折后售价为120元,求原价。
2.呈现(10分钟)展示分式方程的定义、特点及解法。
通过PPT课件,让学生清晰地了解分式方程的基本概念和解题步骤。
3.操练(10分钟)让学生独立解决一些简单的分式方程问题。
教师巡视课堂,解答学生的疑问,指导学生掌握解题方法。
4.巩固(10分钟)分析典型例题,引导学生总结解题方法。
苏科版数学八年级下册《10.5 分式方程》教学设计

苏科版数学八年级下册《10.5 分式方程》教学设计一. 教材分析《苏科版数学八年级下册》中的“10.5 分式方程”是一节重要的数学课程。
本节课的主要内容是让学生掌握分式方程的解法及其应用。
分式方程是初中数学中的一个重要知识点,它既考察了学生对分式的理解,又考察了学生对方程的求解能力。
在教材中,分式方程的引入是为高中阶段更深入的数学学习打下基础。
因此,本节课的教学设计应注重学生对分式方程概念的理解,及其解法的掌握。
二. 学情分析八年级的学生已经掌握了分式的基本知识,对解一元一次方程、一元二次方程等也有了一定的理解。
但学生在解决分式方程时,往往因为对分式的理解不深,导致解题步骤不清晰,解法不当。
因此,在教学设计中,要充分考虑学生的已有知识,帮助学生在理解分式的基础上,掌握分式方程的解法。
三. 教学目标1.知识与技能:使学生掌握分式方程的解法,并能应用于实际问题中。
2.过程与方法:培养学生解决实际问题的能力,提高学生的逻辑思维能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队合作意识。
四. 教学重难点1.重点:分式方程的解法及其应用。
2.难点:对分式方程解法的理解,以及如何在实际问题中应用。
五. 教学方法1.情境教学法:通过生活实例引入分式方程,使学生能更好地理解概念。
2.案例教学法:通过典型例题,讲解分式方程的解法,使学生能熟练运用。
3.小组合作学习:鼓励学生分组讨论,培养学生的团队合作意识。
六. 教学准备1.课件:制作与课程内容相关的课件,辅助教学。
2.例题:挑选具有代表性的例题,用于讲解和练习。
3.作业:设计具有针对性的作业,巩固所学知识。
七. 教学过程1.导入(5分钟)通过一个生活实例,引入分式方程的概念。
例如,假设某商品的原价是x元,现在进行打折活动,如果打8折,则售价为0.8x元;如果打9折,则售价为0.9x 元。
问:如果售价相同,原价是多少?2.呈现(10分钟)呈现一些分式方程,让学生观察和分析。
苏科版数学八年级下册10.5《分式方程》说课稿1

苏科版数学八年级下册10.5《分式方程》说课稿1一. 教材分析《分式方程》是苏科版数学八年级下册第10.5节的内容,本节课主要让学生掌握分式方程的解法及其应用。
分式方程是初中数学中的重要内容,也是学生进一步学习高中数学的基础。
通过本节课的学习,学生可以培养解决实际问题的能力,提高逻辑思维和运算能力。
二. 学情分析八年级的学生已经掌握了分式的基本知识,对解一元一次方程、一元二次方程等有了深入的理解。
但学生在解决实际问题时,往往对将实际问题转化为方程的形式感到困难。
因此,在教学过程中,教师需要关注学生对实际问题转化为方程的意识的培养,以及学生在解分式方程过程中可能出现的困难。
三. 说教学目标1.知识与技能目标:让学生掌握分式方程的解法,能解简单的分式方程。
2.过程与方法目标:通过解决实际问题,培养学生将实际问题转化为方程的能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,提高学生解决实际问题的能力。
四. 说教学重难点1.教学重点:分式方程的解法及其应用。
2.教学难点:将实际问题转化为分式方程,以及解分式方程的过程中可能出现的运算问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法、小组合作学习法等。
2.教学手段:利用多媒体课件、黑板、粉笔等。
六. 说教学过程1.导入新课:通过一个实际问题引入分式方程的概念,激发学生的兴趣。
2.知识讲解:讲解分式方程的解法,引导学生掌握解题方法。
3.案例分析:分析几个典型的分式方程案例,让学生学会将实际问题转化为方程。
4.课堂练习:布置一些分式方程练习题,巩固所学知识。
5.课堂小结:总结本节课的主要内容,提醒学生注意解题中的易错点。
6.课后作业:布置一些实际的题目,让学生运用所学知识解决实际问题。
七. 说板书设计板书设计要清晰、简洁,突出本节课的重点内容,主要包括:1.分式方程的定义2.分式方程的解法3.实际问题转化为分式方程的方法4.分式方程的解题步骤八. 说教学评价教学评价主要从学生的课堂表现、作业完成情况、课后练习成绩等方面进行。
苏科版数学八年级下册10.5《分式方程》说课稿3

苏科版数学八年级下册10.5《分式方程》说课稿3一. 教材分析苏科版数学八年级下册10.5《分式方程》是学生在学习了分式、分式运算的基础上,进一步深入研究分式方程的性质和求解方法。
本节课的内容包括分式方程的定义、分式方程的解法以及分式方程的应用。
通过本节课的学习,学生能够掌握分式方程的基本概念,了解分式方程的解法,并能够运用分式方程解决实际问题。
二. 学情分析学生在学习本节课之前,已经掌握了分式的基本概念和运算方法,具备了一定的逻辑思维能力和问题解决能力。
但是,对于分式方程这一概念可能还比较陌生,需要通过实例和练习来进一步理解和掌握。
此外,学生可能对于分式方程的解法和解题思路还不够清晰,需要教师的引导和讲解。
三. 说教学目标1.知识与技能目标:学生能够理解分式方程的定义,掌握分式方程的解法,并能够运用分式方程解决实际问题。
2.过程与方法目标:学生通过自主学习和合作交流,培养观察、思考、归纳和推理的能力。
3.情感态度与价值观目标:学生能够积极参与数学学习,体验数学的乐趣,培养对数学的兴趣和自信心。
四. 说教学重难点1.教学重点:分式方程的定义、解法以及应用。
2.教学难点:分式方程的解法和应用,特别是解题思路的建立和运用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和合作学习法,引导学生主动探究和解决问题。
2.教学手段:利用多媒体课件和教学素材,辅助学生理解和掌握分式方程的知识。
六. 说教学过程1.导入:通过一个实际问题,引入分式方程的概念,激发学生的兴趣和思考。
2.知识讲解:讲解分式方程的定义和解法,通过实例和练习让学生理解和掌握。
3.解题方法讲解:讲解解题思路和方法,引导学生运用分式方程解决实际问题。
4.练习与讨论:学生进行练习和合作交流,巩固所学知识和技能。
5.总结与拓展:总结本节课的主要内容,提出拓展性问题,激发学生的思考和探究欲望。
七. 说板书设计板书设计应突出分式方程的核心概念和解题方法,包括:1.分式方程的定义2.分式方程的解法3.解题思路和方法板书设计应简洁明了,条理清晰,方便学生理解和记忆。
10.5分式方程-苏科版八年级数学下册教案

10.5 分式方程-苏科版八年级数学下册教案1. 教学目标1.1 知识目标•了解分式方程的概念;•学会解一元一次分式方程;•学会通过分式方程解决实际问题。
1.2 能力目标•能够运用所学知识解决实际问题;•提高学生的数学思维能力。
1.3 教育目标•培养学生的逻辑思维能力;•培养学生的钻研精神和创新意识。
2. 教材分析2.1 教材内容本节课讲解的是分式方程,主要内容包括:•分式方程的定义及基本性质;•解一元一次分式方程的方法;•通过分式方程解决实际问题。
2.2 教学重点•解一元一次分式方程的方法。
2.3 教学难点•通过分式方程对实际问题进行建模和求解。
3. 教学过程设计3.1 教学准备•按照教学计划准备教材、教具、实际问题等;•根据学生程度提前设置几道分式方程的例题。
3.2 教学过程3.2.1 导入环节首先,教师简单介绍分式方程的概念和定义,并引导学生讨论分式方程在实际生活中的应用。
3.2.2 概念讲解接着,教师详细讲解分式方程的基本概念和性质,帮助学生深入理解分式方程的概念。
3.2.3 知识点讲解通过一些例题的讲解,教师讲解解一元一次分式方程的方法,并帮助学生理解各个步骤的含义。
3.2.4 练习环节教师设置几个实际问题,让学生根据所学知识建立分式方程,并求解问题。
3.2.5 活动扩展通过一些适当的合作活动,如小组讨论、竞赛等形式,促进学生之间知识的分享和交流。
3.3 教学总结在本节课的最后,教师对本节课所学知识进行总结,并对学生的表现进行评价和指导。
4. 教学反思本节课通过讲解分式方程、解一元一次分式方程的方法和实际问题的求解,让学生更加深入地理解了分式方程的概念和性质,同时培养了学生的逻辑思维能力和数学计算能力。
在今后的教学中,应当注重引导学生将所学知识应用到实际问题中,进一步培养学生的问题意识和解决问题的能力。
八年级数学下册教案-10.5 分式方程13-苏科版

1.用方程描述数量之间的相等关系的一般步骤是什么?
2.问题1中,设甲每天加工x件,则乙每天加工______件
甲加工20件用_______天,乙加工24件用_______天,
可得方程___________________
问题2中,设原两位数的十位数字为x,则原两位数为________,
课 题
10.5分式方程
【学习目标】
1.能从实际问题中得出分式方程,理解分式方程的概念
2.掌握可化为一元一次方程的分式方程的解法
第一次备课(通案)
第二次备课(个案)
【板书课题】10.5分式方程
【学习目标】
1.能从实际问题中得出分式方程,理解分式方程的概念
2.掌握可化为一元一次方程的分式方程的解法
【自学指导一】
【当堂检测】
口答
.
学生先独立解答,然后展示交流,教师点评.
日清内容
大本
第三次备课(教学反思)
学生能够通过自主探索,认识并了解分式方程的定义,并且能够正确解决分式方程的相关题目。只是对于部分学困生,要加强方法的指导。
新两位数为_________,可得方程_________|
问题3中,设自行车的速度为x千米̸小时,则汽车的速度为____
千米̸小时,自行车行1பைடு நூலகம்千米用_______小时,汽车行15千米用
____小时,可的方程___________
观察你所得到的方程,他们有什么共同特征?
同学们,知识点明确的请举手。好,下面就比一比,看谁能正确回答自我检测一的问题。
自学指导二:
认真看书114页探索和例1内容,思考下列问题:
1.如何寻找最简公分母?
苏科版八年级数学下册教案:10.5分式方程

3、解关于 的方程 有增根,求 的值.(10分)
【课堂练习】
1.以下是方程 去分母的结果,其中正确的是()
A. B. C. D.
2.在下列方程中,关于 的分式方程的个数有()
① ②. ③ ④.
⑤ ⑥ .
A.2个B.3个C.4个D.5个
3.分式 的值为1时,m的值是()
A.2 B.-2 C.-3 D.3
例1:若方程 有增根,则a的值是______。
例2:当 为何值时,关于 的分式方程 会产生增根?
例3:若分式方程 (其中k为常数)产生增根,则增根是()
A.x=6 B.x=5 C.x=k D.无法确定
【对应练习】
1.若分式方程 无解,则 的值为().
A、-1 B、1C、 D、-2
2.若解分式方程 产生增根,则m的值是()
学生姓名:
年级:
科目:
授课日期:月日
上课时间:时分------时分合计:小时
教学目标
1.理解分式方程的意义;
2.了解解分式方程的基本思路和解法;
3.理解解分式方程时,可能无解的原因,并掌握解分式方程的验根方法。
重难点导航
1.解分式方程的基本思路和解法;
2.理解解分式方程时可能无解的原因。
分式方程
知识点一:分式方程的定义
8.在正数范围内定义一种运算☆,其规则为 ☆ = ,根据这个规则 ☆ 的解为()
A. B. C. 或1D. 或
9.若分式方程 无解,那么 的值应为
10.解下列分式方程
(1) (2)
(3) (4)
11.先化简代数式 ,然后选取一个使你喜欢的 的值代入求值.
12.若方程 的解是正数,求a的取值范围。
校八年级数学下册 10.5分式方程教案 (新版)苏科版 教案
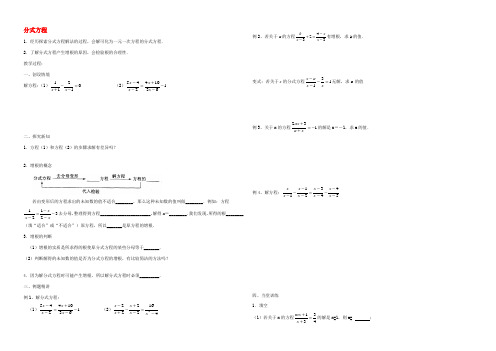
分式方程1.经历探索分式方程解法的过程,会解可化为一元一次方程的分式方程. 2.了解分式方程产生增根的原因,会检验根的合理性. 教学过程: 一、创设情境 解方程:(1)12011x x -=+- (2)163104245--+=--x x x x二、探究新知1.方程(1)和方程(2)的步骤求解有差异吗?2.增根的概念若由变形后的方程求出的未知数的值不适合________,那么这种未知数的值叫做________.例如:方程32121---=-xxx 去分母,整理得到方程_______________________,解得x =________.我们发现,所得的根________(填“适合”或“不适合”)原方程,所以_______是原方程的增根. 3.增根的判断(1)增根的实质是所求得的根使原分式方程的某些分母等于_______. (2)判断解得的未知数的值是否为分式方程的增根,有比较简洁的方法吗?4.因为解分式方程时可能产生增根,所以解分式方程时必须_________. 三、例题精讲 例1、解分式方程: (1)163104245--+=--x x x x (2)41622222-=-+-+-x x x x x例2、若关于x 的方程4233k xx x -+=--有增根,求k 的值.变式:若关于x 的分式方程131=---xx a x 无解,求a 的值例3、关于x 的方程132-=++xa ax 的解是x =-1,求a 的值.例4、解方程:5443211-----=----x x x x x x x x四、当堂训练 1.填空(1)若关于x 的方程4331=++x mx 的解是x=1,则m= ;(2)若方程xmx x --=-525有增根5=x ,则______=m ; (3)如果分式方程11+=+x mx x 无解,则m= ; 2.解方程: (1)1432222-=++-x x x x x (2)1114132+=-+-x x x x3.关于x 的方程xx x x m x x 12122-=+-+,当m 为何值时,会产生增根?。
2020八年级数学下册 第十章 分式 10.5 分式方程(3)教案 (新版)苏科版
自主先学当堂检测交流展示检测反馈小结反思
教具:多媒体等
教
学
过
程
教
学
过
程
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
一、情境引入
列方程(组)解应用题的一般步骤是什么?
关键是什么?
1.京沪 铁路是我国东部沿海地区纵贯南北的大动脉,全长1462 km,是我国最繁忙的干线之一.如果货运列车的速度为akm/h,快速列车的速度是货运列车的2倍,那么:
10.5分式方程
教学
目标
1、能将实际问题中的等量关系用分式方程表示,列出分式方程解决简单的实际问题,并能根据实际问题的意义检验所得的结果是否合理.
2、发展学生分析问题、解决问题的能力,渗 透数学的转化思想,培养学生的应用意识.
重点
如何结合实际分 析问题,列出分式方程.
难点
如何结合实际分析问题,列出分式方程.
五、小结反思
1.分式方程解应用题的一般步骤有哪些?
2.在学习过程中你还存在哪些问题?
(1)根 据题意设末知数;
( 2)分析题意寻找等量关系,列方程;
(3)解所列方程;
(4)检验所列方程的解是否符合题意;
(
交流问难
分组展示板演并讲解学生讲解
试试看,学生思考如何列式,谈谈可以有几种方法。
学生认真完成练习后,小组内讨论交流。
学生说说
用分式方程解实际问题的一般步骤
板
书
设
计
教学
札记
讲清:
1、找准等量关系。
2、用分式方程解决实际问题的一般步骤
3、根据实际问题的意义检验所得的结果是否合理。
八年级数学下册10-5分式方程教案3(新版)苏科版

八年级数学下册10-5分式方程教案3(新版)苏科版教学目标:1.能将实际问题中的等量关系用分式方程表示,列出分式方程解决简单的实际问题,并能根据实际问题的意义检验所得的结果是否合理;2.发展分析问题、解决问题的能力。
重点、难点:列出分式方程解决简单的实际问题。
教学过程一.【预学指导】初步感知、激发兴趣1.列方程(组)解应用题的一般步骤是什么?2.2010年春季我国西南五省持续干旱,旱情牵动着全国人民的心。
“一方有难.八方支援”,某厂计划生产1800吨纯净水支援灾区人民,为尽快把纯净水发往灾区,工人把每天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任务.求原计划每天生产多少吨纯净水?①设原计划每天生产x吨纯净水,根据题意可列出方程:②这是一个什么方程?并解这个方程,解完后应注意什么?③你认为用分式方程解应用题的一般步骤是什么?二.【问题探究】师生互动、揭示通法问题1. 为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务。
这样,这两个小组的每个同学就要比原计划多做4面。
如果这3个小组的人数相等,那么每个小组有多少名学生?问题2.甲.乙两公司各为“见义勇为基金会”捐款30000元,已知乙公司比甲公司人均多捐款20元,且甲公司的人数比乙公司的人数多20%。
问甲.乙两公司各有多少人?问题3. 小明买软面笔记本共用去12元,小丽买硬面笔记本共用去21元,已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同本数的笔记本吗?三.【变式拓展】能力提升、突破难点问题4.轮船在顺水中航行20千米与逆水中航行10千米所用时间相同,水流速度为2.5千米/小时,求轮船的静水速度问题5.某校九年级两个班各为某地震灾区捐款1800元.已知2班比1班人均捐款多4元,2班的人数比1班的人数少10%.请你根据上述信息,就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题,并写出解题过程.四.【回扣目标】学有所成、悟出方法用分式方程解实际问题的一般步骤是什么?五.【板书】六.教学反思。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10.5 分式方程(1)
教学目标:
1.使学生理解分式方程的意义.
2.使学生掌握可化为一元一次方程的分式方程的一般解法.
3.了解解分式方程解的检验方法.
4.在学生掌握了分式方程的一般解法和分式方程验根方法的基础上,使学生进一步掌握可化为一元一次方程的分式方程的解法,使学生熟练掌握解分式方程的技巧.
5.通过学习分式方程的解法,使学生理解解分式方程的基本思想是把分式方程转化成整式方程,把未知问题转化成已知问题,从而渗透数学的转化思想.
教学重点:
(1)可化为一元一次方程的分式方程的解法.
(2)分式方程转化为整式方程的方法及其中的转化思想.
教学难点:
检验分式方程解的原因
课时数:3
过程
等的未知数的值,叫做方程的解.
分式方程.
船在静水中的最大航速为
江水的流速为多少?
分式方程的一般步骤:
看结果是不是零;使最简公分母为零的根不是原方程的解,必须舍。
