核磁共振氢谱图怎么看
核磁共振氢谱图怎么看(谷风参考)

7
2
CH3CH2O
5
4
CH3 CH3CH2O
5
4
CH3
O
O
1
经验学习
2
20
5.3 帮助分析图谱的一些辅助手段
• 5.3.4 溶剂效应 • 苯、吡啶等溶剂具有强的磁各向异性,
在样品溶液中加入少量此类溶剂,它们会 对样品分子的不同部位产生不同的屏蔽作 用。由此可以使样品的1HNMR谱发生较大 的变化,有时,可以使重叠的峰组分开。 • 例:下面的化合物的1HNMR谱:
• (4) 应该具有与大量的溶剂易于混溶的性质;
• (5) 应该尽可能是易于挥发的物质,以便于回收 样品。
经验学习
9
5.2 分析图谱时,经常碰到的一些问题
• 5.2.1.4 常用的标准物质 • TMS (四甲基硅) • DSS: (CH3)3SiCH2CH2CH2SO3Na
经验学习
10
5.2 分析图谱时,经常碰到的一些问题
DMSO-d6、CD3COCD3、CD3OD、C6D6、 C5D5N、CD3CN等。
经验学习
8
5.2 分析图谱时,经常碰到的一些问题
• 5.2.1.3 标准
• 内标准的选择条件:
• (1) 必须具有高度的化学惰性;
• (2) 必须是磁各向同性的,或者接近于磁各向同 性的;
• (3) 应该给出一个简单的、尖锐的和易于识别的 共振信号;
CH
• 其结果,原来的羟基峰消失,同时,与 羟基相连的次甲基峰左移1-2ppm。
经验学习
19
5.3 帮助分析图谱的一些辅助手段
• 如果羟基为酚羟基,则加三氟醋酸酐后, 羟基的邻、对位氢的峰也发生左移。
• 例:下面两个化合物的区别(应用三氟醋 酸酐确定羟基的位置):
氢谱谱图解析步骤

谱图的解析NMR谱法一般经历如下的步骤进行谱图的解析:★与IR法相同,首先尽可能了解清楚样品的一些自然情况,以便对样品有一些大概的认识;通过元素分析获得化合物的化学式,计算不饱和度Ω;★根据化学位移值确认可能的基团,一般先辨认孤立的,未偶合裂分的基团,即单峰,即不同基团的1H之间距离大于三个单键的基团及一些活泼氢基团,如甲基醚、甲基酮()、甲基叔胺()、甲基取代的苯等中的甲基质子及苯环上的质子,活泼氢为―O―H,,-SH等;然后再确认偶合的基团。
从有关图或表中的δ可以确认可能存在的基团,这时应注意考虑影响δ的各种因素如电负性原子或基团的诱导效应、共轭效应、磁的各向异性效应及形成氢键的影响等;★根据偶合裂分峰的重数、偶合常数,判断基团的连接关系。
先解析一级光谱,然后复杂光谱。
进行复杂光谱解析时,应先进行简化;★根据积分高度确定出各基团中质子数比,印证偶合裂分多重峰所判断的基团连接关系;★通过以上几个程序,一般可以初步推断出可能的一种或几种结构式。
然后,反过来,从可能的结构式按照一般规律预测可能产生的NMR谱,与实际谱图对照,看其是否符合,从而可以推断出某种最可能的结构式。
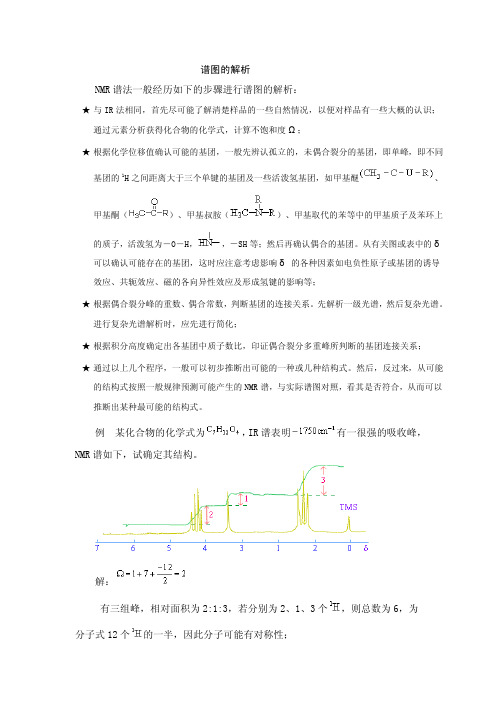
例某化合物的化学式为,IR谱表明有一很强的吸收峰,NMR谱如下,试确定其结构。
解:有三组峰,相对面积为2:1:3,若分别为2、1、3个,则总数为6,为分子式12个的一半,因此分子可能有对称性;????IR显示~1750cm-1有一强峰,应有存在,且分子中有4个O,则可能有2个;处有一组三重峰,可能为-CH,且受裂分,而处有一组四重峰,与是典型的3组分;而δ较大,可能为的组分;?处有一单峰,相对面积为1,则是一个与碳基相连的孤立(不偶合)的,可能为所以可能有的结合。
而此结合的、O的数目为分子式的一半,而C原子数一半多半个原子。
因此可以推测出整个分子的中间C原子为对称的结构,可能为验证:以炔可能结构,推测其NMR谱,与实验谱图比较,结果相符合。
氢谱谱图解析步骤讲述
谱图的解析NMR谱法一般经历如下的步骤进行谱图的解析:★与IR法相同,首先尽可能了解清楚样品的一些自然情况,以便对样品有一些大概的认识;通过元素分析获得化合物的化学式,计算不饱和度Ω;★根据化学位移值确认可能的基团,一般先辨认孤立的,未偶合裂分的基团,即单峰,即不同基团的1H之间距离大于三个单键的基团及一些活泼氢基团,如甲基醚、甲基酮()、甲基叔胺()、甲基取代的苯等中的甲基质子及苯环上的质子,活泼氢为―O―H,,-SH等;然后再确认偶合的基团。
从有关图或表中的δ可以确认可能存在的基团,这时应注意考虑影响δ的各种因素如电负性原子或基团的诱导效应、共轭效应、磁的各向异性效应及形成氢键的影响等;★根据偶合裂分峰的重数、偶合常数,判断基团的连接关系。
先解析一级光谱,然后复杂光谱。
进行复杂光谱解析时,应先进行简化;★根据积分高度确定出各基团中质子数比,印证偶合裂分多重峰所判断的基团连接关系;★通过以上几个程序,一般可以初步推断出可能的一种或几种结构式。
然后,反过来,从可能的结构式按照一般规律预测可能产生的NMR谱,与实际谱图对照,看其是否符合,从而可以推断出某种最可能的结构式。
例某化合物的化学式为,IR谱表明有一很强的吸收峰,NMR谱如下,试确定其结构。
解:有三组峰,相对面积为2:1:3,若分别为2、1、3个,则总数为6,为分子式12个的一半,因此分子可能有对称性;IR显示~1750cm-1有一强峰,应有存在,且分子中有4个O,则可能有2个;处有一组三重峰,可能为-CH3,且受裂分,而处有一组四重峰,与是典型的组分;而δ较大,可能为的组分;处有一单峰,相对面积为1,则是一个与碳基相连的孤立(不偶合)的,可能为所以可能有的结合。
而此结合的、O的数目为分子式的一半,而C原子数一半多半个原子。
因此可以推测出整个分子的中间C原子为对称的结构,可能为验证:以炔可能结构,推测其NMR谱,与实验谱图比较,结果相符合。
核磁共振氢谱解析步骤

核磁共振氢谱解析步骤
核磁共振氢谱解析步骤如下:
1.观察图谱是否符合要求:如四甲基硅烷的信号是否正常、杂音大
不大、基线是否平、积分曲线中没有吸收信号的地方是否平整。
如果存在问题,需要重新测试图谱。
2.根据积分曲线,观察各信号的相对高度,计算样品化合物分子式
中的氢原子数目:可以利用可靠的甲基信号或孤立的次甲基信号为标准计算各信号峰的质子数目。
3.先解析图中CH3O、CH3N、、CH3C=O、CH3C=C、CH3-C等孤
立的甲基质子信号,然后再解析偶合的甲基质子信号。
4.解析羧基、醛基、分子内氢键等低磁场的质子信号。
5.解析芳香核上的质子信号。
核磁一般氢谱和碳谱的解析步骤

核磁一般氢谱和碳谱的解析步骤分析氢谱有如下的步骤。
(1) 区分出杂质峰、溶剂峰、旋转边带。
杂质含量较低,其峰面积较样品峰小很多,样品和杂质峰面积之间也无简单的整数比关系。
据此可将杂质峰区别出来。
氘代试剂不可能100%氘代,其微量氢会有相应的峰,如CDCl3中的微量CHCl3在约7.27ppm处出峰。
边带峰的区别请阅6.2.1。
(2) 计算不饱和度。
不饱和度即环加双键数。
当不饱和度大于等于4时,应考虑到该化合物可能存在一个苯环(或吡啶环)。
(3) 确定谱图中各峰组所对应的氢原子数目,对氢原子进行分配。
根据积分曲线,找出各峰组之间氢原子数的简单整数比,再根据分子式中氢的数目,对各峰组的氢原子数进行分配。
(4) 对每个峰的δ、J都进行分析。
根据每个峰组氢原子数目及δ值,可对该基团进行推断,并估计其相邻基团。
对每个峰组的峰形应仔细地分析。
分析时最关键之处为寻找峰组中的等间距。
每一种间距相应于一个耦合关系。
一般情况下,某一峰组内的间距会在另一峰组中反映出来。
通过此途径可找出邻碳氢原子的数目。
当从裂分间距计算J值时,应注意谱图是多少兆周的仪器作出的,有了仪器的工作频率才能从化学位移之差Δδ(ppm)算出Δν(Hz)。
当谱图显示烷基链3J耦合裂分时,其间距(相应6-7Hz)也可以作为计算其它裂分间距所对应的赫兹数的基准。
(5) 根据对各峰组化学位移和耦合常数的分析,推出若干结构单元,最后组合为几种可能的结构式。
每一可能的结构式不能和谱图有大的矛盾。
(6) 对推出的结构进行指认。
每个官能团均应在谱图上找到相应的峰组,峰组的δ值及耦合裂分(峰形和J值大小)都应该和结构式相符。
如存在较大矛盾,则说明所设结构式是不合理的,应予以去除。
通过指认校核所有可能的结构式,进而找出最合理的结构式。
必须强调:指认是推结构的一个必不可少的环节。
如果未知物的结构稍复杂,在推导其结构时就需应用碳谱。
在一般情况下,解析碳谱和解析氢谱应结合进行。
氢谱谱图解析步骤

氢谱谱图解析步骤谱图得解析NMR谱法一般经历如下得步骤进行谱图得解析:★与IR法相同,首先尽可能了解清楚样品得一些自然情况,以便对样品有一些大概得认识;通过元素分析获得化合物得化学式,计算不饱与度Ω;★根据化学位移值确认可能得基团,一般先辨认孤立得,未偶合裂分得基团,即单峰,即不同基团得1H之间距离大于三个单键得基团及一些活泼氢基团,如甲基醚、甲基酮()、甲基叔胺()、甲基取代得苯等中得甲基质子及苯环上得质子,活泼氢为―O―H,,-SH等;然后再确认偶合得基团。
从有关图或表中得δ可以确认可能存在得基团,这时应注意考虑影响δ得各种因素如电负性原子或基团得诱导效应、共轭效应、磁得各向异性效应及形成氢键得影响等;★根据偶合裂分峰得重数、偶合常数,判断基团得连接关系。
先解析一级光谱,然后复杂光谱。
进行复杂光谱解析时,应先进行简化;★根据积分高度确定出各基团中质子数比,印证偶合裂分多重峰所判断得基团连接关系;★通过以上几个程序,一般可以初步推断出可能得一种或几种结构式。
然后,反过来,从可能得结构式按照一般规律预测可能产生得NMR 谱,与实际谱图对照,瞧其就是否符合,从而可以推断出某种最可能得结构式。
例某化合物得化学式为,IR谱表明有一很强得吸收峰,NMR谱如下,试确定其结构。
解:有三组峰,相对面积为2:1:3,若分别为2、1、3个,则总数为6,为分子式12个得一半,因此分子可能有对称性;IR显示~1750cm-1有一强峰,应有存在,且分子中有4个O,则可能有2个;处有一组三重峰,可能为-CH,且受裂分,而处有一组四重峰,与就是典型得3组分;而δ较大,可能为得组分; 处有一单峰,相对面积为1,则就是一个与碳基相连得孤立(不偶合)得,可能为所以可能有得结合。
而此结合得、O得数目为分子式得一半,而C原子数一半多半个原子。
因此可以推测出整个分子得中间C原子为对称得结构,可能为验证:以炔可能结构,推测其NMR谱,与实验谱图比较,结果相符合。
核磁共振氢谱几种解析方法(精华版)

2.3核磁共振氢谱解析方法1、核磁共振氢谱谱图的解析方法a.检查整个氢谱谱图的外形、信号对称性、分辨率、噪声、被测样品的信号等。
b.应注意所使用溶剂的信号、旋转边带、C卫星峰、杂质峰等。
c.确定TMS的位置,若有偏移应对全部信号进行校正。
d.根据分子式计算不饱和度u。
e.从积分曲线计算质子数。
f.解析单峰。
对照附图I是否有-CH3-O-、CHCOCH3N=、CH3C、RCOCH2Cl、RO-CH2-Cl等基团。
g.确定有无芳香族化合物。
如果在6.5-8.5范围内有信号,则表示有芳香族质子存在。
如出现AA`BB`的谱形说明有芳香邻位或对位二取代。
h.解析多重峰。
按照一级谱的规律,根据各峰之间的相系关系,确定有何种基团。
如果峰的强度太小,可把局部峰进行放大测试,增大各峰的强度。
i.把图谱中所有吸收峰的化学位移值与附图I相对照,确定是何官能团,并预测质子的化学环境。
j.用重水交换确定有无活泼氢。
k.连接各基团,推出结构式,并用此结构式对照该谱图是否合理。
再对照已知化合物的标准谱图。
2、核磁共振氢谱谱图解析举例例1:已知某化合物分子式为C3H7NO2。
测定氢谱谱图如下所示,推定其结构。
解析计算不饱和度u=1,可能存在双键,1.50和1.59ppm有小峰,峰高不大于1个质子,故为杂质峰。
经图谱可见有三种质子,总积分值扣除杂质峰按7个质子分配。
从低场向高场各峰群的积分强度为2:2:3,可能有-CH2-、-CH2-、-CH3-基团。
各裂分峰的裂距(J),低场三重峰为7Hz,高场三重峰为8Hz,所以这两个三峰没有偶合关系,但它们与中间六重峰有相互作用。
这六重峰的质子为2个,所以使两边信号各裂分为三重峰。
则该化合物具有CH3-CH2-CH2-结构单元。
参考所给定的分子式应为CH3-CH2-CH2-NO2,即1-硝基丙烷。
例2:已知某化合物分子式为C7H16O3,其氢谱谱图如下图所示,试求其结构。
解析计算不饱和度u=0,为饱和化合物。
氢谱谱图解析步骤(图文借鉴)

谱图的解析NMR谱法一般经历如下的步骤进行谱图的解析:★与IR法相同,首先尽可能了解清楚样品的一些自然情况,以便对样品有一些大概的认识;通过元素分析获得化合物的化学式,计算不饱和度Ω;★根据化学位移值确认可能的基团,一般先辨认孤立的,未偶合裂分的基团,即单峰,即不同基团的1H之间距离大于三个单键的基团及一些活泼氢基团,如甲基醚、甲基酮()、甲基叔胺()、甲基取代的苯等中的甲基质子及苯环上的质子,活泼氢为―O―H,,-SH等;然后再确认偶合的基团。
从有关图或表中的δ可以确认可能存在的基团,这时应注意考虑影响δ的各种因素如电负性原子或基团的诱导效应、共轭效应、磁的各向异性效应及形成氢键的影响等;★根据偶合裂分峰的重数、偶合常数,判断基团的连接关系。
先解析一级光谱,然后复杂光谱。
进行复杂光谱解析时,应先进行简化;★根据积分高度确定出各基团中质子数比,印证偶合裂分多重峰所判断的基团连接关系;★通过以上几个程序,一般可以初步推断出可能的一种或几种结构式。
然后,反过来,从可能的结构式按照一般规律预测可能产生的NMR谱,与实际谱图对照,看其是否符合,从而可以推断出某种最可能的结构式。
例某化合物的化学式为,IR谱表明有一很强的吸收峰,NMR谱如下,试确定其结构。
解:有三组峰,相对面积为2:1:3,若分别为2、1、3个,则总数为6,为分子式12个的一半,因此分子可能有对称性;IR显示~1750cm-1有一强峰,应有存在,且分子中有4个O,则可,且受裂分,而能有2个;处有一组三重峰,可能为-CH3处有一组四重峰,与是典型的组分;而δ较大,可能为的组分;处有一单峰,相对面积为1,则是一个与碳基相连的孤立(不偶合)的,可能为所以可能有的结合。
而此结合的、O的数目为分子式的一半,而C原子数一半多半个原子。
因此可以推测出整个分子的中间C原子为对称的结构,可能为验证:以炔可能结构,推测其NMR谱,与实验谱图比较,结果相符合。
氢谱谱图解析步骤

谱图的解析(一)NMR谱法一般经历如下的步骤进行谱图的解析:★与IR法相同,首先尽可能了解清楚样品的一些自然情况,以便对样品有一些大概的认识;通过元素分析获得化合物的化学式,计算不饱和度Ω;★根据化学位移值确认可能的基团,一般先辨认孤立的,未偶合裂分的基团,即单峰,即不同基团的1H之间距离大于三个单键的基团及一些活泼氢基团,如甲基醚、甲基酮()、甲基叔胺()、甲基取代的苯等中的甲基质子及苯环上的质子,活泼氢为―O―H,,-SH等;然后再确认偶合的基团。
从有关图或表中的δ可以确认可能存在的基团,这时应注意考虑影响δ的各种因素如电负性原子或基团的诱导效应、共轭效应、磁的各向异性效应及形成氢键的影响等;★根据偶合裂分峰的重数、偶合常数,判断基团的连接关系。
先解析一级光谱,然后复杂光谱。
进行复杂光谱解析时,应先进行简化;★根据积分高度确定出各基团中质子数比,印证偶合裂分多重峰所判断的基团连接关系;★通过以上几个程序,一般可以初步推断出可能的一种或几种结构式。
然后,反过来,从可能的结构式按照一般规律预测可能产生的NMR谱,与实际谱图对照,看其是否符合,从而可以推断出某种最可能的结构式。
例某化合物的化学式为,IR谱表明有一很强的吸收峰,NMR谱如下,试确定其结构。
解:有三组峰,相对面积为2:1:3,若分别为2、1、3个,则总数为6,为分子式12个的一半,因此分子可能有对称性;IR显示~1750cm-1有一强峰,应有存在,且分子中有4个O,则可能有2个;处有一组三重峰,可能为-CH,且受裂分,而处有一组四重峰,与3是典型的组分;而δ较大,可能为的组分;处有一单峰,相对面积为1,则是一个与碳基相连的孤立(不偶合)的,可能为所以可能有的结合。
而此结合的、O的数目为分子式的一半,而C原子数一半多半个原子。
因此可以推测出整个分子的中间C原子为对称的结构,可能为验证:以炔可能结构,推测其NMR谱,与实验谱图比较,结果相符合。
谱图分析课件第2章核磁共振氢谱

峰的裂分与自旋系统
峰的裂分
由于相邻氢原子核的相互作用,一个峰可能会分裂成多个小峰。根据裂分的程 度和规律,可以推断出分子内部的氢原子排列方式和相互位置关系。
自旋系统
表示一组相互作用的氢原子核,根据自旋系统的类型,可以判断分子内部的结 构和对称性。
05
氢谱的局限性与发展趋势
氢谱的局限性
分辨率较低
由于氢原子在分子中的分布较为 广泛,导致氢谱的分辨率较低, 难以区分相近的化学环境。
受样品限制
氢谱分析需要使用液体样品,对 于固体样品和不易溶解的物质, 氢谱分析存在局限性。
对仪器要求高
氢谱分析需要高精度和高灵敏度 的核磁共振谱仪,仪器成本较高, 普及程度有限。
氢谱的表示方法
氢谱通常以频率或波数表示,横 坐标为化学位移,纵坐标为信号
强度。
化学位移表示氢原子核所处的化 学环境,即周围的官能团类型, 通过化学位移可以推断出氢原子
所属的化合物类型。
信号强度表示该化学环境下氢原 子核的数量,信号强度越大,表
示该类型的氢原子数量越多。
02
氢谱的组成与特征
峰的位置与化学位移
注意事项
确保实验过程中样品温度和磁场稳定性,避免外界干扰,及时记录异常情况。
数据处理与分析方法
数据处理
对采集的原始数据进行预处理,如基线校正、相位调整等,以提 高谱图质量。
峰识别与标注
根据峰的位置、强度和形状,识别和标注不同氢原子类型。
数据解析与推断
结合化学位移、耦合常数等信息,解析氢原子所处的化学环境, 推断分子结构。
人工智能技术在数据处理和分析方面具有 优势,与核磁共振技术结合有望提高氢谱 分析的效率和准确性。
核磁共振氢谱 解析图谱的步骤

核磁共振氢谱解析图谱的步伐之迟辟智美创作核磁共振氢谱核磁共振技术发展较早,20世纪70年代以前,主要是核磁共振氢谱的研究和应用.70年代以后,随着傅里叶变换波谱仪的出生,13C—NMR的研究迅速开展.由于1H—NMR的灵敏度高,而且积累的研究资料丰富,因此在结构解析方面1H—NMR的重要性仍强于13C—NMR.解析图谱的步伐 1.先观察图谱是否符合要求;①四甲基硅烷的信号是否正常;②杂音年夜不年夜;③基线是否平;④积分曲线中没有吸收信号的处所是否平整.如果有问题,解析时要引起注意,最好重新测试图谱. 2.区分杂质峰、溶剂峰、旋转边峰(spinning side bands)、13C卫星峰(13C satellite peaks)(1)杂质峰:杂质含量相对样品比例很小,因此杂质峰的峰面积很小,且杂质峰与样品峰之间没有简单整数比的关系,容易区别.(2)溶剂峰:氘代试剂不成能到达100%的同位素纯度(年夜部份试剂的氘代率为99-99.8%),因此谱图中往往呈现相应的溶剂峰,如CDCL3中的溶剂峰的δ值约为7.27 ppm处.(3)旋转边峰:在测试样品时,样品管在1H-NMR仪中快速旋转,当仪器调节未到达良好工作状态时,会呈现旋转边带,即以强谱线为中心,呈现出一对对称的弱峰,称为旋转边峰.(4)13C卫星峰:13C具有磁距,可以与1H偶合发生裂分,称之为13C卫星峰,但由13C的天然丰度只为1.1%,只有氢的强峰才华观察到,一般不会对氢的谱图造成干扰. 3.根据积分曲线,观察各信号的相对高度,计算样品化合物分子式中的氢原子数目.可利用可靠的甲基信号或孤立的次甲基信号为标准计算各信号峰的质子数目. 4.先解析图中CH3O、CH3N、、CH3C=O、CH3C=C、CH3-C等孤立的甲基质子信号,然后再解析偶合的甲基质子信号. 5.解析羧基、醛基、分子内氢键等低磁场的质子信号. 6.解析芳香核上的质子信号.7.比力滴加重水前后测定的图谱,观察有无信号峰消失的现象,了解分子结构中所连活泼氢官能团.8.根据图谱提供信号峰数目、化学位移和偶合常数,解析一级类型图谱.9.解析高级类型图谱峰信号,如黄酮类化合物B环仅4,-位取代时,呈现AA,BB,系统峰信号,二氢黄酮则呈现ABX系统峰信号.10. 如果一维1H-NMR难以解析分子结构,可考虑测试二维核磁共振谱配合解析结构.11. 组合可能的结构式,根据图谱的解析,组合几种可能的结构式.12. 对推出的结构进行指认,即每个官能团上的氢在图谱中都应有相应的归属信号.四. 核磁共振碳谱(13C—(1)溶剂峰:虽然碳谱不受溶剂中氢的干扰,但为兼顾氢谱的测定及磁场需要,仍常采纳氘代试剂作为溶剂,氘代试剂中的碳原子均有相应的峰.(2)杂质峰:杂质含量相对样品少很多,其峰面积极小,与样品化合物中的碳呈现的峰不成比例.(3)测试条件的影响:测试条件会对所测谱图有较年夜影响.如脉冲倾斜角较年夜而脉冲间隔不够长时,往往招致季碳不出峰;扫描宽度不够年夜时,扫描宽度以外的谱线会折叠到图谱中来;等等,均造成解析图谱的困难.根据分子式计算的不饱和度,推测图谱烯碳的情况.若谱线数目即是分子式中碳原子数目,说明分子结构无对称性;若谱线数目小于分子式中碳原子数目,说明分子结构有一定的对称性.另外,化合物中碳原子数目较多时,有些核的化学环境相似,可能δ值发生重叠现象,应予以注意.δ值的分区碳原子年夜致可分为三个区(1)高δ值区δ>165ppm,属于羰基和叠烯区:①分子结构中,如存在叠峰,除叠烯中有高δ值信号峰外,叠烯两端碳在双键区域还应有信号峰,两种峰同时存在才说明叠烯存在;②δ>200 ppm的信号,只能属于醛、酮类化合物;③160-180ppm的信号峰,则归属于酸、酯、酸酐等类化合物的羰基.(2)中δ值区δ90-160ppm(一般情况δ为100-150ppm)烯、芳环、除叠烯中央碳原子外的其他SP2杂化碳原子、碳氮三键碳原子都在这个区域出峰.(3)低δ值区δ<100ppm,主要脂肪链碳原子区:①不与氧、氮、氟等杂原子相连的饱和的δ值小于55ppm;②炔碳原子δ值在70-100ppm,这是不饱和碳原子的特例.由低核磁共振或APT(attached proton test)、DEPT(distortionless enhancement by polarization transfer)等技术可确定碳原子的级数,由此可计算化合物中与碳原子相连的氢原子数.若此数目小于分子式中的氢原子数,二者之差值为化合物中活泼氢的原子数.先推导出结构单位,并进一步组合成若干可能的结构式.将核磁共振碳谱中各信号峰在推出的可能结构式上进行指认,找出各碳谱信号相应的归属,从而在被推导的可能结构式中找出最合理的结构式,即正确的结构式.。
核磁共振氢谱 解析图谱的步骤

核磁共振氢谱解析图谱的步调之马矢奏春创作核磁共振氢谱核磁共振技术发展较早,20世纪70年代以前,主要是核磁共振氢谱的研究和应用。
70年代以后,随着傅里叶变换波谱仪的诞生,13C—NMR的研究迅速开展。
由于1H—NMR的灵敏度高,而且积累的研究资料丰富,因此在结构解析方面1H—NMR的重要性仍强于13C—NMR。
解析图谱的步调 1.先观察图谱是否符合要求;①四甲基硅烷的信号是否正常;②杂音大不大;③基线是否平;④积分曲线中没有吸收信号的地方是否平整。
如果有问题,解析时要引起注意,最好重新测试图谱。
2.区分杂质峰、溶剂峰、旋转边峰(spinning side bands)、13C卫星峰(13C satellite peaks) (1)杂质峰:杂质含量相对样品比例很小,因此杂质峰的峰面积很小,且杂质峰与样品峰之间没有简单整数比的关系,容易区别。
(2)溶剂峰:氘代试剂不成能达到100%的同位素纯度(大部分试剂的氘代率为99-99.8%),因此谱图中往往呈现相应的溶剂峰,如CDCL3中的溶剂峰的δ值约为7.27 ppm 处。
(3)旋转边峰:在测试样品时,样品管在1H-NMR仪中快速旋转,当仪器调节未达到良好工作状态时,会出现旋转边带,即以强谱线为中心,呈现出一对对称的弱峰,称为旋转边峰。
(4)13C卫星峰:13C具有磁距,可以与1H偶合发生裂分,称之为13C卫星峰,但由13C的天然丰度只为1.1%,只有氢的强峰才干观察到,一般不会对氢的谱图造成干扰。
3.根据积分曲线,观察各信号的相对高度,计算样品化合物分子式中的氢原子数目。
可利用可靠的甲基信号或孤立的次甲基信号为尺度计算各信号峰的质子数目。
4.先解析图中CH3O、CH3N、、CH3C=O、CH3C=C、CH3-C等孤立的甲基质子信号,然后再解析偶合的甲基质子信号。
5.解析羧基、醛基、分子内氢键等低磁场的质子信号。
6.解析芳香核上的质子信号。
7.比较滴加重水前后测定的图谱,观察有无信号峰消失的现象,了解分子结构中所连活泼氢官能团。
核磁共振氢谱图怎么看ppt课件

• 双共振技术的应用主要包括自旋去偶和核 的Overhauser效应(NOE)。
核磁共振氢谱图怎么看
30
5.4 双照射(双共振)技术
• 5.4.1 自旋去偶 • 相互偶合的核,使峰发生裂分。峰的裂分需要
核磁共振氢谱图怎么看
10
5.2 分析图谱时,经常碰到的一些问题
• 5.2.1.5 图谱的记录 • 核磁共振图谱给出化学位移δ值,也有以
频率表示的。
核磁共振氢谱图怎么看
11
核磁共振氢谱图怎么看
12
5.2 分析图谱时,经常碰到的一些问题
• 5.2.3 杂质峰与溶剂峰
• 在核磁共振氢谱中,经常会碰到杂质峰。杂质 峰一般可以通过其峰面积进行鉴别:如果某峰的 积分面积与其它峰相比不成比例,则可断定其为 杂质峰。
核磁共振氢谱图怎么看
4
核磁共振氢谱图怎么看
5
5.1 核磁共振氢谱分析的一般步骤
在完成了对核磁氢谱的分析以后,(要广 泛查阅有关文献,比对有关数据),根据分 析结果,确定需进一步开展的测试项目。
核磁共振氢谱图怎么看
6
5.2 分析图谱时,经常碰到的一些问题
• 5.2.1 核磁共振氢谱的测定:
• 5.2.1.1 样品
则是绝对数值,与仪器的频率成正比。 (例如,Δδ若为0.1ppm,在60MHz的仪器 上,它相当于6Hz;在400MHz的仪器上, 它相当于40Hz)。
核磁共振氢谱图怎么看
26
5.3 帮助分析图谱的一些辅助手段
• 由于以上3个方面的原因,在不同频率的 NMR波谱仪上所测同一样品的谱图形状是 不同的,且仪器频率越高,图谱越趋简单 化。
核磁共振谱图解析 ppt课件

PPT课件
33
用NOESY方法对异构体的鉴别
•
在有机合成反应中会经常出现异构体 ,在异构体构型的鉴别 中,NOE是一种非常有效的手段。NOE谱对有机化合物结构、构 型、构象的鉴定能够提供重要信息. NOE谱可以采用一维方式或 二维方式 ,我们通常都采用二维谱图的方式,因为二维谱方便快 捷,可观察的信息全。 • NOE主要用来确定两种质子在分子立体空间结构中是否距 离相近。要求两种质子的空间距离小于5A. 从以上可以看出 NOE和空间因素很有关系,和相隔的化学键数无关,所以在分析 NOE谱图时候,一定要能画出结构的立体构型以便解析。下面是 用NOE方法来鉴别异构体的简单例子。
下面是四氢糖醇的结构图,可以看出手性碳对2,3,4,5位氢的空间上的影响.
PPT课件
2.5
1.188 2.373
2.0
2.944
4 5
4
1.000
1.5
1.955 1.941 1.936 1.922 1.918 1.910 1.907 1.904 1.899 1.895 1.884 1.867 1.853 1.848 1.664 1.658 1.650 1.645 1.638 1.632 1.628 1.619 1.610 1.602 1.589
10-14 (DMSO); 7-10 (CDCl3) 8-10 (峰型尖锐) 5-8 (并且两个氢会分开) 7-13 9-12
PPT课件
12
PPT课件
13
PPT课件
14
PPT课件
15
PPT课件
16
PPT课件
17
PPT课件
18
PPT课件
19
PPT课件
20
核磁共振氢谱图谱解析

核磁共振氢谱图谱解析1. 引言核磁共振氢谱是一种利用核磁共振技术研究物质中氢原子的化学环境和结构的方法。
氢是最常见的元素之一,广泛存在于化学化工、生物医药等领域。
通过核磁共振氢谱图谱的解析,可以了解样品的分子结构、官能团和化学环境等信息,对于化学合成、物质性质研究、质量控制等具有重要意义。
本文将介绍核磁共振氢谱图谱的基本原理、谱峰解析步骤和谱峰解析的应用实例,帮助读者更好地理解和应用核磁共振氢谱图谱解析技术。
2. 核磁共振氢谱基本原理核磁共振(Nuclear Magnetic Resonance, NMR)基于原子核的磁性和电磁波的相互作用,通过施加磁场和射频脉冲来激发样品中的氢原子核,根据吸收或发射电磁波的频率差异来获得谱图信息。
核磁共振氢谱图谱的横坐标表示化学位移或称为化学位移标尺(Chemical Shift, δ),单位为ppm(parts per million)。
纵坐标表示吸收强度或强度积分。
3. 核磁共振氢谱图谱解析步骤3.1 样品准备样品是进行核磁共振氢谱图谱解析的基础,需要制备纯度高、浓度适宜的样品。
样品制备时要注意避免杂质的干扰,需选用适合的溶剂,并校正溶剂的化学位移标尺。
3.2 光谱仪参数设置在进行核磁共振实验前,需要根据样品的特点和要研究的问题来调整光谱仪的参数。
如调节磁场强度、扫描速度、脉冲宽度和接收增益等。
3.3 谱峰解析核磁共振谱峰的位置、形状和峰面积等参数与样品的结构和环境密切相关,通过分析谱峰的特征来推断样品的化学结构。
谱峰解析通常包括以下几个方面的内容:3.3.1 化学位移解析化学位移是谱图上谱峰的位置信息,表示了不同原子在化学环境中所受到的磁场强度的差异。
通过与参考物质的化学位移进行比较,可以推断样品中含有的官能团和化学结构。
3.3.2 耦合常数解析耦合常数是指谱图上峰之间的距离信息,用于描述不同耦合离子对之间的相互作用。
通过分析谱峰之间的相对位置和大小关系,可以预测样品中的化学键和官能团。
核磁共振氢谱解析方法

核磁共振氢谱解析方法核磁共振(Nuclear Magnetic Resonance, NMR)是一种广泛应用于化学、生物化学、医学等领域的分析技术。
其中,核磁共振氢谱分析是最常见也是最重要的核磁共振技术之一、通过测定样品中氢原子的核磁共振现象,可以获得关于物质结构、分子运动、相互作用等方面的信息。
核磁共振氢谱的解析方法包括信号强度的归属和信号位置的解读等方面。
首先,核磁共振氢谱的解析方法通常涉及信号强度的归属。
在核磁共振氢谱中,不同化学环境下的氢原子会表现出不同的化学位移,并以峰的形式出现在谱图中。
根据这些峰的积分强度可以推测化学位移的数量关系。
因为化学位移受到化学键的极性和电子云密度的影响,不同化学环境下的氢原子会有不同的化学位移。
通过和参考标准物质的化学位移进行比较,可以准确确定样品中各个峰的归属。
其次,核磁共振氢谱的解析方法还涉及信号位置的解读。
不同化学环境下的氢原子在核磁共振谱图中会出现在不同的位置。
一般来说,氢原子所在的官能团会对化学位移产生明显的影响。
因此,通过分析氢原子在谱图中的位置,可以初步判断物质中存在的官能团。
此外,还可以通过同位素效应、溶剂效应等对信号位置进行解读。
通过综合这些信息,可以进一步确定分子的结构。
除了以上两个方面,核磁共振氢谱的解析方法还包括对耦合常数和峰形的解析。
在核磁共振谱图中,不同化学位移的氢原子之间会发生磁耦合。
耦合常数可以提供关于化学键的数目和相互作用方式的信息。
通过检测氢原子之间的耦合模式,可以推测出分子中的基团。
此外,峰的形状也可以提供有关官能团之间相互作用的信息。
通过对峰形的解析,可以了解分子的动力学行为和分子内的相互作用等。
总之,核磁共振谱图中的信号强度、位置、耦合常数和峰形等都可以提供关于物质结构和性质的重要信息。
通过对这些信息的解析,可以确定分子的结构和官能团的存在,为进一步研究物质的性质和反应机制提供重要的线索。
核磁共振氢谱解析方法的应用,对于化学、生物化学和医药等领域的研究具有重要的意义。
核磁共振氢谱图课件

环境,从而确定有机化合物的分子结构。
确定碳原子的类型和连接方式
02
结合氢谱图和碳谱图,可以推断出碳原子的类型和连接方式,
进一步确定有机化合物的骨架结构。
判断手性分子构型
03
通过氢谱图可以确定手性分子的构型,对于不对称合成和手性
识别具有重要意义。
蛋白质结构的解析
确定氨基酸序列
通过氢谱图结合其他谱图,可以解析蛋白质的一级结构,即氨基 酸的排列顺序。
误差控制
采取适当的措施,控制实 验误差,提高实验结果的 准确性。
安全注意事项
了解氢谱图实验的安全风 险,如高磁场、射频辐射 等,注意安全操作规程。
THANKS FOR WATCHING
感谢您的观看
峰的耦合
在某些情况下,氢原子之间可能存在耦合作用。这种耦合作用可能导致相邻氢原子的共振频率发生改变。通过对 耦合现象的分析,可以获得关于分子中氢原子耦合作用的信息。
CHAPTER 04
氢谱图的应用
有机化合物结构的鉴定
确定氢原子的类型和数目
01
通过氢谱图,可以清晰地显示出不同类型氢原子的数目和化学
确定蛋白质三级结构
通过氢谱图分析蛋白质分子内部氢原子的相互作用和运动,有助于 解析蛋白质的三级结构。
研究蛋白质相互作用
氢谱图可以用来研究蛋白质之间的相互作用,如配体与受体之间的 结合方式以及结合常数等。
药物分子的结构研究
确定药物分子的化学结构
氢谱图是研究药物分子化学结构的重要手段之一,可以确定药物 分子中氢原子的类型和数目以及它们的连接方式。
峰的对称性
峰的对称性反映了氢原子在分子中的构型或构象。某些分子可能具有多个构型或 构象,这些构型或构象可以通过氢谱的峰对称性来区分。通过对峰对称性的分析 ,可以获得关于分子构型或构象的信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
OH OH
OH OH
C CH CH2 COOH O CH3
1
C CH2 CH COOH
O
CH3
2
5.3 帮助分析图谱的一些辅助手段
• 5.3.3 三氟醋酸酐试剂
• 样品中如果含有羟基,加三氟醋酸酐后 会有如下反应:
O
OH
O C CF3
CH
(CF3CO)2O
CH
• 其结果,原来的羟基峰消失,同时,与 羟基相连的次甲基峰左移1-2ppm。
5.1 核磁共振氢谱分析的一般步骤
• (3) 计算偶合常数:应用偶合常数的知识, 可以确定分子的立体构型等。
5.1 核磁共振氢谱分析的一般步骤
在完成了对核磁氢谱的分析以后,(要广 泛查阅有关文献,比对有关数据),根据分 析结果,确定需进一步开展的测试项目。
5.2 分析图谱时,经常碰到的一些问题
• 双共振技术是在扫描射频H1(υ1)扫描的同 时,再加上另一个照射射频H2(υ2)来照射某 一特定核,使其达到饱和(高速往返于各 自旋态之间)状态。其结果能使图谱发生 很大的变化。
5.4 双照射(双共振)技术
• 在双共振实验中,通常采用的符号如下: • (1) 用H0表示外磁场; • (2) 用H1或υ1表示扫描射频; • (3) 用H2或υ2表示照射射频 • (4)用A{X}表示被观测核为A,被干扰
核磁共振氢谱的分析
5.1 核磁共振氢谱分析的一般步骤
• 核磁共振氢谱的分析大体上可以分为以 下三个步骤:
• (1) 看峰的位置(即化学位移)和峰的面 积(即氢原子数目):应用化学位移的知 识,结合谱峰面积,可以确定(或大致确 定)化合物中含氢官能团的种类。
5.1 核磁共振氢谱分析的一般步骤
• (2) 看峰的形状(即各个峰的偶合裂分情 况):应用n+1规律或二级偶合裂分的知识, 可确定(或大致确定)分子中基团和基团 间的相互关系,区分出自旋体系的种类。
5.4 双照射(双共振)技术
• 以1-溴丙烷的双共振自旋去偶1HNMR谱 示意图为例:
5.4 双照射(双共振)技术
• 5.4.2 核的Overhauser效应(nuclear Overhauser effect, NOE)
• 如果分子内两组自旋核在空间的距离小 于5 (不一定相互偶合),那么,在双共 振实验中,当用照射射频照射其中的一组 核,使其共振饱和时,则可引起另一组核 的共振峰强度的增强。这种由于双共振引 起的谱峰强度增强的效应,称为核的 Overhauser效应。
• 5.2.1.2 溶剂 • 做核磁共振图谱测试所用溶剂本身最好
不含氢,含氢的溶剂应是重氢试剂。、 • 常用的溶剂有:CCl4、CDCl3、D2O、
DMSO-d6、CD3COCD3、CD3OD、C6D6、 C5D5N、CD3CN等。
5.2 分析图谱时,经常碰到的一些问题
• 5.2.1.3 标准 • 内标准的选择条件: • (1) 必须具有高度的化学惰性; • (2) 必须是磁各向同性的,或者接近于磁各向同
5.2 分析图谱时,经常碰到的一些问题
• 5.2.1.5 图谱的记录 • 核磁共振图谱给出化学位移δ值,也有以
频率表示的。
5.2 分析图谱时,经常碰到的一些问题
• 5.2.3 杂质峰与溶剂峰 • 在核磁共振氢谱中,经常会碰到杂质峰。杂质
峰一般可以通过其峰面积进行鉴别:如果某峰的 积分面积与其它峰相比不成比例,则可断定其为 杂质峰。 • 核磁共振氢谱中的溶剂峰包括样品本身残留的 溶剂(如结晶溶剂、合成或提取时所用溶剂等) 和做测定时所用溶剂的溶剂峰。样品本身残留的 溶剂的谱峰要根据样品的具体情况做具体分析。 做1HNMR测试时所用溶剂的溶剂峰比较容易识别。
• (3) 1HNMR谱图的复杂程度由Δυ/J的数 值所决定。J的数值反映了原子核磁矩间相 互干扰(作用能量)的大小,是化合物分 子所固有的属性,不因作图条件的改变而 改变。化学位移之差以ppm计,是相对数值, 不随仪器的频率的改变而改变;但以Hz计, 则是绝对数值,与仪器的频率成正比。 (例如,Δδ若为0.1ppm,在60MHz的仪器 上,它相当于6Hz;在400MHz的仪器上, 它相当于40Hz)。
如果样品中含有活泼氢,在作完图谱后, 往样品管里滴加几滴重水,震荡,然后重 新作图,则相应的谱峰由于其活泼氢已被 氘交换而消失。由此可以完全确定活泼氢 的存在。
5.3 帮助分析图谱的一些辅助手段
• 5.3.2 重氢氧化钠交换
• 重氢氧化钠交换可以把羰基的α-氢交换 掉。这个方法对于测定化学结构有很大帮 助。
• 5.2.1 核磁共振氢谱的测定: • 5.2.1.1 样品 • 做核磁共振实验所需样品要比较纯,一
般情况下,纯度要求达到95%以上。 • 为了得到分辨率很高的图谱,一般情况
下,应将样品用溶剂溶解。 • 溶液的浓度视仪器的灵敏度、化合物的
分子量以及所测核磁共振图谱的类型而定。
5.2 分析图谱时,经常碰到的一些问题
核(被照射核)为X。
5.4 双照射(双共振)技术
• 在双共振实验中,当被观测核与被干扰核 为同种类核时,称为同核双共振;如1H{1H}; 当被观测核与被干扰核为不同种类的核时, 称为异核双共振;如13C{1H}。
• 双共振技术的应用主要包括自旋去偶和核 的Overhauser效应(NOE)。
5.4 双照射(双共振)技术
• 5.3.4 溶剂效应 • 苯、吡啶等溶剂具有强的磁各向异性,
在样品溶液中加入少量此类溶剂,它们会 对样品分子的不同部位产生不同的屏蔽作 用。由此可以使样品的1HNMR谱发生较大 的变化,有时,可以使重叠的峰组分开。 • 例:下面的化合物的1HNMR谱:
5.3 帮助分析图谱的一些辅助手段
• 例:下面的化合物的1HNMR谱: •
5.3 帮助分析图谱的一些辅助手段
• 如果羟基为酚羟基,则加三氟醋酸酐后, 羟基的邻、对位氢的峰也发生左移。
• 例:下面两个化合物的区别(应用三氟醋 酸酐确定羟基的位置):
OH O
7
OCH2CH3
2
CH3CH2O O OH
7
2
CH3CH2O
5
4
CH3 CH3CH2O
5
4
CH3
O
O
1
2
5.3 帮助分析图谱的一些辅助手段
性的; • (3) 应该给出一个简单的、尖锐的和易于识别的
共振信号; • (4) 应该具有与大量的溶剂易于混溶的性质; • (5) 应该尽可能是易于挥发的物质,以便于回收
样品。
5.2 分析图谱时,经常碰到的一些问题
• 5.2.1.4 常用的标准物质 • TMS (四甲基硅) • DSS: (CH3)3SiCH2CH2CH2SO3Na
5.4 双照射(双共振)技术
• NOE常用于分子立体构型的确定,也可 在易混淆的共振峰的归属中作为参考。
• 例1:异香兰醛甲氧基取代位置的确定。
CHO
HB
HA
HC
OH
OCH3
• 例2: 黄酮类化合物tamarixetin 3-O-α-Lribopyranoside的结构确定
N
H0
2
H0
5.3 帮助分析图谱的一些辅助手段
• (2) 氢原子核在外加磁场H0中的实受磁场H 核与H0的关系:
•
H核=H0(1-σ)
• 其中σ为屏蔽常数,核的化学环境。H0σ 为氢原子核的核外电子所产生的抗磁场,
它的数值与H0成正比。
5.3 帮助分析图谱的一些辅助手段
5.2 分析图谱时,经常碰到的一些问题
• 5.2.3 受阻旋转
•
•
具有
O C
NM类e 结构的化合物,氮上的孤电子对
Me
• 能与羰基发生共轭,使CO―N键具有部分双键性 质,从而旋转不能自由,因此,两个甲基表现为 两种化学位移,这种现象称为受阻旋转。
5.3 帮助分析图谱的一些辅助手段
• 5.3.1 重氢交换 • 活泼氢在溶液中可以进行不断的交换。
• 5.4.1 自旋去偶 • 相互偶合的核,使峰发生裂分。峰的裂分需要
一定的条件,即相互偶合的核在其各自旋态(如 1H在+1/2和-1/2自旋态)的时间必须大于某一时 间标度(一般情况下,应大于10-1秒)。在通常 的测试条件下,如果不存在化学交换,相互偶合 的核可以满足这一峰裂分的条件。但是,当用一 个方法破坏上述条件时,就可以去掉偶合。
5.4 双照射(双共振)技术
• 双共振技术使被干扰的核达到了饱和 (即高速往返于各自旋态之间),从而, 使其在各自旋态的时间很短,结果,该核 与其它自旋核之间的偶合作用消失。这就 是自旋去偶现象。
• 自旋去偶的主要作用是确定质子间的相 互偶合关系。相应地,它可以准确确定某 一多重峰的化学位移,找出隐藏的信号。
5.3 帮助分析图谱的一些辅助手段
• 由于以上3个方面的原因,在不同频率的 NMR波谱仪上所测同一样品的谱图形状是 不同的,且仪器频率越高,图谱越趋简单 化。
• 另外,高频仪器的使用可以改善仪器的 信噪比,提高灵敏度。
5.4 双照射(双共振)技术
• 双共振(double resonance)又叫双照 射(double irradiation)
O
O
• 当用CDCl3做溶剂时,异丙基的两个甲基以 及另一个甲基的峰重叠非常严重,不能区
分。如改用C6D6作溶剂,则三个甲基可以 获得较好的分离。
HO
OR OH O
OMe OH R=ribo
5.3 帮助分析图谱的一些辅助手段
• 5.3.5 使用高场仪器
• 高场仪器的使用可以简化图谱:
• (1) 氢原子核绕磁场进动有一定的角速度ω。ω 与外加磁场的磁场强度H0成正比,具有如下关系 式:
