初一几何证明典型例题
初中数学几何证明经典试题(含答案)【范本模板】
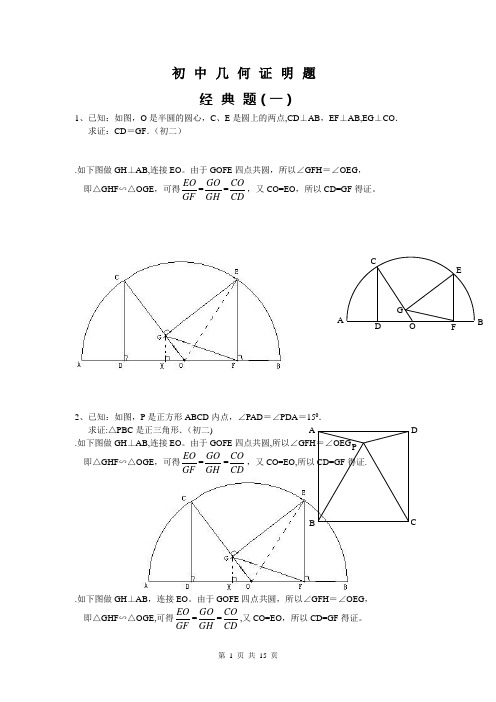
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证..如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初一几何证明典型例题

初一几何证明典型例题1、已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC 在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=2ADBC2、已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2ABCDEF21证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴△BCF≌△EDF (S、A、S)∴ BF=EF,∠CBF=∠DEF连接BE在△BEF中,BF=EF∴∠EBF=∠BEF。
∵ ∠ABC=∠AED。
∴ ∠ABE=∠AEB。
∴ AB=AE。
在△ABF和△AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ABF≌△AEF。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE,EF//AB,求证:EF=ACBACDF21E 过C作CG∥EF交AD的延长线于点GCG∥EF,可得,∠EFD=CGDDE =DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC 为等腰三角形,AC=CG又 EF=CG∴EF=ACA4、已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD =∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠AB C=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF ∵CE⊥AB ∴∠CEB=∠CEF =90 ∵EB=EF,CE=CE,∴△CEB≌△CEF ∴∠B=∠CFE ∵∠B +∠D=180,∠CFE+∠CFA=180 ∴∠D=∠CFA ∵AC平分∠BAD ∴∠DAC=∠FAC ∵AC=AC ∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
(完整版)初中几何证明题五大经典(含答案)
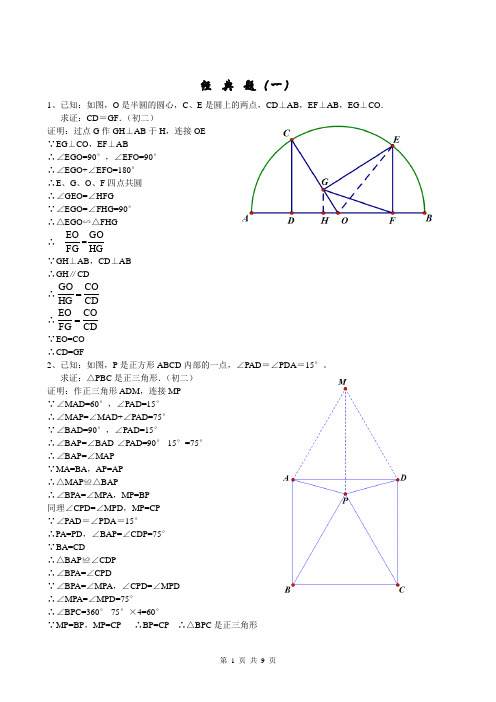
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初一几何证明典型例题

初一几何证明典型例题 Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】戴氏教育达州西外校区名校冲刺戴氏教育温馨提醒:暑假两个月是学习的最好时机,可以在两个月里,复习旧知识,学习新知识,承上,还能启下。
在这个炎热的假期,祝你学习轻松愉快。
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23、4、证明:连接BF 和EFA BC DEF 2 1ADBC∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF≌△∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
已知:∠1=∠2,CD=DE ,EFP 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-ABBA CD F2 1 E A在AC 上取点E , 使AE =AB 。
∵AE =AB AP =AP ∠EAP =∠BAE , ∴△EAP≌△BAP ∴PE =PB 。
PC <EC +PE∴PC <(AC -AE )+PB ∴PC -PB <AC -AB 。
(完整版)七年级几何证明题训练(含答案),推荐文档

1. 已知:如图11所示,∆ABC 中,∠=C 90于E ,且有AC AD CE ==。
求证:DE =122. 已知:如图 求证:BC =3. 已知:如图13所示,过∆ABC 的顶点A ,在∠A 内任引一射线,过B 、C 作此射线的垂线BP 和CQ 。
设M 为BC 的中点。
求证:MP =MQ4. ∆ABC 中,∠=︒⊥BAC AD BC 90,于D ,求证:()AD AB AC BC <++14【试题答案】1. 证明:取ΘAC ADAF CDAFC =∴⊥∴∠= 又∠+∠=︒∠+∠=︒14901390,∴∠=∠=∴≅∴=∴=4312ΘAC CEACF CED ASA CF EDDE CD∆∆()2. 分析:本题从已知和图形上看好象比较简单,但一时又不知如何下手,那么在证明一条线段等于两条线段之和时,我们经常采用“截长补短”的手法。
“截长”即将长的线段截ΘΘCB CE BCD ECD CD CD CBD CEDB EBAC B BAC E=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22又∠=∠+∠BAC ADE E∴∠=∠∴=∴==ADE E AD AEBC CE ,3. 证明:延长PM ΘCQ AP BP BP CQ PBM ⊥∴∴∠=∠,// 又BM CM =,∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线ΘAD BC AD AEBC AE AD⊥∴<∴=>,22()ΘAB AC BCBC AB AC BC AD AB AC BC AD AB AC BC +>∴<++∴<++∴<++2414。
初中数学几何证明试题(含答案)
第 6 页 共 15 页
4.如下图连接 AC 并取其中点 Q,连接 QN 和 QM,所以可得∠QMF=∠F,∠QNM=∠
DEN 和∠QMN=∠QNM,从而得出∠DEN=∠F。
经 典 题(二)
1.(1)延长 AD 到 F 连 BF,做 OG⊥AF,
又∠F=∠ACB=∠BHD, 可得 BH=BF,从而可得 HD=DF, 又 AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM
BE AD
= ,即 AD•BC=BE•AC,
①
BC AC
又∠ACB=∠DCE,可得△ABC∽△DEC,既得
AB = DE ,即 AB•CD=DE•AC,
②
AC DC
由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
第 11 页 共 15 页
4.过 D 作 AQ⊥AE
(2)连接 OB,OC,既得∠BOC=1200,
从而可得∠BOM=600, 所以可得 OB=2OM=AH=AO, 得证。
第 7 页 共 15 页
3.作 OF⊥CD,OG⊥BE,连接 OP,OA,OF,AF,OG,AG,OQ。 由于 AD = AC = CD = 2FD = FD , AB AE BE 2BG BG
(2)过 P 点作 BC 的平行线交 AB,AC 与点 D,F。
由于∠APD>∠ATP=∠ADP,
推出 AD>AP
①
又 BP+DP>BP
②
和 PF+FC>PC
③
又 DF=AF
④
由①②③④可得:最大 L< 2 ;
七年级数学典型几何证明50题

七年级数学典型几何证明50题初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)A BC DEF 21 ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF =CG ∠CGD=∠EFD又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE6、如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
初中经典几何证明练习题(含问题详解)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQOP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中几何证明题

.
例3 如图, 在一个房间内, 有一个梯子斜靠在墙上, 梯子顶端距地面的垂直距离MA为a米, 此时梯子 的倾斜角为75°.若梯子底端距离地面的垂直距 离NB为b米, 梯子的倾斜角为45°.求房子的宽AB.
M
D
N
75° 45°
.
3. 步骤规范 这里主要是我们许多同学会疏忽的共 性问题,由于证明的书写要体现严谨 的思路,但基于数学语言的不熟练和 思路的不清晰以及不少同学的粗枝大 叶的性格,经常会出现跳跃步骤的现 象.
.
4.逻辑规范 (1)思路不清晰,书写时常颠三倒四; (2)依据不符或简化, 如: ∵∠CAB=∠ACD. ∴AB∥CD.(内错角相等)
.
(3)角的正确表示 同样在上面证明中,也有同学将角的符号表
示错误 或者漏写. 证明: (2)∵△ABC≌△BAD, ∴AC=BD. 又∵OA=OB, ∴ OC=OD. ∴∠C=ODC.
.
2. 格式规范 “∵∴” 的书写和推出符号的使用应统一. ∵△ABC≌△BAD =〉 AC=BD. 又∵OA=OB, =〉 OC=OD =〉 ∠OCD=∠ODC.
几何证明题如何书写才算规范
.
●怎样才算规范
1.语言规范 常见的数学语言使用要规范.如: (1)表示逻辑关系的因为、所以的简化符 号不能乱写, 因为用“∵”,所以用“∴” ;
.
(2)三角形的表示形式要规范 例(2010南京市第21题) 如图,四边形
ABCD的对角线AC.BD相交于点O, △ABC≌△BAD. 求证:(1)OA=OB;(2)AB∥CD. 证明: (1)∵ABC≌BAD, ∴∠CAB=∠DBA. ∴OA=OB.
七年级上册几何证明题

七年级上册几何证明题
好的,以下是一道七年级上册几何证明题:
题目:已知△ABC和直线l,过△ABC的顶点A,B分别作AB和AB的垂线
与直线l交于点P,Q。
求证:点P,Q在同一直线上。
为了证明点P,Q在同一直线上,我们可以按照以下步骤逐步推导:
第一步,由于过一点A有且只有一条直线与已知直线l垂直,所以点A、P、Q三点共线。
第二步,同理,由于过一点B有且只有一条直线与已知直线l垂直,所以点B、P、Q三点共线。
第三步,根据两点确定一条直线,我们知道A、B两点确定一条直线,而点P、Q都在该直线上,所以点P、Q在同一直线上。
综上,我们证明了过三角形的顶点作垂线与直线的交点在同一直线上。
七年级上册几何证明题

七年级上册几何证明题引言在数学学科中,几何证明题是一种重要的题型。
通过解答几何证明题,不仅能够帮助学生提高对几何形状的理解,还能够培养学生的逻辑思维能力和推理能力。
本文将介绍七年级上册的一些典型的几何证明题,并提供相应的解答。
题目一:等腰三角形的性质证明题目描述:证明等腰三角形的两底角相等。
证明过程: 1. 假设三角形ABC是一个等腰三角形,其中AB=AC。
2. 根据等腰三角形的定义,我们知道AB=AC,即两边的长度相等。
3. 由于等腰三角形的两边相等,所以两个底角也一定相等。
4. 因此,我们可以得出结论:等腰三角形的两底角相等。
题目二:垂直线段的性质证明题目描述:证明垂直线段相互垂直。
证明过程: 1. 假设线段AB和线段CD是两条垂直线段。
2. 根据垂直线段的定义,我们知道线段AB和CD的斜率相乘等于-1。
3. 过点A和点C分别作AB所在直线和CD所在直线的垂线,设交点为E。
4. 根据直线的性质,垂直相交的两条直线所成的角度为90度,即角AED为直角。
5. 同理,过点B和点D分别作AB所在直线和CD所在直线的垂线,设交点为F。
6. 根据直线的性质,垂直相交的两条直线所成的角度为90度,即角BFD为直角。
7. 因此,我们可以得出结论:垂直线段相互垂直。
题目三:等边三角形的性质证明题目描述:证明等边三角形的三个内角都为60度。
证明过程: 1. 假设三角形ABC是一个等边三角形,其中AB=BC=AC。
2. 根据等边三角形的定义,我们知道AB=BC=AC,即三边的长度都相等。
3. 由于等边三角形的三边相等,所以三个角度也相等。
4. 假设角A的度数为x度,那么角B和角C的度数也分别为x度。
5. 根据角的性质,三个角的度数之和等于180度,所以x + x + x = 180。
6. 解以上方程,得到x = 60度。
7. 因此,我们可以得出结论:等边三角形的三个内角都为60度。
结论几何证明题是数学学科中的重要题型,通过解答这些题目,可以帮助学生加深对几何形状的理解。
初一几何证明题及答案

初一几何证明题及答案【篇一:七年级数学几何证明题(典型)】3.已知,如图,在△ abc中,ad,ae分别是△ abc的高和角平分线,若∠b=30dc4、一个零件的形状如图,按规定∠a=90o ,∠c=25o,∠b=25o,检验已量得∠bdc=150o,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
db5、如图,已知df∥ac,∠c=∠d,你能否判断ce∥bd?试说明你的理由 aebc8、如图,ad⊥bc于d,eg⊥bc于g,∠e =∠1,求证ad平分∠bac。
e3gdc10、如图,将一副三角板叠放在一起,使直角的顶点重合于o,则∠aoc+∠dob11、如图,将两块直角三角尺的直角顶点c叠放在一起. (1)若∠dce=35,求∠acb的度数;(2)若∠acb=140,求∠dce的度数;(3)猜想:∠acb与∠dce有怎样的数量关系,并说明理由12、已知:直线ab与直线cd相交于点o,∠boc=45,(1)如图1,若eo⊥ab,求∠doe的度数;(2)如图2,若eo平分∠aoc,求∠doe的度数.13、已知?aob,p为oa上一点.(1)过点p画一条直线pq,使pq∥ob;(2)过点p画一条直线pm,使pm⊥oa交ob于点m;(3)若?aob?40?,则?pmo? ?adecodbad cob16、已知:线段ab=5cm,延长ab到c,使ac=7cm,在ab的反向延长线上取点d,使bd=4bc,设线段cd的中点为e,问线段ae 是线段cd的几分之一?【篇二:初中数学几何证明经典试题(含答案)】题(一)1、已知:如图,o是半圆的圆心,c、e是圆上的两点,cd⊥ab,ef⊥ab,eg⊥co.求证:cd=gf.(初二).如下图做gh⊥ab,连接eo。
由于gofe四点共圆,所以∠gfh=∠oeg, 即△ghf∽△oge,可得eogf=gogh=cocd,又co=eo,所以cd=gf得证。
eadofb2、已知:如图,p是正方形abcd内点,∠pad=∠pda=150.求证:△pbc是正三角形.(初二) a.如下图做gh⊥ab,连接eo。
初一上册几何证明题(精选多篇)

初一上册几何证明题(精选多篇)第一篇:初一上册几何证明题初一上册几何证明题1.在三角形abc中,∠acb=90°,ac=bc,e是bc边上的一点,连接ae,过c作cf ⊥ae于f,过b作bd⊥bc交cf的延长线于d,试说明:ae=cd。
满意回答因为ae⊥cf,bd⊥bc所以∠afc=90°,∠dbc=90°又∠acb=90°,所以∠ace=∠dbc因为∠cae+∠aec=90°∠ecf+∠aec=90°所以∠cae=∠ecf又ac=bc所以△ace全等于△cbd(asa)所以ae=cd像这类题目,一般用全等较好做些2.如图所示,已知ad、bc相交于o,∠a=∠d,试说明∠c=∠b.解:证1:∠a=∠d=====>ab∥cd=====>∠c=∠b(内错角相等)证2:△abo内角和180=△cdo内角和180∠a=∠d∠aob=∠d0c∴∠c=∠b证明:显然有:∠aob=∠cod(两直线相交,对顶角相等)又∠a=∠d,且三角形三个内角的和等于180º∴一定有∠c=∠b.3.(1)d是三角形abc的bc边上的点且cd=ab,角adb=角bad,ae是三角形abd的中线,求证ac=2ae。
(2)在直角三角形abc中,角c=90度,bd是角b的平分线,交ac于d,ce垂直ab于e,交bd于o,过o作fg平行ab,交bc于f,交ac于g。
求证cd=ga。
延长ae至f,使ae=ef。
be=ed,对顶角。
证明abe全等于def。
=》ab=df,角b=角edf角adb=角bad=》ab=bd,cd=ab=》cd=df。
角ade=bad+b=adb+edf。
ad=ad=》三角形adf全等于adc=》ac=af=2ae。
题干中可能有笔误地方:第一题右边的e点应为c点,第二题求证的cd不可能等于ga,是否是求证cd=fa或cd=co。
初一几何证明题

初一几何证明题1.已知AB∥CD,∠1=∠2,证明:∠XXX∠XXX。
根据平行线内角相等的性质,可得∠1=∠2=∠XXX。
同时,因为AB∥CD,所以∠BEF+∠EFC=180°,即∠BEF=180°-∠XXX。
代入前面的等式,可得∠XXX∠XXX。
2.如图2,AB∥CD,∠3∶∠2=3∶1,求∠1的度数。
根据平行线内角相等的性质,可得∠1=180°-∠2.又因为∠3∶∠2=3∶1,所以∠3=3x,∠2=x。
代入前面的等式,可得∠1=180°-x。
因此,∠1+∠2+∠3=180°,即4x=180°,x=45°。
代入前面的等式,可得∠1=135°。
3.如图3,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,求∠XXX的度数。
根据直角三角形的性质,可得∠CEA=90°。
又因为CE⊥AF,所以∠EAF=90°-∠F=50°。
根据三角形内角和为180°的性质,可得∠EFA=180°-∠F-∠EAF=90°。
因为AB∥CD,所以∠XXX∠EFA=90°。
4.如图4,EF∥AD,∠1=∠2,∠BAC=80°。
求证:∠AGD=100°。
因为EF∥AD,所以∠AGD=∠AGE。
又因为∠BAC=80°,所以∠XXX°-∠BAC/2=50°。
因为∠1=∠2,所以∠DGE=∠AGE=180°-∠1-∠GAC=50°。
因此,∠AGD=∠AGE=50°+∠DGE=100°。
5.如图5,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的XXX°方向。
求∠C的度数。
根据题意,可画出如图6所示的图形。
(完整word版)七年级数学几何证明题
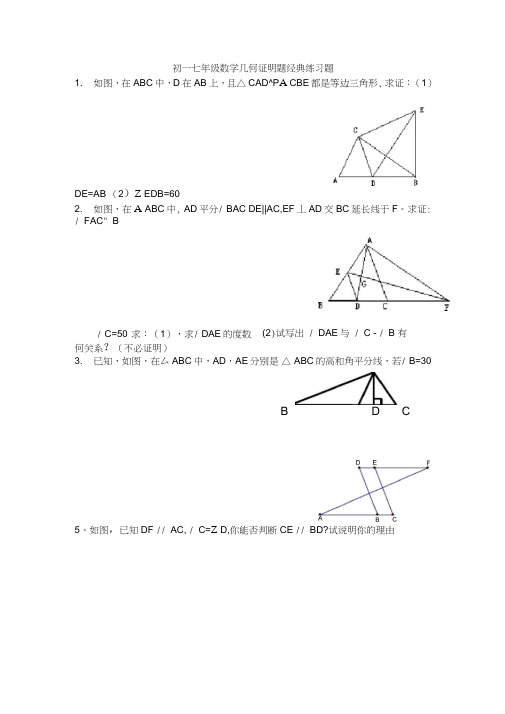
初一七年级数学几何证明题经典练习题1. 如图,在ABC 中,D 在AB 上,且△ CAD^P A CBE 都是等边三角形, 求证:(1)DE=AB (2)Z EDB=602. 如图,在A ABC 中, AD 平分/ BAC DE||AC,EF 丄AD 交BC 延长线于F 。
求证: / FAC " B3. 已知,如图,在厶ABC 中,AD ,AE 分别是 △ ABC 的高和角平分线,若/ B=30 B D C5、如图,已知DF // AC, / C=Z D,你能否判断CE // BD?试说明你的理由/ C=50°求:(1),求/ DAE 的度数 何关系?(不必证明)(2)试写出 / DAE 与 / C - / B 有6、如图,△ ABC中,D在BC的延长线上,过D作DE丄AB于E,交AC于F.已知/ A=30 ° ,Z FCD=80° ,求/D。
A87、如图,BE 平分/ ABD , CF 平分/ ACD , BE 、CF 交于 G , 若/ BDC = 140。
,/ BGC = 110。
,则 / A ?8、如图,AD 丄BC 于D , EG 丄BC 于G ,Z E =Z 1,求证 AD 平分/ BAC9、如图,直线。
丘交厶ABC 的边AB AC 于 D E,交BC 延长线于F , 若/ B = 67°,/ ACB= 74°,/ AED= 48°,求/ BDF 的度数•10、如图,将一副三角板叠放在一起,使直角的顶点重 合于O,贝U/ AOC / DOB11、如图,将两块直角三角尺的直角顶点C 叠放在一起 (1) 若/ DCE=3&求/ ACB 的度数;(2) 若/ ACB=140,求/ DCE 的度数; (3) 猜想:/ ACB 与/ DCE 有怎样的数量关系,并说明理由 AE12、已知:直线AB 与直线CD 相交于点O ,/ B0C= 45° ,(1) 如图1,若E0丄AB ,求/ D0E 的度数;(2) 如图2,若E0平分/ AOC ,求/ DOE 的度数.13、已知 AOB , P 为0A 上一点. (1)过点P 画一条直线PQ ,使PQ // 0B ;(2)过点P 画一条直线PM ,使PM 丄0A 交0B 于点M ;14、如图。
初中经典几何证明练习题集(含答案解析)
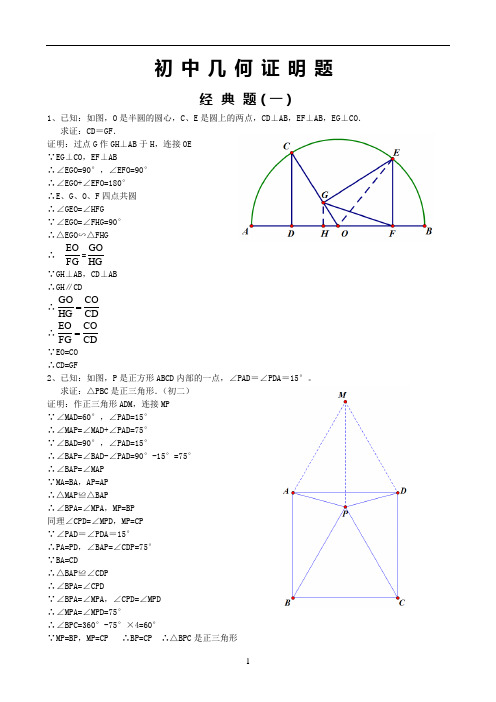
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
戴氏教育达州西外校区名校冲刺戴氏教育温馨提醒:暑假两个月是学习的最好时机,可以在两个月里,复习旧知识,学习新知识,承上,还能启下。
在这个炎热的假期,祝你学习轻松愉快。
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2ADBC证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)A BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC∠FDE =∠GDC (对顶角) ∴△EFD ≌△CGDBA CDF2 1 EEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC4、已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BDA∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
在BC上截取BF=AB,连接EF ∵BE平分∠ABC∴∠ABE=∠FBE又∵BE=BE∴⊿ABE≌⊿FBE(SAS)∴∠A=∠BFE∵AB//CD∴∠A+∠D=180º∵∠BFE+∠CFE=180º∴∠D=∠CFE又∵∠DCE=∠FCECE平分∠BCDCE=CE∴⊿DCE≌⊿FCE(AAS)∴CD=CF∴BC=BF+CF=AB+CD7. P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB在AC上取点E,使AE=AB。
∵AE=ABAP=AP∠EAP=∠BAE,∴△EAP≌△BAP ∴PE=PB。
PC<EC+PE∴PC<(AC-AE)+PB ∴PC-PB<AC-AB。
8. 已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE证明:在AC上取一点D,使得角DBC=角C ∵∠ABC=3∠C∴∠ABD=∠ABC-∠DBC=3∠C-∠C=2∠C;∵∠ADB=∠C+∠DBC=2∠C;∴AB=AD∴AC –AB =AC-AD=CD=BD 在等腰三角形ABD中,AE是角BAD的角平分线,∴AE垂直BD∵BE⊥AE∴点E一定在直线BD上,在等腰三角形ABD中,AB=AD,AE垂直BDP DACB∴点E也是BD的中点∴BD=2BE∵BD=CD=AC-AB∴AC-AB=2BE9. 如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.解:延长AD至BC于点E,∵BD=DC ∴△BDC是等腰三角形∴∠DBC=∠DCB又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2即∠ABC=∠ACB∴△ABC是等腰三角形∴AB=AC在△ABD和△ACD中AB=AC∠1=∠2BD=DC∴△ABD和△ACD是全等三角形(边角边)∴∠BAD=∠CAD∴AE是△ABC的中垂线∴AE⊥BC∴AD⊥BC10. 如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA证明:∵OM平分∠POQ∴∠POM=∠QOM∵MA⊥OP,MB⊥OQ∴∠MAO=∠MBO=90∵OM=OM∴△AOM≌△BOM (AAS)∴OA=OB∵ON=ON∴△AON≌△BON (SAS)∴∠OAB=∠OBA,∠ONA=∠ONB∵∠ONA+∠ONB=180∴∠ONA=∠ONB=90∴OM⊥AB11. 如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.证明:在AB上取F,使AF=AD,连接EF ∵AE平分∠DAB∴∠DAE=∠FAE在⊿ADE和⊿AFE中PEDCBAAD =AF ∠DAE=∠FAE AE = AE∴⊿ADE ≌⊿AFE (SAS ) ∴∠ADE=∠AFE ∵AB//CD∴∠ADE+∠C=180º ∵∠AFE+∠BFE=180º ∴∠C=∠BFE ∵ BE 平分∠ABC ∠CBE=∠FBE 在⊿BFE 和⊿BCE 中∠C=∠BFE ∠CBE=∠FBECE=CE∴⊿BFE ≌⊿BCE (AAS ) ∴CB=BF∴AB=AF+FB=AD+BC12. 如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF{{(2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.(1)证:∵DE⊥AC于E,BF⊥AC于F,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA(HL)∴DE=BF.在△DEM和△BFM中∠DEM=∠BFM∠DME=∠BMFDE=BF∴△DEM≌△BFM(AAS)∴MB=MD,ME=MF(2) 证:∵DE⊥AC于E,BF⊥AC于F,∴∠DEC=∠BFA=90°,DE∥BF,在Rt△DEC和Rt△BFA中,∵AF=CE,AB=CD,∴Rt△DEC≌Rt△BFA(HL)在△DEM 和△BFM 中 ∠DEM=∠BFM ∠DME=∠BMF DE=BF∴△DEM ≌△BFM(AAS) ∴MB=MD ,ME=MF13如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE . 证:∵∠CEB=∠CAB=90°∠ADB=∠CDE在△ABD 中,∠ABD = 180°-∠CAB-∠ADB 在△CED 中,∠DCE = 180°-∠CEB-∠CDE ∴∠ABD =∠DCE 在△ABD 和△ACF 中∠DAB=∠CAFAB=AC ∠ABD =∠DCF ∴△ABD ≌△ACF(ASA){FE D CBA{∵BD是∠ABC的平分线∴∠FBE =∠CBE在△FBE和△CBE中∠FBE =∠CBEBE=BE∠BEF =∠BEC∴△FBE≌△CBE(ASA)∴CE=FE CF=2CE∴BD=2CE14. 如图:DF=CE,AD=BC,∠D=∠C。
求证:△AED≌△BFC。
证明:∵DF=CE,∴DF-EF=CE-EF,即DE=CF,在△AED和△BFC中,∵AD=BC,∠D=∠C ,DE=CF ∴△AED≌△BFC(SAS)FED CBA15. 如图:AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。
求证:AM是△ABC的中线。
证明:∵BE‖CF∴∠E=∠CFM,∠EBM=∠FCM ∵BE=CF∴△BEM≌△CFM∴BM=CM∴AM是△ABC的中线M FE CBA16.AB=AC,DB=DC,F是AD的延长线上的一点。
求证:BF=CF证:在△ABD与△ACD中AB=ACBD=DCAD=AD∴△ABD≌△ACD(SSS)∴∠ADB=∠ADC∴∠BDF=∠FDC在△BDF与△FDC中BD=DC∠BDF=∠FDCDF=DF∴△FBD≌△FCD(SAS) ∴BF=FCFDC BA17. 如图:AB=CD,AE=DF,CE=FB。
求证:AF=DE。
证:∵CF=CE+EF EB=EF+FB又∵CE=FB∴CF=EB在△CDF与△ABE中AB=CDAE=DFBE=CF∴△CDF≌△ABE(SSS) ∴∠DCB=∠ABF在△ABF与△CDE中{ { {AB=CD∠ABF =∠DCEBF=CE∴△ABF≌△CDE (SAS) ∴AF=EDFEDCB A18. 公园里有一条“Z”字形道路ABCD,如图所示,其中AB∥CD,在AB,CD,BC 三段路旁各有一只小石凳E,F,M,且BE=CF,M在BC的中点,试说明三只石凳E,F,M恰好在一条直线上.证明:连接EF∵AB∥CD∴∠B=∠C∵M是BC中点∴BM=CM在△BEM和△CFM中BE=CF∠B=∠C ∴△BEM≌△CFM(SAS)∴CF=BEBM=CM19. 已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:AE =AF。
证:连接AC∵在△ADC和△ABC中AD=ABDC=BCAC=AC∴△ADC≌△ABC(SSS){ { {∴∠B=∠D∵E 、F 分别是DC 、BC 的中点 又∵BC =DC ∴DE=BF∵在△ADE 和△ABF 中 AD=AB∠D=∠B DE=BF∴△ADE ≌△ABF (SAS )∴AE=AF20. 如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6. 证明:∵在△ADC 和△ABC 中∠BAC=∠DAC ∠BCA=∠DCA AC=AC∴△ADC ≌△ABC (AAS ) ∵AB=AD ,BC=CD 在△DEC 与△BEC 中CE=CE ∠BCA=∠DCA ∴△DEC ≌△BEC (SAS ) ∴∠DEC=∠BEC654321E DCBABC=CD21.如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F 。
