第三章 弹性本构方程.ppt

单位体积中具有的应变能，称为应变能密度或比能。
变分法是研究泛函求极值的方法。弹性力学问题的变 分法，也称为能量法，是和弹性体的应变能或应变余能 密切相关的，是有限元法的基础。
一、一维状态
细长直杆，长度为L，横截面积为S，两端受拉力P作用。
产生的伸长量为DL，外力作的功为：
单位体积的应变能U0为：
单位体积的应变能U0代表应力-应变曲线中阴影部分的面积。 单位体积的应变余能U0为：
产生的x方向应变：
产生的x方向应变：
叠加
产生的x方向应变：
同理：
剪应变：
物理方程：
说明：
1.方程表示了各向同性材料的应力与应 变的关系，称为广义Hooke定义。也称 为本构关系或物理方程。
2.方程组在线弹性条件下成立。
三. 体积应变与体积弹性模量
令： 则： 令：
sm称为平均应力; q 称为体积应变
这些方程还不能解决弹塑性力学问题。
需要研究应力与应变之间的物理关系，即本构关系。 对应的函数方程称为物理方程，或本构方程。
• 材料的应力与应变关系需通过实验确定的。
• 本构方程实际是应力与应变关系实验结果的数学 描述。
• 由于实验的局限性，通常由简单载荷实验获得应 力与应变关系结果，建立描述相应的数学模型， 再将数学模型用于复杂载荷情况的分析。（用一 定实验验证结果）
具有一个弹性对称面的各向异性体, 弹性常数 有13个。单斜晶体(如正长石)具有这类弹性对称。
• 如果在物体内的任意一点有三个互相正交的弹性对 称面, 这种物体称为正交各向异性体。如: 煤块、均 匀的木材、叠层胶木、复合材料等
正交各向异性体有9个弹性常数。其弹性矩阵为
3.横观各向同性体
如物体内任意一点, 在平行于某一 平面的所有各个方向都有相同的弹性性 质, 这类正交异性体为横观各向同性体。 如不同层次的土壤、复合板材等。
当自变量(应变)很小时，式（１）中的各表达式可用泰 勒级数展开．略去二阶及以上的高阶微量，则式（１）中 的第一式展开为：
表示应变分量为零时的值，由基本假设，初始应力为 零．故
表示函数f1对应变分量的一阶偏导数在应变分量为零 时的值，等于一个常数
故, 式（１）可用一个线性方程组表示（线弹性体）
式（２）是纯数学推导结果，实际上与虎克定律线性关 系一致，是在弹性小变形条件下弹性体内任一点的应力与应 变的一般关系式．
• 弹性矩阵为
• 极端各向异性体的特点:
(1) 当作用正应力 时, 不仅会产生正应变
,
还会引起剪应变
。
(2) 当作用剪应力时, 不仅会产生剪应变, 也会引起正 应变。
2.正交各向异性体 如在均匀体内, 任意一点都存在着一个对称面,
在任意两个与此面对称的方向上, 材料的弹性性质 都相同。 称为具有一个弹性对称面的各向异性体。 该对称面称为弹性对称面, 垂直于弹性对称面的方 向称为物体的弹性主方向。
对线弹性材料，利用本构方程 应变余能U0为：
• 本章重点：
本 构 方 程
K E
3(1 2 )
应变能：
对线弹性材料，
一、三维状态
• 三向应力状态下，六个应力分量和六个应变分量。由能量 守恒原理，各应力分量的合力只在其对应的应变分量所引 起的变形位移上做功。
• 总的应变能为各应力分量对应的应变能之和，即：
令：
比较：
本构方程能量形式
满足上式的弹性材料称为超弹性材料。特点：在任意 加载-卸载循环下，材料不发生能量耗散。
三、. 弹性常数
1. 极端各向异性体:
物体内的任一点, 沿各个方向的性能都不相 同, 则称为极端各向异性体. (这种物体的材料极 少见)
即使在极端各向异性条件下, 式(2)中的36个 弹性常数也不是全部独立.
由能量守恒定律和应变能理论可证明,弹性常数 之间存在关系
36个弹性常数减少到21个. 弹性矩阵是对称矩阵.
横观各向同性体只有五个 弹性常数, 弹性矩阵为
4.各向同性体
物体内任意一点, 沿任何方向的弹性性质都相同。 各向同性体只有两个独立的弹性常数, 弹性矩阵为:
比较: 可见:
§3-3 弹性应变能
弹性体受外力作用后产生变形，外力在其作用位置的 变形上做功。忽略速度、热交换和温度等因素，则外力所 做的功全部转换为应变能储存在物体的内部。
• 例如：材料单轴拉伸应力-应变曲线：
s 塑形变形
s 塑形变形

e 线弹性
e 非线弹性
二. 各向同性材料的广义Hooke定律（本构方程） • 由材料力学已知，Hooke定律可表示为：
单向拉压
纯剪切 横向与纵向变形关系
E为拉压弹性模量； G为剪切弹性模量
为泊松比
对复杂应力状态，在弹性力学假设条件下，应用叠加原理： 考虑x方向的正应变：
式（２）中的系数 有３６个．
称为弹性常数，共
由均匀性假设，弹性体各点作用同样应力 时，必产生同样的应变，反之亦然．因此 为 常数，其数值由弹性体材料的性质而定．
式（２）推导过程未引用各向同性假设， 故可适用于极端各向异性体、正交各向异性体、 二维各向同性体以及各向同性体等．
式（２）可用矩阵表示
式(3)可用简写为 称为弹性矩阵.
四. 物理方程的其他表示形式
物理方程：
用应变表示应力：
或： ✓ 各种弹性常数之间的关系
§3-2 线弹性体本构方程的一般表达式
弹性条件下，应力与应变有唯一确定的对应关系，三维 应力状态下，一点的应力取决于该点的应变状态，应力是应 变的函数（或应变是应力的函数） 6个应力分量可表述为6个应变分量的函数。
中篇 弹性力学
第三章 弹性本构方程
§3-1 应力—应变关系的一般表达 §3-2 各向异性线弹性体 §3-3 各向同性线弹性体 §3-4 弹性应变能与弹性应变余能
§3-1 应力—应变关系
一、本构方程
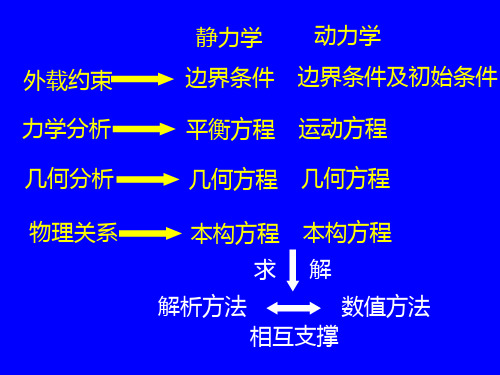
从静力学的角度对应力进行了分析 从几何学的角度对应变进行了分析
平衡微分方程 几何方程和变形协调方程
上述方程适用于任意连续物体，包括弹性力学和塑 性力学。