二维热传导方程有限差分法的MATLAB实现
matlab fdm算法

matlab fdm算法MATLAB是一种强大的数值计算软件,广泛应用于科学、工程和技术领域。
有许多算法和方法可以使用MATLAB实现,其中包括有限差分法(FDM)算法。
本文将介绍MATLAB中的FDM算法以及其在数值计算中的应用。
FDM算法是一种常见的数值计算方法,适用于求解偏微分方程(PDE)。
它将连续的PDE转化为离散的差分方程,然后利用离散的差分方程进行求解。
FDM算法在数值计算中具有广泛的应用,尤其适用于求解边值问题、热传导问题和流体动力学问题。
在MATLAB中,实现FDM算法需要以下几个关键步骤:1. 网格生成:选择适当的网格,并将待求解的区域离散化为小的网格单元。
常见的网格包括一维网格、二维网格和三维网格。
2. 差分形式:将偏微分方程转化为差分方程。
根据PDE的特性和问题的具体要求,选择适当的差分形式。
3. 离散化:将PDE中的微分算子和边界条件在网格上进行离散化。
常见的离散化方法有中心差分、前向差分和后向差分。
4. 矩阵构建:将离散化的差分方程转化为一个线性方程组。
这可以使用矩阵乘法和向量操作来实现。
5. 解线性方程组:使用MATLAB中的线性代数函数来解决离散化的线性方程组。
常见的函数包括LU分解、迭代法和共轭梯度法等。
6. 后处理:根据实际问题的需要,对求解结果进行后处理。
可以绘制网格图、等值线图等来展示结果。
下面,我们将以一个简单的热传导问题为例,演示MATLAB中的FDM算法。
假设我们要求解一个一维热传导问题,该问题的偏微分方程为:dT/dt = alpha * d^2T/dx^2其中,T是温度,t是时间,x是空间位置,alpha是热扩散系数。
首先,我们需要定义问题的参数和边界条件。
假设热扩散系数alpha为1,边界条件为T(0) = 0,T(1) = 100。
我们将空间区域[0,1]离散化为10个网格单元,时间区域[0,1]离散化为100个时间步长。
接下来,我们可以使用MATLAB中的差分形式来离散化偏微分方程。
matlab差分方程

matlab差分方程MATLAB是一种广泛使用的计算机辅助工具,其中包含了许多实用算法和解决方案。
差分方程是MATLAB中非常重要的一种工具,可以用于模拟和解决各种差分方程问题。
下面将介绍如何使用MATLAB来解决差分方程问题。
首先在MATLAB窗口中打开一个新的脚本文件(Ctrl+N),左侧显示脚本编辑器的窗口。
在窗口中输入以下内容:function dy = diffeq(t,y)dy = zeros(2,1);dy(1) = y(2);dy(2) = -0.1*y(2) - y(1) - 10*(y(1)^3);在这个脚本中,我们定义了一个名为“diffeq”的函数,它有两个参数(t和y)。
该函数返回一个长度为2的dy向量,dy是y的导数(dy/dt)。
在本例中,我们使用了系统描述的常见方法:x'=f(x,t),y是系统状态向量。
换句话说,我们将梯度设置为我们想要模拟的方程。
一旦函数被定义,我们现在可以开始运行模拟。
接下来,我们将使用MATLAB的ODE求解器来解决我们的差分方程问题。
我们可以这样编写代码:[t,y] = ode45(@diffeq,[0 30],[1 0]);在这里,ode45是MATLAB中用于解决常微分方程的函数,它需要三个参数。
第一个参数是定义我们的方程的函数(即我们之前声明的diffeq函数),第二个参数是我们期望的时间范围(从0到30,单位为秒),第三个参数是初值(在这个例子中,我们使用y(0)=1和y'(0)=0作为初值)。
运行后,MATLAB会将结果存储在两个向量t和y中,我们可以使用下面的代码来显示不同时间点t的y值:plot(t,y(:,1),'-')在此代码中,我们使用plot函数来绘制y的前一个元素(我们的状态向量正在被建模)以及时间t之间的关系。
结果应该是一个类似于与时间的函数y(t)的曲线。
这个值可以根据不同的初值和系统变量被改变。
matlab有限差分法

matlab有限差分法一、前言Matlab是一种广泛应用于科学计算和工程领域的计算机软件,它具有简单易学、功能强大、易于编程等优点。
有限差分法(Finite Difference Method)是一种常用的数值解法,它将微分方程转化为差分方程,通过对差分方程进行离散化求解,得到微分方程的数值解。
本文将介绍如何使用Matlab实现有限差分法。
二、有限差分法基础1. 有限差分法原理有限差分法是一种通过将微分方程转化为离散形式来求解微分方程的数值方法。
其基本思想是将求解区域进行网格划分,然后在每个网格点上进行逼近。
假设要求解一个二阶常微分方程:$$y''(x)=f(x,y(x),y'(x))$$则可以将其转化为离散形式:$$\frac{y_{i+1}-2y_i+y_{i-1}}{h^2}=f(x_i,y_i,y'_i)$$其中$h$为网格步长,$y_i$表示在$x_i$处的函数值。
2. 一维情况下的有限差分法对于一维情况下的常微分方程:$$\frac{d^2 y}{dx^2}=f(x,y,y')$$可以使用中心差分法进行离散化:$$\frac{y_{i+1}-2y_i+y_{i-1}}{h^2}=f(x_i,y_i,y'_i)$$这个方程可以写成矩阵形式:$$A\vec{y}=\vec{b}$$其中$A$为系数矩阵,$\vec{y}$为函数值向量,$\vec{b}$为右端项向量。
三、Matlab实现有限差分法1. 一维情况下的有限差分法假设要求解的方程为:$$\frac{d^2 y}{dx^2}=-\sin(x)$$首先需要确定求解区域和网格步长。
在本例中,我们将求解区域设为$[0,2\pi]$,网格步长$h=0.01$。
则可以通过以下代码生成网格:```matlabx = 0:0.01:2*pi;```接下来需要构造系数矩阵和右端项向量。
根据上面的公式,系数矩阵应该是一个三对角矩阵,可以通过以下代码生成:```matlabn = length(x)-2;A = spdiags([-ones(n,1), 2*ones(n,1), -ones(n,1)], [-1 0 1], n, n); ```其中`spdiags`函数用于生成一个稀疏矩阵。
二维传热方程c-n有限差分python

二维传热方程c-n有限差分python二维传热方程,也称为二维热传导方程,是一个描述温度分布随时间变化的重要偏微分方程。
对于一个均匀的二维区域,该方程可以表示为:∂T/∂t = α(∂²T/∂x² + ∂²T/∂y²)其中,T表示温度,t表示时间,x和y表示空间坐标,α表示热扩散率。
为了解决这个方程,可以使用有限差分法(Finite Difference Method)。
该方法将连续的空间离散化为一系列离散的网格点,并使用差分近似来求解方程。
下面是一个使用Python实现二维传热方程有限差分法的简单示例代码:```pythonimport numpy as npimport matplotlib.pyplot as plt# 定义区域和网格大小nx, ny = 100, 100x = np.linspace(0, 1, nx)y = np.linspace(0, 1, ny)dx, dy = x[1] - x[0], y[1] - y[0]# 定义初始温度分布T = np.zeros((nx, ny))T[nx//2, ny//2] = 100# 定义时间步长和总时间dt = 0.01nt = 1000# 定义热扩散率alpha = 0.01# 迭代求解温度分布for n in range(nt):T_new = np.zeros((nx, ny))for i in range(1, nx-1):for j in range(1, ny-1):T_new[i, j] = T[i, j] + alpha*dt*((T[i+1, j] - 2*T[i, j] + T[i-1, j])/(dx**2) + (T[i, j+1] - 2*T[i, j] + T[i, j-1])/(dy**2))T = T_new# 可视化结果plt.imshow(T, extent=(0, 1, 0, 1), origin='lower', cmap='hot')plt.colorbar(label='Temperature')plt.xlabel('x')plt.ylabel('y')plt.show()```在上述代码中,我们首先定义了一个100x100的网格,并将中心点设置为初始温度100度。
热传导方程有限差分法的MATLAB实现

△t
n
nn
关于
t
的二阶中心差商[10]:
坠2u 坠x2
≈
uj+1
-2uj +uj-1 (△x)2
,对方
程进行离散。 离散后的方程为:
n n-1
n
nn
uj -uj △t
=a2
uj+1
-2uj +uj-1 (△x)2
。
令
:r=
a2·△t (△x)2
,即
n
n
n
n-1
(1+2r)uj -r·uj+1 -r·uj-1 =uj 。 可化为矩阵形式:
摘 要:对于有界热传导齐次方程的混合问题,用分离变量法求解往往很复杂。 为了更好地
理解热传导方程的解,使用 MATLAB 软件将方程的解用图像表示出来。 通过区域转换的思想,
利用 MATLAB 编程实现一定区域内热传导方程的有限差分方法,数值表明了方法的可行性和
稳定性。
关键词:热传导方程;有限差分;MATLAB
方法, 把控制方程中的导数用网格节点上的函数值
的差商代替进行离散,从而 建立以网格节点上的值
为未知数的代数方程组。
1 求解热传导方程的基本思想
基本思想是把连续的定解区域用有限个离散点
构成的网格来代替, 这些离散点称作网格的节点;
把连续定解区域上的连续变量的函数用在网格上定
义的离散变量函数来近似; 把原方程和定解条件中
x0(ii+1)=ii*ox; end u=sin(pi*x0/l); % t=0 时 u(x,t)的值 r=a^2*ot/(ox)^2; for ii=1:n
%数据的输入 B=zeros(M-1,1);%存放系数矩阵主对角线元素 A=zeros (M-2,1);%存放系数矩阵主对角线元素下 方次对角线的元素 C=zeros (M-2,1);%存放系数矩阵主对角线元素上 方次对角线的元素 S=zeros(M-1,1);%存放右端的常数项 for ii=1:M-2
【毕业设计(论文)】二维热传导方程有限差分法的MATLAB实现

第1章前言1.1问题背景在史策教授的《一维热传导方程有限差分法的MATLAB实现》和曹刚教授的《一维偏微分方程的基本解》中,对偏微分方程的解得MATLAB实现问题进行过研究,但只停留在一维中,而实际中二维和三维的应用更加广泛。
诸如粒子扩散或神经细胞的动作电位。
也可以作为某些金融现象的模型,诸如布莱克-斯科尔斯模型与Ornstein-uhlenbeck过程。
热方程及其非线性的推广形式也被应用与影响分析。
在科学和技术发展过程中,科学的理论和科学的实验一直是两种重要的科学方法和手段。
虽然这两种科学方法都有十分重要的作用,但是一些研究对象往往由于他们的特性(例如太大或太小,太快或太慢)不能精确的用理论描述或用实验手段来实现。
自从计算机出现和发展以来,模拟那些不容易观察到的现象,得到实际应用所需要的数值结果,解释各种现象的规律和基本性质。
科学计算在各门自然科学和技术科学与工程科学中其越来越大的作用,在很多重要领域中成为不可缺少的重要工具。
而科学与工程计算中最重要的内容就是求解科学研究和工程技术中出现的各种各样的偏微分方程或方程组。
解偏微分方程已经成为科学与工程计算的核心内容,包括一些大型的计算和很多已经成为常规的计算。
为什么它在当代能发挥这样大的作用呢?第一是计算机本身有了很大的发展;第二是数值求解方程的计算法有了很大的发展,这两者对人们计算能力的发展都是十分重要的。
1.2问题现状近三十年来,解偏微分方程的理论和方法有了很大的发展,而且在各个学科技术的领域中应用也愈来愈广泛,在我国,偏微分方程数值解法作为一门课程,不但在计算数学专业,而且也在其他理工科专业的研究生的大学生中开设。
同时,求解热传导方程的数值算法也取得巨大进展,特别是有限差分法方面,此算法的特点是在内边界处设计不同于整体的格式,将全局的隐式计算化为局部的分段隐式计算。
而且精度上更好。
目前,在欧美各国MATLAB的使用十分普及。
在大学的数学、工程和科学系科,MATLAB苏佳园:二维热传导方程有限差分法的MATLAB实现被用作许多课程的辅助教学手段,MATLAB也成为大学生们必不可少的计算工具,甚至是一项必须掌握的基本技能。
利用matlab程序解决热传导问题-推荐下载

1、题目及要求
1. 原始题目及要求 2. 各节点的离散化的代数方程 3. 源程序 4. 不同初值时的收敛快慢 5. 上下边界的热流量(λ=1W/(m℃)) 6. 计算结果的等温线图 7. 计算小结 题目:已知条件如下图所示:
二、各节点的离散化的代数方程
各温度节点的代数方程
ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4 te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4 ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4
0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0; -1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0; 0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0; 0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0; 0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0; 0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0; 0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0; 0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0; 0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1; 0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0; 0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0; 0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1; 0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12]; b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4; yy=xx; [X,Y]=meshgrid(xx,yy); Z=reshape(x,4,4); Z=Z' contour(X,Y,Z,30) Z= 139.6088 150.3312 153.0517 153.5639
利用matlab程序解决热传导问题

哈佛大学能源与环境学院课程作业报告作业名称:传热学大作业——利用matlab程序解决热传导问题院系:能源与环境学院专业:建筑环境与设备工程学号:姓名:盖茨比2015年6月8日一、题目及要求1.原始题目及要求2.各节点的离散化的代数方程3.源程序4.不同初值时的收敛快慢5.上下边界的热流量(λ=1W/(m℃))6.计算结果的等温线图7.计算小结题目:已知条件如下图所示:二、各节点的离散化的代数方程各温度节点的代数方程ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4 te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4tm=(2*i+300+n)/24; tn=(2*j+m+p+200)/24; to=(2*k+p+n+200)/24; tp=(l+o+100)/12 三、源程序【G-S迭代程序】【方法一】函数文件为:function [y,n]=gauseidel(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0;0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0;0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]';[x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.1523 84.1429 67.9096 63.3793 62.4214 20.1557 15.4521 14.8744 14.7746 【方法2】>> t=zeros(5,5);t(1,1)=100;t(1,2)=100;t(1,3)=100;t(1,4)=100;t(1,5)=100;t(2,1)=200;t(3,1)=200;t(4,1)=200;t(5,1)=200;for i=1:10t(2,2)=(300+t(3,2)+t(2,3))/4 ;t(3,2)=(200+t(2,2)+t(4,2)+t(3,3))/4;t(4,2)=(200+t(3,2)+t(5,2)+t(4,3))/4;t(5,2)=(2*t(4,2)+200+t(5,3))/4;t(2,3)=(100+t(2,2)+t(3,3)+t(2,4))/4;t(3,3)=(t(3,2)+t(2,3)+t(4,3)+t(3,4))/4; t(4,3)=(t(4,2)+t(3,3)+t(5,3)+t(4,4))/4; t(5,3)=(2*t(4,3)+t(5,2)+t(5,4))/4;t(2,4)=(100+t(2,3)+t(2,5)+t(3,4))/4;t(3,4)=(t(3,3)+t(2,4)+t(4,4)+t(3,5))/4;t(4,4)=(t(4,3)+t(4,5)+t(3,4)+t(5,4))/4;t(5,4)=(2*t(4,4)+t(5,3)+t(5,5))/4;t(2,5)=(2*t(2,4)+300+t(3,5))/24;t(3,5)=(2*t(3,4)+t(2,5)+t(4,5)+200)/24;t(4,5)=(2*t(4,4)+t(3,5)+t(5,5)+200)/24;t(5,5)=(t(5,4)+t(4,5)+100)/12;t'endcontour(t',50);ans =100.0000 200.0000 200.0000 200.0000 200.0000 100.0000 136.8905 146.9674 149.8587 150.7444 100.0000 102.3012 103.2880 103.8632 104.3496 100.0000 70.6264 61.9465 59.8018 59.6008 100.0000 19.0033 14.8903 14.5393 14.5117【Jacobi迭代程序】函数文件为:function [y,n]=jacobi(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0; 0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0; 0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0; 0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0; 0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=jacobi(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6); xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)n =97Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.152384.1429 67.9096 63.3793 62.421420.1557 15.4521 14.8744 14.7746四、不同初值时的收敛快慢1、[方法1]在Gauss 迭代和Jacobi 迭代中,本程序应用的收敛条件均为norm(y-x0)>=eps ,即使前后所求误差达到e 的-6次方时,跳出循环得出结果。
二维热传导方程 matlab

二维热传导方程是描述二维热传导过程的数学模型,它在工程、物理、地球科学等领域都有重要应用。
在实际工程问题中,我们经常需要求解二维热传导方程,以预测物体表面的温度分布、热量传递速率等参数。
Matlab是一个强大的数学软件,通过Matlab我们可以很方便地求解二维热传导方程,并得到预期的结果。
一、二维热传导方程的基本形式二维热传导方程可以用偏微分方程的形式表示为:∂u/∂t = k(∂²u/∂x² + ∂²u/∂y²)其中,u(x, y, t)是温度分布随时间和空间的变化,k是热传导系数。
二、Matlab中求解二维热传导方程的方法在Matlab中,我们可以采用有限差分法(finite difference method)求解二维热传导方程。
有限差分法将偏微分方程离散化,转化为代数方程组,然后通过迭代求解得到数值解。
具体步骤如下:1. 离散化空间和时间变量,将连续的空间区域和时间区间分割成若干个小区间。
2. 利用二阶中心差分格式对二维热传导方程进行离散化,得到代数方程组。
3. 利用Matlab中的矩阵运算和迭代方法,求解代数方程组,得到数值解。
三、Matlab代码示例下面是一个简单的Matlab代码示例,用于求解二维热传导方程:```matlab定义参数和初始条件Lx = 1; Ly = 1; 区域大小Nx = 100; Ny = 100; 离散化网格数T = 1; 总时间Nt = 100; 时间步数k = 1; 热传导系数dx = Lx/Nx; dy = Ly/Ny;dt = T/Nt;x = 0:dx:Lx; y = 0:dy:Ly;[X, Y] = meshgrid(x, y);u = sin(pi*X).*sin(pi*Y); 初始温度分布迭代求解for n = 1:Ntun = u;for i = 2:Nx-1for j = 2:Ny-1u(i, j) = un(i, j) + k*dt/dx^2*(un(i+1, j)-2*un(i, j)+un(i-1, j)) + k*dt/dy^2*(un(i, j+1)-2*un(i, j)+un(i, j-1));endendend可视化结果figure;surf(X, Y, u);xlabel('x'); ylabel('y'); zlabel('Temperature');```以上代码首先定义了区域大小、离散化网格数、总时间、热传导系数等参数,然后利用有限差分法进行迭代求解,最后利用Matlab绘制了温度分布的三维图像。
二维热传导方程有限容积法的MATLAB实现

温度/(℃)
参数类型 无限大板厚度 L 厚度方向坐标 x 密度 ρ 比热 c 大板初始温度 Ti 流体温度 T f 热传导系数 λ 换热系数 h
N n
[8]
界类型定义不同源项 S, 并将其代入到方程组的迭代 求解中, 从而在数学物理模型上体现不同方式向物 理介质内的有限容积单元传递热量, 下面分三种情 况进行讨论: (1) 给定热流密度 q 边界条件 T 2 j - T1 j 热流密度 q = - λ , 边界温度系数 aW = δx w 又有源项 S u 2 j = q aW 2 j = 0 , 元温度: T1 j = q
基金项目: 国家自然科学基金 (No.10901067) ; 中央高校基本科研业务费专项资金 (No.2011-1a-023) 。 作者简介: 薛琼 ( 1980— ) , 女, 博士, 讲师, 主要研究领域为微分几何及其应用; 肖小峰 ( 1979— ) , 男, 讲师。E-mail: 18986258401@ 收稿日期: 2011-12-08 修回日期: 2012-01-30 CNKI 出版日期: 2012-05-21 DOI: 10.3778/j.issn.1002-8331.2012.24.044 /kcms/detail/11.2127.TP.20120521.1142.073.html
199
通过式 (1) 和式 (3) 推导出, 具体如下式:
ì ρ c ¶T = ¶ æ λ ¶T ö + S ï ¶τ ¶x è ¶x ø ï ¶T | | = h T - T ¶T | =0 ï ¶x | |x = 0 λ 1 f ¶x |x = 0.06 ï 0 ía P T P = a E T E + aW TW + S u Dx + a0 PT P ï 0 ïa P = a E + aW + a P - S P Dx ï 0 ρcDV λe λw ïa P = Dτ a E = δx aW = δx e w î
热传导方程有限差分法的MATLAB实现

万方数据万方数据万方数据万方数据热传导方程有限差分法的MATLAB实现作者:史策作者单位:西安建筑科技大学,理学院,陕西,西安,710055刊名:咸阳师范学院学报英文刊名:JOURNAL OF XIANYANG NORMAL UNIVERSITY年,卷(期):2009,24(4)被引用次数:0次1.曹钢,王桂珍,任晓荣.一维热传导方程的基本解[J].山东轻工业学院学报,2005,19(4):76-80.2.万正苏,方春华,张再云.关于热传导方程有限差分区域分解并行算法精度的注记[J].湖南理工学院学报(自然科学版),2007,20(3):12-14.3.StephenJ.Chapman.MATLAB编程[M].邢树军,郑碧波,译.北京:科学出版社,2008.4.田兵.用MATLAB解偏微分方程[J].阴山学刊,2006,20(4):12-13.5.王飞,裴永祥.有限差分方法的MATLAB编程[J].新疆师范大学学报(自然科学版),2003,22(4):21-27.6.王宝红.热传导方程的可视化探讨[J].忻州师范学院学报,2008,24(2):31-36.7.李先枝.热传导方程差分解法的最佳网格[J].河南大学学报(自然科学版),2004,34(3):16-18.8.赵德奎,刘勇.MATLAB在有限差分数值计算中的应用[J].四川理工学院学报,2005,18(4):61-64.9.谢焕田,吴艳.拉普拉斯有限差分法的MATLAB实现[J].四川理工学院学报,2008,21(3):1-2.10.南京大学数学系计算数学专业.偏微分方程数值解法[M].北京:科学出版社,1979.1.学位论文申卫东热传导方程有限差分区域分解算法研究2003区域分解算法是在并行机上求解偏微分方程数值解的一种较自然的方法.该方法先将偏微分方程求解区域划分为若干个子区域,然后在各个子区域并行求解.全文共五章.第一章为引言,简要介绍了热传导方程并行算法的概况及该文所讨论的基本内容.在第二章,我们在内边界点为等距分划的多子区域条件下,得到Dawson等人关于求解热传导方程区域分解算法差分解的误差估计.在第三章,我们以Saul'yev非对称格式作内边界处理,发展了新的区域分解算法,得到了差分解的先验误差估计,并与Dawson等人的算法作了比较.给出了关于算法计算精度的数值结果.在第四章,我们发展了一些新技术,在子区域的边界处采用小时间步长古典显式格式求解,构造了新的区域分解算法,得到了差分解的先验误差估计.给出了关于算法计算精度的数值结果.在第五章,我们在二维热传导方程求解上扩充了Dawson等人的区域分解算法.给出了关于算法计算精度的数值结果.第六章为该研究工作的主要结论.2.期刊论文张守慧.王文洽.ZHANG Shou-hui.WANG Wen-qia热传导方程有限差分逼近的数学Stencil及其新型迭代格式-山东大学学报(理学版)2006,41(6)将Stencil应用于偏微分方程有限元差分逼近过程,以两类差分格式为基础建立了求解热传导方程的两种新型迭代算法.此两种算法与经典的Jacobi方法同样具有并行的性质,但比Jacobi方法收敛快.给出的算例说明方法的适用性.3.期刊论文吕桂霞.马富明.Lü Guixia.Ma Fuming二维热传导方程有限差分区域分解算法-数值计算与计算机应用2006,27(2)本文讨论了一类数值求解二维热传导方程的并行差分格式.在这个算法中,通过引进内界点将求解区域分裂成若干子区域.在子区域间内界点上采用非对称格式计算,一旦这些点的值被计算出来,各子区域间的计算可完全并行.本文得到了稳定性条件和最大模误差估计.它表明我们的格式有令人满意的稳定性,并且有着较高的收敛阶.4.学位论文田源地下煤火三维数理模型正演数值模拟2006本文首先给出了几个地下煤火随空间、温度变化的动态和稳态热数学物理模型及其简化模型。
最新利用matlab程序解决热传导问题

哈佛大学能源与环境学院课程作业报告作业名称:传热学大作业——利用matlab程序解决热传导问题院系:能源与环境学院专业:建筑环境与设备工程学号:5201314姓名:盖茨比2015年6月8日一、题目及要求1.原始题目及要求2.各节点的离散化的代数方程3.源程序4.不同初值时的收敛快慢5.上下边界的热流量(λ=1W/(m℃))6.计算结果的等温线图7.计算小结题目:已知条件如下图所示:二、各节点的离散化的代数方程各温度节点的代数方程ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4tm=(2*i+300+n)/24; tn=(2*j+m+p+200)/24; to=(2*k+p+n+200)/24; tp=(l+o+100)/12三、源程序【G-S迭代程序】【方法一】函数文件为:function [y,n]=gauseidel(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0; -1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0; 0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0; 0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.1523 84.1429 67.9096 63.3793 62.4214 20.1557 15.4521 14.8744 14.7746【方法2】>> t=zeros(5,5);t(1,1)=100;t(1,2)=100;t(1,3)=100;t(1,4)=100;t(1,5)=100;t(2,1)=200;t(3,1)=200;t(4,1)=200;t(5,1)=200;for i=1:10t(2,2)=(300+t(3,2)+t(2,3))/4 ;t(3,2)=(200+t(2,2)+t(4,2)+t(3,3))/4;t(4,2)=(200+t(3,2)+t(5,2)+t(4,3))/4;t(5,2)=(2*t(4,2)+200+t(5,3))/4;t(2,3)=(100+t(2,2)+t(3,3)+t(2,4))/4;t(3,3)=(t(3,2)+t(2,3)+t(4,3)+t(3,4))/4; t(4,3)=(t(4,2)+t(3,3)+t(5,3)+t(4,4))/4; t(5,3)=(2*t(4,3)+t(5,2)+t(5,4))/4;t(2,4)=(100+t(2,3)+t(2,5)+t(3,4))/4;t(3,4)=(t(3,3)+t(2,4)+t(4,4)+t(3,5))/4;t(4,4)=(t(4,3)+t(4,5)+t(3,4)+t(5,4))/4;t(5,4)=(2*t(4,4)+t(5,3)+t(5,5))/4;t(2,5)=(2*t(2,4)+300+t(3,5))/24;t(3,5)=(2*t(3,4)+t(2,5)+t(4,5)+200)/24;t(4,5)=(2*t(4,4)+t(3,5)+t(5,5)+200)/24;t(5,5)=(t(5,4)+t(4,5)+100)/12;t'endcontour(t',50);ans =100.0000 200.0000 200.0000 200.0000 200.0000 100.0000 136.8905 146.9674 149.8587 150.7444 100.0000 102.3012 103.2880 103.8632 104.3496 100.0000 70.6264 61.9465 59.8018 59.6008 100.0000 19.0033 14.8903 14.5393 14.5117【Jacobi迭代程序】函数文件为:function [y,n]=jacobi(A,b,x0,eps) D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0;0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0;0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=jacobi(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6); xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)n =97Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.152384.1429 67.9096 63.3793 62.421420.1557 15.4521 14.8744 14.7746四、不同初值时的收敛快慢1、[方法1]在Gauss迭代和Jacobi迭代中,本程序应用的收敛条件均为norm(y-x0)>=eps,即使前后所求误差达到e的-6次方时,跳出循环得出结果。
热传导方程几种差分格式的MATLAB数值解法比较

热传导方程几种差分格式的MATLAB数值解法比较
冯立伟
【期刊名称】《沈阳化工大学学报》
【年(卷),期】2011(025)002
【摘要】对求解热传导方程的几种差分格式进行分析,并讨论使用MATLAB编程求解偏微分方程的方法.编制几种差分格式的MATLAB程序,使用算例进行数值实验,在不同网格比情况下,比较几种算法的优劣.
【总页数】5页(P179-182,191)
【作者】冯立伟
【作者单位】沈阳化工大学数理系,辽宁沈阳110142
【正文语种】中文
【中图分类】O241.82
【相关文献】
1.热传导方程几种差分格式的MATLAB数值解法比较 [J], 冯立伟
2.热传导方程非局部初边值问题的向前Euler差分格式和向后Euler差分格式 [J], 潘祝山
3.热传导方程非局部初边值问题的向前Euler差分格式和向后Euler差分格式 [J], 潘祝山
4.基于Crank-Nicolson差分与Newton迭代法的非线性热传导方程数值解法 [J], 高忠社
5.一类基于Crank-Nicolson差分格式的非线性热传导方程数值解 [J], 高忠社
因版权原因,仅展示原文概要,查看原文内容请购买。
二维 热传导方程 matlab

二维热传导方程在实际工程问题中有着广泛的应用。
热传导方程描述了热量在空间和时间中的传播规律,而二维热传导方程则特指热量在二维平面上的传播情况。
在工程领域,我们经常需要利用数值方法来求解二维热传导方程,而MATLAB作为一款强大的工程计算软件,提供了丰富的工具和函数来进行热传导方程的数值求解。
让我们回顾一下二维热传导方程的基本形式,它通常可以表示为:\[ \frac{\partial u}{\partial t} = \alpha \left( \frac{\partial^2u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) \]其中,\( u(x, y, t) \) 是温度场的分布,\( \alpha \) 是热扩散系数。
这个偏微分方程描述了温度场随时间和空间的演化规律,是研究热传导问题的基本方程之一。
在实际工程中,我们经常需要利用数值方法求解二维热传导方程,特别是在复杂几何结构和边界条件下。
MATLAB提供了丰富的数值求解工具,最常用的是有限差分法。
有限差分法将空间离散化为网格,用差分格式逼近偏微分方程,然后利用迭代方法求解离散化的代数方程组,得到温度场的数值解。
为了使用MATLAB进行二维热传导方程的数值求解,我们需要进行以下基本步骤:1. 网格划分:将求解区域进行网格划分,确定空间离散化的步长。
2. 边界条件处理:根据实际问题确定边界条件,例如固定温度、热通量等。
3. 数值格式选取:选择合适的差分格式逼近偏微分方程,通常采用显式或隐式格式。
4. 迭代求解:利用MATLAB提供的迭代方法,求解离散化后的代数方程组,得到温度场的数值解。
在实际工程中,二维热传导方程的数值求解往往涉及到复杂的边界条件、材料参数、热源分布等。
我们需要对MATLAB的数值求解工具有深入的理解和熟练的应用,才能准确地模拟和分析实际问题。
在我看来,二维热传导方程的数值求解是工程领域中非常重要的课题之一。
有限元二维热传导波前法MATLAB程序

有限元二维热传导波前法MATLAB程序科技论文2009-12-28 02:40:17 阅读226 评论15 字号:大中小江岩声•二维热传导有限元•使用高斯消去法解线性方程组的二维热传导有限元程序•波前法的基本概念与算法•使用波前法解线性方程组的二维热传导有限元程序•消元过程•波前法与高斯消去法的效率之比较•小结:波前法的过去、现在和未来波前法是求解线性方程组的一种方法,广泛用于有限元程序。
它最初由英国人(?)B.M. Irons于1970在“国际工程计算方法杂志”上发表。
30多年来,波前法有了不少变种。
本文所用算法,采于法国人Pascal JOLY所著《Mise en Oeuvre de la Méthode des Eléments Finis》。
这本书是我1993年在比利时一家书店买的,书中有一节"波前法",六页纸,解释了基本概念和算法,但没有程序,也没有细节讨论。
我曾花了两个半天的时间,在网上寻找波前法程序,或更详细的资料,没有找到(需要花钱才能看的文献不算)。
倒是看到不少中国人,也在寻找。
一些人说,波前法程序太难懂了。
通过自己编写程序,我同意这些人的说法,确实难。
我还真很少编如此耗费脑力的程序。
完工之后,我曾对朋友老王说,有了算法,编程序还这么难,当初想出算法的人,真是了不起。
现将我对波前法的理解和编程体会解说如下,供感兴趣的网友参考,也为填补网络上波前法空白。
二维热传导有限元波前法和有限元密不可分。
因而,在编写波前法程序之前,必须有个有限元程序。
为了简化问题,最好是能解算一个节点上只有一个自由度的问题的有限元程序,而且要尽可能地简单。
我手边现有的有限元程序都不符合这个要求。
就决定先开发一个解算二维热传导问题的MATLAB有限元程序。
二维热传导问题的微分方程是其中T 是温度,Kx 和Ky 分别是x 和y 方向上的热传导系数,q 是热源。
对于这样的比较经典的二阶微分方程,如何导出有限元表达式?这个问题,是有限元的首要问题!我相信,许许多多学过有限元的人,甚至每天都在用有限元的人,并不真的十分明了。
有限差分法及matlab实现

U i1, j , k U i−1, j , k U i , j 1, kU i , j −1, kU i , j , k1 U i , j , k−1 = 6U i , j , k ρ ----- (1) ⋯ ∂ x 2 ∂ x2 6 ∂ x3 ∂ U 1 ∂2 U 1 ∂3 U U i , j 1, k =U i , j ,k ⋯ ∂ y 2 ∂ y2 6 ∂ y3 ∂ U 1 ∂2 U 1 ∂ 3 U U i , j , k1 =U i , j ,k ⋯ ∂ z 2 ∂ z2 6 ∂ z3 ∂ U 1 ∂2 U 1 ∂3 U U i−1, j , k =U i , j , k− − ⋯ ∂ x 2 ∂ x2 6 ∂ x3 ∂ U 1 ∂2 U 1 ∂3 U U i , j 1, k =U i , j , k− − ⋯ ∂ y 2 ∂ y2 6 ∂ y3 ∂ U 1 ∂2 U 1 ∂ 3 U U i , j , k1 =U i , j , k− − ⋯ ∂ z 2 ∂ z2 6 ∂ z3 U i1, j , k =U i , j ,k
= 6U i , j , k ρ
这就是泊松方程的有限差分形式,以下估计该方程的精度: 由泰勒公式,易知有以下结果:
∂U 1 ∂2 U 2 1 ∂3 U 3 h h h ⋯ ∂x 2 ∂ x2 6 ∂ x3 ∂U 1 ∂ 2 U 2 1 ∂3 U 3 U x , y k, z =U x , y , z k k k ⋯ ∂y 2 ∂ y2 6 ∂ y3 2 3 ∂U 1∂ U 2 1∂ U 3 U x , y , z l =U x , y , z l l l ⋯ ∂z 2 ∂ z2 6 ∂ z3 U x h , y , z =U x , y , z
有限差分法解热传导问题

y
0Hale Waihona Puke y xx y 4tm,n
2tm1,n
2x
qw
tm,n1
tm,n1
Φm,n
x2
1
(2) 外部角点
qw
y 2
tm1,n tm,n x
y 2 qw
x 2
qw
x 2
tm,n1 y
tm,n
Φ m,n
x 2
y 2
x2 m,n
x 2
同样可得:
2t tm,n1 2tm,n tm,n1 o(y2 )
y2 m,n
y 2
建立离散方程
对于二维稳态导热问题,在直角坐标中,其导热 微分方程为:
2t x 2
2t y 2
v
0
其节点方程为:
ti1, j
2ti, j
x2
= 流出控制体的总热流量+控制体内能的增量
建立离散方程
内部节点:Φm1,n Φm1,n Φm,n1 Φm,n1 0
(m,n+1)
y
Φ上 Φ下 Φ左+Φ右 0
y
y o
(m-1,n)
x
x
(m, n) (m,n-1)
x
(m+1,n)
建立离散方程
Φ上 Φ下 Φ左+Φ右 Φv 0
NDSolve[{D[u[x,t],t]=D[u[x,t],{x,2}],u[x,0]=-x*(1x),Derivative[1,0][u][0,t]=0,Derivative[1,0][u][1,t]=3u[1,t],u,{x,0,1},{t,0,0.3}]
用有限差分法和Matlab计算二维热加工温度场分析
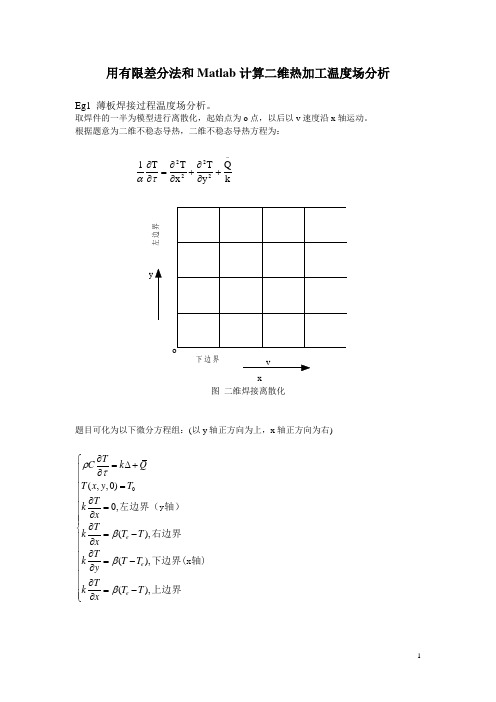
用有限差分法和Matlab 计算二维热加工温度场分析Eg1 薄板焊接过程温度场分析。
取焊件的一半为模型进行离散化,起始点为o 点,以后以v 速度沿x 轴运动。
根据题意为二维不稳态导热,二维不稳态导热方程为:k Qy T x T T 12222-+∂∂+∂∂=∂∂ταyx 左边界下边界图 二维焊接离散化题目可化为以下微分方程组:(以y 轴正方向为上,x 轴正方向为右)(,,0)0,(),(),(),e e e TC k QT x y TTk xT k T T x Tk T T y Tk T T x ρτβββ∂⎧=∆+⎪∂⎪=⎪⎪∂=⎪∂⎪⎪∂⎨=-⎪∂⎪∂⎪=-⎪∂⎪∂⎪=-⎪∂⎩左边界(y 轴)右边界下边界(x 轴)上边界需要的参数(均已cm,cal,g 为单位,所以不必换算):参数数值 备注 ρ7.82 g/cm 3 密度 v0.4 cm/s 焊接速度 h1cm 板厚度 Qm 4000 cal/cm 3 热源分布密度 β0.0008cal/cm 2·s ·℃ 换热系数 Te ,T 020℃ 周边介质温度,初始温度 k 0.1 cal/c m ·s ·℃ 导热系数用PDE Tool 解题步骤如下:1. 区域设置单击工具,在窗口拉出一个矩形,双击矩形区域,在Object Dialog 对话框输入Left 为0,Bottom 为0,Width 为2,Height 为2。
与默认的坐标相比,图形小的看不见,所以要调整坐标显示比例。
方法:选择Options->Axes Limits,把X ,Y 轴的自动选项打开。
设置Options->Application 为Heat Transfer (设置程序应用热传输模型)2. 设置边界条件单击,使边界变红色,然后分别双击每段边界,打开Boundary Conditions 对话框,设置边界条件(根据边界条件)。
二位热传导方程第二类边界有限差分法

这是一个关于热传导方程的问题,可以使用有限差分法进行求解。
首先,我们需要定义一个二维热传导方程:
∂u/∂t = α (∂²u/∂x² + ∂²u/∂y²)
其中,u表示温度,t表示时间,x和y表示空间坐标,α表示热扩散率。
然后,我们可以使用第二类边界有限差分法来求解这个方程。
将方程进行离散化处理,得到如下的差分方程:
u_i,j^(n+1) = u_i,j^n + Δt/α * [(u_i+1,j^n - 2u_i,j^n + u_i-1,j^n)/Δx² + (u_i,j+1^n - 2u_i,j^n + u_i,j-1^n)/Δy²]
其中,u_i,j^(n) 表示在时刻n,坐标为(i, j) 处的温度值,Δt 表示时间步长,Δx 和Δy 表示空间步长。
我们可以使用这个差分方程来迭代求解温度场的变化。
需要注意的是,在边界处需要考虑边界条件。
具体的边界条件可以根据实际问题的需求进行设定。
以上就是使用第二类边界有限差分法求解二维热传导方程的基本步骤。
热传导方程以及matlab求解

热传导方程及matlab求解1. 热传导方程的概念热传导方程是描述物质内部温度分布随时间变化的数学模型。
它是热力学基本方程之一,描述了热能在物体内传递和扩散的过程。
热传导方程通常表示为:$$\frac{\partial u}{\partial t} = \alpha \nabla^2 u$$其中,u表示温度分布,t表示时间,$\alpha$表示热扩散系数,$\nabla^2$表示拉普拉斯算子。
热传导方程可以根据不同的物理条件和边界条件进行不同形式的推导和求解。
2. 热传导方程的重要性热传导方程在工程、地球科学、生物学和材料科学等领域都有着广泛的应用。
通过研究热传导方程,可以深入理解物质内部温度变化的规律,从而优化材料设计、改进能源利用效率,甚至预测地球内部热量分布等方面都有着重要的意义。
3. 热传导方程的matlab求解Matlab作为一种强大的科学计算软件,对热传导方程的求解有着很好的支持。
通过Matlab中的偏微分方程求解工具包,可以方便地对热传导方程进行数值求解。
一般来说,使用Matlab求解热传导方程的步骤包括定义方程、设定边界条件和初值条件、选择合适的数值求解方法,并进行模拟计算。
4. 个人观点和理解对于热传导方程及其在Matlab中的求解,我个人认为这是一个非常有意思且实用的课题。
热传导方程作为热力学基本方程之一,在工程领域有着很重要的应用,而Matlab作为科学计算软件的代表,在求解热传导方程时具有高效、准确的优势。
通过学习热传导方程及在Matlab中的求解,不仅可以深入理解热传导的物理过程,还能够提升数值计算及编程的能力。
总结通过本文的介绍,我们了解了热传导方程的基本概念、重要性以及在Matlab中的求解方法。
热传导方程作为描述物质内部温度分布变化的数学模型,对于研究物质热传导过程有着重要意义。
而Matlab作为强大的科学计算软件,对于求解热传导方程也有着很好的支持。
希望通过本文的介绍,读者能对热传导方程及其在Matlab中的求解有更深入的理解,并能够在相关领域应用这些知识。
