材料力学作业参考解答
材料力学习题及答案
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 导电性答案:D2. 根据胡克定律,当材料受到正应力时,其应变与应力成正比,比例系数称为:A. 杨氏模量B. 剪切模量C. 泊松比D. 屈服强度答案:A3. 在材料力学中,材料的屈服强度是指:A. 材料开始发生塑性变形的应力B. 材料发生断裂的应力C. 材料发生弹性变形的应力D. 材料发生脆性断裂的应力答案:A4. 材料的疲劳寿命与下列哪一项无关?A. 材料的疲劳极限B. 应力循环次数C. 材料的弹性模量D. 应力循环的幅度答案:C5. 在材料力学中,下列哪一项不是材料的力学性能指标?A. 硬度B. 韧性C. 密度D. 冲击韧性答案:C二、简答题(每题5分,共10分)6. 简述材料力学中弹性模量和剪切模量的区别。
答:弹性模量,也称为杨氏模量,是描述材料在受到正应力作用时,材料的纵向应变与应力成正比的比例系数。
剪切模量,也称为刚度模量,是描述材料在受到剪切应力作用时,材料的剪切应变与剪切应力成正比的比例系数。
7. 什么是材料的疲劳寿命,它与哪些因素有关?答:材料的疲劳寿命是指材料在反复加载和卸载过程中,从开始加载到发生疲劳断裂所需的循环次数。
它与材料的疲劳极限、应力循环的幅度、材料的微观结构和环境因素等有关。
三、计算题(每题15分,共30分)8. 一根直径为20mm的圆杆,材料的杨氏模量为200GPa,当受到100N的拉力时,求圆杆的伸长量。
答:首先计算圆杆的截面积A = π * (d/2)^2 = π * (0.02/2)^2m^2 = 3.14 * 0.01 m^2。
然后根据胡克定律ΔL = F * L / (A * E),其中 L 为杆长,假设 L = 1m,代入数值得ΔL = 100 * 1 / (3.14* 0.01 * 200 * 10^9) m = 7.96 * 10^-6 m。
材料力学习题解答

解: (3) 梁可简化, 为图示简朴支梁。
B
(m / 2)a 6EI
ma 12EI
(逆时针)
wC 0
mm
m
2
B
C
m
m
2a a a a a 2a
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
解: (4) 梁可简化,为图示简朴支梁。 B
q
2qqaa22
C
B
qa3 24EI
φ w3 w2
q EI a
A a/4
θ w1
w1
a 4
qa3 a qa4 24EI 4 96EI
w2
q 8EI
a 4
4
qa 4 2048EI
φ w3
w3
a 4
a 3EI
1 2
q
a 4
2
a 4
qa 4 384EI
w2
w
w1
w2
w3
15qa 4 2048EI
7.试用叠加法计算图示各梁C点旳挠度。
解: (1) 梁可简化, 为图示悬臂梁。
A
B
F (2a)2 2EI
Fa 2 2EI
B
3Fa 2 2EI
(逆时针)
wC
wA
F (2a)3 3EI
( Fa3 3EI
Fa 2 2EI
a)
F
F
B C
Fa
a
a
F
a
BF
C
F
11Fa3 wC 6EI (向下)
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
A
先考虑载荷作用下梁旳变形。
材料力学试题及答案

材料力学试题及答案一、选择题(每题2分,共20分)1. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 塑性C. 硬度D. 韧性2. 材料在拉伸过程中,当应力达到屈服点后,材料将:A. 断裂B. 产生永久变形C. 恢复原状D. 保持不变3. 材料的弹性模量是指:A. 材料的密度B. 材料的硬度C. 材料的抗拉强度D. 材料在弹性范围内应力与应变的比值4. 根据材料力学的胡克定律,下列说法正确的是:A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成线性关系5. 材料的疲劳寿命是指:A. 材料的总寿命B. 材料在循环加载下达到破坏的周期数C. 材料的断裂寿命D. 材料的磨损寿命6. 材料的屈服强度是指:A. 材料在弹性范围内的最大应力B. 材料在塑性变形开始时的应力C. 材料的抗拉强度D. 材料的极限强度7. 材料的断裂韧性是指:A. 材料的硬度B. 材料的抗拉强度C. 材料抵抗裂纹扩展的能力D. 材料的屈服强度8. 材料力学中的泊松比是指:A. 材料的弹性模量B. 材料的屈服强度C. 材料在拉伸时横向应变与纵向应变的比值D. 材料的断裂韧性9. 在材料力学中,下列哪一项是衡量材料脆性程度的指标?A. 弹性模量B. 屈服强度C. 断裂韧性D. 泊松比10. 材料在受力过程中,当应力超过其极限强度时,将:A. 发生弹性变形B. 发生塑性变形C. 发生断裂D. 恢复原状答案1. C2. B3. D4. A5. B6. B7. C8. C9. C10. C试题二、简答题(每题10分,共30分)1. 简述材料力学中材料的三种基本力学性质。
2. 解释什么是材料的疲劳现象,并简述其对工程结构的影响。
3. 描述材料在拉伸过程中的四个主要阶段。
答案1. 材料的三种基本力学性质包括弹性、塑性和韧性。
弹性指的是材料在受到外力作用时发生变形,当外力移除后能够恢复原状的性质。
塑性是指材料在达到一定应力水平后,即使外力移除也无法完全恢复原状的性质。
材料力学的试题及答案

材料力学的试题及答案一、选择题1. 材料力学中,下列哪个选项不是材料的基本力学性质?A. 弹性B. 塑性C. 韧性D. 硬度答案:D2. 根据材料力学的理论,下列哪个选项是正确的?A. 材料在弹性范围内,应力与应变成正比B. 材料在塑性变形后可以完全恢复原状C. 材料的屈服强度总是高于其抗拉强度D. 材料的硬度与弹性模量无关答案:A二、填空题1. 材料力学中,应力是指_______与_______的比值。
答案:单位面积上的压力;受力面积2. 在材料力学中,材料的弹性模量E与_______成正比,与_______成反比。
答案:杨氏模量;泊松比三、简答题1. 简述材料力学中材料的三种基本变形类型。
答案:材料力学中材料的三种基本变形类型包括拉伸、压缩和剪切。
2. 描述材料的弹性模量和屈服强度的区别。
答案:弹性模量是指材料在弹性范围内应力与应变的比值,反映了材料的刚性;屈服强度是指材料开始发生永久变形时的应力值,反映了材料的韧性。
四、计算题1. 已知一材料的弹性模量E=200 GPa,杨氏模量E=210 GPa,泊松比ν=0.3,试计算该材料的剪切模量G。
答案:G = E / (2(1+ν)) = 200 / (2(1+0.3)) = 200 / 2.6 ≈ 76.92 GPa2. 某材料的抗拉强度为σt=300 MPa,若该材料承受的应力为σ=200 MPa,试判断材料是否发生永久变形。
答案:由于σ < σt,材料不会发生永久变形。
五、论述题1. 论述材料力学在工程设计中的重要性。
答案:材料力学是工程设计中的基础学科,它提供了对材料在力作用下行为的深入理解。
通过材料力学的分析,工程师可以预测材料在各种载荷下的响应,设计出既安全又经济的结构。
此外,材料力学还有助于新材料的开发和现有材料性能的优化。
2. 讨论材料的疲劳寿命与其力学性能之间的关系。
答案:材料的疲劳寿命与其力学性能密切相关。
材料的疲劳寿命是指在循环载荷作用下材料能够承受的循环次数。
材料力学试题及答案

材料力学试题及答案一、选择题(每题5分,共25分)1. 下列哪个选项是材料力学的基本假设之一?A. 材料是各向同性的B. 材料是各向异性的C. 材料是均匀的D. 材料是线弹性的答案:A2. 在材料力学中,下列哪个公式表示杆件的正应力?A. σ = F/AB. τ = F/AC. σ = F/LD. τ = F/L答案:A3. 当材料受到轴向拉伸时,下列哪个选项是正确的?A. 拉伸变形越大,材料的强度越高B. 拉伸变形越小,材料的强度越高C. 拉伸变形与材料的强度无关D. 拉伸变形与材料的强度成正比答案:B4. 下列哪种材料在拉伸过程中容易发生断裂?A. 钢材B. 铸铁C. 铝合金D. 塑料答案:B5. 下列哪个选项表示材料的泊松比?A. μ = E/GB. μ = G/EC. μ = σ/εD. μ = ε/σ答案:C二、填空题(每题10分,共30分)6. 材料力学研究的是材料在______作用下的力学性能。
答案:外力7. 材料的强度分为______强度和______强度。
答案:屈服强度、断裂强度8. 材料在受到轴向拉伸时,横截面上的正应力公式为______。
答案:σ = F/A三、计算题(每题25分,共50分)9. 一根直径为10mm的圆钢杆,受到轴向拉伸力F=20kN 的作用,求杆件横截面上的正应力。
解:已知:d = 10mm,F = 20kNA = π(d/2)^2 = π(10/2)^2 = 78.5mm^2σ = F/A = 20kN / 78.5mm^2 = 255.8N/mm^2答案:杆件横截面上的正应力为255.8N/mm^2。
10. 一根长度为1m的杆件,受到轴向拉伸力F=10kN的作用,已知材料的弹性模量E=200GPa,泊松比μ=0.3,求杆件的伸长量。
解:已知:L = 1m,F = 10kN,E = 200GPa,μ = 0.3ε = F/(EA) = 10kN / (200GPa × π(10mm)^2) =0.025δ = εL = 0.025 × 1000mm = 25mm答案:杆件的伸长量为25mm。
材料力学作业参考解答
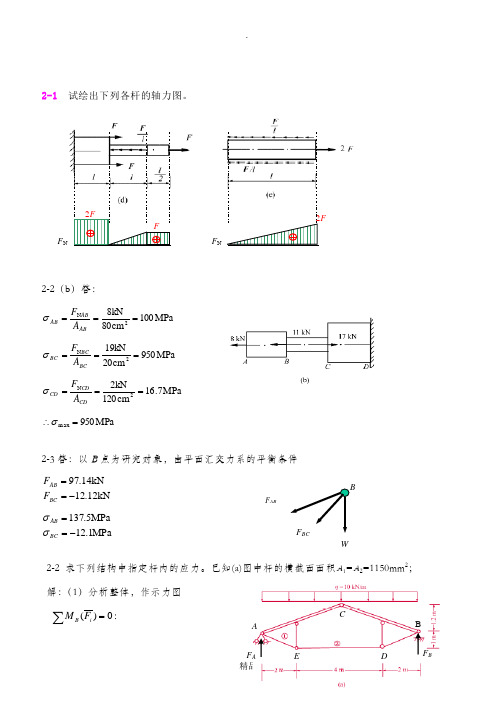
2-1 试绘出下列各杆的轴力图。
2-2(b )答:MPa 100cm 80kN82N ===AB AB AB A F σ MPa 950cm 209kN12N ===BC BC BC A F σ MPa 7.16cm120kN22N ===CD CD CD A F σ MPa 950max =∴σ2-3答:以B 点为研究对象,由平面汇交力系的平衡条件kN12.12kN 14.97-==BC AB F FMPa1.12MPa5.137-==BC AB σσ2-2 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:F2FF N2FF NA CB F ABF BCWE F N1F N3F N2β(c)041088=⨯⨯-⨯A F 40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=⨯+⨯-⨯q F F A N2(404402)36.36kN 2.2N F ⨯-⨯==3262236.361031.62MPa 115010N F A σ-⨯===⨯杆(3)分析铰E ,示力图见(c )∑=0ixF:0sin 12=-βN N F F22122140.65kN 2N N F F +=⨯=3161137.961035.3MPa 115010N F A σ-⨯===⨯杆2-3 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F -=+⨯⨯⨯=AB 段最大轴力在A 处6N 1212(0.5300.540)107812.0kNA F -=++⨯+⨯⨯⨯= CF AF CyF CxN2(b)ABC12.012.0F N (kN)3N 2612.010400MPa 30mm 3010BB F σ--⨯===⨯3N 2612.010300MPa 40mm 4010AA F σ--⨯===⨯杆件最大正应力为400MPa ,发生在B 截面。
材料力学课后答案

材料力学课后答案1. 弹性力学基础题。
题目,一根长为L的均匀横截面圆柱形杆,端部固定,另一端受力F,求受力端的应变。
解答,根据弹性力学的基本公式,应变ε=σ/E,其中σ为应力,E为弹性模量。
由于杆的横截面积为A,受力F导致的应力σ=F/A。
因此,受力端的应变ε=F/(AE)。
2. 弹性力学应用题。
题目,一根钢丝的长度为L,直径为d,受力F时产生的应力为σ,求其应变。
解答,首先计算钢丝的横截面积A=πd^2/4,然后根据应变ε=σ/E,其中E为钢的弹性模量,求得应变ε=σ/(E)。
3. 材料的破坏。
题目,一块材料在受力时产生的应力达到了其屈服强度,求此时的应变。
解答,当材料的应力达到屈服强度时,材料开始发生塑性变形,此时的应变无法简单地通过弹性力学公式来计算。
需要通过材料的本构关系来确定应变。
4. 弯曲应力与应变。
题目,一根横截面为矩形的梁,在受力时产生的最大应力为σ,求其最大应变。
解答,根据梁的弯曲应力公式σ=My/I,其中M为弯矩,y为梁的截面离中性轴的距离,I为梁的惯性矩。
最大应变发生在最大应力处,由应变ε=σ/E,可以求得最大应变。
5. 拉伸与压缩。
题目,一根长为L的杆在受拉力F时产生的应变为ε,求其长度变化量。
解答,根据胡克定律,拉伸或压缩材料的长度变化量ΔL=εL。
6. 应变能。
题目,一根长为L的弹簧,在受力F时产生的应变为ε,求其弹性势能。
解答,弹簧的弹性势能U=1/2kε^2,其中k为弹簧的弹性系数。
根据ε=F/(kL),代入可得弹性势能U=1/2F^2/(kL)。
7. 疲劳破坏。
题目,一根金属材料在受到循环载荷时,经过了n次循环后发生疲劳破坏,求其疲劳寿命。
解答,根据疲劳寿命公式N=K(σ_max)^(-1/α),其中N为疲劳寿命,K为材料常数,σ_max为循环载荷的最大应力,α为材料的疲劳指数。
代入循环载荷的应力值,可以求得疲劳寿命。
8. 蠕变。
题目,一根材料在高温下受到持续载荷时发生了蠕变,求其蠕变应变。
材料力学作业解答

材料力学作业解答1.弹簧的力学行为弹簧是一种具有弹性的材料,它可以在受力时发生弹性形变,并且能够恢复到原始形状。
弹簧的力学行为可以通过胡克定律来描述。
根据胡克定律,弹簧的形变与施加在它上面的力成正比,即F=k*x,其中F是施加在弹簧上的力,k是弹簧的弹性系数,x是弹簧的形变量。
2.弹簧的应变能和弹性势能当弹簧被拉伸或压缩时,它会储存一定量的应变能。
弹簧的应变能可以通过下式计算:U=(1/2)*k*x^2,其中U是弹簧储存的应变能,k是弹簧的弹性系数,x是弹簧的形变量。
3.伸长弹簧的应变能假设一个弹簧的弹性系数为k,它被拉伸或压缩x长度。
根据胡克定律,施加在弹簧上的力可以通过F = k * x计算得到。
通过积分力在形变路径上的关系,可以得到弹簧的应变能。
假设初始长度为L,拉伸后的长度为L+x,则弹簧的伸长应变能可以计算如下:U = ∫[0, L+x] F(x)dx = ∫[0, x] k * x dx = (1/2) k * x^24.剪切应力和剪切应变剪切应力是作用于物体上的横截面内的剪切力与该横截面上的面积之比。
剪切应变是物体在受到剪切应力时产生的形变。
剪切应力和剪切应变之间的关系可以通过剪切弹性模量来描述。
剪切弹性模量G可以通过下式计算:G=τ/γ,其中τ是剪切应力,γ是剪切应变。
5.弯曲应力和弯曲应变弯曲应力是作用于物体上的弯曲力与该物体的横截面想对距离之比。
弯曲应变是物体在受到弯曲应力时产生的形变。
弯曲应力和弯曲应变之间的关系可以通过弯曲弹性模量来描述。
弯曲弹性模量E可以通过下式计算:E=σ/ε,其中σ是弯曲应力,ε是弯曲应变。
6.斯特拉因准则斯特拉因准则描述了材料在达到破坏点之前的应力和应变行为。
根据斯特拉因准则,当材料达到其屈服点时,应力和应变之间的关系可以通过单一的线性方程来描述。
这个线性方程表明了在屈服点之前,应力与应变之间的比例关系。
7.杨氏模量和泊松比杨氏模量是一种描述材料刚度的量度,它可以表示应力与应变之间的比例关系。
(完整版)材料力学课后习题答案
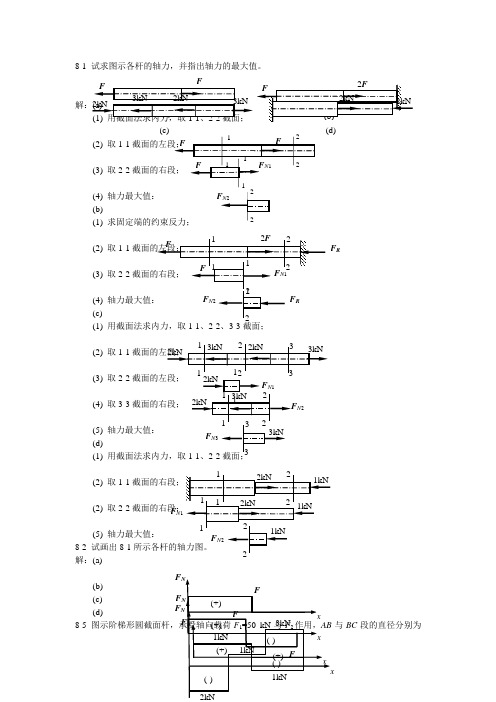
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
材料力学全部习题解答

弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解:1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解:1 建立平衡方程 由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得: FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算 联立方程1和方
程(2);得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于 塑5 性% 材料;
15
解:杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I( za) I( zR ) =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;,y轴不变; 图示截面对z,轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y
材料力学精选练习题及答案

材料力学精选练习题及答案
材料力学,是力学中的一个重要分支,它主要研究物质的力学
性质和形变行为。
在工程实践中,材料力学的知识和技能非常重要,不仅是理论基础,更是工程设计和制造中必不可少的一部分。
以下是材料力学的一些精选练习题及答案,供大家参考和学习。
1、弹性力学
题目:一个长为L,横截面积为A的钢杆,弹性模量为E,要
求它在受到一定的拉力F后产生的伸长量为δ,求钢杆所受的应力和应变。
解答:应力σ=F/A,应变ε=δ/L,弹性模量E=σ/ε,所以σ=F/A,ε=F/(AE),将δ带入ε可得σ=F(L/AE),ε=F/(AE)。
2、塑性力学
题目:在压缩试验中,一块铜板被加压后,其长度由原来的L
缩短至L',试求其应变。
解答:应变ε=(L-L')/L。
3、断裂力学
题目:一个半径为a的圆柱体被沿着一直径破裂,试求其破裂力F。
解答:破裂力F=πa^2σ_max。
4、疲劳力学
题目:在疲劳试验中,一个试件经过n个周期后发生失效,试求其循环应力幅值σ_a和平均应力σ_m。
解答:循环应力幅值σ_a和平均应力σ_m可根据试件的应力-应变曲线以及可能失效的总循环数和n计算得出。
5、复合材料力学
题目:一个由纤维和基材组成的复合材料,在受到一定的横向压力后,试求其纵向伸长量。
解答:通过复合材料的材料性质和几何体积参数可以计算出纵向伸长量。
以上是一些基本的材料力学练习题,希望对大家有所帮助。
在学习过程中,还需要不断积累和练习,才能真正掌握材料力学的知识和技能,为工程实践提供有力的支持和保障。
材料力学练习题与答案-全

材料力学练习题与答案-全1.当T三Tp时,剪切虎克定律及剪应力互等定理。
A、虎克定律成立,互等定理不成立B、虎克定律不成立,互等定理成立(正确答案)C、均不成立D、二者均成立2.木榫接头,当受F力作用时,接头的剪切面积和挤压面积分别是A、ab,lcB、cb,lbC、lb,cb(正确答案)D、lc,ab3.在下列四种材料中,()不可以应用各向同性假设。
A、铸钢B、玻璃C、松木(正确答案)D、铸铁4.一细长压杆当轴向压力P达到临界压力Pcr时受到微小干扰后发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形。
A、有所缓和B、完全消失(正确答案)C、保持不变D、继续增大;5.矩形截面偏心受压杆件发生变形。
A、轴向压缩、平面弯曲B、轴向压缩、平面弯曲、扭转C、轴向压缩、斜弯曲(正确答案)D、轴向压缩、斜弯曲、扭转6.当杆件处于弯扭组合变形时,对于横截面的中性轴有这样的结论,正确的是:A、一定存在(正确答案)B、不一定存在C、一定不存在7.梁在某一段内作用有向下的分布载荷时,在该段内它的弯矩图为。
A、上凸曲线;(正确答案)B、下凸曲线;C、带有拐点的曲线;D、斜直线8.图示结构中,AB为钢材,BC为铝,在P力作用下()A、AB段轴力大B、BC段轴力大C、轴力一样大(正确答案)D、无法判断9.圆截面的悬臂梁在自由端受集中力的作用,若梁的长度增大一倍,其他条件不变,最大挠度是原来的倍。
图片2.pngA、2B、16C、8(正确答案)D、410.托架由横梁与杆组成。
若将杆由位于梁的下方改为位于梁的上方,其他条件不变,则此托架的承载力。
A、提高(正确答案)B、降低C、不变D、不确定11.单位长度的扭转角e与()无关A、杆的长度(正确答案)B、扭矩C、材料性质D、截面几何性质12.矩形截面拉弯组合变形时,对于横截面的中性轴有以下的结论。
正确的是:。
A、过形心B、过形心且与ZC轴有一夹角;C、不过形心,与ZC轴平行;(正确答案)D、不过形心,与ZC轴有一夹角。
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料力学习题大全及答案
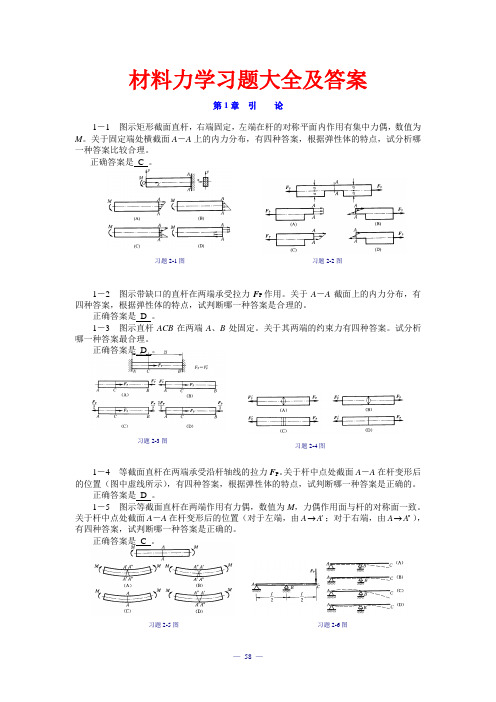
习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A )d d Q x F d M(B )d d Q x F (C )d d Q x F (D )d d Q xF 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
(参考资料)材料力学习题解答(拉伸、压缩与剪切)

2
1.5m
10kN
D
C
B
A
1m
1m
1.5m
1
1.5m
解:(1) 以整体为研究对象,易见 A 处的水平约束反力为零; (2) 以 AB 为研究对象(B 处不带销钉)
XBB
B
A
由平衡方程知 (3) 以杆 BD 为研究对象
D
YBB
RA
X B = YB = RA = 0
N2
10kN
C
B
由平衡方程求得 (4) 杆内的应力为
1m
1m
N1
∑ mC = 0 N1 ×1 − 10 ×1 = 0
N1 = 10KN
∑Y = 0 N 2 − N1 − 10 = 0
N 2 = 20KN
3
σ1
=
N1 A1
=
π
10 ×103 × 0.012 /
4
= 127MPa
σ2
=
N2 A2
=
π
20 ×103 × 0.022 / 4
=
63.7 MPa
2.7. 冷镦机的曲柄滑块机构如图所示。镦压工件时连杆接近水平位置,承受的镦压力 P=1100kN 。连杆的截面为矩形,高与宽之比为 h/b=1.4。材料为 45 钢,许用应力为 [σ]=58MPa,试确定截面尺寸 h 和 b。
N3 = 3P
4P 3P
(+)
x
2.3. 作用图示零件上的拉力 P=38kN,试问零件内最大拉应力发生于哪个横截面上?并求其 值。
20
P
φ22
1
材料力学1 (答案)

材料力学请在以下五组题目中任选一组作答,满分100分。
第一组:计算题(每小题25分,共100分)1. 梁的受力情况如下图,材料的a。
若截面为圆柱形,试设计此圆截面直径。
10kNq/m2. 求图示单元体的:(1)图示斜截面上的应力;(2)主方向和主应力,画出主单元体;(3)主切应力作用平面的位置及该平面上的正应力,并画出该单元体。
60x解:(1)、斜截面上的正应力和切应力:MPa MPa o 95.34,5.6403030=-=--τσ(2)、主方向及主应力:最大主应力在第一象限中,对应的角度为0067.70=α,则主应力为:MPa MPa 0.71),(0.12131-==σσ(3)、主切应力作用面的法线方向:0/20/167.115,67.25==αα 主切应力为:/2/104.96ααττ-=-=MPa此两截面上的正应力为:)(0.25/2/1MPa ==αασσ,主单元体如图3-2所示。
x图3-10.MPa0.25图3-23. 图中所示传动轴的转速n=400rpm,主动轮2输入功率P2=60kW,从动轮1,3,4和5的输出功率分别为P1=18kW,P3=12kW,P4=22kW,P5=8kW。
试绘制该轴的扭矩图。
4. 用积分法求图所示梁的挠曲线方程和转角方程,并求最大挠度和转角。
各梁EI均为常数。
第二组:计算题(每小题25分,共100分)1. 简支梁受力如图所示。
采用普通热轧工字型钢,且已知= 160MPa。
试确定工字型钢型号,并按最大切应力准则对梁的强度作全面校核。
(已知选工字钢No.32a:W = 692.2 cm3,Iz = 11075.5 cm4)解:1.FRA = FRB= 180kN(↑)kN·mkN·mkNm3由题设条件知:W = 692.2 cm2,Iz = 11075.5 cm4cmE截面:MPaMPa2. A+、B-截面:MPaMPa3.C-、D+截面:MPaMPa∴选No.32a工字钢安全。
材料力学相关习题答案

材料力学相关习题答案材料力学相关习题答案材料力学是工程力学的一个重要分支,研究材料在受力过程中的力学性质和变形行为。
在学习材料力学的过程中,习题是不可或缺的一部分。
通过解答习题,我们可以更好地理解和应用所学的理论知识。
在本文中,我将为大家提供几道材料力学相关习题的答案,希望能对大家的学习有所帮助。
1. 一根长度为L、截面积为A的均匀杆材,受到一个沿着杆轴方向的拉力F。
求杆材的应力和应变。
解答:根据杆材的应力定义,应力等于受力F与截面积A的比值。
即σ = F/A。
应变定义为杆材的变形量与原始长度的比值。
即ε = ΔL/L。
2. 一根长度为L、截面积为A的杆材,其杨氏模量为E。
如果在杆材上施加一个拉力F,使其产生弹性变形,求变形后的杆材长度。
解答:根据胡克定律,弹性变形下的应力与应变之间存在线性关系。
即σ = Eε。
应变可以表示为杆材长度的变化量与原始长度的比值。
即ε = ΔL/L。
根据上述两个公式,我们可以得到F/A = EΔL/L。
由此可以解得变形后的杆材长度为L + ΔL = FL/(AE)。
3. 一个圆形截面的钢材柱,直径为D,长度为L。
当柱受到一个压力P时,求杆材的应力和应变。
解答:圆形截面的面积可以表示为A = πD^2/4。
根据杆材的应力定义,应力等于受力P与截面积A的比值。
即σ = P/A。
应变可以表示为杆材长度的变化量与原始长度的比值。
即ε = ΔL/L。
由于该杆材受到压力,所以应变为负值。
4. 一根长度为L、截面积为A的杆材,其杨氏模量为E。
如果在杆材上施加一个压力P,使其产生弹性变形,求变形后的杆材长度。
解答:根据胡克定律,弹性变形下的应力与应变之间存在线性关系。
即σ = Eε。
应变可以表示为杆材长度的变化量与原始长度的比值。
即ε = ΔL/L。
根据上述两个公式,我们可以得到P/A = EΔL/L。
由此可以解得变形后的杆材长度为L + ΔL = -PL/(AE)。
通过以上几道习题的解答,我们可以看到材料力学中的一些基本概念和公式的应用。
材料力学的试题及答案

材料力学的试题及答案一、选择题(每题2分,共20分)1. 材料力学研究的对象是什么?A. 材料的化学性质B. 材料的力学性质C. 材料的热学性质D. 材料的电学性质2. 材料力学中,下列哪一项不是基本力学性质?A. 弹性B. 韧性C. 硬度D. 塑性3. 材料力学中,应力的定义是什么?A. 力与面积的比值B. 力与体积的比值C. 力与长度的比值D. 面积与力的比值4. 材料力学中,下列哪一项不是材料的基本变形形式?A. 拉伸B. 压缩C. 扭转D. 膨胀5. 材料力学中,弹性模量表示什么?A. 材料的硬度B. 材料的韧性C. 材料的弹性D. 材料的塑性二、简答题(每题10分,共30分)6. 简述材料力学中材料的三种基本力学性质。
7. 解释材料力学中的应力-应变曲线,并说明其各阶段的意义。
8. 什么是材料的屈服强度,它在工程设计中的重要性是什么?三、计算题(每题25分,共50分)9. 一根直径为20mm,长度为200mm的圆杆,在两端受到100kN的拉伸力。
如果材料的弹性模量为200GPa,求圆杆的伸长量。
10. 一个直径为50mm,长为100mm的空心圆筒,内径为40mm,受到一个扭矩为500N·m。
如果材料的剪切模量为80GPa,求圆筒的最大剪切应力。
答案一、选择题1. B. 材料的力学性质2. C. 硬度3. A. 力与面积的比值4. D. 膨胀5. C. 材料的弹性二、简答题6. 材料力学中材料的三种基本力学性质包括弹性、塑性和韧性。
弹性是指材料在受到外力作用后能恢复原状的能力;塑性是指材料在达到一定应力后,即使撤去外力也不会完全恢复原状的性质;韧性是指材料在断裂前能吸收和分散能量的能力。
7. 应力-应变曲线是描述材料在受力过程中应力与应变之间关系的曲线。
它通常包括弹性阶段、屈服阶段、强化阶段和颈缩阶段。
弹性阶段表示材料在受力后能够完全恢复原状;屈服阶段是材料开始产生永久变形的点;强化阶段是材料在屈服后继续承受更大的应力而不断裂;颈缩阶段是材料接近断裂前发生的局部变细现象。
(完整版)材料力学习题册答案..

练习1 绪论及基本概念1-1 是非题(1)材料力学是研究构件承载能力的一门学科。
( 是 )(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
(是 )(3)构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
( 是 ) (4)应力是内力分布集度。
(是 )(5)材料力学主要研究构件弹性范围内的小变形问题。
(是 ) (6)若物体产生位移,则必定同时产生变形。
(非 ) (7)各向同性假设认为,材料沿各个方向具有相同的变形。
(F )(8)均匀性假设认为,材料内部各点的力学性质是相同的。
(是)(9)根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(非) (10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(非 )1-2 填空题(1)根据材料的主要性质对材料作如下三个基本假设:连续性假设 、均匀性假设 、 各向同性假设 。
(2)工程中的 强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。
(3)保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性 三个方面。
(4)图示构件中,杆1发生 拉伸 变形,杆2发生 压缩 变形, 杆3发生 弯曲 变形。
(5)认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设 。
根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6)图示结构中,杆1发生 弯曲 变形,构件2发生 剪切 变形,杆件3发生 弯曲与轴向压缩组合。
变形。
(7)解除外力后,能完全消失的变形称为 弹性变形 ,不能消失而残余的的那部分变形称为 塑性变形 。
(8)根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。
1-3 选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1 试绘出下列各杆的轴力图。
2-2(b )答:MPa 100cm 80kN82N ===AB AB AB A F σ MPa 950cm 209kN12N ===BC BC BC A F σ MPa 7.16cm120kN22N ===CD CD CD A F σ MPa 950max =∴σ2-3答:以B 点为研究对象,由平面汇交力系的平衡条件kN12.12kN 14.97-==BC AB F FMPa1.12MPa5.137-==BC AB σσ2-2 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:F2FF N2FF NA ECDB F AF BF ABF BCWE F N1F N3F N2β(c)041088=⨯⨯-⨯A F 40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=⨯+⨯-⨯q F F A N2(404402)36.36kN 2.2N F ⨯-⨯==3262236.361031.62MPa 115010N F A σ-⨯===⨯杆(3)分析铰E ,示力图见(c )∑=0ixF:0sin 12=-βN N F F22122140.65kN 2N N F F +=⨯=3161137.961035.3MPa 115010N F A σ-⨯===⨯杆2-3 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F -=+⨯⨯⨯=AB 段最大轴力在A 处6N 1212(0.5300.540)107812.0kN A F -=++⨯+⨯⨯⨯=CF AqF CyF CxF N2(b)ABC12.012.0F N (kN)3N 2612.010400MPa 30mm 3010BB F σ--⨯===⨯3N 2612.010300MPa 40mm 4010AA F σ--⨯===⨯杆件最大正应力为400MPa ,发生在B 截面。
2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比ν。
解:加载至58.4kN 时,杆件横截面中心正应力为3N 2458.410330.48MPa 1.5104F A σπ-⨯==⨯⨯= 线应变:333Δ0.910 4.51020010l l ε--⨯===⨯⨯弹性模量:33330.48MPa73.410MPa 4.510E σε-===⨯⨯侧向线应变:310467.115022.0-⨯==,ε 泊松比:,0.326εμε==2-6图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm 2;下段为铝制,长300mm ,截面尺寸为200×200mm 2。
当柱顶受F 力作用时,柱子总长度减少了0.4mm ,试求F 值。
已知E 钢=200GPa ,E 铝=70GPa 。
解:柱中的轴力都为F ,总的变形(缩短)为:120.20.3Δg l F Fl E A E A =+ 12399Δ0.20.30.4100.20.3200100.10.170100.20.21931.0kNg l lF E A E A -=⎡⎤+⎢⎥⎢⎥⎣⎦⨯=⎡⎤+⎢⎥⨯⨯⨯⨯⨯⨯⎣⎦=2-7 图示等直杆AC ,材料的容重为ρg ,弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
解: AB 段内轴力 N1F F gAx ρ=-- BC 段内轴力 N22F F gAx ρ=--B 点位移为杆BC 的伸长量: 22(2)d 2 1.5lB lF gAx x Fl gAl EA EAρρ∆-++==-⎰2-8 图示结构中,AB 可视为刚性杆,AD 为钢杆,面积A 1=500mm 2,弹性模量E 1=200GPa ;CG 为铜杆,面积A 2=1500mm 2,弹性模量E 2=100GPa ;BE 为木杆,面积A 3=3000mm 2,弹性模量E 3=10GPa 。
当G 点处作用有F =60kN 时,求该点的竖直位移ΔG 。
解:(1)求①、②杆轴力 由平衡方程可以求出:N1N3N2240kN320kN 360kNFF F F F F =-=-=-=-==(2)求杆的变形34N11961140101Δ410m 2001050010AD F l l E A ---⨯⨯===-⨯⨯⨯⨯(压缩) 34N22962260100.5Δ210m 10010150010CG F l l E A --⨯⨯===⨯⨯⨯⨯(拉伸) 36N33963320101Δ 6.6710m 1010300010BE F l l E A ---⨯⨯===-⨯⨯⨯⨯(压缩) (3)由几何关系:421321ΔΔΔ 6.8910m 33G l l l ∆-=-⨯-=(下降) 2-9答:任一截面上轴力为F ,由212d d b l x -= 22)2(4)(b d x A +=π得面积为222122])([4)2(4)(lld x d d b d x A +-=+=ππ伸长量为⎰⎰+-==∆l ll d x d d E xFl x EA x F l 0222120])[(d 4)(d π 214d d E Flπ=2-11 图示一挡水墙示意图,其中AB 杆支承着挡水墙,各部分尺寸均已示于图中。
若AB 杆为圆截面,材料为松木,其容许应力[σ]=11MPa ,试求AB 杆所需的直径。
解:(1)求水压力的合力:21240kN P h b γ==(2)作示力图(a )由平衡方程求轴力2N 3N ()0:0.60.4011.11kNOi MF F P F =⨯⨯-⨯==∑ (3)由强度条件,设计截面尺寸:F NP 3m4m2mxb bN 3632[]411.1110/(1110) 1.28610m 3.58cm F A d d σσπ-=≤≥⨯⨯⋅⨯=⨯≥ 2-10答:对水塔∑=0AM ,021********=⨯+⨯+⨯FkN F 2503-=∑=0ixF ,02/21002=⨯+FkN F 4.14121003-=-=∑=0iyF,04002/2321=++⨯+F F FkN F 501-=][/11c N A F σ≤,21500mm A ≥][/22c N A F σ≤,221414mm A ≥ ][/33c N A F σ≤,232500mm A ≥2-12 图示结构中的CD 杆为刚性杆,AB 杆为钢杆,直径d =30mm ,容许应力[σ]=160MPa ,弹性模量E =2.0×105MPa 。
试求结构的容许荷载F 。
解:(1)求AB 杆的轴力F N∑=0)(i CF M:N N sin 302 2.502.5F F F F⨯-⨯==(2)由强度条件求[]F[][][]N 462.591016010445.2kN2.5F F A A F σσσπ-=≤⇒≤⨯⨯⨯⨯==F AxF AyF N1FF N2△ϕl 2△l 12-14 图示AB 为刚性杆,长为3a 。
A 端铰接于墙壁上,在C 、B 两处分别用同材料、同面积的①、②两杆拉住,使AB 杆保持水平。
在D 点作用荷载F 后,求两杆内产生的应力。
设弹性模量为E ,横截面面积为A 。
解:1.本题为超静定问题,见图(a),设AB 杆产生角位移ϕ∆,则 ϕϕ∆=∆∆=∆a l a l 3,21, 2.由Hooke 定律:ϕϕ∆=∆=∆=∆=EA l aEA F EA l aEAF N N 5.1222113.由平衡方程:∑=0)(i AF M:EAFaF aEA aEA aF aF aF N N 5.5225.402321=∆=∆+∆=-+ϕϕϕ 4.由Hooke 定律:FF EA F F F EA F N N 5454.05.525.15.13636.05.5221=⨯=∆===∆=ϕϕσ①A FAF N 3636.01== σ②AFAF N 5454.02==2-15 两端固定,长度为l ,横截面面积为A ,弹性模量为E 的正方形杆,在B 、C 截面处各受一F 力作用。
求B 、C 截面间的相对位移。
F F F NAABCD(a)F NA F F N (b)解: 1.本题为超静定问题解除A 截面处约束,代之约束力NA F ,见图(a ) A 截面的位移为杆件的总变形量EA Fl EA l F EA l F F EA l F F EA l F l l l A NA NA NA NA CDBC AB -=-+-+=∆+∆+∆=∆3)2(3)(3 2.由约束条件 0=∆A 得:FF EA FlEA l F NA NA ==-03.见图(b),求BC 段轴力 由平衡条件可知: 0=N F所以B,C 截面相对位移为 03==∆EAl F N BC-1-3-1 试作下列各杆的扭矩图。
3-2 一直径d =60mm 的圆杆,其两端受外力偶矩T =2kN ·m 的作用而发生扭转。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
(G =80GPa )。
解:横截面上切应力大小沿半径线性分布,方向垂直半径33P 213200047.2MPa3.140.06/160.02/331.4MPaT W ττττ===⨯===4max 3/ 5.910rad G γτ-==⨯3-3 从直径为300mm 的实心轴中镗出一个直径为150mm 的通孔而成为空心轴,问最大切应力增大了百分之几?解:实心轴max13P116x xM M W d τπ==空心轴max 234P216(10.5)x xM M W d τπ==-最大切应力增大了4343max 2max14max1316160.5(10.5)100%100%100% 6.67%1610.5x xxM M d d M dττππτπ---⨯=⨯=⨯=-3τ1τ10010 Mx(N·m) 21 Mx(kN·m)5 3-2-3-4 一端固定、一端自由的钢圆轴,其几何尺寸及受力情况如图所示(空心处有两段,内径10mm ,外径30mm ),试求: (1)轴的最大切应力。
(2)两端截面的相对扭转角(G =80GPa)。
解:(1)作扭矩图, AB 段中最大切应力 max 36P6035.56MPa 31016x M W πτπ-===⨯⨯CD 段中最大切应力 ()()max 946P 644031101616401024MPa 2713x M W πτπα---==⨯⨯-⨯⨯=⨯=-所以轴中,MPa 56.35max =τ (2)相对扭转角分四段计算P1P1P2P2400.2300.1300.1600.15ΔΔΔΔΔDC CE EB BA GI GI GI GI ππππϕϕϕϕϕ⨯⨯⨯⨯=+++=+++P1P2P1P211121112GI GI G I I πππ⎛⎫=+=+ ⎪⎝⎭()94844811120.011426rad 118010310133103232πππ---⎛⎫⎪=+= ⎪⨯⨯⨯-⨯⨯ ⎪⎝⎭3-2 一变截面实心圆轴,受图示外力偶矩作用,求轴的最大切应力。
