简单复合函数的导数
5.2.3简单复合函数的导数

= − =
可以发现,
′ = = ∙ = ′ ∙ ′
合作探究
复合函数的求导法则
一般地,对于由函数 y=f(u)和u=g(x)复合而成的函数 = (())
5.2.3简单复合函数的导数
人教A版(2019)
选择性必修第二册
新知导入
思考
如何求函数 = ( − ) 的导数呢 ?
新知讲解
函数 = ( − ) 不是由基本初等函数通过加、减、乘、
除运算得到的,所以无法用现有的方法求它的导数.
下面,先分析这个函数的结构特点.
若设 = − ( >
(2)函数 = + 的中间变量为 = 2 + 1 . 则函数的导数为,
′ = ′ ∙ ′ = ′ ∙ + ′ = = +
课堂练习
1 (3) = (− + )
(5) =
(4) = ( − )
(6) =
−
),则
=
从而 = ( − )可以看成是由 = 和 = − ( >
)
经过“复合”得到的,即 y 可以通过中间变量 u 表示为自变量 x
的函数.
新知讲解
复合函数
对于两个函数 y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数
合函数的求导法则,有
′
=
′
∙
′
′
=
∙ + ′ = × = +
(2)函数 = −.+ 可以看作函数 = 和 = −. + 的复合函数.根据复合
22人教版高中数学新教材选择性必修第二册--5.2.3 简单复合函数的导数

成,所以 ′ ()
=
′
⋅
′
1
= ⋅2=
2
,得 ′ (1)
2+1
=
2
.
3
探究点二 复合函数与导数四则运算法则的综合
例 求下列函数的导数:
(1) = sin 2 + cos 2 ;
[答案] 解法一(复合函数求导):
对于函数 = sin 2 ,令 = 2 ,则 = sin ,
所以 ′ = ′ ⋅ ′ = cos ⋅ 2 = 2 cos 2 .
对于函数 = cos 2 ,令 = 2 ,则 = cos ,
所以 ′ = ′ ⋅ ′ = −sin ⋅ 2 = −2 sin 2 .
所以函数 = sin 2 + cos 2 的导数为 ′ = 2 cos 2 − 2 sin 2 = 2 2sin(2 +
由题意,得
3
2
+ =
3
2
,故 = 0 .
综上所述, = 0, = −1 .
1. 函数 = (2021 − 3)3 的导数 ′ = (
D
)
A. 3(2021 − 3)2
B. −9
C. 9(2021 − 3)2
D. −9(2021 − 3)2
2. 下列求导数结果正确的是(
3π
).
4
解法二(利用导数的四则运算法则):
∵ = sin 2 + cos 2 = 2 sin cos + (cos + sin ) ⋅ (cos − sin ) ,
∴ ′ = 2 cos 2 − 2 sin2 + (cos − sin )2 − (sin + cos )2
数学选择性必修二 第五章 5.2.3 简单复合函数的导数

5.2.3简单复合函数的导数学习目标 1.进一步运用导数公式和导数运算法则求函数的导数.2.了解复合函数的概念,掌握复合函数的求导法则.知识点复合函数的导数1.复合函数的概念一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).思考函数y=log2(x+1)是由哪些函数复合而成的?答案函数y=log2(x+1)是由y=log2u及u=x+1两个函数复合而成的.2.复合函数的求导法则一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数与函数y=f(u),u=g(x)的导数间的关系为y′x=y′u·u′x,即y对x的导数等于y对u的导数与u对x的导数的乘积.1.y=cos 3x由函数y=cos u,u=3x复合而成.(√)2.函数f(x)=sin(2x)的导数为f′(x)=cos 2x.(×)3.函数f(x)=e2x-1的导数为f′(x)=2e2x-1.(√)一、求复合函数的导数例1求下列函数的导数:(1)y=1(1-3x)4;(2)y=cos(x2);(3)y=log2(2x+1);(4)y=e3x+2.解(1)令u=1-3x,则y=1u4=u-4,所以y′u=-4u-5,u′x=-3.所以y′x=y′u·u′x=12u-5=12 (1-3x)5.(2)令u =x 2,则y =cos u ,所以y ′x =y ′u ·u ′x =-sin u ·2x =-2x sin(x 2). (3)设y =log 2u ,u =2x +1,则y x ′=y u ′u x ′=2u ln 2=2(2x +1)ln 2.(4)设y =e u ,u =3x +2, 则y x ′=(e u )′·(3x +2)′ =3e u =3e 3x +2.反思感悟 (1)求复合函数的导数的步骤(2)求复合函数的导数的注意点:①分解的函数通常为基本初等函数;②求导时分清是对哪个变量求导;③计算结果尽量简洁. 跟踪训练1 求下列函数的导数: (1)y =11-2x; (2)y =5log 2(1-x ); (3)y =sin ⎝⎛⎭⎫2x +π3. 解 (1)()12=12,y x --设y =12u -,u =1-2x ,则y ′x =()1212u 'x '⎛⎫- ⎪⎝⎭-()32212u -⎛⎫-⋅ ⎪⎝⎭=- ()32=12x .--(2)函数y =5log 2(1-x )可看作函数y =5log 2u 和u =1-x 的复合函数, 所以y ′x =y ′u ·u ′x =5(log 2u )′·(1-x )′ =-5u ln 2=5(x -1)ln 2.(3) 设y =sin u ,u =2x +π3,则y x ′=(sin u )′⎝⎛⎭⎫2x +π3′=cos u ·2=2cos ⎝⎛⎭⎫2x +π3. 二、复合函数与导数的运算法则的综合应用 例2 求下列函数的导数: (1)y =ln 3xe x ;(2)y =x 1+x 2;(3)y =x cos ⎝⎛⎭⎫2x +π2sin ⎝⎛⎭⎫2x +π2. 解 (1)∵(ln 3x )′=13x ×(3x )′=1x ,∴y ′=(ln 3x )′e x -(ln 3x )(e x )′(e x )2=1x -ln 3x e x =1-x ln 3x x e x.(2)y ′=(x 1+x 2)′=x ′1+x 2+x (1+x 2)′ =1+x 2+x 21+x 2=(1+2x 2)1+x 21+x 2.(3)∵y =x cos ⎝⎛⎭⎫2x +π2sin ⎝⎛⎭⎫2x +π2 =x (-sin 2x )cos 2x =-12x sin 4x ,∴y ′=⎝⎛⎭⎫-12x sin 4x ′=-12sin 4x -x2cos 4x ·4 =-12sin 4x -2x cos 4x .反思感悟 (1)在对函数求导时,应仔细观察及分析函数的结构特征,紧扣求导法则,联系学过的求导公式,对不易用求导法则求导的函数,可适当地进行等价变形,以达到化异求同、化繁为简的目的.(2)复合函数的求导熟练后,中间步骤可以省略,即不必再写出函数的复合过程,直接运用公式,从外层开始由外及内逐层求导. 跟踪训练2 求下列函数的导数: (1)y =sin 2x3;(2)y =sin 3x +sin x 3;(3)y =x ln(1+x ).解 (1)方法一 ∵y =1-cos 23x2,∴y ′=⎝ ⎛⎭⎪⎫12-cos 23x 2′=13sin 23x . 方法二 y ′=2sin x 3cos x 3·13=23sin x 3cos x3 =13sin 23x . (2)y ′=(sin 3x +sin x 3)′ =(sin 3x )′+(sin x 3)′ =3sin 2x cos x +cos x 3·3x 2 =3sin 2x cos x +3x 2cos x 3.(3)y ′=x ′ln(1+x )+x [ln(1+x )]′ =ln(1+x )+x 1+x.三、与切线有关的综合问题例3 (1)曲线y =ln(2x -1)上的点到直线2x -y +3=0的最短距离是( ) A. 5 B .2 5 C .3 5 D .0 答案 A解析 设曲线y =ln(2x -1)在点(x 0,y 0)处的切线与直线2x -y +3=0平行. ∵y ′=22x -1,∴0=|x x y'=22x 0-1=2,解得x 0=1,∴y 0=ln(2-1)=0,即切点坐标为(1,0).∴切点(1,0)到直线2x -y +3=0的距离为d =|2-0+3|4+1=5,即曲线y =ln(2x -1)上的点到直线2x -y +3=0的最短距离是 5.(2)设f (x )=ln(x +1)+x +1+ax +b (a ,b ∈R ,a ,b 为常数),曲线y =f (x )与直线y =32x 在(0,0)点相切.求a ,b 的值. 解 由曲线y =f (x )过(0,0)点,可得ln 1+1+b =0,故b =-1. 由f (x )=ln(x +1)+x +1+ax +b , 得f ′(x )=1x +1+12x +1+a ,则f ′(0)=1+12+a =32+a ,即为曲线y =f (x )在点(0,0)处的切线的斜率. 由题意,得32+a =32,故a =0.反思感悟 (1)求切线的关键要素为切点,若切点已知便直接使用,切点未知则需先设再求.两直线平行与垂直关系与直线的斜率密切相关,进而成为解出切点横坐标的关键条件. (2)在考虑函数问题时首先要找到函数的定义域.在解出自变量的值或范围时也要验证其是否在定义域内.跟踪训练3 (1)已知函数f (x )=k +ln xe x(k 为常数,e =2.718 28…是自然对数的底数),曲线y =f (x )在点(1,f (1))处的切线与x 轴平行,则k 的值为 . 答案 1解析 由f (x )=ln x +ke x,得f ′(x )=1-kx -x ln xx e x,x ∈(0,+∞).由于曲线y =f (x )在点(1,f (1))处的切线与x 轴平行, 所以f ′(1)=0,因此k =1.(2)设曲线y =e ax 在点(0,1)处的切线与直线x +2y +1=0垂直,则a = .该切线与坐标轴围成的面积为 . 答案 2 14解析 令y =f (x ),则曲线y =e ax 在点(0,1)处的切线的斜率为f ′(0), 又切线与直线x +2y +1=0垂直,所以f ′(0)=2. 因为f (x )=e ax ,所以f ′(x )=(e ax )′=e ax ·(ax )′=a e ax , 所以f ′(0)=a e 0=a ,故a =2.由题意可知,切线方程为y -1=2x ,即2x -y +1=0. 令x =0得y =1;令y =0得x =-12.∴S =12×12×1=14.1.(多选)函数y=(x2-1)n的复合过程正确的是() A.y=u n,u=x2-1 B.y=(u-1)n,u=x2 C.y=t n,t=(x2-1)n D. t=x2-1, y=t n答案AD2.函数y=(2 020-8x)3的导数y′等于()A.3(2 020-8x)2B.-24xC.-24(2 020-8x)2D.24(2 020-8x)2答案C解析y′=3(2 020-8x)2×(2 020-8x)′=3(2 020-8x)2×(-8)=-24(2 020-8x)2.3.函数y=x2cos 2x的导数为()A.y′=2x cos 2x-x2sin 2xB.y′=2x cos 2x-2x2sin 2xC.y′=x2cos 2x-2x sin 2xD.y′=2x cos 2x+2x2sin 2x答案B解析y′=(x2)′cos 2x+x2(cos 2x)′=2x cos 2x+x2(-sin 2x)·(2x)′=2x cos 2x-2x2sin 2x.4.已知f(x)=ln(3x-1),则f′(1)=.答案3 2解析∵f′(x)=33x-1,∴f′(1)=33-1=32.5.曲线y=ln(2-x)在点(1,0)处的切线方程为.答案x+y-1=0解析∵y′=-12-x=1x-2,∴y′|x=1=11-2=-1,即切线的斜率是k=-1,又切点坐标为(1,0).∴y=ln(2-x)在点(1,0)处的切线方程为y=-(x-1),即x+y-1=0.1.知识清单: (1)复合函数的概念. (2)复合函数的求导法则. 2.方法归纳:转化法.3.常见误区:求复合函数的导数时不能正确分解函数;求导时不能分清是对哪个变量求导;计算结果复杂化.1.(多选)下列函数是复合函数的是( ) A .y =-x 3-1x +1B .y =cos ⎝⎛⎭⎫x +π4C .y =1ln xD .y =(2x +3)4答案 BCD解析 A 不是复合函数,B ,C ,D 均是复合函数, 其中B 由y =cos u ,u =x +π4复合而成;C 由y =1u ,u =ln x 复合而成;D 由y =u 4,u =2x +3复合而成. 2.函数y =x ln(2x +5)的导数为( ) A .ln(2x +5)-x2x +5B .ln(2x +5)+2x2x +5C .2x ln(2x +5) D.x 2x +5答案 B解析 ∵y =x ln(2x +5), ∴y ′=ln(2x +5)+2x2x +5.3.函数y =x 3e cos x 的导数为( ) A .y ′=3x 2e cos x +x 3e cos x B .y ′=3x 2e cos x -x 3e cos x sin x C .y ′=3x 2e cos x -x 3e sin x D .y ′=3x 2e cos x +x 3e cos x sin x答案 B解析 y ′=(x 3)′e cos x +x 3(e cos x )′=3x 2e cos x +x 3e cos x ·(cos x )′=3x 2e cos x -x 3e cos x sin x . 4.曲线y =x e x-1在点(1,1)处切线的斜率等于( )A .2eB .eC .2D .1 答案 C解析 ∵y =x e x -1,∴y ′=e x -1+x e x -1, ∴k =y ′|x =1=e 0+e 0=2,故选C.5.已知直线y =x +1与曲线y =ln(x +a )相切,则a 的值为( ) A .1 B .2 C .-1 D .-2 答案 B解析 设切点坐标是(x 0,x 0+1), 依题意有⎩⎪⎨⎪⎧1x 0+a =1,x 0+1=ln (x 0+a ),由此得x 0+1=0,x 0=-1,a =2.6.函数y =sin 2x cos 3x 的导数是 . 答案 y ′=2cos 2x cos 3x -3sin 2x sin 3x 解析 ∵y =sin 2x cos 3x ,∴y ′=(sin 2x )′cos 3x +sin 2x (cos 3x )′=2cos 2x cos 3x -3sin 2x sin 3x .7.已知函数f (x )的导函数为f ′(x ),若f (x )=f ′⎝⎛⎭⎫π9sin 3x +cos 3x ,则f ′⎝⎛⎭⎫π9= . 答案 33解析 ∵f (x )=f ′⎝⎛⎭⎫π9sin 3x +cos 3x , ∴f ′(x )=f ′⎝⎛⎭⎫π9·3cos 3x -3sin 3x , 令x =π9可得f ′⎝⎛⎭⎫π9=f ′⎝⎛⎭⎫π9×3cos π3-3sin π3 =32 f ′⎝⎛⎭⎫π9-3×32, 解得f ′⎝⎛⎭⎫π9=3 3.8.点P 是f (x )=(x +1)2上任意一点,则点P 到直线y =x -1的最短距离是 ,此时点P 的坐标为 . 答案728⎝⎛⎭⎫-12,14 解析 与直线y =x -1平行的f (x )=(x +1)2的切线的切点到直线y =x -1的距离最短.设切点为(x 0,y 0),则f ′(x 0)=2(x 0+1)=1,∴x 0=-12,y 0=14.即P ⎝⎛⎭⎫-12,14到直线y =x -1的距离最短. ∴d =⎪⎪⎪⎪-12-14-1(-1)2+12=728.9.求下列函数的导数: (1)y =ln(e x +x 2); (2)y =102x +3; (3)y =sin 4x +cos 4x .解 (1)令u =e x +x 2,则y =ln u .∴y ′x =y ′u ·u ′x =1u ·(e x +x 2)′=1e x +x 2·(e x+2x )=e x +2x e x +x 2.(2)令u =2x +3,则y =10u ,∴y ′x =y ′u ·u ′x =10u ·ln 10·(2x +3)′=2×102x +3ln 10.(3)∵y =sin 4x +cos 4x =(sin 2x +cos 2x )2-2sin 2 x ·cos 2 x =1-12sin 2 2x =1-14(1-cos 4x )=34+14cos 4x . ∴y ′=-sin 4x .10.曲线y =e sin x 在点(0,1)处的切线与直线l 平行,且与l 的距离为2,求直线l 的方程. 解 ∵y =e sin x , ∴y ′=e sin x cos x , ∴y ′|x =0=1.∴曲线y =e sin x 在点(0,1)处的切线方程为 y -1=x ,即x -y +1=0. 又直线l 与x -y +1=0平行, 故直线l 可设为x -y +m =0. 由|m -1|1+(-1)2=2得m =-1或3.∴直线l 的方程为x -y -1=0或x -y +3=0.11.曲线y =e-2x+1在点(0,2)处的切线与直线y =0和y =x 围成的三角形的面积为( )A.13B.12C.23D .1答案 A解析 依题意得y ′=e -2x·(-2)=-2e-2x,y ′|x =0=-2e-2×0=-2.所以曲线y =e -2x+1在点(0,2)处的切线方程是y -2=-2x ,即y =-2x +2.在坐标系中作出直线y =-2x +2,y =0与y =x 的图象,如图所示.因为直线y =-2x +2与y =x 的交点坐标是⎝⎛⎭⎫23,23, 直线y =-2x +2与x 轴的交点坐标是(1,0), 所以结合图象可得,这三条直线所围成的三角形的面积为12×1×23=13.12.(多选)已知点P 在曲线y =4e x +1上,α为曲线在点P 处的切线的倾斜角,则α的取值可以是( )A.π4B.π2C.3π4D. 7π8 答案 CD 解析 因为y =4e x+1, 所以y ′=-4e x (e x +1)2=-4e x e 2x +2e x +1=-4e x +1e x +2. 因为e x >0,所以e x +1e x ≥2(当且仅当x =0时取等号),所以y ′∈[-1,0), 所以tan α∈[-1,0). 又因为α∈[0,π), 所以α∈⎣⎡⎭⎫3π4,π.13.设函数f (x )=cos(3x +φ)(0<φ<π),若f (x )+f ′(x )是奇函数,则φ= . 答案 π6解析 ∵f ′(x )=-3sin(3x +φ),∴f (x )+f ′(x )=cos(3x +φ)-3sin(3x +φ),令g (x )=cos(3x +φ)-3sin(3x +φ),∵其为奇函数,∴g (0)=0,即cos φ-3sin φ=0,∴tan φ=33, 又0<φ<π,∴φ=π6. 14.已知f (x )为偶函数,当x <0时,f (x )=ln(-x )+3x ,则曲线y =f (x )在点(1,-3)处的切线方程是 .答案 y =-2x -1解析 设x >0,则-x <0,f (-x )=ln x -3x ,又f (x )为偶函数,所以f (x )=ln x -3x ,f ′(x )=1x-3,f ′(1)=-2, 所以切线方程为y =-2x -1.15.已知f ⎝⎛⎭⎫1x =x 1+x ,则f ′(x )等于( )A.11+xB .-11+x C.1(1+x )2D .-1(1+x )2答案 D解析 由f ⎝⎛⎭⎫1x =x 1+x =11x+1,得f (x )=1x +1, 从而f ′(x )=-1(1+x )2,故选D. 16.(1)已知f (x )=e πx sin πx ,求f ′(x )及f ′⎝⎛⎭⎫12;(2)在曲线y =11+x 2上求一点,使过该点的切线平行于x 轴,并求切线方程. 解 (1)∵f (x )=e πx sin πx ,∴f ′(x )=πe πx sin πx +πe πx cos πx=πe πx (sin πx +cos πx ).∴f ′⎝⎛⎭⎫12=2e sin +cos 22πππ⎛⎫π ⎪⎝⎭ 2e .π=π(2)设切点坐标为P (x 0,y 0),由题意可知0=|0.x x y'=又y ′=-2x (1+x 2)2, ∴0=|x x y'=-2x 0(1+x 20)2=0. 解得x 0=0,此时y 0=1.即该点的坐标为P (0,1),切线方程为y -1=0.。
江苏省2020年高二数学第12讲 简单复合函数的导数 课件

(2) y
=
ln(2 x )由y
=
ln
u及u=2x复合而成,yⅱu =
ቤተ መጻሕፍቲ ባይዱ
1 u
, ux
=
2,
yⅱu ?ux
2, u
又y
=
ln(2x)= ln
x
+ ln
2,
yⅱx =
1 x
=
yu
?u?x符合猜想.
2.3法则论证
对于y = (3x - 1)2, yu = u2,ux = 3x - 1 yⅱx = 6(3x - 1),yu = 2u,u?x = 3
核心任务
如何获得复合函数的求导法则?
如何理解复合函数的求导法则? 如何运用复合函数的求导法则?
01 简单复合函数的定义 ------研究对象的确定
1.1复合函数的概念
由基本初等函数复合而成的函数,称为复合函数. 如y = ln(5x +1)由y = ln u及u = 5x +1复合而成. y = f (j (x))由y = f (u)及u =j (x)复合而成.
考察特殊的位置:x =1时,u = 2 思考:此时yⅱ x =12,yu = 4,u?x = 3分别代表什么含义?
y¢x =12表示此时y增加的速度是x增加速度的12倍, yu¢= 4表示此时y增加的速度是u增加速度的4倍, u¢x = 3表示此时u增加的速度是x增加速度的3倍.
2.2法则归纳
若y = f (u),u = ax +b,则yⅱ x = yu ?u?x,即 yⅱ x = yu ?a
例2:求下列函数的导数
(1) y = (2x - 3)3
(2) y = 1 3x - 1
(1) y = (2x - 3)3可由y = u3及u = 2x - 3复合而成,从而
5.2 5.2.3 简单复合函数的导数

5.2.3简单复合函数的导数考点学习目标核心素养复合函数的导数能够利用导数的运算法则推导出简单复合函数f(ax+b)的导数,并能利用它求其他复合函数的导数数学抽象、数学运算复合函数的导数的应用会用复合函数的导数求解相关问题数学运算问题导学预习教材P78倒数第一行~P80的内容,并思考下列问题:1.复合函数的定义是什么?2.如何求复合函数的导数?1.复合函数的概念一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).2.复合函数的求导法则复合函数y=f(g(x))的导数与函数y=f(u),u=g(x)的导数间的关系为y′x=y′u·u′x,即y对x的导数等于y对u的导数与u对x的导数的乘积.■名师点拨在复合函数定义中,y是因变量,x是自变量,u是中间变量,因变量y是中间变量u的函数,中间变量u是自变量x的函数.1.判断正误(正确的打“√”,错误的打“×”)(1)函数y =2x +5+ln x ,y =ln(2x +5)和y =sin(x +2)都是复合函数.( ) (2)函数y =ln(3x +1)是函数y =ln u ,u =3x +1的复合函数.( ) 答案:(1)× (2)√2.函数y =(x 2-1)n 的复合过程正确的是( ) A .y =u n ,u =x 2-1 B .y =(u -1)n ,u =x 2 C .y =t n ,t =(x 2-1)n D .y =(t -1)n ,t =x 2-1答案:A3.已知f (x )=sin n x ,则f ′(x )=( ) A .n sin n -1x B .n cos n -1xC.cos n x D .n sin n -1x ·cos x解析:选D.由于f (x )=sin n x ,由函数y =t n ,t =sin x 复合而成,所以y ′x =y ′t ·t ′x =nt n -1·cos x =n sin n -1x ·cos x .4.已知f (x )=ln(2x +5),则f ′(1)=____________. 解析:因为f ′(x )=12x +5(2x +5)′=22x +5, 所以f ′(1)=22×1+5=27.答案:27探究点1 简单复合函数求导求下列函数的导数. (1)y =e cos x +1;(2)y =log 2(2x +1); (3)y =2sin ⎝ ⎛⎭⎪⎫3x -π6;(4)y =11-2x . 【解】 (1)设y =e u ,u =cos x +1,则y′x=y′u·u′x=e u·(-sin x)=-e cos x+1·sin x.(2)设y=log2u,u=2x+1,则y′x=y′u·u′x=2u ln 2=2(2x+1)ln 2.(3)设y=2sin u,u=3x-π6,则y′x=y′u·u′x=2cos u×3=6cos(3x-π6).(4)设y=u-12,u=1-2x,则y′x=y′u·u′x=(u-12)′·(1-2x)′=-12u-32×(-2)=(1-2x)-32.(1)求复合函数导数的步骤(2)求复合函数导数的注意点:①分解的函数通常为基本初等函数;②求导时分清是对哪个变量求导;③计算结果尽量简洁.求下列函数的导数.(1)y=103x-2;(2)y=ln(e x+x2);(3)y=sin4x+cos4x.解:(1)令u=3x-2,则y=10u,所以y′x=y′u·u′x=10u ln 10·(3x-2)′=3×103x-2·ln 10.(2)令u=e x+x2,则y=ln u,所以y′x=y′u·u′x =1 u·(e x+x2)′=1e x+x2·(e x+2x)=e x+2xe x+x2.(3)因为y=sin4x+cos4x=(sin2x+cos2x)2-2sin2x·cos2x=1-12sin22x=1-14(1-cos 4x)=34+14cos 4x,所以y′=⎝⎛⎭⎪⎫34+14cos 4x′=-sin 4x.探究点2复合函数与导数的运算法则的综合应用求下列函数的导数.(1)y=ln 3xe x;(2)y=x1+x2;(3)y=x cos(2x+π2)sin(2x+π2).【解】(1)因为(ln 3x)′=13x×(3x)′=1x,所以y′=(ln 3x)′e x-(ln 3x)(e x)′(e x)2=1x-ln 3xe x=1-x ln 3xx e x.(2)y′=(x1+x2)′=x′1+x2+x(1+x2)′=1+x2+x21+x2=(1+2x2)1+x21+x2.(3)因为y=x cos(2x+π2)sin(2x+π2)=x(-sin 2x)cos 2x=-12x sin 4x,所以y′=⎝⎛⎭⎪⎫-12x sin 4x′=-12sin 4x-x2cos 4x·4=-12sin 4x-2x cos 4x.(1)在对函数求导时,应仔细观察及分析函数的结构特征,紧扣求导法则,联系学过的求导公式,对不易用求导法则求导的函数,可适当地进行等价变形,以达到化异求同、化繁为简的目的.(2)复合函数的求导熟练后,中间步骤可以省略,即不必再写出函数的复合过程,直接运用公式,从外层开始由外及内逐层求导.求下列函数的导数.(1)y =sin 2x3;(2)y =sin 3x +sin x 3; (3)y =11-x;(4)y =x ln(1+x ). 解:(1)因为y =1-cos 23x2,所以y ′=⎝ ⎛⎭⎪⎪⎫12-cos23x 2′=13sin 23x . (2)y ′=(sin 3x +sin x 3 )′=(sin 3x )′+(sin x 3)′ =3sin 2x cos x +cos x 3·3x 2 =3sin 2x cos x +3x 2cos x 3. (3)y ′=0-(1-x )′1-x=-12(1-x )-12(1-x )′1-x=12(1-x )1-x.(4)y ′=x ′ln(1+x )+x [ln(1+x )]′=ln(1+x )+x 1+x. 探究点3 复合函数的导数与导数几何意义的综合应用设f(x)=ln(x+1)+x+1+ax+b(a,b∈R),曲线y=f(x)与直线y=3 2x在(0,0)点相切,求a,b的值.【解】由曲线y=f(x)过(0,0)点,可得ln 1+1+b=0,故b=-1.由f(x)=ln(x+1)+x+1+ax+b,得f′(x)=1x+1+12x+1+a,则f′(0)=1+12+a=32+a,即为曲线y=f(x)在点(0,0)处的切线的斜率.由题意,得32+a=32,故a=0.本类题正确的求出复合函数的导数是前提,审题时注意所给点是否是切点,挖掘题目的隐含条件,求出参数,解决已知经过一定点的切线问题,寻求切点是解决问题的关键.曲线y=e sin x在(0,1)处的切线与直线l平行,且与l的距离为2,求直线l的方程.解:设u=sin x,则y′=(e sin x)′=(e u)′(sin x)′=cos x·e sin x,即y′|x=0=1,则切线方程为y-1=x-0,即x-y+1=0.因为直线l与切线平行,可设直线l的方程为x-y+c=0.两平行线间的距离d=|c-1|2=2⇒c=3或c=-1.故直线l的方程为x-y+3=0或x-y-1=0.1.函数y =(2 016-8x )3的导数等于( ) A .3(2 016-8x )2 B .-24x C .-24(2 016-8x )2D .24(2 016-8x )2解析:选C.y ′=3(2 016-8x )2×(2 016-8x )′ =3(2 016-8x )2×(-8)=-24(2 016-8x )2.2.函数y =x 2cos ⎝ ⎛⎭⎪⎫2x -π3的导数为( )A .y ′=2x cos ⎝ ⎛⎭⎪⎫2x -π3-x 2sin ⎝ ⎛⎭⎪⎫2x -π3 B .y ′=2x cos ⎝ ⎛⎭⎪⎫2x -π3-2x 2sin ⎝ ⎛⎭⎪⎫2x -π3C .y ′=x 2cos ⎝ ⎛⎭⎪⎫2x -π3-2x sin ⎝ ⎛⎭⎪⎫2x -π3D .y ′=2x cos ⎝ ⎛⎭⎪⎫2x -π3+2x 2sin ⎝ ⎛⎭⎪⎫2x -π3 解析:选 B.y ′=(x 2)′cos ⎝ ⎛⎭⎪⎫2x -π3+x 2⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫2x -π3′=2x cos ⎝ ⎛⎭⎪⎫2x -π3+x 2⎣⎢⎡⎦⎥⎤-sin ⎝ ⎛⎭⎪⎫2x -π3⎝ ⎛⎭⎪⎫2x -π3′=2x cos ⎝ ⎛⎭⎪⎫2x -π3-2x 2sin ⎝ ⎛⎭⎪⎫2x -π3. 3.函数y =1(3x -1)2的导数是( )A.6(3x -1)3B.6(3x -1)2C .-6(3x -1)3D .-6(3x -1)2解析:选C.y ′=⎣⎢⎡⎦⎥⎤1(3x -1)2′=-2(3x -1)3·(3x -1)′=-6(3x -1)3,故选C. 4.己知f (x )=ln(3x -1),则f ′(1)=__________ . 解析:因为f ′(x )=13x -1·(3x -1)′=33x -1,所以f ′(1)=32. 答案:325.设曲线y =e ax 在点(0,1)处的切线与直线x +2y +1=0垂直,则a =__________.解析:由题意知y ′|x =0=a e ax |x =0=a =2.答案:2[A 基础达标]1.(多选)下列函数是复合函数的是( ) A .y =-x 3-1x +1 B .y =cos ⎝ ⎛⎭⎪⎫x +π4C .y =1ln xD .y =(2x +3)4解析:选BCD.A 中的函数是一个多项式函数;B 中的函数可看作函数u =x +π4,y =cos u 的复合函数;C 中的函数可看作函数u =ln x ,y =1u 的复合函数;D 中的函数可看作函数u =2x +3,y =u 4的复合函数,故选BCD.2.函数y =⎝ ⎛⎭⎪⎫x +1x 5的导数为( )A .y ′=5⎝ ⎛⎭⎪⎫x +1x 4B .y ′=5⎝ ⎛⎭⎪⎫x +1x 4⎝ ⎛⎭⎪⎫1+1xC .y ′=5⎝ ⎛⎭⎪⎫x +1x 4⎝ ⎛⎭⎪⎫1-1x 2D .y ′=5⎝ ⎛⎭⎪⎫x +1x 4⎝ ⎛⎭⎪⎫x +1x解析:选C.函数y =⎝ ⎛⎭⎪⎫x +1x 5是函数y =u 5与u =x +1x 的复合函数,所以y ′x=y ′u ·u ′x =5⎝ ⎛⎭⎪⎫x +1x 4⎝ ⎛⎭⎪⎫1-1x 2.3.函数y =x ln(2x +5)的导数为( ) A .ln(2x +5)-x2x +5B .ln(2x +5)+2x2x +5C .2x ln(2x +5)D.x 2x +5解析:选 B.y ′=[x ln(2x +5)]′=x ′ln(2x +5)+x [ln(2x +5)]′=ln(2x +5)+x ·12x +5·(2x +5)′=ln(2x +5)+2x 2x +5. 4.已知直线y =x +1与曲线y =ln(x +a )相切,则a 的值为( ) A .1 B .2 C .-1D .-2解析:选B.设切点坐标是(x 0,x 0+1),依题意有⎩⎪⎨⎪⎧1x 0+a =1,x 0+1=ln (x 0+a ),解得x 0=-1,a =2.5.曲线y =e -2x +1在点(0,2)处的切线与直线y =0和y =x 围成的三角形的面积为( )A.13 B.12 C.23 D .1解析:选A.y ′|x =0=-2e -2×0=-2,所以曲线在点(0,2)处的切线方程为y =-2x +2.由⎩⎪⎨⎪⎧y =-2x +2,y =x ,解得x =y =23,所以A ⎝ ⎛⎭⎪⎫23,23,所以围成的三角形的面积为12×23×1=13.6.函数y =sin 2x cos 3x 的导数是__________. 解析:因为y =sin 2x cos 3x , 所以y ′=(sin 2x )′cos 3x +sin 2x (cos 3x )′ =2cos 2x cos 3x -3sin 2x sin 3x .答案:2cos 2x cos 3x -3sin 2x sin 3x7.曲线y =x e x -1在点(1,1)处的切线的斜率为__________.解析:y ′x =e x -1+x e x -1=(x +1)e x -1,故曲线在点(1,1)处的切线的斜率为2.答案:28.若y =f (x )=(2x +a )2且f ′(2)=20,则a =________.解析:令u =2x +a ,则y ′x =y ′u ·u ′x =(u 2)′(2x +a )′=4(2x +a ),则f ′(2)=4(2×2+a )=20,所以a =1.答案:19.求函数y =a sin x3+b cos 22x (a ,b 是常数)的导数.解:因为⎝ ⎛⎭⎪⎫a sin x 3′=a cos x 3⎝ ⎛⎭⎪⎫x 3′=a 3cos x 3,又(cos 22x )′=⎝ ⎛⎭⎪⎫12+12cos 4x ′=12(-sin 4x )×4=-2sin 4x ,所以y =a sin x3+b cos 2 2x 的导数为y ′=⎝ ⎛⎭⎪⎫a sin x 3′+b (cos 22x )′=a 3cos x 3-2b sin 4x .10.曲线y =e 2x cos 3x 在(0,1)处的切线与直线l 平行,且与l 的距离为5,求直线l 的方程.解:由y ′=(e 2x cos 3x )′ =(e 2x )′cos 3x +e 2x (cos 3x )′ =2e 2x cos 3x +e 2x (-3sin 3x ) =e 2x (2cos 3x -3sin 3x ), 得y ′|x =0=2.则切线方程为y -1=2(x -0), 即2x -y +1=0.因为直线l 与切线平行,可设直线l 的方程为2x -y +c =0,两平行线间的距离d =|c -1|5=5⇒c =6或c =-4.故直线l 的方程为2x -y +6=0或2x -y -4=0.[B 能力提升]11.己知点P 在曲线y =4e x +1上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是( )A.⎣⎢⎡⎭⎪⎫0,π4 B.⎣⎢⎡⎭⎪⎫π4,π2 C.⎝ ⎛⎦⎥⎤π2,3π4 D.⎣⎢⎡⎭⎪⎫3π4,π 解析:选D.y ′=-4e x (e x +1)2=-4e x (e x )2+2e x +1=-4e x +1ex +2. 因为e x+1e x ≥2,所以e x +1e x +2≥4, 所以y ′∈[-1,0),即tan α∈[-1,0),所以α∈⎣⎢⎡⎭⎪⎫3π4,π. 12.在等比数列{}a n 中,a 1=2,a 8=4,函数f (x )=x (x -a 1)·(x -a 2)·…·(x -a 8),则f ′(0)=__________.解析:因为f ′(x )=x ′(x -a 1)(x -a 2)·…·(x -a 8)+x (x -a 1)′(x -a 2)·…·(x -a 8)+…+x (x -a 1)(x -a 2)·…·(x -a 8)′=(x -a 1)(x -a 2)·…·(x -a 8)+x (x -a 2)·…·(x -a 8)+…+x (x -a 1)(x -a 2)·…·(x -a 7),所以f ′(0)=a 1·a 2·…·a 8=(a 1a 8)4=84=4 096.答案:4 09613.已知f (x )为偶函数,当x ≤0时,f (x )=e -x -1-x ,则曲线y =f (x )在点(1,2)处的切线方程是________.解析:设x >0,则-x <0,f (-x )=e x -1+x .因为f (x )为偶函数,所以f (x )=e x -1+x ,f ′(x )=e x -1+1,f ′(1)=2,即所求的切线方程为y -2=2(x -1),即2x -y =0.答案:2x -y =014.设曲线y =e -x (x ≥0)在点M (t ,e -t )处的切线l 与x 轴,y 轴围成的三角形面积为S (t ).(1)求切线l 的方程;(2)求S (t )的解析式.解:(1)因为y =e -x ,所以y ′x =(e -x )′=-e -x ,当x =t 时,y ′x =-e -t .故切线方程为y -e -t =-e -t (x -t ),即x +e t y -(t +1)=0.(2)令y =0,得x =t +1.令x =0,得y =e -t (t +1).所以S (t )=12(t +1)·e -t (t +1)=12(t +1)2e -t (t ≥0).[C 拓展探究]15.设曲线y =ln(2x -1)上的点到直线l :2x -y +3=0的最短距离.解:作出直线l :2x -y +3=0和曲线y =ln(2x -1)的图象可知它们无公共点,所以平移直线l ,当l 与曲线相切时,切点到直线l 的距离就是曲线上的点到直线l 的最短距离,y ′=12x -1(2x -1)′=22x -1. 设切点为P (x 0,y 0),所以22x 0-1=2,所以x 0=1, 所以y 0=ln(2×1-1)=0,P (1,0).所以曲线y =ln(2x -1)上的点到直线l :2x -y +3=0的最短距离为P (1,0)到直线l :2x -y +3=0的距离,|2×1-0+3|22+12=55= 5.最短距离d=。
人教A版选择性必修第二册5.2.3简单复合函数的导数

= 3时的导数,并解释它的实际意义.
− )可以看作函数
2
= 18和 =
2
3
− 的复合函数,
2
根据复合函数的求导法则,有:
2
’
2
2
= ∙ = (18) ∙ ( − ) = 18 ×
= 12( − ).
3
2
3
3
2
3
新知探索
l
l
一般地,对于由函数
= ()和 = ()复合而成的函数 =
(()),它的导数与函数 = (), = ()的导数间的关
系为 ’ = ’ ∙ ’ .
即对的导数等于对的导数与对的导数的乘积.
新知探索
辨析1.判断正误.
(1)若() = 2 ,则 ’ () = 2 .(
则 ’ =
1
(−2 )’ (1 −
3
2 2 )’ =
2 )−
(2):设
2. ,
2(1 − 2=
1 −3
(− 2 )
2
∙ (−4) =
1
− (1
2
3
− 2 2 )−2 (−4)
=
= , = + ,
则 ’ = ( )’ ()’ ( + )’ = ∙ () ∙ = = ( + ) ∙ (+) .
练习
变2.设曲线 = − ( + 1)在 = 0处的切线方程为2 − +1 = 0,则 =______.
解:∵ = − ( + 1),
’
∴ =
1
−
,
简单复合函数的求导法则学习教育课件PPT

推论:[c· f(x)]’ = c f’(x)
3)
课前练习:
1 1 1. y x( x 2 ), 求y '; x x x x 2. y x sin cos , 求y '; 2 2
2
3. y x cos( x), 求y ';
1 4. y , 求y '; sin x 5 x x x sin x 5. y , 求y '. 2 x
(2) y 3 x 2 x 1; (4) y ( a bx n ) m;
引例1:求函数y=(3x-1)2的导数.
已知y (3x 1) , 那么 y ' (3x 1) 2 (9x 6x 1)' 18x 6
2 2 '
函数y (3x 1)2 又可以看成由y u 2 , u 3x 1复合而成,
问题:如何求y (3x 2) 的导数?
2
① y x y 3x 2 9 x 12x 4 18 x 12
'
'
2'
2
'
y ( 3 x 2) 是一个复函数, ② 其实,
2
由 yu
yu
2
与 u 3 x 2 复合而成 .
2u
6 x 4 ; ux
复合函数的求导法则:
复合函数对自变量的导数,等于已知函数对中间变量f(u) 的导数,乘以中间变量 u ( x ) 对自变量的导数.
注意: 1、法则可以推广到两个以上的中间变量; 2、求复合函数的导数,关键在于分清函数的复合关系,合理选定 中间变量,明确求导过程中每次是哪个变量相对于哪个变量求导.
高中数学简单复合函数的求导法则

2u , ux 3, 从而 yx y 则 yu u ux 18 x 12
练习:指出下列函数是怎样复合而成的. 1 3 (1) y sin (1 ) (2) y (1 sin 2 x)4 x (3) y cos ln( x 1)
2
(4) y ae
2 x2 1
例:求下列函数的导数 (1) y (2 x 3)2
yx ' yu ' ux ' (u 2 )'(2x 3)' 4u 8x 12
(2) y e
0.05 x 1
yx ' yu ' ux ' (eu ) '(0.05x 1) ' 0.05e 0.05e
二、导数运算法则
[ f ( x) g ( x)]' f ( x)' g ( x)' [ f ( x) g ( x)]' f ( x)' g ( x) f ( x) g ( x)' f ( x) f ( x)' g ( x) f ( x) g ( x)' [ ]' 2 g ( x) [ g ( x)]
§5 简单复合函数的求导法则
一、基本初等函数的求导公式
1.若y c(c是常数),则y / 0; 2.若y x (是实数),则y / x 1; 3.若y a x (a 0, a 1),则y / a x ln a 特别地(e x ) / e x ; 4.若y log x(a 0, a 1),则y /
想一的导数 把平方式展开,利用导数的四则运算法则求导. 是否还有用其它的办法求导呢? 2).又如我们知道函数y=1/x2的导数是y’=- 2/x 3 那么函数y=1/(3x-2)2的导数又是什么呢?
5.2.3简单复合函数的导数课件(人教版)

变式.(1) 若存B. C. D.
(2) 若曲线 在点 处的切线与直线 平行,且切线与 之间的距离为 ,求直线 的方程.
(2) ;
(3) ;
(4) .
(5) .
问题探究
(5) .
方法总结
练习巩固
1.
2.
求下列函数的导数
例1 求下列函数的导数:
(1) ;
(2) ;
(3) ;
(4) ;
(5) .
变式.求下列函数的导数:
(1) ;
(2) ;
(3) .
蓝本P107
复习回顾
◆ 知识点 导数的运算法则
已知 , 为可导函数.
(1) ______________.
(2) ______________________,特别地, ________.
(3) _ ________________
蓝本P108
小试牛刀
求下列函数的导数
(1) ;
复习回顾
◆ 知识点二 基本初等函数的导数公式
1.若 ( 为常数),则 ____.
2.若 ( ,且 ),则 ________.
3.若 ,则 _______.
4.若 ,则 ________.
5.若 ( ,且 ),则 _________;特别地,若 ,则 _____.
6.若 ( ,且 ),则 _ _____;特别地,若 ,则 _ ___.
[素养小结]求复合函数的导数时,应把握好以下环节:
(1)选取恰当的中间变量,使构成复合函数的基本初等函数符合求导法则中的函数结构;
(2)从外到内,层层剥皮,依次求导;
人教版高中数学选择性必修第二册5.2.3 简单的复合函数的导数

复合函数的求导过程就是对复合函数由外层向里求导,每 次求导都是针对着最外层的相应变量进行的,直至求到最里层为 止,所谓最里层是指可以直接引用基本公式表进行求导.
课时学案
题型一 明确复合关系
例 1 指出下列函数的复合关系:
(1)y=(2-x2)3;
(2)y=sinx2;
(3)y=cosπ4-x; (4)y=lnsin(3x-1).
2.若可导函数 f(x)满足 f′(3)=9,则 f(3x2)在 x=1 处的导数 值为_____54___.
解析 ∵[f(3x2)]′=f′(3x2)(3x2)′=6xf′(3x2), ∴f(3x2)在 x=1 处的导数值为 6×1×f′(3)=54.
3.求下列函数的导数:
(1)y=sin22x+π3; (2)y=cos22x;
【解析】 (1)设 y=u2,u=-2x+1,则 y′x=y′u·u′x=2u·(- 2)=-4(-2x+1)=8x-4.
(2)设 y=eu,u=x-1,则 y′x=y′u·u′x=eu·1=ex-1.
(3) 设
y = log2u , u = 2x + 1 , 则
y′x
=
y′u
·
u
′
x
=
2 uln2
【解析】 ∵y= x21-3x=(x2-3x)-12, ∴y′=-12(x2-3x)-32·(x2-3x)′ =-12(x2-3x)-32·(2x-3). ∴曲线 y= x21-3x在点4,12处的切线斜率为 k=y′|x=4=- 12(42-3×4)-32·(2×4-3)=-156. ∴曲线在点4,12处的切线方程为 y-12=-156(x-4),即 5x +16y-28=0.
【解析】 (1)函数的导数 f′(x)=12· 3x12+1·6x= 3x32x+1, 则曲线在点(1,2)处的切线斜率 k=f′(1)= 33+1=32,则对应 的切线方程为 y-2=32(x-1), 即 3x-2y+1=0. (2)y′=x(1-x2)-32,令 y′=0,得 x=0,∴y=1.
数学北师大版选修2-2教材基础第二章§5简单复合函数的求导法则含答案

§5 简单复合函数的求导法则
前面我们学习了简单函数的求导和导数的四则运算,但如果我们遇到层次关系较多的函数,这样的函数我们怎样求它的导数呢? 高手支招1细品教材
一、复合函数的定义
一般地,对于两个函数y=f(u)和u=φ(x ),如果通过变量u ,y 可以表示成x 的函数,那么称这个函数为函数y=f(u)和u=φ(x)的复合函数。
如:y=2
x e ,y=lntanx 都是复合函数. 状元笔记 复合函数y=f (φ(x))对自变量x 的导数等于函数y=f (u)关于中间变量u 的导数与中间变量u 关于自变量x 的导数的乘积。
二、复合函数的求导法则
如果函数u=φ(x)在点x 可导,而函数y=f(u)在对应点u=φ(x)可导,则复合函数y=f (φ(x ))在点x 可导,且其导数为:y′=(f (u ))′=f′(u)·φ′(x).
三、利用复合函数的求导法则求复合函数的导数的步骤
1。
分解复合函数为基本初等函数,适当选取中间变量;
2。
求每一层基本初等函数的导数,注意是对哪一个变量求导;
3。
每层函数求导后,需把中间变量转化为自变量的函数;
4.对于层数比较多的复合函数,可由外向里逐层求导.
【示例】求y=655-
x 的导数. 解:y′=[(5x 65-21)]′=21·(5x 65-21)-·5=65
525-x .
高手支招2基础整理
本节的主要内容是复合函数的概念,复合函数的求导法则及其应用。
本节的知识结构如下:。
简单复合函数的导数-高考数学复习PPT

1 C.ln 3
解析
f′(x)=(x-11)ln
,故 3
f′(2)=ln13.
D.-ln13
1 2 3 4 5 6 7 8 9 10 11 12 13 14
索引
2.若函数y=x(1-ax)2(a>0),且y′|x=2=5,则a=( A )
A.1
B.-1
C.2
D.-2
解析 y′=(1-ax)2-2ax(1-ax),
3.注意1个易错点 对复合函数求导不完全.
索引
拓展延伸分层精练 核心素养达成
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
一、基础达标
1.设f(x)=log3(x-1),则f′(2)=( C )
A.ln 3
B.-ln 3
解析 设直线 y=x+1 与曲线 y=ln(x+a)相切于点(x0,y0),则 y0=1+x0,y0= ln(x0+a), 又 y′=x+1 a, ∴y′|x=x0=x0+1 a=1,即 x0+a=1. 又 y0=ln(x0+a),∴y0=0,∴x0=-1,∴a=2.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
索引
训练3 曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面
积为( A )
A.13
B.12
C.23
D.1
解析 对 y=e-2x+1 求导得 y′=-2e-2x,则 y′|x=0=-2e-2×0=-2,
∴曲线 y=e-2x+1 在点(0,2)处的切线方程为 y=-2x+2.
索引
7.某铁路线新开行“绿巨人”动力集中复兴号动车组,最高时速为160 km/h.假 设“绿巨人”开出站一段时间内,速度v(m/s)与行驶时间t(s)的关系为v=0.4t + 0.6t2 , 则 出 站 后 “ 绿 巨 人 ” 速 度 首 次 达 到 24 m/s 时 的 加 速 度 为
简单复合函数的求导法则

简单复合函数的求导法则复合函数的求导是微积分中的重要概念之一,常用于解决实际问题中的导数计算。
在本文中,将介绍简单复合函数和复合函数的求导法则,以及一些例题的解答。
简单复合函数指的是由一个基本函数和一个简单函数复合而成的函数。
例如,如果有一个函数y=f(u)和另一个函数u=g(x),那么可以通过将这两个函数进行复合得到一个新的函数y=f(g(x))。
我们可以使用链式法则来计算这个复合函数的导数。
链式法则是求导中最基本的方法之一,它可以帮助我们计算复合函数的导数。
链式法则的表达式为:(dy/dx) = (dy/du)*(du/dx) 或者 f'(g(x))=f'(u)*g'(x)其中,dy/dx表示函数y关于x的导数,dy/du表示函数y关于u的导数,du/dx表示函数u关于x的导数。
举个例子,如果y=sin(3x)和u=3x,那么我们可以将它们复合为y=sin(u),然后利用链式法则求导。
首先通过求导公式得到dy/du=cos(u),然后通过将du/dx代入得到dy/dx=cos(u)*3、因此,我们得出了函数y=sin(3x)的导数为dy/dx=3*cos(3x)。
复合函数指的是由两个以上的函数复合而成的函数。
与简单复合函数不同,复合函数的求导需要使用多次链式法则来计算。
下面是一些常见的复合函数求导法则:1.和法则如果一个函数可以表示为两个函数之和的形式,那么它的导数等于这两个函数的导数之和。
即,如果y=f(x)+g(x),那么dy/dx=f'(x)+g'(x)。
比如,对于函数y=x^2+3x,我们可以将其分解为f(x)=x^2和g(x)=3x两个函数的和。
然后分别求导得到f'(x)=2x和g'(x)=3、最后,将两个导数相加得到dy/dx=2x+32.差法则如果一个函数可以表示为两个函数之差的形式,那么它的导数等于这两个函数的导数之差。
简单复合函数的导数 课件-高中数学人教A版(2019)选择性必修第二册
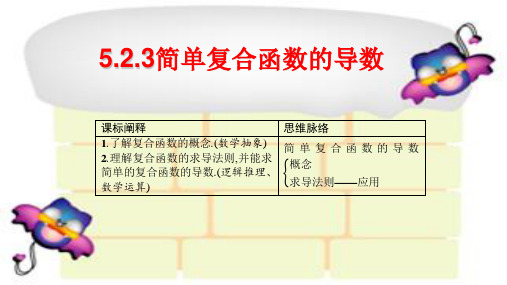
)
x
(
1
x
)
.
2
5 1 x
1 x
5 1 x
(1 x)
5
1
2 2
2
2
2
y
(2
x
3)
1
x
(2
x
3)(1 x ) ;
解:
1
2 2
讲
课
人
:
邢
启
强
1
1
y 4 x(1 x ) (2 x 2 3) (1 x 2 ) 2 2 x
2
2
3
即曲线 y=ln(2x-1)上的点到直线 2x-y+3=0 的最短距离是 5.
讲
课
人
:
邢
启
强
(2)令y=f(x),则曲线y=eax在点(0,1)处的切线的斜率为f'(0),又切线与直线x+2y+1=0垂直,
所以f'(0)=2.因为f(x)=eax,所以f'(x)=(eax)'=eax·(ax)'=aeax,所以f'(0)=ae0=a,故a=2.
讲
课
人
:
邢
启
强
13
典型例题
例4(1)曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是(
A. 5
B.2 5
C.3 5
)
D.0
(2)设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a=
.
分析:(1)设 P(x0,y0)→由 y'|= =2 求P(x ,y )→由点到直线的距离求最小值
简单复合函数的求导法则名师公开课获奖课件百校联赛一等奖课件

例题讲解
例3 求
y (2 x 1)5旳导数.
解:设 y u5 , u 2 x 1, 则
yx yu ux (u5 )u (2 x 1)x 5u4 2 5(2x 1)4 2 10(2x 1)4
求下列函数旳导数.
(1) y (2x 1)5 ;
(2) y ln(5x 1);
解:(1) (2)
y ln(ln x).
y cos(1 x 2 )
一般旳,对于两个函数
y f (u) 和 u g(x) 经过变量 y、u 能够表达成 x 旳函数 y f (g(x)) 那么称这个函数为 y f (u) 和 u g(x)
旳复合函数
要求掌握内层函数为一次复合函数旳导数
复合函数旳导数
(2) y sin x2由 y sin u, u x复2 合而成.
(3)y 成.
cos
4
x
由
y cos u, u
4
x复合而
(4) y ln sin(3 x 1)由 y ln u, u sin v, v 3 x 1复合而成.
复合函数旳导数
新讲课
例2 写出由下列函数复合而成旳函数: (1)y ln u,u ln x (2)y cos u,u 1 x2
π cosu π cosπx φ.
复习检测
复习检测
复习检测
y um , u a bxn.
y sin u, u 1 1 x
*
问题: 如何求y (3x 2)2的导数?
① y'x y' [(3x 2)2]' 9x2 12x 4 ' 18x 12
② 其实,y (3x 2)2 是一种复合函数,
由 y u2 与 u 3x 2复合而成.
5.2.3简单复合函数的导数课件(人教版)

y通过中间变量u表示成x的函数.
复合函数
一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u, y可以表示成x的函数,那么称这个函数为函数y=f(u)和 u=g(x)的复合函数,记作y=f(g(x)).
试一试
指出以下函数是由哪些函数复合而成的?
(1)y=log2(x+1) (2)y=(3x+5)3
(3)y=e-0.05x+1
y=log2u和u=x+1 y=u3和u=3x+5 y=eu和u=-0.05x+3
探究:如何求复合函数的导数?以函数 y=sin2x 为例,研究其导数.
y′ =(sin2x)′=(2sinxcosx)′=2 (sinxcosx)′ =2[ (sinx)′cosx + sinx (cosx)′] = 2[cos2x-sin2x]=2cos2x
特别地,[cf ( x)] ___cf__(_x_)__;
f (x)
f ( x)g( x) f ( x)g( x)
(3)
g(
x)
[g( x)]2
.
学习新知
思考 如何求函数y=ln(2x-1)的导数?
LOGO
函数y= ln(2x-1)不是由基本初等函数通过加、减、乘、除运算得到的, 所以无 法用现有的方法求它的导数.
[解] 解法一:f′(x)=2f′(2-x)·(2-x)′-2x+8=-2f′(2-x)-2x+8, 则f′(1)=-2f′(1)-2+8,得f′(1)=2. 又f(1)=2f(1)-1+8-8,得f(1)=1, 故曲线y=f(x)在点(1,f(1))处的切线方程为y-1=2(x-1), 即y=2x-1.
巩固练习 1.曲线y=e-5x+2在点(0,3)处的切线方程为________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 分解——求导——相乘——回代
课后作业:
课本 P24 练习 No.2;
课本 P26 习题1.2 No.2、7、13.
求下列函数的导数:
(1) y (2x 3)3; (2) y ln(5x 1) (3) y 1 ; (4) y cos(1 2x)
3x 1
例写出由下列函数复合而成的函数,并 求它们的导数。
⑴ y cosu u 1 x2
⑵ ; y ln, u
u, ln x
.
解:⑴
y cos(1 x 2 )
[ f (x)] g(x)
f (x)g(x) f (x)g(x) g 2 ( x)
其中g(x) 0
简单复合函数 的导数
楚水实验学校高二数学备课组
复合函数: 由几个函数复合而成的函数,叫复合函数.
由函数 y f (u)与 u (x) 复合而成
的函数一般形式是 y f [(x)]
,其中u称为中间变量.
法则2:
[Cf (x)] Cf (x).(C为常数)
法则3:两个函数的积的导数,等于
第一个函数的导数乘以第二个函数
加 乘 上第一个函数 以第二个函数
的导数
[ f (x)g(x)] f (x)g(x) f (x)g(x).
法则4 :两个函数的商的导数,等于分 子的导数与分母的积,减去分母的导数 与分子的积,再除以分母的平方,即:
2 cos2 x 2 sin 2 x
2 cos2x
另一方面: 将函数 y sin 2x
看作是函数 y sin u
和函数 u 2x
分 解
复合函数,并分别求对应变量的导数如下:
yu (sin u) cosu ux (2x) 2
求 导
两个导数相乘,得
yu
ux
(cos u) 2
相 乘
量对自变量的导数 ,即 y'x y'u u'x
复合函数求导的基本步骤是:
(1)分解 (2)求导 (3)相乘 (4)回代
数学运用
试说明下列函数是怎样复合而成的
(1) y (2x 3)3; (2) y ln(5x 1) (3) y 1 ; (4) y cos(1 2x)
3x 1
数学运用
#39;x y'u u'x
建构数学 一般地,我们有u=ax+b时,有
若 y=f(u),u=ax+b,则 y'x y'u u'x
即:y'x y'u a
• 对于一般的复合函数,结论也成立 。 • 复合函数的求导法则 • 复合函数对自变量的导数,等于已
知函数对中间变量的导数,乘以中间变
y 2x sin(1 x2 )
⑵ y ln(ln x) y (x ln x)1
• 1、求下列函数的导数:
(1) y (2x 3)2;(2) y (1 3x)3;
(3) y e2x; (4) y ln 1 x
2、求曲线y=sin2x在点P(π,0)处的 切线方程。
小结 :
• ⑴复合函数的求导,要注意分析复 合函数的结构,引入中间变量,将复 合函数分解成为较简单的函数,然后 再用复合函数的求导法则求导;
知识回顾:基本求导公式:
(1)(kx b) k,特殊的:C 0(C为常数)
(2)(x )' x1(为常数)
(3)(ax )' axlna(a 0,且a 1)
(4)(log ax)'
1 xlna
(a 0,且a
1)
(5)(ex )' ex
(6)(lnx) ' 1 x
(7)(sinx )' cosx (8)(cosx) ' sinx
目前我们所研究的简单复合函数的导数 仅限于形如f(ax+b)的复合函数
问题探究:
求函数 y (3x 2)2 的导数 。
方法一:
yx [(3x 2)2] (9x2 12x 4) 18x 12
方法二:将函数 y (3x 2)2
看作是函数 y u2 和函数 u 3x 2
复合函数,并分别求对应变量的导数如下:
根据导数的概念,求函数导数的过程可以 用下面的流程图来表示
给定函数y f(x)
计算 y f(x x) f(x)
x
x
x 0
y A(x) x
f (x) A(x)
法则1: 两个函数的和(或差)的 导数,等于这两个函数的导数的和 (或差),即:
[ f (x) g(x)] f (x) g(x).
yu (u2 ) 2u ux (3x 2) 3
两个导数相乘,得
yu ux 2u 3 2(3x 2)3 18x 12
从而有 y'x y'u u'x
问题探究:
考察函数 y sin 2x 的导数 。
一方面 : y sin 2x 2sin x cos x
yx (sin 2x)
(2 sin x; cos x) 2(sin x) cos x 2 sin x (cosx)
