华师大版-数学-七年级上册-3.4 整式的加减 练习
七年级数学上册第3章整式的加减3.4.4整式的加减同步测试题新版华东师大版

第三章3.4.4 整式的加减同步测试题一、选择题1.计算(6a2-5a+3)-(5a2+2a-1)的结果是()A.a2-3a+4 B.a2-3a+2 C.a2-7a+2 D.a2-7a+4 2.化简5(2x-3)+4(3-2x)的结果为()A.2x-3 B.2x+9 C.8x-3 D.18x-3 3.用2a+5b减去4a-4b的一半,应当得到()A.4a-b B.b-a C.a-9b D.7b4.加上5x2-3x-5等于3x的代数式是()A.-5x2+6x+5 B.5+5x2 C.5x2-6x-5 D.5x2-5 5.一个长方形的一边长是2a+3b,另一边长是a+b,则这个长方形的周长是() A.12a+16b B.6a+8bC.3a+8b D.6a+4b6.一个多项式与x2-2x+1的和是3x-2,则这个多项式为()A.x2-5x+3 B.-x2+x-1 C.-x2+5x-3 D.x2-5x-137.已知a+2b=5,则代数式3(2a-3b)-4(a-3b+1)+b的值为()A.14 B.10 C.6 D.不能确定8.若多项式2x3-8x2+x-1与多项式x3+(3m+1)x2-5x+7的差不含二次项,则m的值为() A.4 B.-4 C.3 D.-3二、填空题9.化简:(x2+y2)-3(x2-2y2)=_______.10.一根铁丝的长为5a+4b,剪下一部分围成一个长为a,宽为b的长方形,则这根铁丝还剩下_______.三、解答题11.化简:(1)(5m2-3n)-3(m2-2n);(2)7ab-3(a2-2ab)-5(4ab-a2).12.先化简,再求值:(2x2-12+3x)-4(x-x2+12),其中x=-12.13.给出三个多项式:X=2a2+3ab+b2,Y=3a2+3ab,Z=a2+ab,请你任选两个进行加法或减法运算.14.已知某三角形的一条边长为m +n ,另一条边长比这条边长大m -3,第三条边长等于2n -m ,求这个三角形的周长.15.某校有A ,B ,C 三个课外活动小组,A 小组有学生(x +2y)名,B 小组学生人数是A 小组学生人数的3倍,C 小组比A 小组多3名学生,问A ,B ,C 三个课外活动小组共有多少名学生?16.先化简,再求值:(1)2(a 2-ab)-3(2a 2-ab),其中a =-2,b =3;(2)3x 2y -[2xy 2-2(xy -32x 2y)+xy]+3xy 2,其中x =3,y =-13.17.已知小明的年龄是m 岁,小红的年龄比小明年龄的2倍少4岁,小华的年龄比小红的年龄的12多1岁,求这三名同学的年龄之和.18.一位同学做一道题:已知两个多项式A ,B ,计算2A +B.他误将“2A +B ”写成“A +2B ”,求得结果是9x 2-2x +5.已知B =x 2+3x -3,求正确答案.19.做大、小长方体纸盒,尺寸如下:(单位:cm )(1)做大纸盒比做小纸盒多用材料多少平方厘米?(2)当a =10,b =5,c =2时,做这两个纸盒共用材料多少平方厘米?参考答案二、选择题1.计算(6a2-5a+3)-(5a2+2a-1)的结果是(D)A.a2-3a+4 B.a2-3a+2 C.a2-7a+2 D.a2-7a+4 2.化简5(2x-3)+4(3-2x)的结果为(A)A.2x-3 B.2x+9 C.8x-3 D.18x-3 3.用2a+5b减去4a-4b的一半,应当得到(D)A.4a-b B.b-a C.a-9b D.7b4.加上5x2-3x-5等于3x的代数式是(A)A.-5x2+6x+5 B.5+5x2 C.5x2-6x-5 D.5x2-5 5.一个长方形的一边长是2a+3b,另一边长是a+b,则这个长方形的周长是(B) A.12a+16b B.6a+8bC.3a+8b D.6a+4b6.一个多项式与x2-2x+1的和是3x-2,则这个多项式为(C)A.x2-5x+3 B.-x2+x-1 C.-x2+5x-3 D.x2-5x-137.已知a+2b=5,则代数式3(2a-3b)-4(a-3b+1)+b的值为(C)A.14 B.10 C.6 D.不能确定8.若多项式2x3-8x2+x-1与多项式x3+(3m+1)x2-5x+7的差不含二次项,则m的值为(D) A.4 B.-4 C.3 D.-3二、填空题9.化简:(x2+y2)-3(x2-2y2)=-2x2+7y2.10.一根铁丝的长为5a+4b,剪下一部分围成一个长为a,宽为b的长方形,则这根铁丝还剩下3a+2b.三、解答题11.化简:(1)(5m2-3n)-3(m2-2n);解:原式=5m2-3n-3m2+6n=2m2+3n.(2)7ab-3(a2-2ab)-5(4ab-a2).解:原式=7ab-3a2+6ab-20ab+5a2=-7ab+2a2.12.先化简,再求值:(2x 2-12+3x)-4(x -x 2+12),其中x =-12. 解:原式=2x 2-12+3x -4x +4x 2-2 =6x 2-x -52. 当x =-12时,原式=32+12-52=-12.13.给出三个多项式:X =2a 2+3ab +b 2,Y =3a 2+3ab ,Z =a 2+ab ,请你任选两个进行加法或减法运算.解:答案不唯一,如:X -Z =(2a 2+3ab +b 2)-(a 2+ab)=a 2+2ab +b 2,Y -X =(3a 2+3ab)-(2a 2+3ab +b 2)=a 2-b 2.14.已知某三角形的一条边长为m +n ,另一条边长比这条边长大m -3,第三条边长等于2n -m ,求这个三角形的周长.解:(m +n)+(m -3)+(m +n)+(2n -m)=2m +4n -3.15.某校有A ,B ,C 三个课外活动小组,A 小组有学生(x +2y)名,B 小组学生人数是A 小组学生人数的3倍,C 小组比A 小组多3名学生,问A ,B ,C 三个课外活动小组共有多少名学生?解:B 小组学生人数为3(x +2y)名,C 小组学生人数为[(x +2y)+3]名.(x +2y)+3(x +2y)+(x +2y)+3=5(x +2y)+3=(5x +10y +3)名.答:A ,B ,C 三个课外活动小组共有(5x +10y +3)名学生.16.先化简,再求值:(1)2(a 2-ab)-3(2a 2-ab),其中a =-2,b =3;解:原式=-4a 2+ab.当a =-2,b =3时,原式=-4×(-2)2+(-2)×3=-22.(2)3x 2y -[2xy 2-2(xy -32x 2y)+xy]+3xy 2,其中x =3,y =-13. 解:原式=3x 2y -2xy 2+2xy -3x 2y -xy +3xy 2=xy 2+xy.当x =3,y =-13时,原式=3×(-13)2+3×(-13)=-23.17.已知小明的年龄是m 岁,小红的年龄比小明年龄的2倍少4岁,小华的年龄比小红的年龄的12多1岁,求这三名同学的年龄之和.解:m +(2m -4)+[12(2m -4)+1]=m +2m -4+m -2+1=(4m -5)岁. 答:这三名同学的年龄之和是(4m -5)岁.18.一位同学做一道题:已知两个多项式A ,B ,计算2A +B.他误将“2A +B ”写成“A +2B ”,求得结果是9x 2-2x +5.已知B =x 2+3x -3,求正确答案.解:由题意知A =9x 2-2x +5-2(x 2+3x -3)=9x 2-2x +5-2x 2-6x +6=7x 2-8x +11,则2A +B =2(7x 2-8x +11)+x 2+3x -3=14x 2-16x +22+x 2+3x -3=15x 2-13x +19.19.做大、小长方体纸盒,尺寸如下:(单位:cm )(1)做大纸盒比做小纸盒多用材料多少平方厘米?(2)当a=10,b=5,c=2时,做这两个纸盒共用材料多少平方厘米?解:(1)做小纸盒所用的材料为:2(2a·3b+2ac+3bc)=12ab+4ac+6bc,做大纸盒所用的材料为:2(3a·4b+3a·2c+4b·2c)=24ab+12ac+16bc,故做大纸盒比做小纸盒多用材料:24ab+12ac+16bc-(12ab+4ac+6bc)=(12ab+8ac+10bc)cm2.(2)当a=10,b=5,c=2时,做这两个纸盒共用材料:(12ab+4ac+6bc)+(24ab+12ac+16bc)=36ab+16ac+22bc=36×10×5+16×10×2+22×5×2=2 340(cm2).。
七年级数学上册第三章整式的加减3-4整式的加减作业新版华东师大版

3.4整式的加减
1.化简的结果是()
A. B. C. D.
2.当时,可化为()
A. B. C. D.
3.已知多项式,,且,则多项式C为()
A. B. C. D.
4.已知关于的多项式合并后结果为0,则与的关系是.
5.三个连续自然数中最小的一个是,则它们的和是.
6.已知三个数在数轴上的位置如图3-4所示,化简.
7.若,则代数式.
8.已知,则A=.
9.已知,求的值.
10.已知,求的值.(用的代数式表示)
11.一个两位数,它的十位数字是,个位数字是,若把它的十位数字与个位数字对调,将得到一个新的两位数,计算原数与新数的和与差,请回答:这个和能被11整除吗?差能被多少整除?
参考答案:
1.C
2.B
3.B
4.互为相反数
5.
6.
7.4006
8.
9.-10.
10.解:原式=.
11.解:原数为,新数为,和为,能被11整除.差为
,能被9整除.。
七年级数学上册 3.4 整式的加减 3.4.4.2 化简求值跟踪训练(含解析)(新版)华东师大版-(

化简求值一.选择题(共8小题)1.已知A=2a2﹣3a,B=2a2﹣a﹣1,当a=﹣4时,A﹣B=()A.8 B.9 C.﹣9 D.﹣72.已知x2﹣3xy=9,xy﹣y2=4,则代数式y2﹣x2值为()A.﹣7 B.1 C.7 D.﹣13.已知a+2b=3,则代数式2(2a﹣3b)﹣3(a﹣3b)﹣b的值为()A.﹣3 B.3 C.﹣6 D.64.若x+y=3,xy=1,则﹣5x﹣5y+3xy的值为()A.﹣12 B.﹣14 C.12 D.185.已知,那么﹣(3﹣x+y)的结果为()A.B.C.D.6.已知A=3a2+b2﹣c2,B=﹣2a2﹣b2+3c2,且A+B+C=0,则C=()A.a2+2C2B.﹣a2﹣2c2C.5a2+2b﹣4c2D.﹣5a2﹣2b2+4c27.已知x﹣y=3,那么代数式3(x﹣y)2﹣2(x﹣y)﹣2(x﹣y)2+x﹣y的值是()A. 3 B.27 C.6 D.98.当(b≠0)时,(8a﹣7b)﹣(4a﹣5b)等于()A.0 B.b C.2b D.4b二.填空题(共7小题)9.若x﹣y=﹣1,xy=2,则xy﹣x+y= _________ .10.如果m、n是两个不相等的实数,且满足m2﹣2m=1,n2﹣2n=1,那么代数式2m2+4n2﹣4n+1994=_________ .11.若x﹣y看成一个整体,则化简(x﹣y)2﹣3(x﹣y)﹣4(x﹣y)2+5(x+y)的结果是_________ .12.如果a<0,ab<0,则化简|a﹣b|+1﹣(a﹣b+3)的结果是_________ ,若a﹣b=﹣1,则其值为_________ .13.已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值为_________ .14.已知a+b=﹣7,ab=10,则代数式(3ab+6a+4b)﹣(2a﹣2ab)的值为_________ .15.若多项式2x2+3x+7的值为10,则多项式6x2+9x﹣7的值为_________ .三.解答题(共7小题)16.求代数式2x3﹣5x2+x3+9x2﹣3x3﹣2的值,其中x=.17.先化简,再求值:4(x﹣y)﹣2(3x+y)+1,其中.18.已知a﹣2=0,求代数式3a﹣6+a2﹣4a+5的值.19.先化简,再求值:(3a2﹣ab+7)﹣(5ab﹣4a2+7),其中a=2,b=.20.先化简,再求值:(1)(6a﹣1)﹣(2﹣5a)﹣,其中a=2;(2)(3a2﹣ab+7)﹣(5ab﹣4a2+7),其中a=2,b=.21.以知|m+n﹣2|+|mn+3|2=0,求﹣3的值.22.化简求值:若a=﹣3,b=4,c=﹣,求7a2bc﹣{8a2cb﹣}的值.第三章整式加减.2化简求值参考答案与试题解析一.选择题(共8小题)1.已知A=2a2﹣3a,B=2a2﹣a﹣1,当a=﹣4时,A﹣B=()A.8 B.9 C.﹣9 D.﹣7考点:-整式的加减—化简求值.分析:-根据整式的加减,可化简整式,根据代数求值,可得答案.解答:-解:A﹣B=2a2﹣3a﹣(2a2﹣a﹣1)=2a2﹣3a﹣2a2+a+1=﹣2a+1,把a=﹣4代入原式,得﹣2a+1=﹣2×(﹣4)+1=9,故选:B.点评:-本题考查了整式的化简求值,先化简再求值,注意减法时要先添括号.2.已知x2﹣3xy=9,xy﹣y2=4,则代数式y2﹣x2值为()A.﹣7 B.1 C.7 D.﹣1考点:-整式的加减—化简求值.专题:-计算题.分析:-已知等式变形后,相加即可求出原式的值.解答:-解:x2﹣3xy=9①,xy﹣y2=4②,①+②×3得:x2﹣3xy+3xy﹣3y2=21,整理得:y2﹣x2=﹣7.故选A.点评:-此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.3.已知a+2b=3,则代数式2(2a﹣3b)﹣3(a﹣3b)﹣b的值为()A.﹣3 B.3 C.﹣6 D.6考点:-整式的加减—化简求值.专题:-计算题.分析:-原式去括号合并,将已知等式代入计算即可求出值.解答:-解:∵a+2b=3,∴原式=4a﹣6b﹣3a+9b﹣b=a+2b=3,故选B.点评:-此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.4.若x+y=3,xy=1,则﹣5x﹣5y+3xy的值为()A.﹣12 B.﹣14 C.12 D.18考点:-整式的加减—化简求值.分析:-本题可对﹣5x﹣5y+3xy进行转换,可转换为﹣5(x+y)+3xy,题中已知x+y=3,xy=1,代入即可.解答:-解:由分析可得:﹣5x﹣5y+3xy=﹣5(x+y)+3xy,已知x+y=3,xy=1,代入可得﹣5x﹣5y+3xy=﹣12.故答案为:A.点评:-本题考查整式的加减及化简求值,看清题中所给条件.5.已知,那么﹣(3﹣x+y)的结果为()A.B.C.D.考点:-整式的加减—化简求值.分析:-把﹣(3﹣x+y)去括号,再把代入即可.解答:-解:原式=﹣3+x﹣y,∵,∴上式=﹣,故选A.点评:-本题考查了整式的化简求值,是基础题型.6.已知A=3a2+b2﹣c2,B=﹣2a2﹣b2+3c2,且A+B+C=0,则C=()A.a2+2C2B.﹣a2﹣2c2C.5a2+2b﹣4c2D.﹣5a2﹣2b2+4c2考点:-整式的加减—化简求值.分析:-由A+B+C=0知,C=﹣(A+B),然后把A,B的值代入即可.解答:-解:∵A+B+C=0,∴C=﹣(A+B)=﹣(3a2+b2﹣c2﹣2a2﹣b2+3c2)=﹣(a2+2c2)=﹣a2﹣2c2,故选B.点评:-本题考查了整式的加减,主要是去括号原则的运用.7.已知x﹣y=3,那么代数式3(x﹣y)2﹣2(x﹣y)﹣2(x﹣y)2+x﹣y的值是()A. 3 B.27 C.6 D.9考点:-整式的加减—化简求值.专题:-计算题.分析:-将x﹣y=3代入原式计算即可得到结果.解答:-解:将x﹣y=3代入得:原式=3(x﹣y)2﹣2(x﹣y)﹣2(x﹣y)2+x﹣y=27﹣6﹣18+3=6.故选C.点评:-此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.8.当(b≠0)时,(8a﹣7b)﹣(4a﹣5b)等于()A.0 B.b C.2b D.4b考点:-整式的加减—化简求值.专题:-计算题.分析:-所求式子利用去括号法则去括号后,合并得到最简结果,将已知的等式代入计算即可求出值.解答:-解:∵a=,∴(8a﹣7b)﹣(4a﹣5b)=8a﹣7b﹣4a+5b=4a﹣2b=4×﹣2b=2b﹣2b=0.故选A.点评:-此题考查了整式的加减﹣化简求值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.二.填空题(共7小题)9.若x﹣y=﹣1,xy=2,则xy﹣x+y= 3 .考点:-整式的加减—化简求值.分析:-根据x﹣y=﹣1,xy=2,将xy﹣x+y变形后可得出结果.解答:-解:xy﹣x+y=xy﹣(x﹣y),将x﹣y=﹣1,xy=2代入得:xy﹣x+y=xy﹣(x﹣y)=3.点评:-本题考查整式的加减,属于基础题,化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面,也是一个常考的题材.10.如果m、n是两个不相等的实数,且满足m2﹣2m=1,n2﹣2n=1,那么代数式2m2+4n2﹣4n+1994= 2008 .考点:-整式的加减—化简求值.分析:-主要利用根与系数的关系得出m+n=2,把所求的代数式变形得出关于m+n的形式,整体代入即可求值.解答:-解:根据题意可知m,n是x2﹣2x﹣1=0两个不相等的实数根.则m+n=2,又m2﹣2m=1,n2﹣2n=12m2+4n2﹣4n+1994=2(2m+1)+4(2n+1)﹣4n+1994=4m+2+8n+4﹣4n+1994=4(m+n)+2000=4×2+2000=2008.点评:-主要考查了代数式求值问题.代数式中的字母表示的数没有明确告知,而是隐含在题设中,首先应从题设中获取关于n,m的代数式的值,然后把所求的代数式变形整理出题设中的形式,利用“整体代入法”求代数式的值.11.若x﹣y看成一个整体,则化简(x﹣y)2﹣3(x﹣y)﹣4(x﹣y)2+5(x+y)的结果是﹣3(x﹣y)2+2(x﹣y).考点:-整式的加减—化简求值.分析:-根据合并同类项的法则,可化简整式.解答:-解:原式=+=(x﹣y)2+(﹣3+5)(x+y)=﹣3(x﹣y)2+2(x﹣y).故答案为:﹣3(x﹣y)2+2(x,y).点评:-本题考查了整式的化简求值,利用了合并同类项,把(x﹣y)2、(x﹣y)当作整体是解题的关键.12.如果a<0,ab<0,则化简|a﹣b|+1﹣(a﹣b+3)的结果是﹣2a+2b﹣2 ,若a﹣b=﹣1,则其值为0 .考点:-整式的加减—化简求值.分析:-由a<0,ab<0,得出b>0,进一步根据绝对值的意义和去括号的法则化简合并得出答案即可.解答:-解:∵a<0,ab<0,∴b>0,∴|a﹣b|+1﹣(a﹣b+3)=﹣a+b+1﹣a+b﹣3=﹣2a+2b﹣2;若a﹣b=﹣1,则原式=﹣2(a﹣b)﹣2=2﹣2=0.故答案为:﹣2a+2b﹣2;0.点评:-此题考查整式的加减混合运算与化简求值,注意题目已知条件的理解和运用.13.已知a﹣b=3,c+d=2,则(b+c)﹣(a﹣d)的值为﹣1 .考点:-整式的加减—化简求值.分析:-运用整式的加减运算顺序,先去括号,再合并同类项.解答时把已知条件代入即可.解答:-解:原式=b+c﹣a+d=c+d﹣a+b=(c+d)﹣(a﹣b)=2﹣3=﹣1.点评:-本题考查整式的加减运算,解此题的关键是注意整体思想的应用.14.已知a+b=﹣7,ab=10,则代数式(3ab+6a+4b)﹣(2a﹣2ab)的值为22 .考点:-整式的加减—化简求值.分析:-先去括号,再合并同类项,最后代入求出即可.解答:-解:(3ab+6a+4b)﹣(2a﹣2ab)=3ab+6a+4b﹣2a+2ab=5ab+4a+4b=5ab+4(a+b)当a+b=﹣7,ab=10时,原式=5×10+4×(﹣7)=22,故答案为:22.点评:-本题考查了整式的加减和求值,用了整体代入思想,即分别把a+b和ab当作一个整体来代入.15.若多项式2x2+3x+7的值为10,则多项式6x2+9x﹣7的值为 2 .考点:-整式的加减—化简求值.分析:-由题意得2x2+3x=3,将6x2+9x﹣7变形为3(2x2+3x)﹣7可得出其值.解答:-解:由题意得:2x2+3x=36x2+9x﹣7=3(2x2+3x)﹣7=2.点评:-本题考查整式的加减,整体思想的运用是解决本题的关键.三.解答题(共7小题)16.求代数式2x3﹣5x2+x3+9x2﹣3x3﹣2的值,其中x=.考点:-整式的加减—化简求值.分析:-本题应先将原式合并同类项,再将x的值代入,即可解出本题.解答:-解:原式=2x3+x3﹣3x3+9x2﹣5x2﹣2=4x2﹣2,当x=时,原式=1﹣2=﹣1.点评:-本题考查了整式的化简.整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.17.先化简,再求值:4(x﹣y)﹣2(3x+y)+1,其中.考点:-整式的加减—化简求值.分析:-先去括号,再合并同类项,最后代入求值.解答:-解:原式=4x﹣4y﹣6x﹣2y+1,=﹣2x﹣6y+1,当x=1,y=﹣时,原式=﹣2×1﹣6×(﹣)+1=﹣2+2+1=1.点评:-去括号时,当括号前面是负号,括号内各项都要变号;合并同类项时把系数相加减,字母与字母的指数不变.18.已知a﹣2=0,求代数式3a﹣6+a2﹣4a+5的值.考点:-整式的加减—化简求值.专题:-计算题.分析:-先求出a的值,再将a=2代入即可解答.解答:-解:解法一:3a﹣6+a2﹣4a+5=a2﹣a﹣1.由a﹣2=0得a=2,原式=22﹣2﹣1=1.解法二:3a﹣6+a2﹣4a+5=3(a﹣2)+(a﹣2)2+1,因为a﹣2=0,原式=3×0+02+1=1.若有其它方法酌情给分.点评:-本题考查的是代数式求值、整体代入思想的知识.19.先化简,再求值:(3a2﹣ab+7)﹣(5ab﹣4a2+7),其中a=2,b=.考点:-整式的加减—化简求值.分析:-本题应先将括号去掉,然后合并同类项,将方程化为最简式,最后把a、b的值代入计算即可.解答:-解:原式=3a2﹣ab+7﹣5ab+4a2﹣7=7a2﹣6ab,当a=2,b=时,原式=24.点评:-本题考查了整式的运算,整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.20.先化简,再求值:(1)(6a﹣1)﹣(2﹣5a)﹣,其中a=2;(2)(3a2﹣ab+7)﹣(5ab﹣4a2+7),其中a=2,b=.考点:-整式的加减—化简求值.分析:-(1)根据去括号的法则,可去掉括号,根据合并同类项,可化简整式,根据代数式求值,可得答案;(2)根据去括号的法则,可去掉括号,根据合并同类项,可化简整式,根据代数式求值,可得答案.解答:-解:(1)(6a﹣1)﹣(2﹣5a)﹣=6a﹣1﹣2+5a+(1﹣a)=6a﹣1﹣2+5a+1﹣a=10a﹣2,把a=2代入原式,得10a﹣2=10×2﹣2=18;(2)(3a2﹣ab+7)﹣(5ab﹣4a2+7)=3a2﹣ab+7﹣5ab+4a2﹣7=7a2﹣6ab,把a=2,b=代入原式,得7a2﹣6ab=7×2﹣6×2×=14﹣4=10.,点评:-本题考查了整式的化简求值,注意去括号的法则:括号前是正号去掉括号不变号,括号前是负号去掉括号要变号.21.以知|m+n﹣2|+|mn+3|2=0,求﹣3的值.22.考点:-整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.专题:-计算题.分析:-利用非负数的性质求出m+n与mn的值,代入原式计算即可得到结果.解答:-解:∵|m+n﹣2|+|mn+3|2=0,∴m+n=2,mn=﹣3,则原式=(﹣3+2)﹣3×(4+9)=﹣1﹣39=﹣40.点评:-此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.22.化简求值:若a=﹣3,b=4,c=﹣,求7a2bc﹣{8a2cb﹣}的值.23.考点:-整式的加减—化简求值.分析:-本题应对代数式进行去括号,合并同类项,将代数式化为最简式,然后把a,b,c的值代入即可.注意去括号时,如果括号前是负号,那么括号中的每一项都要变号;合并同类项时,只把系数相加减,字母与字母的指数不变.解答:-解:原式=7a2bc﹣8a2cb+=﹣a2bc+a2bc+ab﹣2a2bc=﹣2a2bc+ab当a=﹣3,b=4,c=﹣时,原式==.点评:-化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面,也是一个常考的题材.。
七年级数学上册 3.4 整式的加减 3.4.4.1 整式加减跟踪训练(含解析)(新版)华东师大版-(
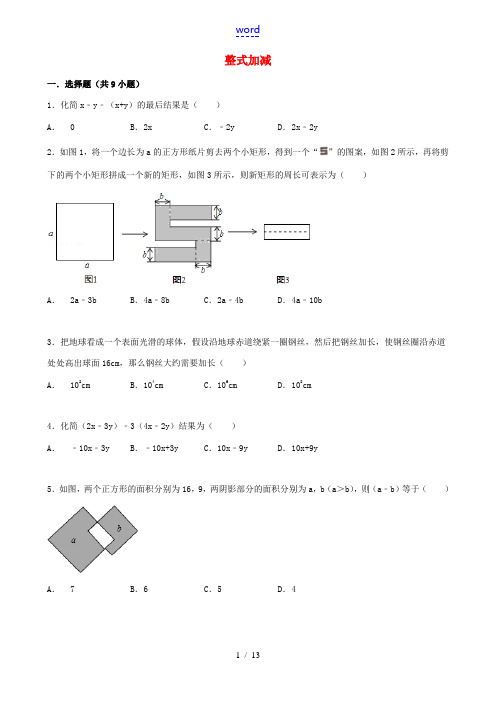
整式加减一.选择题(共9小题)1.化简x﹣y﹣(x+y)的最后结果是()A.0 B.2x C.﹣2y D.2x﹣2y2.如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为()A.2a﹣3b B.4a﹣8b C.2a﹣4b D.4a﹣10b3.把地球看成一个表面光滑的球体,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,那么钢丝大约需要加长()A.102cm B.104cm C.106cm D.108cm4.化简(2x﹣3y)﹣3(4x﹣2y)结果为()A.﹣10x﹣3y B.﹣10x+3y C.10x﹣9y D.10x+9y5.如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a﹣b)等于()A.7 B.6 C.5 D.46.把四X形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是()A.4mcm B.4ncm C.2(m+n)cm D.4(m﹣n)cm7.化简(﹣2a)2﹣(﹣2a)2(a≠0)的结果是()A.0 B.2a2C.﹣4a2D.﹣6a28.已知有一整式与(2x2+5x﹣2)的和为(2x2+5x+4),则此整式为()A. 2 B.6 C.10x+6 D.4x2+10x+29.已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是()A.﹣5x﹣1 B. 5x+1 C.﹣13x﹣1 D.13x+1二.填空题(共6小题)10.如图.在正方形ABCD的边长为3,以A为圆心,2为半径作圆弧.以D为圆心,3为半径作圆弧.若图中阴影部分的面积分为S1、S2.则S1﹣S2= _________ .11.计算:3(2x+1)﹣6x= _________ .12.在数轴上有示a、b、c三个实数的点的位置如图所示化简式子:|b﹣a|+|c﹣a|﹣|c﹣b|= _________ .13.已知A=3x﹣2,B=1+2x,则A﹣B= _________ .14.一个多项式与m2+m﹣2的和是m2﹣2m.这个多项式是_________ .15.化简:(x2+y2)﹣3(x2﹣2y2)= _________ .三.解答题(共6小题)16.化简:3(2x2﹣y2)﹣2(3y2﹣2x2).17.先化简再求值:若A=9a3b2﹣5b3﹣1,B=﹣7a2b3+8b3+2,求A+B+A,3B﹣A的值.18.有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a﹣c|+|b﹣c|+|a﹣b|.19.2(x2﹣x+1)﹣2(﹣2x+3x2)+(1﹣x)20.化简:4xy2﹣3x2y﹣{3x2y+xy2﹣}.21.“小马虎”在计算“M+N”时,误将“M+N”看成“M﹣N”,结果答案为xy﹣yz+5zx,如果N=7xy﹣yz+xz,你能求出正确的结果吗?第三章整式加减.1整式加减参考答案与试题解析一.选择题(共9小题)1.化简x﹣y﹣(x+y)的最后结果是()A.0 B.2x C.﹣2y D.2x﹣2y考点:-整式的加减.专题:-计算题.分析:-原式去括号合并即可得到结果.解答:-解:原式=x﹣y﹣x﹣y=﹣2y.故选C.点评:-此题考查了整式的加减,熟练掌握运算法则是解本题的关键.2.如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为()A.2a﹣3b B.4a﹣8b C.2a﹣4b D.4a﹣10b考点:-整式的加减;列代数式.专题:-几何图形问题.分析:-根据题意列出关系式,去括号合并即可得到结果.解答:-解:根据题意得:2=4a﹣8b.故选B点评:-此题考查了整式的加减,以及列代数式,熟练掌握运算法则是解本题的关键.3.把地球看成一个表面光滑的球体,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,那么钢丝大约需要加长()A.102cm B.104cm C.106cm D.108cm考点:-整式的加减;圆的认识.分析:-根据圆的周长公式分别求出半径变化前后的钢丝长度,进而得出答案.解答:-解:设地球半径为:rcm,则地球的周长为:2πrcm,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,故此时钢丝围成的圆形的周长变为:2π(r+16)cm,∴钢丝大约需要加长:2π(r+16)﹣2πr≈100(cm)=102(cm).故选:A.点评:-此题主要考查了圆的周长公式应用以及科学记数法等知识,根据已知得出图形变化前后的周长是解题关键.4.化简(2x﹣3y)﹣3(4x﹣2y)结果为()A.﹣10x﹣3y B.﹣10x+3y C.10x﹣9y D.10x+9y考点:-整式的加减.分析:-先按照去括号法则去掉整式中的小括号,再合并整式中的同类项即可.解答:-解:(2x﹣3y)﹣3(4x﹣2y)=2x﹣3y﹣12x+6y=﹣10x+3y.故选B.点评:-本题考查了整式的加减、去括号法则两个考点.解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.5.如图,两个正方形的面积分别为16,9,两阴影部分的面积分别为a,b(a>b),则(a﹣b)等于()A.7 B.6 C.5 D.4考点:-整式的加减.专题:-计算题;压轴题.分析:-设重叠部分面积为c,(a﹣b)可理解为(a+c)﹣(b+c),即两个正方形面积的差.解答:-解:设重叠部分面积为c,a﹣b=(a+c)﹣(b+c)=16﹣9=7,故选A.点评:-本题考查了等积变换,将阴影部分的面积之差转换成整个图形的面积之差是解题的关键.6.把四X形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是()A.4mcm B.4ncm C.2(m+n)cm D.4(m﹣n)cm考点:-整式的加减.专题:-压轴题.分析:-本题需先设小长方形卡片的长为a,宽为b,再结合图形得出上面的阴影周长和下面的阴影周长,再把它们加起来即可求出答案.解答:-解:设小长方形卡片的长为a,宽为b,∴L上面的阴影=2(n﹣a+m﹣a),L下面的阴影=2(m﹣2b+n﹣2b),∴L总的阴影=L上面的阴影+L下面的阴影=2(n﹣a+m﹣a)+2(m﹣2b+n﹣2b)=4m+4n﹣4(a+2b),又∵a+2b=m,∴4m+4n﹣4(a+2b),=4n.故选:B.点评:-本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.7.化简(﹣2a)2﹣(﹣2a)2(a≠0)的结果是()A.0 B.2a2C.﹣4a2D.﹣6a2考点:-整式的加减.分析:-应按照整式运算顺序,先算乘方,再算整式的加减.解答:-解:原式=4a2﹣4a2=0.故选A.点评:-整式的加减运算实际上就是去括号、合并同类项,这是各地中考的常考点.对于本题注意先算乘方,再算整式的加减.8.已知有一整式与(2x2+5x﹣2)的和为(2x2+5x+4),则此整式为()A. 2 B.6 C.10x+6 D.4x2+10x+2考点:-整式的加减.专题:-计算题.分析:-由于一整式与(2x2+5x﹣2)的和为(2x2+5x+4),那么把(2x2+5x+4)减去(2x2+5x﹣2)即可得到所求整式.解答:-解:依题意得(2x2+5x+4)﹣(2x2+5x﹣2)=2x2+5x+4﹣2x2﹣5x+2=6.故选B.点评:-本题考查的是有理数的运算能力.正确理解题意是解题的关键.9.已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是()A.﹣5x﹣1 B.5x+1 C.﹣13x﹣1 D.13x+1考点:-整式的加减.专题:-计算题.分析:-本题涉及多项式的加减运算,解答时根据各个量之间的关系作出回答.解答:-解:设这个多项式为M,则M=3x2+4x﹣1﹣(3x2+9x)=3x2+4x﹣1﹣3x2﹣9x=﹣5x﹣1.故选:A.点评:-此题考查了整式的加减运算,解决此类题目的关键是熟练运用多项式的加减运算、去括号法则.括号前添负号,括号里的各项要变号.二.填空题(共6小题)10.如图.在正方形ABCD的边长为3,以A为圆心,2为半径作圆弧.以D为圆心,3为半径作圆弧.若图中阴影部分的面积分为S1、S2.则S1﹣S2=﹣9 .考点:-整式的加减.专题:-几何图形问题.分析:-先求出正方形的面积,再根据扇形的面积公式求出以A为圆心,2为半径作圆弧、以D为圆心,3为半径作圆弧的两扇形面积,再求出其差即可.解答:-解:∵S正方形=3×3=9,S扇形ADC==,S扇形EAF==π,∴S1﹣S2=S扇形EAF﹣(S正方形﹣S扇形ADC)=π﹣(9﹣)=﹣9.故答案为:﹣9.点评:-本题考查的是整式的加减,熟知整式的加减实质上是合并同类项是解答此题的关键.11.计算:3(2x+1)﹣6x= 3 .考点:-整式的加减.专题:-计算题.分析:-原式去括号合并即可得到结果.解答:-解:原式=6x+3﹣6x=3.故答案为:3.点评:-此题考查了整式的加减,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.12.在数轴上有示a、b、c三个实数的点的位置如图所示化简式子:|b﹣a|+|c﹣a|﹣|c﹣b|= 0 .考点:-整式的加减;数轴;绝对值.专题:-计算题.分析:-由数轴上点右边的数总比左边的数大,判断出a,b及c的大小,进而确定出b﹣a,c﹣a及c﹣b 的正负,利用绝对值的代数意义化简绝对值运算,合并即可得到结果.解答:-解:由数轴上点的位置可得:c<0<a<b,∴b﹣a>0,c﹣a<0,c﹣b<0,∴|b﹣a|+|c﹣a|﹣|c﹣b|=b﹣a+a﹣c+c﹣b=0.故答案为:0点评:-此题考查了整式的加减运算,涉及的知识有:数轴上点的表示,绝对值的代数意义,以及合并同类项法则,判断出绝对值号中式子的正负是解本题的关键.13.已知A=3x﹣2,B=1+2x,则A﹣B= x﹣3 .考点:-整式的加减.分析:-首先表示出A﹣B,然后去括号、合并同类项即可求解.解答:-解:原式=(3x﹣2)﹣(1+2x)=3x﹣2﹣1﹣2x=x﹣3.故答案是:x﹣3.点评:-本题考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.14.一个多项式与m2+m﹣2的和是m2﹣2m.这个多项式是﹣3m+2 .考点:-整式的加减.专题:-常规题型.分析:-根据一多项式与m2+m﹣2的和是m2﹣2m,利用两多项式的和减去已知多项式求出未知个多项式即可.解答:-解:∵一多项式与m2+m﹣2的和是m2﹣2m.∴这个多项式是:m2﹣2m﹣(m2+m﹣2)=﹣3m+2.故答案为:﹣3m+2.点评:-此题主要考查了整式的加减运算,根据已知得出两多项式的和减去已知多项式求出未知个多项式是解决问题的关键.15.化简:(x2+y2)﹣3(x2﹣2y2)= ﹣2x2+7y2.考点:-整式的加减.分析:-本题考查了整式的加减运算,解答时要先去括号,再合并同类项得出结果.解答:-解:原式=x2+y2﹣3x2+6y2=﹣2x2+7y2.点评:-整式的加减运算,是各地中考的常考点.解决此类题目的关键是去括号法则,注意运用乘法的分配律,不要漏乘括号里的项.三.解答题(共6小题)16.化简:3(2x2﹣y2)﹣2(3y2﹣2x2).考点:-整式的加减.分析:-熟练运用去括号法则去括号,然后合并同类项.注意去括号时,如果括号前是负号,那么括号中的每一项都要变号;合并同类项时,只把系数相加减,字母与字母的指数不变.解答:-解:3(2x2﹣y2)﹣2(3y2﹣2x2)=6x2﹣3y2﹣6y2+4x2=10x2﹣9y2.点评:-关键是去括号.①不要漏乘;②括号前面是“﹣”,去括号后括号里面的各项都要变号.17.先化简再求值:若A=9a3b2﹣5b3﹣1,B=﹣7a2b3+8b3+2,求A+B+A,3B﹣A的值.考点:-整式的加减.分析:-根据题意将A,B直接代入进而合并同类项得出即可.解答:-解:∵A=9a3b2﹣5b3﹣1,B=﹣7a2b3+8b3+2,∴A+B+A=9a3b2﹣5b3﹣1﹣7a2b3+8b3+2+9a3b2﹣5b3﹣1=18a3b2﹣7a2b3﹣2b3;3B﹣A=3×(﹣7a2b3+8b3+2)﹣(9a3b2﹣5b3﹣1)=﹣21a2b3﹣9a3b2+29b3+7.点评:-此题主要考查了整式的加减运算,正确合并同类项是解题关键.18.有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a﹣c|+|b﹣c|+|a﹣b|.考点:-整式的加减;数轴;绝对值.分析:-由图知,b>0,a﹣c<0,b﹣c>0,a﹣b<0,根据正数的绝对值等于它本身,负数的绝对值等于它的相反数可得,|b|+|a﹣c|+|b﹣c|+|a﹣b|=b+c﹣a+b﹣c+b﹣a=3b.解答:-解:由数轴得,a<c<0<b,∴b>0,a﹣c<0,b﹣c>0,a﹣b<0,∴|b|+|a﹣c|+|b﹣c|+|a﹣b|=b+c﹣a+b﹣c+b﹣a=3b﹣2a.点评:-本题考查了整式的加减,绝对值与数轴,用两种不同的方法即几何方法和代数方法进行求解.通过比较,可以发现借助数轴用几何方法化简含有绝对值的式子,比较有关数的大小有直观、简捷,举重若轻的优势.19.2(x2﹣x+1)﹣2(﹣2x+3x2)+(1﹣x)考点:-整式的加减.专题:-计算题.分析:-原式去括号合并即可得到结果.解答:-解:原式=2x2﹣2x+2+4x﹣6x2+1﹣x=﹣4x2+x+3.点评:-此题考查了整式的加减,熟练掌握运算法则是解本题的关键.20.化简:4xy2﹣3x2y﹣{3x2y+xy2﹣}.考点:-整式的加减.专题:-计算题.分析:-原式去括号合并即可得到结果.解答:-解:原式=4xy2﹣3x2y﹣3x2y﹣xy2+2xy2﹣4x2y+x2y﹣2xy2=3xy2﹣9x2y.点评:-此题考查了整式的加减,熟练掌握运算法则是解本题的关键.21.“小马虎”在计算“M+N”时,误将“M+N”看成“M﹣N”,结果答案为xy﹣yz+5zx,如果N=7xy﹣yz+xz,你能求出正确的结果吗?考点:-整式的加减.分析:-首先用结果xy﹣yz+5zx加上N=7xy﹣yz+xz,得出M,再进一步算出M+N算得正确的结果.解答: -解:(xy﹣yz+5zx)+(7xy﹣yz+xz)+(7xy﹣yz+xz)=xy﹣yz+5zx+7xy﹣yz+xz+7xy﹣yz+xz=xy+7xy+7xy﹣yz﹣yz﹣yz+5zx+xz+xz=15xy﹣3yz+7zx.正确的结果是15xy﹣3yz+7zx.点评:-此题考查整式的加减运算,根据题意列出算式,进一步利用去括号的方法和合并同类项的方法解决问题.。
3华东师大版初中数学七年级上册专题训练.4 整式的加减

3.4整式的加减一、选择题1.如果代数式4y2-2y+5的值为7,那么代数式2y2-y+1的值等于()A.2B.3C.-2D.42.下面的式子,正确的是()A.3a2+5a2=8a4B.5a2b-6ab2=-ab2C.6xy-9yx=-3xyD.2x+3y=5xy3.一个多项式加上x2y-3xy2得2x2y-xy2,则这个多项式是()A.3x2y-4xy2 C.x2y+2xy2B.x2y-4xy2 D.-x2y-2xy24.若A=x2-5x+2,B=x2-5x-6,则A与B的大小关系是()A.A>BB.A=BC.A<BD.无法确定5.若A=5a2-4a+3,B=3a2-4a+2,则A与B的大小关系是()A.A=B B.A>B C.A<B D.以上都可能成立6.当x=-1时,2ax3-3bx+8的值为18,则12b-8a+2的值为()A.40B.42C.46D.567.已知一个多项式与3x2+9x的和等于3x2+4x-1,则这个多项式是()A.-5x-1B.5x+1C.-13x-1D.13x+18.三个连续奇数,中间的一个是2n+1(n是整数),则这三个连续奇数的和为()A.2n-1B.2n+3C.6n+3D.6n-39.若A和B都是五次多项式,则A-B一定是()A.十次多项式B.五次多项式C.次数不高于5的整式D.次数不高于5的多项式二、填空题10.如果x=1时,代数式2ax3+3bx+4的值是5,那么x=-1时,代数式2ax3+3bx+4的值是__________.11.定义ab ab为二阶行列式,规定它的运算法则为cd cd=ad-bc,那么二阶行列式23x-1x+1=____________.三、解答题12.化简:(1)7-3x-4x2+4x-8x2-15;(2)2(2a2-9b)-3(-4a2+b);“ b 3(3) 8x 2-[-3x-(2x 2-7x-5)+3]+4x.13.先化简,后求值:(1)(5x-3y-2xy)-(6x+5y-2xy),其中 x = -5 , y = -1;(2)若 a - 2 + (b + 3)2 = 0 ,求 3a 2b -[2ab 2-2(ab -1.5a 2b )+ab]+3ab 2 的值.14.有这样一道题目: 当 a =0.35, =-0.28 时,求多项式 7a 3- (2a 3b -a 2b -a 3)+ (6a 3b-3a 2b )-(10a 3-3)的值”.小敏在计算时把 a =0.35,b =-0.28 抄成了 a =-0.35,b=0.28,结果她的结果也是正确的,你知道这是为什么吗?15.某工厂第一车间有 m 人,第二车间的人数比第一车间的人数的 2 倍少 5 人,第三车间的人数比第一车间的人数的 3 倍还多 7 人,则第三车间的人数比第一、第二车间的人数的和多还是少?请说明理由.16.已知A=2x2-9x-11,B=3x2-6x+4,求:(1)A-B;(2)12A+2B.17.图中的数阵是由全体奇数排成的.(1)图中平行四边形框内的九个数之和与中间的数有什么关系?(2)在图中任意作一个类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由.这九个数之和能等于2016,2018或2025吗?若能,请写出这九个数中最小的一个;若不能,请说出理由.18.一辆出租车从A地出发,在一条东西走向的街道上营运,每次行驶的路程(向东记为正)记录如下(9<x<26,单位:km):第一次第二次第三次第四次x1-x2x-52(9-x)(1)说出这辆出租车每次行驶的方向.(2)这辆出租车一共行驶了多少路程?答案一、1.A 2.C 3.C 4.A5.B分析:可用作差法:A-B=5a2-4a+3-(3a2-4a+2)=5a2-4a+3-3a2+4a-2=2a2+1.因为a2≥0,所以2a1+1≥1,所以A-B>0,即A>B.6.B分析:把x=-1代入2ax3-3bx+8得2a×(-1)3—36×(-1)+8=-2a+3b+8.因为此式的值为18,所以-2a+3b+8=18,所以3b-2a=10,所以12b-8a=40,所以12b-8a+2=40+2=42.7.A分析:设这个多项式为M,则M=3x2+4x-1-(3x2+9x)=3x2+4x-1-3x2-9x=-5x-1.8.C分析:已知三个连续奇数中的中间一个为2n+1(n为整数),那么,较小的一个为2n-1,较大的一个为2n+3,所以这三个奇数的和为(2n-1)+(2n+1)+(2n+3)=6n+3.9.C分析:当A,B中含字母的项不都相同时,A-B是次数不高于5的多项式;当A,B 中含字母的项都相同时,A-B为常数,此时是单项式,属于整式,故选C.二、10.3分析:把x=1代入2ax3+3bx+4=5,进行变形,然后利用整体代入法求值.因为当x=1时,代数式2ax3+3bx+4的值是5,所以2a+3b+4=5,即2a+3b=1.当x=-1时,2ax3+3bx+4=-2a-3b+4=-(2a+3b)+4=-1+4=3.11.-x+5分析:由题意得2(x+1)-3(x-1)=2x+2-3x+3=-x+5.三、12、(1)-12x2+x-8;(2)16a2-21b;(3)10x2-8.13.(1)-x-8y=13;(2)ab2+ab=12.14.解:7a3-3(2a3b-a2b-a3)+(6a3b-3a2b)-(10a3-3)=7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3+3=(7a3+3a3-10a3)-6a3b+6a3b+3a2b-3a2b+3=3.因为3是常数,不含字母a和b,所以无论a,b是何值,结果都不变.故小敏将a,b抄错时,结果也是正确的.15.解:第三车间的人数比第一、第二车间的人数的和多12人,理由如下:由题意得,第二车间的人数为2m-5,第三车间的人数为3m+7,所以3m+7-(2m-5+m)=3m+7-(3m-5)=3m+7-3m+5=12>0,故第三车间的人数比第一、第二车间的人数的和多12人.16.解:(1)A-B=(2x2-9x-11)-(3x2-6x+4)=2x2-9x-11-3x2+6x-4=-x2-3x-15;= x 2- x - + 6x 2 - 12x + 8 = 7 x 2 - x + .所以 x>0, - x <0 ,x -5>0,2(9-x )<0.(2)因为 | x | + - x + | x - 5 | + | 2(9 - x) |所以这辆出租车一共行驶了 x - 23⎪ km .A + 2B =(2) 1 1(2 x 2 - 9x - 11) + 2(3x 2 - 6x + 4)2 29 11 33 52 2 2 217.解:(1)平行四边形框内的九个数之和是中间的数的 9 倍.(2)任意作一个类似(1)中的平行四边形框,规律仍然成立,理由:不妨设平行四边形框中间的数为 n ,则这九个数按大小顺序依次为(n -18),(n -16),(n -14), (n -2) ,n ,(n +2),(n +14),(n +16),(n +18).显然,其和为 9n ,是 n 的 9 倍.这九个数之和不能等于 2 016.若和为 2 016,则 9n =2 016,n =224,是偶数,显然不在数阵中,这九个数之和也不能等于 2 018,因为 2 018 不能被 9 整除.这九个数之和能等于 2 025,中间数为 225,最小的数为 225-18=207.题后总结:方框形题要从横行和竖列两个方面找数字间的规律.18.解:(1)因为 9<x<26,1 2又因为向东为正,所以这辆出租车第一次向东行驶,第二次向西行驶,第三次向东行驶,第四次向西行驶.121= x + x + x - 5 - 2(9 - x)21= x + x + x - 5 - 18 + 2x2 = 9x - 23 2 ,⎛ 9 ⎫ ⎝ 2 ⎭。
整式的加减 华东师大版数学七年级上册素养提升练(含解析)

第3章整式的加减3.4整式的加减3.4.4 整式的加减基础过关全练知识点整式的加减1.已知多项式A=x2+2y2-z2,B=-4x2+3y2+2z2,那么A+B= ()A.5x2-y2-z2B.3x2-5y2+z2C.3x2+5y2+z2D.-3x2+5y2+z22.(2023河南许昌禹州期中)多项式2x2-7x+3减去5x2-x-4的结果是()A.-3x2-6x+7B.-3x2-8x-1C.7x2-8x+7D.-3x2-6x-13.【新独家原创】多项式2m+5n与3m+2n的和比它们的差多 ()A.6m+4nB.4m+4nC.6m-4nD.-6m+4n4.(2023湖南郴州永兴期末)一个多项式加上3x2-6x+4得到-7x2+x+1,则这个多项式是.,则5(a2-2ab)-[a2-5.(2023江西宜春丰城中学期中)若a=-3,b=133b+3(ab+b)]= .6.化简:(1)(2023吉林榆树期末)(3a2-a+7)-(-4a2+2a+6);(2)5(3a2b-ab2)-4(-ab2+3a2b).7.【教材变式·P112T8】先化简,再求值.(1)(2023山西阳泉期末)3(a2-4a)-(-2a+4a2),其中a=-1;(2)(2023吉林长春外国语学校期末)2(x2y-2xy)-3(x2y-3xy)+x2y,其中x=-1,y=1;5(3)(2023四川泸州泸县四中期末)(2a2−b2−3ab)-(a2-3ab)-(−a2+12ab),其中a=1,b=-2;2(4)(2023河南南阳唐河期末)2xy-[1(5xy−16x2y2)−2(xy−4x2y2)],其中x=-12,y=4;2(5)(2023重庆九龙坡渝高中学期末)3(xy2-2xy)-2(3y2x-3yx+1)+4xy2,其中x,y满足(x-2)2+|2y+1|=0;(6)(2023北京平谷期末)3(a2b+a-2b)-2(a2b+a)-(a2b-5b-1),其中a、b满足a-b=5.8.【一题多变】(2022河南周口太康朱口一中入学测试)已知A=x2+xy-y2,B=3x2-4xy-2y2.(1)化简2A-(2B-A);(2)若x=-1,y=2,对(1)的化简结果求值.[变式1](2023陕西汉中宁强期末)小明在计算A-B时,误将A-B看成了A+B,结果求出的答案是-2x2-x+3,已知B=4x2-5x-6.请你帮他纠错,正确地算出A-B.[变式2](2023河南南阳第一完全学校期末)已知A=3x2-x+2y-4xy,B=2x2-3x-y+xy. (1)当x+y=-6,xy=-1,求2A-3B的值;7(2)若2A-3B的值与x的取值无关,求2A-3B的值.能力提升全练9.【整体思想】(2023云南昭通绥江期中,11,★☆☆)若x-2y=3,则代数式x-2y-2(y-x)-(x-3)的值为 ()A.-3B.3C.6D.910.【代数推理】(2022四川内江期末,10,★☆☆)如果M=x2-3x+5,N=-x2-3x+2,那么M 与N的大小关系是()A.M<NB.M=NC.M>ND.无法确定11.(2022内蒙古包头中考,17,★☆☆)若一个多项式加上3xy+2y2-8,结果得2xy+3y2-5,则这个多项式为.12.(2023山东济南高新区期末,16,★★☆)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,如下:-x2-4xy+4y2=-x2+3y2,则被捂住的多项式是.13.(2022陕西榆林绥德期末,12,★★☆)王华乘公交车去公园玩,王华上车时,发现车上共有(4x+2y)人,车到中途时,有一半人下车,但又上来若干人,这时公交车上共有(8x-4y)人,则中途上车的有人.14.【数形结合思想】(2023吉林松原前郭期末,19,★★☆)已知有理数a、b、c在数轴上对应点的位置如图所示.解答下列各题:(1)用“>”或“<”填空:a-b0,b-c0,c-a0,b+c0;(2)化简:|a-b|+|b-c|-|c-a|+|b+c|.15.【代数推理】(2023湖北黄石阳新期中,23,★★☆)一个正两位数的个位数字是a,十位数字比个位数字大2.(1)请列式表示这个两位数,并化简;(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新两位数与原两位数的和能被22整除.素养探究全练16.【运算能力】(2022四川眉山仁寿期末)已知A=2a2b-3ab2+abc,小明错将“2A-B”看成“2A+B”,算得结果C=2a2b-5ab2+4abc.(1)求B;(2)求2A-B;(3)小明说2A-B的值与c的取值无关,对吗?若a=-2,b=-1,求2A-B的值.答案全解全析基础过关全练1.D A+B=x2+2y2-z2+(-4x2+3y2+2z2)=x2+2y2-z2-4x2+3y2+2z2=-3x2+5y2+z2.故选D.2.A 根据题意知,(2x2-7x+3)-(5x2-x-4)=2x2-7x+3-5x2+x+4=-3x2-6x+7,故选A.3.A 根据题意,得[(2m+5n)+(3m+2n)]-[(2m+5n)-(3m+2n)]=(2m+5n+3m+2n)-(2m+5n-3m-2n)=(5m+7n)-(-m+3n)=5m+7n+m-3n=6m+4n,故选A.4.答案-10x2+7x-3解析根据题意,得这个多项式为-7x2+x+1-(3x2-6x+4)=-7x2+x+1-3x2+6x-4=-10x2+7x-3.故答案为-10x2+7x-3.5.答案49解析5(a2-2ab)-[a2-3b+3(ab+b)]=5a2-10ab-(a2-3b+3ab+3b)=5a2-10ab-a2-3ab=5a2-a2-10ab-3ab=4a2-13ab,当a=-3,b=13时,原式=4×(-3)2-13×(-3)×13=36+13=49.故答案为49.6.解析(1)原式=3a2-a+7+4a2-2a-6=7a2-3a+1.(2)原式=15a2b-5ab2+4ab2-12a2b=3a2b-ab2.7.解析(1)3(a2-4a)-(-2a+4a2)=3a2-12a+2a-4a2=-a2-10a,当a=-1时,原式=-(-1)2-10×(-1)=-1+10=9.(2)2(x2y-2xy)-3(x2y-3xy)+x2y=2x2y-4xy-3x2y+9xy+x2y=5xy,当x=-1,y=15时,原式=5×(-1)×15=-1.(3)原式=2a 2-b 2-32ab -a 2+3ab +a 2-12ab =2a 2+ab -b 2,当a =1,b =-2时,原式=2×12+1×(-2)-(-2)2=2-2-4=-4.(4)原式=2xy -(52xy −8x 2y 2−2xy +8x 2y 2)=2xy -12xy =32xy ,当x =-12,y =4时,原式=32×(−12)×4=-3.(5)原式=3xy 2-6xy -6y 2x +6yx -2+4xy 2=xy 2-2,∵(x -2)2+|2y +1|=0,∴x =2,y =-12, ∴原式=2×(−12)2-2=12-2=-32. (6)3(a 2b +a -2b )-2(a 2b +a )-(a 2b -5b -1)=3a 2b +3a -6b -2a 2b -2a -a 2b +5b +1=a -b +1,∵a -b =5,∴原式=6.8.解析 (1)∵A =x 2+xy -y 2,B =3x 2-4xy -2y 2,∴2A -(2B -A )=2A -2B +A =3A -2B =3(x 2+xy -y 2)-2(3x 2-4xy -2y 2)=3x 2+3xy -3y 2-6x 2+8xy +4y 2=-3x 2+11xy +y 2.(2)当x =-1,y =2时,-3x 2+11xy +y 2=-3×(-1)2+11×(-1)×2+22=-3×1+(-22)+4=-3+(-22)+4=-21.[变式1] 解析 由题意得,A =(-2x 2-x +3)-(4x 2-5x -6)=-2x 2-x +3-4x 2+5x +6=-6x 2+4x +9,则A -B =(-6x 2+4x +9)-(4x 2-5x -6)=-6x 2+4x +9-4x 2+5x +6=-10x 2+9x +15.[变式2] 解析 (1)∵A =3x 2-x +2y -4xy ,B =2x 2-3x -y +xy ,∴2A -3B =2(3x 2-x +2y -4xy )-3(2x 2-3x -y +xy )=6x 2-2x +4y -8xy -6x 2+9x +3y -3xy =7x +7y -11xy ,当x +y =-67,xy =-1时,2A -3B =7x +7y -11xy =7(x +y )-11xy =7×(−67)-11×(-1)=-6+11=5. (2)∵2A -3B =7x +7y -11xy =(7-11y )x +7y ,∴当2A -3B 的值与x 的取值无关时,7-11y =0,∴y =711,∴2A -3B =0+7×711=4911.能力提升全练9.D ∵x-2y=3,∴原式=x-2y-2y+2x-x+3=2x-4y+3=2(x-2y)+3=6+3=9,故选D.10.C 因为M-N=(x2-3x+5)-(-x2-3x+2)=x2-3x+5+x2+3x-2=2x2+3>0,所以M>N.故选C.11.答案y2-xy+3解析由题意得,这个多项式为(2xy+3y2-5)-(3xy+2y2-8)=2xy+3y2-5-3xy-2y2+8=y2-xy+3.故答案为y2-xy+3.12.答案4xy-y2解析由题意得被捂住的多项式是-x2+3y2-(-x2-4xy+4y2)=-x2+3y2+x2+4xy-4y2=4xy-y2.故答案为4xy-y2.13.答案(6x-5y)(4x+2y)=8x-4y-2x-y=6x-5y,则中途上车的有(6x-5y)人.解析根据题意得,(8x-4y)-12故答案为(6x-5y).14.解析(1)根据数轴可知,-1<c<0<b<1<a<2,∴a-b>0,b-c>0,c-a<0,b+c<0,故答案为>;>;<;<.(2)原式=(a-b)+(b-c)+(c-a)-(b+c)=a-b+b-c+c-a-b-c=-b-c.15.解析(1)由题意可得这个两位数为10(a+2)+a=11a+20.(2)由题意可得,新两位数是10a+a+2=11a+2,故新两位数与原两位数的和是11a+2+11a+20=22(a+1),故新两位数与原两位数的和能被22整除.素养探究全练16.解析(1)由题意可知B=C-2A=(2a2b-5ab2+4abc)-2(2a2b-3ab2+abc)=2a2b-5ab2+4abc-4a2b+6ab2-2abc=-2a2b+ab2+2abc.(2)2A-B=2(2a2b-3ab2+abc)-(-2a2b+ab2+2abc)=4a2b-6ab2+2abc+2a2b-ab2-2abc=6a2b-7ab2.(3)对.当a=-2,b=-1时,原式=6×(-2)2×(-1)-7×(-2)×(-1)2=6×4×(-1)-7×(-2)×1=-24+14=-10.。
七年级数学上册 3.4 整式的加减巩固训练 华东师大版

3.4 整式的加减基础巩固训练一、选择题1、 下列各组中的两个单项式,属于同类项的是( )A.6xy 和6xyzB.3x 与35C.22a b 与212ab - D.40.85xy 与4y x - 2、 下列各式中,合并同类项结果正确的是( )3、 A.235325x x x += B.222538mn m n m n +=4、 C.660xy yx -= D.2232a a a -=5、 若213a x y -与2b xy 是同类项,则a b的值是( ) A.32 B.2 C.3 D.126、 在下列单项式中,说法正确的是( )①36x ②23xy ③20.37y x -④214x -⑤213xy z A.没有同类项 B.②与③是同类项 C. ②与⑤是同类项 D. ①与④是同类项7、 下列添括号正确的是( )A.323272867(286)x x x x x x --+=--+B.()()a b c d a d b c -+-=--+C.225623(562)3a ab a b a ab a b ---=-+--D.27(27)a b c a b c -+=--8、 化简(53)3(2)a a b a b --+-的结果是( )A.2aB.6b -C.26a b -二、填空题1、单项式22224,6,3,a b ab a b a b --的和是。
2、两个单项式2212m a b 与412n a b -的和是一个单项式,那么m =,n =。
3、当k =时,多项式21383x kxy xy -+-中不含xy 项。
4、把()a b -看作一个整体,合并同类项7()3()2()a b a b a b -----=5、某三角形第一条边长(2)a b -厘米,第二条边比第一条边长()a b +厘米,第三条边比第一条边的2倍少b 厘米,那么这个三角形的周长是厘米。
三、解答题已知2244A x xy y =-+,225B x xy y =+-,求:A -3B ;②3A+B 。
华师大版初中数学七年级上册《3.4.4 整式的加减》同步练习卷(含答案解析

华师大新版七年级上学期《3.4.4 整式的加减》同步练习卷一.解答题(共50小题)1.计算(1)﹣×(+3);(2)3(4a2﹣2ab3)﹣2(5a2﹣3ab3)2.化简:2(x2﹣5xy)﹣3(﹣6xy+x2)3.王老师给同学们出了一道化简的题目:2(2x2y+x)﹣3(x2y﹣2x),小亮同学的做法如下:2(2x2y+x)﹣3(x2y﹣2x)=4x2y+x﹣3x2y﹣2x=x2y﹣x.请你指出小亮的做法正确吗?如果不正确,请指出错在哪?并将正确的化简过程写下来.4.计算化简(1)﹣24﹣2×(﹣3)+|﹣2﹣5|÷(﹣1)2017.(2)6a2﹣2[(﹣3a2b+5ab2)﹣2(5a2b﹣3ab2)].5.2xy2﹣3(2x2﹣xy2+2)+(7x2﹣5xy2).6.已知:A=4a2﹣7ab+b,且B=2a2+6ab+7.(1)求A﹣2B.(2)若A+B+C=0,求C所表示的多项式.7.一般情况下不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;(3)若(m,n)是“相伴数对”,求代数式m﹣﹣[4m﹣2(3n﹣1)]的值.8.阅读下面的解题过程:计算2(﹣4a+3b)﹣3(a﹣2b).解:原式=(﹣8a+6b)﹣(3a﹣6b)(第一步)=﹣8a+6b﹣3a﹣6b (第二步)=﹣11a+12b (第三步)回答:(1)上面解题过程中有两步错误,第一处是第步;第二处是第步.(2)请给出正确的计算过程.9.化简:(1)a﹣(3a+b)+(a﹣5b)(2)5abc﹣2a2b﹣[3abc﹣3(4ab2+a2b)].10.数轴上点A对应的数为a,点B对应的数为b,且多项式﹣﹣2xy+5的次数为a,常数项为b.(1)直接写出:a=,b=.(2)数轴上点A、B之间有一动点P(不与A、B重合),若点P对应的数为x,试化简:|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|.(3)若M=3b2﹣2a2+5ab,N=4ab﹣2b2﹣a2,求3M﹣4N的值.11.已知a是绝对值等于4的负数,b是最小的正整数,c的倒数的相反数是﹣2,(1)求a,b,c的值;(2)求:4a2b3﹣[2abc+(5a2b3﹣7abc)﹣a2b3].12.小兵喜欢研究数学问题,在计算整式的加减(﹣4x2﹣7+5x)+(2x﹣3+3x2)的时候,想到了小学的列竖式加减法,令A=﹣4x2﹣7+5x,B=2x﹣3+3x2,然后将两个整式关于x进行降幂排列,A=﹣4x2+5x﹣7,B=3x2+2x﹣3,最后只要写出其各项系数对齐同类项进行竖式计算如下:所以,(﹣4x2﹣7+5x)+(2x﹣3+3x2)=﹣x2+7x﹣10若A=﹣4x2y2+2x3y﹣5xy3+2x4,B=3x3y+2x2y2﹣y4﹣4xy3,请你按照小兵的方法,先对整式A,B关于某个字母进行降幂排列,再写出其各项系数进行竖式计算A ﹣B,并写出A﹣B值.13.化简:(1)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b);(2)7x+2(x2﹣2)﹣4(x2﹣x+3).14.已知天平左边托盘中的物体重量为x,右边托盘中的物体重量为y,其中x=30(1+a2)﹣3(a﹣a2),y=31﹣[a﹣2(a2﹣a)﹣31a2](1)化简x和y;(2)请你想一想,天平会倾斜吗?如果出现倾斜,将向哪边倾斜?请说明理由.15.设A=﹣x﹣4(x﹣y)+(﹣x+y).(1)当x=﹣,y=1时,求A的值;(2)若y﹣3x=2,则(1)中A=.16.已知A=﹣3x2﹣2mx+3x+1,B=2x2+mx﹣1(1)求5A﹣3(A﹣B)的值(2)若(1)中的值与x的值无关,求m的值.17.化简下列各式:(1)5(a2b﹣2ab2)﹣4(3a2b﹣2ab2).(2)﹣2x2﹣[3y2﹣2(x2﹣3y2)+6].18.若定义=ad﹣bc,如:=2×b﹣a×(﹣1)=2b+a①计算,并指出结果是几次几项式.②若|x﹣3+y|与(xy+4)2互为相反数,求①式的值.19.计算.(1)5(2x﹣7y)﹣3(4x﹣10y);(2)(5a﹣3b)﹣3(a2﹣2b);(3)3(3a2﹣2ab)﹣2(4a2﹣ab)(4)2x﹣[2(x+3y)﹣3(x﹣2y)].20.化简(1)(2x2﹣+3x)﹣4(x﹣x2+)(2)x﹣2(x﹣)﹣(﹣)21.化简求值:2(a2﹣ab)﹣3(2a2﹣ab),其中a=﹣2,b=3.22.先化简再求值:2x2y﹣[3xy2﹣2(xy2+2x2y)],其中x=,y=﹣2.23.已知代数式A=﹣6x2y+4xy2﹣5,B=﹣3x2y+2xy2﹣3.(1)求A﹣B的值,其中x=1,y=﹣2.(2)请问A﹣2B的值与x,y的取值是否有关系,试说明理由.24.已知A=2ab﹣a,B=﹣ab+2a.(1)计算:5A+4B;(2)当|a+2|+(3﹣b)2=0,求5A+4B的值.25.先化简,再求值:2xy﹣(4xy﹣4x2y2)+2 (3xy﹣5x2y2),其中x,y满足(x+1)2+|y﹣2|=0.26.先化简,再求值:(1),其中x=3,y=﹣.(2)已知a+b=7,ab=10,求代数式(5ab+4a+7b)+(6a﹣3ab)﹣(4ab﹣3b)的值.27.先化简,再求值:3(a2b﹣ab)﹣2(ab﹣3a2b+1),其中a=,b=6.28.先化简,再求值:5(3a2b﹣ab2)﹣3(﹣ab2+4a2b),其中a=﹣,b=.29.先化简,再求值:x﹣2(x﹣y2)﹣(﹣x+y2),其中x=3,y=﹣.30.先化简,再求值:(1)5x2﹣[2xy﹣3(xy+2)+4x2]﹣xy.其中x=﹣2,y=;(2)已知a=﹣1,b=2,求2a2﹣[8ab+(ab﹣4a2)]﹣ab的值.31.计算:(1)m2+2m+2m2﹣3m;(2)先化简,再求值:(ab﹣3a2)﹣[5ab﹣2(2a2﹣ab)],其中a=﹣2,b=1.32.先化简再求值:2m﹣2(m2+m﹣1),其中m=﹣2.33.先化简,再求代数式的值:2(x2y+xy2)﹣2(x2y﹣2)﹣(xy2+2),其中x=2018,y=﹣1.34.先化简,再求值:3a2b﹣6ab2﹣2(2a2b﹣3ab2﹣2),其中a=﹣1.b=2.35.先化简,再求值.4ab﹣[(a2+5ab﹣b2)﹣2(a2+3ab﹣b2),其中a=﹣1,b=2.36.先化简,再求值.已知|x﹣3|+(y+)2=0,先化简再求值:3x2y﹣[2xy2﹣3(xy﹣x2y)+xy]+5xy2 37.先化简,后求值.求2(a2b+ab2)﹣5(2ab2﹣1+a2b)﹣2的值,其中a=1,b=﹣2.38.①计算:3(2x2﹣xy)﹣2(3x2+xy﹣1)②先化简,再求值:2(ab2﹣2a2b)﹣3(ab2﹣a2b)+(2ab2﹣2a2b)其中:a=2,b=1.39.(1)先化简,再求值:3x2y﹣[2xy2﹣2(xy﹣x2y)+xy]+3xy2,其中x=3,y=﹣;(2)已知2x2﹣3x=7,求整式6x﹣4x2+5的值.40.化简:(1)3x2﹣3(x2﹣2x+1)+4;(2)先化简再求值:3x2y﹣[2xy2﹣2(xy﹣1.5x2y)+xy]+3xy2,其中x=﹣3,y=﹣2.41.(1)计算:﹣3(2a2﹣2ab)+4(a2+ab﹣6)(2)化简求值:12(x2y﹣xy2)+5(xy2﹣x2y)﹣2x2y,其中x=,y=﹣5.42.先化简,再求值(﹣2x2+xy﹣y2)+2(x2﹣xy);其中x=2,y=﹣.43.先化简,再求值:5x2y﹣[x2﹣3(xy2﹣2x2y)+3xy2],其中x=6,|y|=,且xy<0.44.化简(1)求3a2﹣ab+1减4a2+6ab﹣7所得的差;(2)化简,求值4x2y﹣[6xy﹣2(3xy﹣2)﹣x2y]+1,其中x=﹣,y=8.45.先化简,再求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=﹣,b=.46.化简求值:﹣3xy2﹣2(xy﹣x2y)﹣(3x2y﹣2xy2),其中x=﹣4,y=.47.化简后求值:3(x2y+xy2)﹣3(x2y﹣1)﹣4xy2﹣3,其中x、y满足|x﹣2|+(y+)2=0.48.先化简,再求值:2(a2﹣ab)﹣3(a2﹣ab),其中,a=﹣2,b=3.49.先化简,再求值已知|x﹣2|+(y+1)2=0,求2x2﹣[5xy﹣3(x2﹣y2)]﹣5(﹣xy+y2)的值.50.先化简,再求值:2x﹣[3x﹣2(x﹣1)﹣3],其中x=﹣2.华师大新版七年级上学期《3.4.4 整式的加减》同步练习卷参考答案与试题解析一.解答题(共50小题)1.计算(1)﹣×(+3);(2)3(4a2﹣2ab3)﹣2(5a2﹣3ab3)【分析】(1)原式先计算乘方运算,再计算乘除运算即可得到结果;(2)原式去括号合并即可得到结果.【解答】解:(1)原式=﹣×3÷(﹣)=6;(2)原式=12a2﹣6ab3﹣10a2+6ab3=2a2.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.2.化简:2(x2﹣5xy)﹣3(﹣6xy+x2)【分析】原式去括号合并即可得到结果.【解答】解:原式=2x2﹣10xy+18xy﹣3x2=﹣x2+8xy.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.3.王老师给同学们出了一道化简的题目:2(2x2y+x)﹣3(x2y﹣2x),小亮同学的做法如下:2(2x2y+x)﹣3(x2y﹣2x)=4x2y+x﹣3x2y﹣2x=x2y﹣x.请你指出小亮的做法正确吗?如果不正确,请指出错在哪?并将正确的化简过程写下来.【分析】根据整式的运算法则即可求出答案.【解答】解:不正确,去括号时出错2(2x2y+x)﹣3(x2y﹣2x)=4x2y+2x﹣3x2y+6x=x2y+8x【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算法则,本题属于基础题型.4.计算化简(1)﹣24﹣2×(﹣3)+|﹣2﹣5|÷(﹣1)2017.(2)6a2﹣2[(﹣3a2b+5ab2)﹣2(5a2b﹣3ab2)].【分析】(1)先计算乘方,再计算乘除,最后计算加减即可;(2)去括号合并同类项即可;【解答】解:(1)﹣24﹣2×(﹣3)+|﹣2﹣5|÷(﹣1)2017.=﹣16+6+7﹣1=﹣4(2)6a2﹣2[(﹣3a2b+5ab2)﹣2(5a2b﹣3ab2)]=6a2+6a2b﹣10ab2+20a2b﹣12ab2=6a2+26a2b﹣22ab2.【点评】本题考查整式的加减,熟练掌握去括号法则、合并同类项法在是解题的关键.5.2xy2﹣3(2x2﹣xy2+2)+(7x2﹣5xy2).【分析】先去括号,然后合并同类项即可.【解答】解:原式=2xy2﹣6x2+3xy2﹣6+7x2﹣5xy2=﹣6+x2.【点评】本题考查了整式的加减,整式加减的实质就是去括号、合并同类项.去括号时,要注意两个方面:一是括号外的数字因数要乘括号内的每一项;二是当括号外是“﹣”时,去括号后括号内的各项都要改变符号.6.已知:A=4a2﹣7ab+b,且B=2a2+6ab+7.(1)求A﹣2B.(2)若A+B+C=0,求C所表示的多项式.【分析】根据整式的运算法则即可求出答案.【解答】解:(1)A﹣2B=4a2﹣7ab+b﹣2a2﹣12ab﹣14=﹣19ab+b﹣14(2)由A+B+C=0,得C=﹣A﹣B=﹣(4a2﹣7ab+b)﹣(2a2+6ab+7)=﹣4a2+7ab﹣b﹣2a2﹣6ab﹣7=﹣6a2+ab﹣b﹣7【点评】本题考查整式的运算法则,解题的关键是熟练运用整式运算法则,本题属于基础题型.7.一般情况下不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;(3)若(m,n)是“相伴数对”,求代数式m﹣﹣[4m﹣2(3n﹣1)]的值.【分析】(1)利用“相伴数对”的定义化简,计算即可求出b的值;(2)写出一个“相伴数对”即可;(3)利用“相伴数对”定义得到9m+4n=0,原式去括号整理后代入计算即可求出值.【解答】解:(1)∵(1,b)是“相伴数对”,∴+=,解得:b=﹣;(2)(2,﹣)(答案不唯一);(3)由(m,n)是“相伴数对”可得:+=,即=,即9m+4n=0,则原式=m﹣n﹣4m+6n﹣2=﹣n﹣3m﹣2=﹣﹣2=﹣2.【点评】此题考查了整式的加减,以及代数式求值,弄清题中的新定义是解本题的关键.8.阅读下面的解题过程:计算2(﹣4a+3b)﹣3(a﹣2b).解:原式=(﹣8a+6b)﹣(3a﹣6b)(第一步)=﹣8a+6b﹣3a﹣6b (第二步)=﹣11a+12b (第三步)回答:(1)上面解题过程中有两步错误,第一处是第二步;第二处是第三步.(2)请给出正确的计算过程.【分析】(1)根据去括号的法则及合并同类项的法则,即可作出判断.(2)先去括号,然后合并同类项,计算得出结果.【解答】解:(1)第一处错误在第二步;第二处错误在第三步;(2)2(﹣4a+3b)﹣3(a﹣2b)原式=(﹣8a+6b)﹣(3a﹣6b)(第一步)=﹣8a+6b﹣3a+6b (第二步)=﹣11a+12b.(第三步)【点评】本题考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.9.化简:(1)a﹣(3a+b)+(a﹣5b)(2)5abc﹣2a2b﹣[3abc﹣3(4ab2+a2b)].【分析】(1)原式去括号合并即可得到结果;(2)原式去括号合并即可得到结果.【解答】解:(1)原式=a﹣3a﹣b+a﹣5b=﹣a﹣6b;(2)原式=5abc﹣2a2b﹣3abc+12ab2+3a2b=2abc+12ab2+a2b.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.10.数轴上点A对应的数为a,点B对应的数为b,且多项式﹣﹣2xy+5的次数为a,常数项为b.(1)直接写出:a=3,b=5.(2)数轴上点A、B之间有一动点P(不与A、B重合),若点P对应的数为x,试化简:|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|.(3)若M=3b2﹣2a2+5ab,N=4ab﹣2b2﹣a2,求3M﹣4N的值.【分析】(1)根据多项式的次数与常数项的定义即可求解;(2)由题意可得3<x<5,根据绝对值的意义去掉绝对值符号,再化简即可;(3)将M、N分别代入3M﹣4N,去括号、合并同类项即可.【解答】解:(1)∵多项式﹣﹣2xy+5的次数为a,常数项为b,∴a=3,b=5.故答案为3,5;(2)依题意,得3<x<5,则|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|=(2x+6)+4(5﹣x)﹣(6﹣x)+(3x﹣9)=2x+6+20﹣4x﹣6+x+3x﹣9=2x+11;(3)∵M=3b2﹣2a2+5ab,N=4ab﹣2b2﹣a2,∴3M﹣4N=3(3b2﹣2a2+5ab)﹣4(4ab﹣2b2﹣a2)=9b2﹣6a2+15ab﹣16ab+8b2+4a2=17b2﹣2a2﹣ab.【点评】本题考查了整式的加减,绝对值的意义,多项式的有关定义,掌握定义与法则是解题的关键.11.已知a是绝对值等于4的负数,b是最小的正整数,c的倒数的相反数是﹣2,(1)求a,b,c的值;(2)求:4a2b3﹣[2abc+(5a2b3﹣7abc)﹣a2b3].【分析】(1)根据题意即可求出a、b、c的值;(2)先将原式化简,然后将a、b、c的值代入即可求出答案.【解答】解:(1)由题意可知:a=﹣4,b=1,c=(2)当a=﹣4,b=1,c=时,原式=4a2b3﹣(2abc+5a2b3﹣7abc﹣a2b3)=4a2b3﹣(4a2b3﹣5abc)=4a2b3﹣4a2b3+5abc=5abc=5×(﹣4)×1×=﹣10【点评】本题考查学生的运算能力,解题的关键是熟练运用整式的运算法则,本题属于基础题型.12.小兵喜欢研究数学问题,在计算整式的加减(﹣4x2﹣7+5x)+(2x﹣3+3x2)的时候,想到了小学的列竖式加减法,令A=﹣4x2﹣7+5x,B=2x﹣3+3x2,然后将两个整式关于x进行降幂排列,A=﹣4x2+5x﹣7,B=3x2+2x﹣3,最后只要写出其各项系数对齐同类项进行竖式计算如下:所以,(﹣4x2﹣7+5x)+(2x﹣3+3x2)=﹣x2+7x﹣10若A=﹣4x2y2+2x3y﹣5xy3+2x4,B=3x3y+2x2y2﹣y4﹣4xy3,请你按照小兵的方法,先对整式A,B关于某个字母进行降幂排列,再写出其各项系数进行竖式计算A ﹣B,并写出A﹣B值.【分析】先对整式A,B关于字母x进行降幂排列,再写出其各项系数,列出竖式计算A﹣B即可.【解答】解:A=2x4﹣2x3y﹣4x2y2﹣5xy3,B=3x3y+2x2y2﹣4xy3﹣y4,A的各项系数为:2+2﹣4﹣5+0,B的各项系数为:0+3+2﹣4﹣1,列竖式计算如下:,所以,A﹣B=2x4﹣x3y﹣6x2y2﹣xy3+y4.【点评】本题考查了整式的加减,多项式的排列,掌握合并同类项的法则是解题的关键.13.化简:(1)5(3a2b﹣ab2)﹣4(﹣ab2+3a2b);(2)7x+2(x2﹣2)﹣4(x2﹣x+3).【分析】(1)原式去括号合并即可得到结果;(2)原式去括号合并即可得到结果.【解答】解:(1)原式=15a2b﹣5ab2+4ab2﹣12a2b=3a2b﹣ab2;(2)原式=7x+2x2﹣4﹣2x2+4x﹣12=11x﹣16.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.14.已知天平左边托盘中的物体重量为x,右边托盘中的物体重量为y,其中x=30(1+a2)﹣3(a﹣a2),y=31﹣[a﹣2(a2﹣a)﹣31a2](1)化简x和y;(2)请你想一想,天平会倾斜吗?如果出现倾斜,将向哪边倾斜?请说明理由.【分析】(1)x与y去括号合并即可得到结果;(2)利用作差法判断x与y的大小,即可作出判断.【解答】解:(1)x=30+30a2﹣3a+3a2=33a2﹣3a+30,y=31﹣a+2a2﹣2a﹣2+31a2=33a2﹣3a+29;(2)天平会向左边倾斜,其理由是:∵x﹣y=(33a2﹣3a+30)﹣(33a2﹣3a+29)=1>0,∴x>y,∴天平会向左边倾斜.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.15.设A=﹣x﹣4(x﹣y)+(﹣x+y).(1)当x=﹣,y=1时,求A的值;(2)若y﹣3x=2,则(1)中A=4.【分析】(1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;(2)把已知等式代入计算即可求出值.【解答】解:(1)A=﹣x﹣4x+y﹣x+y=﹣6x+2y,当x=﹣,y=1时,原式=2+2=4;(2)由y﹣3x=2,得到A=2(﹣3x+y)=4,故答案为:4【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.16.已知A=﹣3x2﹣2mx+3x+1,B=2x2+mx﹣1(1)求5A﹣3(A﹣B)的值(2)若(1)中的值与x的值无关,求m的值.【分析】(1)将A、B代替的代数式代入5A﹣3(A﹣B),去括号、合并同类项即可得;(2)根据整式的值与x的值无关知x的系数为0,据此列出关于m的方程,解之可得.【解答】解:(1)原式=5(﹣3x2﹣2mx+3x+1)﹣3[(﹣3x2﹣2mx+3x+1)﹣(2x2+mx ﹣1)]=﹣15x2﹣10mx+15x+5﹣3(﹣3x2﹣2mx+3x+1﹣2x2﹣mx+1)=﹣15x2﹣10mx+15x+5﹣3(﹣5x2﹣3mx+3x+2)=﹣15x2﹣10mx+15x+5+15x2+9mx﹣9x﹣6=﹣mx+6x﹣1;(2)原式=(6﹣m)x﹣1,∵该整式值与x的值无关,∴6﹣m=0,解得:m=6.【点评】本题主要考查整式的加减,整式的加减其实质就是去括号、合并同类项,所以解题的关键是掌握去括号、合并同类项的法则.17.化简下列各式:(1)5(a2b﹣2ab2)﹣4(3a2b﹣2ab2).(2)﹣2x2﹣[3y2﹣2(x2﹣3y2)+6].【分析】根据整式的运算法则即可求出答案.【解答】解:(1)原式=5a2b﹣10ab2﹣12a2b+8ab2=﹣7a2b﹣2ab2(2)原式=﹣2x2﹣[3y2﹣2x2+6y2+6]=﹣2x2﹣[9y2﹣2x2+6]=﹣2x2﹣y2+x2﹣3=﹣y2﹣x2﹣3【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算法则,本题属于基础题型.18.若定义=ad﹣bc,如:=2×b﹣a×(﹣1)=2b+a①计算,并指出结果是几次几项式.②若|x﹣3+y|与(xy+4)2互为相反数,求①式的值.【分析】根据题意给出的运算法则以及整式的运算法则即可求出答案.【解答】解:①原式=5(﹣2y)﹣(9x﹣2xy﹣y+7)=xy﹣10y﹣9x+2xy+y﹣7=﹣9x﹣9y﹣7②由于|x﹣3+y|与(xy+4)2互为相反数,∴|x﹣3+y|+(xy+4)2=0,∴∴xy=﹣4,x+y=3∴原式=xy﹣9(x+y)﹣7=﹣18﹣9×3﹣7=﹣18﹣27﹣7=﹣52【点评】本题考查整式的运算,解题的关键熟练运用整式的运算法则,本题属于基础题型.19.计算.(1)5(2x﹣7y)﹣3(4x﹣10y);(2)(5a﹣3b)﹣3(a2﹣2b);(3)3(3a2﹣2ab)﹣2(4a2﹣ab)(4)2x﹣[2(x+3y)﹣3(x﹣2y)].【分析】根据整式的运算法则即可求出答案.【解答】解:(1)原式=10x﹣35y﹣12x+30y=﹣2x﹣5y(2)原式=5a﹣3b﹣3a2+6b=﹣3a2+5a+3b(3)原式=9a2﹣6ab﹣8a2+2ab=a2﹣4ab(4)原式=2x﹣(2x+6y﹣3x+6y)=3x﹣12y【点评】本题考查整式的运算法则,解题的关键是熟练运用整式的运算法则,本题属于基础题型.20.化简(1)(2x2﹣+3x)﹣4(x﹣x2+)(2)x﹣2(x﹣)﹣(﹣)【分析】(1)原式去括号合并即可得到结果;(2)原式去括号合并即可得到结果.【解答】解:(1)原式=2x2﹣+3x﹣4x+4x2﹣2=6x2﹣x﹣;(2)原式=x﹣2x+y2+x﹣y2=y2.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.21.化简求值:2(a2﹣ab)﹣3(2a2﹣ab),其中a=﹣2,b=3.【分析】直接去括号进而合并同类项,再把已知代入即可.【解答】解:2(a2﹣ab)﹣3(2a2﹣ab)=2a2﹣2ab﹣6a2+3ab=﹣4a2+ab,把a=﹣2,b=3代入得:原式=﹣22.【点评】此题主要考查了整式的加减,正确合并同类项是解题关键.22.先化简再求值:2x2y﹣[3xy2﹣2(xy2+2x2y)],其中x=,y=﹣2.【分析】本题先进行化简,进行同类项合并,然后再代入x=,y=﹣2进行求值.【解答】解:2x2y﹣[3xy2﹣2(xy2+2x2y)]=2x2y﹣(3xy2﹣2xy2﹣4x2y)=2x2y﹣3xy2+2xy2+4x2y=6x2y﹣xy2.当x=,y=﹣2时,原式=6×()2×(﹣2)﹣×(﹣2)2=6××(﹣2)﹣×4=﹣3﹣2=﹣5.【点评】本题考查整式的化简求值,通过同类项合并进行化简后,代入求值即可.23.已知代数式A=﹣6x2y+4xy2﹣5,B=﹣3x2y+2xy2﹣3.(1)求A﹣B的值,其中x=1,y=﹣2.(2)请问A﹣2B的值与x,y的取值是否有关系,试说明理由.【分析】(1)先计算A﹣B的值,再将x和y的值代入可得结果;(2)先计算A﹣2B的值,再将x和y的值代入可得结果;【解答】解:(1)A﹣B=(﹣6x2y+4xy2﹣5)﹣(﹣3x2y+2xy2﹣3),=﹣6x2y+4xy2﹣5+3x2y﹣2xy2+3,=﹣3x2y+2xy2﹣2,当x=1,y=﹣2时,原式=﹣3×12×(﹣2)+2×1×(﹣2)2﹣2,=6+8﹣2,=12;(2)A﹣2B=(﹣6x2y+4xy2﹣5)﹣2(﹣3x2y+2xy2﹣3),=﹣6x2y+4xy2﹣5+6x2y﹣4xy2+6,=1;∴其值与x,y的值无关.【点评】本题主要考查整式的混合运算﹣化简求值,解题的关键是熟练掌握整式的混合运算顺序和运算法则.24.已知A=2ab﹣a,B=﹣ab+2a.(1)计算:5A+4B;(2)当|a+2|+(3﹣b)2=0,求5A+4B的值.【分析】(1)将A,B所代表的代数式代入,然后去括号、合并同类项即可得;(2)先根据非负数的性质得出a,b的值,再代入化简后的式子计算可得.【解答】解:(1)∵A=2ab﹣a,B=﹣ab+2a,∴5A+4B=5(2ab﹣a)+4(﹣ab+2a)=10ab﹣5a﹣4ab+8a=6ab+3a;(2)∵|a+2|+(3﹣b)2=0,∴a+2=0,3﹣b=0,则a=﹣2,b=3,∴5A+4B=6ab+3a=6×(﹣2)×3+3×3=﹣36+9=﹣27.【点评】本题主要考查整式的加减﹣化简求值,解题的关键是熟练掌握整式的加减运算顺序和运算法则及非负数的性质.25.先化简,再求值:2xy﹣(4xy﹣4x2y2)+2 (3xy﹣5x2y2),其中x,y满足(x+1)2+|y﹣2|=0.【分析】原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.【解答】解:∵(x+1)2+|y﹣2|=0,∴x=﹣1,y=2,则原式=2xy﹣2xy+2x2y2+6xy﹣10x2y2=﹣8x2y2+6xy,当x=﹣1,y=2时,原式=﹣32﹣12=﹣44.【点评】此题考查了整式的加减﹣化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.26.先化简,再求值:(1),其中x=3,y=﹣.(2)已知a+b=7,ab=10,求代数式(5ab+4a+7b)+(6a﹣3ab)﹣(4ab﹣3b)的值.【分析】(1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;(2)原式去括号整理后,将已知等式代入计算即可求出值.【解答】解:(1)原式=3x2y﹣2xy2+2xy﹣3x2y+3xy2=xy2+2xy,当x=3,y=﹣时,原式=﹣2=﹣1;(2)原式=5ab+4a+7b+6a﹣3ab﹣4ab+3b=﹣2ab+10(a+b),当a+b=7,ab=10时,原式=﹣20+70=50.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.27.先化简,再求值:3(a2b﹣ab)﹣2(ab﹣3a2b+1),其中a=,b=6.【分析】原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:原式=3a2b﹣3ab﹣2ab+6a2b﹣2=9a2b﹣5ab﹣2,当a=,b=6时,原式=6﹣10﹣2=﹣6.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.28.先化简,再求值:5(3a2b﹣ab2)﹣3(﹣ab2+4a2b),其中a=﹣,b=.【分析】原式去括号合并得到最简结果,将a与b的值代入计算即可求出值.【解答】解:原式=15a2b﹣5ab2+3ab2﹣12a2b=3a2b﹣2ab2,当a=﹣,b=时,原式=3×(﹣)2×﹣2×(﹣)×()2=+=.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.29.先化简,再求值:x﹣2(x﹣y2)﹣(﹣x+y2),其中x=3,y=﹣.【分析】原式去括号、合并得到最简结果,将y的值代入计算即可求出值.【解答】解:原式=x﹣2x+y2+x﹣y2=y2,当y=﹣时,原式=×=.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.30.先化简,再求值:(1)5x2﹣[2xy﹣3(xy+2)+4x2]﹣xy.其中x=﹣2,y=;(2)已知a=﹣1,b=2,求2a2﹣[8ab+(ab﹣4a2)]﹣ab的值.【分析】(1)原式去括号合并得到最简结果,将x与y的值代入计算即可求出值.(2)原式去括号合并得到最简结果,将a与b的值代入计算即可求出值.【解答】解:(1)原式=5x2﹣2xy+3(xy+2)﹣4x2﹣xy=5x2﹣2xy+xy+6﹣4x2﹣xy=x2﹣2xy+6,当x=﹣2,y=时,原式=(﹣2)2﹣2×(﹣2)×+6=4+2+6=12;(2)原式=2a2﹣8ab﹣(ab﹣4a2)﹣ab=2a2﹣8ab﹣ab+2a2﹣ab=4a2﹣9ab,当a=﹣1,b=2时,原式=4×(﹣1)2﹣9×(﹣1)×2=4+18=22.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.31.计算:(1)m2+2m+2m2﹣3m;(2)先化简,再求值:(ab﹣3a2)﹣[5ab﹣2(2a2﹣ab)],其中a=﹣2,b=1.【分析】(1)合并同类项即可得;(2)原式去括号、合并同类项化成最简形式,再将a,b的值代入计算可得.【解答】解:(1)原式=3m2﹣m;(2)原式=ab﹣3a2﹣5ab+2(2a2﹣ab)=ab﹣3a2﹣5ab+4a2﹣2ab=a2﹣6ab,当a=﹣2,b=1时,原式=(﹣2)2﹣6×(﹣2)×1=4+12=16.【点评】本题主要考查考查整式的加减﹣化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.32.先化简再求值:2m﹣2(m2+m﹣1),其中m=﹣2.【分析】先去括号,再合并同类项化简原式,继而将m的值代入计算可得.【解答】解:原式=2m﹣2m2﹣2m+2=﹣2m2+2,当m=﹣2时,原式=﹣2×(﹣2)2+2=﹣2×4+2=﹣8+2=﹣6.【点评】本题主要考查考查整式的加减﹣化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.33.先化简,再求代数式的值:2(x2y+xy2)﹣2(x2y﹣2)﹣(xy2+2),其中x=2018,y=﹣1.【分析】原式去括号、合并同类项化成最简形式,再将x,y的值代入计算可得.【解答】解:原式=2x2y+2xy2﹣2x2y+4﹣xy2﹣2=xy2+2,当x=2018,y=﹣1时,原式=2018×(﹣1)2+2=2020.【点评】本题主要考查考查整式的加减﹣化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.34.先化简,再求值:3a2b﹣6ab2﹣2(2a2b﹣3ab2﹣2),其中a=﹣1.b=2.【分析】原式去括号、合并同类项化成最简形式,再将a,b的值代入计算可得.【解答】解:原式=3a2b﹣6ab2﹣4a2b+6ab2+4=﹣a2b+4,当a=﹣1,b=2时,原式=﹣1×(﹣1)2×2+4=﹣2+4=2.【点评】本题主要考查考查整式的加减﹣化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.35.先化简,再求值.4ab﹣[(a2+5ab﹣b2)﹣2(a2+3ab﹣b2),其中a=﹣1,b=2.【分析】原式合并得到最简结果,将各自的值代入计算即可求出值.【解答】解:4ab﹣[(a2+5ab﹣b2)﹣2(a2+3ab﹣b2),=4ab﹣a2﹣5ab+b2+2a2+6ab﹣b2=5ab+a2把a=﹣1,b=2代入5ab+a2=5×(﹣1)×2+(﹣1)2=﹣9.【点评】考查了整式的加减﹣化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.注意整体思想的运用.36.先化简,再求值.已知|x﹣3|+(y+)2=0,先化简再求值:3x2y﹣[2xy2﹣3(xy﹣x2y)+xy]+5xy2【分析】利用非负数的性质求出x与y的值,原式合并得到最简结果,将各自的值代入计算即可求出值.【解答】解:根据题意,可得:x﹣3=0,y+=0,解得:x=3,y=﹣,3x2y﹣[2xy2﹣3(xy﹣x2y)+xy]+5xy2==把x=3,y=﹣代入==9【点评】考查了整式的加减﹣化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.注意整体思想的运用.同时考查了非负数的性质.37.先化简,后求值.求2(a2b+ab2)﹣5(2ab2﹣1+a2b)﹣2的值,其中a=1,b=﹣2.【分析】原式去括号、合并同类项化简,再将a,b的值代入计算可得.【解答】解:原式=2a2b+2ab2﹣10ab2+5﹣5a2b﹣2=﹣3a2b﹣8ab2+3,当a=1,b=﹣2时,原式=﹣3×12×(﹣2)﹣8×1×(﹣2)2+3=6﹣32+3=﹣23【点评】本题主要考查整式的加减﹣化简求值,解题的关键是掌握去括号、合并同类项法则.38.①计算:3(2x2﹣xy)﹣2(3x2+xy﹣1)②先化简,再求值:2(ab2﹣2a2b)﹣3(ab2﹣a2b)+(2ab2﹣2a2b)其中:a=2,b=1.【分析】①先去括号,再合并同类项即可得;②原式去括号、合并同类项即可化简原式,再将a,b的值代入计算可得.【解答】解:①原式=6x2﹣3xy﹣6x2﹣2xy+2=﹣5xy+2;②原式=2ab2﹣4a2b﹣3ab2+3a2b+2ab2﹣2a2b=ab2﹣3a2b,当a=2,b=1时,原式=2×12﹣3×22×1=2﹣12=﹣10.【点评】本题主要考查整式的加减﹣化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.39.(1)先化简,再求值:3x2y﹣[2xy2﹣2(xy﹣x2y)+xy]+3xy2,其中x=3,y=﹣;(2)已知2x2﹣3x=7,求整式6x﹣4x2+5的值.【分析】(1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;(2)原式变形后,将已知等式代入计算即可求出值.【解答】解:(1)原式=3x2y﹣2xy2+2xy﹣3x2y﹣xy+3xy2=xy2+xy,当x=3,y=﹣时,原式=﹣;(2)∵2x2﹣3x=7,∴3x﹣2x2=﹣7,则原式=2(3x﹣2x2)+5=﹣14+5=﹣9.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.40.化简:(1)3x2﹣3(x2﹣2x+1)+4;(2)先化简再求值:3x2y﹣[2xy2﹣2(xy﹣1.5x2y)+xy]+3xy2,其中x=﹣3,y=﹣2.【分析】(1)原式去括号合并即可得到结果;(2)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.【解答】解:(1)原式=3x2﹣3x2+6x﹣3+4=6x+1;(2)原式=3x2y﹣2xy2+2xy﹣3x2y﹣xy+3xy2=xy2+xy,当x=﹣3,y=﹣2时,原式=﹣12+6=﹣6.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.41.(1)计算:﹣3(2a2﹣2ab)+4(a2+ab﹣6)(2)化简求值:12(x2y﹣xy2)+5(xy2﹣x2y)﹣2x2y,其中x=,y=﹣5.【分析】(1)去括号、合并同类项即可得;(2)原式去括号、合并同类项化简后,把x,y的值代入计算可得.【解答】解:(1)原式﹣6a2+6ab+4a2+4ab﹣24=﹣2a2+10ab﹣24;(2)原式=12x2y﹣4xy2+5xy2﹣5x2y﹣2x2y=5x2y+xy2,当x=,y=﹣5时,原式=5×()2×(﹣5)+×52=﹣1+5=4.【点评】本题主要考查整式的加减﹣化简求值,解题的关键是掌握整式的加减运算顺序和运算法则.42.先化简,再求值(﹣2x2+xy﹣y2)+2(x2﹣xy);其中x=2,y=﹣.【分析】原式去括号合并得到最简结果,把x,y的值代入计算即可求出值.【解答】解:原式=﹣2x2+xy﹣y2+2x2﹣xy=xy﹣y2,将x=2,y=﹣代入原式=×2×(﹣)﹣(﹣)2=﹣﹣=﹣.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.43.先化简,再求值:5x2y﹣[x2﹣3(xy2﹣2x2y)+3xy2],其中x=6,|y|=,且xy<0.【分析】原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.【解答】解:∵x=6,|y|=,且xy<0,∴x=6,y=﹣,原式=5x2y﹣x2+3xy2﹣6x2y﹣3xy2=﹣x2y﹣x2,当x=6,y=﹣时,原式=18﹣36=﹣18.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.44.化简(1)求3a2﹣ab+1减4a2+6ab﹣7所得的差;(2)化简,求值4x2y﹣[6xy﹣2(3xy﹣2)﹣x2y]+1,其中x=﹣,y=8.【分析】(1)根据题意列出关系式,去括号合并即可得到结果;(2)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.【解答】解:(1)根据题意得:(3a2﹣ab+1)﹣(4a2+6ab﹣7)=3a2﹣ab+1﹣4a2﹣6ab+7=﹣a2﹣7ab+8;(2)原式=4x2y﹣6xy+6xy﹣4+x2y+1=5x2y﹣3,当x=﹣,y=8时,原式=10﹣3=7.【点评】此题考查了整式是加减,熟练掌握运算法则是解本题的关键.45.先化简,再求值:5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=﹣,b=.【分析】先去括号、合并同类项化简原式,再将a、b的值代入计算可得.【解答】解:原式=15a2b﹣5ab2﹣ab2﹣3a2b=12a2b﹣6ab2,当a=﹣,b=时,原式=12×(﹣)2×﹣6×(﹣)×()2=1+=.【点评】本题主要考查整式的加减﹣化简求值,解题的关键是掌握整式的加减的本质即为去括号、合并同类项.46.化简求值:﹣3xy2﹣2(xy﹣x2y)﹣(3x2y﹣2xy2),其中x=﹣4,y=.【分析】先去括号、合并同类项化简原式,再将x,y的值代入计算可得.【解答】解:原式=﹣3xy2﹣2xy+3x2y﹣3x2y+2xy2=﹣xy2﹣2xy,当x=﹣4,y=时,原式=﹣(﹣4)×﹣2×(﹣4)×=1+4=5.【点评】本题主要考查整式的加减﹣化简求值,解题的关键是掌握整式的加减的本质即为去括号、合并同类项.47.化简后求值:3(x2y+xy2)﹣3(x2y﹣1)﹣4xy2﹣3,其中x、y满足|x﹣2|+(y+)2=0.【分析】先去括号、合并同类项化简原式,再根据非负数的性质得出x,y的值,继而将x,y的值代入计算可得.【解答】解:原式=3x2y+3xy2﹣3x2y+3﹣4xy2﹣3=﹣xy2,∵|x﹣2|+(y+)=0,∴x﹣2=0 y+=0,于是x=2,y=﹣,当x=2,y=﹣时,原式=﹣xy2=﹣2×(﹣)2=﹣.【点评】本题主要考查非负数的性质与整式的加减﹣化简求值,解题的关键是掌握整式的加减的本质即为去括号、合并同类项.48.先化简,再求值:2(a2﹣ab)﹣3(a2﹣ab),其中,a=﹣2,b=3.【分析】先去括号,再合并同类项化简原式,再将a,b的值代入计算可得.【解答】解:原式=2a2﹣2ab﹣3a2+3ab=﹣a2+ab,当a=﹣2,b=3时,原式=﹣(﹣2)2+(﹣2)×3=﹣4﹣6=﹣10.【点评】本题主要考查整式的加减﹣化简求值,解题的关键是掌握整式的加减的本质即为去括号、合并同类项.49.先化简,再求值已知|x﹣2|+(y+1)2=0,求2x2﹣[5xy﹣3(x2﹣y2)]﹣5(﹣xy+y2)的值.【分析】先去括号、合并同类项化简原式,继而根据非负数的性质得出x,y的值,再将x,y的值代入计算可得.【解答】解:原式=2x2﹣5xy+3(x2﹣y2)﹣5(﹣xy+y2)=2x2﹣5xy+3x2﹣3y2+5xy﹣5y2=5x2﹣8y2,因为|x﹣2|+(y+1)2=0,所以x=2,y=﹣1,所以,原式=5×22﹣8×(﹣1)2=20﹣8=12.【点评】本题主要考查整式的加减﹣化简求值与非负数的性质,解题的关键是掌握整式的加减的本质即为去括号、合并同类项.50.先化简,再求值:2x﹣[3x﹣2(x﹣1)﹣3],其中x=﹣2.【分析】本题要先去括号再合并同类项,对原代数式进行化简,然后把x的值代入计算即可.【解答】解:原式=2x﹣(3x﹣2x+2﹣3)=2x﹣3x+2x﹣2+3=x+1,当x=﹣2时,原式=﹣2+1=﹣1.【点评】本题主要考查整式的加减﹣化简求值,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.。
华东师大版数学 七年级上册 3.4 整式的加减 课后练习题

一、单选题
1. 下列计算正确的是()
A.a3﹣a2=a B.a2•a3=a6C.(a﹣b)2=a2﹣b2D.(﹣a2)3=﹣a6
2. 下列各式中,与是同类项的是()
D.
A.B.
C.
3. 下列运算中,正确的是()
A.4a+2b=6ab B.2a3+3a2=5a5
C.3a2b﹣3ba2=0 D.5a2﹣4a2=1
4. 下列运算中,正确的是()
A.B.
C.D.
5. 若与是同类项,且它们的和为0,则m,n的值分别为( ) A.0,2 B.0,1 C.2,0 D.0,-1
二、填空题
6. 已知,则代数式的值为______.
7. 已知关于,的单项式与的和仍是单项式,则______.
8. 写两个多项式__________、_________,使它们的差为a2+b2.
三、解答题
9. 已知一个三角形院墙,第一条边长为3a+2b,第二条边比第一边长a﹣b,第三条边比第二条边短2a.
(1)求这个三角形的周长(用含有a、b表示).
(2)当求a=2米,b=1米时,这个三角形的周长是多少米?
(3)在(2)的条件下,围成院墙的材料20米以内收费每米180元,超过的部分每米只收费150元,请问围成这个三角形的院墙至少要花费多少钱?
10. 先化简,再求值:,其中,
11. 化简:
(1)
(2)。
华师大版七年级数学上册同步练习:3.4.4整式的加减.docx

整式的加减(30分钟50分)一、选择题(每小题4分,共12分)1.一个多项式A与多项式B=2x2-3xy-y2的差是多项式C=x2+xy+y2,则A等于( )A.x2-4xy-2y2B.-x2+4xy+2y2C.3x2-2xy-2y2D.3x2-2xy2.已知A=2a2-3a,B=2a2-a-1,当a=-4时,A-B等于( )A.8B.9C.-9D.-73.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )A.4mcmB.4ncmC.2(m+n)cmD.4(m-n)cm二、填空题(每小题4分,共12分)4.化简:(x2+2y2)-3(x2-2y2)=________.5.某校组织若干师生到恩施大峡谷进行社会实践活动.若学校租用45座的客车x 辆,则余下20人无座位;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是________.6.如果M=3x2-2xy-4y2,N=4x2+5xy-y2,则4M-N的值为________.三、解答题(共26分),另一边长是周长与4的差的一7.(8分)三角形的周长为a,它的一边长是周长的14半,求第三边的长.8.(8分)已知M=4x2-3x+2,N=6x2-3x+6,试比较M,N的大小.【拓展延伸】9.(10分)有这样一道题:“先化简,再求值:,b=-0.39.”(7a3-6a3b+3a2b)-(-3a3-6a3b+3a2b)-10a3+2,其中a=-313,b=-0.39”是多余的条件;小玉马上反对说:这个多项小宝说:本题中“a=-313式中每一项都含有a和b,不给出a,b的值怎么能求出多项式的值呢?你同意哪名同学的观点?请说明理由.答案解析1.【解析】选D.因为A与B的差是C,所以A=B+C,即A=(2x2-3xy-y2)+(x2+xy+y2)=2x2-3xy-y2+x2+xy+y2=3x2-2xy.2.【解析】选B.A-B=(2a2-3a)-(2a2-a-1)=2a2-3a-2a2+a+1=-2a+1.当a=-4时,A-B=-2×(-4)+1=8+1=9.3.【解析】选B.设小长方形的长为acm,宽为bcm,所以上面的阴影周长为:2(n-a+m-a)cm,下面的阴影周长为:2(m-2b+n-2b)cm,所以总周长为:[4m+4n-4(a+2b)]cm,又因为a+2b=m,所以4m+4n-4(a+2b)=4m+4n-4m=4n(cm).4.【解析】原式=x2+2y2-3x2+6y2=-2x2+8y2.答案:-2x2+8y25.【解析】因为学校租用45座的客车x辆,则余下20人无座位,所以师生的总人数为45x+20,又因为租用60座的客车则可少租用2辆,所以乘坐最后一辆60座客车的人数为45x+20-60(x-3)=45x+20-60x+180=200-15x.答案:200-15x6.【解析】4M-N=4(3x2-2xy-4y2)-(4x2+5xy-y2)=12x2-8xy-16y2-4x2-5xy+y2=8x2-13xy-15y2.答案:8x2-13xy-15y27.【解析】依题意得,第一边长为a,4第二边长为12(a-4), 所以第三边长为a-a 4-12(a-4) =a-a 4-12a+2=14a+2. 8.【解析】比较M,N 大小可用作差的方法,将差与0进行比较,当M-N>0时,M>N;当M-N=0时,M=N;当M-N<0时,M<N.M-N=4x 2-3x+2-(6x 2-3x+6)=4x 2-3x+2-6x 2+3x-6=-2x 2-4=-(2x 2+4).因为2x 2+4>0,所以-(2x 2+4)<0,即M-N<0,所以M<N.9.【解析】同意小宝的观点.因为(7a 3-6a 3b+3a 2b)-(-3a 3-6a 3b+3a 2b)-10a 3+2=7a 3-6a 3b+3a 2b+3a 3+6a 3b-3a 2b- 10a 3+2=2,所以本题中a=-313,b=-0.39是多余的条件.关闭Word 文档返回原板块初中数学试卷桑水出品。
2022-2023学年华东师大版七年级数学上册《3-4整式的加减》同步练习题(附答案)

2022-2023学年华东师大版七年级数学上册《3.4整式的加减》同步练习题(附答案)一.选择题1.如果单项式﹣xy b+1与x a﹣2y3是同类项,那么(a﹣b)2022=()A.1B.﹣1C.52022D.﹣520222.若4a2b n﹣1与a m b2是同类项,则m+n的值是()A.6B.5C.4D.33.下列说法中,错误的是()A.单项式2mn2与﹣5m2n是同类项B.单项式的次数是2C.单项式﹣x2y3的系数是﹣1D.多项式a3+2ab﹣1是三次三项式二.填空题4.如果单项式2a x﹣3b2与﹣ab y是同类项,那么多项式a x+3a y﹣1的次数是次.5.在等号右边的横线上填空:2m﹣n+1=2m﹣();3x+2y+1=3x﹣().6.填空a﹣(b﹣c+d)=a﹣d+()7.若一个多项式与﹣3x2+5x﹣7的和是﹣x2+2x﹣6,则这个多项式为.8.王老师在黑板上书写了一个正确的整式加减运算等式,随后用手盖住了一部分,如图所示,所盖住的部分为.9.有一道题目是:一个整式A减去x2﹣y2,小张误当成了加法计算,结果得到一个整式x2+y2,那么原来的整式A是.10.单项式x m+1y2﹣n与2y2x3的和仍是单项式,则m n=.三.解答题11.已知单项式x b y a+1与单项式﹣5x6﹣b y2是同类项,c是多项式2mn﹣5m﹣n﹣3的次数.(1)a=,b=,c=.(2)若关于x的二次三项式ax2+bx+c的值是3,求代数式2019﹣2x2﹣6x的值.12.合并同类项:(1)7a+3a2+2a﹣a2+3.(2)a2﹣3a﹣3a2+a2+a﹣8.13.合并下列各式的同类项:(1)a+2b+3a﹣2b;(2)3x2+6x+5﹣4x2+7x﹣6;(3)x2y﹣3xy2+2yx2﹣y2x;(4)3(x+y)2﹣(x﹣y)+2(x+y)2+(x﹣y)﹣5(x+y)2(提示:把(x﹣y)和(x+y)各看作一个字母因式).14.化简:(1)5m+2n﹣m﹣3n;(2)3a2﹣1﹣2a﹣5+3a﹣a2;(3)ab2﹣5a2b﹣a2b+0.75ab2;(4)4(m+n)﹣5(m+n)+2(m+n).15.先化简,再求值:3(a2b﹣2ab2﹣1)﹣2(2a2b﹣3ab2)+1,其中a=2,b=﹣1.16.先化简,再求值:﹣3[y﹣(3x2﹣3xy)]﹣[y+2(4x2﹣4xy)],其中x=﹣4,y=.17.先化简,再求值:(1)(﹣3mx2+mx﹣3)﹣(﹣1﹣mx2﹣mx),其中m=2,x=﹣3;(2),其中a、b满足|a+3|+(b﹣2)2=0.18.先化简,再求值:4xy﹣[2(x2+xy﹣2y2)﹣3(x2﹣2xy+y2)],其中x,y满足.19.(1)如图,数轴上的点A,B,C分别表示有理数a,b,c.化简:|a|﹣|b+2|﹣|a+c|﹣|b+1|+|1﹣c|;(2)已知关于x、y的多项式(3y﹣ax2﹣3x﹣1)﹣(﹣y+bx﹣2x2)中不含x项和x2项,且﹣x+b=0,求代数式:﹣x﹣b的值.20.如果多项式x4﹣(a﹣1)x3+5x2﹣(b+1)x﹣1中不含x的三次项和x的一次项,求|﹣7a﹣b3|的值.21.已知整式﹣x2+2y﹣mx+5﹣nx2+6x﹣20y的值与字母x的取值无关.求m2﹣2mn﹣n3的值.参考答案一.选择题1.解:∵单项式﹣xy b+1与x a﹣2y3是同类项,∴a﹣2=1,b+1=3,解得:a=3,b=2,∴(a﹣b)2022=(3﹣2)2022=12022=1.故选:A.2.解:∵4a2b n﹣1与a m b2是同类项,∴m=2,n﹣1=2,∴m=2,n=3,∴m+n=2+3=5,故选:B.3.解:A.2mn2与﹣5m2n所含字母相同,但相同字母的指数不相同,不是同类项,故选项A符合题意;B.单项式的次数是2,说法正确,故选项B不合题意;C.单项式﹣x2y3的系数是﹣1,说法正确,故选项C不合题意;D.多项式a3+2ab﹣1是三次三项式,说法正确,故选项D不合题意;故选:A.二.填空题4.解:因为单项式2a x﹣3b2与﹣ab y是同类项,所以x﹣3=1,y=2,所以x=4,y=2,所以多项式a x+3a y﹣1的次数是4次.故答案为:4.5.解:2m﹣n+1=2m﹣(n﹣1);3x+2y+1=3x﹣(﹣2y﹣1).故答案为:n﹣1;﹣2y﹣1.6.解:a﹣(b﹣c+d)=a﹣d+(﹣b+c),故答案为:﹣b+c7.解:由题意可得:﹣x2+2x﹣6﹣(﹣3x2+5x﹣7)=﹣x2+2x﹣6+3x2﹣5x+7=2x2﹣3x+1.故答案为:2x2﹣3x+1.8.解:由题意可得,所盖住的部分为:x2﹣5x+1﹣(﹣3x+2)=x2﹣5x+1+3x﹣2=x2﹣2x﹣1.故答案为:x2﹣2x﹣1.9.解:由题意可得,A=(x2+y2)﹣(x2﹣y2)=x2+y2﹣x2+y2=2y2,故答案为:2y2.10.解:依题意得:m+1=3,2﹣n=2,m=2,n=0,∴m n=20=1.故答案为:1.三.解答题11.解:(1)因为单项式x b y a+1与单项式﹣5x6﹣b y2是同类项,所以a+1=2,b=6﹣b,所以a=1,b=3,因为c是多项式2mn﹣5m﹣n﹣3的次数,所以c=2.故答案为:1,3,2.(2)依题意得:x2+3x+2=3,所以x2+3x=1,所以2019﹣2x2﹣6x=2019﹣2(x2+3x)=2019﹣2×1=2017.12.解:(1)7a+3a2+2a﹣a2+3=(7a+2a)+(3a2﹣a2)+3=9a+2a2+3;(2)a2﹣3a﹣3a2+a2+a﹣8=(1﹣3+)a2+(﹣3+)a﹣8=﹣a2﹣a﹣8.13.解:(1)原式=(1+3)a+(2﹣2)b=4a;(2)原式=(3﹣4)x2+(6+7)x+(5﹣6)=﹣x2+13x﹣1;(3)原式=(1+2)x2y+(﹣3﹣1)xy2=3x2y﹣4xy2;(4)原式=(3+2﹣5)(x+y)2+(1﹣1)(x﹣y)=0.14.解:(1)5m+2n﹣m﹣3n=4m﹣n;(2)3a2﹣1﹣2a﹣5+3a﹣a2=2a2+a﹣6;(3)ab2﹣5a2b﹣a2b+0.75ab2=ab2﹣5a2b﹣a2b+ab2=ab2﹣a2b;(4)4(m+n)﹣5(m+n)+2(m+n)=(4﹣5+2)(m+n)=m+n.15.解:原式=3a2b﹣6ab2﹣3﹣4a2b+6ab2+1=﹣a2b﹣2,当a=2,b=﹣1时,原式=﹣22×(﹣1)﹣2=﹣4×(﹣1)﹣2=4﹣2=2.16.解:﹣3[y﹣(3x2﹣3xy)]﹣[y+2(4x2﹣4xy)]=﹣3y+3(3x2﹣3xy)﹣y﹣2(4x2﹣4xy)=﹣3y+9x2﹣9xy﹣y﹣8x2+8xy=x2﹣xy﹣4y,当x=﹣4,y=时,原式=(﹣4)2﹣(﹣4)×﹣4×=16+1﹣1=16.17.解:(1)(﹣3mx2+mx﹣3)﹣(﹣1﹣mx2﹣mx)=﹣mx2+mx﹣1+1+mx2+mx=mx,当m=2,x=﹣3时,原式=×2×(﹣3)=﹣4;(2)∵|a+3|+(b﹣2)2=0,∴a+3=0,b﹣2=0,∴a=﹣3,b=2,∴=2ab2﹣a﹣b﹣2ab2﹣a2b+b+a=﹣a2b,当a=﹣3,b=2时,原式=﹣×(﹣3)2×2=﹣×9×2=﹣6.18.解:∵,∴,,∴,.原式=4xy﹣(2x2+2xy﹣4y2﹣3x2+6xy﹣3y2)=4xy﹣(﹣x2+8xy﹣7y2)=4xy+x2﹣8xy+7y2=x2﹣4xy+7y2===3.19.解:(1)∵a<﹣2<b<﹣1,0<c<1,∴b+2>0,a+c<0,b+1<0,1﹣c>0,∴|a|﹣|b+2|﹣|a+c|﹣|b+1|+|1﹣c|=﹣a﹣(b+2)﹣(﹣a﹣c)﹣(﹣b﹣1)+1﹣c=﹣a﹣b﹣2+a+c+b+1+1﹣c=0.(2)原式=3y﹣ax2﹣3x﹣1+y﹣bx+2x2=(2﹣a)x2﹣(b+3)x+4y﹣1,由题意得2﹣a=0,b+3=0,解得a=2,b=﹣3,∵x2﹣x﹣3=0,∴x1=2,x2=﹣1,当x=2时,原式=×23﹣3×22﹣2﹣(﹣3)=8﹣12﹣2+3=﹣3,当x=﹣1时,原式=×(﹣1)3﹣3×(﹣1)2﹣2﹣(﹣3)=﹣1﹣3﹣2+3=﹣3.∴﹣x﹣b的值为﹣3.20.解:因为多项式x4﹣(a﹣1)x3+5x2﹣(b+1)x﹣1不含x的三次项和一次项,所以a﹣1=0,b+1=0,所以a=1,b=﹣1,所以|﹣7a﹣b3|=|﹣7﹣(﹣1)3|=6.21.解:﹣x2+2y﹣mx+5﹣nx2+6x﹣20y=(﹣1﹣n)x2+(6﹣m)x+5﹣18y,∵整式﹣x2+2y﹣mx+5﹣nx2+6x﹣20y的值与字母x的取值无关,∴﹣1﹣n=0,6﹣m=0,解得n=﹣1,m=6,∴m2﹣2mn﹣n3===.。
七年级数学上册 3.4 整式的加减 3.4.1 同类项跟踪训练(含解析)(新版)华东师大版-(新版)

同类项一.选择题(共9小题)1.若﹣5x2y m与x n y是同类项,则m+n的值为()A. 1 B.2 C.3 D.42.下列各式中,与2a的同类项的是()A.3a B.2ab C.﹣3a2D.a2b3.如果单项式﹣x a+1y3与x2y b是同类项,那么a、b的值分别为()A.a=1,b=3 B.a=1,b=2 C.a=2,b=3 D.a=2,b=24.已知代数式﹣3x m﹣1y3与x n y m+n是同类项,那么m、n的值分别是()A.B.C.D.5.如果代数式4x2a﹣1y与是同类项,那么()A.a=2,b=﹣6 B.a=3,b=﹣8 C.a=2,b=﹣5 D.a=3,b=﹣96.已知与﹣x3y2n是同类项,则(nm)2010的值为()A.2010 B.﹣2010 C.1 D.﹣17.已知单项式﹣3x2m﹣n y4与x3y m+2n是同类项,则m n的值为()A.B.3 C.1 D.28.单项式﹣x a+b y a﹣1与3x2y是同类项,则a﹣b的值为()A. 2 B.0 C.﹣2 D.19.若2a m b2m+3n与a2n﹣3b8的和仍是一个单项式,则m,n的值分别是()A.1,1 B.1,2 C.1,3 D.2,1二.填空题(共7小题)10若代数式2a3b n+2与﹣3a m﹣2b是同类项,则mn= _________ .11.若单项式2x2y m与﹣3x n y3是同类项,则m+n的值是_________ .12.若代数式﹣4x6y与x2n y是同类项,则常数n的值为_________ .13.已知﹣2x m﹣1y3和x n y m+n是同类项,则(n﹣m)2012= _________ .14.已知代数式2a3b n+1与﹣3a m﹣2b2是同类项,则2m+3n= _________ .15.当m= _________ 时,﹣x3b2m与x3b是同类项.16.如果单项式﹣3a2m﹣n b与4a3m+n b5m+8n是同类项,那么两个单项式的积为_________ .三.解答题(共7小题)17.如果单项式2mx a y与﹣5nx2a﹣3y是关于x,y的单项式,且它们是同类项.(1)(7a﹣22)2004的值.(2)若2mx a y+5nx2a﹣3y=0,求(2m+5n)2005的值.18.己知3a m•b4与﹣5a4•b n﹣1是同类项,求m+n的值.19.已知﹣3x4+m y与x4y3n是同类项,求代数式m100+(﹣3n)99﹣mn的值.20.已知﹣5.1×10m x2y n与3n x m+1y n是同类项,求当合并同类项后,单项式的系数是正数时,n的最小值是几?当n取最小值时,合并同类项后的单项式的系数和次数是几?21.若关于x,y的单项式2ax m y与5bx2m﹣3y是同类项,且a,b不为零.(1)求(4m﹣13)2009的值.(2)若2ax m y+5bx2m﹣3y=0,且xy≠0,求的值.22.阅读下面第(1)题的解答过程,然后解答第(2)题.(1)已知﹣2x m+5n y5与4x2y m﹣3n是同类项,求m+n的值.解:根据同类项的意义,可知x的指数相同,即:m+5n=2.y的指数也相同,即m﹣3n=5.所以:(m+5n)+(m﹣3n)=2+5,即:2m+2n=2(m+n)=7所以:(2)已知x m﹣3n y7与是同类项,求m+2n的值.23.若单项式的和仍是单项式,求m,n的值.第三章整式加减.1同类项参考答案与试题解析一.选择题(共9小题)1.若﹣5x2y m与x n y是同类项,则m+n的值为()A. 1 B.2 C.3 D.4考点:-同类项.分析:-根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程等式,求出n,m的值,再相加即可.解答:-解:∵﹣5x2y m和x n y是同类项,∴n=2,m=1,m+n=2+1=3,故选:C.点评:-本题考查同类项的知识,注意掌握同类项定义中的两个“相同”:同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,是易混点,因此成了中考的常考点.2.下列各式中,与2a的同类项的是()A.3a B.2ab C.﹣3a2D.a2b考点:-同类项.分析:-本题是同类项的定义的考查,同类项是所含的字母相同,并且相同字母的指数也相同的项.中的字母是a,a的指数为1,解答:-解:2a中的字母是a,a的指数为1,A、3a中的字母是a,a的指数为1,故A选项正确;B、2ab中字母为a、b,故B选项错误;C、中字母a的指数为2,故C选项错误;D、字母与字母指数都不同,故D选项错误,故选:A.点评:-考查了同类项的定义.同类项一定要记住两个相同:同类项是所含的字母相同,并且相同字母的指数也相同.3.如果单项式﹣x a+1y3与x2y b是同类项,那么a、b的值分别为()A.a=1,b=3 B.a=1,b=2 C.a=2,b=3 D.a=2,b=2考点:-同类项.分析:-根据同类项是字母相同相同,且相同的字母的指数也相同,可得答案.解答:-解:单项式﹣x a+1y3与x2y b是同类项,a+1=2,b=3,a=1,b=3,故选:A.点评:-本题考查了同类项,相同的字母的指数也相同是解题关键.4.已知代数式﹣3x m﹣1y3与x n y m+n是同类项,那么m、n的值分别是()A.B.C.D.考点:-同类项;解二元一次方程组.分析:-本题考查同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,根据同类项的定义中相同字母的指数也相同,可先列出关于m和n的二元一次方程组,再解方程组求出它们的值.解答:-解:由同类项的定义,得,解得.故选C.点评:-同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,是易混点,因此成了中考的常考点.解题时注意运用二元一次方程组求字母的值.5.如果代数式4x2a﹣1y与是同类项,那么()A.a=2,b=﹣6 B.a=3,b=﹣8 C.a=2,b=﹣5 D.a=3,b=﹣9考点:-同类项.分析:-根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,根据同类项的定义中相同字母的指数也相同,即可求得a和b的值.解答:-解:根据同类项的定义可知:2a﹣1=5,3a+b=1,解得:a=3把a=3代入到3a+b=1,解得:b=﹣8.故选B.点评:-本题考查同类项定义,判断两个项是不是同类项,一看所含字母是否相同,二看相同字母的指数是否相同.6.已知与﹣x3y2n是同类项,则(nm)2010的值为()A.2010 B.﹣2010 C.1 D.﹣1考点:-同类项.专题:-探究型.分析:-先根据同类项的定义列出方程组,求出n、m的值,再把m、n的值代入代数式进行计算即可.解答:-解:∵与﹣x3y2n是同类项,∴,解得,∴2010=(﹣1)2010=1.故选C.点评:-本题考查的是同类项的定义,能根据同类项的定义列出关于m、n的方程组是解答此题的关键.7.已知单项式﹣3x2m﹣n y4与x3y m+2n是同类项,则m n的值为()A.B.3 C.1 D.2考点:-同类项.专题:-计算题.分析:-根据同类项的定义得到2m﹣n=3,m+2n=4,然后解方程组,再把方程组的解代入m n进行计算即可.解答:-解:∵单项式﹣3x2m﹣n y4与x3y m+2n是同类项,∴2m﹣n=3,m+2n=4,解方程组,得,∴m n=21=2.故选D.点评:-本题考查了同类项的定义:所含字母相同,并且相同字母的次数也分别相同的项叫同类项.8.单项式﹣x a+b y a﹣1与3x2y是同类项,则a﹣b的值为()A. 2 B.0 C.﹣2 D.1考点:-同类项;解二元一次方程组.分析:-本题考查同类项的定义,由同类项的定义可先求得a和b的值,从而求出它们的差.解答:-解:由同类项得定义得,,解得,则a﹣b=2﹣0=2.故选A.点评:-同类项定义中的两个“相同”:相同字母的指数相同,是易混点,因此成了中考的常考点.9.若2a m b2m+3n与a2n﹣3b8的和仍是一个单项式,则m,n的值分别是()A.1,1 B.1,2 C.1,3 D.2,1考点:-同类项;解二元一次方程组.分析:-根据同类项的定义即可列出方程组,求出m、n的值即可.解答:-解:依题意,得,将①代入②,可得2(2n﹣3)+3n=8,即4n﹣6+3n=8,即7n=14,n=2.则m=1.故选B.点评:-本题考查的是同类项和方程的综合题目.两个单项式的和为单项式,则这两个单项式必须是同类项.二.填空题(共7小题)10.若代数式2a3b n+2与﹣3a m﹣2b是同类项,则mn= ﹣5 .考点:-同类项.分析:-根据同类项是字母相同,且相同字母的指数也相同,可得m、n的值再根据有理数的乘法,可得答案.解答:-解:2a3b n+2与﹣3a m﹣2b是同类项,m﹣2=3,n+2=1,m=5,n=﹣1,mn=5×(﹣1)=﹣5,故答案为:﹣5.点评:-本题考查了同类项,相同字母的指数也相同是解题关键.11.若单项式2x2y m与﹣3x n y3是同类项,则m+n的值是 5 .考点:-同类项.分析:-根据同类项的定义(所含字母相同,相同字母的指数相同)求出n,m的值,再代入代数式计算即可.解答:-解:∵单项式2x2y m与﹣3x n y3是同类项,∴m=3,n=2,∴m+n=3+2=5.故答案为5.点评:-本题考查同类项的定义:所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项.注意:①一是所含字母相同,二是相同字母的指数也相同,两者缺一不可;②同类项与系数的大小无关;③同类项与它们所含的字母顺序无关;④所有常数项都是同类项.12.若代数式﹣4x6y与x2n y是同类项,则常数n的值为 3 .考点:-同类项.专题:-计算题.分析:-根据同类项的定义得到2n=6解得n值即可.解答:-解:∵代数式﹣4x6y与x2n y是同类项,∴2n=6解得:n=3故答案为:3.点评:-本题考查了同类项的定义:所含字母相同,并且相同字母的次数也分别相同的项叫做同类项.13.已知﹣2x m﹣1y3和x n y m+n是同类项,则(n﹣m)2012= 1 .考点:-同类项.专题:-计算题.分析:-根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程求出m,n的值,再代入代数式计算即可.解答:-解:∵﹣2x m﹣1y3和x n y m+n是同类项,∴m﹣1=n,3=m+n,解得m=2,n=1,所以(n﹣m)2012=(1﹣2)2012=1.故答案为:1.点评:-本题考查了同类项的定义,注意同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,是易混点,因此成了中考的常考点.解题时注意运用二元一次方程组求字母的值.14.已知代数式2a3b n+1与﹣3a m﹣2b2是同类项,则2m+3n= 13 .考点:-同类项.分析:-本题考查同类项的定义(所含字母相同,相同字母的指数相同),可得:m﹣2=3,n+1=2,解方程即可求得m,n的值,从而求出2m+3n的值.解答:-解:由同类项的定义,可知m﹣2=3,n+1=2,解得n=1,m=5,则2m+3n=13.故答案为:13点评:-同类项定义中的两个“相同”:所含字母相同,相同字母的指数相同,是易混点,因此成了中考的常考点.15.当m= 0.5 时,﹣x3b2m与x3b是同类项.考点:-同类项.专题:-计算题.分析:-利用同类项的定义计算即可求出m的值.解答:-解:由﹣x3b2m与x3b是同类项,得到2m=1,解得:m=0.5,点评:-此题考查了同类项,熟练掌握同类项的定义是解本题的关键.16.如果单项式﹣3a2m﹣n b与4a3m+n b5m+8n是同类项,那么两个单项式的积为﹣12a5b2.考点:-同类项;单项式乘单项式.分析:-根据同类项的定义,相同字母的指数相同得到关于m、n的方程组,通过解方程组求得它们的值,然后将其代入两个单项式,利用单项式的乘法法则进行解答即可.解答:-解:∵单项式﹣3a2m﹣n b与4a3m+n b5m+8n是同类项,∴,解得,则这两个单项式是﹣3a b与4b,∴﹣3a b×4b=﹣12a5b2.故答案是:﹣12a5b2.点评:-本题考查了同类项的定义和整式的乘法,根据同类项定义中相同字母的指数相同确定出具体的单项式是解题的关键.三.解答题(共7小题)17.如果单项式2mx a y与﹣5nx2a﹣3y是关于x,y的单项式,且它们是同类项.(1)(7a﹣22)2004的值.(2)若2mx a y+5nx2a﹣3y=0,求(2m+5n)2005的值.考点:-同类项.专题:-计算题.分析:-(1)根据同类项所含字母相同,相同字母的指数相同可得a的值,代入求解即可;(2)利用2mx a y+5nx2a﹣3y=0,得出它们的系数和为0,进而得出答案.解答:-解:(1)∵单项式是同类项,∴2a﹣3=a,∴a=3,∴(7a﹣22)2004=1;(2)∵2mx a y+5nx2a﹣3y=0,2mx a y与﹣5nx2a﹣3y是关于x,y的单项式,且它们是同类项,∴2m+5n=0,∴(2m+5n)2005=0.点评:-此题主要考查了同类项,利用同类项定义得出系数关系是解题关键.18.己知3a m•b4与﹣5a4•b n﹣1是同类项,求m+n的值.考点:-同类项.分析:-根据同类项是字母相同,且相同字母的指数相同,可得m,n的值,根据有理数的加法运算,可得答案.解答:-解:∵3a m•b4与﹣5a4•b n﹣1是同类项,∴m=4,n﹣1=4,n=5,m+n=×4+5=2+5=7.点评:-本题考查了同类项,同类项是字母相同,且相同字母的指数相同.19.已知﹣3x4+m y与x4y3n是同类项,求代数式m100+(﹣3n)99﹣mn的值.考点:-同类项;代数式求值.分析:-利用同类项的定义求出m,n的值,代入代数式求值即可.解答:-解:∵﹣3x4+m y与x4y3n是同类项,∴4+m=4,3n=1,∴m=0,n=,∴m100+(﹣3n)99﹣mn=0+(﹣1)﹣0=﹣1.点评:-本题主要考查了同类项及代数式求值,解题的关键是根据同类项的定义求出m,n的值.20.已知﹣5.1×10m x2y n与3n x m+1y n是同类项,求当合并同类项后,单项式的系数是正数时,n的最小值是几?当n取最小值时,合并同类项后的单项式的系数和次数是几?考点:-同类项;单项式.分析:-本题考查同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,根据同类项的定义中相同字母的指数也相同,可求得m和n的值,根据合并同类项法则合并同类项即可.解答:-解:由﹣5.1×10m x2y n与3n x m+1y n是同类项,得m=1,﹣5.1×10x2y n+3n x2y n=(﹣51+3n)x2y n,由﹣51+3n>0得n最小是4,即(﹣51+34)x2y4=30x2y4,合并同类项后,单项式的系数是30,次数是6.点评:-本题考查的是同类项的定义,同类项定义中的两个“相同”:(1)所含字母相同,(2)相同字母的指数相同,是易混点,还要注意同类项与字母的顺序无关,与系数无关,以及合并同类项的法则,难度适中.21.若关于x,y的单项式2ax m y与5bx2m﹣3y是同类项,且a,b不为零.(1)求(4m﹣13)2009的值.(2)若2ax m y+5bx2m﹣3y=0,且xy≠0,求的值.考点:-同类项.分析:-根据同类项的定义列出方程,求出m的值.(1)将m的值代入代数式计算.(2)将m的值代入2ax m y+5bx2m﹣3y=0,且xy≠0,得出2a+5b=0,即a=﹣2.5b.代入求得的值.解答:-解:单项式2ax m y与5bx2m﹣3y是同类项,且a,b不为零.m=2m﹣3,解得m=3(1)将m=3代入,(4m﹣13)2009=﹣1.(2)∵2ax m y+5bx2m﹣3y=0,且xy≠0,∴(2a+5b)x3y=0,∴2a+5b=0,a=﹣2.5b.∴=﹣点评:-同类项定义中的两个“相同”:所含字母相同,相同字母的指数相同,是易混点,因此成了中考的常考点.22.阅读下面第(1)题的解答过程,然后解答第(2)题.(1)已知﹣2x m+5n y5与4x2y m﹣3n是同类项,求m+n的值.解:根据同类项的意义,可知x的指数相同,即:m+5n=2.y的指数也相同,即m﹣3n=5.所以:(m+5n)+(m﹣3n)=2+5,即:2m+2n=2(m+n)=7所以:(2)已知x m﹣3n y7与是同类项,求m+2n的值.考点:-同类项.分析:-根据(1)小题的解题方法,结合同类项的概念直接进行计算.解答:-解:根据同类项的意义,可知x的指数相同,即:m﹣3n=3.y的指数也相同,即3m+11n=7.所以:(m﹣3n)+(3m+11n)=3+7,即:4m+8n=4(m+2n)=10所以:m+2n=.点评:-本题主要考查了同类项的概念,注意类比方法的运用.23.若单项式的和仍是单项式,求m,n的值.考点:-同类项;解二元一次方程组.专题:-计算题.分析:-由同类项的定义,即相同字母的指数相同,得到关于m、n的方程组,即可求得m和n的值.解答:-解:由同类项的定义,得,解得m=1,n=﹣0.5.故答案为m=1,n=﹣0.5.点评:-本题主要考查同类项的定义这类题目的解题关键是从同类项的定义出发,列出方程(组)并求解.。
七年级数学上册 3.4 整式的加减专题训练 (新版)华东师大版

3.4 整式的加减专题一 同类项与去(添)括号1. 若5a |x |b 2与—0.2a 3b |y |是同类项,则x 、y 的值分别是( )A .x =±3,y =±2B .x =3,y =2C .x =—3,y =—2D .x =3,y =—22. 已知代数式—31x a +b y a ﹣1与3x 2y 的和是单项式,则a ﹣b 的相反数为( ) A .2 B .0C .﹣2D .13. 已知a —b =—3,c +d =2,则(a ﹣d )—b +c )的值为( )A .﹣5B .1C .5D .﹣1专题二 整式的加减运算4. 有理数a ,b ,c 在数轴上的位置如图所示,式子|a |+|b |+|a +b |+|c -b |化简结果为( )A .2a +3b -cB .3b -cC .c -bD .3b +c5. 现规定一种运算: a ※b=ab +a -b ,其中a 、b 为有理数,化简a ※b +(b -a ) ※2,并求出当a =—21,b =2时该式的值.状元笔记【知识要点】1.同类项:所含字母相同、并且相同字母的指数也分别相同的项叫做同类项.几个常数项也是同类项.2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.合并同类项的法则是:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.3.去括号法则:(1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都改变正负号.(2)括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.4.添括号法则:(1)所添括号前面是“+”号,括到括号里的各项都不改变正负号.(2)所添括号前面是“-”号,括到括号里的各项都改变正负号.5.整式的加减运算的一般步骤:(1)去括号;(2)合并同类项.【温馨提示(针对易错)】1.辨认同类项时要注意:(1)同类项与系数大小没有关系;(2)同类项与它们所含字母的顺序没有关系.2.去(添)括号要严格按照法则进行,防止出现符号错误.【方法技巧】1.添括号是否正确,可以用去括号检验一下.2.在进行整式的加减求值时,除了化简后直接代入求值外,有时可以用整体代入、变形代入等特殊方法.答案1. A 【解析】 ∵5a |x|b 2与—0.2a 3b |y|是同类项,∴|x|=3,|y|=2,解得x=±3,y=±2.故选A .2. C 【解析】 ∵代数式—31x a+b y a ﹣1与3x 2y 的和是单项式, ∴代数式—31x a+b y a ﹣1与3x 2y 是同类项, ∴a+b=2,a —1=1,解得:a=2,b=0.∴a —b=2,即a ﹣b 的相反数是—2.故选C .3. A 【解析】 根据题意有(a —d )—(b+c )=(a —b )—(c+d )=—3—2=—5,故选A .4. B 【解析】 由已知得a <0、b >0、a +b >0、b -c <0,所以|a|+|b|+|a +b|+|b -c|=-a +b +(a +b )+(b -c )=-a +b +a +b +b -c =3b —c.5. 解: a ※b=ab+a -b, (b -a) ※2=(b -a)×2+(b -a)-2, a ※b +(b -a) ※2=ab+a -b+2b -2a +b -a -2=ab —2a +2b -2.当a =﹣21,b =2时,原式=(—21)×2—2×(—21)+2×2-2=-1+1+4-2=2.。
华师大版数学七年级上册-3.4-整式的加减

解 (1) 设长方形的长为x米,则它的宽为2 x米.由图不
3
难知道,做这个窗框所需材料的长度为
11x 9 2 x πx 3
=11x 6x πx
=(17 π)(x 米)
(2) 当x=0.4时,
=(3+5)x2y-(4-2)xy2+(5-3) =8x2y-2xy2+2
合并同类项的法则: 把同类项的系数相加,所得的结果作为系数,字母和字母
的指数保持不变.
例3 合并下列多项式中的同类项:
(1)2a2b-3a2b+ 1 a2b
2
解 2a2b-3a2b+1 a2b
2
三项都是同类项
=(2 3 1)a2b
解 原式=x2-y2-6x2+9y2 =-5x2+8y2
(3)7a2b-(-4a2b+5ab2)-2(2a2b-3ab2).
解 原式=7a2b+4a2b-5ab2-4a2b+6ab2 =7a2b+ab2
4.计算:
(1)117x+138x-38x 解 原式=117x+(138x-38x)
=117x+100x =217x (3)136x-87x+57x 原式=136x-(87x-57x) =136x-30x =106x
1.去括号: (1)(a-b)+(-c-d); 解 原式=a-b-c-d
(3)-(a-b)+(-c-d); 原式=-a+b-c-d
(2)(a-b)-(-c-d); 原式=a-b+c+d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.4 整式的加减
1.若与是同类项,则a +b 的值是() A.1 B.2 C.3 D.4
2.在下列单项式中,说法正确的是()
①②③④⑤ A.没有同类项 B.②与③是同类项 C. ②与⑤是同类项 D. ①与④是同类项
3.下列添括号正确的是()
A.
B.
C.
D.
4.化简的结果是()
A. B. C. D.0
5.单项式的和是.
6.两个单项式与的和是一个单项式,那么,.
7.当时,多项式中不含项.
8.把看作一个整体,合并同类项.
9.某三角形第一条边长厘米,第二条边比第一条边长厘米,第三条边比第一条边的2倍少b 厘米,那么这个三角形的周长是厘米.
10.已知,,求:①A -3B ;②3A +B .
11.,其中.
12.
,其中.
213
a x y -2
b xy 3
6x 23xy 20.37y x -214x -213xy z 323272867(286)x x x x x x --+=--+()()a b c d a d b c -+-=--+225623(562)3a ab a b a ab a b ---=-+--27(27)a b c a b c -+=--(53)3(2)a a b a b --+-2a 6b -26a b -22224,6,3,a b ab a b a b --2212m a b 412
n a b -m =n =k =21383x kxy xy -+
-xy ()a b -7()3()2()a b a b a b -----=(2)a b -()a b +2244A x xy y =-+225B x xy y =+-332323[(67)]2(34)x x x x x x x -+----1x =-222221382(33)(3)3535x x xy y x xy y -+-+++1,22
x y =-=
参考答案:
1.C
2.B
3.D
4.A
5. 6. 3 2 7.19 8. 9. 10.⑴⑵
11.-15
12. 4 2222ab a b -+2()a b -94a b -22716x xy y -+22
13112x xy y --。
