弯曲正应力切应力与强度条件演示文稿
材料力学课件第5章

M
zM
x
等截面梁
y
注意 当梁为变截面梁时, max 并不一定
发生在|M|max 所在面上.
22
5.3 横力弯曲时梁横截面上的正应力 弯曲正应力强度条件
h
常用图y形Wz
c b
Wz =Iz /ymax
z
Wz
Iz h
bh3 2 12 h
bh2 6
2
h2
h1
y
c
z
Wz
Iz h1
1 ( b1h13 h1 6
z
于是
M
E
Iz
M
得
1 M
EIz
y
x
代入
E
y得
My
Iz
15
5.2 纯弯曲时梁横截面上的正应力
常用图形y、Iz
h
y
1.矩形
dy
c
y z
Iz
Ay2 d A
h 2
y2b d y bh3
h 2
12
b
y
同理:
Iy
hb3 12
z
Iz
b1h13 12
b2h23 12
c
b2 b1
同理: I y
h1b13 12
y
12 rp
mn
x2
x
x1
12
dx
'=
x2 FN1
FN2
'=
38
5.4 横力弯曲时梁横截面上的切应力 弯曲切应力强度条件
F
Fx 0
FN 2 FN1 dx b
x1
y
12 rp mn
x2
x
12
dx
材料力学弯曲应力_图文

§5-3 横力弯曲时的正应力
例题6-1
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
120
1.C 截面上K点正应力 2.C 截面上最大正应力
B
x
180
K
30 3.全梁上最大正应力 z 4.已知E=200GPa,
FBY
C 截面的曲率半径ρ y
解:1. 求支反力
x 90kN M
x
(压应力)
目录
目录
§5-2 纯弯曲时的正应力
正应力分布
z
M
C
zzy
x
dA σ
y
目录
§5-2 纯弯曲时的正应力
常见截面的 IZ 和 WZ
圆截面 空心圆截面
矩形截面 空心矩形截面
目录
§5-3 横力弯曲时的正应力
横力弯曲
6-2
目录
§5-3 横力弯曲时的正应力
横力弯曲正应力公式
弹性力学精确分析表明 ,当跨度 l 与横截面高度 h 之比 l / h > 5 (细长梁)时 ,纯弯曲正应力公式对于横 力弯曲近似成立。 横力弯曲最大正应力
§5-3 横力弯曲时的正应力
q=60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
120
2. C 截面最大正应力
B
x
180
K
30 C 截面弯矩 z
FBY
y
C 截面惯性矩
x 90kN M
x
目录
§5-3 横力弯曲时的正应力
q=60kN/m
A
1m
FAY
C
l = 3m
秦飞编著《材料力学》第7章 弯曲应力

秦飞 编著《材料力学》 第7章 弯曲应力
14
7.1 弯曲正应力
弯曲正应力公式
各种型钢的Iz、Wz值均可以从附录的型钢规格表中查到。
常用截面:矩形截面
bh 3 Iz 12
y max
h 2
bh 2 Wz 6
h
b
对于直径为D的实心圆形截面
πD Iz 64
4
ymax
C
拉
z
M
z
C
压
拉 y y
秦飞 编著《材料力学》 第7章 弯曲应力 8
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(2)静力平衡关系 由平面假设,横截面上只有正应力σ。纯弯曲情况下,梁横 截面上的内力只有Mz=M,轴力和 My等其他内力均为零,则
dA 0
A
中性轴
z dA 0
A
由这3个静力平衡方
y
与y成正比,沿截面高
度线性变化。
秦飞 编著《材料力学》 第7章 弯曲应力
ρ为中性层曲率半径
10
7.1 弯曲正应力
纯弯曲时梁横截面上的正应力
(4)物性关系
y 将 代入物性关系,得: y E E
可见,梁横截面上的弯曲正应力 (normal stress in bending) 与y成正比, 即 (1)沿截面高度线性分布; (2)在中性层处为零,在上、下表面 处最大。
My Iz
—弯曲正应力公式
此公式适用于所有横截面具有纵向对称轴的梁,如圆形截 面、工字形截面和T形截面。 由公式: 正比于y。 沿高度线性分布。 中性轴处=0。
秦飞 编著《材料力学》 第7章 弯曲应力 13
横力弯曲时的正应力

应力,纯弯曲时所作的平面假设和单向受力假设都不成立. 虽然横力弯曲与纯弯曲存在这些差异,但进一步的分析表
明,工程中常用的梁,纯弯曲时的正应力计算公式,可以精确的 计算横力弯曲时横截面上的正应力.
等直梁横力弯曲时横截面上的正应力公式为 σ M ( x) W
l
F
独立弯曲,近似地认为每片上承担
的外力等于 F / n
解:每一薄片中的最大正应力
h
z
b
l
F
σmax
M max Wz
F l n 1 b (h)2
6Fl bh2
n
6n
h
z
b
若用刚度足够的螺栓将薄片联紧,杆就会象整体梁一样弯曲
最大正应力等于
σmax
M max Wz
Fl
1 6
bh2
6Fl bh2
1m
1m
2.5kN
1m 最大负弯矩在截面B上
-
+
M B 4kN m
B截面
80
4kN
σt max
M B y1 Iz
27.2MPa
[σt]
20
σ c max
M B y2 Iz
46.2MPa
[σc]
C截面
120
20
σt max
MC y2 Iz
28.8MPa
[σt]
例题3 由 n 片薄片组成的梁,当每 片间的磨擦力甚小时,每一薄片就
对形心轴z的惯性矩为 Iz =763cm4 , y1 =52mm,校核梁的强度.
20
F1=9kN
F2=4kN
80
y1
A C
弯曲应力及强度计算
工程背景
第2页/共32页
1999年1月4日,我国重庆市綦江县彩虹
桥发生垮塌,造成:
40人死亡;
14人受伤;
直接经济损失631万元。
第3页/共32页
由工程实例可知:
工程中存在大量与弯曲强度有关的问题。
弯曲强度问题的研究对避免受弯结构的破坏 具有十分重要的意义。
研究弯曲强度问题
受弯构件内 应力的分布规律
12.75103 139103 403107
43.98MPa
如果T截面倒置会如何???
第19页/共32页
* 梁的剪应力强度条件
一、梁横截面上的剪应力
Q—横截面上的剪力
QS
* z
IZb
IZ—横截面对中性轴的惯性矩
S*Z—所求应力点以上或以下部分截面对中性轴的静矩 b—所求应力点的截面宽度
剪应力沿截面高度呈抛物线分布,在中性轴处最 大,在上下边缘处为零。
成变截面的。横截面沿梁轴变化的梁,称为变截面梁。
F A
F A
h(x) B
z
b
B
各个横截面具有同样强度的梁称为等强度梁,等强度梁是一种
理想的变截面梁。但是,考虑到加工制造以及构造上的需要等,实际 构件往往设计成近似等强的。
第29页/共32页
小结:
一、梁的应力:
横截面上的正应力: M y ; Iz
等直梁 max
Mmax所在横截面 离中性轴最远处
max
Mmax IZ
ymax
等直梁的最大弯曲正应力公式
第12页/共32页
* 梁的正应力强度计算
max
M max IZ
ymax
设 ymax为到中性轴的最远距离
材料力学 弯曲应力与强度条件

150 50
A
l 2
B
l 2
96 .4 C 50
200
z
M max
FL 16kNm 4
y
max max
200 50 96.4 153.6mm 96.4mm
max
My max IZ My max IZ
24.09MPa 15.12MPa
max
例题
长为2.5m的工字钢外伸梁,如图示,其外伸部分为0.5m,梁上 承受均布荷载,q=30kN/m,试选择工字钢型号。已知工字钢抗弯 强度[σ]=215MPa。
q 30 kN m
A
0.5m
解:1、求支反力,画梁的弯矩图,确 定危险截面 FA 46.9KN , FB 28.1KN
E
y
X
A
0:
y
A
N dA E
A
dA
E
A
ydA 0
S Z ydA yc A 0(中性轴通过截面形心)
M
A
Z
0:
M Z ydA M
A
M yE dA
y
E
y 2 dA 令: y 2 dA I Z A
C截面
c
B
B截面
∴铸铁梁工作安全。如果T截面倒
例题
A
y 铸铁制作的悬臂梁,尺寸及受力如图示,图中F=20kN。梁 的截面为T字形,形心坐标yc=96.4mm。已知材料的拉伸许用应 150 力和压缩许用应力分别为[σ]+=40MPa, [σ]-=100MPa。试 校核梁的强度是否安全。 F 50 96 .4
工程力学5

B
l Fl
| M |max Fl 1.2 F N m
查附录型钢表3,
x
4 3
Wz 185cm 1.85 10 m
3
M
由: 得: 故:
M max Wz
1.2F (1.85 104 ) (170 106 )
[ F ]max
185 170 26.2kN 1.2
* N2 * N1
* * 得 dFS=FN F 2 N1
其中 dFS= bdx
* FN 2 dA Ay
* FN 1
M dM y1dA Ay Iz M dM y1dA Ay Iz
Ay
* FN 2
M dM Sz Iz
M F Sz Iz
* N1
dFS
p
(4)由于y、z轴就是横截面的形心主轴,从而可得到启示:当横 截面没有对称轴时,只要外力偶作用在形心主轴之一(例如 y轴)所构成的纵向平面内,上述公式仍适用。 (5)对于用铸铁、木材以及混凝土等材料制成的梁,在应用上述
公式时,都带有一定的近似性。
例5-1 T形截面外伸梁尺寸及受力如图所示。已知横截面对中性轴
§5-2
横力弯曲时梁的正应力及其强度条件 梁的合理截面
q
一.横力弯曲时梁的正应力及其强度条件
q b
M ( x)
z h
l
y
b
Fs ( x)
由于τ的存在,横截面发生翘曲(§5-3)。平面假设不成立, 且还有沿y的挤压正应力。 由弹性力学结果表明,当l/h≥5时,用(5-2)式计算跨中截面的 最大正应力,其误差≤1.07%。所以工程中仍用纯弯曲时的正应 力公式,计算横力弯曲时的正应力。但要注意,横力弯曲时, 弯矩是x的函数,所以
第18讲梁横力弯曲时横截面上的切应力

第18讲教学方案——弯曲切应力、弯曲强度条件§7-3 弯曲切应力梁受横弯曲时,虽然横截面上既有正应力σ,又有剪应力 τ。
但一般情况下,剪应力对梁的强度和变形的影响属于次要因素,因此对由剪力引起的剪应力,不再用变形、物理和静力关系进行推导,而是在承认正应力公式(6-2)仍然适用的基础上,假定剪应力在横截面上的分布规律,然后根据平衡条件导出剪应力的计算公式。
1.矩形截面梁对于图6-5所示的矩形截面梁,横截面上作用剪力Q 。
现分析距中性轴z 为y 的横线1aa 上的剪应力分布情况。
根据剪应力成对定理,横线1aa 两端的剪应力必与截面两侧边相切,即与剪力Q 的方向一致。
由于对称的关系,横线1aa 中点处的剪应力也必与Q 的方向相同。
根据这三点剪应力的方向,可以设想1aa 线上各点剪应力的方向皆平行于剪力Q 。
又因截面高度h 大于宽度b ,剪应力的数值沿横线1aa 不可能有太大变化,可以认为是均匀分布的。
基于上述分析,可作如下假设:1)横截面上任一点处的剪应力方向均平行于剪力 Q 。
2)剪应力沿截面宽度均匀分布。
基于上述假定得到的解,与精确解相比有足够的精确度。
从图6-6a 的横弯梁中截出dx 微段,其左右截面上的内力如图6-6b 所示。
梁的横截面尺寸如图6-6c 所示,现欲求距中性轴z 为y 的横线1aa 处的剪应力 τ。
过1aa 用平行于中性层的纵截面11cc aa 自dx 微段中截出一微块(图6-6d )。
根据剪应力成对定理,微块的纵截面上存在均匀分布的剪应力 τ'。
微块左右侧面上正应力的合力分别为1N 和2N ,其中*1I 1**z zAzA S I M dA I My dA N ===⎰⎰σ (a ) *1II 2)()(**z z Az A S I dM M dA I y dM M dA N +=+==⎰⎰σ (b)式中,*A 为微块的侧面面积,)(II I σσ为面积*A 中距中性轴为 1y 处的正应力,⎰=*1*A z dA y S 。
弯曲强度计算
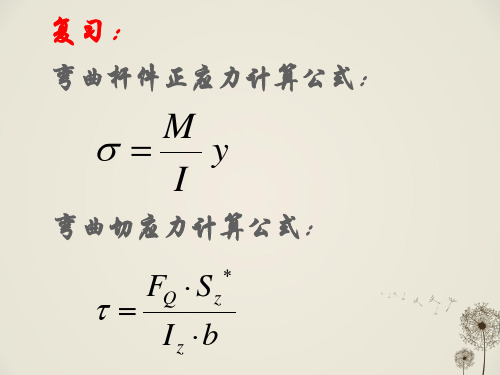
I y 令
Wz
Iz ymax
则
z max
max
M Wz
式中 Wz——抗弯截面系数。在M相同的情况
下,Wz 愈大, max就愈小,梁便不容易破坏。可见
,抗弯截面系数反映截面抵抗弯曲破坏的能力。
(2) 脆性材料杆件和中性轴不在对称轴的 截面,最大拉应力和最大压应力不一定发生
在同一截面,所以,最大正应力公式表示为
RA 26 KN
RB 34 KN
M max 136 KN m
Wz
M max
2
136 106 2 170
400 cm3
a z
b
y
M
τmin
τmax τmin
二、强度计算
1. 强度校核
max
M max Wz
2. 设计截面
max
FQ
S* z max
Iz b
Wz M max
圆截面:
Wz
Iz ymax
d 4
d
64 2
d3
32
矩形截面:
Wz
Iz ymax
bh3 12 h2
bh2 6
3. 确定许用荷载
M max Wz
力强度,甚至由切应力强度条件来控制:
(1)梁的跨度较小或荷载作用在支座附时。
(2)某些组合截面梁(如焊接的工字形钢板梁
),当腹板厚度与高度之比小于相应型钢的相应
比值时。
(3)木梁或玻璃等复合材料梁。
3.主应力强度条件
当截面为三块矩形钢板 焊接而成的工字形:
1
2
2
2
2
3
2
2
2
2
mmaxaxMM2I1Iyzyzmmaaxx
弯曲正应力、切应力与强度条件

M
C
拉
Z
C
Z
中性轴
拉
y
中性轴
y
压
中性轴将横截面分为 受拉 和 受压 两部分。
M yAz(
d)A E
Az
y dA
E
I
yz
0
Iyz0
因为 y 轴是横截面的对称轴,所以 Iyz 一定为零。 该式自动满足
中性轴是横截面的形心主惯性轴
M ZAy(
d)A E
A
y2 dA
E
Iz
M
1M
EI z
基本假设2: 纵向纤维无挤压假设
纵向纤维间无正应力。
公式推导
d
用两个横截面从梁中假想地截取 长为 dx 的一段 。
由平面假设可知,在梁弯曲时,
这两个横截面将相对地旋转一个
角度 d 。
横截面的转动将使梁的凹边的纵 向线段缩短,凸边的纵向线段伸 长。由于变形的连续性,中间必 有一层纵向线段 O1O2 无长度改 变。此层称为 中性层 。
m M
FS m
m
m
M
FS
m
m
只有与切应力有关的切向内力元素 dFS = dA 才能合成剪力 只有与正应力有关的法向内力元素 dFN = dA 才能合成弯矩 所以,在梁的横截面上一般既有 正应力,又有 切应力
一,纯弯曲梁横截面上的正应力
RA
P
P RB
C a
P
+
D a
+
P
+
Pa
推导 纯弯曲 梁横截面上正应力的计算公式。 几何 物理 静力学
2 假想地从梁段上截出体积元素 mB1
m'
m z
材料力学 第10章 弯曲应力及强度

a
Φ14
30 工件
Fa x
10.4 弯曲强度条件
例10-5 梁的载荷及截面尺寸如图所示,材料的容许拉应力
[t]=40MPa、容许压应力[c] =100MPa,试校核该梁的强度。
q=10kN/m
F=20kN
AB 2m
CD 3m 1m
q=10kN/m
A
B
FB M
F=20kN
C
D
FD
10kN.m
x
157.5 200 30
10.3 横力弯曲时梁的切应力
三、其它形状截面
T型截面
圆形截面
环形截面
max
z
max
FSS
* z,m
ax
I zb1
z
max
z
max
max
4 3
FS A
max
2
FS A
10.3 横力弯曲时梁的切应力
21 560
例10-2 56a号工字钢制成的简支梁如图所示,F=150kN,求最大 切应力及最大切应力所在截面上K点处的切应力。
ad bc
a
d
b
c
σσ
M
ττ
10.2 纯弯曲时梁的正应力
3. 变形几何关系
o1o2 dx ρdθ
k1k2 (ρ y)dθ Δl=k1k2 k1k2 ( ρ y)dθ ρdθ ydθ
dx 中性层
y o1
o2
k1
k2
dx 变形前
o
d
o1
o2
k1
k 2
变形后
10.2 纯弯曲时梁的正应力
第10章 弯曲应力及弯曲强度
10.1 引言 10.2 纯弯曲时梁的正应力 10.3 横力弯曲时梁的切应力 10.4 弯曲强度条件 10.5 提高梁弯曲强度的措施
第五章 弯曲应力1

§5–4 弯曲切应力
一、梁横截面上的切应力
1、矩形截面梁
(1)两个假设 (a)切应力与剪力平行 (b)切应力沿截面宽度均匀分布
(2)分析方法
F1 F2 m n
q(x)
z
m
n
mn
x
dx
h yo
A1
B1
x
z
y
x
A
B
A1
B1
y bm
n
dx
FN1
A
ym
B
FN2
n
z
z
m
n
y
x
A1 dFS’
B1
FN1
A
B FN2
查型钢表中,20a号工字钢,有
Iz
S
* z
max
17.2cm
d=7mm
F
AC
B
5m
FSmax
据此校核梁的切应力强度
*
F S F Smax z ,max
max
I d ( I )d z
Smax z
+
S* z ,max
30 103
24.9MPa [ ] 以上两方面的强度条件都满
D
z
4
1
1
22
a1
Wz3
bh2 6
4a13 6
1.67Wz1
合理放置截面
bh2 WZ 左 6
WZ 右
hb2 6
三、采用等强度梁
梁各横截面上的最大正应力都相等,并均达到材料的许用应力,
则称为等强度梁. 例如,宽度b保持不变而高度可变化的矩形截面简支梁,若设
第六章弯曲应力2
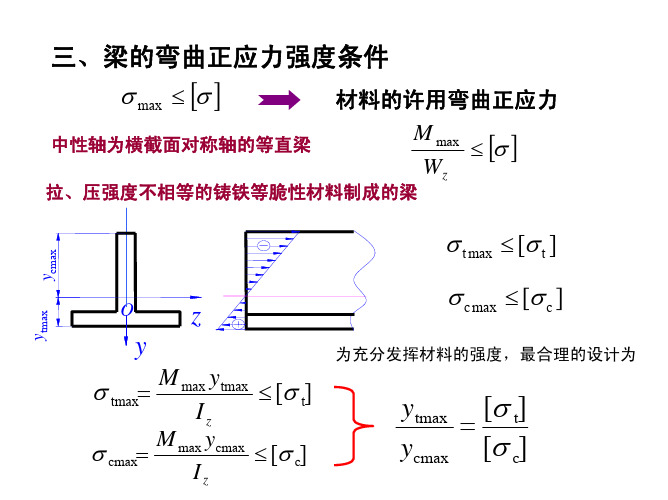
120
C 形心 86 z 134
Fb/4
压应力
拉应力
20
y 20
拉应力 C截面 B截面
压应力
可见:压应力强度条件由B截面控制,拉应力 强度条件则B,C截面都要考虑.
Fb/2
40 180
拉应力
120
C 形心 86 z 134
Fb/4 考虑截面B :
20
压应力
y 20
σ t,max
M B y2 F / 2 × 2 × 10 3 mm (86 mm ) = = ≤ 30 MPa 3 4 Iz 5493 × ×10 mm
1
∑X =N
F s S z dM S z τ1 = = dx bI z bI z
由切应力互等定理可知
( M + dM ) S z N1 = Iz
τ1
y
τ
y x
F s S z τ = I zb
σ
σ1
图C
注意:Fs为横截面的剪力;Iz 为整个横截 面对 z 轴的惯性矩;b为所求点对应位置 * 截面的宽度;S z 为所求点对应位置以外 的面积对Z轴的静矩.
M C y1 F / 4 × 2 × 10 3 mm (134 mm ) ≤ 30 MPa = = 4 4 Iz 5493 × 10 mm F ≤ 24.6 kN
拉应力
(
)
因此梁的强度由截面B上的最大拉应力控制
[ F ] = 19.2 kN
例:图示槽型截面梁,Iz=100*106mm4,y1=200mm,y2=50mm, 〔σt〕=45MPa,〔σ c 〕=120MPa.校核梁的强度.
b
3,矩形截面剪应力的分布:
h A* = b( y ) 2
第五章 弯曲应力

三类条件
物理关系
静力关系
1.变形几何关系
m a
n
a
m a o b m
n a o dx
b m
dx
b n
b n
假设oo层为中性层 变形前:aa = bb = oo = dx
m M a
o b m
n a M M
d M
dx
o b n
m o
b′
n o
b′
m
n
变形后:假设中性层oo层变形后的曲率半径为,则
max
M [ ] Wz max
(2) 设计截面尺寸
(3) 计算许用载荷
M Wz [ ]
M max Wz [ ]
例2. T形截面铸铁梁,已知[σt]=30MPa,[σc]=60MPa, 试 80 校核梁的强度。
9kN
A 1m
4kN
B D 1m
20
CLeabharlann 1m120讨论: 1.横截面是绕中性轴转动。 (中性层不伸长也不缩短,中性轴是中性层与横截
面的交线 。) 上部受压
当M > 0时 下部受拉 上部受拉 下部受压
当M < 0时
讨论: 2.纵向纤维的伸长或者缩短与它到中性层的
距离成正比。
m
n′
n a
y
a
y
b m
b
中性层 n′
中性轴 横截面
n
定量分析
与圆轴扭转问题相似,弯曲问题的理论分析也 必须包含三类条件。 变形几何关系
结论: 1.横截面上只存在正应力。
(纵向线与横向线保持直角。)
2.正应力分布不是均匀的。
(纵向线中既有伸长也有缩短的。)
弯曲应力-材料力学

max
Mymax Iz
工程力学 Engineering Mechanics
典型例题
例1 图示矩形截面梁,梁上载荷q=100kN/m,梁跨度l=6m,截面尺寸:
b=400mm,h=600mm,材料许用应力[]=100MPa,试判断该梁是否安全。
弹性力学精确分析表明,当跨度l与横截面高度h之比l/h>5(细长梁)时, 纯弯曲正应力公式对于横力弯曲近似成立。
横力弯曲最大正应力
max
M max ymax Iz
弯曲正应力适用范围 细长梁的纯弯曲或横力弯曲 横截面惯性积Iyz=0 弹性变形阶段
工程力学 Engineering Mechanics
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解:(3)求解正应力
My Iz
惯性矩
Iz
1 12
50 903
3.0375106 mm4
弯矩
M 10kN.m
典型例题
例1 求图示矩形截面梁指定截面上对应点的正内力。
10kN
1
A
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解:(3)求解正应力
M max
1 8
ql 2
1 8
q
62
q
533.3kN/m
练习1
受均布载荷作用的简支梁如图,求 ① 1-1截面上1、2两点的正应力; ② 1-1截面上的最大正应力; ③ 全梁的最大正应力; ④ 已知E=200GPa,求1-1截面的曲率半径。
第十章 工程力学之弯曲应力
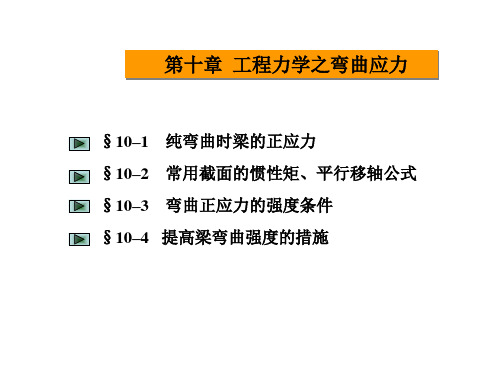
max拉MWm1ax [拉] ; max压MWm2ax [压]
式中W1和W2分别是相应于最大拉应力 max拉和最大压应力 max压 的抗弯截面模量,[ 压 ] 为材料的许用拉应力,[ 拉 ]为
材料的许用压应力。
例10-1 某冷却塔内支承填料用的梁,可简化为受均布载荷 的简支梁,如图10-8所示。已知梁的跨长为3m,所受均布
加载之前,先在梁的侧面,分别画上与梁轴线垂直的横线mn、 m1n1,与梁轴线平行的纵线ab、a1b1,前二者代表梁的横截面;
后二者代表梁的纵向纤维。如图10-2(a)所示。
在梁的两端加一对力偶,梁处于纯弯曲状态,将产生如图 10-2(b)、图10-2(c)所示的弯曲变形,可以观察到以下 现象:
•两条横线仍为直线,仍与纵线垂直,只是横线间作相对 转动,由平行线变为相交线。
2. 梁的变形规律
可以证明,纯弯曲梁变形后的轴线为一段圆弧。将图10-2(b)
中代表横截面的线段mn和m1n1延长,相交于C点,C点就是梁轴 弯曲后的曲率中心。若用 表示这两个横截面的夹角, 表
示中性层 故有
O
1
O
2
的曲率半径,因为中性层的纤维长度
O
1
O
2
不变,
O1O2
在如图10-2所示的坐标系中,y轴为横截面的对称轴,z轴为
如图10-1(a)所示的简支梁,其剪 力图如图10-1(b)所示,弯矩图如图 10-1(c)所示。可以看出梁中间一段 的剪力为零,而弯矩为常数,即为纯
弯曲; AC 和DB 段上既有剪力,又有
弯矩,为横力弯曲。
一、变形的几何关系
1. 梁的变形特点
如图10-2(a)所示,取梁的纵向对称面为xy平面。梁上的 外载荷就作用在这个平面内,梁的轴线在弯曲变形后也位于这 个平面内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§9—3 梁截面上的正应力
当梁上有横向外力作用时,一般情况下,梁的横截面上既又弯矩 M , 又有剪力 FS 。
m M
FS m
m
FS
m
m
M
m
只有与切应力有关的切向内力元素 dFS = dA 才能合成剪力 只有与正应力有关的法向内力元素 dFN = dA 才能合成弯矩 所以,在梁的横截面上一般既有 正应力,又有 切应力
M
O
dA y
Z
Z
x
dA
y
E E y
F N A dA
E
A
ydA
E
Sz
0
My
A z (dA)
E
A z
y dA
E
I
yz
0
MZ
A
y (dA)
E
A
y2 dA
E
Iz
M
F
N
A
dA
E
A
ydA
E
Sz
0
SZ 0
中性轴必通过横截面的形心
中性轴过截面形心且与横截面的对称轴 y 垂直
C
Z
中性轴
。此层称为 中性层 。
O1O2 的长度为 dx 。
O1
dx
O2
中性层与横截面的交线称 为 中性轴 。
中性轴与横截面的 对称轴成正交 。
d
O1
dx
O2
中性层与中性轴
d
横截面的 对称轴
横截面
O1
dx
O2
中性层
中性轴
d Z
x
y
将梁的轴线取为 x 轴 。
O1
dx
O2
横截面的对称轴取为 y 轴 。
中性轴取为 z 轴 。
Iz
(1)应用公式时,一般将 M ,y 以绝对值代入。根据梁变形 的实际情况直接判断 的正,负号。
为中性层上的纵向线段 O1O2
变弯后的曲率半径。
在横截面上取距中性轴为 y 处 的纵向线 AB。
作 O2B1 与 O1A 平行。 O2B1 的长度为 y 。
d
O1
y
A
dx
O2
d
y B
B1
AB1 为变形前 AB 的长度
B1B 为 AB1 的伸长量 AB1 为 A 点的纵向线应变。
l AB1 B1 B
E E y
上式说明,横截面上任一点处的正应力 与该点到中性轴的距 离 y 成正比 ;
在距中性轴为 y 的同一横线上 各点处的 正应力 均相等 。
Z
O
x
y
y1
y
需要解决的问题 如何确定 中性轴的位置 ? 如何计算 ?
σ
Eε
E
y
ρ
M
中性轴
3,静力学方面
在横截面上法向内力元素 dA 构成了空间平行力系。
横力弯曲时的正应力
横力弯曲时横截面上有切应力(翘曲)
平面假设 不再成立
此外, 横力弯曲时纵向纤维无挤压假设也不成立.
由弹性力学的理论,有结论:
当梁的长度l与横截面的高度h的比值:
l 5 h
则用纯弯曲的正应力公式计算横力弯曲时的正应
力有足够的精度。
l / h > 5 的梁称为细长梁。
4,讨论
My
l
AB1 O1O2
y(d )
dx
d
O1
y
A
dx
O2
d
y
B dx
B1
AB1 B1 B y(d )
AB1 O1O2 dx
中性层的曲率为
1 d dx
y
d
O1
y
A
dx
O2
d
y
dx
B
B1
y
该式说明 , 和 y 坐标成正比 , 因而, 横截面上到中性轴等 远的各点,其线应变相等。
M
1 M
EI z
EIz 称为截面的抗弯刚度
E E y
My
Iz
该式为等直梁 纯弯曲 时横截面上任一点处正应力的计算公式
式中 :
M
横截面上的弯矩。
Iz
横截面对中性轴的惯性矩。
y
求应力点的 y 坐标 。
公式的适用性
My
Iz
由于推导过程并未用到矩形截面条件,因而 公式适用于任何横截面具有纵向对称面,且 载荷作用在对称面内的情况。 公式是对等直梁得到的。对缓慢变化的变截 面梁和曲率很小的曲梁也近似成立。 公式是从纯弯曲梁推得,是否适用于一般情 形(横力弯曲)?
一,纯弯曲梁横截面上的正应力
RA
P
P RB
C a
P +
D a
+ P
+
Pa
P
C a
P +
P D
a
+ P
+
Pa
横力弯曲
梁的横截面上同时有弯 矩和剪力的弯曲。
纯弯曲 梁的横截面上只有弯矩 没有剪力的弯曲。
横截面上只有正应 力而无切应力。
推导 纯弯曲 梁横截面上正应力的计算公式。
几何
物理
实验: 取 一 纯弯曲 梁来研究 。
基本假设2: 纵向纤维无挤压假设
纵向纤维间无正应力。
公式推导
d
用两个横截面从梁中假想地截取 长为 dx 的一段 。
由平面假设可知,在梁弯曲时, 这两个横截面将相对地旋转一个 角度 d 。
横截面的转动将使梁的凹边的纵向线段缩短 d
,凸边的纵向线段伸长。由于变形的连续性 ,中间必有一层纵向线段 O1O2 无长度改变
dA
M
O
dA y
Z
1 dA Z
x
dA
y
该空间平行力系简化为 x 轴方向的主矢
F N AdA
对y 轴和 z 轴主矩
M y A z(dA) M Z A y(dA)MO源自dA yZZ
x
dA
y
F N AdA 0 M y A z(dA) 0
M Z A y(dA) M
该梁段各横截面上 FN 和 My 均 等于零, 而 Mz 就是横截面上 的弯矩 M 。
d
O1
y
A
dx
O2
d
y
ddxx
B
B1
d
O1
y
A
dx
O2
d
y
ddxx
B
B1
y
Z
O
x
y y
2,物理方面 假设: 纯弯曲时横截面上各点处的处于单轴应力状态 。 材料在线弹性范围内工作,且拉,压弹性模量相等 。 由单轴应力状态下的 胡克定律 可得物理关系
=E
y
E
E E y
上式为横截面上 正应力 变化规律的表达式。
y
C
Z
中性轴
y
压
M
M
C
拉
Z
C
Z
中性轴
拉
y
中性轴
y
压
中性轴将横截面分为 受拉 和 受压 两部分。
My
A z (dA)
E
A z
y dA
E
I
yz
0
I yz 0
因为 y 轴是横截面的对称轴,所以 Iyz 一定为零。
该式自动满足
中性轴是横截面的形心主惯性轴
MZ
A
y (dA)
E
A
y2 dA
E
Iz
静力学
1,几何方面
m
n
a
a
b
b
m
n
梁在加力前先在其侧面上画上一系列的横向线(如 mm ,nn 等) 以及横向线相垂直的一系列的纵向线 (如 aa ,bb 等) 。
m
n
a
a
b
b
m
n
m
m
梁变形后观察到的现象 (1)变形前相互平行的纵向直线(aa ,bb 等),变形后均为
圆弧线(a’a’ ,b’b’等 ),且靠上部的缩短靠下部的伸长。
m
n
a
a
b
b
m
n
m m’
m n’
n’ m’
(2)变形前垂直于纵向直线的横向线( mm , nn 等)变形后仍 为直线( m’m’ , n’n’ 等) ,但相对转了一个角度,且与 弯曲后的纵向线垂直。
纯弯曲的变形特征
基本假设1: 平面假设 变形前为平面的横截 面变形后仍为平面, 且仍垂直于梁的轴线。
