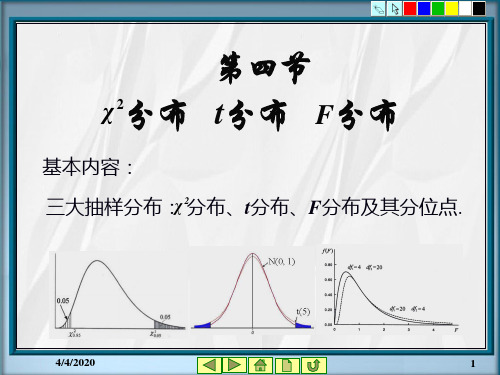
X~2分布、t分布和f分布的性质及近似计算

以下为三个分布的动画演示程序，直接运行：function dandn(action)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%% 《X~2分布、t分布和f分布的性质及近似计算》%% 制作人：幸玮石岩顾秋容% All Rights Reserved % 2008.12%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%无输入参数时进行初始程序,否则调界面参数if nargin<1,action='initialize';else%看是哪种分布data=get(gco,'UserData');pdflabel=data(4);%图形显示参数，调试时用switch pdflabelcase 1xstart=0; %x轴起始点width=120; %x轴范围xdis=30; %x轴刻度间距lenth=0.24; %y轴范围ydis=0.03; %y轴刻度间距speed=0.6; %动画演进速率case 2width=6;xdis=3;lenth=0.42;ydis=0.05;speed=0.5;case 3width=2;xdis=0.5;lenth=4;ydis=0.4;speed=0.8;endend%初始化模块if strcmp(action,'initialize')%数据初始化%分布函数选择pdflabel=0;d=inputdlg({'输入分布函数类型:'},'选择分布函数',1,{'x2'});if strcmp(d,'x2')pdflabel=1;elseif strcmp(d,'t')pdflabel=2;elseif strcmp(d,'f')pdflabel=3;end%不符合的输入报错if pdflabel==0errordlg('分布函数只能选择x2,t与f')returnend%整体用户界面建立，图形显示窗口嵌入figNumber=figure( ...'Name','Changing of the X~2 destribution function', ...'NumberTitle','off', ...'Visible','off');axes( ...'Units','normalized', ...'Visible','off', ...'Position',[0.06 0.065 0.70 0.9]);%显示初始现实画面switch pdflabelcase 1%初始显示参数xstart=0; %x轴起始点width=120; %x轴范围xdis=30; %x轴刻度间距lenth=0.24; %y轴范围ydis=0.03; %y轴刻度间距%画背景图plot([xstart xstart+width],[lenth lenth],'b');hold onplot([xstart xstart+width],[lenth lenth],'r');plot([xstart xstart+width],[lenth lenth],'black'); legend('X~2分布','正态分布');axis([xstart xstart+width 0 lenth]);grid onset(gca,'XTick',xstart:xdis:xstart+width);set(gca,'YTick',0:ydis:lenth);hold off%分布函数动画初始参数m=0;n=1;case 2width=6;xdis=3;lenth=0.42;ydis=0.05;plot([-width -width width],[0 lenth lenth],'b');hold onplot([-width -width width],[0 lenth lenth],'r--'); plot([-width -width width],[0 lenth lenth],'black'); legend('T分布','正态分布');grid onaxis([-width width 0 lenth]);set(gca,'XTick',-width:xdis:width);set(gca,'YTick',0:ydis:lenth);hold offm=0;n=2;otherwisewidth=2;xdis=0.5;lenth=4;ydis=0.4;plot(width,0,'b');hold onplot(width,0,'r');legend('f分布','正态分布');axis([0 width 0 lenth]);grid onset(gca,'XTick',0:xdis:width);set(gca,'YTick',0:ydis:lenth);hold off%f分布输入nn=inputdlg({'输入n的值:'},'获取n',1,{'5'});n=str2double(n{1});if n<=4errordlg('要使正态逼近式成立n必须大于4!')returnendm=1;end%按钮显示位置top=0.95;left=0.80;btnWid=0.15;btnHt=0.08;spacing=0.02;%“Start”按钮btnNumber=1;labelStr='Start';callbackStr='dandn(''start'')';%显示按钮btnPos=[left top-btnHt btnWid btnHt];uicontrol( ...'Style','pushbutton', ...'Units','normalized', ...'Position',btnPos, ...'String',labelStr, ...'Callback',callbackStr, ...'UserData',[btnNumber m n pdflabel]); %调用时的句柄参数传递%关闭按钮yPos=top-(btnHt+spacing);uicontrol( ...'Style','push', ...'Units','normalized', ...'Position',[left yPos-btnHt btnWid btnHt], ...'String','Close', ...'Callback','close(gcf)');set(figNumber,'Visible','on'); %显示初始图像%“Start”按钮执行程序elseif strcmp(action,'start')%参数初始化data=get(gco,'UserData');method=data(1);m=data(2);n=data(3);%“Stop”按钮设置，点击开始后替换“Start”按钮btnNumber=2;labelStr='Stop';callbackStr='dandn(''stop'')';top=0.95;left=0.80;btnWid=0.15;btnHt=0.08;btnPos=[left top-btnHt btnWid btnHt];stophld=uicontrol( ...'Style','pushbutton', ...'Units','normalized', ...'Position',btnPos, ...'String',labelStr, ...'Callback',callbackStr, ...'UserData',[btnNumber m n pdflabel]);%画图程序switch pdflabelcase 1while(method==1) %当未点击“Stop”则继续执行%画x2分布密度函数a=n/2; b=2;x=xstart:0.1:xstart+width;y=gampdf(x,a,b);plot(x,y,'b','EraseMode','normal');hold on%画近似正太分布密度函数y1=normpdf(x,n,(2*n)^0.5);plot(x,y1,'r-');%图形参数调节axis([xstart xstart+width 0 lenth]);set(gca,'XTick',xstart:xdis:xstart+width);set(gca,'YTick',0:ydis:lenth);grid on;legend('X~2分布','正态分布');%显示当前ntemp=num2str(floor(n));str=strcat('n=',temp);text(92,0.2,str);%显示当前最大间距dis=num2str(max(abs(y-y1)));str=strcat('dis=',dis);text(92,0.187,str);%动画指令drawnow;hold off;n=n+speed;%看stop是否按下data=get(gco,'UserData');method=data(1);%更新传递参数set(stophld,'Userdata',[btnNumber m n pdflabel]);endcase 2while(method==1)%画t分布密度函数x=-width:0.1:width;y=tpdf(x,n);plot(x,y,'EraseMode','normal');hold on%画近似正太分布密度函数y1=normpdf(x,0,(n/(n-2))^0.5);plot(x,y1,'r--');%图形参数调节axis([-width width 0 lenth]);set(gca,'XTick',-width:xdis:width);set(gca,'YTick',0:ydis:lenth);grid on;legend('T分布','正态分布');%显示当前ntemp=num2str(floor(n));z=strcat('n=',temp);text(3.3,0.335,z);%显示当前最大间距dis=num2str(max(abs(y-y1)));str=strcat('dis=',dis);text(3.3,0.315,str);%动画指令drawnow;hold off;n=n+speed;%看stop是否按下data=get(gco,'UserData');method=data(1);%更新传递参数set(stophld,'Userdata',[btnNumber m n pdflabel]);endotherwisewhile(method==1)%画f分布密度函数x=0:0.01:width;y=fpdf(x,m,n);plot(x,y,'EraseMode','normal');hold on%画近似正太分布密度函数y1=normpdf(x,n/(n-2),(2*n^2*(m+n-2)/m/(n-2)^2/(n-4))^0.5); plot(x,y1,'r');%图形参数调节axis([0 width 0 lenth]);set(gca,'XTick',0:xdis:width);set(gca,'YTick',0:ydis:lenth);grid on;legend('f分布','正态分布');%显示当前mtemp1=num2str(floor(m));str=strcat('m=',temp1);text(1.55,3.32,str);%显示当前ntemp2=num2str(floor(n));str=strcat('n=',temp2);text(1.78,3.32,str);%显示当前最大间距dis=num2str(max(abs(y-y1)));str=strcat('dis=',dis);text(1.55,3,str);%动画指令drawnow;hold off;m=m+speed;%看stop是否按下data=get(gco,'UserData');method=data(1);%更新传递参数set(stophld,'Userdata',[btnNumber m n pdflabel]);endend%“Close”按钮执行程序elseif strcmp(action,'stop')data=get(gco,'UserData'); %读原有传递数据top=0.95;left=0.80;btnWid=0.15;btnHt=0.08;%用“continue”按钮替代“StopbtnNumber=1;labelStr='Continue';callbackStr='dandn(''continue'')';data(1)=btnNumber; %更新按钮标识btnPos=[left top-btnHt btnWid btnHt];uicontrol( ...'Style','pushbutton', ...'Units','normalized', ...'Position',btnPos, ...'String',labelStr, ...'Callback',callbackStr, ...'UserData',data);%“continue”按钮执行程序elseif strcmp(action,'continue')%读取传递数据data=get(gco,'UserData');method=data(1);m=data(2);n=data(3);%用“Stop”按钮替代“continue”btnNumber=2;labelStr='Stop';callbackStr='dandn(''stop'')';top=0.95;left=0.80;btnWid=0.15;btnHt=0.08;btnPos=[left top-btnHt btnWid btnHt];conthld=uicontrol( ...'Style','pushbutton', ...'Units','normalized', ...'Position',btnPos, ...'String',labelStr, ...'Callback',callbackStr, ...'UserData',[btnNumber m n pdflabel]);%动画switch pdflabelcase 1while(method==1)%画系x2分布密度函数a=n/2; b=2; %画x2分布密度函数x=xstart:0.1:xstart+width;y=gampdf(x,a,b);plot(x,y,'b','EraseMode','normal');hold on%画近似正太分布密度函数y1=normpdf(x,n,(2*n)^0.5);plot(x,y1,'r-');%图形参数调节axis([xstart xstart+width 0 lenth]);set(gca,'XTick',xstart:xdis:xstart+width);set(gca,'YTick',0:ydis:lenth);grid on;legend('X~2分布','正态分布');%显示当前ntemp=num2str(floor(n));str=strcat('n=',temp);text(92,0.2,str);%显示当前最大间距dis=num2str(max(abs(y-y1)));str=strcat('dis=',dis);text(92,0.187,str);%动画指令drawnow;hold offn=n+speed;%看stop是否按下data=get(gco,'UserData');method=data(1);%更新传递参数set(conthld,'UserData',[btnNumber m n pdflabel]);endcase 2while(method==1)x=-width:0.1:width;y=tpdf(x,n);plot(x,y,'EraseMode','normal');hold on%画近似正太分布密度函数y1=normpdf(x,0,(n/(n-2))^0.5);plot(x,y1,'r--');%图形参数调节axis([-width width 0 lenth]);set(gca,'XTick',-width:xdis:width);set(gca,'YTick',0:ydis:lenth);grid on;legend('T分布','正态分布');%显示当前ntemp=num2str(floor(n));z=strcat('n=',temp);text(3.3,0.335,z);%显示当前最大间距dis=num2str(max(abs(y-y1)));str=strcat('dis=',dis);text(3.3,0.315,str);%动画指令drawnow;hold offn=n+speed;%看stop是否按下data=get(gco,'UserData');method=data(1);%更新传递参数set(conthld,'UserData',[btnNumber m n pdflabel]);endotherwisewhile(method==1)x=0:0.01:width;y=fpdf(x,m,n);plot(x,y,'EraseMode','normal');hold on%画近似正太分布密度函数y1=normpdf(x,n/(n-2),(2*n^2*(m+n-2)/m/(n-2)^2/(n-4))^0.5); plot(x,y1,'r');%图形参数调节axis([0 width 0 lenth]);set(gca,'XTick',0:xdis:width);set(gca,'YTick',0:ydis:lenth);grid on;legend('f分布','正态分布');%显示当前mtemp1=num2str(floor(m));str=strcat('m=',temp1);text(1.55,3.32,str);%显示当前ntemp2=num2str(floor(n));str=strcat('n=',temp2);text(1.78,3.32,str);%显示当前最大间距dis=num2str(max(abs(y-y1)));str=strcat('dis=',dis);text(1.55,3,str);%动画指令drawnow;hold offm=m+speed;%看stop是否按下data=get(gco,'UserData');method=data(1);%更新传递参数set(conthld,'UserData',[btnNumber m n pdflabel]);endendend。