希望杯九年级数学竞赛试卷
初三希望杯试题及答案

初三希望杯试题及答案一、选择题(每题4分,共40分)1. 下列哪个数是无理数?A. 2B. √2C. 0.5D. 1/3答案:B2. 一个等腰三角形的两边长分别为3和5,那么它的周长是多少?A. 11B. 13C. 16D. 无法确定答案:B3. 以下哪个函数是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = x答案:D4. 一个圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 100πD. 125π答案:C5. 以下哪个方程的解是x=2?A. x^2 - 4x + 4 = 0B. x^2 - 5x + 6 = 0C. x^2 - 6x + 9 = 0D. x^2 - 7x + 12 = 0答案:A6. 一个数列的前三项为1,2,3,从第四项开始,每一项是其前三项的和,那么这个数列的第10项是多少?A. 40B. 47C. 52D. 55答案:B7. 一个二次函数的图像开口向上,且与x轴有两个交点,那么它的判别式Δ是多少?A. Δ > 0B. Δ = 0C. Δ < 0D. 无法确定答案:A8. 以下哪个图形是中心对称图形?A. 矩形B. 等边三角形C. 等腰梯形D. 圆答案:D9. 一个多项式f(x) = ax^3 + bx^2 + cx + d,其中a,b,c,d均为整数,且f(1) = 6,f(-1) = -6,那么a + b + c + d的值是多少?A. 0B. 2C. 4D. 6答案:B10. 以下哪个不等式组有解?A. x + y < 2B. x - y > 0C. x + y < 2 和 x - y > 0D. x - y > 0 和 x - 2y < 0答案:C二、填空题(每题4分,共20分)11. 一个直角三角形的两直角边长分别为6和8,那么它的斜边长是________。
希望杯初三试题及答案

希望杯初三试题及答案一、选择题(每题3分,共30分)1. 下列哪项是正确的?A. 圆的周长是其直径的π倍B. 圆的周长是其半径的2π倍C. 圆的面积是其半径的π倍D. 圆的面积是其直径的π倍答案:B2. 以下哪个数是无理数?A. 3.14B. √2C. 0.33333D. 1/3答案:B3. 一元二次方程ax²+bx+c=0(a≠0)的根与系数的关系是?A. x₁+x₂=-b/aB. x₁+x₂=b/aC. x₁x₂=c/aD. x₁x₂=-b/a答案:A4. 以下哪个选项是等腰三角形的特征?A. 两边相等B. 两角相等C. 三边相等D. 三角相等答案:A5. 以下哪个是完全平方数?A. 23B. 25C. 27D. 29答案:B6. 以下哪个是质数?A. 2B. 9C. 10D. 12答案:A7. 以下哪个是反比例函数?A. y=xB. y=1/xC. y=x²D. y=x+1答案:B8. 以下哪个是一次函数?A. y=2x+3B. y=x²+1C. y=1/xD. y=x/2+1答案:A9. 以下哪个是正弦函数?A. y=sin(x)B. y=cos(x)C. y=tan(x)D. y=cot(x)答案:A10. 以下哪个是余弦函数?A. y=sin(x)B. y=cos(x)C. y=tan(x)D. y=cot(x)答案:B二、填空题(每题3分,共30分)1. 一个等边三角形的每个内角是______度。
答案:602. 一个数的相反数是-5,那么这个数是______。
答案:53. 一个数的绝对值是4,那么这个数可以是______或______。
答案:4,-44. 一个数的平方是36,那么这个数可以是______或______。
答案:6,-65. 一个数的立方是-27,那么这个数是______。
答案:-36. 一个数的倒数是1/4,那么这个数是______。
答案:47. 一个数的平方根是3,那么这个数是______。
第二十四届希望杯竞赛初三第1试
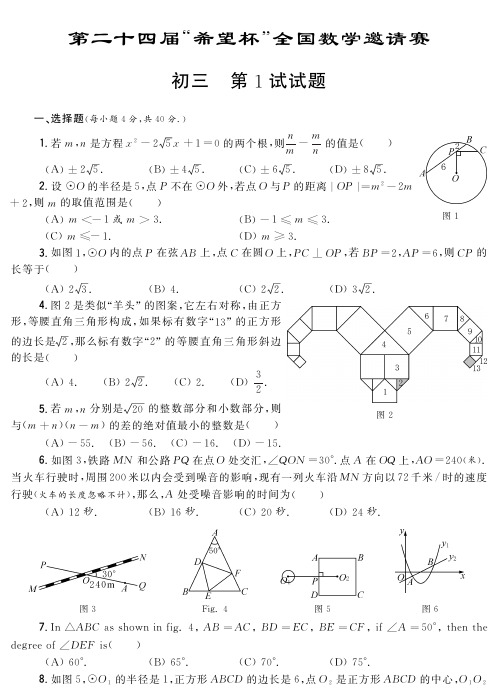
第二十四届 希望杯 全国数学邀请赛初三㊀第1试试题一、选择题(每小题4分,共40分.)图11.若m ,n 是方程x 2-25x +1=0的两个根,则n m -mn的值是()(A )ʃ25.(B )ʃ45.(C )ʃ65.(D )ʃ85.2.设☉O 的半径是5,点P 不在☉O 外,若点O 与P 的距离|O P |=m 2-2m +2,则m 的取值范围是()(A )m <-1或m >3.(B )-1ɤm ɤ3.(C )m ɤ-1.(D )m ȡ3.3.如图1,☉O 内的点P 在弦A B 上,点C 在圆O 上,P C ʅO P ,若B P =2,A P =6,则C P 的长等于()(A )23.(B )4.(C )22.(D )32.图24.图2是类似 羊头 的图案,它左右对称,由正方形,等腰直角三角形构成,如果标有数字 13 的正方形的边长是2,那么标有数字 2的等腰直角三角形斜边的长是()(A )4.(B )22.(C )2.(D )32.5.若m ,n 分别是20的整数部分和小数部分,则与(m +n )(n -m )的差的绝对值最小的整数是()(A )-55.(B )-56.(C )-16.(D )-15.6.如图3,铁路MN 和公路P Q 在点O 处交汇,øQ O N =30ʎ.点A 在O Q 上,A O =240(米).当火车行驶时,周围200米以内会受到噪音的影响,现有一列火车沿MN 方向以72千米/时的速度行驶(火车的长度忽略不计),那么,A 处受噪音影响的时间为()(A )12秒.(B )16秒.(C )20秒.(D )24秒.图3F i g .4图5图67.I n әA B C a s s h o w n i n f i g.4,A B =A C ,B D =E C ,B E =C F ,i føA =50ʎ,t h e n t h e d e gr e e o føD E F i s ()(A )60ʎ.(B )65ʎ.(C )70ʎ.(D )75ʎ.8.如图5,☉O 1的半径是1,正方形A B C D 的边长是6,点O 2是正方形A B C D 的中心,O 1O 2垂直A D 于P 点,O 1O 2=8.若将☉O 1绕点P 按顺时针方向旋转360ʎ,在旋转过程中,☉O 1与正方形A B C D 的边只有一个公共点的情况一共出现()(A )3次.(B )5次.(C )6次.(D )7次.9.如图6,在同一个坐标系内,二次函数y 1=a x 2+b x +c (a ʂ0)和一次函数y 2=d x +e (d ʂ0)的图象相交于点A (m ,n )和点B (p ,q ).当y 1<y 2时,用m ,p 表示x 的取值范围,则是()(A )m <x <p .(B )x <m .(C )x >p .(D )x >m.图710.如图7,在正方形A B C D 中,点M ㊁N 分别在边A B ㊁B C 上运动(不与正方形的顶点重合),且B N =2AM ,若图中的三个阴影三角形中至少有两个相似,则这样的点M 有()(A )1个.(B )2个.(C )3个.(D )4个.二㊁A 组填空题(每小题4分,共40分.)11.已知实数a ,b 不相等,并且a 2+1=5a ,b 2+1=5b ,则1a 2+1b2=.12.I f a 1=1-1m ,a 2=1-1a 1,a 3=1-1a 2, ,t h e n a 2013i n t e r m s o f m i s .13.如图8,在3ˑ2的方格纸上,以某三个格点为顶点的三角形中,等腰三角形共有个.14.若实数x ,y ,z 使2x +y +z =0和3x +2y +5z =0成立,并且z ʂ0,则2x 2-y 2+2z 2-4x yx 2-5z 2+7x z的值是.15.若一个三角形的三边的长是2,13,17,则此三角形的面积是.16.已知抛物线y =a x 2+b x +c (a ʂ0)与x 轴的交点坐标为(-1,0),(3,0),当-2ɤx ɤ5时,y 的最大值为12,则该抛物线的解析式为.图8图9图10图1117.如图9,直角梯形纸片A B C D 中,A D ʊB C ,A B ʅB C ,A B =10,B C =25,A D =15,以B D 为折痕,将әA B D 折起,旋转180ʎ后,点A 到点A 1,则凹五边形B D C E A 1的面积为.18.如图10,将边长为a 的正方形A B C D 绕其顶点C 顺时针旋转45ʎ,得四边形A ᶄB ᶄC D ᶄ,则图中阴影部分的面积是.19.I f (a +4)2-(a -3)2=7,t h e n t h e v a l u e r a n ge of r e a l n u m b e r a i s .20.如图11,从边长为5的正方形纸片A B C D 中剪去直角әE B F (点E 在边A B 上,点F 在边B C 上).若E B +B F =15,则五边形A E F C D 的面积的最小值是.三㊁B 组填空题(每小题8分,共40分.)21.图12是由若干个棱长为1厘米的正方体堆成的几何体,它的三视图中,面积最大的是平方厘米,这个几何体的体积是立方厘米.22.如图13,在әA B C 中,øA =30ʎ,A B =A C =2,B D 是边A C 上的高,利用此图可求得t a n15ʎ=,B C=.23.在直角坐标系内,如果一个点的横坐标和纵坐标都是整数,则称该点为整点.若凸n边形的顶点都是整点,并且多边形内部及其边上没有其它整点,则n=.图12图13图14图1524.如图14,直角梯形A B C D中,A B=1.5,C D=2,A F=1,A D=3,A BʊE FʊC D,øA= 90ʎ,分别以A D,F E所在的直线为x轴,y轴建立坐标系(A D,F E为正方向),若抛物线y=a x2+b x +c过点B㊁C,并且它的顶点M在线段E F上,则a=,b=,c=.25.如图15,әA B C中,øB=90ʎ,øA=60ʎ,A B=A D=2,点M在D C上,以M为圆心,以DM为半径的半圆切边B C于点N,交M C于点P,则DM=,曲边әN C P的面积= .附加题(每小题10分,共20分.)1.若f(x)=6x3-11x2+a x-6可以被g(x)=2x-3整除,则a=,当f(x) >0时,x的取值范围是.2.有一堆黑,白围棋子,如果从中每次取出3枚黑子和2枚白子,当黑子被取完或剩下1枚或2枚时,则还剩35枚白子,如果每次取出5枚黑子和7枚白子,当白子被取完或剩下不足7枚时,则还剩下35枚黑子,那么这堆棋子中,原有黑子枚,白子枚.初三第1试答案。
初三历年希望杯试题及答案

初三历年希望杯试题及答案希望杯数学竞赛是一项面向中学生的数学竞赛活动,旨在激发学生对数学的兴趣和热爱。
以下是一份模拟的初三希望杯试题及答案,供参考:初三希望杯数学竞赛模拟试题一、选择题(每题3分,共15分)1. 下列哪个数不是有理数?A. πB. √2C. 1/3D. 0.33333(无限循环小数)答案:A2. 如果一个直角三角形的两条直角边分别为3和4,那么斜边的长度是:A. 5B. 6C. 7D. 8答案:A3. 一个数的平方根是它本身,这个数是:A. 0B. 1C. -1D. 以上都不是答案:A4. 下列哪个代数式不是同类项?A. 3x^2B. -2x^2C. 5xD. 3x^3答案:C5. 如果一个多项式f(x) = ax^3 + bx^2 + cx + d,其中a ≠ 0,那么f(x)的导数是:A. 3ax^2 + 2bx + cB. 3ax^3 + 2bx^2 + cxC. 3ax + 2bx + cD. 3ax^2 + 2bx + d答案:A二、填空题(每题4分,共20分)6. 一个圆的半径为5,那么它的面积是________。
答案:25π7. 如果一个函数f(x) = kx + b,其中k ≠ 0,那么这个函数的斜率是________。
答案:k8. 一个等差数列的首项是2,公差是3,那么它的第5项是________。
答案:179. 如果两个相似三角形的对应边之比为2:3,那么它们的面积之比为________。
答案:4:910. 一个二次方程x^2 - 5x + 6 = 0的根是________。
答案:2, 3三、解答题(每题10分,共30分)11. 证明:如果一个三角形是直角三角形,那么它的斜边的平方等于两条直角边的平方和。
证明:设直角三角形的两条直角边分别为a和b,斜边为c。
根据勾股定理,我们有:\[ c^2 = a^2 + b^2 \]这证明了直角三角形斜边的平方确实是两条直角边平方和。
希望杯初三试题及答案

希望杯初三试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的?A. 圆的周长是直径的π倍B. 圆的周长是半径的2π倍C. 圆的周长是直径的2π倍D. 圆的周长是半径的π倍答案:C2. 一个数的平方根是它本身的数是:A. 0B. 1C. -1D. 以上都是答案:D3. 以下哪个函数是一次函数?A. y = 2x + 3B. y = x^2 + 1C. y = 1/xD. y = x^3 - 2答案:A4. 以下哪个方程是一元二次方程?A. 3x + 2 = 0B. x^2 - 4x + 4 = 0C. 2x^3 - 5x + 1 = 0D. x/2 + 3 = 0答案:B5. 以下哪个图形是中心对称图形?A. 等边三角形B. 矩形C. 等腰梯形D. 圆答案:D6. 两个相似三角形的对应边长比为2:3,它们的周长比为:A. 2:3B. 3:4C. 4:5D. 6:9答案:A7. 一个等腰三角形的底角为45°,那么顶角的度数是:A. 45°B. 90°C. 60°D. 75°答案:B8. 一个正五边形的内角和为:A. 540°B. 720°C. 900°D. 1080°答案:B9. 一个数列的前三项为1, 2, 4,从第四项开始,每一项是前三项的和,那么第六项是:A. 13B. 21C. 34D. 55答案:C10. 以下哪个选项是正确的?A. √2是有理数B. π是无理数C. 0.333...是无理数D. √3是有理数答案:B二、填空题(每题3分,共30分)11. 一个直角三角形的两直角边长分别为3和4,那么斜边长为______。
答案:512. 一个数的立方根是它本身的数是______。
答案:0,1,-113. 一个二次函数y = ax^2 + bx + c的顶点坐标为(h, k),那么h = ______。
希望杯初三数学竞赛试卷

一、选择题(每题5分,共25分)1. 若一个数的平方根是2,那么这个数是()A. 4B. -4C. 8D. -82. 在直角坐标系中,点A(2,3)关于原点对称的点是()A. (-2,-3)B. (2,-3)C. (-2,3)D. (3,-2)3. 若a、b、c是等差数列,且a+b+c=0,则a²+b²+c²的值为()A. 0B. 3C. 6D. 94. 已知函数f(x)=x²-2x+1,那么f(2x)的值为()A. 4x²-4x+1B. 4x²-8x+1C. 4x²-8x+4D. 4x²-4x+45. 在等腰三角形ABC中,AB=AC,且∠B=40°,则∠C的度数为()A. 40°B. 50°C. 60°D. 70°二、填空题(每题5分,共25分)6. 若a=√2+√3,b=√2-√3,则a+b的值为______。
7. 在直角坐标系中,点P(-2,3)关于y轴对称的点是______。
8. 已知等差数列{an}的首项为2,公差为3,那么第10项an的值为______。
9. 若函数f(x)=ax²+bx+c的图像开口向上,且a>0,b=0,则函数的对称轴为______。
10. 在等腰三角形ABC中,AB=AC,且∠B=30°,则∠C的度数为______。
三、解答题(每题10分,共30分)11. 已知数列{an}的通项公式为an=2n-1,求前n项和S_n。
12. 在直角坐标系中,点A(-2,3)关于直线y=x的对称点为B,求点B的坐标。
13. 已知等差数列{an}的首项为3,公差为2,求第10项an的值。
四、应用题(每题10分,共20分)14. 小明骑自行车从A地到B地,已知A、B两地的距离为10km,小明以每小时15km的速度匀速行驶,求小明从A地到B地所需的时间。
第12届“枫叶新希望杯”全国数学大赛九年级(B卷)

第12届“枫叶新希望杯”全国数学大赛九年级(B 卷)一、单选题1.下列图形中,只用一把无刻度的直尺不能画出对称轴的是( )A .菱形B .正三角形C .正方形D .正五边形 2.小王记录了2月份连续16天的最高气温,并整理成如下表格:那么这16天每天的最高气温的中位数是( )A .12.5B .13C .13.5D .143.如图,ABO V 为等边三角形,且B 点坐标为()2,0,以原点O 为位似中心,将ABO V 放大到CDO V,若点C 的坐标为()2,m ,则ABO V 与CDO V 的面积之比为( )A .1:3B .1:4C .2:7D .2:94.如图,7个大小相同的正方体堆积在一起,其主视图是( )A .B .C .D .5.如图,某小区有一块长24米,宽8米的矩形空地,物业公司计划在其中建3个相同的矩形绿地,三块绿地与周边之间为等宽的人行通道,三块绿地之间有两条等宽的小路,人行通道的宽度是小路宽度的2倍,且三块绿地的面积之和为72平方米.若设人行通道的宽度为x 米,可列方程( )A .28120x x -+=B .210160x x -+=C .212200x x -+=D .2219240x x -+=6.蜂巢的构造非常美丽、科学,蜂巢的一部分如图所示,由5个相同的正六边形组成,称正六边形的顶点为格点,线段AB 为正六边形的对角线,若格点C 使得ABC V 为等腰三角形,则这样的点C 共有( )A .4个B .5个C .6个D .7个7.如图A 、B 、C 是固定在桌面上的三根小棒,其中A 上有5个大小不同的圆片,从上到下,圆片的直径依次增大.现要将这5个圆片移动到B 上,要求:①每次只能移动一个圆片;②圆片只能在A 、B 、C 之间移动;③大圆片不能放在小圆片上面.那么完成这件事情最少要移动圆片( )A .31次B .33次C .17次D .25次8.如图,点O 为矩形ABCD 的中心,8,6,AB BC B ==e 的半径为2,点P 是B e 上一个动点,则AOP V 面积的最小值为( )A .9B .8C .7.2D .7二、填空题9.10.在221m m □□的□中任意填上“+”或者“-”号,所得的代数式为完全平方式的概率是. 11.抛物线2y ax c =+与x 轴交于()(),0,,0A m B n ,与y 轴交于C ,当ABC V 为直角三角形时,a c 、满足的关系为:.12.甲、乙两人同时从A 地出发,以各自的速度匀速向B 地走去,甲到达B 后立即以原来速度的1.5倍返回,直到与乙相遇.若甲、乙两人之间的距离(米)与两人行走的时间x (分钟)之间的函数图像如图所示,则甲、乙相遇时,距离A 地米.13.如图,沿一条母线将圆锥剪开并展平,得到一个扇形,若圆锥的母线长25cm l =,扇形的圆心角100.8θ=︒,则圆锥的体积为3cm .(结果保留π)14.若函数()211y mx m x m =++++与一次函数y x =-恰有一个交点,则m 的值为.15.如图,正方形ABCD 的顶点A 在x 轴上,顶点B 在y 轴上,顶点C D 、在反比例函数8(0)y x x=>的图像上,1A 是反比例函数图像上点D 右侧的一点,以1DA 为边作正方形111DA B C ,若1B 恰好在x 轴上,则1A 的坐标为.16.如图,在正方形ABCD 中,E F 、分别在边BC CD 、上,且45,EAF BD ∠=︒分别与AE AF 、交于点G H 、,连接FG EF 、.下列结论:①45AFG ∠=︒;②2FEC BAE ∠=∠;③AH HF DH HG ⋅=⋅;④BE DF EF +=. 其中正确的有.(填序号)三、解答题17.如图,在平面直角坐标系中,格点小正方形的边长为1,ABC V 的顶点均在格点上,将ABC V 绕点O 顺时针旋转90︒,得到A B C '''V .(1)直接写出A B C '''、、点的坐标A ':_______,B ':_______,C ':_______.(2)在旋转过程中,点A 运动的路径长_______(结果保留π)18.如图,AB 是O e 的直径,点,C D 是圆上两点,且AD 平分,BAC AD ∠交BC 于E .(1)求证:ADB BDE △∽△;(2)若106AB AC ==,,求DE 的长度.19.中国古代数学家秦九韶和古希腊数学家海伦分别提出了一般三角形面积的计算方法:①S =②S =(其中a b c 、、为三角形的三边长,,2a b c p S ++=为面积)(1) (2)如图,线段6MN =,点B 在MN 上,且4MB =,点A 是线段MB 上一点,分别以AB 、为圆心,AM BN 、的长为半径画圆,A e 和B e 交于点P ,直接写出PAB V 的面积的最大值:_______.20.如图1,直线2y x =+与抛物线2y x =交于A B 、两点.(1)直接写出AB 、两点的坐标:_______; (2)如图2,点()0,C m 在y 轴上运动,过点C 作直线l x ∥轴,在点C 运动的过程中,若l 上恰有一点P ,使得90APB ∠=︒,直接写出m 的值:_______;(3)如图3,将抛物线2y x =及直线AB 整体向右平移一个单位长度,A B 、对应点分别为A B ''、,平移后,新抛物线的顶点为G ,直线A B ''交x 轴于,M B N x '⊥轴于N ,点Q 是抛物线上B G '之间的一个动点,GQ 交B N '于,E B Q '交x 轴于F ,求证:()FN MN EN ⋅+为定值.。
初三希望杯竞赛试题及答案

初三希望杯竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是二次方程的解?A. x = 1B. x = 2C. x = 3D. x = 4(答案:B)2. 如果一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 15π厘米C. 20π厘米D. 25π厘米(答案:C)3. 根据题目给出的函数y = 2x + 3,当x = 1时,y的值是多少?A. 5B. 6C. 7D. 8(答案:A)4. 一个数的平方根是4,这个数是多少?A. 16B. 8C. 12D. 10(答案:A)5. 一个直角三角形的两条直角边分别为3和4,斜边的长度是多少?A. 5B. 6C. 7D. 8(答案:A)6. 一个班级有30名学生,其中15名男生和15名女生。
如果随机选择一名学生,选择男生的概率是多少?A. 1/2B. 1/3C. 2/3D. 3/4(答案:A)7. 如果a和b是互质数,那么a和b的最大公约数是多少?A. aB. bC. 1D. ab(答案:C)8. 一个数列的前三项是1, 1, 2,如果这个数列是等差数列,那么第四项是多少?A. 3B. 4C. 5D. 6(答案:A)9. 一个长方体的长、宽和高分别是3米、2米和1米,它的体积是多少?A. 6立方米B. 8立方米C. 10立方米D. 12立方米(答案:A)10. 如果一个正方体的棱长是2厘米,那么它的表面积是多少?A. 12平方厘米B. 24平方厘米C. 36平方厘米D. 48平方厘米(答案:B)二、填空题(每题4分,共20分)1. 一个数的立方根是3,那么这个数是 _ 。
(答案:27)2. 如果一个三角形的内角和是180度,那么一个四边形的内角和是多少度?(答案:360度)3. 一个数的倒数是1/4,那么这个数是 _ 。
(答案:4)4. 如果一个分数的分子是5,分母是10,那么这个分数化简后的结果是 _ 。
(答案:1/2)5. 一个圆的直径是14厘米,那么它的半径是 _ 厘米。
二十五届希望杯初三二试有答案

第二十五届 希望杯 全国数学邀请赛初三㊀第2试试题一㊁选择题(每小题4分,共40分.)1.I fb o t h a a n d c a r e r e a l n u m b e r s ,2a n d 3a r e t h e t w o s o l u t i o n s o f t h e e qu a t i o n a x 2-10x +c =0f o r x ,t h e n t h e v a l u e o f a +c i s ()(A )10.(B )12.(C )14.(D )16.图12.如图1,在әA B C 中,B C >C A >A B ,D ㊁E ㊁F 分别是A B ㊁B C ㊁C A 边上的点,D E ʊA C ,F D ʊC B ,若A D ʒD B =1ʒ2,则图中的相似三角形有()对.(A )3.(B )4.(C )5.(D )6.3.若a -b =4,a b +c 2+4=0,则a 的值是()(A )2.(B )3.(C )4.(D )5.4.将抛物线y =x 2先向左平移1个单位,再向下平移2个单位,则所得的抛物线的解析式是()(A )y =x 2-2x +1.(B )y =x 2+2x -1.(C )y =x 2+4x +3.(D )y =x 2-2x -1.5.若3x 2-x =1,则9x 4+12x 3-2x 2-7x +2014的值是()(A )2013.(B )2014.(C )2015.(D )2016.6.半径分别是1,2的☉O 1和☉O 2相外切,若半径是3的☉O 3和它们都相切,则满足条件的☉O 3的个数是()(A )6.(B )3.(C )4.(D )5.7.给如图2所示的无水游泳池注水,如果进水速度是均匀的,那么,泳池内水的高度h 随时间t 变化的图象可能是()图28.三角形内的一点和三角形三个顶点的连线将三角形分成三部分,若这三部分的面积比是1ʒ2ʒ3,则这样的点的个数是()(A )1.(B )3.(C )6.(D )9.9.G i v e n p o s i t i v e i n t e g e r m w h i c h i s n o l a r g e r t h a n 10,a n d m 2014+2014mc a nb ed i v i de db y5,t h e n t h en u m b e r o f s u c h m i s()图3(A )2.(B )3.(C )4.(D )5.10.如图3,在平面直角坐标系x O y 中,点A (2,0),M (0,33),N (5,23),N B ʅx 轴于点B ,P 为MN 上一动点,则P A +P B 的最小值为()(A )33.(B )23.(C )323.(D )343.二㊁填空题(每小题4分,共40分.)11.若y =a x 2+b x +c (a ʂ0)的图象如图4所示,则a b c 的值是(填: 正数 ㊁ 负数 或 0 ).12.若关于x 的方程x 2+p x +q =0有两个负根,则直线y =p x +q 不经过第象限.(填: 一 ㊁ 二 ㊁ 三 或 四 )13.已知{x +x y +y =6,x 2+y 2=12,则x 3+y 3的值是.14.在әA B C 中,A C =8,B C =6,øA C B =90ʎ,C D ʅA B 于点D ,若әA B C ㊁әA C D ㊁әB C D的内切圆的半径分别是r 1,r 2,r 3,则r 1+r 2+r 3的值是.15.若关于x 的方程x 2-(m +5)|x |+4=m 恰有3个实数解,则实数m =.16.在平面直角坐标系x O y 中,若直线x =-1,x =3,y =3,y =kx -2围成的四边形的面积是16,则k =.图4F i g .5图6图717.A ss h o w ni n F i g .5,t h e r ea r e3s q u a r e s i nt h er i g h tt r i a n gl e .T h es i d e so ft h et w o s m a l l e r s q u a r e s a r e a a n d4.T h e s i d eo f t h e s qu a r e i n t h em i d d l e i s x ,t h e n x =(i n t e r m s o f a ).18.如图6,在边长为2的正方形A B C D 内有等边三角形C D E ,A C 交D E 于点F ,则S әC F E =.19.如图7,将长为4,宽为2的长方形A B C D 绕顶点A 顺时针旋转90ʎ到达A B ᶄC ᶄD ᶄ,图中的两段弧线分别是顶点C ㊁D 经过的路径,则阴影部分的面积为.(π取3)20.长与宽的比是2ʒ1的长方形称为 特征长方形 .用宽分别为a 1,a 2,a 3,a 4,a 5(a 1<a 2<a 3<a 4<a 5)的5个 特征长方形 拼成的大长方形,记为(a 1,a 2,a 3,a 4,a 5),则大长方形(1,2,a 3,a 4,a 5)的面积最大是.三、解答题.21.(本题满分10分)如图8,在边长为1的正方形A B C D 中,以A 为圆心㊁A B 为半径的弧与以D C 为直径的半圆交于点E ,连结D E 并延长交B C 于F ,连结B E 并延长交D C 于G .(1)求D G ʒG C 的值;(2)求四边形E F C G 的面积.图8图9图1022.(本题满分15分)如图9,排球场总长18m ,设球网高为2m ,运动员站在离网3m 的线上(图中虚线所示)正对网前跳起将球水平击出.以击球点为原点,建立如图10的直角坐标系,球运动的轨迹方程是y =5x 2v2(x ,y 单位:m ),其中v 是球被击出时的速度(单位:m /s ).(1)设击球点在3m 线的正上方,高度为2.5m ,求使球既不触网也不出界的击球速度的范围;(2)若击球点在3m 线的正上方,当高度小于h (单位:m )时,无论水平击球的速度多大,球不是触网就是越界,求h .23.(本题满分15分)如图11,有一束光线,从中心为O 的圆环的A 点射入,在圆环内经过两次反射后从A 点射出;如图12,从A 点射入的光线经过三次反射后从A 点射出.图11图12图13图14(1)如图13,若从A 点射入的光线经过五次反射后从A 点射出,求从A 点射入的光线和圆环半径O A 的夹角α的度数;(2)如图14,若从A 点射入的光线和圆环半径O A 的夹角是50ʎ,则经过几次反射后光线从A 点射出?初三第2试答案21.(1)=2DG GC.(2)760CGEF S =.22.(1)击球速度的范围是v <<;(2)若击球点在3m 线的正上方3215m 处,则无论水平击球的速度多大,球不是触网就是越界.23.(1)60α=︒.(2)经过8次反射后,从A 点出来.。
第12届“枫叶新希望杯”全国数学大赛九年级(A卷)

第12届“枫叶新希望杯”全国数学大赛九年级(A 卷)一、单选题1.若a b 、均为实数,下列说法正确的是( )A .若a b 、互为相反数,则1ab=- B a =C .若1ab =,则a 的倒数是bD .22a b +是一个正数2.下列说法中,正确的是( )A .任意掷一枚质地均匀的硬币10次,正面向上的次数一定是5次B .想了解某种饮料中含色素的情况,宜采用普查C .甲、乙两组数据,若22S S >甲乙,则乙组数据波动大D .“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件3.如图,正六边形的边长为1,顶点A 与原点重合,将对角线AB 绕点A 顺时针旋转,使得点B 落在数轴上的点C 处,则点C 表示的数是( )A .1B C .32D .24.一次函数y ax b =+与反比例函数cy x=在同一平面直角坐标系中的图像如图所示,则二次函数2y ax bx c =++的图像可能是( )A .B .C .D .5.已知m n 、是方程232160x x +-=的两个实数根,则( ) A .23m n +=B .16mn =-C .22529m n +=D .22329mn m n +=6.阅读材料:求函数22221x xy x x +=++的最小值,方法如下:将原函数化为关于x 的一元二次方程,得()()22210y x y x y -+-+=,x 为实数,则()2Δ(21)42140y y y y =---=+≥,则14y ≥-,即y 的最小值为14-.根据材料,函数2232114x x y x x +=++的最小值为( ) A .14-B .13-C .12-D .1-7.如图,在矩形ABCD 中,3,4AB AD ==,连接AC ,以对角线AC 为边,按顺时针方向作矩形ABCD 的相似矩形11AB C C ;再连接1AC ,以对角线1AC 为边,按顺时针方向作矩形11AB C C 的相似矩形221AB C C L L 依次类推,则矩形1n n n AB C C -的面积为( )A .221354nn -⨯B .212354n n -⨯C .1354n n +⨯D .1354nn -⨯8.如图,点C 是»AB 的中点,CD AB ⊥于点D ,点P 是»AB 上的一个动点(不与A B 、重合),,M N 分别是»AP,»PB的中点,若3AB CD ==,则MN 的长( )A .等于6B .随点P 的运动而变化,最大值是6C .随点P 的运动而变化,最小值是6D .随点P 的运动而变化,没有最值二、填空题9.分解因式:2221a b a --+=.10.设a ,b 是一个直角三角形两条直角边的长,且()()2222248a b a b ++-=,则这个直角三角形的斜边长为.11.如图,在ABC V 中,,40,AB AC BAC ACB =∠=︒∠的平分线交ABC V 的外接圆于点D ,点E 是ABC V 的内心,连接AD AE 、,则DAE ∠=度.12.如图,直线分别与坐标轴交于()03A ,,()90B ,两点,若称横纵坐标都是整数的点为整点,那么AOB V 内(含边界)的整点共有个.13.若a b 11a b-的值为.14.如图,点()(),6,8,A a B b 在函数(0,0)k y k x x=>>的图像上,将该函数图像向上平移3个单位长度得到一条新的曲线,点AB 、的对应点分别为A B ''、.若图中阴影部分的面积为9,则k 的值为.15.如图,菱形ABCD 的边长为2,60A ∠=︒,将它绕对角线的交点顺时针旋转90︒,旋转后的图形与原图形重叠的部分(阴影部分)的周长为.16.如图,抛物线2y ax bx c =++的对称轴是=1x -.且过点5,02⎛⎫- ⎪⎝⎭,有下列结论:①0abc >;②240a b c -+=;③30a c +<;④关于x 的方程210ax bx c +++=有两个不相等的实数根;其中所有正确的结论是.(填写正确结论的序号)三、解答题17.已知实数a 满足2220160a a +-=,求22221415411a a a a a a a -++⨯-++-+的值. 18.贝贝和星星一起玩抽卡片游戏,4张卡片A 、B 、C 、D 的正面分别画有4个不同的图形(背面相同),将4张卡片洗均匀后倒扣在桌面上,两人轮流从中抽出1张卡片(放回).(1)用树形图或列表法表示他们抽卡片的所有情况;(2)若两人抽出的卡片相同,则称两人“心灵相通”,求他们“心灵相通”的概率;(3)若两人抽出的卡片不同,但两张卡片上的图形既是轴对称图形又是中心对称图形,则称两人“心有灵犀”,求他们“心有灵犀”的概率.19.希希开了一家网店,计划销售甲、乙两种商品.若甲商品每件利润25元,乙商品每件利润30元,则每周能卖出甲商品200件,乙商品80件,经调查,甲商品零售单价每降价1元,每周可多销售10件;乙商品零售单价每降价1元,每周可多销售5件,为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x (x 为整数)元.(1)直接写出甲、乙两种商品每周的销售量y (件)与降价x (元)之间的函数关系式:y =甲_______,y =乙_______.(2)求出希希每周销售甲、乙两种商品获得的总利润W (元)与降价x (元)之间的函数关系式;(3)如果每周两种商品的销售总量不超过380件,希希每周销售甲、乙两种商品获得的总利润最大是多少?20.如图1,M e 与x 轴交于()()2,08,0A B -、两点,与y 轴交于点C ,抛物线26y ax ax b=-+过、、A B C 三点.(1)求抛物线的解析式;(2)如图2,动点P 从点B 出发,以1个单位/秒的速度向点A 运动,运动时间为t 秒,连接PC BC 、,当45BCP ∠=︒时,求t 的值;(3)如图3,过点P 作PQ PC ⊥交直线BC 于点Q ,当3C Q B Q =时请直接写出t 的值:_______.。
初三希望杯培训题

“希望杯〞数学邀请赛培训题1一.选择题〔以下每题的四个选择支中,仅有一个是正确的〕1.-7的绝对值是〔〕〔A〕-7 〔B〕7 〔C〕-〔D〕2.1999-的值等于〔〕〔A〕-2001 〔B〕1997 〔C〕2001 〔D〕19993.下面有4个命题:①存在并且只存在一个正整数和它的相反数相同。
②存在并且只存在一个有理数和它的相反数相同。
③存在并且只存在一个正整数和它的倒数相同。
④存在并且只存在一个有理数和它的倒数相同。
其中正确的命题是:〔〕〔A〕①和②〔B〕②和③〔C〕③和④〔D〕④和①c的同类项是〔〕〔A〕4bc a〔B〕4ca b〔C〕ac b〔D〕ac b5.某工厂七月份生产某产品的产量比六月份减少了20%,假设八月份产品要到达六月份的产量,那么八月份的产量比七月份要增加〔〕〔A〕20%〔B〕25%〔C〕80%〔D〕75%6.,,,四个数中,与的差的绝对值最小的数是〔〕〔A〕〔B〕〔C〕〔D〕7.如果x=―, Y=0.5,那么X―Y―2X的值是( )(A)0 (B) (C)(D) ―8.ax+b=0和mx+n=0关于未知数x的同解方程,那么有〔〕〔A〕a+m>0. 〔B〕mb≥an.〔C〕mb≤an.〔D〕mb=an.9.〔-1〕+〔-1〕-〔-1〕×〔-1〕÷〔-1〕的结果是〔〕〔A〕-1 〔B〕1 〔C〕0 〔D〕210.以下运算中,错误的选项是〔〕〔A〕2X+3X=5X〔B〕2X-3X=-1〔C〕2X·3X=6X〔D〕2X÷4X=11.a<0,化简,得( )(A) 2 (B) 1 (C) 0 (D) -212.计算〔-1〕+〔-1〕÷|-1|的结果是〔〕〔A〕0 〔B〕1 〔C〕-1 〔D〕213.以下式子中,正确的选项是〔〕〔A〕a·a=a. 〔B〕(x)=x.〔C〕3=9. 〔D〕3b·3c=9bc.14.-|-3|的相反数的负倒数是〔〕〔A〕-〔B〕〔C〕-3 〔D〕315.十月一日亲朋聚会,小明统计大家的平均年龄恰是38岁,老爷爷说,两年前的十月一日也是这些人相聚,那么两年前相聚时大家的平均年龄是〔〕岁。
希望杯九年级数学竞赛试卷,满分120分,试题可打印

希望杯九年级数学竞赛试卷,满分120分,试题可打印希望杯九年级数学竞赛试卷注意:满分120分,试题可打印一、选择题(共30题,每题4分,共120分)1.已知函数y = 2x + 3,如果x的值为5,求y的值。
A. 8B. 10C. 13D. 152.已知三角形ABC,AB = 5cm,AC = 8cm,BC = 7cm,判断该三角形是否为直角三角形。
A. 是B. 否3.已知一等差数列的公差为3,前三项分别为2,5,8,求这个数列的通项公式。
A. an = n - 1B. an = 2n - 1C. an = 3n - 1D. an = 3n + 14.已知一等差数列的首项为3,公差为7,且第五项为31,求该等差数列的前十项和。
A. 120B. 150C. 180D. 2105.已知函数y = 4x^2 + 3x - 2,求当x = -2时的y值。
A. -14B. -16C. -18D. -206.已知三角形ABC,AB = 4cm,BC = 5cm,AC = 6cm,判断该三角形的形状。
A. 锐角三角形B. 直角三角形C. 钝角三角形7.若正方形的边长为6cm,求其对角线的长度。
A. 6cmB. 9cmC. 12cmD. 18cm8.已知函数y = -2x^2 + 5x + 3,求其对称轴的方程。
A. x = 5/4B. x = -5/4C. x = -5/2D. x = 5/29.已知直角三角形的一个锐角为45°,求另一锐角的度数。
A. 30°B. 45°C. 60°D. 90°10.已知函数y = x^3 + 2x^2 - x + 1,求当x = -1时的y值。
A. 0B. 2C. 4D. 611.已知三角形ABC的边长分别为4cm,5cm,7cm,求其面积。
A. 6cm^2B. 8cm^2C. 10cm^2D. 12cm^212.已知一个等差数列,首项为2,公差为4,求第10项的值。
第14届“枫叶新希望杯”全国数学大赛初中第十四届九年级(B卷)

第14届“枫叶新希望杯”全国数学大赛初中 第十四届九年级(B 卷)一、单选题1.下列图形是中心对称图形的有( ).①正方形;②长方形;③等边三角形;④线段;⑤平行四边形.A .1个B .2个C .3个D .4个2.在半径为1的O e 中,弦AB =AB 所对的圆周角的度数为( ). A .45︒ B .30︒ C .45︒或135︒ D .60︒或120︒3.有下列函数:①y x =-;②1y x =-;③1(0)y x x=-<;④221y x x =+-.当自变量x 在各自的取值范围之内时,其中y 随x 的增大而增大的函数有( ).A .1个B .2个C .3个D .4个4.如图,在直角ABC V 中,34,sin ,5AB ABC O =∠=e 与AB AC 、都相切,且圆心在斜边BC 上,则O e 的半径为( ).A .127B .107C .138D .1695.如图为一个抛物线形建筑物的示意图,底部宽为8米,4.2米高处宽为6米,则这个建筑物的高度为( ).A .9.2米B .9.4米C .9.6米D .9.8米6.现有2张红桃、3张黑桃、4张方块,将这9张扑克牌洗匀后背面朝上,再从中抽出2张牌,抽出的这2张牌花色相同的概率是( )A .12 B .518 C .1318 D .13367.已知抛物线22y ax x =++.当a p =时,抛物线22y ax x =++与x 轴的正半轴相交于点(),0M m ;当a q =时,抛物线22y ax x =++与x 轴的正半轴相交于点(),0N n .若点M 在点N 的左边,则p 与q 的大小关系是( ).A .p q <B .p q =C .p q >D .无法比较8.如图,抛物线()21:0,0l y ax b a b =+交x 轴于点A B 、(点A 在点B 右侧),交y 轴于点C .将抛物线绕点A 旋转180︒,得到抛物线2l ,它与x 轴的另一个交点为点D ,顶点为点E .若四边形BCDE 为矩形,则a b 、应满足的关系式为( ).A .12ab =-B .1ab =-C .2ab =-D .3ab =-二、填空题9.计算()()sin60cos45cos30sin45︒-︒︒+︒=.10.如图,数学活动小组为了测量学校旗杆AB 的高度,使用长为2m 的竹竿CD 作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在地面O 处重合,测得5m,17m OD BD ==,则旗杆AB 的高为m .11.若关于x 的一元二次方程()()2215450k x k x k k -++++-=有一个根是0,则k =.12.已知函数()22152100521002y x x x x =-++-+,当150x ≤≤,且x 为整数时,所有函数值的和为. 13.如图,直线4y x =+与反比例函数3(0)y x x=-<的图象相交于点AB 、,与反比例函数(0)k y x x =>的图象相交于点C ,若:2:3AB BC =,则k 的值为.14.如图,两半圆的圆心点12O O 、分别在直角ABC V 的两直角边AB AC 、上,直径分别为AB CD 、,如果两半圆相外切,且10AB AC ==,那么图中阴影部分的面积为.15.如图,在等边ABC V 内有一点P ,使得::7:8:9APC APB BPC ∠∠∠=,那么以AP ,BP ,CP 的长度为边长的三角形的三个内角的大小之比为.16.已知正整数n 满足不等式89910+<L ,则n 的取值共有个.三、解答题17.若关于x 的一元二次方程()2220ax ax x a -=-≠有两个不相等的实数根,且这两个实数根都是正整数,求整数a 的值.18.已知反比例函数8y x =的图象与正比例函数12y x =的图象相交于点 A B 、,与另一个正比例函数的图象相交于点C D 、,其中点A C 、在第一象限.若四边形ACBD 的面积为24,求点C 的坐标.19.如图1,AB 为O e 的直径,弦CD 垂直平分OB ,在AB 的延长线上取一点E ,使得BE BC =.(1)求证:CE 是O e 的切线;(2)如图2,若2BC =,点F 在O e 上,且BCF △的内心是CD 上的点G ,求线段DG 的长度.20.如图1,抛物线()()42y a x x =+-与x 轴交于A B 、两点(A 在B 的左侧),交y 轴于C 点.(1)当38a =-时,点P 在直线x t =上,若满足90APC ∠=︒的点P 恰有一个,直接写出t 的值; (2)如图2,四边形DEFG 是ABC V 的内接矩形,当矩形DEFG 的面积S 取最大值时,连接EG 并延长交抛物线于点M ,求MG EG的值.。
希望杯历年真题集(九年级)-附答案

目录第二十二届“希望杯”全国数学邀请赛(第1试) (3)第二十三届“希望杯”全国数学邀请赛(第1试) (7)第二十三届“希望杯”全国数学邀请赛(第2试) (11)第二十四届“希望杯”全国数学邀请赛(第1试) (15)第二十四届“希望杯”全国数学邀请赛(第2试) (19)第二十五届“希望杯”全国数学邀请赛(第1试) (23)第二十五届“希望杯”全国数学邀请赛(第2试) (27)第二十六届“希望杯”全国数学邀请赛(第1试) (31)第二十六届“希望杯”全国数学邀请赛(第2试) (35)第二十七届“希望杯”全国数学邀请赛(第1试) (40)第二十八届“希望杯”全国数学邀请赛(第1试) (43)参考答案 (47)第二十二届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.假期里王老师有一个紧急通知,要用电话尽快通知给50个同学,假设每通知一个同学需要1分钟时间,同学接到电话后也可以相互通知,那么要使所有同学都接到通知最快需要的时间为( )A .8分钟B .7分钟C .6分钟D .5分钟 2.若关于x 的一元二次方程()2320a b x ax b +++=有唯一解,则这个解是( )A .23-B .32-C .23D .323.如图,已知////AD EF BC ,::1:2:4AD EF BC =,则梯形AEFD 与梯形EBCF 的面积之比为( )A .1:2B .1:3C .1:4D .2:34.一个兵乓球队有男队员6人,女队员5人,其中男、女左撇子分别有3人和2人,若从这个球队任意抽取2人,则抽到2个左撇子的概率是( )A .211 B .511 C .15D .251215.已知x ,y 都是负整数,且满足66xy x=-,则y 的最小值为( ) A .3- B .4- C .5- D .6-6.已知等腰ABC 中,,30AB AC BAC =∠=︒,AD 为BC 边上的高,P 点在AC 上,E 点在AD 上,若PE EC +的最小值为4,则ABC 的面积为( )A .8B .16C .32D .647.如图,AB 是圆O 的直径,点C 平分AB ,点D 平分AC ,DB 、CA 交于点E ,则DEEB的值( )A .13B .14 C .1 D8.已知直线()0y kx k =<与双曲线2y x=-交于点()11A x y ,和()22B x y ,两点,则122138x y x y -的值是( ) A .10- B .5- C .5 D .109.用一些棱长是1的小正方体堆成一个立体,下图分别是它的俯视图和主视图,则这个立体的表面积(含下底面面积)的值最小是( )A .42B .43C .44D .4610.如图,在ABC 中,BAC ∠、BCA ∠的平分线相交于点I ,若35B ∠=,BC AI AC =+,则BAC ∠的度数为( )A .60B .70C .80D .90二、A 组填空题(每小题4分,共40分)11.如图,正六边形的边向外延长一倍,连接端点后又构成一个大的正六边形,则小正六边形与大正六边形的面积之比为 ;12.若对于p 的任意值,抛物线2231y x px p =-++都过一个定点,则这个定点的坐标是 ; 13.如图,正方形ABCD 的边长为 4,E 点在BC 上,以E 为圆心,EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则EC = ;14.在锐角ABC 中,54AB AC ==,,则BC 的取值范围是 ;15.袋中装有大小相同的黑球、白球、红球各2个,规定:取出一个黑球计0分,取出一个白球计1 分,取出一个红球计2分;在抽取这些球的时候,看不到球的颜色.甲先取出3个球,不再放回袋中,然后,乙取出剩余的3个球;取出球的总积分多者获胜.则甲乙成平局的概率为 ;16.不等式21x x a -+-≥对所有实数x 都成立,则 a 的最大值是 ; 17.如图,设M 是ABC 的重心,过M 的直线分别交边AB AC 、于P Q 、 两点,且APm PB=,AQ n QC =,则11m n+= ;18.已知抛物线()20y ax bx c c =++≠与x 轴的交点坐标为()()1,0,3,0-,当25x -≤≤时,y 的最大值为12,则该抛物线的解析式为 ;19.已知平面直角坐标系中有()1,3A ,()3,1B 两点,在x y 、轴上分别找一点C D 、,使四边形的周长最小,则最小周长为 ;20.明明用计算器求代数式()a b c +的值.他依次按出“,,,,,a b c ⨯+=”,显示11;当他依次按“,,,,b c a +⨯=”,显示14 (其中,,a b c 均为正整数).这时他才明白不按括号时,计算器先做乘法再做加法.那么如果他按键正确(该加括号时加括号)时,显示结果应为 ;三、B 组填空题(每小题 8 分,共 40 分)21.已知代数式22 342x xy y x by ---+-能分解为两个关于x y 、的一次式的乘积,则b = 或 ; 22.已知,,x y z 是三个非负实数,满足3252x y z x y z ++=+-=,,若2S x y z =+-,则S 的最大值为 最小值为 ;23.已知()2f x ax bx c =++,若()01f =,并且()()12f x f x x +-=,则()1f = ,()1f -= ,a = ,b = ;24.如图,在平面直角坐标系中,矩形OABC 的顶点A C 、分别在轴上,顶点B 在()14,8,点E F 、分别在OA 、 OB 、上.将AEF 沿EF 对折,使点A 落在线段BC 上的点D 处.经过抛物线()2220y ax abx ab c c =-++<顶点P 的每一条直线总平分矩形OABC 的面积.若点P 在线段DE 上,AF 的长为整数,且已知抛物线与线段EF 仅有一个交点,则点F 的坐标是 ,a 的取值范围是 ;25.某种在同一平面内进行传动的机械装置如左图,右图是它的示意图.其工作原理是:滑块Q 在平直滑道l 上可以左右滑动,在Q 滑动的过程 中,连杆PQ 也随之运动,并且PQ 带动连杆OP 绕定点O 摆动.在摆动过程中,两连杆的接点P 在以OP 为半径的O 上运动.数学兴趣小组为进一步研究其中所蕴含的数学知识,过点O 做 OH l ⊥于点H ,并测得4OH = 分米,3PQ = 分米,2OP = 分米.则点Q 在l 上 允许滑动的最大距离为 分米,点P在O 上的最大移动路线长为 分米;第二十三届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.如图1所示,一个正方体和一个圆柱体紧靠在一起,则它们的主视图是( )图1 A B C D2.完成一项工作,甲单独做需a 天,乙单独做需b 天,甲乙合作需c 天,则丙单做全部工作所需的天数是( )A .abc ab ac bc -- B .abc ab ac bc +- C .ab ac bcabc++ D .()ab c b a c --3.已知1,0,1x ≠-,则1111x x x x x x -+++-+的值可能是( ) A .比3大的数 B .比3-小的数 C .1,3±± D .比3-大,并且比3小的数4.如图,梯形ABCD 中,//AB CD ,两条对角线交于点E .已知ABE 的面积是a ,CDE 的面积是b ,则梯形ABCD 的面积是( )A .22a b +B )a b +C .2D .()2a b +5.已知a ,b 是实数,关于x 的不等式组的解集表示在数轴上如图所示,则这个不等式组是( )A .11ax bx >⎧⎨>⎩B .11ax bx >⎧⎨<⎩C .11ax bx <⎧⎨>⎩D .11ax bx <⎧⎨<⎩6.如图,AB BC ⊥,AB BC =,点D 在BC 上,以D 为直角顶点作等腰直角,则当D 从B 运动到C 的过程中,点E 的运动轨迹是( )A .圆弧B .抛物线C .线段D .双曲线7.已知实数1234,,,x x x x 满足条件1231234234134124x x x a x x x a x x x a x x x a ++=⎧⎪++=⎪⎨++=⎪⎪++=⎩其中1234a a a a <<<,则1234,,,x x x x 的大小关系是( )A .1234x x x x <<<B .2314x x x x <<<C .3214x x x x <<<D .4321x x x x <<< 8.已知23x ≤≤,则函数()21y x =-的取值范围是( )A .14y ≤≤和916y ≤≤B .116y ≤≤C .49y ≤≤D .19y ≤≤ 9.如图,已知梯形ABCD 中,//AB DC A C αβ∠=∠=,,,则:AD BC 等于( )A .sin :cos αβB .sin :sin αβC .sin :sin βαD .cos :sin αβ10.若关于x 的二次函数221y x mx =-+的图像与端点在()1,1-和()3,4的线段只有一个交点,则m 的取值可能是( )A .52B .13-C .12D .13二、A 组填空题(每小题4分,共40分)11.若两位数除以他的数字和等于7,则这样的两位数有 个. 12.已知21x y -=,则22425x y x y ---+= ;13.二次函数2y ax bx c =++的图象如图所示,已知2OB OA OA OC =<,,则,,a b c 满足的关系式是 ;14.如图,已知A B C 、、三点在同一个圆上,并且AB 是圆O 的直径,若点C 到AB 的距离5CD =,则圆O 的面积最小是;15.如图,在边长为1的正方形中,分别以四个顶点为圆心,作半径为1的圆弧,则图中阴影部分的面积是 ;16.如图,在梯形ABCD 中,2//76BA CD AD AB AB CD m BC m ⊥===,,,,,若以BC 为直径的圆与AD 没有公共点,则m 的取值范围是 ;17.设()f x 是关于x 的多项式,()f x 除以()21x +,余式是3;()2f x 除以()32x -,余式是4-,那么,()3f x 除以()242x x --,余式是 ;18.已知实数,a b 满足3a ab b ++=,若m a ab b =-+,则m 的取值范围是 ;19.Tom’s computer has password,which contains only numbers from 0 to 9.If the probability to guess the right password only one time is less than12012,then at least the password has digits. 20.Suppose point ()1,A m - is on the graph of the function 2y x=-,,,,B C D respectively,are point As symmetric points of x -axis,origin,y-axis.Then the area of the quadrilateral ABCD is ;三、B 组填空题(每小题8分,共40分) 21.反比例函数1k y x =和一次函数2y k x b =+的图象交于点2(3,)3M -和点()1,2N -,则1k = ,2k = ,一次函数的图象交x 轴于点 ;22.已知,a b 是实数,且2210a a -=,则a = ,b = ;23.已知,a b 是有理数,1x =是方程20x ax b -+=的一个解,则a 的值是 ,b 的值是 ; 24.如图,已知ABC 中,CD AB ⊥于点D ,26BD AD CD ==,,8cos 9ACD ∠=,BE 是AC 边上的高,则AD = ,BE = ;25.已知点A B Pa=︒,∠=,点M是上的动点,且使ABM为等腰三角形.若45、、是O上不同的三点,APB a则所有符合条件的点M有个,若满足题意的点M有2个,则a=;第二十三届 “希望杯”全国数学邀请赛(第2试)一、 选择题(每小题4分,共40分) 1.若反比例函数k y x =的图像经过点1,22⎛⎫- ⎪⎝⎭,则k 的值为( ) A .1- B .1 C .4- D .42.已知二次函数2y ax bx c =++的图像如图所示,则下列代数式的值恒为正值的是( )A .abcB .acC .bcD .ab3.若存在12x ≤≤,使得2120ax -->,则a 的取值范围是( )A .14a <-B .34a >C .1344a -<<D .14a <-或34a >4.直线k y x k=总是下列哪个函数图像的对称轴?( )A .y k x =B .ky x=C .2y kx =D .y kx = 5.若实数,,a b c 满足2222221,2,3,a b b c c a +=+=+=则ab bc ca ++的最小值为( )A .B .C .D 6.如图,双曲线(0)ky k x=>经过Rt AOB ∆的斜边AB 的中点C ,,AF AO ⊥,BF BO ⊥,AF BF 与双曲线分别交于点,D E ,若8,6,OA OB ==则四边形ODFE 的面积是( )A .12B .24C .36D .407.对于实数a ,规定[]a 表示不大于a 的最大整数,如[][]2.12, 1.52,=-=-则方程[][]224x y +=的解在xOy 坐标系中的图像是( )A B C D 8.某商店对于某个商品的销售量与获利做了统计,得到下表:若获利是销售量的二次函数,则该商店获利的最大值是( )A .9万元B .9.25万元C .9.5万元D .10万元9.如图,已知长方形ABCD 的边长32AB AD ==,,点E 在BC 边上,且AE EF ⊥,EF 交CD 于F ,设,BE x FC y ==,则当点E 从点B 运动到点C 时,y 关于x 的函数图像是( )A B C D10.若凸n 边形12n A A A 适合以下:(1)1100A ∠=,(2)18,1,2,,1,k k A A k n +∠=∠+=-则n 的值是( )A .5B .6C .7D .8 二、A 组填空题(每小题4分,共40分)11.若ABC ∆是半径为1的圆的内接三角形,BC =则A ∠= ; 12.方程11112012201420162018x x x x -=-----的解是x = ; 13.如图,P 是等边ABC ∆内一点,3,4,5,AP BP PC ===则APB ∠= ;14.边长为整数,且周长为2012的等腰三角形有 个.15.已知关于x 的一元二次方程222(1)(1)0x m x m --+-=有两个不相等的实根,αβ,若224,αβ+=则m = ; 16.已知ABC ∆的三个顶点的坐标分别为(1,5),(6,2),(1,2),A B C ----则ABC ∆外接圆半径的长度为 ;17.已知坐标平面xOy ,Rt ABC ∆中的直角顶点是A ,点B 与点O 重合,点C 在坐标轴上,则点C 的坐标是 ;18.已知350,x y z -+=并且230x y z ++=,则2222223323x y z xy yz zx x y z-+++-+-的值等于 ; 19.α和β是方程2210x x --=的两根,2α和2β是20x mx n ++=的两根,点(,)m n 在一次函数(3)y kx n =+-的图像上,则此函数的解析式是 .它的图像与xOy 坐标平面内的坐标轴围成的图形的面积是 ; 20.如图5,在直角梯形ABCD 中,,90,AB CD BAD ADC ∠=∠=∥两条对角线的交点为O ,O 与AD 相切,并与以AD 为直径的O '内切,已知AD 长为h ,则梯形ABCD 的面积是 ;三、解答题(每题都要写出推算过程) 21.解方程44(2)820x x +--=22.如图所示,已知二次函数28y x bx =-++的图像与x 轴交于,A B 两点,与y 轴交于点C ,且(4,0)B . (1)求二次函数的解析式及其图像的顶点D 的坐标;(2)若点(,0)M p 是x 轴上的一个动点,则当MC MD -取得最大值时,求p 的值;(3)如果点(,)E m n 是二次函数28y x bx =-++的图像上的一个动点,且ABE ∆是钝角三角形,求m 的取值范围.23.给你若干个边长都是1的正三角形,正方形,正五边形,正六边形,从其中任选两种(个数不限),将它们拼接,要求是:(1)使某边重合;(2)两种图形中的任何一种不得有公共部分.问:(1)用选出的两种图形围成正n 边形,如:用3个正方形和3个正六边形围成一个正三角形ABC (如下图). 请你再举两例,并作图说明.(2) 对于(1)中的正n 边形,求它的外接圆的半径.第二十四届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.若m n 、是方程210x -+=的两个根,则n mm n-的值是( )A .±B .±C .±D .±2.设O 的半径是5,点P 不在O 外,若点O 与P 的距离222OP m m =-+,则m 的取值范围是( ) A .1m <-或3m > B .13m -≤≤ C .1m ≤- D .3m ≥3.如图,O 内的点P 在弦AB 上,点C 在圆O 上,PC OP ⊥,若2BP =,6AP =,则CP 的长等于( )A .B .4C .D .4.如图是类似“羊头的”图案,它左右对称,由正方形,等腰直角三角形构成,如果标有数字“13”的正方形的边长是,那么标有数字“2”的等腰直角三角形的斜边的长是( )A .4B .C .2D .325.若m n 、()()m n n m +-的差的绝对值最小的整数是( ) A .55- B .56- C .16- D .15-6.如图,铁路MN 和公路PQ 在点O 处交汇,30QON ∠=︒,点A 在OQ 上,240AO = (米),当火车行驶时,周围200米以内未受到噪音的影响,现有一列火车沿MN 方向意72千米/时的速度行驶(火车的长度忽略不计),那么,A 处受噪音影像的时间为( )A .12秒B .16秒C .20秒D .24秒 7.InABC as shown in fig, ,,AB AC BD EC BE CF ===,if 50A ∠=︒,then the degree of DEF ∠ is ( )A .60︒B .65︒C .70︒D .75︒8.如图5,2O 的半径是1,正方形ABCD 的边长是6,点2O 是正方形ABCD 的中心,12O O 垂直AD 于P 点,128O O =,若将1O 绕点P 按顺时针方向旋转360°,在旋转过程中,与正方形ABCD 的边只有一个公共点的情况一共出现( )A .3次B .5次C .6次D .7次9.如图,在同一个平面直角坐标系内,二次函数()120y ax bx c a =++≠和一次函数()20y dx e d =+≠的图象相交于点(),A m n 和点(),B p q ,当12y y <时,用,m p 表示x 的取值范围,则是( )A .m x p <<B .x m <C .x p >D .x m >10.如图,在正方形ABCD 中,点M N 、分别在边AB BC 、上运动(不与正方形的顶点重合),2BN AM =,若图中的三个阴影三角形中至少有两个相似,则这样的点M 有( )A .1个B .2个C .3个D .4个二、A 组填空题(每小题4分,共40分)11.已知实数,a b 不相等,并且2215,15,a a b b +=+=则2211a b+= ; 12.If 111a m=-, 2111a a =-, 3211a a =-,...,then 2013a in terms of m is;13.如图,在3×2的方格纸上,以某三个格点为顶点的三角形中,等腰三角形共有 个.14.若实数,,x y z 使20x y z ++=和3250x y z ++=成立,并且0z ≠,则2222222457x y z xy x z xz -+--+的值是 ;15, ,则此三角形的面积是 ;16.已知抛物线2(0)y ax bx c c =++≠与x 轴的交点坐标为()1,0-,()3,0,当25x -≤≤时,y 的最大值为12,则该抛物线的解析式为 ;17.如图,直角梯形纸片ABCD 中,//AD BC ,AB BC ⊥,10AB =,25BC =,15AD =,以BD 为折痕,将ABD 折起,旋转180°后,点A 到点1A ,则凹五边形1BDCEA 的面积为 ;18.如图,将边长为a 的正方形ABCD 绕其顶点C 顺时针旋转45︒,得四边形A B C D '''',则图中阴影部分的面积是 ;19.If7,then the value range of real number a is ;20.如图,从边长为5的正方形纸片ABCD 中剪去直角EBF (点E 在边AB 上,点F 在边BC 上),EB BF +=则五边形AEFCD 的面积的最小值是 ;三、B 组填空题(每小题8分,共40分)21.下图是由若干个棱长为1厘米的正方形堆成的几何体,它的三视图中,面积最大的是 平方厘米,这个几何体的体积是 立方厘米22.如图,在ABC 中,502A AB AC ∠=︒==,,BD 是边AC 上的高,利用此图可求得tan15︒= ;BC = ;23.在直角坐标系内,如果一个点的横坐标和纵坐标都是整数,则称该点为整点,若凸n 边形的顶点都是整点,并且多边形内部及其边上没有其它整点,则n = ;24.如图,直角梯形中, 1.5213////90AB CD AF AD AB EF CD A ====∠=︒,,,,,,分别以AD FE ,所在的直线为x 轴、y 轴建立坐标系(,AD FE 为正方向)若抛物线过点B C 、,并且它的顶点M 在线段EF 上,则a = b = c = ;25.如图,ABC 中,90602B A AB AD ∠=︒∠=︒==,,,点M 在DC 上,以M 为圆心,以DM 为半径的半圆切边BC 于点N ,交MC 于点P ,则DM = 曲边的面积= ;附加题(每小题10分,共20分)1.若()326116f x x x ax =-+-可以被()23g x x =-整除,则a = 当()0f x >时,x 的取值范围是 ;2.有一堆黑,白围棋子,如果从中每次取出3枚黑子和2枚白子,当黑子被取完或剩下1枚或2枚时,则还剩35枚白子,如果每次取出5枚黑子和7枚白子,当白子被取完或剩下不足7枚时,则还剩下35枚黑子,那么这堆棋子中,原有黑子 枚,白子 枚;第二十四届“希望杯”全国数学邀请赛(第2试)一、选择题(每小题4分,共40分)1.如图,矩形ABCD 中,2AB =,1AD =,点M 在边DC 上,若AM 平分DMB ∠,则AMD ∠的大小是( )A .75B .60C .45D .302 )A .B .-C .D .-3.一个矩形被直线分成面积为,x y 的两部分,则y 与x 之间的函数关系只可能是( )A B C D 4.函数31x y x x-=-中,x 的取值范围是( ) A .0以外的一切实数 B .0,1-以外的一切实数 C .1±以外的一切实数 D .0,1±以外的一切实数5 )A .1B .2C .3D .4 6.代数式25x x -++( )A .有最小值,没有最大值B .有最大值,没有最小值C .既有最小值,也有最大值D .既没有最小值,也没有最大值7.如图,△ABC 中,AB=2,BC=4,CA=3,平行于BC 的直线l 过△ABC 的内心I ,分别交边AB AC 、于点D E 、,则ADE 的周长是( )A .5B .6C .7D .88.若动点)M x y (,到定点A 324⎛⎫⎪⎝⎭,的距离等于M 到直线54y =的距离,则动点)M x y (,的轨迹( )A .双曲线B .抛物线C .双曲线的一支D .一条直线9.不等式0a 的解是( ) A .0a ≠ B .1a >或1a <- C .1a >或10a -<< D .0a >或1a <-10.如图,ABC 中,1,2,90AB AC ABC ==∠=,若BD EF GH 、、都垂直于AC DE FG HI 、、、都垂直于BC ,则阴影HIC 的面积与ABC 的面积的比是( )A .634⎛⎫ ⎪⎝⎭ B .6324⎛⎫⨯ ⎪⎝⎭ C 634⎛⎫⎪⎝⎭D .62334⎛⎫⨯ ⎪⎝⎭二、填空题(每小题4分,共40分)112=的根是 ; 12.若正n 边形的一个外角为5︒,则n = ;13.已知关于x 的方程224220x x p p --++=的一个根为p ,则p = ;14.平面直角坐标系内,一只跳蚤停在点()5,0处,它要跳到点()6,0处,它每一跳都是飞越5个长度单位,并且总是跳到整点(坐标都是整数的点),也不从原路返回,那么,当它跳到点()6,0时,至少跳了 次 15.将一个圆分成三个相同的扇形,将其中一个卷成圆锥,锥顶对锥底圆周上任意两点的最大张角的余弦值是 ;16.将相同的平行四边形和相同的菱形镶嵌成如图所示的图案.设菱形中较小角为x 度,平行四边形中较大角为y 度,则y 与x 的关系式是 ;17.ABC 中,3,5,120AC BC ACB ==∠=,点M 平分AB ,则tan MCA ∠= ,MC = ;18.方程组3322181x y z x y z +=-⎧⎨+=-⎩的正整数解(),,x y z 是 ; 19.ABC 的三条高依次是643AD BE CF ===,,,则cos C = ,ABC 的面积是 ; 20.已知()f x 是一个多项式,若()f x 除以()1x -,余5;若()f x 除以()2x +,余2,则()f x 除以()()12x x -+,得到的余式是 ;三、解答题(每题都要写出推算过程) 21.(本题满分10分)已知二次函数24y mx x m =+++的图象在直线2y =-的上方. (1)求m 的取值范围;(2)当2m =时,求此二次函数的图象在x 轴上截得的线段长.22.(本题满分15分)一家商店销售某种计算器,开始按定价(小于200元的整数元)售出,后来按定价的六折售出,当售出200台时,共得款30498元.问:打折前,按定价售出了多少台?23.(本题满分15分)设()0)f x x =>(1)将()f x(a b ,是不同的整数)的形式;(2)求()f x 的最大值及相应的x 的值.第二十五届“希望杯”全国数学邀请赛(第1试)一、选择题(每小题4分,共40分)1.以下三角形中,与图1中的三角形相似的是( )图1 A B C D2.某商品原价200元,先降价%a ,又提价%a ,售价是182元,则下列关系式中正确的是( )A .()()2001%1%182a a -÷+=B .()()1821%1%200a a -÷+=C .()()2001%1%182a a +÷-=D .()()1821%1%200a a ÷-÷+= 3.一个几何体的三视图如图所示,则该几何体可能是下列四个选项中的( )主视图 左视图 俯视图A B C D4.若关于x 的一元二次方程()2223560m x x m m -++-+=的常数项为0,则m 的值是( )A .2B .3C .2或3D .0 5.方程20142014x x -=-的正整数解有( )A .2013个B .2014个C .2015个D .无穷多个6.在ABC 中,若AC =BC AB =ABC 的面积为( )A B . C .112D .67.Given equationx ,then the number of solutions for this equation is ( )A .0B .1C .2D .countless8.若()()6xx+=,则x =( )A .2B .2-C .2±D .12±9.如图,AB AC AD DE EC BC ====,,则ABC ∠的度数为( )A .30︒B .40︒C .45︒D .60︒ 10.如图,设AB 是O 的弦,CD 是O 的直径,且CD 与AB 相交,若CABOABm SS=-,OABn S=,则( )A .2m n >B .2m n =C .2m n <D .m 与2n 的大小关系无法确定. 二、A 组填空题(每小题4分,共40分)11.若2420y y ++=,则22224y y y =-+ ;12.如图,矩形ABCD 中,60AB =,23BD BC CD =+,则BC = ;13.InABC as shown in Fig., 40BAC ∠=︒.Both BD and CD are the interior angle bisectors of ABC which intersect atpoint D , BE and CE are exterior angle bisectors of ABC which intersect at point E ,then BDC BEC ∠-∠= °14.有1,2,5,10g g g g 的砝码各2个,从中任取2个放在已经平衡的天平的两端,则天平依然保持平衡的概率P = ;15.如图,将等边ABC 的外接圆对折,使点A 与弧BC 的中点F 重合,折痕与边AB AC 、分别交于点D E 、.若3BC =,则ADE 的面积是 ;16.如图,Rt ABC 中,9021C AC BC ∠=︒==,,,若以C 为圆心,CB 为半径的圆交AB 于点D ,则AD DB= ;17.在平面直角坐标系中,抛物线C 经过点()()3,87,8A B ,,且与x 轴恰有一个交点,则抛物线C 上纵坐标为32的两个点的距离为 ;18.如图,等边AFG 被线段BC DE ,分割成周长相等的三部分:等边三角形ACB 、梯形BCED 、梯形DEGF ,其面积分别为123S S S ,,,若263S =,则12S S -= ;19.如图,四边形ABCD 中,90571ABC CDA AD DC AB BC ∠=∠=︒====,,,,则BD = ; 20.正方体骰子的每个面内都写了一个正整数.随意地投掷这样的两个骰子,若朝上的两个面内的数的和为偶数的概率最小为P ,则P = ;三、B 组填空题(每小题8分,共40分.)21.若关于x 的方程()()()()2424x x p p --=--的两个实数根12x x ,是某直角三角形的两条直角边的长,则此直角三角形的面积最大是 ,此时P = ;22.If ,x y and z satisfy the equation x y z ++,then x y z ++= ,and xyz = ;23.若ABC 的三条边长,,a b c 满足2101261b c bc a a +==-+,,则ABC 的周长等于 ,面积等于 ;24.如图,在平面直角坐标系x O y --中,反比例函数()0ky x x=>的图象交矩形OBCD 的边BC 于点E ,交CD 于F 点,且14DF CD =,若四边形OECF 的面积为24,则k = ,OEFS= ;25.在直角坐标系xOy 中,抛物线2y ax bx c =++(,,a b c 是正整数)与x 轴有两个不同的交点()()12,0,,0A x B x .若1x 和2x 都大于1,则abc 的最小值是 ,此时a b c ++= ;第二十五届“希望杯”全国数学邀请赛(第2试)一、选择题(每小题4分,共40分)1.If both a and c are real numbers , 2and 3are the two solutions of the equation 2100ax x c -+= for x ,then the value of a c + is ( )A .10B .12C .14D .162.如图,在ABC 中,BC CA AB >>,D E F 、、分别是AB BC CA 、、边上的点,//,//DE AC FD CB ,若 :1:2AD DB =,则图中的相似三角形有( )对。
第24届希望杯初三第1试试题及答案

第二十四届“希望杯”全国数学邀请赛初三 第1试试题一、选择题(每小题4分,共40分)1.若n m ,是方程01522=+-x x 的两个根,则n m m n -的值是( ) (A )52± (B )54± (C )56± (D )58±2.设⊙O 的半径是5,点P 不在⊙O 外,若点O 与P 的距离|OP|=222+-m m ,则m 的取值范围是( )(A )1-<m 或3>m(B )31≤≤-m (C )1-≤m (D )3≥m3.如图1,⊙O 内的点P 在弦AB 上,点C 在圆O 上,PC ⊥OP ,若BP=2,AP=6,则CP 的长等于( )(A )32 (B )4 (C )22 (D )234.图2是类似“羊头”的图案,它左右对称,由正方形,等腰直角三角形构成,如果标有数字“13”的正方形的边长是2,那么标有数字“2”的等腰直角三角形斜边的长是( )(A )4 (B )22 (C )2 (D )23 5.若n m ,分别是20的整数部分和小数部分,则与))((m n n m -+的差的绝对值最小的整数是( )(A )-55 (B )-56 (C )-16 (D )-156.如图3,铁路MN 和公路PQ 在点O 处交汇,∠QON=30ο,点A 在OQ 上,AO=240米,当火车行驶时,周围200米以内会受到噪音的影响,现有一列火车沿MN 方向以72千米/时的速度行驶(火车的长度忽略不计),那么,A 处受噪音影响的时间为( )(A )12秒 (B )16秒 (C )20秒 (D )24秒∆ABC as 7.Inshown in fig.4, AB=AC, BD=EC, BE=CF, if ∠A=50ο,then the degree of ∠DEF is ( )(A )60ο (B )65ο (C )70ο (D )75ο8.如图5,⊙O 1的半径是1,正方形ABCD 的边长是6,点O 2是正方形ABCD 的中心,O 1O 2垂直AD 于P 点,O 1O 2=8,若将⊙O 1绕点P 按顺时针方向旋转360ο,在旋转过程中,⊙O 1与正方形ABCD 的边只有一个公共点的情况一共出现( )(A )3次 (B )5次 (C )6次 (D )7次9.如图6,在同一个坐标系内,二次函数)0(21≠++=a c bx ax y 和一次函数)0(2≠+=d e dx y 的图象相交于点),(n m A 和点),(q p B ,当21y y <时,用p m ,表示x 的取值范围,则是( )(A )p x m << (B )m x < (C )p x > (D )m x >10.如图7,在正方形ABCD 中,点M 、N 分别在边AB 、BC 上运动(不与正方形的顶点重合),且BN=2AM ,若图中的三个阴影三角形中至少有两个相似,则这样的点M 有()(A )1个 (B )2个 (C )3个 (D )4个二、A 组填空题(每小题4分,共40分)11.已知实数b a ,不相等,并且b b a a 51,5122=+=+,则=+2211b a 12.If ,,11,11,1123121Λa a a a m a -=-=-=then 2013a in terms of m is 13.如图8,在23⨯的方格纸上,以某三个格点为顶点的三角形中,等腰三角形共有 个。
希望杯初三试题及答案

希望杯初三试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的?A. 圆的周长公式为C=2πrB. 圆的面积公式为A=πr²C. 圆的周长公式为C=πdD. 圆的面积公式为A=2πr²答案:B2. 已知函数y=2x+3,当x=1时,y的值为:A. 1B. 3C. 5D. 7答案:C3. 一个数的平方根是4,这个数是:A. 16B. 8C. 4D. 2答案:A4. 一个等腰三角形的两边长分别为3和5,那么第三边的长度是:A. 2B. 3C. 5D. 8答案:C5. 一个数的立方根是2,这个数是:A. 6B. 8C. 4D. 2答案:C6. 一个直角三角形的两个直角边长分别为3和4,那么斜边的长度是:A. 5B. 6C. 7D. 8答案:A7. 一个数的倒数是2,这个数是:A. 1/2C. 1/4D. 1/8答案:A8. 一个数的绝对值是5,这个数可能是:A. 5B. -5C. 5或-5D. 0答案:C9. 一个数的相反数是-3,这个数是:A. 3B. -3C. 0答案:A10. 一个数的平方是9,这个数可能是:A. 3B. -3C. 3或-3D. 9答案:C二、填空题(每题4分,共20分)11. 一个数的平方根是3,这个数是______。
答案:912. 一个数的立方根是-2,这个数是______。
答案:-813. 一个直角三角形的两个直角边长分别为6和8,那么斜边的长度是______。
答案:1014. 一个等腰三角形的两边长分别为4和6,那么第三边的长度是______。
答案:4或615. 一个数的倒数是1/3,这个数是______。
答案:3三、解答题(每题10分,共50分)16. 已知函数y=3x-5,求当x=2时,y的值。
解:将x=2代入函数y=3x-5,得y = 3*2 - 5 = 6 - 5 = 1答:当x=2时,y的值为1。
17. 已知一个直角三角形的两个直角边长分别为5和12,求斜边的长度。
希望杯初三数学竞赛试题

希望杯初三数学竞赛试题希望杯数学竞赛是一项旨在激发学生对数学学习兴趣和提高数学素养的竞赛活动。
以下是一份模拟的初三数学竞赛试题,供参赛者参考:一、选择题(每题3分,共15分)1. 下列哪个数是无理数?A. πB. 0.3333...C. √4D. 1/32. 如果一个二次方程的判别式是负数,那么这个方程:A. 有两个实数根B. 没有实数根C. 有一个实数根D. 有一个虚数根3. 函数y = 2x^2 - 3x + 1的顶点坐标是:A. (3/4, -1/8)B. (-3/2, 11/4)C. (3/2, -11/4)D. (1/2, 1)4. 一个圆的半径为5,那么它的面积是:A. 25πB. 50πC. 100πD. 125π5. 如果一个三角形的三边长分别为3, 4, 5,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能构成三角形二、填空题(每题2分,共10分)6. 一个数的平方根是4,那么这个数是________。
7. 一个正六边形的内角是________。
8. 如果一个数列的前三项是2, 5, 11,那么第四项是________。
9. 一个圆的周长是44cm,那么它的直径是________。
10. 一个长方体的长、宽、高分别是2cm, 3cm, 4cm,那么它的体积是________。
三、解答题(共75分)11.(10分)解方程:x^2 - 5x + 6 = 0。
12.(15分)证明:如果一个三角形的两边和其中一边上的高相等,那么这个三角形是直角三角形。
13.(15分)求函数y = 3x - 2在x = 1处的切线方程。
14.(15分)一个长方体的长、宽、高分别是a, b, c,求证:这个长方体的对角线长度为√(a^2 + b^2 + c^2)。
15.(20分)某工厂计划生产一批产品,每件产品的成本是c元,售价是p元。
如果工厂希望获得的利润是总收入的20%,求工厂应该生产多少件产品才能达到这个目标。
