解析几何知识点总结复习
解析几何的基本知识点总结

解析几何的基本知识点总结解析几何是几何学的一个分支,它利用坐标系和代数方法研究几何问题。
通过对解析几何的基本知识点的总结,我们可以更好地理解和应用解析几何的方法。
本文将就解析几何的基本概念、坐标系、直线和曲线等知识点进行详细阐述。
一、基本概念1. 点:解析几何中的基本单位,用坐标表示,通常用大写字母表示,如点A(x₁, y₁)。
2. 线段:由两点确定的有限线段,在解析几何中用两点的坐标表示,如线段AB:AB = √[(x₂-x₁)²+(y₂-y₁)²]。
3. 中点:线段的中点即为线段两端点的均值,设线段AB的中点为M,则M的坐标为[(x₁+x₂)/2, (y₁+y₂)/2]。
4. 斜率:表示直线斜率的概念,在解析几何中常用字母k表示,直线的斜率为k=(y₂-y₁)/(x₂-x₁)。
5. 角度:两条直线之间的旋转角度,用度数或弧度表示。
二、坐标系1. 笛卡尔坐标系:由水平的x轴和垂直的y轴组成,交点为原点O(0,0)。
在这个坐标系下,点的位置可以用有序数对(x, y)表示。
2. 极坐标系:由原点O和极径、极角两个坐标轴组成,极径表示点到原点的距离,极角表示点与x轴正半轴的夹角。
三、直线与曲线1. 直线:由一次方程表示的线段,在解析几何中用方程的形式表示,如直线方程为y=kx+b。
2. 曲线:不是直线的线段,在解析几何中的表示较为复杂,可以通过方程、参数方程或极坐标方程表示,常见的曲线有圆、椭圆、双曲线、抛物线等。
四、常见图形的解析几何表示1. 圆:圆心为(h, k),半径为r,其方程表示为(x-h)²+(y-k)²=r²。
2. 椭圆:椭圆的中心为(h, k),长轴为2a,短轴为2b,其方程表示为(x-h)²/a²+(y-k)²/b²=1。
3. 双曲线:双曲线的中心为(h, k),两支曲线的焦点分别为(f₁, k)和(-f₂, k),其方程表示为(x-h)²/a²-(y-k)²/b²=1。
解析几何基础核心知识汇总

解析几何基础核心知识汇总解析几何是数学中一个重要的分支,涉及到平面和空间中点、线、面等几何元素的研究和分析。
以下是解析几何的基础核心知识的汇总。
1. 坐标系坐标系是解析几何中非常重要的概念。
平面坐标系一般使用直角坐标系,用x和y轴来表示平面上的点的坐标。
空间坐标系则使用三维直角坐标系,用x、y和z轴来表示空间中的点的坐标。
2. 点的坐标和距离在解析几何中,点的坐标表示了点在坐标系中的位置。
对于平面中的点,一般使用一对有序实数来表示(x,y)。
空间中的点则需要使用三个有序实数来表示(x,y,z)。
点之间的距离可以使用距离公式来计算。
在平面上,两点A (x1,y1)和B(x2,y2)之间的距离可以计算为:$d = \sqrt{(x2-x1)^2 + (y2-y1)^2}$在空间中,两点A(x1,y1,z1)和B(x2,y2,z2)之间的距离可以计算为:$d = \sqrt{(x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2}$3. 直线和曲线在解析几何中,直线可以使用方程来表示。
例如,在平面坐标系中,一条直线可以由方程y = mx + c来表示,其中m为斜率,c 为截距。
曲线则可以使用方程或参数方程来表示。
常见的曲线方程包括圆、椭圆、双曲线等。
4. 曲线的切线和法线切线和法线是解析几何中研究曲线的重要概念。
切线是曲线上某一点处的切线,它与曲线在该点处相切,具有与曲线相切的方向。
我们可以通过计算曲线在该点处的斜率来求得切线的方程。
法线是曲线上某一点处与切线垂直的直线,它垂直于切线。
法线的斜率与切线的斜率互为相反数,可以通过切线的方程来求得法线的方程。
5. 平面和空间的几何关系解析几何还研究了平面与平面之间、平面与直线之间、直线与直线之间、平面与曲线之间以及曲线与曲线之间的几何关系。
常见的几何关系包括垂直、平行、相交、共面、共线等。
这些是解析几何的基础核心知识的汇总。
深入掌握这些基础知识,有助于我们在解析几何的研究和应用中更加熟练和准确地处理各种几何问题。
解析几何知识点总结

解析几何知识点总结解析几何是数学中的一个重要分支,主要研究的是几何图形的性质、变换和关系等问题。
本文将对解析几何的一些基本知识点进行总结和讲解,希望能够帮助读者更好地理解和掌握相关概念和方法。
一、坐标系和坐标表示法在解析几何中,我们常常使用坐标系和坐标表示法来描述几何图形的位置和性质。
一般而言,我们可以使用二维笛卡尔坐标系或三维笛卡尔坐标系来构建坐标系。
在二维笛卡尔坐标系中,我们通常使用直角坐标系,其中 x 轴和 y 轴是垂直的。
在三维笛卡尔坐标系中,我们则使用直角坐标系,其中 x 轴、y 轴和 z 轴互相垂直。
在坐标表示法中,我们使用有序数对或有序数组来表示点、线、面等几何图形的位置。
例如,对于二维平面上的点 A,我们可以使用(x, y) 的形式表示其坐标;对于三维空间中的点 B,我们可以使用 (x, y, z) 的形式表示其坐标。
同样地,对于平面上的线段 AB,我们可以使用 AB 来表示其长度;对于空间中的线段 AB,我们可以使用AB 来表示其长度。
二、直线和曲线的方程在解析几何中,我们常常需要通过方程来描述直线和曲线的性质。
对于直线而言,我们可以使用一般式或点斜式的方程来描述。
一般式方程形如 Ax + By + C = 0,其中 A、B、C 是实数且不同时为零。
点斜式方程形如 y = kx + b,其中 k 和 b 是实数且 k 不为零。
两种方程形式都能够方便地描述直线的性质和特点。
对于曲线而言,我们常常使用几种常见的方程来描述。
例如,圆的方程可以使用标准式方程或一般式方程来表示。
标准式方程形如 (x-a)^2+(y-b)^2=r^2,其中(a, b) 是圆心的坐标,r 是半径的长度。
一般式方程形如 Ax^2 + By^2 + Cx + Dy + E = 0,其中 A、B、C、D、E 是实数且不同时为零。
其他曲线如椭圆、双曲线、抛物线等都有各自的方程形式。
三、向量和矢量运算在解析几何中,向量是一个重要的概念。
高中数学解析几何知识点总结大全

高中数学解析几何知识点总结大全解析几何是高中数学的重要分支之一,通过运用代数和几何的方法来研究几何图形的性质和变换。
下面是高中数学解析几何的知识点总结,供参考:一、直线与平面的位置关系1.直线与平面的交点个数:直线和平面可以有0个、1个或无数个交点。
2.平面与平面的位置关系:两个平面可以相交、平行或重合。
二、向量及其代数运算1.向量的概念:向量是具有大小和方向的量。
2.向量的表示方法:向量可以用有向线段或坐标表示。
3.向量的加法:向量的加法满足平行四边形法则。
4.向量的数乘:向量的数乘是一个向量与一个实数的乘积。
5.向量的数量积:向量的数量积是两个向量之间的乘积,结果是一个实数。
6.向量的乘法运算法则:分配律、结合律和交换律。
三、直线及其方程1.平面直角坐标系:平面直角坐标系包括坐标轴、坐标原点和相应的正方向。
2.直线的方程:直线可以用一般式、点斜式、两点式或截距式表示。
3.直线的性质:平行、垂直、斜率、倾斜角等。
4.直线的位置关系:两条直线可以相交、平行或重合。
四、曲线及其方程1.圆的方程:圆可以用标准方程、一般方程或截距方程表示。
2.椭圆、双曲线和抛物线的方程:椭圆、双曲线和抛物线可以用一般式表示。
3.曲线的性质:焦点、准线、离心率等概念的理解。
4.曲线的位置关系:两条曲线可以相交、相切或没有交点。
五、空间直线及其方程1.空间直线的方程:空间直线可以用对称式、参数方程或直角坐标式表示。
2.空间直线的位置关系:两条空间直线可以相交、平行或重合。
3.空间直线与平面的位置关系:空间直线可以与平面相交、平行或测度为零。
六、空间曲线及其方程1.空间曲线的方程:空间曲线可以用参数方程或直角坐标式表示。
2.空间曲线与平面的位置关系:空间曲线可以与平面相交、触及或完全包含。
七、立体图形1.点、线、面、体的概念:点是没有长度、宽度和高度的,线是一系列相连的点,面是一系列相连的线,体是一系列相连的面。
2.立体图形的表面积:立方体、长方体、正方体、球体、圆柱体、圆锥体和棱锥体的表面积计算公式。
高中数学中的平面解析几何知识点总结

高中数学中的平面解析几何知识点总结高中数学中的平面解析几何是一个重要的知识板块,它将代数与几何巧妙地结合在一起,为我们解决几何问题提供了全新的思路和方法。
下面就让我们一起来详细梳理一下平面解析几何的相关知识点。
一、直线1、直线的方程点斜式:若直线过点\((x_0,y_0)\),斜率为\(k\),则直线方程为\(y y_0 = k(x x_0)\)。
斜截式:若直线斜率为\(k\),在\(y\)轴上的截距为\(b\),则直线方程为\(y = kx + b\)。
两点式:若直线过点\((x_1,y_1)\)和\((x_2,y_2)\),则直线方程为\(\frac{y y_1}{y_2 y_1} =\frac{x x_1}{x_2 x_1}\)。
截距式:若直线在\(x\)轴、\(y\)轴上的截距分别为\(a\)、\(b\)(\(a\neq 0\),\(b\neq 0\)),则直线方程为\(\frac{x}{a} +\frac{y}{b} = 1\)。
一般式:\(Ax + By + C = 0\)(\(A\)、\(B\)不同时为\(0\))。
2、直线的位置关系平行:两条直线\(y_1 = k_1x + b_1\)和\(y_2 = k_2x + b_2\)平行,当且仅当\(k_1 = k_2\)且\(b_1 \neq b_2\);对于一般式直线\(A_1x + B_1y + C_1 = 0\)和\(A_2x + B_2y + C_2 = 0\)平行,当且仅当\(A_1B_2 A_2B_1 = 0\)且\(A_1C_2 A_2C_1 \neq0\)。
垂直:两条直线\(y_1 = k_1x + b_1\)和\(y_2 = k_2x + b_2\)垂直,当且仅当\(k_1k_2 =-1\);对于一般式直线\(A_1x + B_1y + C_1 = 0\)和\(A_2x + B_2y + C_2 = 0\)垂直,当且仅当\(A_1A_2 + B_1B_2 = 0\)。
解析几何知识点总结大全

解析几何知识点总结大全几何知识点总结大全 1过两点有且只有一条直线2两点之间线段最短3同角或等角的补角相等4同角或等角的余角相等5过一点有且只有一条直线和直线垂直6直线外一点与直线上各点连接的所有线段中,垂线段最短7平行公理经过直线外一点,有且只有一条直线与这条直线平行8假如两条直线都和第三条直线平行,这两条直线也互相平行9同位角相等,两直线平行10内错角相等,两直线平行11同旁内角互补,两直线平行12两直线平行,同位角相等13两直线平行,内错角相等14两直线平行,同旁内角互补15定理三角形两边的和大于第三边16推论三角形两边的差小于第三边17三角形内角和定理三角形三个内角的和等于18018推论1直角三角形的两个锐角互余19推论2三角形的一个外角等于和它不相邻的两个内角的和20推论3三角形的一个外角大于任何一个和它不相邻的内角21全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等23角边角公理有两角和它们的夹边对应相等的两个三角形全等24推论有两角和其中一角的对边对应相等的两个三角形全等25边边边公理有三边对应相等的两个三角形全等26斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27定理1在角的平分线上的点到这个角的两边的间隔相等28定理2到一个角的两边的间隔一样的点,在这个角的平分线上29角的平分线是到角的两边间隔相等的所有点的集合30等腰三角形的性质定理等腰三角形的两个底角相等31推论1等腰三角形顶角的平分线平分底边并且垂直于底边32等腰三角形的顶角平分线、底边上的中线和高互相重合33推论3等边三角形的各角都相等,并且每一个角都等于6034等腰三角形的断定定理假如一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35推论1三个角都相等的三角形是等边三角形36推论2有一个角等于60的等腰三角形是等边三角形37在直角三角形中,假如一个锐角等于30那么它所对的直角边等于斜边的一半38直角三角形斜边上的中线等于斜边上的一半39定理线段垂直平分线上的点和这条线段两个端点的间隔相等40逆定理和一条线段两个端点间隔相等的点,在这条线段的垂直平分线上41线段的垂直平分线可看作和线段两端点间隔相等的所有点的集合42定理1关于某条直线对称的两个图形是全等形43定理2假如两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3两个图形关于某直线对称,假如它们的对应线段或延长线相交,那么交点在对称轴上45逆定理假如两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a+b=c47勾股定理的逆定理假如三角形的三边长a、b、c有关系a+b=c,那么这个三角形是直角三角形48定理四边形的内角和等于36049四边形的外角和等于36050多边形内角和定理n边形的内角的和等于(n-2)18051推论任意多边的外角和等于36052平行四边形性质定理1平行四边形的对角相等53平行四边形性质定理2平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3平行四边形的对角线互相平分56平行四边形断定定理1两组对角分别相等的四边形是平行四边形57平行四边形断定定理2两组对边分别相等的四边形是平行四边形58平行四边形断定定理3对角线互相平分的四边形是平行四边形59平行四边形断定定理4一组对边平行相等的四边形是平行四边形60矩形性质定理1矩形的四个角都是直角61矩形性质定理2矩形的对角线相等62矩形断定定理1有三个角是直角的四边形是矩形63矩形断定定理2对角线相等的平行四边形是矩形64菱形性质定理1菱形的四条边都相等65菱形性质定理2菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(ab)267菱形断定定理1四边都相等的四边形是菱形68菱形断定定理2对角线互相垂直的平行四边形是菱形69正方形性质定理1正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1关于中心对称的两个图形是全等的72定理2关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理假如两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形断定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理假如一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79推论1经过梯形一腰的中点与底平行的直线,必平分另一腰80推论2经过三角形一边的中点与另一边平行的直线,必平分第三边81三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)2S=Lh83(1)比例的根本性质假如a:b=c:d,那么ad=bc假如ad=bc,那么a:b=c:d84(2)合比性质假如a/b=c/d,那么(ab)/b=(cd)/d85(3)等比性质假如a/b=c/d=…=m/n(b+d+…+n0),那么(a+c+…+m)/(b+d+…+n)=a/b86平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88定理假如一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91相似三角形断定定理1两角对应相等,两三角形相似(ASA)92直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93断定定理2两边对应成比例且夹角相等,两三角形相似(SAS)94断定定理3三边对应成比例,两三角形相似(SSS)95定理假如一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96性质定理1相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97性质定理2相似三角形周长的比等于相似比98性质定理3相似三角形面积的比等于相似比的平方99任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值圆是定点的间隔等于定长的.点的集合102圆的内部可以看作是圆心的间隔小于半径的点的集合103圆的外部可以看作是圆心的间隔大于半径的点的集合104同圆或等圆的半径相等105到定点的间隔等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和线段两个端点的间隔相等的点的轨迹,是着条线段的垂直平分线107到角的两边间隔相等的点的轨迹,是这个角的平分线108到两条平行线间隔相等的点的轨迹,是和这两条平行线平行且间隔相等的一条直线109定理不在同一直线上的三个点确定一条直线110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112推论2圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115推论在同圆或等圆中,假如两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等118推论2半圆(或直径)所对的圆周角是直角;90的圆周角所对的弦是直径119推论3假如三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121①直线L和⊙O相交d?r②直线L和⊙O相切d=r③直线L和⊙O相离d?r122切线的断定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1经过圆心且垂直于切线的直线必经过切点125推论2经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论假如两个弦切角所夹的弧相等,那么这两个弦切角也相等130相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等131推论假如弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134假如两个圆相切,那么切点一定在连心线上135①两圆外离d?R+r②两圆外切d=R+r③两圆相交R-r?d?R+r(R?r)④两圆内切d=R-r(R?r)⑤两圆内含d?R-r(R?r)136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成n(n3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆139正n边形的每个内角都等于(n-2)180/n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积Sn=pnrn/2p表示正n边形的周长142正三角形面积3a/4a表示边长143假如在一个顶点周围有k个正n边形的角,由于这些角的和应为360,因此k(n-2)180/n=360化为(n-2)(k-2)=4 144弧长计算公式:L=nR/180145扇形面积公式:S扇形=nR/360=LR/2146内公切线长=d-(R-r)外公切线长=d-(R+r)。
解析几何学知识点总结

解析几何学知识点总结一、点、线、面的基本概念1. 点:点是几何学中的基本概念,它没有长、宽、高,只有位置,用来表示物体的位置。
在几何学中,我们经常用坐标系来表示点的位置。
2. 线:线是由一系列无限延伸的点构成的,它没有宽度,只有长度。
除了直线,还有曲线、射线等概念。
3. 面:面是由一系列线构成的,它有长度和宽度,但没有高度。
在几何学中,我们研究的一般是平面,即二维空间中的面。
二、直线和角1. 直线的性质:直线是无限延伸的,没有起点和终点。
直线上的任意两点确定了一条直线,直线是几何学中的基本要素。
2. 角:角是由两条射线共同起点构成的。
角的大小用度来表示,是几何学中重要的角度概念。
角的度数和弧度数可以相互转换,角的正弦、余弦、正切等三角函数也是很重要的。
三、多边形和圆1. 多边形:多边形是由有限个直线段构成的封闭图形,它有顶点、边和面。
在几何学中,我们所研究的多边形一般是指正多边形,它是边相等、角相等的多边形。
多边形的面积和周长是多边形的重要性质。
2. 圆:圆是一种特殊的曲线,是由到一个定点距离相等的所有点构成的。
圆是几何学中的重要图形,它的半径、直径、圆心、圆周长和面积都是圆的重要性质。
四、立体几何1. 立体图形:在几何学中,我们研究的不仅仅是平面图形,还有立体图形。
立体图形是有长度、宽度和高度的,像正方体、长方体、圆柱体、圆锥体和球体等图形都属于立体图形的范畴。
2. 立体图形的体积和表面积:立体图形的体积和表面积是立体图形的重要性质,它们是我们在实际应用中经常要用到的。
五、坐标系和向量1. 坐标系:在几何学中,我们经常用坐标系来表示点的位置。
常见的坐标系有直角坐标系、极坐标系和球坐标系等。
2. 向量:向量是具有大小和方向的物理量,它是几何学中的重要概念。
向量的加法、减法、数乘、数量积和向量积都是向量的重要运算。
这些是几何学中的一些重要知识点,它们涵盖了几何学的基本概念和性质。
几何学是一门非常宝贵的学科,它在很多领域都有着重要的应用价值。
解析几何知识点总结

解析几何知识点总结一、直线1、直线的倾斜角直线倾斜角的范围是0, π)。
当直线与 x 轴平行时,倾斜角为 0;当直线与 x 轴垂直时,倾斜角为π/2 。
2、直线的斜率经过两点 P₁(x₁, y₁),P₂(x₂, y₂)(x₁≠x₂)的直线的斜率 k =(y₂ y₁)/(x₂ x₁)。
当直线的倾斜角α≠π/2 时,直线的斜率 k =tanα 。
3、直线的方程(1)点斜式:y y₁= k(x x₁) ,其中(x₁, y₁) 是直线上的一点,k 是直线的斜率。
(2)斜截式:y = kx + b ,其中 k 是斜率,b 是直线在 y 轴上的截距。
(3)两点式:(y y₁)/(y₂ y₁) =(x x₁)/(x₂ x₁) ,其中(x₁, y₁),(x₂, y₂) 是直线上的两点。
(4)截距式:x/a + y/b = 1 ,其中 a 是直线在 x 轴上的截距,b是直线在 y 轴上的截距。
(5)一般式:Ax + By + C = 0 (A、B 不同时为 0)。
4、两条直线的位置关系(1)平行:若两条直线的斜率都存在,分别为 k₁,k₂,则 k₁=k₂;若两条直线的一般式方程分别为 A₁x + B₁y + C₁= 0 ,A₂x+ B₂y + C₂= 0 ,则 A₁B₂ A₂B₁= 0 且 A₁C₂ A₂C₁ ≠ 0 。
(2)垂直:若两条直线的斜率都存在,分别为 k₁,k₂,则k₁k₂=-1 ;若两条直线的一般式方程分别为 A₁x + B₁y + C₁=0 ,A₂x + B₂y + C₂= 0 ,则 A₁A₂+ B₁B₂= 0 。
5、点到直线的距离点 P(x₀, y₀) 到直线 Ax + By + C = 0 的距离 d =|Ax₀+ By₀+ C| /√(A²+ B²) 。
6、两条平行线间的距离两条平行线 Ax + By + C₁= 0 ,Ax + By + C₂= 0 (C₁≠C₂)间的距离 d =|C₁ C₂| /√(A²+ B²) 。
高中数学解析几何知识点总结

高中数学解析几何知识点总结解析几何是数学中的一个重要分支,它是几何和代数的结合,通过代数方法研究几何问题。
在高中数学学习中,解析几何是一个重要的知识点,它涉及到直线、圆、曲线等图形的性质和相关定理。
下面将对高中数学解析几何的知识点进行总结。
一、直线的方程。
1.点斜式方程。
点斜式方程是解析几何中直线的一种常见方程形式,它的形式为y-y₁=k(x-x₁),其中(x₁,y₁)为直线上的一点,k为直线的斜率。
利用点斜式方程,可以方便地确定直线的位置和性质。
2.一般式方程。
一般式方程是直线的另一种常见方程形式,它的形式为Ax+By+C=0,其中A、B、C为常数且A和B不同时为0。
一般式方程可以直接得到直线的斜率和截距,方便进行直线的分析和运算。
二、圆的方程。
1.标准方程。
圆的标准方程是(x-a)²+(y-b)²=r²,其中(a,b)为圆心坐标,r为半径。
通过标准方程,可以直接得到圆的圆心和半径,方便进行圆的性质和位置分析。
2.一般方程。
圆的一般方程是x²+y²+Dx+Ey+F=0,其中D、E、F为常数。
一般方程可以通过配方和化简得到圆的标准方程,也可以直接得到圆的圆心坐标和半径长度。
三、曲线的方程。
1.抛物线的方程。
抛物线的一般方程为y=ax²+bx+c,其中a、b、c为常数且a≠0。
抛物线是解析几何中的重要曲线,通过抛物线的方程可以确定抛物线的开口方向、顶点坐标等重要性质。
2.椭圆的方程。
椭圆的一般方程为(x-h)²/a²+(y-k)²/b²=1,其中(h,k)为椭圆的中心坐标,a、b分别为椭圆在x轴和y轴上的半轴长度。
椭圆是解析几何中的另一种重要曲线,通过椭圆的方程可以确定椭圆的中心、长短轴长度等重要性质。
综上所述,高中数学解析几何知识点总结包括直线的方程、圆的方程和曲线的方程。
通过对这些知识点的学习和掌握,可以帮助学生更好地理解和运用解析几何知识,提高数学解题能力。
数学解析几何考点梳理

数学解析几何考点梳理数学解析几何是高中数学的重要组成部分,考试中常常出现的一个大模块。
在解析几何中,我们研究几何图形与代数关系之间的联系,通过代数的方法来解决几何问题。
解析几何考点较多,本文将对常见的解析几何考点进行梳理和总结。
一、平面几何基础知识回顾在学习解析几何之前,我们首先需要回顾一些平面几何的基础知识。
这包括点、线、向量等的定义与性质。
比如,我们需要了解点的坐标表示方法,如(x, y)表示平面上的一个点;线的方程表示形式,如一般式、点斜式等;向量的定义及其运算法则,如加法、数乘等。
这些基础知识在后续的解析几何学习中起着重要的作用。
二、直线的方程与性质直线是解析几何中的重要图形,研究直线的方程与性质是解析几何的核心内容之一。
常见的直线方程有一般式方程、点斜式方程、两点式方程等。
我们需要了解不同方程形式之间的转换关系,并能根据要求求解直线的方程。
此外,还需要掌握直线与坐标轴的交点求解方法,以及直线的斜率和与坐标轴的夹角等性质。
三、曲线的方程除了直线,解析几何还研究了各种曲线的方程。
常见的曲线包括圆、椭圆、抛物线和双曲线等。
对于这些曲线,我们需要了解它们的定义、性质以及其与坐标轴的交点求解方法。
此外,还需要学会根据给定的条件确定曲线的方程,以及根据方程确定曲线的形状和位置等。
四、点、线、面的位置关系解析几何中研究了点、线、面的位置关系。
其中,点到线的距离及其相关性质是考试中常见的考点之一。
我们需要学会求解点到直线的距离,并能根据给定的条件确定点与直线的位置关系。
此外,还需要了解点到平面的距离的计算方法,以及点与平面之间的位置关系等。
五、向量及其运算向量是解析几何的重要工具,涉及到向量的定义、运算及其性质的学习。
我们需要了解向量的加法、减法、数量积和向量积等运算法则,以及向量的模、方向角和共线性等基本性质。
此外,还需要掌握向量之间的运算规律,并能根据给定条件解决相关的几何问题。
六、平面的方程在解析几何中,研究了平面的方程。
高中数学解析几何知识点总结

高中数学解析几何知识点总结一、基本概念1. 点、直线和平面•点:在平面上,点是最基本的几何对象,可以用坐标表示。
在空间中,点可以用三维坐标表示。
•直线:由无数个点连成的无限延伸的轨迹,可以由两个不重合的点唯一确定。
•平面:由无数点在同一平面上组成。
2. 基本图形•线段:连接两点的线段,有起点和终点,可以用线段的长度表示。
•射线:一个起点和一个终点在同一条直线上的线段,有起始点但没有终结点。
•角:由两条半直线和公共端点组成,以顶点为中心点,夹在两条半直线之间。
二、坐标系与向量1. 坐标系•笛卡尔坐标系:直角坐标系,是一个由两条垂直的坐标轴组成的平面,用于表示点的位置。
•极坐标系:以一个点为极点,在此点设一根射线作为极轴,并规定每一个点到该射线的距离和与该射线正方向所成角度来表示该点的坐标。
2. 向量•向量的定义:向量是有大小和方向的量,表示一段膨胀或者收缩的箭头。
•向量的运算:向量可以做加法和乘法运算,具备平移、缩放和旋转的特性。
•向量的表示:向量可以用有序数组、列矩阵或坐标表示。
三、直线与圆1. 直线的方程•点斜式方程:通过已知点和斜率来表示直线的方程。
•斜截式方程:通过截距和斜率来表示直线的方程。
•两点式方程:通过两个已知点来表示直线的方程。
•一般式方程:直线的一般方程为Ax + By + C = 0。
2. 圆的方程•标准方程:圆的标准方程为(x−a)2+(y−b)2=r2,其中(a,b)为圆心坐标,r为半径长度。
•一般方程:圆的一般方程为x2+y2+Dx+Ey+F=0。
四、曲线与曲面1. 二次曲线•椭圆:由平面上到两个定点的距离之和为常数的点的轨迹组成。
•抛物线:由平面上到一个定点的距离与到一条定直线的距离相等的点的轨迹组成。
•双曲线:有两个定点F1和F2称为焦点,对于任意一点P的到两个焦点的距离之差是常数。
2. 二次曲面•椭球面:由空间中到两个定点的距离之和为常数的点的轨迹组成。
•抛物面:由空间中到一个定点的距离与到一条定直线的距离相等的点的轨迹组成。
2024高考数学解析几何知识点总结与题型分析

2024高考数学解析几何知识点总结与题型分析随着时间的推移,我们离2024年的高考越来越近。
数学作为高考的一门重要科目,解析几何是其中的一个重点内容。
为了帮助同学们更好地复习解析几何,并在高考中取得好成绩,本文将对2024高考数学解析几何的知识点进行总结与题型分析。
1. 直线与平面1.1 直线的方程直线的一般方程为Ax + By + C = 0,其中A、B、C为常数。
根据直线的特点,我们可以将其方程转化为其他形式,如点斜式、两点式、截距式等,以便于解题。
1.2 平面的方程平面的一般方程为Ax + By + Cz + D = 0,其中A、B、C、D为常数。
类似于直线的情况,根据平面的性质,我们可以将其方程转化为点法式、截距式等形式。
2. 空间几何体2.1 球球是解析几何中的一个重要概念。
其方程为(x-a)^2 + (y-b)^2 + (z-c)^2 = r^2,其中(a, b, c)为球心坐标,r为半径长度。
2.2 圆锥曲线圆锥曲线包括圆、椭圆、双曲线和抛物线。
通过对几何体的方程进行适当的变化,可以得到不同类型的圆锥曲线方程。
掌握其特点和方程形式,对于解析几何的学习非常重要。
3. 空间几何关系3.1 直线与直线的位置关系直线与直线的位置关系包括相交、平行、重合等情况。
根据两条直线的方程,我们可以通过求解方程组或直线的斜率等方式,判断它们之间的空间位置关系。
3.2 直线与平面的位置关系直线与平面的位置关系包括相交、平行、重合等情况。
根据直线的方程和平面的方程,我们可以通过代入求解或者检验点的方法,判断它们之间的位置关系。
4. 解析几何的常见题型4.1 直线与平面的交点求解给定直线和平面的方程,我们需要求解它们的交点。
通过将直线方程代入平面方程中,可以得到关于未知变量的方程组,进而求解出交点的具体坐标。
4.2 距离计算在解析几何中,我们常常需要计算点、直线或平面之间的距离。
对于给定的两点,我们可以利用距离公式进行计算;对于直线和平面,我们可以利用点到直线/平面的距离公式进行计算。
高中数学解析几何知识点总结

高中数学解析几何知识点总结一、引言解析几何是高中数学的重要分支,它通过坐标系统将几何问题转化为代数问题,使得复杂的几何图形和关系可以通过代数方法进行分析和解决。
本篇文章旨在总结高中数学解析几何的核心知识点,为学习和复习提供参考。
二、坐标系统1. 笛卡尔坐标系:由两条垂直的数轴构成,分别为x轴和y轴,交点为原点。
2. 坐标点:在坐标系中,任意一点的位置由一对数值(x, y)确定。
3. 距离公式:点A(x1, y1)和点B(x2, y2)之间的距离为√[(x2-x1)²+(y2-y1)²]。
三、直线方程1. 斜率:直线的倾斜程度,用k表示,计算公式为k=(y2-y1)/(x2-x1)。
2. 点斜式:直线方程y-y1=k(x-x1),其中(x1, y1)为直线上的一点。
3. 斜截式:直线方程y=kx+b,其中b为直线与y轴的交点。
4. 两点式:直线方程(y-y1)/(y2-y1)=(x-x1)/(x2-x1),用于两点确定的直线。
5. 一般式:直线方程Ax+By+C=0,其中A、B、C为常数。
四、圆的方程1. 标准圆:圆心在原点,半径为r的圆的方程为x²+y²=r²。
2. 一般圆:圆心为(a, b),半径为r的圆的方程为(x-a)²+(y-b)²=r²。
五、圆锥曲线1. 椭圆:中心在原点,焦点在x轴上的椭圆方程为(x/a)²+(y/b)²=1,其中a>b。
2. 双曲线:中心在原点,焦点在x轴上的双曲线方程为(x/a)²-(y/b)²=1,其中a, b>0。
3. 抛物线:顶点在原点,对称轴为y轴的抛物线方程为y=ax²。
六、空间解析几何1. 三维坐标系:在平面坐标系的基础上增加z轴,形成三维空间坐标系。
2. 空间直线:通过对称性、方程组或参数方程来描述空间中的直线。
2024年高考数学平面解析几何的复习方法总结

2024年高考数学平面解析几何的复习方法总结一、理清知识框架平面解析几何是高中数学的重要内容,复习时首先要理清知识框架,明确各个知识点的内容和重点。
可以根据教材或参考书的章节来进行分类整理,将知识点归纳为直线方程、圆方程、二次曲线方程等等,并注意各个知识点之间的联系和线索。
二、复习关键知识点1. 直线方程:掌握直线的点斜式、斜截式、一般式等多种表示方法,能够灵活转换直线方程,解决直线的位置关系、距离、角平分线等相关问题。
2. 圆方程:了解标准方程和一般方程的定义和性质,能够根据给定条件列出圆的方程,解决圆与直线、圆与圆之间的位置关系、切线、切点等问题。
3. 二次曲线方程:熟练掌握抛物线、双曲线和椭圆的方程表示方法,注意各个二次曲线的基本性质和特点,能够画出二次曲线的图像,解决与二次曲线相关的各种问题。
4. 曲线的判别:掌握判别方程的基本方法,了解直线与二次曲线的位置关系的判别式和条件,能够根据判别式解决相关的问题。
三、掌握基本解题思路1. 了解解题步骤:解决平面解析几何问题通常遵循以下步骤:确定已知条件;列出方程或不等式;解方程或不等式得到未知量的取值范围;根据问题要求,对方程的解或取值范围进行判断与选择。
2. 注意问题的本质:平面解析几何考察的是几何图形的性质和位置关系,因此,在解答问题时要分析问题的本质,结合具体的几何意义去解决。
四、多练习典型题目1. 题海战术:平面解析几何的题目类型较多,考察灵活性较强,因此,在复习过程中要多做一些典型题目,掌握不同类型题目的解题思路和技巧。
2. 整理常见题型:将遇到的题目整理成不同的题型,比如直线方程的求法、圆方程的求法、二次曲线图像的分析等,通过总结常见的题型,加深对知识点的理解,提高解题效率。
五、查缺补漏1. 平时及时记录:在复习过程中,及时记录自己遇到的问题和不理解的知识点,并寻找相关的资料进行补充和学习。
2. 寻求帮助:如果自己在复习过程中遇到难题或困惑,可以向老师、同学或家长寻求帮助,共同解决问题。
高中数学解析几何总结非常全

高中数学解析几何总结非常全解析几何是数学中一个非常重要的分支,它凭借着坐标系的引入和解析法的运用,把几何图形的特征用精确的数学语言描述。
本篇文章主要围绕高中数学解析几何的知识点进行总结,旨在帮助读者更好的掌握该学科。
一、平面直角坐标系平面直角坐标系指由二维直角坐标系(x,y) 和坐标平面上给定的一个原点(O) 共同构成的平面。
坐标系的基础知识对解析几何的学习至关重要,因此我们需要掌握如下概念:1. 笛卡尔坐标系平面直角坐标系又称为笛卡尔坐标系,是二维空间中的一种坐标系。
该坐标系中,平面上的任意一点P的坐标(x,y) 是由P点在x轴、y轴上的投影所确定的。
2. 坐标轴平面直角坐标系中的两条坐标轴分别是x轴和y轴,它们相交于坐标系的原点O。
3. 坐标变化在平面直角坐标系中,任意一点P(x,y) 关于x轴、y轴、原点O的对称点分别是P'(x,-y)、P'(-x,y) 和P'(-x,-y)。
二、直线及其方程解析几何中的直线是平面上的一种基本几何元素,由于它们的性质非常重要,因此直线及其方程的知识点也是解析几何中的核心内容。
我们需要掌握以下知识点:1. 直线的方程直线的一般式和斜截式是解析几何中最为常用的两种方程。
(1)直线的一般式:Ax+By+C=0在直线的一般式中,A、B、C 均为实数,其中 A 和 B 不同时为零。
(2)直线的斜截式:y=kx+b在直线的斜截式中,k 为直线的斜率,即斜线的倾斜程度。
斜率为0的直线是水平线,斜率为正数的直线是上升的,斜率为负数的直线是下降的。
2. 直线的截距式直线的截距式比较简单,它是指直线在x、y轴上截距所组成的一种方程形式,可以用来求解直线的截距。
3. 直线之间的关系直线之间的关系有平行、垂直等多种情况,我们需要掌握这些关系的性质和求解方法。
三、圆与圆的方程圆是解析几何中的另一个重要几何元素,它可以用一个点和一个距离来描述。
在本篇文章中,我们需要掌握以下知识点:1. 圆的一般式圆的一般式为(x-a)²+(y-b)²=r²,其中(a,b)为圆心坐标,r为圆的半径。
解析几何知识点管综

解析几何知识点管综一、直线。
1. 直线的倾斜角与斜率。
- 倾斜角α:直线l向上的方向与x轴正方向所成的最小正角,α∈[0,π)。
- 斜率k = tanα(α≠(π)/(2)),经过两点P_1(x_1,y_1),P_2(x_2,y_2)(x_1≠x_2)的直线的斜率k=(y_2 - y_1)/(x_2 - x_1)。
2. 直线方程的几种形式。
- 点斜式:y - y_0=k(x - x_0)(直线过点(x_0,y_0),斜率为k)。
- 斜截式:y = kx + b(k为斜率,b为直线在y轴上的截距)。
- 两点式:(y - y_1)/(y_2 - y_1)=(x - x_1)/(x_2 - x_1)(x_1≠ x_2,y_1≠ y_2,直线过两点(x_1,y_1),(x_2,y_2))。
- 截距式:(x)/(a)+(y)/(b)=1(a≠0,b≠0,a为x轴上的截距,b为y轴上的截距)。
- 一般式:Ax + By+C = 0(A、B不同时为0)。
3. 两直线的位置关系。
- 平行:l_1:y = k_1x + b_1,l_2:y = k_2x + b_2,则l_1∥ l_2Leftrightarrow k_1 = k_2且b_1≠ b_2;对于l_1:A_1x + B_1y + C_1 = 0,l_2:A_2x + B_2y + C_2 = 0,l_1∥ l_2Leftrightarrow(A_1)/(A_2)=(B_1)/(B_2)≠(C_1)/(C_2)。
- 垂直:l_1:y = k_1x + b_1,l_2:y = k_2x + b_2,则l_1⊥ l_2Leftrightarrowk_1k_2=- 1;对于l_1:A_1x + B_1y + C_1 = 0,l_2:A_2x + B_2y + C_2 = 0,l_1⊥l_2Leftrightarrow A_1A_2 + B_1B_2 = 0。
- 相交:联立两直线方程求解交点坐标。
专题-解析几何知识点汇总(全)
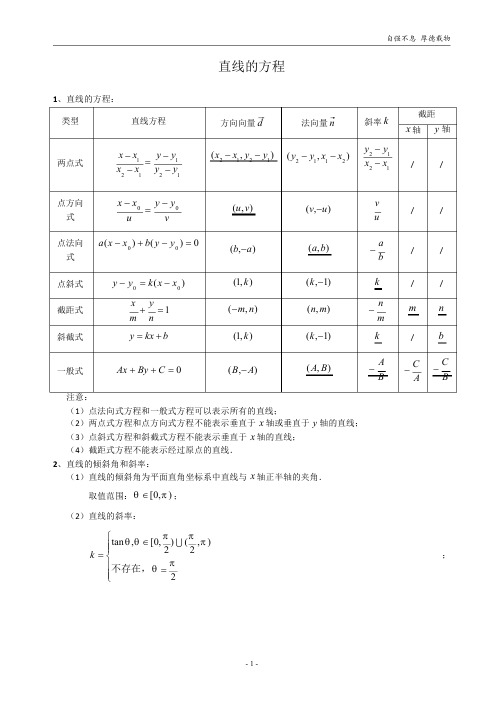
直线的方程1、直线的方程:类型直线方程方向向量d法向量n斜率k截距x轴/y轴/两点式x x1y y1x2x1y2y1(x2x1,y2y1)(y2y1,x1x2)y2y1x2x1点方向式点法向式点斜式截距式斜截式x xy yu va(x x) b(y y) 0(u,v)(v, u)vuab//(b, a)(1,k)( m,n)(1,k)(B, A)(a,b)(k, 1)(n,m)(k, 1)(A,B)//y yk(x x)x y1m ny kx bAx By C 0knm//m/nbCBkAB一般式C A注意:(1)点法向式方程和一般式方程可以表示所有的直线;(2)两点式方程和点方向式方程不能表示垂直于x轴或垂直于y轴的直线;(3)点斜式方程和斜截式方程不能表示垂直于x轴的直线;(4)截距式方程不能表示经过原点的直线.2、直线的倾斜角和斜率:(1)直线的倾斜角为平面直角坐标系中直线与x轴正半轴的夹角.取值范围: [0, );(2)直线的斜率:tan , [0,) (, )22k不存在,2;k 0 0k 2 0 0k tan 在[0, )和 k 不存在 = 2(2, )上单调递增.2k 0 2 y 2 y 1(3)若直线过点(x x ,x 1 x 21,y 1),(x 2,y 2),则该直线的斜率k 2 x 1,k R .不存在,x 1 x 23、两条直线的位置关系:已知l 1:a 1x b 1y c 1 0,l 2:a 2x b 2y c 2 0,则(1)系数法:①l 1 l 2 a 1a 2 b 1b 2 0;特别地,若l 1的斜率为k 1,l 2的斜率为k 2,l 1 l 2 k 1 k 2 1;②l 1与l 2相交 a 1b 2 a 2b 1;③l 1与l 2重合 a 1:b 1:c 1 a 2:b 2:c 2;④l 与l a 1:b 1 a 2:b 212平行 a .1:c 1 a 2:c 2或b 1:c 1 b 2:c 2(2)向量法:已知l 的法向量为 n11 (a 1,b 1),l 2的法向量为n 2 (a 2,b 2),则①l l12 n 1 n 20 a 1a 2 b 1b 2 0;特别地,若l 1的斜率为k 1,l 2的斜率为k 2,则l 1 l 2 k 1 k 2 1;②l l1与2相交 n 1与n 2不平行 a 1b 2 a 2b 1;③l 1与l 2平行或重合 n 1与n 2平行 a 1b 2 a 2b 1.(3)行列式法:已知Da 1b 1a ,Db 1xc 12b 2c 2b ,D y a 1c 12a 2c ,则21l 1与l2相交 D 0;②l1与l2重合 D D x D y 0;则③1与2平行 l l D 0.D x、D y 不全为零4、两条相交直线l 1:a 1x b 1y c 1 0和l 2:a 2x b 2y c 2 0的夹角 :(1)若l 1、l 2的法向量分别为n 1 (a 1,b 2)、n 2 (a 2,b 2),且l 1、l 2的方向向量分别为d 1、d 2,则n n 2cos 1n 1 n 2a 1a 2b 1b 2a 12 b 12 a 22 b 22d 1 d 2 或cos, [0,];2d 1 d 2(2)若l 1、l 2的斜率分别为k 1、k 2,且l 1到l 2的角为 1,l 2到l 1的角为 2,则tank k 1k k 2k 1 k 2, [0,);tan 1 2,tan 2 1.1 k 1k 21 k 1k 21 k 1k 225、点到直线的距离公式:(1)点P (x 0,y 0)到直线l :Ax By C 0的距离为dAx 0 By 0 CA B22;(2)直线l 1:Ax By C 1 0与直线l 2:Ax By C 2 0的距离为dC 1 C 2A B22.6、直线l :Ax By C 0同侧/异侧:(1)Ax 0 By 0 C 0(A 0) P (x 0,y 0)在直线l :Ax By C 0(A 0)的右侧;Ax 0 By 0 C 0(A 0) P (x 0,y 0)在直线l :Ax By C 0(A 0)的左侧.(2)点M (x 1,y 1)、N (x 2,y 2)在直线l 同侧 (Ax 1 By 1 C )(Ax 2 By 2 C ) 0;点M (x 1,y 1)、N (x 2,y 2)在直线l 异侧 (Ax 1 By 1 C )(Ax 2 By 2 C ) 0.7、点关于直线的对称问题:点直线P (x 0,y 0)x 轴P (x 0, y 0)y 轴P ( x 0,y 0)y xP (y 0,x 0)y xP ( y 0, x 0)x mP (2m x 0,y 0)y n P (x 0,2n y 0)对称点补充:①点P(x0,y)关于直线y x b的对称的点为P (yb,xb);②点P(x0,y)关于直线y x b的对称的点为P (b y,b x);A(n y) B(m x)③点P(x0,y)关于直线Ax By C 0的对称点P (m,n)满足 m x.n yA B C 022或者P (m,n),其中 8、三线共点问题:三条互不平行的直线l1:a1x b1y c10,直线l2:a2x b2y c20,直线l3:a3x b3y c30共m x0 2AD Ax By C,D 022.A Bn y0 2BDa1点的充要条件是a2b1b2b3c1c20.c3a39、直线系方程:具有某一个共同性质的一簇直线称为直线系.(1)平行直线系:①斜率为k0(常数)的直线系:,例:y 2x b;y kx b(b为参数)②平行于直线A0x By 0的直线系:Ax By C 0(C为参数).(2)过已知点的直线系:①以斜率k作为参数的直线系:y y0 k(x x),直线过定点(x,y);②以斜率k作为参数的直线系:y kx b0,直线过定点(0,b).③过两条直线l1:A1x B1y C10,l2:A2x B2y C20的交点的直线系:A 1x B1y C1(A2x B2y C2) 0( 为参数).注意:对于①②,过定点且平行于y轴或与y轴重合的直线不在直线系内;对于③,其中直线l2不在直线系内.10、定直线上动点与两定点距离和差问题:(1)定直线上动点与两定点距离和:问题已知定直线l上动点P,两个定点A、B,求PA PB的取值范围.取值范围A、B在l的解答步骤同侧 A B,AB, ①作点A关于l的对称点A ;②联结A B,交l于M;③点M为最小值状态点.①联结AB交l于M;②点M为最小值状态点.异侧(2)定直线上动点与两定点距离差:已知定直线l上动点P,两个定点A、B,点A、B到l的距离分别为d1、d2,问题直线AB与直线l的夹角为 ,求PA PB的取值范围.A、B在l的d1与d2的大小关系d1d2取值范围解答步骤①联结AB并延长交l于M;②点M为最大值状态点./①联结BA并延长交l于M;②点M为最小值状态点.①作点A关于l的对称点A ;②联结A B并延长交l于M;③点M为最大值状态点./①作点A关于l的对称点A ;②联结BA 并延长交l于M;2AB cos ,ABAB,ABAB,AB cos同侧d1 d2d 1 d2d 1 d2A B cos ,A BA B,A BA B,AB cos异侧d1d2d1d2点M为最小值状态点.曲线的方程(一)曲线的方程概论1、轴对称的两个曲线:曲线对称轴曲线F(x,y) 0x轴F(x, y) 0y轴y x y x x m y n F( x,y) 0F(y,x) 0F( y, x) 0F(2m x,y) 0F(x,2n y) 0补充:①曲线F (x ,y ) 0关于y x b 对称的曲线方程为F (y b ,x b ) 0;②曲线F (x ,y ) 0关于y x b 对称的曲线方程为F (b y ,b x ) 0.2、中心对称的两个曲线:曲线对称中心曲线F (x ,y ) 03、轴对称的曲线:曲线对称轴条件(m ,n )F (2m x ,2n y ) 0F (x ,y ) 0y x F (y ,x ) F (x ,y )补充:y x F ( y , x ) F (x ,y )x mF (2m x ,y ) F (x ,y )y nF (x ,2n y ) F (x ,y )a b对称。
解析几何知识点总结(高考复习)

1. 直线与方程5、两点间距离公式:P 1P 2 = x 2 - x 12+ y 2 - y 1 2( )( )1、倾斜角与斜率: k = tan α =2、直线方程:y2 - y 1 x 2 - x 16、点到直线距离公式:Ax 0 + By 0 + Cd =A 2+B 2⑴点斜式: ⑵斜截式: ⑶两点式:⑷截距式:⑸一般式:y - y 0 = k (x - x 0)y = kx + by - y 1 y 2 - y 1x - x 1=- x 1x 2x y+= 1a bAx + By + C = 07、两平行线间的距离公式:l 1: Ax + By + C 1 = 0 与 l 2 : Ax + By + C 2 = 0平行,C 1- C 2 则d = A 2+B 22. 圆与方程1、圆的方程:⑴ 标准方程: (x - a )2 + (y - b )2 = r 23、对于直线:l 1 : y = k 1 x + b 1 , l 2 : y = k 2 x + b 2 有:⑴ l 1 // l 2 k 1 = k 2?;b 1 ≠b 2⑵l 1 和 l 2 相交 ? k 1 ≠k 2 ;k 1 = k 2;⑶ l 1 和 l 2 重合 ?= b 2 b 1⑷l 1 ⊥l 2 ? k 1k 2 = - 1.4、对于直线:l 1 : A 1 x + B 1 y + C 1 = 0,有:l 2 : A 2 x + B 2 y + C 2 = 0A 1B 2 = A 2B 1 ⑴l 1 // l 2 ?;B 1C 2 ≠B 2C 1⑵ l 1 和 l 2 相交 ? A 1B 2 ≠A 2 B 1;⑶ l 1 和 l 2 A 1 B 2 = A 2 B 1 重合 ?= B 2C 1 ;B 1C 2⑷l 1 ⊥l 2 ? A 1 A 2 + B 1 B 2 = 0.其中 圆心为 (a,b) ,半径为 r .⑵ 一般方程: x 2 + y 2 + Dx + Ey + F = 0.D E 1 22其中 圆心为 (-, - ) ,半径为 r =D + E-4F .2222、直线与圆的位置关系直线 Ax + By + C = 0 与圆 ( x - a) 2 + ( y - b)2 = r 2的位置关系有三种 :d > r ? 相离 ? ? < 0 ; d = r ? 相切 ? ? = 0 ; d < r ?相交 ? ? > 0 .弦长公式: l = 2 r 2 - d 2= 1+ k 2( x 1 - x 2 ) 2 - 4 x 1 x 23、两圆位置关系: d = O 1 O 2 ⑴外离: d > R + r ; ⑵外切: d = R + r ;⑶相交: R - r < d < R + r ;⑷内切: d = R - r ;⑸内含: d < R - r .3、空间中两点间距离公式:P 1 P 2 = (x 2 - x 1 )2 + (y 2 - y 1 )2 + (z 2 - z 1 )2焦点的位置图形3.椭圆焦点在 x 轴上焦点在y轴上标准方程第一定义x 2+y2= 1(a > b > 0)a2b2到两定点 F1、F2的距离之和等于常数y2x2a2+b2 = 1(a > b > 0 )2 a,即| MF1| + | MF2|= 2a(2a >| F1F2|)第二定义范围顶点轴长与一定点的距离和到一定直线的距离之比为常数- a ≤x ≤a 且 - b ≤y ≤bΑ1 (- a,0)、Α2 (a,0)Β1 (0, - b)、Β2 (0,b)长轴的长 = 2aMFe ,即= e (0 < e <1)-b ≤x ≤b 且- a≤y≤aΑ1 (0, - a)、Α2 (0,a)Β1 (- b,0)、Β2 (b,0)短轴的长 = 2b对称性焦点焦距离心率准线方程关于 x 轴、 y 轴对称,关于原点中心对称F1(- c,0 )、 F2(c,0 )F1(0, - c )、 F2(0, c)F1F2 = 2c(c2 = a2 - b2 )c222b2ec a- b1(0e1)= a=a2= a 2=- a2<<x =±a 2y =±a2c c焦半径左焦半径:MF1= a + ex0下焦半径: MF1= a + ey0 M ( x0, y0 )右焦半径:MF 2= a - ex0上焦半径: MF 2= a - ey0焦点三角形面积S MF F2=b2tanθ(F1 MF2 )?12θ= ∠通径过焦点且垂直于长轴的弦叫通径:HH′2b2=a(焦点)弦长公式A( x1, y1 ), B( x2, y2 ) , AB = 1+ k 2 x1 - x2 = 1 + k 2( x1 - x2 )2 - 4x1 x24.双曲线焦点的位置焦点在 x 轴上焦点在y轴上图形标准方程第一定义第二定义范围顶点轴长对称性焦点x 2y2y 2x22-2 = 1(a > 0, b > 0)2- 2 = 1(a > 0, b > 0)a b a b到两定点 F1、F2的距离之差的绝对值等于常数 2a,即 | MF1 | - | MF2 | = 2a ( 0 < 2a <| F1F2 | )与一定点的距离和到一定直线的距离之比为常数 e ,即MF= e ( e > 1)dx ≤- a 或 x ≥a , y ∈R y ≤- a 或 y ≥a ,x∈RΑ1 (- a,0 )、Α2 (a,0 )Α1 (0, - a ) 、Α2 (0,a )实轴的长 = 2a虚轴的长= 2b关于 x 轴、 y 轴对称,关于原点中心对称F1(- c,0 )、 F2(c,0 )F1(0, - c )、 F2(0, c)焦距离心率准线方程渐近线方程焦半径M ( x0, y0 )焦点三角形面积通径注意F1F2 = 2c(c2 = a2 + b2 )ec c2a2+ b21b2(e1)= a=a2=a2=+a2>x =±a2y =±a2c cy = ±bx y = ±axa b左焦:MF1= ex0 + a左焦:MF1= ey0 + a M 在右支= ex0 - aM 在上支= ey0 - a 右焦:MF 2右焦:MF 2左焦:MF1 = - ex0 - a左焦:MF1 = - ey0 - a M 在左支M 在下支右焦:MF 2= - ex0 + a右焦:MF 2= - ey0 + aS b2cotθ( F MF)? MF1F2=2θ= ∠12过焦点且垂直于长轴的弦叫通径:HH′2b2=a2222若双曲线方程为x2-y2 =1?渐近线方程:x2 -y2= 0 ?y = ±bxa b a b a若渐近线方程为y =±bx ?x±y= 0?x 2-y 2= λ双曲线可设为22a ab a b2222若双曲线与x2-y 2= 1 有公共渐近线,可设为x2-y2= λa b a b注意 ? PF1 F2中结合定义PF1-PF2 =2a与余弦定理 cos ∠F1PF2,将有关线段PF1、 PF2、 F1F2和角结合起来。
解析几何知识点总结复习

一、直线与方程基础:1、直线的倾斜角α:[0,)απ∈2、直线的斜率k : 2121tan y y k x x α-==-; 注意:倾斜角为90°的直线的斜率不存在。
3、直线方程的五种形式:①点斜式:00()y y k x x -=-;②斜截式:y kx b =+;③一般式:0Ax By C ++=;④截距式:1x y a b+=; ⑤两点式:121121y y y y x x x x --=-- 注意:各种形式的直线方程所能表示和不能表示的直线。
4、两直线平行与垂直的充要条件:1111:0l A x B y C ++=,2222:0l A x B y C ++=,1l ∥2l 12211221A B A B C B C B =⎧⇔⎨≠⎩; 1212120l l A A B B ⊥⇔+= .5、相关公式:①两点距离公式:11(,)M x y ,22(,)N x y ,MN =②中点坐标公式:11(,)M x y ,22(,)N x y ,则线段MN 的中点1122(,)22x y x y P ++; ③点到直线距离公式:00(,)P x y ,:0l Ax By C ++=,则点P 到直线l的距离d =④两平行直线间的距离公式:11:0l Ax By C ++=,22:0l Ax By C ++=, 则平行直线1l 与2l之间的距离d =;⑤到角公式:(补充)直线1111:0l A x B y C ++=到直线2222:0l A x B y C ++=的角为θ,(0,)(,)22ππθπ∈,则2112tan 1k k k k θ-=+⋅ .(两倾斜角差的正切) 二、直线与圆,圆与圆基础:1、圆的标准方程:222()()x a y b r -+-=;确定圆的两个要素:圆心(,)C a b ,半径r ;2、圆的一般方程:220x y Dx Ey F ++++=,(2240D E F +->);3、点00(,)P x y 与圆222:()()C x a y b r -+-=的位置关系:点00(,)P x y 在圆⇔22200()()x a y b r -+-<;点00(,)P x y 在圆上⇔22200()()x a y b r -+-=;点00(,)P x y 在圆外⇔22200()()x a y b r -+->;4、直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=的位置关系:从几何角度看:令圆心(,)C a b 到直线:0l Ax By C ++=的距离为d ,相离⇔d r >;相切⇔=d r ;相交⇔0d r ≤<;若直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=相交于两点M ,N ,则弦长MN =从代数角度看:联立:0l Ax By C ++=与圆222:()()C x a y b r -+-=,消去y (或x )得一元二次方程,24b ac ∆=-,相离⇔0∆<;相切⇔0∆=;相交⇔0∆>;相交时的弦长1212MN x x y y =-=- . 5、圆与圆的位置关系:相离,外切,相交,切,含 .圆2221111:()()O x x y y r -+-=;圆2222222:()()O x x y y r -+-=, 根据这三个量之间的大小关系来确定:12r r -,12O O ,12r r +;相离⇔1212O O r r >+;外切⇔1212O O r r =+;相交⇔121212r r O O r r -<<+;切⇔1212O O r r =-;含⇔12120O O r r ≤<-;6、两圆2221111:()()O x x y y r -+-=①;圆2222222:()()O x x y y r -+-=②若相交,则相交弦所在的直线方程的求法:交轨法:①式-②式,整理化简即可得到相交弦所在直线方程 .三、椭圆:1、(第一)定义:12122PF PF a F F +=>;P2、椭圆标准方程及离心率:焦点在x轴上的椭圆标准方程为:22221(0)x ya ba b+=>>;:a长半轴;b:短半轴;:c半焦距 .椭圆中a,b,c的关系:222a b c=+;椭圆的离心率(0,1)cea=∈ .3、弦长公式:直线:l y kx b=+与椭圆2222:1()x yC m nm n+=≠交于两点11(,)M x y,22(,)N x y,则相交时的弦长1212MN x x y y=-=- .弦长公式是由两点距离公式与两点斜率公式推导出来,故适用性比较广。
总结解析几何中的常见考点

总结解析几何中的常见考点解析几何是高中数学中的一个重要分支,涉及到平面几何和空间几何的知识。
在解析几何的学习过程中,我们经常会遇到一些常见的考点。
本文将对解析几何中的几个重要考点进行总结和分析。
一、直线与平面的方程在解析几何中,直线和平面的方程是我们首先要学习和掌握的内容。
直线的方程可以通过点斜式、两点式、截距式等多种方式表示。
平面的方程则可以用一般式、点法式、法向量式等表示。
掌握这些方程的转化和应用是解析几何的基础。
在解析几何的考试中,通常会考察直线与平面的相交、平行和垂直等关系。
我们需要根据给定条件,判断两者之间的几何性质,并利用相应的方程进行求解。
二、直线和平面的交点问题直线与平面的交点问题是解析几何中的一个重要考点。
当我们已知一条直线和一个平面的方程时,我们可以通过联立这两个方程,求解它们的交点坐标。
在解答这类问题时,我们需要注意方程的转化和方程的解的唯一性。
在实际问题中,直线和平面的交点问题也有着广泛的应用。
比如在计算机图形学中,我们常常需要计算直线与平面的交点坐标,以便进行图形的绘制和变换。
三、直线与平面的位置关系研究直线与平面的位置关系是解析几何中的一个重要内容。
直线可以与平面相交、平行或者垂直。
我们需要了解判断直线与平面位置关系的几何条件和数学方法,应用到具体问题中。
在解析几何的考试中,常常会涉及到直线与平面的位置关系的判断和求解。
我们需要根据给定条件,运用相关的定理和公式,确定直线与平面的位置关系,并给出相应的证明过程。
四、空间几何体的计算空间几何体的计算是解析几何中的一个重要考点。
我们需要掌握球、柱、锥、棱柱等几何体的体积和表面积的计算方法。
在计算过程中,我们需要根据几何体的具体形状和给定的条件,运用相关的公式和技巧,进行数据的代入和计算。
在解析几何的学习和考试中,空间几何体的计算问题常常出现。
掌握几何体的计算方法,能够帮助我们进一步理解和应用解析几何的知识。
总结:解析几何是高中数学中的重要内容,涉及到直线与平面的方程、交点问题以及位置关系的判断和求解,同时还包括空间几何体的计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、直线与方程基础:1、直线的倾斜角α: [0,)απ∈2、直线的斜率k :2121tan y y k x x α-==-;注意:倾斜角为90°的直线的斜率不存在。
3、直线方程的五种形式: ①点斜式:00()y y k x x -=-; ②斜截式:y kx b =+; ③一般式:0Ax By C ++=; ④截距式:1x yab+=; ⑤两点式:121121y y y y x x x x --=-- 注意:各种形式的直线方程所能表示和不能表示的直线。
4、两直线平行与垂直的充要条件:1111:0l A x B y C ++=,2222:0l A x B y C ++=,1l ∥2l 12211221A B A B C B C B =⎧⇔⎨≠⎩;1212120l l A A B B ⊥⇔+= .5、相关公式:①两点距离公式:11(,)M x y ,22(,)N x y ,MN =②中点坐标公式:11(,)M x y ,22(,)N x y , 则线段MN 的中点1122(,)22x y x y P ++; ③点到直线距离公式: 00(,)P x y ,:0l Ax By C ++=, 则点P 到直线l的距离d =;④两平行直线间的距离公式:11:0l Ax By C ++=,22:0l Ax By C ++=, 则平行直线1l 与2l之间的距离d =;⑤到角公式:(补充)直线1111:0l A x B y C ++=到直线2222:0l A x B y C ++=的角为θ,(0,)(,)22ππθπ∈,则2112tan 1k k k k θ-=+⋅ .(两倾斜角差的正切) 二、直线与圆,圆与圆基础:1、圆的标准方程:222()()x a y b r -+-=; 确定圆的两个要素:圆心(,)C a b ,半径r ;2、圆的一般方程:220x y Dx Ey F ++++=,(2240D E F +->);3、点00(,)P x y 与圆222:()()C x a y b r -+-=的位置关系: 点00(,)P x y 在圆内⇔ 22200()()x a y b r -+-<; 点00(,)P x y 在圆上⇔ 22200()()x a y b r -+-=;点00(,)P x y 在圆外⇔ 22200()()x a y b r -+->;4、直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=的位置关系: 从几何角度看:令圆心(,)C a b 到直线:0l Ax By C ++=的距离为d , 相离⇔d r >; 相切⇔=d r ; 相交⇔0d r ≤<;若直线:0l Ax By C ++=与圆222:()()C x a y b r -+-=相交于两点M ,N ,则弦长MN = 从代数角度看:联立:0l Ax By C ++=与圆222:()()C x a y b r -+-=, 消去y (或x )得一元二次方程,24b ac ∆=-, 相离⇔0∆<; 相切⇔0∆=; 相交⇔0∆>;相交时的弦长1212MN x x y y =-=- . 5、圆与圆的位置关系: 相离,外切,相交,内切,内含 . 圆2221111:()()O x x y y r -+-=;圆2222222:()()O x x y y r -+-=, 根据这三个量之间的大小关系来确定:12r r -,12O O ,12r r +; 相离⇔1212O O r r >+;外切⇔1212O O r r =+; 相交⇔121212r r O O r r -<<+; 内切⇔1212O O r r =-; 内含⇔12120O O r r ≤<-;6、两圆2221111:()()O x x y y r -+-=①;圆2222222:()()O x x y y r -+-=②若相交,则相交弦所在的直线方程的求法:交轨法: ①式-②式,整理化简即可得到相交弦所在直线方程 .三、椭圆:1、(第一)定义:12122PF PF a F F +=>;2、椭圆标准方程及离心率:焦点在x 轴上的椭圆标准方程为:22221(0)x y a b a b +=>>;:a 长半轴;b :短半轴;:c 半焦距 .椭圆中a ,b ,c 的关系:222a b c =+; 椭圆的离心率(0,1)ce a=∈ . 3、弦长公式:直线:l y kx b =+与椭圆2222:1()x y C m n m n+=≠交于两点11(,)M x y ,22(,)N x y ,则相交时的弦长1212MN x x y y =-=- . 弦长公式是由两点距离公式与两点斜率公式推导出来,故适用性比较广。
4、中点弦结论(点差法):椭圆2222:1()x y C m n m n+=≠上的两点11(,)M x y ,22(,)N x y ,弦MN 的中点1212(,)22x x y y P ++, 则22MN OPn k k m⋅=- .5、焦点三角形面积:椭圆2222:1(0)x y C a b a b+=>>的两个焦点分别为1F 、2F ,点P 是椭圆C上除左、右端点外的一点,令12F PF θ∠=,则:122tan2PF F S b θ∆=⋅ .该公式是由三角形面积公式、椭圆第一定义、余弦定理结合三角恒等变换推导出来。
6、直线与椭圆位置关系:联立:0l Ax By C ++=与椭圆2222:1()x y C m n m n+=≠,消去y (或x )得一元二次方程,24b ac ∆=-,相离⇔0∆<; 相切⇔0∆=; 相交⇔0∆>;7、与点坐标相关的面积公式:(0,0)O ,11(,)A x y ,22(,)B x y ,点O ,A ,B 不在一条直线上,则:122112OAB S x y x y ∆=-. 该公式是由三角形面积公式、余弦定理结合三角恒等式推导出。
四、双曲线:(类比椭圆来学习双曲线) 1、定义:12122PF PF a F F -=<;2、双曲线标准方程及离心率、渐近线方程:焦点在x 轴上的双曲线标准方程为:22221(0,0)x y a b a b -=>>;:a 实半轴;b :虚半轴;:c 半焦距 .双曲线中a ,b ,c 的关系:222c a b =+; 双曲线的离心率(1,)c e a=∈+∞ ;焦点在x 轴上的双曲线的渐近线方程为b y x a=±; 焦点到渐近线的距离d b = .焦点在y 轴上的双曲线相关性质可以类比。
3、弦长公式:直线:l y kx b =+与双曲线2222:1(0,0)x y C a b a b-=>>交于两点11(,)M x y ,22(,)N x y ,则相交时的弦长1212MN x x y y =-=- . 4、中点弦结论(点差法):双曲线2222:1(0,0)x y C a b a b-=>>上的两点11(,)M x y ,22(,)N x y ,弦MN 的中点1212(,)22x x y y P ++, 则22MN OPb k k a⋅= . 5、焦点三角形面积:双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点分别为1F 、2F ,点P 是双曲线C 上除左、右端点外的一点,令12F PF θ∠=,则:122tan2PF F b S θ∆=.6、直线与双曲线位置关系:①当直线l 与双曲线C 的其中一条渐近线重合时,显然直线l 与双曲线C 无交点;②当直线l 与双曲线C 的其中一条渐近线平行时,有且仅有一个交点,此时联立直线方程与双曲线方程,会得到一个一次方程(二次项系数为0);③当直线l 与双曲线C 的渐近线既不平行也不重合时,此时联立直线方程与双曲线方程,消去y (或x )得一元二次方程,24b ac ∆=-, 相离⇔0∆<;相切⇔0∆=; 相交⇔0∆>;五、抛物线:1、定义:P l PF d -= (到定点的距离等于到定直线的距离的这样的2、标准方程:22(0)y px p =>(开口朝右的抛物线,开口朝其它方向的抛物线方程及其它性质可以类比。
) 焦点(,0)2p F ,准线:2p l x =-,离心率1e =. 3、常见性质: ① 普通的弦长公式:直线y kx b =+与抛物线22(0)y px p =>相交于两点11(,)M x y ,22(,)N x y , 12y y - .②过焦点(,0)2p F 的特殊弦长公式及12x x 与12y y :(i )若弦MN 过焦点(,0)2p F ,则弦长1222sin pMN x x p α=++= (α为倾斜角);(ii )2124p x x =,212y y p =- .③过抛物线2:2(0)C y px p =>的顶点(0,0)O 作两条互相垂直的射线OM 、ON 分别与抛物线C 交于两点M ,N ,弦MN 与x 轴交于点P ,则(2,0)P p ,即:4OP OF =.反之亦然,即:若4OP OF =,则90MON ∠=︒.4、抛物线中过焦点弦的其它性质(补充,作为了解,切记不能死记硬背。
如死记硬背,如下知识点不如不用掌握。
可以尝试证明。
) 设MN 是过抛物线22(0)y px p =>焦点F 的弦,11(,)M x y ,22(,)N x y , 如图(抛物线图2), 则:①22sin MON p S α∆=; ②112MF NF p+=; ③以MN 为直径的圆与准线相切; ④90PFQ ∠=︒;⑤以MF 或NF 为直径的圆与y 轴相切 . 5、直线与抛物线的位置关系:①若直线与抛物线的对称轴平行或重合,则有一个交点;②若直线与抛物线的对称轴不平行,也不垂直,则根据判别式∆的符号来确定交点个数;③若直线与抛物线的对称轴垂直,画图数形结合很容易判断交点个数。
圆锥曲线大题常见题型(归纳总结): 题型一、求点的轨迹问题: 常见方法:①直接法:(设出所求点(,)P x y ,根据题意列出等式,建立起y 与x 的关系。
) 如椭圆的标准方程的求出,本身就是利用这种方法。
②几何定义法:根据题意画出图形,通过已知条件及所学知识(如三角形中位线、圆与圆内切与外切,直线与圆相切的等价条件)得出所求点(,)P x y 满足圆的几何定义或椭圆、双曲线、抛物线的定义,从而求出点的轨迹方程;③伴随动点转化法: 该类题型的特征往往是: 其中一个动点如点00(,)Q x y 的轨迹方程是已知的,另有一个定点A 或多个定点,所求动点(,)P x y 与定点A 和动点00(,)Q x y 有着一定关系。
