多元积分计算方法总结
多元函数积分计算方法

多元函数积分计算方法在数学中,多元函数积分是一种重要的计算方法,能够求解多元函数在给定区域上的面积、体积以及相关的物理量。
本文将介绍一些常见的多元函数积分计算方法,帮助读者更好地理解和应用这一数学工具。
一、重积分的定义重积分是单变量函数积分的推广,用于求解多元函数在给定区域上的面积或体积。
设函数f(x,y)在区域D上有定义,D的边界可以用曲线C表示,则重积分的定义为:∬_D▒〖f(x,y)dA=lim(Δx→0,Δy→0)∑▒f(x_i^*,y_j^*)ΔA〗其中,ΔA为区域D中小面积元素,f(x_i^*,y_j^*)为该小面积元素上一点的函数值。
二、二重积分的计算方法1. 矩形区域上的二重积分计算若D为矩形区域,可以采用迭代积分的方法求解二重积分。
先对x 进行积分,再对y进行积分,即:∬_D▒〖f(x,y)dA=∫_(a_y)^(b_y)▒(∫_(a_x)^(b_x)▒f(x,y)dxdy)〗2. 极坐标下的二重积分计算对于极坐标下的积分区域D,可以将二重积分转化为极坐标形式进行计算。
设D在极坐标下的表示为(r,θ),则二重积分的计算公式为:∬_D▒〖f(x,y)dA=∫_(θ_1)^(θ_2)▒(∫_(r_1(θ))^(r_2(θ))▒f(rcosθ,rsinθ)rdθ)〗三、三重积分的计算方法1. 直角坐标系下的三重积分计算若函数f(x,y,z)在空间区域V上有定义,则三重积分的计算公式为:∭_V▒〖f(x,y,z)dV=∫_(a_z)^(b_z)▒(∫_(a_y)^(b_y)▒(∫_(a_x)^(b_x)▒f(x,y,z)dxdydz )〗2. 柱坐标系或球坐标系下的三重积分计算对于柱坐标或球坐标下的积分区域V,可以将三重积分转化为柱坐标或球坐标形式进行计算。
具体转化公式可以根据坐标系关系进行推导,然后套用相应的公式进行计算。
四、应用举例1. 面积计算对于二维平面上的函数f(x,y),可以通过二重积分来计算给定区域D的面积。
(整理)多元函数积分

(整理)多元函数积分多元函数积分1. 利用积分区域的对称性化简多元函数的积分1.1 利用积分区域的对称性化简多元函数的重积分题型一计算积分区域具有对称性,被积函数具有奇偶性的重积分类型(一)计算积分区域具有对称性、被积函数具有奇偶性的二重积分常用下述命题简化计算二重积分.命题1 若f(x,y)在积分区域D 上连续,且D 关于y 轴(或x 轴)对称,则(1)f(x,y)是D 上关于x (或y )的奇函数时,有??=Ddxdy y x f 0),(;(2)f(x,y)是D 上关于x (或y )的偶函数时,有=D D dxdy y x f dxdy y x f 1),(2),(;其中D 1是D 落在y 轴(或x 轴)一侧的那一部分区域.命题2 若D 关于x 轴、y 轴对称,D 1为D 中对应于x ≥0,y ≥0(或x ≤0,y ≤0)的部分,则-=--=-=-=D D y x f y x f y x f y x f y x f y x f dxdy y x f dxdy y x f ).,(),(),(,0),,(),(),(,),(4),(1或命题3 设积分区域D 对称于原点,对称于原点的两部分记为D 1和D 2.(1);),(2),(),,(),(1==--D D d y x f d y x f y x f y x f σσ则若(2).0),(),,(),(??=-=--Dd y x f y x f y x f σ则若命题4 积分区域D 关于y x ,具有轮换对称性,则+==DD D d x y f y x f d x y f d y x f σσσ)],(),([21),(),( 记D 位于直线y=x 上半部分区域为D 1,则-===D D y x f x y f y x f x y f dxdy y x f dxdy y x f ),,(),(,0),,(),( ,),(2),(1类型(二)计算积分区域具有对称性,被积函数具有奇偶性的三重积分.常用下述命题简化具有上述性质的三重积分的计算.命题1若Ω关于xOy 平面对称,而Ω1是Ω对应于z ≥0的部分,则Ω∈?=-Ω∈?--=-=ΩΩ;),,(),,,(),,(,),,(2,),,(),,,(),,(,0),,(1z y x z y x f z y x f d z y x f z y x z y x f z y x f d z y x f υυ 若Ω关于yOz 平面(或zOx 平面)对称,f 关于x (或y )为奇函数或偶函数有类似结论.命题2 若Ω关于xOy 平面和xOz 平面均对称(即关于x 轴对称),而Ω1为Ω对应于z ≥0,y ≥0的部分,则=ΩΩ为奇函数;或关于,当为偶函数,关于当z y f z y f d z y x f d z y x f 0,,),,(4),,(1υυ 若Ω关于xOz 平面和yOz 平面均对称(即关于z 轴对称),或者关于xOy 平面和yOz 平面均对称,那么也有类似结论.命题3 如果积分区域Ω关于三个坐标平面对称,而Ω1是Ω位于第一象限的部分,则=ΩΩ为奇函数;或或关于,当均为偶函数,关于当z y x f z y x f d z y x f d z y x f 0,,,),,(8),,(1υυ 命题4 若积分区域Ω关于原点对称,且被积函数关于x,y,z 为奇函数,即.0),,(),,,(),,(=----=Ωυd z y x f z y x f z y x f 则题型三计算积分区域具有轮换对称性的三重积分命题5 如果积分区域关于变量x,y,z 具有轮换对称性(即x 换成y,y 换成z,z 换成x ,其表达式不变),则ΩΩΩΩ++===υυυυd y x z f x z y f z y x f d y x z f d x z y f d z y xf )],,(),,(),,([31),,(),,(),,(.1.2 利用积分区域的对称性化简第一类曲线积分、曲面积分题型一计算积分曲线(面)具有对称性的第一类曲线(面)积分类型(一)计算积分曲线具有对称性的第一类曲线积分命题1.2.1 设曲线L 关于y 轴对称,则=??,0,),(2),(1L L ds y x f s d y x f 是奇函数,关于是偶函数,关于x y x f x y x f ),(),( 其中L 1是L 在x ≥0的那段曲线,即L 1是L 在y 轴右侧的部分;若曲线L 关于x 轴对称,则有上述类似结论.命题1.2.2 设f(x,y)在分段光滑曲线L 上连续,若L 关于原点对称,则=??,LL ds y x f s d y x f ),(2,0),( 为偶函数,关于若为奇函数,关于若),(),(),(),(y x y x f y x y x f 其中L 1为L 的右半平面或上半平面部分.类型(二)计算积分曲面具有对称性的第一类曲面积分第一类曲面积分的奇偶对称性与三重积分类似,可利用下述命题简化计算.命题1.2.3 设积分曲面Σ关于yOz 对称,则=∑∑1),,(2,0),,(dS z y x f dS z y x f 为偶函数,关于当为奇函数,关于当x z y x f x z y x f ),,(),,( 其中Σ1是Σ在yOz 面的前侧部分.若Σ关于另外两坐标面有对称性,则有类似结论.注意不能把Σ向xOy 面上投影,因第一类曲面积分的Σ投影域面积不能为0.题型二计算平面积分曲线关于y=x 对称的第一类曲线积分命题1.2.4 若L 关于直线y=x 对称,则??=L Lds x y f ds y x f ),(),(. 题型三计算空间积分曲线具有轮换对称性的第一类曲线积分命题1.2.5 若曲线Γ方程中的三变量x,y,z 具有轮换对称性,则ΓΓΓΓΓΓ====ds z ds y ds x zds yds xds 222,. 1.3 利用积分区域的对称性化简第二类曲线积分、曲面积分题型一计算积分曲线具有对称性的第二类曲线积分第二类曲线积分的奇偶对称性与第一类曲线积分相反,有下述结论.命题1.3.1 设L 为平面上分段光滑的定向曲线,P(x,y),Q(x,y)连续,(1)L 关于y 轴对称,L 1是L 在y 轴右侧部分,则=??,),(2,0),(1L L dx y x P dx y x P 为偶函数;关于若为奇函数,关于若x y x P x y x P ),(),( =??,),(2,0),(Q 1L L dy y x Q dy y x .),(),(为奇函数关于若为偶函数,关于若x y x Q x y x Q (2)L 关于x 轴对称,L 1为L 在x 轴上侧部分,则=??,),(2,0),(1L L dx y x P dx y x P 为奇函数;关于若为偶函数,关于若y y x P y y x P ),(),( =??,),(2,0),(1L L dy y x Q dy y x Q .),(),(为偶函数关于若为奇函数,关于若y y x Q y y x Q (3)L 关于原点对称,L 1是L 在y 轴右侧或x 轴上侧部分,则+=+,2,0),(),(1L L L Qdy Pdx dy y x Q dx y x P .),(),(),,(),(),(),,(为奇函数关于若为偶函数,关于若y x y x Q y x P y x y x Q y x P (4)L 关于y=x 对称,则.),(),(),(),(),(),(+-=+=+-LL L dx x y Q dy x y P dx x y Q dy x y P dy y x Q dx y x P 即若L 关于y=x 对称,将x 与y 对调,则L 关于直线y=x 翻转,即L 化为L —.因而第二类曲线积分没有轮换对称性.题型二计算积分曲面具有对称性的第二类曲面积分命题1.3.2 设Σ关于yOz 面对称,则=∑∑,0,),,(2),,(1dydz z y x P dydz z y x P .),,(),,(为偶函数关于当为奇函数,关于当x z y x P x z y x P 其中Σ1是Σ在yOz 面的前侧部分.这里对坐标y 和z 的第二类曲面积分只能考虑Σ关于yOz 面的对称性,而不能考虑其他面,这一点也与第一类曲面积分不同.2. 交换积分次序及转换二次积分题型一交换二次积分的积分次序※直接例题,无讲解.题型二转换二次积分转换二次积分是指将极坐标系(或直角坐标系)下的二次积分转换成直角坐标系(或极坐标系)下的二次积分.由极坐标系(或直角坐标系)下的二次积分的内外层积分限写出相应的二重积分区域D 的极坐标(或直角坐标)表示,再确定该区域D 在直角坐标系(或极坐标系)中的图形,然后配置积分限.3. 计算二重积分题型一计算被积函数分区域给出的二重积分含绝对值符号、最值符号max 或min 及含符号函数、取整函数的被积函数,实际上都是分区域给出的函数,计算其二重积分都需分块计算.题型二计算圆域或部分圆域上的二重积分当积分区域的边界由圆弧、过原点的射线(段)组成,而且被积函数为)(22y x f y x m n +或)/(x y f y x m n 的形状时,常作坐标变换θθsin ,cos r y r x ==,利用极坐标系计算比较简单.为此,引进新变量r,θ,得到用极坐标(r ,θ)计算二重积分的公式:=')sin ,cos (),(D D rdrd r r f dxdy y x f θθθ (其中rd θdr 是极坐标系下的面积元素). 用极坐标系计算的二重积分,就积分区域来说,常是圆域(或其一部分)、圆环域、扇形域等,可按其圆心所在位置分为下述六个类型(其中a,b,c 均为常数).类型(一)计算圆域x 2+y 2≤a 上的二重积分. 类型(二)计算圆域x 2+y 2≤2ax 上的二重积分.类型(三)计算圆域x 2+y 2≤-2ax 上的二重积分.类型(四)计算圆域x 2+y 2≤2ay 上的二重积分.类型(五)计算圆域x 2+y 2≤-2ay 上的二重积分.类型(六)计算圆域x 2+y 2≤2ax+2by+c 上的二重积分.4. 计算三重积分题型一计算积分区域的边界方程均为一次的三重积分当积分区域Ω主要由平面围成时,宜用直角坐标系计算,如果积分区域Ω的边界方程中含某个坐标变量的方程只有两个,则可先对该坐标变量积分。
2多元函数积分的计算公式

2多元函数积分的计算公式多元函数积分是微积分中的重要内容,用于计算多元函数在给定区域上的面积、体积以及质量等问题。
在本文中,我将介绍多元函数积分的定义、计算方法以及一些重要性质。
1.多重积分的定义多重积分是对多元函数在给定区域上的进行求和的过程。
对于二重积分来说,可以表示为:\[ \iint_D f(x,y) dA \]其中,f(x,y)是定义在平面区域D上的函数,dA表示面积元素。
对于三重积分来说,可以表示为:\[ \iiint_V f(x,y,z) dV \]其中,f(x,y,z)是定义在空间区域V上的函数,dV表示体积元素。
2.多重积分的计算方法多重积分的计算方法有两种:直接计算和间接计算。
直接计算是通过将积分区域划分成小的子区域,然后在每个子区域上计算函数值,并将所有结果相加。
间接计算是通过将多重积分转化为一重积分进行计算。
对于二重积分,可以使用极坐标转换将其转化为一重积分。
极坐标转换公式为:\[ x = r\cos(\theta) \]\[ y = r\sin(\theta) \]面积元素dA可以表示为:\[ dA = r dr d\theta \]将这个转换应用于二重积分计算中,可以得到:\[ \iint_D f(x,y) dA = \int_\alpha^\beta\int_{r_1(\theta)}^{r_2(\theta)} f(r\cos(\theta), r\sin(\theta)) r dr d\theta \]其中,\(\alpha\)和\(\beta\)是极角的范围,\(r_1(\theta)\)和\(r_2(\theta)\)是每个极角对应的极径范围。
对于三重积分,可以使用柱面坐标或球面坐标进行转换。
柱面坐标转换公式为:\[ x = r\cos(\theta) \]\[ y = r\sin(\theta) \]\[z=z\]体积元素dV可以表示为:\[ dV = r dr d\theta dz \]将这个转换应用于三重积分计算中,可以得到:\[ \iiint_V f(x,y,z) dV = \int_\alpha^\beta\int_{r_1(\theta)}^{r_2(\theta)} \int_{z_1(r, \theta)}^{z_2(r, \theta)} f(r\cos(\theta), r\sin(\theta), z) r dz dr d\theta \]其中,\(\alpha\)和\(\beta\)是极角的范围,\(r_1(\theta)\)和\(r_2(\theta)\)是每个极角对应的极径范围,\(z_1(r, \theta)\)和\(z_2(r, \theta)\)是每个极径和极角对应的高度范围。
多元函数微积分学总结

多元函数微积分学总结多元函数微积分学是微积分学的一个重要分支,研究多个变量之间的关系以及对这些变量的变化进行分析和计算。
本文将对多元函数微积分学的主要内容进行总结,并介绍常见的方法和技巧。
一、空间坐标系和极坐标系在多元函数微积分学中,我们通常使用空间坐标系和极坐标系来描述多维空间中的点和曲线。
空间坐标系是由三个相互垂直的坐标轴x、y、z组成,用来表示三维空间中的点。
我们可以通过向量运算、平面的方程等方式来研究空间中的曲线、曲面以及相关的计算方法。
极坐标系是在平面上建立的坐标系,由极径r和极角θ组成。
极坐标系可以用来描述平面上的点和曲线,通过坐标变换的方法可以与空间坐标系进行转换。
二、多元函数的极限和连续性多元函数的极限和连续性是多元函数微积分学的基础概念。
类似于一元函数的极限和连续性,多元函数的极限和连续性也可以通过定义、性质等方式进行研究和计算。
对于多元函数的极限,我们需要考虑函数在不同方向上的极限以及函数在某点处的极限。
通过使用极限的定义和极限运算法则,我们可以判断多元函数在某点处的极限是否存在,并进行具体的计算。
多元函数的连续性与一元函数的连续性类似,即函数在某点附近的函数值和极限值之间存在一个足够小的常数δ,使得当自变量的取值在这个常数范围内时,函数值的变化足够小。
通过使用连续函数的定义和连续性的性质,我们可以判断多元函数在某点处是否连续,并进行具体的计算。
三、多元函数的偏导数和全微分多元函数的偏导数和全微分是研究多元函数变化的重要工具,在微积分学中有着广泛的应用。
对于多元函数的偏导数,我们可以通过定义和偏导数的性质来进行计算。
偏导数可以表示函数在某个方向上的变化率,它在多个方向上的值决定了函数的变化趋势和比例。
通过计算偏导数和一阶偏导数的矩阵,我们可以得到多元函数的梯度,进而进行更复杂的分析和计算。
多元函数的全微分则广义地描述了函数在某一点附近的变化情况。
全微分可以通过偏导数和偏导数向量的运算来进行计算,并可以表示函数值的一个线性近似。
多元函数的积分

多元函数的积分在数学中,多元函数的积分是一项重要的概念和计算方法。
与一元函数的积分类似,多元函数的积分可以帮助我们求解曲线下的面积、体积等问题,以及解决一些与实际问题相关的计算。
一、二重积分二重积分是多元函数积分中最基础的一种形式。
它的计算方法依赖于重积分的定义以及二重积分的性质。
对于二重积分来说,我们需要将待求的函数转化为极坐标形式、直角坐标形式等,并确定积分区域的范围。
通过分割积分区域成为若干小块,再对每个小块进行积分求和,最后将所有小块的积分结果相加,可以得到二重积分的值。
在实际应用中,二重积分可以用来计算平面图形的面积、求解平面质心等问题。
二、三重积分与二重积分类似,三重积分是多元函数积分中的另一种形式。
三重积分的计算方法也依赖于重积分的定义以及三重积分的性质。
与二重积分不同的是,三重积分需要确定积分区域的范围,并将待求的函数转化为球坐标形式、柱坐标形式等。
同样地,通过分割积分区域成为若干小块,再对每个小块进行积分求和,最后将所有小块的积分结果相加,可以得到三重积分的值。
在实际应用中,三重积分可以用来计算空间图形的体积、质心等问题。
三、重积分的性质重积分具有一些重要的性质,这些性质对于计算积分结果以及简化计算过程都非常有帮助。
其中一些常见的性质包括积分线性性、积分对称性、积分的加法性和积分的估值性等。
积分线性性:对于常数a和b,函数f(x,y)和g(x,y),有∬[D](af(x,y)+bg(x,y))dA = a∬[D]f(x,y)dA + b∬[D]g(x,y)dA。
这个性质使得我们在计算重积分时可以将积分区域分解成若干个子区域进行计算。
积分对称性:如果函数f(x,y)在区域D上关于x轴对称,则有∬[D]f(x,y)dA = 2∬[D1]f(x,y)dA,其中D1是区域D在x轴上方的部分。
类似地,还有关于y轴对称和原点对称的性质。
积分的加法性:对于两个不重叠的区域D1和D2,有∬[D1∪D2]f(x,y)dA = ∬[D1]f(x,y)dA + ∬[D2]f(x,y)dA。
多元函数积分的计算方法技巧
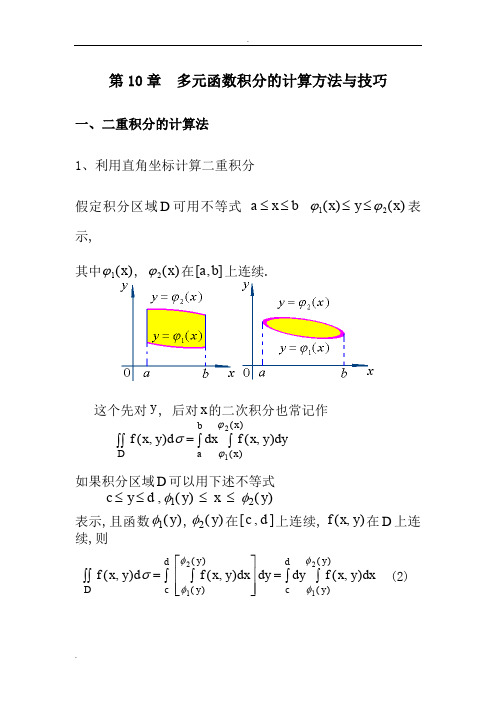
第10章 多元函数积分的计算方法与技巧一、二重积分的计算法1、利用直角坐标计算二重积分假定积分区域可用不等式 表示,其中, 在上连续.这个先对, 后对的二次积分也常记作如果积分区域可以用下述不等式表示,且函数,在上连续,在上连续,则(2)D a x b x y x ≤≤≤≤ϕϕ12()()ϕ1()x ϕ2()x [,]ab y x f x y d dx f x y dy Dabx x (,)(,)()()σϕϕ⎰⎰⎰⎰=12D c y d y x y ≤≤≤≤,()()φφ12φ1()y φ2()y [,]c d f x y (,)D f x y d f x y dx dy dy f x y dx D y y c dc d y y (,)(,)(,)()()()()σφφφφ⎰⎰⎰⎰⎰⎰=⎡⎣⎢⎢⎤⎦⎥⎥=1212显然,(2)式是先对,后对的二次积分.积分限的确定几何法.画出积分区域的图形(假设的图形如下 )在上任取一点,过作平行于轴的直线,该直线穿过区域,与区域的边界有两个交点与,这里的、就是将,看作常数而对积分时的下限和上限;又因是在区间上任意取的,所以再将看作变量而对积分时,积分的下限为、上限为.例1计算, 其中是由抛物线及直线所围成的区域.x yD ],[b a x x y D D ))(,(1x x ϕ))(,(2x x ϕ)(1x ϕ)(2x ϕx y x [,]a b x x a b xyd D⎰⎰σD y x 2=y x =-22.利用极坐标计算二重积分 1、就是极坐标中的面积元素.2、极坐标系中的二重积分, 可以化归为二次积分来计算.其中函数, 在上连续.则注:本题不能利用直角坐标下二重积分计算法来求其精确值.D y y x y :,-≤≤≤≤+1222xyd dy xydx x y dy D y y y y σ⎰⎰⎰⎰⎰==⎡⎣⎢⎤⎦⎥-+-+12221222212[]=+-=-⎰1224582512y y y dy ()rdrd θr →cos θr →sin θrdrd →θf x y dxdyD(,)⎰⎰f r r rdrd D(cos ,sin )θθθ⎰⎰αθβϕθϕθ≤≤≤≤12()()r ϕθ1()ϕθ2()[,]αβf r r rdrd d f r r rdrD(cos ,sin )(cos ,sin )()()θθθθθθαβϕθϕθ⎰⎰⎰⎰=123、使用极坐标变换计算二重积分的原则(1)、积分区域的边界曲线易于用极坐标方程表示( 含圆弧,直线段 );(2)、被积函数表示式用极坐标变量表示较简单( 含, 为实数 ). 例6计算解此积分区域为该区域在极坐标下的表示形式为二、三重积分的计算 1、积分区域可表示成则这就是三重积分的计算公式, 它将三重积分化成先对积()x y 22+ααI dxdyx y a x y a axa a x =+⋅-+>⎰⎰--+-022*******()()D x a x y a a x :,022≤≤-≤≤-+-D r a :,sin -≤≤≤≤-πθθ4002I rdrd r a rd dra r r a d Da a =-=-=⎡⎣⎢⎤⎦⎥⎰⎰⎰⎰⎰----θθθπθθπ44222402202024sin sin arcsin =-=-=--⎰()θθθπππd 402421232Ωa x b y x y y x z x y z z x y ≤≤≤≤≤≤,()(),(,)(,)1212f x y z dv dx dyf x y z dz aby x y x z x y z x y (,,)(,,)()()(,)(,)Ω⎰⎰⎰⎰⎰⎰=1212分变量, 次对,最后对的三次积分.例1计算, 其中为球面及三坐标面所围成的位于第一卦限的立体. 解 在面上的投影区域为确定另一积分变量的变化范围选择一种次序,化三重积分为三次积分z y x xyzdxdydz Ω⎰⎰⎰Ωx y z 2221++=Ωxoy D x y x y xy :,,22100+≤≥≥0122≤≤--z x y ⎰⎰⎰⎰⎰⎰⎰⎰----Ω--==2222102210101010)1(21x y x x dyy x xy dx xyzdzdy dxxdydzxyzd dxx x x x x x dx xy y x xy dyxy y x xy dx x x⎰⎰⎰⎰⎥⎦⎤⎢⎣⎡-----=⎥⎦⎤⎢⎣⎡--=--=--102223210104232103310)1(81)1(41)1(41814141)212121(224812462481246224124241cos sin 81cos sin 41cos sin 41cos cos sin 81cos sin 41cos sin 412052033320204232=⋅⋅⋅⋅-⋅⋅⋅⋅-⋅⋅=--=⎥⎦⎤⎢⎣⎡--=⎰⎰⎰⎰ππππtdtt tdt t dt t tdtt t t t t t2、利用柱面坐标计算三重积分 点的直角坐标与柱面坐标之间有关系式体积为这便是柱面坐标系下的体积元素, 并注意到(1)式有3、利用球坐标计算三重积分直角坐标与球面坐标间的关系为这就是球面坐标系下的体积元素。
多元函数积分学总结

多元函数积分学总结引言多元函数积分学是微积分的一个重要分支,研究的是多个变量的函数在特定区域上的积分计算和性质。
在实际问题中,我们经常需要求解多元函数的积分,以求得面积、体积、质量等物理量。
本文将对多元函数积分学的基本概念、计算方法和应用进行总结和介绍。
一、多元函数积分的基本概念1. 二重积分二重积分是多元函数积分学中最基本的概念之一。
它表示在二维平面上的一个有界区域上对函数进行积分。
二重积分的计算可以通过投影到坐标轴上的两个一元积分来实现。
根据积分区域的形状和函数性质的不同,二重积分可以分为类型I和类型II两种。
•类型I:积分区域为矩形、正方形或一般的可由直线分割成有限个矩形的区域。
•类型II:积分区域不属于类型I的情况,一般需要进行变量替换或极坐标转化来简化计算。
2. 三重积分三重积分是对三维空间内的函数进行积分。
它可以用于计算体积、质量、重心等与物体形状和密度有关的物理量。
三重积分的计算方法较为复杂,一般需要采用适当的坐标变换或者使用球坐标、柱坐标等不同坐标系下的积分公式来进行计算。
二、多元函数积分的计算方法1. Fubini定理Fubini定理是多元函数积分计算的基础定理之一。
它建立了二重积分和三重积分之间的关系,使得计算复杂多元函数积分时可以拆分为若干个简单的积分。
Fubini定理主要有两种形式:对于矩形区域上的二重积分,可以通过交换积分次序将其转化为两次一元积分。
对于空间区域上的三重积分,也可以利用类似的方法进行计算。
2. 极坐标和球坐标对于具有相关几何特性的问题,使用极坐标和球坐标可以简化多元函数积分的计算过程。
极坐标常用于计算平面上的二重积分,而球坐标常用于计算空间中的三重积分。
通过引入极坐标或球坐标的坐标变换,我们可以将原积分区域变换为一个更简单的形式,从而简化积分计算。
在实际应用中,灵活运用极坐标和球坐标可以大大提高计算效率。
三、多元函数积分的应用多元函数积分在物理学、工程学、经济学等领域有广泛的应用。
多元函数的积分

多元函数的积分在数学中,多元函数的积分是一个重要的概念和计算方法。
与一元函数的积分不同,多元函数的积分需要考虑多个自变量和相应的积分变量。
一、多元函数的积分定义对于二元函数f(x, y),其在有界闭区域D上的积分可以定义为:∬f(x, y)dA = limΔx,Δy→0 Σf(xi, yj)ΔA其中,Δx和Δy分别表示x和y方向的分割长度,Σ表示对所有的(i, j)求和,xi和yj表示分割后的小区域的任意点,ΔA表示小区域的面积。
对于n元函数f(x1, x2, ..., xn),其在有界闭区域D上的积分可以定义为:∭f(x1, x2, ..., xn)dV = limΔx1,Δx2,...,Δxn→0 Σf(x1i, x2j, ..., xnk)ΔV其中,Δx1, Δx2, ..., Δxn分别表示各个方向的分割长度,Σ表示对所有的(i1, i2, ..., in)求和,x1i, x2j, ..., xnk表示分割后小区域的任意点,ΔV表示小区域的体积。
二、多元函数的积分计算与一元函数的积分类似,对于多元函数的积分计算也需要借助于定积分的性质、微积分的基本定理和换元积分法等方法。
1. 球坐标和柱坐标对于具有某种对称性的多元函数,可以选择适当的坐标系来简化积分计算。
常用的坐标系有球坐标和柱坐标。
球坐标系适用于具有球对称性的问题,对于三元函数可以表示为:x = rsinθcosφ, y = rsinθsinφ, z = rcosθ其中,r代表点到坐标原点的距离,θ表示点与正z轴的夹角,φ表示点在xy平面上与正x轴的夹角。
柱坐标系适用于具有柱对称性的问题,对于三元函数可以表示为:x = rcosθ, y = rsinθ, z = z其中,r代表点到z轴的距离,θ表示点在xy平面上与正x轴的夹角,z表示点在z轴上的坐标。
2. 积分的性质多元函数的积分具有类似于一元函数积分的一些性质,如线性性质、可加性质、保号性质等。
多重积分方法总结

多重积分方法总结多重积分是微积分的一个重要分支,用于研究二维、三维或更高维空间中的函数性质。
它在实际问题的建模与求解中起到了重要作用。
多重积分方法主要包括定积分、累次积分、面积分和体积分的相关方法。
一、定积分方法定积分是多重积分的基础,可将曲线下方形成的面积看作是一个函数与对应的线段长度之间的关系。
定积分可用于求函数的面积、弧长、几何体积、质量、质心等问题。
利用定积分方法可将区域分割为无穷多的小矩形,通过求和得到区域的总面积。
定积分的计算可以应用牛顿-莱布尼茨公式、变限积分法和微积分基本定理。
二、累次积分方法累次积分是多重积分的另一种重要方法,主要用于求解二重积分和三重积分。
通过不断降维,将多重积分问题转化为单重积分问题。
对于二重积分,可以将区域划分为无穷多的小矩形,求和得到总面积;对于三重积分,可以将区域划分为无穷多的小立方体,求和得到总体积。
累次积分通过反复积分的方式,对于不同变量进行积分,使得积分操作变得相对简单。
三、面积分方法面积分主要用于计算曲面的面积和一些向量场沿曲面的通量。
面积分可以分为第一类和第二类,分别对应于标量场和向量场。
对于第一类面积分,可以通过将曲面分割为无数小小面积片,用累次积分的方法将其进行求和,得到总面积。
对于第二类面积分,需要考虑向量场在曲面上的法向量,通过点乘计算通量。
四、体积分方法体积分主要用于计算三维空间中定义的函数体所围成的体积。
通过将空间划分为无穷多的小体积元,用累次积分的方法对其进行求和,得到总体积。
体积分的计算需要确定积分变量的积分区间,同时还需要确定积分函数在每个小体积元上的取值。
除了上述基本的多重积分方法外,还有一些常见的变量替换方法,如极坐标、球坐标、柱坐标等,可以简化积分计算,并且有时能够使积分过程更加简洁。
此外,对于一些特殊的区域和函数,还可以利用对称性、奇偶性等性质,选择合适的积分区域和变量替换,从而简化多重积分的计算过程。
综上所述,多重积分方法是微积分的重要工具之一,对于求解曲线面积、体积、通量等问题有着广泛的应用。
10多元函数积分中的三个公式计算及运用

10多元函数积分中的三个公式计算及运用在高等数学中,多元函数积分是一个重要的概念,它在应用数学、物理学等领域中都有着广泛的应用。
为了更好地理解和应用多元函数积分,李正元考研高数基础讲义中介绍了十个多元函数积分的基本公式,其中有三个是重要且常用的公式,它们分别是重积分的线性性、变量代换公式和极坐标系下的积分公式。
首先是重积分的线性性。
重积分的线性性是指如果f(x,y)和g(x,y)是定义在闭区域D上的可积函数,c1和c2是常数,那么c1f(x,y)+c2g(x,y)也是定义在D上的可积函数,并且有以下成立的公式:∫∫D [c1f(x, y) + c2g(x, y)]dxdy = c1∫∫D f(x, y)dxdy +c2∫∫D g(x, y)dxdy这个公式的运用非常广泛,在对多元函数进行积分时经常会用到。
其次是变量代换公式。
在计算多元函数积分时,有时可以通过进行变量代换来简化计算。
设有从平面区域D到平面区域D'的可导函数变换x=x(u,v),y=y(u,v),且这个变换是一一对应,那么就有以下变量代换公式:∫∫D' f(x(u, v), y(u, v)),J(u, v),dudv = ∫∫D f(x,y)dxdy其中J(u,v)是变换的雅可比行列式,即J(u,v)=∂(x,y)/∂(u,v)=∂x/∂u*∂y/∂v-∂x/∂v*∂y/∂u。
这个公式在计算复杂的多元函数积分时非常有用,通过适当的变量代换可以将积分区域转化成更简单的形式,从而简化计算过程。
最后是极坐标系下的积分公式。
当积分区域是一个闭圆盘或圆环时,可以使用极坐标系来进行积分计算。
假设f(r,θ)是定义在圆盘或圆环内的连续函数,那么有以下公式成立:∫∫D f(r, θ)rdrdθ = ∫(θ=a to b) ∫(r=0 to R) f(r,θ)rdrdθ其中D表示积分区域,a和b是角度的取值范围,R是极坐标下的积分区域的半径。
多元积分的应用常见公式

多元积分的应用常见公式多元积分是微积分中的重要内容,它在物理学、工程学、经济学等领域中具有广泛的应用。
在多元积分的计算中,我们经常会使用一些常见的公式,这些公式是解决实际问题时的强大工具。
下面我们将介绍一些常见的多元积分应用公式。
1. Fubini定理Fubini定理是多元积分中的重要定理,它用于计算二重积分和三重积分。
Fubini定理的关键思想是将多元积分转化为一元积分的连续积分问题。
对于二重积分,Fubini定理可表示为:∬Rf(x,y)dA=∫a∫b f(x,y)dydx其中R为积分区域,f(x,y)为被积函数,dA表示面积元素。
在积分区域R内,先对y进行积分,再对x进行积分。
对于三重积分,Fubini定理可表示为:∭Gf(x,y,z)dV=∬R∫h(x,y)fdx dy其中G为积分区域,f(x,y,z)为被积函数,dV表示体积元素。
在积分区域G内,先对x进行积分,再对y进行积分,最后对z进行积分。
2.曲线坐标系下的积分公式曲线坐标系下的积分公式是在常见的曲线坐标系(如极坐标系、柱坐标系、球坐标系等)下进行积分的重要工具。
在积分过程中,可以通过合适的坐标变换将被积函数转化为简化形式。
以极坐标系为例,假设R为极坐标系下的积分区域,f(r,θ)为被积函数,则二重积分可表示为:∬Rf(r,θ)dA=∫α∫βf(r,θ)rdr dθ其中α和β分别为极角的起始值和终止值。
3.罗必达法则罗必达法则是计算二重积分和三重积分时常用的方法,它解决了一些复杂的函数积分问题。
罗必达法则的核心思想是通过变量替换将原函数转化为简化形式。
以二重积分为例,假设R为积分区域,f(x,y)为被积函数,需要将其转化为极坐标系下的简化形式。
首先进行变量替换,令x=g(u,v),y=h(u,v),则利用链式法则,可以将f(x,y)转化为f(g(u,v),h(u,v))。
然后计算雅可比行列式,J,通过代入g(u,v)和h(u,v)的偏导数,可得,J,=gh/uv。
多重积分计算方法小结

多重积分计算方法小结多重积分是微积分中的一个重要概念,它是对具有多个自变量的函数进行求积的方法。
在实际问题中,往往需要对多个变量间的关系进行综合考虑,多重积分就提供了一个有效的工具。
多重积分可以分为二重积分和三重积分两种情况,分别对应于二维平面和三维空间中的函数求积。
在计算多重积分时,我们常常需要利用几何图形、物理问题以及正交曲线坐标系等概念和方法。
下面我将对多重积分的计算方法进行小结。
首先,我们来看二重积分的计算方法。
二重积分可以看作是对一个平面区域上的函数进行求积。
二重积分的计算可以分为直角坐标系和极坐标系两种情况。
在直角坐标系下,我们常常利用矩形分割和极限的思想来进行计算。
具体而言,我们将整个积分区域分成若干个小矩形,然后计算每个小矩形上函数值的积累,最后将所有小矩形的积累相加,得到整个区域上函数的积分值。
这种方法又称为“矩形分割法”或“Darboux和”方法。
在极坐标系下,我们常常利用极坐标的性质来简化计算。
具体而言,我们将整个积分区域表示成极坐标下的简单几何形状,如直线段、圆、扇形等,然后利用极坐标变换和对称性来计算积分值。
这种方法又称为“极坐标变换法”。
除了这两种基本方法外,还可以利用换元积分法、对偶积分法和奇偶性等方法来简化计算。
换元积分法是通过坐标变换将积分区域变换成更简单的形式,然后进行计算。
对偶积分法是通过对倒数进行积分变换,将二重积分转化为两个单变量积分,更便于计算。
奇偶性是指若被积函数在积分区域上的对称性,利用奇偶性可以简化计算过程。
接下来我们来看三重积分的计算方法。
三重积分可以看作是对一个空间区域上的函数进行求积。
三重积分的计算可以分为直角坐标系和柱面坐标系两种情况。
在直角坐标系下,我们常常利用分割和极限的思想来进行计算。
具体而言,我们将整个积分区域分成若干个小立方体,然后计算每个小立方体上函数值的积累,最后将所有小立方体的积累相加,得到整个区域上函数的积分值。
这种方法又称为“立方体分割法”。
多元函数分部积分法公式

多元函数分部积分法公式多元函数分部积分法公式是一种用于计算多元函数积分的方法。
通常情况下,多元函数分部积分公式应用于数学和物理学等领域,可以帮助数学家和物理学家准确计算一个多元函数的积分值。
本文将介绍多元函数分部积分法公式的定义和公式,以及如何应用多元函数分部积分法公式计算多元函数的积分值。
一、什么是多元函数分部积分法公式多元函数分部积分法公式又被称为分部积分法,它是一种常见的积分计算方法。
它可以帮助我们准确无误地计算多元函数积分的值。
多元函数分部积分公式可以表示为:∫abf(x)dx=∑nk=1aib(f),其中,a是多元函数f(x)的下限,b是多元函数f(x)的上限,n是多元函数f(x)的积分步数,i是多元函数f(x)积分时,分割点的位置,介于a到b之间。
二、如何计算多元函数分部积分法公式?1、选择积分步数n:积分步数n是积分时的重要准备,它指的是将区间[a,b]等分为n个小段,对每一段区间取固定点代入公式进行计算。
n越大积分精度越高,而且计算量越大。
因此,根据需要结合准确度与计算量灵活选择n值,以保证积分的准确性与可行性。
2、计算每一段小区间的积分值:当选择完积分步数n后,就可以计算每一段小区间的积分值了。
此时,先在每一段小区间中选择一个点,分别代入已定义的f(x)函数,计算每一段小区间的积分值。
三种常用的中心点是:左点、中点和右点,其积分值分别为:ai(fL)、ai(fM)和ai(fR)。
3、利用多元函数分部积分法公式计算总积分值:将n段小区间的积分值相加,便可以得到该区间上多元函数的总积分值,即总分值=∑nk=1aib(f)。
三、总结多元函数分部积分法公式是一种计算多元函数积分的方法,它可以帮助我们准确计算一个多元函数的积分值。
多元函数分部积分公式可以表示为:∫abf(x)dx=∑nk=1aib(f)。
为了计算一个多元函数的总积分值,需要根据积分步数n联合计算每一段小区间的积分值,然后把所有的小区间的积分值加起来便可以求出总积分值。
多元函数求积分

多元函数求积分多元函数求积分是微积分中的重要内容,它包括二重积分和三重积分两种形式。
在进行多元函数求积分时,我们需要根据具体问题选择合适的积分方法。
下面将介绍二重积分和三重积分的概念及计算方法。
一、二重积分二重积分是对二元函数在一个有界闭区域上的积分求解的方法。
具体而言,若有一个二元函数$f(x,y)$,我们要求解其在闭区域$D$上的积分,即$\iint_D f(x,y)dA$。
其中$dA$表示微元面积,$D$表示平面上的一个有界闭区域。
求解二重积分的方法有两种常见的形式:直角坐标下的二重积分和极坐标下的二重积分。
(1)直角坐标下的二重积分对于直角坐标下的二重积分,我们通常采用分割求和的方法。
将有界闭区域$D$分割成许多小面积的区域,然后对每个小区域内的函数值进行求和,最后取极限即可得到积分的结果。
具体操作时,我们可以选择将$D$划分成矩形形状的小区域,然后分别计算每个小矩形的面积$dA$,并求解$f(x,y)$在每个小矩形上的函数值$f(x_i,y_i)$,其中$(x_i,y_i)$表示小矩形的中心点。
最后的二重积分结果可以表示为$\iint_D f(x,y)dA =\lim_{{\Delta x \to 0} \atop {\Delta y \to 0}} \sum_{i,j} f(x_i,y_j)\Delta A$,其中$\Delta x$和$\Delta y$表示相邻小矩形的边长。
(2)极坐标下的二重积分对于具有旋转对称性的问题,极坐标下的二重积分更加便捷。
我们通过引入极坐标系来简化积分的计算。
首先,我们将直角坐标系转换为极坐标系,即$x =r\cos\theta$和$y = r\sin\theta$。
然后,我们需要计算雅可比行列式$J = \left|\begin{array}{cc}\frac{\partial x}{\partial r} &\frac{\partial y}{\partial r} \\ \frac{\partial x}{\partial \theta} &\frac{\partial y}{\partial \theta}\end{array}\right|$。
多元函数积分的计算方法与技巧

多元函数积分的计算方法与技巧1.多元函数的积分表示:多元函数的积分可以表示为定积分或不定积分。
定积分表示函数在一些区域内的积分值,而不定积分表示函数的原函数。
定积分可以通过区域划分进行求解,而不定积分则可以通过变量替换或部分积分等方法进行求解。
2.变量替换法:变量替换法是求解多元函数积分的常用方法之一、通过适当地选取新的变量,可以将原积分转化为一个更容易求解的形式。
常用的变量替换方法包括极坐标变换、柱面坐标变换、球面坐标变换等。
3.分部积分法:分部积分法是求解多元函数积分的常用方法之一、对于乘积形式的积分,可以将其转化为求解导函数的积分。
通过选择合适的函数进行分解,并利用分部积分公式,可以逐步简化积分的形式。
4.对称性与奇偶性:对称性与奇偶性是求解多元函数积分时常用的技巧。
如果被积函数具有其中一种对称性,可以利用对称性简化积分的计算。
另外,如果被积函数是奇函数或偶函数,则可以利用奇偶性质来简化积分计算。
5.积分次序的变换:对于多元函数的积分,积分次序可以任意交换。
通过变换积分次序,可以选择更合适的积分顺序,从而简化积分的计算。
6.积分区域的选择:对于定积分,选择合适的积分区域也可以简化积分计算。
可以通过变换坐标、利用对称性等方法选择一个更简单的区域进行积分。
除了上述方法与技巧之外,求解多元函数积分还需要熟练运用基本的积分公式和求导公式,灵活运用数学分析的知识。
另外,需要注意积分上下限的选择,确保积分区域与被积函数的定义域一致。
对于难题,可以尝试利用数值积分方法进行近似计算。
综合运用上述方法与技巧,可以更高效地求解多元函数积分,并应用于实际问题的求解。
多元函数的多重积分

多元函数的多重积分多元函数的多重积分是微积分的重要内容之一。
在一元函数的积分中,我们主要关注的是对于一维区间上的函数的积分,而多元函数的多重积分则是涉及到多维空间中的函数积分。
多元函数的多重积分包括二重积分和三重积分,它们在数学理论和实际问题的求解中都扮演着重要的角色。
一、二重积分1. 定义对于定义在有界闭区域D上的连续函数f(x,y),我们可以将D划分为若干小区域,每个小区域选取一点(xi,yi)作为代表点,计算出f(xi,yi)的值,并求和得到的极限,这个极限就是二重积分。
记作∬D f(x,y) dxdy。
2. 计算方法二重积分的计算可以通过对x或y进行分步计算,也可以通过坐标变换来简化计算。
其中,极坐标变换、直角坐标到直角坐标变换、直角坐标到柱坐标变换等是常用的坐标变换方法。
二、三重积分1. 定义对于定义在有界闭区域E上的连续函数f(x,y,z),我们可以将E划分为若干小区域,每个小区域选取一点(xi,yi,zi)作为代表点,计算出f(xi,yi,zi)的值,并求和得到的极限,这个极限就是三重积分。
记作∭E f(x,y,z) dxdydz。
2. 计算方法与二重积分类似,三重积分的计算可以通过分步计算或者坐标变换来进行。
3. 应用多重积分的应用非常广泛,包括物理学、工程学、经济学等各个领域。
例如,在物理学中,我们可以利用三重积分来计算物体的质量、静电荷分布、电场强度等;在经济学中,我们可以利用二重积分来计算收入分配的不平等程度等。
综上所述,多元函数的多重积分是数学中重要的一部分,它的理论和应用价值不可忽视。
通过对多重积分的学习和掌握,我们可以更深入地理解函数在多维空间中的性质和行为,为实际问题的求解提供有效的数学工具。
多元函数求积分

多元函数求积分积分是微积分的重要概念之一,用于求解函数的面积、体积、质量、重心等许多物理和几何问题。
在计算积分时,我们常常会遇到多元函数的积分问题,即在多维空间中对多个变量的函数进行积分。
本文将从基本概念、计算方法和相关参考内容三个方面介绍多元函数的积分。
一、基本概念多元函数的积分是在多维空间中对函数的求和过程,可以用于计算函数在某个区域内的总量。
对于二元函数而言,积分可以表示为∮f(x,y)dA,其中∮表示积分,f(x,y)为要积分的函数,dA表示面积元素。
对于三元函数而言,积分可以表示为∭f(x,y,z)dV,其中∭表示积分,f(x,y,z)为要积分的函数,dV表示体积元素。
多元函数的积分可以从二维空间扩展到任意多维空间。
二、计算方法1.直接计算对于简单的多元函数,可以直接计算积分。
首先需要确定积分的边界,即确定积分的区域。
然后按照积分的定义进行计算,将积分区域划分为许多小的面积元素或体积元素,并对每个元素进行积分。
最后将所有小元素的积分结果相加,即得到整个区域内函数的积分结果。
2.变量替换对于复杂的多元函数,可以通过变量替换的方法简化积分计算。
通过合适的变量替换可以将原函数化简为更简单的形式,从而方便求解积分。
通过变量替换,可以将积分区域变换到更加简单的坐标系中,使得计算变得更加容易。
3.极坐标、球坐标、柱坐标等对于涉及到圆、球、柱等几何形状的函数,可以使用极坐标、球坐标、柱坐标等坐标系进行积分计算。
这些坐标系有助于简化函数表达式和积分区域,从而提高计算效率。
三、相关参考内容1.《高等数学》(同济大学数学系编著):该教材是国内高等院校普遍采用的教材,对多元函数的积分有详细的介绍,并提供了许多例题和习题供读者练习。
2.《数学分析教程》(李修文编著):该教材对多元函数的积分理论和计算方法进行了深入的讲解,包括直接计算、变量替换和不同坐标系下的积分计算方法。
3.《多元函数积分学》(孔祥兴编著):该教材从多元函数积分的基本概念入手,详细介绍了多元函数的积分理论和计算方法,并提供了大量例题和习题供读者练习。
高等数学中的多元函数的积分

高等数学中的多元函数的积分高等数学中的多元函数积分高等数学是一门抽象的学科,它以符号理论和逻辑推理为基础,利用数学结构和算法解决复杂的问题。
在高等数学中,多元函数积分是一个非常重要的概念。
多元函数积分是现代数学的基石之一,它与实际问题密切相关,具有广泛的应用范围。
1. 多元函数积分的概念多元函数积分是一种数学工具,它用于计算多元函数在闭合区域上的积分值。
多元函数是指有多个自变量的函数,积分是对多元函数在一个闭合区域上的求和操作。
多元函数积分的概念最早是由黎曼在19世纪中期提出的,现在已经成为现代数学的一部分。
2. 多元函数积分的性质多元函数积分具有以下性质:(1)线性性:若f和g是定义在闭合区域U上的两个多元函数,a和b是常数,则有∫[af(x,y)+bg(x,y)]dxdy=a∫f(x,y)dxdy+b∫g(x,y)dxdy。
(2)可加性:若f是定义在闭合区域U上的多元函数,在它的范围内用一个曲面D把闭合区域分成两个部分U1和U2,则有∫f(x,y)dxdy=∫f(x,y)dxdy+∫f(x,y)dxdy。
3. 多元函数积分的计算方法多元函数积分的计算方法有以下几种:(1)直接计算:即按照定义式进行积分。
这种方法适合于计算简单的多元函数积分。
(2)使用改变变量法:改变变量法是通过变量代换的方式,将多元函数转化为标准形式,并重新计算积分。
这种方法适合于计算复杂的多元函数积分。
(3)使用重积分法:重积分法是把多元函数积分表示为两个一元函数积分的积分形式,再进行计算。
这种方法适合于计算连续多元函数积分。
4. 多元函数积分的应用多元函数积分是解决实际问题的有力工具,它在物理、工程、金融等领域都有广泛的应用。
(1)物理领域:例如,通过多元函数积分可以计算物体的体积、质心、转动惯量等参数。
(2)工程领域:例如,通过多元函数积分可以计算电场、磁场、热量传递等参数。
(3)金融领域:例如,通过多元函数积分可以计算期权和利率等金融指标。
多元函数积分的计算方法技巧
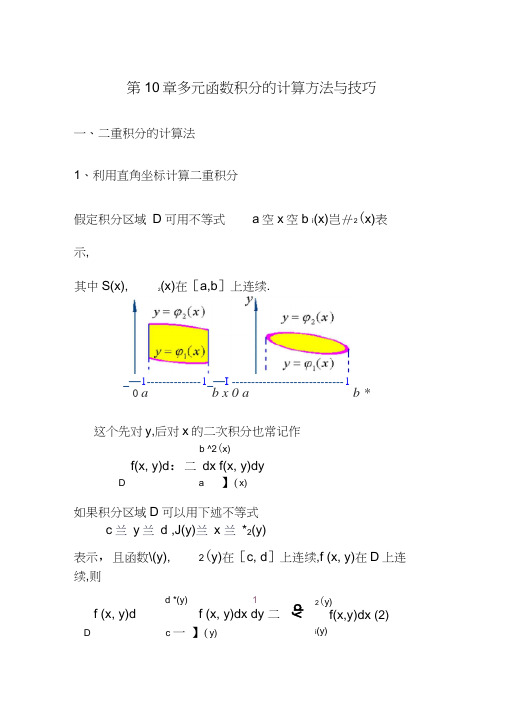
第10章多元函数积分的计算方法与技巧一、二重积分的计算法 1、利用直角坐标计算二重积分假定积分区域 D 可用不等式 a 空x 空b i (x)岂卄 2(x)表示, _—1 -------------- 1_—I ----------------------------- 1 0 a b x 0 a b *这个先对y,后对x 的二次积分也常记作b ^2(x)f(x, y)d :二 dx f(x, y)dy D a 】(x)如果积分区域D 可以用下述不等式c 兰 y 兰d ,J(y)兰 x 兰 *2(y)表示,且函数\(y), 2(y)在[c, d ]上连续,f (x, y)在D 上连续,则d *(y)1f (x, y)df (x, y)dx dy 二Dc 一 】(y)dydi2(y)f(x,y)dx (2)i (y)其中S(x),2(x)在[a,b ]上连续.2显然,(2)式是先对x ,后对y 的二次积分. 积分限的确定几何法.画出积分区域D 的图形(假设的图形如下)在[a, b ]上任取一点x ,过x 作平行于y 轴的直线,该直线穿过区域D ,与区域D 的边界有两个交点(x, i (x ))与(x, 2(x )), 这里的i (x ). 2(x )就是将x ,看作常数而对y 积分时的下限和 上限;又因x 是在区间[a,b ]上任意取的,所以再将x 看作变 量而对x 积分时,积分的下限为a 、上限为b .例1计算D 如,其中D 是由抛物线…及直线…2 所围成的区域. 解:Z)]: 0<x £)2:l<x<4,x-2<y<A/^ 為yda= fj 砂c/b 十fj 秽亦Di\ r>214 V?=\dx \ xydy dx \xycfy 0 — l 工—2V74C A = J- JC -(^-2) 1 2Ld x -勺-Jx4r =0+ f —yx-245dx~~82)2D: _ 1 乞 y 乞 2, y x -2 y 2xyd = dy xydx =D-1 y 21 22 y(y 2)2-2 -i2. 利用极坐标计算二重积分 1、rdrd-就是极坐标中的面积元素2、极坐标系中的二重积分,可以化归为二次积分来计算.:_ 71 _ -£ ) - r - 2⑴其中函数W,二⑴在V / ]上连续.pY)则 f(rcos ,rsin)rdrd 二 d f(rcos,rsin )rdr D:1C)【例5】计算JJt?7 —F 丛创』其中D:x 2 -h y 2 <a 2. D解:加? ms2 2 2\\^~x ~y dxdy = |[e~r -rdrdO D 2 凭 ct 22?z=\ d&\ e~rrdr = J0 0 0 2?r 1 J )朋=兀Q Y0 2注:本题不能利用直角坐标下二重积分计算法来求其精确 值.y 22「1 2 严 d厉X y」2dy-1 yy 5丽458<X ' rcos y rsin dxdy rdrd 匚〉JJ f(rcos,rsin)rdrd0<r<aDT 1尸 ---- e 21住dG 0 < < 2^-3、使用极坐标变换计算二重积分的原则(1)、积分区域的边界曲线易于用极坐标方程表示 (含圆弧, 直线段);⑵、被积函数表示式用极坐标变量表示较简单(含 (x 2 y 2r ,,为实数).解此积分区域为D : 0 乞 x 乞 a , 一 x 乞 y 乞 一 a 一 a 2 一 x 2 该区域在极坐标下的表示形式为D:丁小0 ,°汀」2站32二、三重积分的计算 1、积分区域"可表示成a ^ xb , %(x ) ' y y 2(x ) , ^(x,y )乞 z' Z 2(x, y )by 2(x ) Z 2(x,y ) 贝y !!! f (x, y, z )dv = dx dy f (x, y, z )dzay'x )N (x,y )这就是三重积分的计算公式,它将三重积分化成先对积a -a+\ a 2 _x 2例6计算M dx-xdyx 2 y 2 4a 2 -(x 2 y 2)(a 0)rdrd"D r \ 4a 2 - r 20 -2a si nvd ,dr0 fJIarcsin n -2as in日 r2a2JI2- r 248分变量z ,次对y,最后对x 的三次积分 例1计算…xyzdxdydz ,其中门为球面x^ y^ z^ 1及三坐QJ标面所围成的位于第一卦限的立体 . 解 “在 xoy 面上的投影区域为2 2D xy : x y 「,x 一 0, y — 0确定另一积分变量的变化范围0 岂 z 岂 1 一 X 2 — y 2选择一种次序,化三重积分为三次积分111xyzd xdydzQ1心2c —y 2dx dy xyzdz0 0 01心21dx — xy (10 0 2 12 1 13 13 dx (—xy x y xy )dy0 2 2 2十—1 32 1 4-X y - - xy4 8 06 4 28 6 42x 2 - y 2)dy 0_4xydxI 2 I 3X (1 - X ) X (1 - X ) 11 -0 IL 4n?1 ■J J- _____ 0 I 4 21 sin t cos41 2 1-—x(1 -82 2x) dx-sin t cos 21 - — sin 31 cos 21 -二sin t cos 41 cos tdt 421 dt sin 31 cos 3tdt0 4 2 2 1 4 2兀刁15—sin t cos tdt 082、利用柱面坐标计算三重积分x = r cos 点M的直角坐标与柱面坐标之间有关系式* y = rsinez= z体积为dv 二rdrd ^dz这便是柱面坐标系下的体积元素,并注意到(1)式有I, f (x, y, z)dv 111 f (r cos^ , r sin ^, z)rdrd ^dz3、利用球坐标计算三重积分直角坐标与球面坐标间的关系为x = r sin cos71Iy = r sin sin 二、z = r cos®dv= r2s in ^drd^ d9 这就是球面坐标系下的体积元素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二类曲面积分的向量值函数定义:设 Σ 是定向的光滑曲面,曲面上每一点指定了单位法向量 n=(cosα, cosβ, cosγ),
若 f ( x,y,z ) =P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k 是 定 义 在 Σ 上 的 向 量 值 函 数 , 则 称 ∬Σ f ∙ ndS = ∬Σ [P(x, y, z)cosα +
L
L
L
= 球面 Ω {(x, y, z) | x= 2 + y2 + z2 R2}上,
∫∫ xdydz + ydzdx + xdydz = 4π R3 Σ
∫∫ x2dydz= ∫∫ y2dzdx= ∫∫ z2dxdy= ∫∫ x2dydz + y2dzdx + z2dxdy=
Σ
Σ
Σ
Σ
第一类曲线积分
(cosα,
cosβ,
cosγ)=±
1 √EG−F2
(∂(y,z)
∂(u,v)
,
∂(z,x) ∂(u,v)
,
∂∂((ux,,yv))),dS=√EG
−
F2dudv,则
若向量值函数 f 在 L 上连续,则
� Pdx + Qdy + Rdz = � [P(x, y, z)cosα + Q(x, y, z)cosβ + R(x, y, z)cosγ]ds
例如,光滑曲面Σ 的方程为z=z(x,y), (x,y)∈ D,其中 D 为平面区域。那么
n
=
(cosα,
cosβ,
cosγ)
=
1 ±�1+zx2 (x,y)+zy2 (x,y)
(
−
zx,
−zy,
1),如果取正号,则cosγ
>
0,这时法向量与
z
轴成锐角,意味着
取定了曲面的上侧,反之则取下侧。
dydz dzdx dxdy
2、Gauss 公式计算第二类曲面积分
设空间闭区域 Ω 是由分片光滑的闭曲面Σ所围成,函数 P、Q、R 在 Ω 上具有一阶连续偏导数,则有
∂P ∂Q ∂Q
�
Ω
�∂x
+
∂y
+
∂z �
dxdydz
=
�
Σ
Pdydz + Qdzdx + Rdxdy = �
Σ
[Pcosα + Qcosβ + Rcosγ] dS
算
b
方
� Pdx + Qdy = � [P(x, y(x)) + Q(x, y(x))y′(x)]dx
法
L
a
2、Green 公式计算平面第二类曲线积分
设 D 为平面上由光滑或分片光滑的简单封闭曲线 L 所围的单连通区域,若 P(x,y)、Q(x,y)在 D 上具有连续偏导数,则
∮L
Pdx
+
Qdy
=
∬D
Ω上的连续函数,则∭Ω f(x, y, z)dxdydz = ∫ef dz ∬Ωz f(x, y, z)dxdy。
∬T(D) f(x, y)dxdy = ∬D
f�x(u,
v),
y(u,
v)�|
∂(x,y) ∂(u,v)
|dudv。
2、三重积分的变量代换:
若
f(x,y,z)
是
T(Ω)
上
的
连
续
函
数
,
则
特别,极坐标变换:x=rcosθ,y=rsinθ,0≤ θ ≤ 2π,0≤ r < +∞的 Jacobi 行列式 J=∂(x,y) = r。
2π
dθ
R= r 3dr
π R4
一D
0
0
2
些
计 算
= 椭圆域 Ω
{(x,
y)
|
x2 a2
+
y2 b2
+
≤ 1}
结
∫∫ 论 (x2 + y2 )dσ = abπ (a2 + b2 )
D
4
椭= 球形区域 Ω
{(x,
y, z) |
x2 a2
+
y2 b2
+
z2 c2
≤ 1}
∫∫∫ ∫ ∫ ∫ = ( x2 + y2 + z2 )dv abc = 2π dθ π sinϕdϕ 1 r4dr 4π abc
∫Γ
Pdx
+
Qdy
+
Rdz
=∫∫ Σ
∂R ∂y
−
∂Q ∂z
dydz
+
∂P ∂z
−
∂R ∂x
dzdx
+
∂Q ∂x
−
∂P ∂y
dxdy
=∫∫ Σ
∂ ∂x
∂ ∂y
∂ ∂z
PQ R
cosα
由第一类曲线积分表达为∫Γ Pdx + Qdy + Rdz = ∫Σ∫ ∂∂x
第一类曲面积分
第一类曲线积分通常的计算方法是通过曲线在不同形式的 第一类曲面积分通常的计算方法是将其投影到某个坐标平面上计算相应的二重积分。
一侧的曲面称为定向曲面。
利用 Green 公式计算平面有界区域的面积 S=∮L xdy − ydx
3、Stokes 公式计算空间第二类曲线积分 设 Γ 为分段光滑的空间有向闭曲线,Σ 是以Γ为边界的分片光滑的有向曲面,Γ 的正向与 Σ 的侧符合右手法则,函数 P(x, y, z)、Q(x, y, z)、R(x, y, z)在曲面 Σ(连同边界 Γ)上具有一阶连续偏导数,则有
2π
dθ
π sin ϕdϕ = R r4dr
4π R5
Ω
Ω
0
0
Ω
0
15
对任意由坐标平面分成的半球面有
∫∫∫ ∫∫∫ ∫∫∫ 二重积分
= x2dv = y2dv = z2dv 2π R5
在圆= 域 D {(x, y) | x2 + y2 ≤ R2}(R > 0) 上, Ω
Ω
Ω
15
∫∫ ∫ ∫ (x2 + y= 2 )dσ
L
L
b
= � [P(x(t), y(t), z(t))x′(t) + Q(x(t), y(t), z(t))y′(t) + R(x(t), y(t), z(t))z′(t)]dt
a
二维情形:L:x=x(t),y=y(t), t:a→b
b
� Pdx + Qdy = � [P(x(t), y(t))x′(t) + Q(x(t), y(t))y′(t)]dt
,
J=∂(x,y,z)
∂(r,φ,θ)
=
abcr2sinφ
对于旋转体,或由 z=e 和 z=f 截取的柱面,可考虑用先二后一法,也可考虑(广义)柱坐标变换。
椭球体x2
a2
+
y2 b2
+
zc22≤1可做广义球坐标代换,变换后区域为
{(r, φ, θ)|0 ≤ r ≤ 1,0 ≤ φ ≤ π,0 ≤ θ ≤ 2π}
∂(r,θ,z)
z = z,∞ < ������ < +∞
计
算 方
x = arcosθ, 0 ≤ θ ≤ 2π
(2)、广义柱坐标变换�y = brsinθ, 0 ≤ r < +∞
, J=∂(x,y,z) = abr
∂(r,θ,z)
z = z,∞ < ������ < +∞
法
x = rsinφcosθ, 0 ≤ θ ≤ 2π
(∂Q
∂x
−
∂P)dxdy
∂y
∬Σ Pdydz + Qdzdx + Rdxdy = ∬Σ [Pcosα + Qcosβ + Rcosγ] dS =
±
∬D
[P(x(u,
v,
),
y(u,
v),
z(u,
v))
∂(y,z) ∂(u,v)
+
Q(x(u,
v,
),
y(u,
v),
z(u,
v))
∂(z,x) ∂(u,v)
Q(x, y, z)cosβ + R(x, y, z)cosγ] dS为 f 在 Σ 上的第二类曲面积分。 1、 化为二重积分计算 (1)、曲面 Σ 的方程由参数方程给出:Σ:x=x(u,v),y=y(u,v) ,z=z(u,v), (u,v)∈D,其中 D 为 uv 平面上有分段光滑边界的 有界区域,P、Q、R 在 Σ 上为连续函数。
三重积分:
球= 形区域 Ω {(x, y, z) | x2 + y2 + z2 ≤ R2} 上,
∫∫∫ ∫ ∫ ∫ = (x2 + y2 + z2 )dv 2π d= θ π sinϕdϕ R r4dr 4π R5
Ω
0
0
0
5
∫∫∫ ∫∫∫ ∫∫∫ ∫ ∫ ∫ = x2dv
= y2dv = z2dv
函数,则称∫L f ∙ τds = ∫L [P(x, y, z)cosα + Q(x, y, z)cosβ + R(x, y, z)cosγ]ds为 f 在 L 上的第二类曲线积分。 1、化为定积分计算 (1)、曲线方程由参数方程给出:L:x=x(t),y=y(t),z=z(t),t:a→b
