结构方程模型入门
★结构方程模型要点

★结构方程模型要点一、结构方程模型的模型构成1、变量观测变量:能够观测到的变量(路径图中以长方形表示)潜在变量:难以直接观测到的抽象概念,由观测变量推估出来的变量(路径图中以椭圆形表示)内生变量:模型总会受到任何一个其他变量影响的变量(因变量;路径图会受外生变量:模型中不受任何其他变量影响但影响其他变量的变量(自变量;路中介变量:当内生变量同时做因变量和自变量时,表示该变量不仅被其他变量影响,还可能对其他变量产生影响。
内生潜在变量:潜变量作为内生变量内生观测变量:内生潜在变量的观测变量外生潜在变量:潜变量作为外生变量外生观测变量:外生潜在变量的观测变量中介潜变量:潜变量作为中介变量中介观测变量:中介潜在变量的观测变量2、参数(“未知”和“估计”)潜在变量自身:总体的平均数或方差变量之间关系:因素载荷,路径系数,协方差参数类型:自由参数、固定参数自由参数:参数大小必须通过统计程序加以估计固定参数:模型拟合过程中无须估计(1)为潜在变量设定的测量尺度①将潜在变量下的各观测变量的残差项方差设置为1②将潜在变量下的各观测变量的因子负荷固定为1(2)为提高模型识别度人为设定限定参数:多样本间比较(半自由参数)3、路径图(1)含义:路径分析的最有用的一个工具,用图形形式表示变量之间的各种线性关系,包括直接的和间接的关系。
(2)常用记号:①矩形框表示观测变量②圆或椭圆表示潜在变量③小的圆或椭圆,或无任何框,表示方程或测量的误差单向箭头指向指标或观测变量,表示测量误差单向箭头指向因子或潜在变量,表示内生变量未能被外生潜在变量解释的部分,是方程的误差④单向箭头连接的两个变量表示假定有因果关系,箭头由原因(外生)变量指向结果(内生)变量⑤两个变量之间连线的两端都有箭头,表示它们之间互为因果⑥弧形双箭头表示假定两个变量之间没有结构关系,但有相关关系⑦变量之间没有任何连接线,表示假定它们之间没有直接联系(3)路径系数含义:路径分析模型的回归系数,用来衡量变量之间影响程度或变量的效应大小(标准化系数、非标准化系数)类型:①反映外生变量影响内生变量的路径系数②反映内生变量影响内生变量的路径系数路径系数的下标:第一部分所指向的结果变量第二部分表示原因变量(4)效应分解①直接效应:原因变量(外生或内生变量)对结果变量(内生变量)的直接影响,大小等于原因变量到结果变量的路径系数②间接效应:原因变量通过一个或多个中介变量对结果变量所产生的影响,大小为所有从原因变量出发,通过所有中介变量结束于结果变量的路径系数乘积③总效应:原因变量对结果变量的效应总和总效应=直接效应+间接效应4、矩阵方程式(1)和(2)是测量模型方程,(3)是结构模型方程 测量模型:反映潜在变量和观测变量之间的关系 结构模型:反映潜在变量之间因果关系 5x x ξδ=∧+ (1)y y ηε=∧+ (2) B ηηξζ=+Γ+ (3)三、模型修正1、参考标准模型所得结果是适当的;所得模型的实际意义、模型变量间的实际意义和所得参数与实际假设的关系是合理的;参考多个不同的整体拟合指数;2、修正原则①省俭原则两个模型拟合度差别不大的情况下,应取两个模型中较简单的模型;拟合度差别很大,应采取拟合更好的模型,暂不考虑模型的简洁性;最后采用的模型应是用较少参数但符合实际意义,且能较好拟合数据的模型。
Mplus结构方程模型步骤入门

1数据格式转换由于Mplus只能翻开ASCII格式的文件〔.dat 和-txt文件〕,所以常规的SPSS数据库的数据不能被读取,所以数据分析之前先要将sav格式另存为dat格式.另存为选项里有两类dat 格式,一般可选用“以制表符分隔",当数据量较大时,可选“固定ASCII格式〞.这两类并没有明显特异的使用条件.选择某一种dat格式后,〞将变量名写入表格〞这一项不要勾选.然后保存.一般将该数据文件和mplus语句文件放在一个文件夹.2翻开mplus程序,建立新文件,即点击“new〞.当然,新翻开Mplus程序也会默认这个界面.3编辑命令.这是Mplus分析数据最核心的步骤3.1首先我们可以给该分析起个名字〔该步骤可有可无〕,例如:TITLE: example3.2然后说明我们引用的数据库来自于哪里,也就是刚刚那个DAT文件.命令为:DATA: FILE IS C:\Users\dell\Desktop\MPLUS 结构方程模型教程'数据库.dat;这里面需要注意的是:DATA: FILE IS 〔或者DATA: FILE=〕是固定句式,是必要的.之后“C:\Users\dell\Desktop\MPLUS结构方程模型教程'数据库.dat〞这是DAT文件的保存路径.一般情况下,如果mplus语句文件和dat文件在同一个文件夹中,只需要DATA: FILE IS数据库.dat;但实际上很多情况下,两者即使在同一个文件中,也很可能读不出来,所以必要的话,可将该DAT文件的保存路径写全,这样肯定是没错的.另外,一个命令结束后,必须必须加上“;〞即英文格式下的分号〔除外TITLE〕.3.3写出数据库中所有的变量名称以及本次分析需要的变量名称.这需要根据spss数据库中变量名称顺序来写.VARIABLE: NAMES ARE a1 a2 a3 a4 a5 a6 a7 a8 a9 b1 b2 b3 b4 c1 c2 c3 c4;USEVARIABLES ARES ARE a1 a2 a3 a4 a5 a6 a7 a8 a9 b1 b2 b3 b4 c1 c2 c3 c4;当然这是最根本繁琐的写法,可以直接写为:VARIABLE: NAMES ARE a1-a9 b1-b4 c1-c4;USEVARIABLES ARES ARE a1-a9 b1-b4 c1-c4;不同变量间有空格.由于我们本次分析需要纳入该数据库所有变量,所以上下两行变量是一样的,否那么需要哪些变量,在USEVARIABLES里面纳入哪些变量.3.4分析方法由于MPLUS中针对连续型变量的结构方程模型的默认分析方法是最小二乘法即ML,所以如果使用的方法是这个,那么分析方法语句可以不写,当然也可以写,即ANALYSIS: ESTIMATOR = ML;如果采用其他方法,需要写出来,例如ANALYSIS: ESTIMATOR = MLR;或者ANALYSIS: ESTIMATOR = WLSMV;另外ANALYSIS中还有TYPE语句,MODEL语句,INFORMATION语句,如果没有特殊要求, 我们就根据Mplus的默认方式分析就可,故不用写出来.如果分析采用其他方式,那么需要写出来.命令举例:ANALYSIS: ESTIMATOR = ML; TYPE = GENERAL;MODEL=NOMEANSTRUCTURE; INFORMATION=EXPECTED;3.5模型语句比方我们预期的结构方程模型是这样的:首先我们要将各个观测变量使用“BY〞合并得出三个潜变量,也就是我们研究的自变量y2, 中介变量y1,和因变量y3.语句为:MODEL: y1 BY a1-a9;y2 BY b1-b4;y3 BY c1-c4;然后使用“ON〞来表示各潜变量之间的回归关系,即:y3 ON y1 y2;y1 ON y2;ON前面的是结局变量,后面的是预测变量.所以模型语句合并起来就是:MODEL: y1 BY a1-a9;y2 BY b1-b4;y3 BY c1-c4;y3 ON y1 y2;y1 ON y2;3.6最后一步是输出语句,如果没有特殊要求,我们需要的结构Mplus的默认程序都会呈现. 如果有特殊要求也可以写出来,例如:OUTPUT: SAMPSTAT TECH1 TECH4 STDYX MOD;所以将所有语句写出来就是:TITLE: exampleDATA: FILE IS C:\Users\dell\Desktop\MPLUS 结构方程模型教程'数据库.dat; VARIABLE: NAMES ARE a1 a2 a3 a4 a5 a6 a7 a8 a9 b1 b2 b3 b4 c1 c2 c3 c4; USEVARIABLES ARES ARE a1 a2 a3 a4 a5 a6 a7 a8 a9 b1 b2 b3 b4 c1 c2 c3 c4; MODEL: y1 BY a1-a9;y2 BY b1-b4;y3 BY c1-c4;y3 ON y1 y2;y1 ON y2;如图Mplus - [MptextlJ 药File Edit Wst Mplus Plot Diagr^rrii Windw Help口0 口;制剧善闻|凹坦回|巴 |如国园|小〈国圄| 7-TITLE, exanpleHATA- FILE IS C:培构方程植用强程;俄据反"共:UAKIAiLE: MANE3 IRE a]湛a3 a4 a5 a7 曲酬bL b2 b3 bd. cl c2 c3 3;VSEVAKIAflLES ARES AEE ZL!a2 a4 a5 a7 sB bl bE b3 b4 cl C2凸3;IKiBEL- yl B¥支BY b1-b4;y3 SY C]-E4;y:3 Off yl y2:yl ON y2 t然后点击RUN按钮它会提示你保存该语句保存完成后,结果就出来了.eK :urLpleSU1WAEY OF WITSIS Ni-unber of g roupsNumber of observationsNumber of defiendeirt. variables Number of independent. variablesNunb e r of cont iiiuiiiUE 1 1 at. ent var i ab 19 sEstiiTLatorInfurnation matrixMaximum number of iterations Convergence criterionMazimiiiTL iiLuribe r of st-eepest- descent it er at-ionsInput data file (s)C: XUsers'\del 1\Desktop\,MPLUS 结构方程模型救程 ’\数据库,datInput- data format- FREETHE MODEL ESTIMTION TEMINATED NOFJ1U1LLY(MODEL FIT INFOBJ I UTIONNuitber of Free Parameters5d52 4A B ContimiLiUEAl A2 门Ad A7 A8 A9 El E4 ClC2C3ontmuous latent v ariablesY1Y2叮bserved dependent variables如果想看我们得到的结构方程图的话,点击菜单栏的Diagram ,选择View diagram■ 1 File Edit View Mplus Plot Diagram Window HelpView diagramAlt+ DOpen Di a g rammer这需要JAVA 工具.如果电脑没有的话,会提示你安装安装完,既可以观看图示.1 2967 _uNL OBSERVEDinrn| 0.500D-C420RU Edit Mpkit Vim Diagram Mridow Help4"< 岭-«| U k、i DOQ(OQD:I】叫叫一f j112 5T4($54)\ /M3以y—I47阿/ '咏m)一>3厂1__14?57<P25)/X d 卜,5»(1W>1 174(,3101 0X( DOD:. |IJ C L—27«(ZTO) -、/一、/」gpl?11人… /人工嬴(二?\<nx. LIT、Z *—:3W(3J)I<310( 9«(0«).3 814c必“】为< »1)7 157( l»>2J73( 2]Q>3 皿力啦MRUaP3WC训387(加]319( CU J 157020。
《结构方程模型》课件

SEM 发表的期刊论文有比较优势吗? (Babin, Hair, Boles, 2008)
• 1. 不用SEM 的PAPERS 是否比较容易被拒绝? • 2. 使用SEM 的PAPERS 是否评价比较高? • 3. 使用SEM 是否对reviewers 较有影响力? • 4. 模型适配度好坏是否会影响reviewers评价? • 5. 美国人使用SEM 是否比其它国家的学者多? • 6. 美国人用SEM投稿是否比其它国家的人有优
势?
SEM 常用的名词
• 参数(parameter): – 又称为母数,带有「 未知 」与「 估计」的特
质。如没有特別说明,一般指的是自由参数。 • 自由参数(free parameter): – 在Amos所画的每一条线均是一個参数,除设
为固定参数者外; – 自由估計参数愈多,自由度(df) 愈小。 • 固定参数(fix parameter): – Amos 图上被设定为0 或1或任何数字的线,均
图形
功能说明
图形
功能说明
变量之间的属性拖拽
放大镜检视
维持对称性 放大选取区域 放大路径图
贝氏估计 多群组分析 列印路径图
缩小路径图 路径图整页显示在屏幕上 调整路径图大小符合书面
上一步 下一步 模式搜索
绘制四个观察变量 建立因果关系 调整箭头位置
利用复制功能确保大小一致 内生变量增加残差 调整变量位置
1. SEM 能做些什么?
Structural Equation Modeling(SEM) 是近期成长快速的 统计技术(Herhberger, 2013)
• 愈来愈多的SEM 文章发表在心理学、管理学与社会学期 刊上
• SEM 已成为心理学、管理学与社会学学者最常用的统计 技术
结构方程模型

2. 应用结构方程模型的注意事项
• (1)通径图中 ,内源变量与外源变量间的 关系都是线性的。实际工作中的非线性偏 离被认为是可以忽略的 ,若有强的非线性关 系则应当设法对变量作变换 ,以便可以用线 性作近似;
• (2)结构方程不支持小样本。一般要求样 本容量在 200 以上 ,或是要估计的参数数目 的 5~20 倍;
• proc calis语句是必须的,且此语句还可添 加一些选项,这些选项主要包括:
• (1)数据集选项,如DATA= 使用的数据集 的名字;INRAM= 使用已存在的并被分析 过的模型;OUTRAM= 将模型的说明存入 输出数据集,备以后INRAM调用。
• (2)数据处理选项,如EDF= 在没有使用 原始数据且未指定样本数N时为模型指定自 由度;NOBS= 指定样本数N。
模型修正
• 模型的修正主要包括: • (1) 依据理论或有关假设 ,提出一个或数个合理的
先验模型; • (2) 检查潜变量与指标间的关系 ,建立测量方程模
型; • (3) 若模型含多个因子 ,可以循序渐进地 ,每次只检
验含两个因子的模型 ,确立测量模型部分合理后 , 最后再将所有因子合并成预设的先验模型 ,作总体 检验; • (4) 对每一模型 ,检查标准误、标准化残差、修正 指数、参数期望改变值、χ 2 及各种拟合指数 ,据此 修改模型。
一、结构方程模型简介 1、什么是结构方程模型 2、为什么使用结构方程模型 3、结构方程模型的结构 4、结构方程模型的优点 5、结构方程模型中的变量 6、结构方程模型常用图标
1、什么是结构方程模型 结构方程模型( Structural Equation Model)是基于变量
的协方差矩阵来分析变量之间关系的一种统计方法。所以,有 时候也叫协方差结构分析。
结构方程模型

⑥ 重视多重统计指标的运 用。
7.SEM的样本规模 ① 资料符合常态、无遗漏值
及例外值(Bentler & Chou, 1987)下,样本比例最小为 估计参数的5倍、10倍则 更为适当。 ② 当原始资料违反常态性假 设时,样本比例应提升为 估计参数的15倍。 ③ 以最大似然法(Maximum
02 基本
原1.理模型构建——变量
① 观测变量:能够观测到的变量(路径图中以长方形表示)。 ② 潜在变量:难以直接观测到的抽象概念,由测量变量推估出
来的变量(路径图中以椭圆形表示)。 ③ 内生变量:模型总会受到任何一个其他变量影响的变量(因
变量;路径图会受到任何一个其他变量以单箭头指涉的变量。 ④ 外生变量:模型中不受任何其他变量影响但影响其他变量的
代理:Multivariate Software
④Mplus
设计:BengtMuthén和Linda
01 概念
介绍
6.SEM的技术特性
① 具有理论先验性。
② 同时处理因素的测量关 系和因素之间的结构关 系。
③ 以协方差矩阵的运用为 核心。
④ 适用于大样本分析(样 本数<100,分析不稳定; 一般要>200)。
② 圆或椭圆表示潜在变量;
③ 小的圆或椭圆,或无任何框,表示方程或测量的误差:
单向箭头指向指标或观测变量,表示测量误差;
单向箭头指向因子或潜在变量,表示内生变量未能被外生
潜在变量解释的部分,是方程的误差;
④ 单向箭头连接的两个变量表示假定有因果关系,箭头由原
02 基本
原1.理模型构建——路径图
(2)路径系数 路径分析模型的回归系数,用来衡量变量之间影响程度或变量 的效应大小(标准化系数、非标准化系数)。 分为反映外生变量影响内生变量的路径系数和反映内生变量影 响内生变量的路径系数 路径系数的下标:第一部分所指向的结果变量,第二部分表示 原因变量。
结构方程模型 ppt课件

CONTENTS
01 概念介绍 02 基本原理
03 案例分析
04 实际操作
ppt课件
2
01 概念介绍
1.基本概念
结构方程模型(Structural Equation Modeling, SEM)是一种验证性多元统计分析技术, 是应用线性方程表示观测变量与潜变量之间,以及潜变量之间关系的一种多元统计方法, 其实质是一种广义的一般线性模型。
ppt课件
19
02 基本原理
3.模型拟合——主要拟合度指标
(3)整体模型拟合度
a) χ2卡方拟合指数 检验选定的模型协方差矩阵与观察数据协方差矩阵相匹配的假设。原假设是模型协方差阵等 于样本协方差阵。如果模型拟合的好,卡方值应该不显著。在这种情况下,数据拟合不好的模型被拒绝。
b) RMR 是残差均方根。RMR 是样本方差和协方差减去对应估计的方差和协方差的平方和,再取平均值的平方根。 RMR应该小于0.08,RMR越小,拟合越好。
2.模型评价——参数估计 (1) 假设条件 ① 测量模型误差项δ,ε的均值为零 ② 结构模型的残差项ζ的均值为零 ③ 误差项ε,δ与因子η,ξ之间不相关,误差项ε与δ不相关 ④ 残差项ζ与ξ ,η ,δ之间不相关 (2)参数估计策略 ① 加权最小平方策略(WLS) ② 最大概似法(ML) ③ 无加权最小平方法(ULS) ④ 一般化最小平方法(GLS) ⑤ 渐进分布自由法(ADF)
5
6
结构模型:反映潜在变量之间因果关系
方程式: 1 11 1 1 2 21 1 21 1 2
0 0
B
21
0
结构方程模型基础知识

结构方程这几年热度不减,有必要研究一下它的R语言实现过程,今天先复习一下结构方程的相关理论,参考吉林大学余翠林的ppt一、为什么使用SEM?1、回归分析有几方面的限制:(1)不允许有多个因变量或输出变量(2)中间变量不能包含在与预测因子一样的单一模型中(3)预测因子假设为没有测量误差(4)预测因子间的多重共线性会妨碍结果解释(5)结构方程模型不受这些方面的限制2、S EM的优点:(1)SEM程序同时提供总体模型检验和独立参数估计检验;(2)回归系数,均值和方差同时被比较,即使多个组间交叉;(3)验证性因子分析模型能净化误差,使得潜变量间的关联估计较少地被测量误差污染;(4)拟合非标准模型的能力,包括灵活处理追踪数据,带自相关误差结构的数据库(时间序列分析),和带非正态分布变量和缺失数据的数据库。
3、结构方程模型最为显著的两个特点是:(1)评价多维的和相互关联的关系;(2)能够发现这些关系中没有察觉到的概念关系,而且能够在评价的过程中解释测量误差。
同时具有联系信息技术吸纳能力:SEM能够反映模型中要素之间的相互影响;吸纳能力概念作为一个重要的模型要素,难以直接度量,结构方程模型技术能够更为充分地体现其蕴含的要素信息和影响作用。
二、SEM的基本思想与方法SEM是基于变量的协方差矩阵来分析变量之间关系的一种统计方法,实际上是一般线性模型的拓展,包括因子模型与结构模型,体现了传统路径分析与因子分析的完美结合。
SEM 一般使用最大似然法估计模型(Maxi-Likeliheod , ML)分析结构方程的路径系数等估计值,因为ML法使得研究者能够基于数据分析的结果对模型进行修正。
1、SEM术语(1 )观测变量可直接测量的变量,通常是指标(2)潜变量潜变量亦称隐变量,是无法直接观测并测量的变量。
潜变量需要通过设计若干指标间接加以测量。
(3)外生变量是指那些在模型或系统中,只起解释变量作用的变量。
它们在模型或系统中,只影响其他变量,而不受其他变量的影响。
结构方程模型知识点总结

结构方程模型知识点总结一、SEM的基本概念1.1 潜变量和观察变量SEM中的变量分为潜变量和观察变量两种。
潜变量是无法直接观测到的,但通过观察变量的测量可以间接反映出来的变量,比如抽象的概念、态度或行为。
观察变量是可以直接测量和观察到的变量,它通过对潜变量的测量可以间接反映出来的现象或特征。
1.2 路径图和模型图SEM通过路径图和模型图来表示变量之间的关系。
路径图用箭头表示变量之间的因果关系,箭头的方向表示因果关系的方向,箭头的粗细表示因果关系的强度。
模型图将观察到的变量和潜变量以及它们之间的关系用图形化的方式表达出来。
1.3 测量模型和结构模型SEM包括测量模型和结构模型两个部分。
测量模型用于描述观察变量和潜变量之间的关系,它通过因子分析或确认因素分析来检验观察变量和潜变量之间的关系。
结构模型用于描述潜变量之间的因果关系,它通过路径分析来检验和估计潜变量之间的因果关系。
1.4 模型拟合度和参数估计SEM通过拟合度指标(比如χ²值、RMSEA、CFI等)来检验模型的拟合程度。
拟合度指标可以用来评估模型对观测数据的解释程度。
参数估计则是用来估计模型中的参数,比如路径系数、测量误差和因子之间的协方差等。
二、SEM的应用领域2.1 社会科学研究在社会科学研究中,SEM广泛应用于心理学、教育学、管理学、政治学等领域。
研究者可以利用SEM来检验和估计变量之间的因果关系,比如影响人们行为的因素、组织管理的影响因素等。
2.2 经济学研究在经济学研究中,SEM可以用来检验和估计宏观经济模型或微观经济模型。
研究者可以利用SEM来分析不同变量之间的关系,比如GDP和通货膨胀之间的关系、利率变动对企业盈利的影响等。
2.3 公共卫生研究在公共卫生研究中,SEM可以用来检验和估计潜变量之间的关系,比如疾病和环境因素之间的关系、健康行为和健康状况之间的关系等。
研究者可以利用SEM来揭示潜在的影响因素,从而提出有效的干预措施。
Mplus结构方程模型步骤(入门)
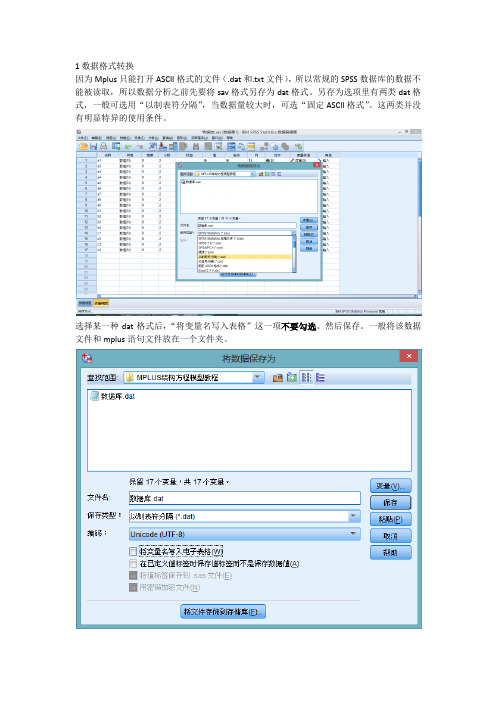
1数据格式转换因为Mplus只能打开ASCII格式的文件(.dat和.txt文件),所以常规的SPSS数据库的数据不能被读取,所以数据分析之前先要将sav格式另存为dat格式。
另存为选项里有两类dat格式,一般可选用“以制表符分隔”,当数据量较大时,可选“固定ASCII格式”。
这两类并没有明显特异的使用条件。
选择某一种dat格式后,“将变量名写入表格”这一项不要勾选。
然后保存。
一般将该数据文件和mplus语句文件放在一个文件夹。
2 打开mplus程序,建立新文件,即点击“new”。
当然,新打开Mplus程序也会默认这个界面。
3 编辑命令。
这是Mplus分析数据最核心的步骤3.1 首先我们可以给该分析起个名字(该步骤可有可无),例如:TITLE: example3.2 然后表明我们引用的数据库来自于哪里,也就是刚刚那个DAT文件。
命令为:DATA: FILE IS C:\Users\dell\Desktop\MPLUS结构方程模型教程\数据库.dat;这里面需要注意的是:DATA: FILE IS (或者DATA: FILE=)是固定句式,是必要的。
之后“C:\Users\dell\Desktop\MPLUS结构方程模型教程\数据库.dat”这是DAT文件的保存路径。
一般情况下,如果mplus语句文件和dat文件在同一个文件夹中,只需要DATA: FILE IS数据库.dat; 但实际上很多情况下,两者即使在同一个文件中,也很可能读不出来,所以必要的话,可将该DAT文件的保存路径写全,这样肯定是没错的。
另外,一个命令结束后,必须必须加上“;”即英文格式下的分号(除外TITLE)。
3.3 写出数据库中所有的变量名称以及本次分析需要的变量名称。
这需要按照spss数据库中变量名称顺序来写。
VARIABLE: NAMES ARE a1 a2 a3 a4 a5 a6 a7 a8 a9 b1 b2 b3 b4 c1 c2 c3 c4;USEVARIABLES ARES ARE a1 a2 a3 a4 a5 a6 a7 a8 a9 b1 b2 b3 b4 c1 c2 c3 c4;当然这是最基本繁琐的写法,可以直接写为:VARIABLE: NAMES ARE a1-a9 b1-b4 c1-c4;USEVARIABLES ARES ARE a1-a9 b1-b4 c1-c4;不同变量间有空格。
结构方程模型最简单易懂的教程PPT学习教案

假设1:工作自主权越高,工作满意度越高。工作自主权是指员工可以 运用相关工作权利的程度。有较高工作自主权的员工,将具有较高的工 作满意度。
假设2:工作负荷越高,工作满意度越低。工作负荷是指工作职责不能 被实现的程度。工作压力会使员工处于有害身心健康的状况中,有碍于 员工对工作的积极态度(House,1980),工作压力会降低工作满意度。
工作内容丰富程度 工作多样性程度
工作单调性 第15页/共33页
y
目前工作满意度 工作兴趣 工作乐趣
工作厌恶程度
(2)模型拟合(model fitting)
模型参数的估计
模型计算(lisrel 软件编程)
表1 标准化路径系数(N=351)
变量
工作自主权 工作负荷 工作单调性
变量间关系
ε1—η1 ε3—η1 ε2—η1
第3页/共33页
线性回归模型及其局限性
y b0 b1x1 b2 x2
1)无法处理因变量(Y)多于一个的情况; 2)无法处理自变量(X)之间的多重共线性; 3)无法对一些不可直接测量的变量进行处理,主
要是一些主观性较强的变量进行测量。如幸福感、 组织认同感、学习能力等; 4)没有考虑变量(自变量、因变量)的测量误差, 以及测量误差之间的关系
SEM包括:回归分析、因子分析(验证性因子分
析、 探索性因子分析)、t检验、方差分析、
比较各组因子均值、交互作用模型、实验设
计
第6页/共33页
结构方程模型的含义
Structural Equation Model,SEM Covariance Structure Modeling,
结构方程模型入门(纯干货!)

结构⽅程模型⼊门(纯⼲货!)⼀、结构⽅程模型的概念结构⽅程模型(Structural Equation Model,简称SEM)是基于变量的协⽅差矩阵来分析变量之间关系的⼀种统计⽅法,因此也称为协⽅差结构分析。
结构⽅程模型属于多变量统计分析,整合了因素分析与路径分析两种统计⽅法,同时可检验模型中的显变量(测量题⽬)、潜变量(测量题⽬表⽰的含义)和误差变量直接按的关系,从⽽活动⾃变量对因变量影响的直接效果、间接效果和总效果。
结构⽅程模型基本上是⼀种验证性的分析⽅法,因此通常需要有理论或者经验法则的⽀持,根据理论才能构建假设的模型图。
在构建模型图之后,检验模型的拟合度,观察模型是否可⽤,同时还需要检验各个路径是否达到显著,以确定⾃变量对因变量的影响是否显著。
⽬前,结构⽅程模型的分析软件较多,如Lisrel、EQS、Amos、Mplus、 Smartpls等等,其中AMOS 的使⽤率甚⾼,因此我们重点了解⼀下使⽤AMOS软件进⾏结构⽅程模型分析的过程。
⼆、结构⽅程模型的相关概念在构建模型假设图,我们⾸先需要了解⼀些有关的基本概念1、显变量显变量有多种称呼,如“观察变量”、“测量变量”、“显性变量”、“观测变量”等等。
从这些称呼中可以看到,显变量的主要含义就是:变量是实际测量的内容,也就是我们问卷上⾯的题⽬。
在Amos中,显变量使⽤长⽅形表⽰。
2、潜变量潜变量也叫潜在变量,是⽆法直接测量,但是可以通过多个题⽬进⾏表⽰的变量。
在Amos中,潜变量使⽤椭圆表⽰。
在使⽤的过程中,我们可以通过这样的⽅式区分显变量和潜变量:在数据⽂件中有具体值的变量就是显变量,没有具体值但可通过多个题⽬表⽰的则是潜变量。
3、误差变量误差变量是不具有实际测量的变量,但必不可少。
在调查中,显变量不可能百分之百的解释潜变量,总会存在误差,这反映在结构⽅程模型中就是误差变量,每⼀个显变量都会有误差变量。
在Amos 中,误差变量使⽤圆形进⾏表⽰(与潜变量类似)。
结构方程模型的原理与应用pdf

结构方程模型的原理与应用一、什么是结构方程模型•结构方程模型(Structural Equation Modeling,简称SEM)是一种多变量统计方法,用于分析观测变量之间的关系以及变量与潜变量之间的关系。
•SEM通过建立数学模型来描述变量之间的关系,并基于数据对模型进行拟合和评估。
它可以帮助研究者探索和解释变量之间的复杂关系,以及验证理论模型是否与实际数据一致。
二、结构方程模型的基本原理•结构方程模型由测量模型和结构模型组成。
测量模型用于描述潜变量与观测变量之间的关系,结构模型则描述了变量之间的因果关系。
•在测量模型中,潜变量是无法直接观测到的,而观测变量是可以被测量到的。
通过观测变量与潜变量之间的关系,可以推断潜变量的存在和性质。
•结构模型描述了变量之间的因果关系,包括直接效应和间接效应。
直接效应表示一个变量对另一个变量的直接影响,而间接效应表示通过其他变量中介作用的影响。
•结构方程模型的参数可以使用最大似然估计或者最小二乘估计来进行估计。
估计得到的参数可以用于验证理论模型是否与实际数据拟合良好。
三、结构方程模型的步骤1.模型规范化:确定潜变量和观测变量,并选择合适的测量指标。
2.建立测量模型:通过测量指标与潜变量之间的关系建立测量模型。
3.建立结构模型:根据理论假设或先验知识,建立变量之间的结构模型。
4.模型拟合:对建立的模型进行拟合,通过比较实际数据和模型估计值,评估模型的拟合度。
5.参数估计:使用最大似然估计或最小二乘估计方法,对模型参数进行估计。
6.模型诊断:通过模型拟合度指标,对模型的各项指标进行诊断,判断模型是否合理。
7.模型修正:如果模型拟合不好,可以对模型进行修正,使用修正指数修正模型。
四、结构方程模型的应用•结构方程模型广泛应用于社会科学研究和教育评估领域。
下面列举一些常见的应用场景:1.教育研究:结构方程模型可以用于研究教育因素对学生学业成绩的影响,分析各个因素之间的关系,以及评估教育政策的有效性。
结构方程模型

分,在测量模型即测量误差,在结构模型中为 干扰变量或残差项,表示内生变量无法被外生 变量及其他内生变量解释的部分。
ηη11== γ ξ + γ111ξ11+ ζ11 ζ1 η 1= γ11 ξ1+ γ12 ξ2 +ζ1
符号表示
潜在变量:被假定为因的外因变量,以ξ(xi/ksi) 表示;假定果的内因变量以η(eta)表示。
外因变量ξ的观测指标称为X变量,内因变量η观测值 表称为Y变量。
它们之间的关系是:①ξ与Y、η与X无关②ξ的协差 阵以Φ(phi)表示③ξ与η的关系以γ表示,即内因 被外因解释的归回矩阵④ξ与X之间的关系,以Λx表 示,X的测量误差以δ表示,δ间的协方差阵以Θε表 示⑥内因潜变量η与η之间以β表示。
观察变量
观察变量作为反映潜在变量的指标变量,可分为反映性指 标与形成性指标两种。
反映性指标又称为果指标,是指一个以上的潜在变量是引 起观察变量或显性变量的因,此种指标能反映其相对应的 潜在变量,此时,指标变量为果,而潜在变量为因。
相对的,形成性指标是指指标变量是成因,而潜在变量被 定义为指标变量的线性组合,因此潜在变量变成内生变量, 指标变量变为没有误差项的外生变量。
SEM包含了许多不同的统计技术
SEM融合了因子分析和路径分析两种统计技 术,可允许同时考虑许多内生变量、外生变量 与内生变量的测量误差,及潜在变量的指标变 量,可评估变量的信度、效度与误差值、整体 模型的干扰因素等。
SEM重视多重统计指标的运用
SEM所处理的是整体模型契合度的程度,关注整体模 型的比较,因而模型参考的指标是多元的,研究者必 须参考多种不同的指标,才能对模型的是陪读做整体 的判断,个别参数显著与否并不是SEM的重点。
结构方程模型入门分解

模型的发展策略
即研究者先利用理论界定出一个起始模型,再搜集一组资料检验其匹配程度。如果不是相当匹配,可运用SEM统计中的某种指数了解需要修正的地方,如果需修正处有着健全的理论可解释则将其修正,这是一般研究者常用的策略。
*
模型识别
对SEM理论不十分清楚的研究者,往往会忽略模型识别的问题,只是将其交给统计软件处理,即不知其中存在诸多复杂的问题,对此应当阅读有关书藉,详细了解模型识别的问题。
01
注:袁振国,教育部社会科学司副司长,北京师范大学教育学院教授、博士生导师。
02
*
*
SEM
结构方程模型(SEM)入门
导言-1
心理学或教育学研究的一个主要目的是通过分析变量与变量之间的关系来揭示心理或教育现象的发展以及变化规律与特点,如相关分析。
X1
X2
r
相关分析(Correlational Analysis)
*
例2
误差 观测变量 负荷量 潜在变量
*
专栏:结构方程模型的构图与模式
*
SEM的模式
测量模式 (measurement model) 测量模式旨在建立测量变量与潜在变量间之关系,主要透过验证性因素分析( CFA)以考验测量模式的效度结构模式。
數學
造句 能力
字彙 能力
加法 能力
計數 能力
=1
採用Single dimension
δ1
δ2
δ3
δ4
δ5
*
Title Confirmatory Factor Analysis for student test performance Observed Variables 文章閱讀 造句能力 字彙能力 加法能力 計數能力 Correlation Matrix= 1 0.722 1 0.714 0.685 1 0.203 0.246 0.170 1 0.095 0.181 0.113 0.585 1 Sample Size=145 Latent Variables 語言 數學 Relationships: 文章閱讀=語言 造句能力=語言 字彙能力=語言 加法能力=數學 計數能力=數學 SET the Covariance of 語言 and 數學 to 1 Path Diagram LISREL OUTPUT SE TV RS MI
结构方程模型初级介绍ppt课件

篮球比赛 是根据 运动队 在规定 的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
例子:员工工作满意度的测量
概念模型:
x
工作方式选择
工作自主权
工作目标调整
任务完成时间充裕度
工作负荷轻重
工作负荷
工作节奏快慢
工作内容丰富程度 工作多样性程度
表2 模型拟合优度结果
指标 DF Χ2 P NFI NNFI CFI IFI GFI AGFI RFI RMR RMSEA
指标值 687 1386.64 0.0 0.901 0.937 0.950 0.951 0.861 0.817 0.861 0.0584 0.0457
篮球比赛 是根据 运动队 在规定 的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
结构方程(structural
equation),描述潜变量之间的
关系,如工作自主权与工作 满意度的关系。
工作自主权
工作满意度
篮球比赛 是根据 运动队 在规定 的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
(一)测量模型
对于指标与潜变量(例如两个工作自主权指标与工作自主权)间的关系,通常 写为以下测量方程:
工作单调性
工作满意度
y
目前工作满意度 工作兴趣 工作乐趣
工作厌恶程度
篮球比赛 是根据 运动队 在规定 的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
(2)模型拟合(model
结构方程模型 ppt课件

结构方程模型
• 模型的修正主要包括: • (1) 依据理论或有关假设 ,提出一个或数个合理的
先验模型; • (2) 检查潜变量与指标间的关系 ,建立测量方程模
型; • (3) 若模型含多个因子 ,可以循序渐进地 ,每次只检
验含两个因子的模型 ,确立测量模型部分合理后 , 最后再将所有因子合并成预设的先验模型 ,作总体 检验; • (4) 对每一模型 ,检查标准误、标准化残差、修正 指数、参数期望改变值、χ 2 及各种拟合指数 ,据此 修改模型。
x1
y1
x2
自信
x3
x4
外向
y2
y3
y4
模型举例
3、结构方程模型的结构
结构方程模型可分为:测量模型和结构模型
(1)测量模型:指标和潜变量之间的关系
x x
y y
说明:
x,y是外源(如:六项社经指标)及内生(如:中、英、数成绩)指标。 δ,ε是X,Y测量上的误差。 Λx是x指标与ξ潜伏变项的关系(如:六项社经地位指标与潜伏社经地位的关 系)。 Λy是y指标与η潜伏变项的关系(如:中、英、数成绩与学业成就间关系)。
• (式6,) 不当 能模 说型 数与 据结数可构据以拟确方合认程时模式,模说,明也型数不据能并 证不 明排 某斥 一模 理
论基础;
• (7) 用同一样本数据 ,以相同数目的待估参数和 不同的组合形式可以产生许多不同模型 ,这些等同 模型哪一个更适合于研究问题 ,应按照模式表达的 意义从专业角度来鉴别;
结构方程模型
• (3) 一个完善的通径图并不表示一定包含尽 可能多的箭头。相反 ,统计学上最感兴趣的 是 ,寻找用尽可能少的箭头去联结尽可能少 的变量 ,而这时的通径图又能对所代表的样 本拟合得好;
结构方程模型讲义

结构方程模型讲义结构方程模型(Structural Equation Modeling,SEM)是一种统计分析方法,多用于研究基于潜变量的复杂系统内在结构的定量关系。
其理论基础源于多元统计分析、因子分析和路径分析,通过建立观察变量与潜变量之间的关系模型,解析出潜变量对观察变量的影响,进而研究变量之间的内在结构关系。
一、SEM的基本概念和特点1.潜变量:潜变量是指无法直接观察或测量的变量,只能通过观察变量来间接反映。
它可以代表一些理论上的构念、心理特质或潜在特征。
2.观察变量:观察变量是可以直接观察和测量的变量,表现为定量或定性的实际测量结果。
3.模型设定:SEM基于研究者对潜变量和观察变量之间关系的理论假设,通过建立潜变量和观察变量之间的关系模型,定量研究变量之间的影响关系。
4.结构关系:SEM通过路径系数来描述潜变量和观察变量之间的关系,并使用结构方程模型来表示这些关系。
路径系数表示了变量之间的直接或间接影响。
二、结构方程模型的步骤1.模型设定:根据研究目的和理论依据,建立潜变量和观察变量之间的关系模型,并确定模型中的指标、因子和路径。
2.数据收集:收集样本数据,并根据所设定的模型变量进行测量,获得观察变量的观测值。
3.模型估计:利用SEM软件,通过最大似然估计等方法求解模型中的参数估计值,包括路径系数、因子载荷和误差项。
4.模型拟合:通过拟合度指标对模型的拟合程度进行评估,检验模型是否与观测数据一致。
如果拟合不理想,可能需要修改或调整模型。
5.结果解释和修正:对模型结果进行解释,解释模型中的路径系数和因子载荷,以及观察变量的解释力。
如果有必要,根据拟合结果调整模型,并进行相应修正。
6.结果验证:通过交叉验证、重测等方法验证模型的鲁棒性和稳定性,确保模型结果的可靠性和稳定性。
结构方程模型的应用领域非常广泛,包括心理学、社会学、教育学、市场营销、财务管理等。
它可以用于研究因果关系、探究复杂系统内在结构、验证理论模型等。
结构方程模型最简单易懂的教程

模型 Mc拟合结果
(93)= 148.61, RMSEA=.040 NNFI = 0.96, CFI = 0.97。 Q8在A负荷为 0.54,在B负荷为 -0.08 因为概念上Q8应与B成正相关,故不合理。 而且这负荷相对低,所以我们选择Mb
简单来说,结构方程模型分 为: 测量方程(measurement equation)测量方程描述潜 变量与指标之间的关系,如 工作方式选择等指标与工作 自主权的关系; 结构方程(structural 满意度的关系。
工作自主权
工作满意度
equation),描述潜变量之间的 关系,如工作自主权与工作
规范拟合指数(NFI),不规范拟合指数(NNFI ),比较拟合指数(CFI),增量拟合指数(IFI) ,拟合优度指数(GFI),调整后的拟合优度指数 (AGFI),相对拟合指数(RFI),均方根残差( RMR),近似均方根残差(RMSEA)等指标用来 衡量模型与数据的拟合程度。 学术界普遍认为在大样本情况下: NFI 、NNFI 、 CFI 、IFI 、GFI、AGFI 、RFI 大于0.9,RMR小于 0.035,RMSEA值小于0.08,表明模型与数据的拟合 程度很好。
例子:员工工作满意度的测量
概念模型:
x
工作自主权
工作方式选择 工作目标调整
y
任务完成时间充裕度
工作负荷轻重 工作节奏快慢 工作内容丰富程度 工作单调性 工作多样性程度
工作负荷
工作满意度
目前工作满意度 工作兴趣 工作乐趣 工作厌恶程度
(2)模型拟合(model fitting)
模型参数的估计
Ma模型修正
结构方程模型讲义_图文

何时能说X引起Y?
X时间在先。(纵向设计) 明确说明因果方向,比如不可逆,或者循环。 (同时测
量设计) 常识、理论、经验研究的成果都可以成为说明的线索。 难以说明怎么办? X与Y之间的关系不因引进第三变量而消失 (统计控制) 。
结构方程模型的结构
结构方程模型可以分为测量方程( measurement)和结构方程(structural equation)两部分
插入新变量
点击Data菜单Insert Variables选项,打开对话框 点击OK键,在光标的左边,一个新变量就被插入到数据文件中 点击Data菜单Define Variables选项激活Define Variables对话框 选中刚才插入的变量 点击Rename键,键入新的变量名 点击OK键回到Define Variables对话框 点击Define Variables对话框中的OK键得到PSF窗口 点击File菜单上Save as选项,在“文件名”字符区键入新的文件名 这样,一个新变量被插入到原有的数据集中并存储为新的文件名
Factor Loading
三个因子与各变量之间的相关系数,称为因子 载荷量(loading)
系数绝对值越大,与相应因子的相关强度越强 。
因子旋转
因子旋转:用一个正交阵右乘已经得到的因子载荷阵(由线性代 数可知,一次正交变化对应坐标系的一次旋转),使旋转后的因 子载荷阵结构简化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
外显指标
收入高低 教育水平
社会经济地位
潜在 变量
SEM主要特点在于能反映潜在变量(Latent variables) 与外显变量(Manifest variable )之关系。
9
方法的进步与革命常常导致相应学科的 进步与革命。就统计方法而盲,回归分析是 相关分析的深人, 而结构方程模型(SEM) 则是对回归分析的深入。
收敛效度(convergent validity):对相同特性(construct, concept, or research variables)使用不同衡量方法(Likert scale, Stapel scale, or semantic differential),所得结果高度相关。
区别效度(discriminant validity):不同建构(construct, 即研究变数或称concept) 彼此之间确实不相同。
0.50~0.95之间; ⑤标准误不能太大。
47
(二)整体模型拟合度指标数值范围及临界值
指標名稱與性質
卡方檢驗 2 test 理論模型與觀察模型的契合程度 2/df(Wheaton et al.) 考慮模式複雜度後的卡方值
適合度指標
GFI(Bentler, 1983) 假設模型可以解釋觀察資料的比例
-
P>.05
-
<2
0-1
>.90
0-1* >.90
0-1
>.50
0-1
>.90
0-1* >.90
適用情形
說明模型解釋力
不受模式複雜度 影響
說明模型解釋力
不受模式複雜度 影響
說明模型的簡單 程度
說明模型較虛無 模型的改善程度
不受模式複雜度
影響
48
(二)整体模型拟合度指标数值范围及临界值
49
50
五、结构方程模型的用途
即研究者事先界定多个可替代的理论模型, 再搜集一组经验资料以检验哪一个理论模型 与经验资料最匹配。譬如对智力既可用 Spearman的二因素理论解释,也可用 Thurstone的群因素理论解释,还可以用卡特 尔的简明层次论解释等,对于哪一种解释方 式最好,以往的统计技术难以处理, SEM却 可以有效地处理这类问题,采用竞争模型更 符合实际情况。
自变量之间可能存在因果关系,因变量也可能是某
个或某几个自变量的原因,有时需要处理多个原因
和多个结果的关系。
特别是会遇到不可直接观测的变量,这种变量
称为潜在变量(Latent Variables) ,诸如社会经济地
位、智力等都不能准确、直接地加以测量。
社会经济地位
潜在变量
智力 8
问题提出
对于潜变量,可用一些外显指标(Observable indicators)来间接测量它们。如用收入高低、教育水 平作为社会经济地位()的测量指标。
16
SEM的模式
测量模式
e1
y1
(measurement
e2
y2
f1
model)
e3
y3
测量模式旨在建立
测量变量与潜在变量间 e4
y4
之关系,主要透过验证
性因素分析( CFA)
e5
y5
f2
以考验测量模式的效度 e6
y6
结构模式。
验证性因素分析 (Confirmatory Factor Analysis,CFA) 17
10
一、结构方程模型的概念
结构方程模型(structural equation modeling,简称 SEM) ,早期称为线性结构关系(Linear Structural Relationships ,简称LISREL) ,是评价理论模型与经 验数据一致性的统计方法。
潜在变量也称为隐变量。 外显变量也称观测变量 ( Observable variable )或测量
35
模型的发展策略
即研究者先利用理论界定出一个起始模型, 再搜集一组资料检验其匹配程度。如果不是 相当匹配,可运用SEM统计中的某种指数了 解需要修正的地方,如果需修正处有着健全 的理论可解释则将其修正,这是一般研究者 常用的策略。
36
模型识别
模型的识别分为低识别、恰好识别和过度识 别三种。
Observed Variables 文章閱讀 造句能力 字彙能力 加法能力 計數能力
Correlation Matrix=
1 0.722 1
相關矩陣
0.714 0.685 1 0.203 0.246 0.170 1
潛伏變數
0.095 0.181 0.113 0.585 1
Sample Size=145 Latent Variables 語言 數學
Path Diagram LISREL OUTPUT SE TV RS MI
MI: 修飾指標
42
軟體操作:學生智力測驗成績 (P.192)
43
軟體操作:學生智力測驗成績 (P.192)
參數最大概似估計、標準誤、t值:
語言:相關性較大、標準誤0.07、t值顯著>2 數學:相關性小、標準誤0.09、t值<2不顯著
加法能力, 計數能力 潛伏變數:語言, 數學
40
路徑圖:學生智力測驗成績 (P.192)
語言
=1
採用Single
dimension
數學
文章 閱讀
造句 能力
字彙 能力
加法 能力
計數 能力
δ1
δ2
δ3
δ4
δ5
χ2、 GFI、AGFI、
41
軟體操作:學生智力測驗成績 (P.192)
指標變數
Title Confirmatory Factor Analysis for student test performance
兩潛伏變數之間 的相關係數為1
殘差變異數估計、 標準誤、t值
44
軟體操作:學生智力測驗成績 (P.192)
卡方值 χ2 = 59.47
GFI = 0.88 <0.90 AGFI= 0.63 <0.80 RMR = 0.14 >0.05
(皆低於可接受水準) 模型配適度不佳
45
學生智力測驗成績-綜合比較
51
五、结构方程模型的用途
(二)侯杰泰(1999) a、验证性因素分析 b、高阶因子分析 c、路径及因果分析 d、多时段(multiwave)设计 e、单形模型(Simplezs Model) f、多组比较
•根据LISREL的 分析程序,SEM 大体分为建立 模型、识别模 型、估计模型, 评估模型和修 正模型五个步 骤。
31
模型界定
模型的界定必须来自健全理论的建构。 模型界定的步骤有三。首先由研究者整理文献与
相关理论,提出建立模型的双向结构表,然后由 专家对结果进行论证,最后根据确定的结构设计 可能的项目。
32
三种模型策略
SEM的基本假设是观测变量的共变数矩阵是 一组参数的函数,而检验一个共变数矩阵有 三种模型策略。
33
验证模型策略
即根据搜集的经验资料严格检验研究者 界定的理论模型,以确定所检验理论模 型是接受还是拒绝,所谓严格检验是指 当模型被拒绝时,不再寻找接受模型的 可能线索。
34
竞争模型策略
注:袁振国,教育部社会科学司副司长,北京师范大学教育学院教授、博士生导师。
1
2
结构方程模型(SEM)入门
云南大学 高等教育研究院 解亚宁
SEM
3
导言-1
心理学或教育学研究的一个主要
目的是通过分析变量与变量之间的关系
来揭示心理或教育现象的发展以及变化
规律与特点,如相关分析。
r
X1
X2
相关分析(Correlational Analysis)
引言
袁振国在译完威廉·维尔斯曼的教育研究方法 导论》后在其前言中评论道“ 总觉得教育研究方 法过于传统,研究的手段也比较落后。而在世纪 年代中期由瑞典统计学家—心理测量学家提出的 结构方程模型(简称SEM)则提供了一种新的统计方 法和研究思路。它能有力地解决教育研究中的问 题,应当引起教育界的重视,理应成为教育研究 的有力工具。
潛在变量路徑分析(Path Analysis with Latent Variables, PA-LV) 19
20
例3:研究生研究论文
21
22
23
24
25
26
模型假设
27
28
29
30
二、结构方程模型分析步骤示意图
首先针对
研究问题,根据 已有的研究资料 提出多个假设模 型,然后收集数 据、进行分析, 通过模型与实际 数据的拟合情况 和模型比较的结 果,确定最终的 结果模hips:
文章閱讀=語言 造句能力=語言 字彙能力=語言
定義指標變數與 潛伏變數之關係
加法能力=數學
計數能力=數學
SET the Covariance of 語言 and 數學 to 1
相關係數為1,不具區別效度
輸出指令 SE: 標準誤 TV: t檢定 RS: 常態化殘差與Q圖
结构方程模型是通过观测变量集合的间的协 方差结构和相关结构出发,从定量的角度建立模 型来研究变量间的因果关系的一种方法。
δ1 δ2 δ3
误差
x1 x2 x3 观测变量
λ1 λ2
λ3
负荷量
ξ 潜在变量
典型的结构方程模型与参数示意图
14
例2
误差
观测变量
负荷量 潜在变量
15
专栏:结构方程模型的构图与模式
卡方值
