自动控制原理课后习题答案第五章

合集下载

自控原理第五章习题参考答案

5-1 5()0.251G s s =+5()0.251G j j ωω=+()A ω=()arctan(0.25)ϕωω=-输入 ()5cos(430)5sin(460) =4r t t t ω=-︒=+︒(4)A ==(4)arctan(0.25*4)45ϕ=-=-︒系统的稳态输出为()(4)*5cos[430(4)]3045)17.68cos(475)17.68sin(415)c t A t t t t ϕ=-︒+=-︒-︒=-︒=+︒ sin cos(90)cos(90)cos(270)αααα=︒-=-︒=+︒或者，()(4)*5sin[460(4)]6045) 17.68sin(415)c t A t t t ϕ=+︒+=+︒-︒=+︒所以，对于cos 信号输入下的稳态输出计算规律与sin 信号作用下计算相同。

5-3（2）1()(1)(12)G s s s =++ 1()(1)(12)G j j j ωωω=++()A ω=()arctan arctan 2ϕωωω=--起点：0ω= (0)1;(0)0A ϕ==︒ 位于正实轴上。

终点：ω→∞ ()0;()180A ϕ∞=∞=-︒+∆ 从第三象限趋于原点因此，，Nyquist 曲线与虚轴有交点，并且满足：()arctan arctan 290ϕωωω=--=-︒ arctan arctan 290ωω+=︒所以有，1/(2)ωω= 21/2ω=()0.473A ω=== 因此，与虚轴的交点为（0，-j0.47）()ω（3）1()(1)(12)G s s s s =++ 1()(1)(12)G j j j j ωωωω=++()A ω=()90arctan arctan 2ϕωωω=-︒--起点：0ω= (0);(0)90A ϕ=∞=︒∆－－位于负虚轴（左侧）无穷远方向终点：ω→∞ ()0;()270A ϕ∞=∞=-︒+∆ 从第二象限趋于原点因此，，Nyquist 曲线与实轴有交点，并且满足：()90arctan arctan 2180ϕωωω=-︒--=-︒ arctan arctan 290ωω+=︒1/(2)ωω= 21/2ω=2()0.673A ω===与实轴的交点为（-0.67，-j0）)ω（4）21()(1)(12)G s s s s =++ 21()()(1)(12)G j j j j ωωωω=++()A ω=()180arctan arctan 2ϕωωω=-︒--起点：0ω= (0);(0)180A ϕ=∞=︒∆－－位于负实轴（上侧）无穷远方向终点：ω→∞ ()0;()360A ϕ∞=∞=-︒+∆ 从第一象限趋于原点因此，，Nyquist 曲线与虚轴有交点，并且满足：()180arctan arctan 2270ϕωωω=-︒--=-︒ arctan arctan 290ωω+=︒1/(2)ωω= 21/2ω=()0.94A ω===与虚轴的交点为（0，j0.94）)ω=5-4（2）10.5ω=，21ω=，1K =，0ν=（3）10.5ω=，21ω=，1K =，1ν=低频段直线（延长线）与0db 线交点的频率为：1/cK νω'=。

《自动控制原理》5章课后习题参考答案.

G S S S =
+
1(
10000(6
.311
2e +=
S S S G
1001.0(11.0(1(1.0(d +++=
S S S S S G 61
.054
.0154.0,
11(2
2
=+==+=
K K
A ω
ωω010
s
900.257.3180 2.16rad
tg ωωω----∙︒=-=,(
(
5
.1,
(5
(6 (7
5.12
K增大和T减少
((1(1(1m K
K s s Ts Ts K
s T s K
Φ=
≈
+++++
K
T m 21=
ζ ,不变(稳定裕度不变
2
22
(12(121b n ωωξξ=-+
-+
5.13
11=+=
p
ssr K e 35
.01
12
416==
=
v
ssr K e %
8.4%100%2
1=⨯=--ξ
πξ
σe 05
.006.13
==≈
ቤተ መጻሕፍቲ ባይዱεξ
ω,S t n s s
rad n n c 8.2707.0707.02=∙=ωωω=0
63
=γdB K g s rad g ∞=∞=ω0,1==r r M ωs
rad n b 4==ωω0
1
1
11006
.787.53.841001.01001.0180180=-=∙-=-+-=----tg

《自动控制原理》胡寿松第五章习题解答

= 0.447 sin(t + 3.4 0 ) − 0.354 cos(2t − 90 0 )
e ss (t ) = c ss (t ) − r (t ) = 0.447 sin(t + 3.4 0 ) − 0.354 cos(2t − 90 0 ) − sin(t + 30 0 ) + cos(2t − 45 0 )
5-4 典型二阶系统的开环传递函数
2 ωn s( s + 2ζω n )
G( s) =
当取 r (t ) = 2 sin t 时，系统的稳态输出
css (t ) = 2 sin(t − 450 )
试确定系统参数 ω n , ζ 。解：根据公式（5-16）和公式（5-17）得到： c ss (t ) = A G B ( jω ) sin(ωt + ϕ + ∠G B ( jω ))
ξ = 0.6532
G( s) H ( s) =
K (τs + 1) ; s 2 (Ts + 1)
K ,τ , T > 0
试分析并绘制 τ > T 和 T > τ 情况下的概略开环幅相曲线。解：相频特性为
ϕ (ω ) = −180 0 + arctan τω − arctan Tω
(1)
τ > T 时， ϕ (ω ) > −180 0 概略开环幅相曲线如下
胡寿松自动控制原理习题解答第五章
5-2 若系统单位阶跃响应为
h(t ) = 1 − 1.8e −4t + 0.8e −9t (t ≥ 0)
试确定系统的频率特性。解：对单位阶跃响应取拉氏变换得：
1 1.8 0.8 36 − + = s s + 4 s + 9 s ( s + 4)( s + 9)

自动控制原理第五章课后答案

五频域分析法2-5-1 系统单位阶跃输入下的输出)0(8.08.11)(94≥+-=--t e e t c tt ,求系统的频率特性表达式。

【解】： 98.048.11)]([L )(1+++-==-s s s t c s C 闭环传递函数)9)(4(36198.048.11)()()(++=+++-==s s ss s s s R s C s G )9tg 4(tg 2211811636)9)(4(36)(ωωωωωωω--+-+⨯+=++=j ej j j G2-5-2系统时，系统的稳态输出（1）)30sin()(0+=t t r ；（2）)452cos(2)(0+=t t r ；（3）)452cos(2)30sin()(00--+=t t t r 。

【解】：求系统闭环传递函数5tg 21254)5(4)(54)(1)()()()(14)(ωωωω--+=+=+=+==+=j B K K B K ej j G s s G s G s R s C s G s s G根据频率特性的定义，以及线性系统的迭加性求解如下：（1）︒===30,1,11θωr A︒--====-3.1151tg )1(178.0264)1()(1j j j B e eeA j G θωω[])7.18sin(78.0)1(sin )1()sin()(12︒+=++=+=t t A A t A t c r c s θθθ（2）︒===45,2,21θωr A︒--==+=-8.2152tg 274.02544)(1j j B e ej G ωω)2.232cos(48.1)(︒+=t t c s（3）)8.662cos(48.1)7.18sin(78.0)(︒--︒+=t t t c s2-5-3 试求图2-5-3所示网络的频率特性，并绘制其幅相频率特性曲线。

【解】：（1）网络的频率特性1)(111)(212212+++=+++=ωωωωωC R R j C jR C j R R C j R j G（2）绘制频率特性曲线)tg (tg 22212121111)(1)(11)(ωωωωωωωT T j eT T jT jT j G ---++=++= 其中1221221,)(,T T C R R T C R T >+==。

自动控制原理及其应用课后习题第五章答案

40 20 0 -20 -20dB/dec 10 1 2ωc -40dB/dec -60dB/dec 40 -40dB/dec
ω
20 0 -20
10 ωc
1
2 -20dB/dec
ω
-60dB/dec
10 ≈1 ω2 0.5 c
ω c=4.5
5 ≈1 ω c=7.9 ω 0.01 c3
第五章习题课 (5-17)
-20
低频段曲线：低频段曲线： 20lgK=20dB φ (ω ) 0 ω1=5 ω2=15 -90 相频特性曲线：相频特性曲线： -180 -270 φ ( )= -90o ω ω=0 φ ( )= -270o ω ω=∞
-60dB/dec
ω
第五章习题课 (5-2)
10(s+0.2) 1.33(5s+1) (5) G(s)= s2(s+0.1)(s+15)=s2(10s+1)(0.67s+1) 解：低频段曲线：低频段曲线： 20lgK=2.5dB
第五章习题课 (5-7)
5-7 已知奈氏曲线，p为不稳定极点个数，已知奈氏曲线，为不稳定极点个数为不稳定极点个数， υ为积分环节个数，试判别系统稳定性。为积分环节个数，试判别系统稳定性。 Im υ=2 (b) p=0 (a) p=0 Im υ=0
ω=0 Re -1 0 ω=0+ -1 0 ω=0 Re
第五章习题课 (5-1)
5-1(1) 已知单位负反馈系统开环传递函数，已知单位负反馈系统开环传递函数，当输入信号r(t)=sin(t+30o)，试求系统的稳态当输入信号，输出。输出。 10 G(s)=(s+1) 10 解： φ(s)= (s+11) 10 = 10 = 10 ω A( )= 2 2 112+1√ 122 =0.905 √ 11 +( ) √ ω φ ( )=-tg-1ω =-tg-1 1 =-5.2o ω 11 11 cs(t)=0.9sin(t+24.8o)

自动控制原理卢京潮主编课后习题答案西北工业大学出版社

自动控制原理卢京潮主编课后习题答案西北工业大学出版社SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第五章线性系统的频域分析与校正习题与解答5-1 试求题5-75图(a)、(b)网络的频率特性。

(a) (b)图5-75 R-C 网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sC R sC R R R s U s U r c ττ (b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c)(1111)()(2122222212ττ 5-2 某系统结构图如题5-76图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(t c s 和稳态误差)(t e s（1） t t r 2sin )(=（2） )452cos(2)30sin()(︒--︒+=t t t r 解系统闭环传递函数为: 21)(+=Φs s 图5-76 系统结构图频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时, 2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ （2）当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5-3 若系统单位阶跃响应试求系统频率特性。

自动控制原理第五章课后习题答案(免费)[1]

自动控制原理第五章课后习题答案（免费）5－１设单位反馈系统的开环传递函数为对系统进行串联校正，满足开环增益及解:① 首先确定开环增益K,00()12lim v s K SG S k →===② 未校正系统开环传函为:012()(1)G s s s =+M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramGm = 70.5 dB (at 200 rad/sec) , P m = 16.5 deg (at 3.39 rad/sec)Frequency (rad/sec)③ 绘制未校正系统的开环对数频率特性,得到幅穿频率 3.4c ω=,对应相位角'0()164,16c G j ωγ∠=-∴=,采用超前校正装置,最大相角 0(180())4016630m c G j ϕγωγ=-+∠+=-+=④ 11sin ,31m αϕαα--=∴=+ 0()(1)KG s s s =+40γ=︒112K s -=⑤ 在已绘图上找出10lg 10lg3 4.77α-=-=-的频率 4.4m ω=弧度/秒令c m ωω=⑥0.128/,0.385/m T s T s ωα=⇒==∴=校正装置的传函为:110.385()110.128Ts s G s Ts s α++==++校正后的开环传函为:012(10.39)()()()(1)(10.13)c s G s G s G s s s s +==++ 校正后1801374340γ=-=>,满足指标要求.-100-50050100M a g n i t u d e (d B )101010101010P h a s e (d e g )Bode DiagramGm = 99.2 dB (at 1.82e+003 rad/sec) , P m = 42.4 deg (at 4.53 rad/sec)Frequency (rad/sec)5－２设单位反馈系统的开环传递函数为要求设计串联迟后校正装置。

《自动控制原理》第5章习题答案

G0 ( s ) =
1 s (0.1s + 1)
特征方程为， D( s ) = 0.1s 2 + s + 1 = 0 ，即，s + 10 s + 10 = 0 ，
2
ω n = 10 = 3.162 ， ζ =
10 = 1.58 ，原系统为过阻尼系统， 2ω n
2
σ % = 0 ， ts >
4
ζω n
解： G ( jω ) =
ω＝0 时， G (0) = 0.4 ，在低频段， L(ω ) = 20 lg 0.4 = −8dB ； ω → ∞ 时， G ( j∞) = 1 ，
在高频段， L(ω ) = 20 lg1 = 0dB 。转折频率 ω1 = 2 ，ω 2 = 5 。串联校正装置是超前校正装置。
-j 3.46
②计算期望主导极点位置。系统期望闭环主导极点具有阻尼系数 ζ =
2 ，自然振荡频率 ω n = 4 2 ， 2
θ = arccosζ = arccos
2 = 450 ，则一个具有期望极点的 2 阶系统特征方程为， 2
s 2 + 8s + 32 = 0
jω
期望极点
期望极点
− p3
j
600
j0.58
− p2
-1
− p1
0 -j
-3
-2
σ
-2
19.150 -1
40.880 0.33 0
119.640
校核相角条件：根据在图中主导极点位置的近似值－0.33 ± j 0.58 和开环极点的位置，作由各开环极点到期望主导极点的向量，
Φ = －119.640 －40.880 －19.150 = －179.670≈－1800

自动控制原理课后习题答案第五章

第五章5-2 若系统单位阶跃响应为49()1 1.80.8tth t ee--=-+试确定系统的频率特性。

分析先求出系统传递函数，用j ω替换s 即可得到频率特性。

解：从()h t 中可求得：(0)0,(0)0h h '==在零初始条件下，系统输出的拉普拉斯变换()H s 与系统输出的拉普拉斯变换()R s 之间的关系为()()()H s s R s =Φ⋅即()()()H s s R s Φ=其中()s Φ为系统的传递函数，又1 1.80.836()[()]49(4)(9)H s L h t s s s s s s ==-+=++++1()[()]R s L r t s ==则()36()()(4)(9)H s s R s s s Φ==++令s j ω=，则系统的频率特性为()36()()(4)(9)H j j R j j j ωωωωωΦ==++5-7 已知系统开环传递函数为)1s T (s )1s T (K )s (G 12++-=;（Ｋ、Ｔ1、Ｔ2＞０）当取ω＝１时， o180)j (G -=ω∠,|Ｇ(ｊω)|＝０.５。

当输入为单位速度信号时，系统的稳态误差为0.1，试写出系统开环频率特性表达式G(ｊω)。

分析：根据系统幅频和相频特性的表达式，代入已知条件，即可确定相应参数。

解：由题意知：()G j ω=21()90arctan arctan G j T T ωωω∠=---因为该系统为Ⅰ型系统，且输入为单位速度信号时，系统的稳态误差为0.1，即1()lim ()0.1ss s e E s K→∞===所以：10K =当1ω=时，(1)0.5G j ==21(1)90arctan arctan 180G j T T ∠=---=-由上两式可求得1220,0.05T T ==，因此10(0.051)()(201)j G j j j ωωωω-+=+5-14 已知下列系统开环传递函数(参数K 、T 、T ｉ＞０，ｉ＝１，2，…，６)(1))1s T )(1s T )(1s T (K)s (G 321+++=(2))1s T )(1s T (s K)s (G 21++=(3))1Ts (s K )s (G 2+=(4))1s T (s )1s T (K )s (G 221++=(5)3s K )s (G =(6)321s)1s T )(1s T (K )s (G ++=(7))1s T )(1s T )(1s T )(1s T (s )1s T )(1s T (K )s (G 432165++++++=(8)1Ts K)s (G -=(9)1Ts K )s (G +--=(10))1Ts (s K)s (G -=其系统开环幅相曲线分别如图5-6(1)～(10)所示，试根据奈氏判据判定各系统的闭环稳定性，若系统闭环不稳定，确定其s 右半平面的闭环极点数。

自控原理习题解答第五章

4 3 2

dk 3 2 4s 18s 20s 8 0 ds

s 1.5s 0.5 3 2 s 3 s 4.5s 5s 2
2
s 3s
3
2 2 2
1.5s 5s 1.5s 4.5s 0.5s 2 0.5s 1.5 0.5
s 0.5s 3 3 2 s 4 s 4.5s 5s 2
1
4 95.58
6求与虚轴的交点
s 1.1s 1.3s 0.5s k 0
4 3 2
s4 s3 s s
2
1 1.1 0.93 0.465 1.21k 1.1k
1.3 0.5 1.1k 0
k
s1
0
2 0.465 1.21k 0,0 k 0.38;0.93s 1.1k 0

4
j
45; l 1 : 3, 4 3 (135)
4
m i 1 i
a
p z
j1
nm

0.5 0.3 j0.96- 0.3 - j0.96- 0 0.275 4
4分离点 2 ss 0.5s 0.6s 1 k 0
试绘制系统的根轨迹图。
2实轴上的根轨迹： 0,0.5 3n m 4, 渐近线的倾角和渐近线与实轴的交点 2l 1 , l 0,1,2
nm l 0 : 1, 2
n
k 答5 - 4Gs Hs ss 0.5 s 2 0.6s 1 1n 4, m 0, p1 0, p 2 -0.5, p 3 0.3 j0.96, p 4 0.3 j0.96

自动控制原理_第5章习题解答-

第5章频率特性法教材习题同步解析一放大器的传递函数为：G (s )=1+Ts K测得其频率响应，当ω=1rad/s 时，稳态输出与输入信号的幅值比为12/2，稳态输出与输入信号的相位差为－π/4。

求放大系数K 及时间常数T 。

解：系统稳态输出与输入信号的幅值比为A ==222172K T ω=+ 稳态输出与输入信号的相位差arctan 45T ϕω=-=-︒，即1T ω=当ω=1rad/s 时，联立以上方程得T =1，K =12放大器的传递函数为：G (s )=121s +已知单位负反馈系统的开环传递函数为5()1K G s s =+ 根据频率特性的物理意义，求闭环输入信号分别为以下信号时闭环系统的稳态输出。

（1）r （t ）=sin （t +30°）；（2）r （t ）=2cos （2t －45°）；（3）r （t ）= sin （t +15°）－2cos （2t －45°）；解：该系统的闭环传递函数为65)(+=Φs s 闭环系统的幅频特性为365)(2+=ωωA闭环系统的相频特性为6arctan )(ωωϕ-=（1）输入信号的频率为1ω=，因此有37375)(=ωA ，()9.46ϕω︒=- 系统的稳态输出537()sin(20.54)37ss c t t ︒=+ （2）输入信号的频率为2ω=，因此有10()A ω=，()18.43ϕω︒=- 系统的稳态输出10()cos(263.43)2ss c t t ︒=- （3）由题（1）和题（2）有对于输入分量1：sin （t +15°），系统的稳态输出如下5371()sin( 5.54)37ss c t t ︒=+ 对于输入分量2：－2cos （2t －45°），系统的稳态输出为102()cos(263.43)ss c t t ︒=-- 根据线性系统的叠加定理，系统总的稳态输出为)4363.632cos(210)537.5sin(37375)(︒︒--+=t t t c ss绘出下列各传递函数对应的幅相频率特性与对数频率特性。

《自动控制原理》答案李红星第五章

5-1
某系统结构图如题 5-1 图所示，试根据频率特性的物理意义，求下列输入信号作用时，
系统的稳态输出 c s (t ) 和稳态误差 e s (t ) （1）（2）
r (t ) = sin 2t r (t ) = sin(t + 30°) − 2 cos( 2t − 45°)
题 5-1 图
解：
系统闭环传递函数为： Φ ( s ) =
(T1 > 0, T2 > 0, T3 > 0, T4 > 0)
又知它们的奈奎斯特曲线如题 5-7 图(a)(b)(c)所示。找出各个传递函数分别对应的奈奎斯特曲线，并判断单位反馈下闭环系统的稳定性
145
题 5-7 图解：三个传递函数对应的奈奎斯特曲线分别为 b, c, a 对 G1 ( s ) =
要求画出以下 4 种情况下的奈奎斯特曲线，并判断闭环系统的稳定性： a． T2 = 0 ；
141
b． 0 < T2 < T1 ； c． 0 < T2 = T1 ； d． 0 < T1 < T2 。解： a．当 T2 = 0 时， Q ( s ) =
K ， s (T1 s + 1)
2
其开环幅相曲线如题 5-5 解图 a 所示， P = 0 ，N=2 则 Z=P+N=2，故在 s 平面右半平面有 2 个闭环极点，闭环系统不稳定； b．当 0 < T2 < T1 时， Q( jω ) =
当 τ > T 时，开环幅相曲线始终处于第三象限，如题 5-4 解图 a 所示；当 T > τ 时，开环幅相曲线始终处于第二象限，如题 5-4 解图 b 所示。
题 5-4 解图 a 开环幅相曲线

自动控制原理(孟华)第5章习题解答

137习题5-1 某系统的单位阶跃响应为c (t ) = 1-e -t +e -2t- e -4t ，试求系统的频率特性。

解：238s+8G(s)(1)(2)(4)s s s s +=+++，将s =j ω代入，得23()8+8()(1)(2)(4)j j G j j j j ωωωωωω+=+++5-2 设系统传递函数为1)1()()(12++=s T s T K s R s C 当输入信号r (t )=A sin ωt 时，试求系统的稳态输出。

解：系统的稳态输出为21()arc tan -arc tan )ss C t t T T ωωω=+5-3画出下列传递函数的Bode 图。

(1) G (s )=1121++s T s T ， ( T 1 > T 2 > 0 ) ； (2) G (s )=1121+-s T s T ， ( T 1 > T 2 > 0 )(3) G (s )=1121++-s T s T ， ( T 1 > T 2 > 0 )解：答案见胡寿松主编《自动控制原理习题集》Page709，B5-13。

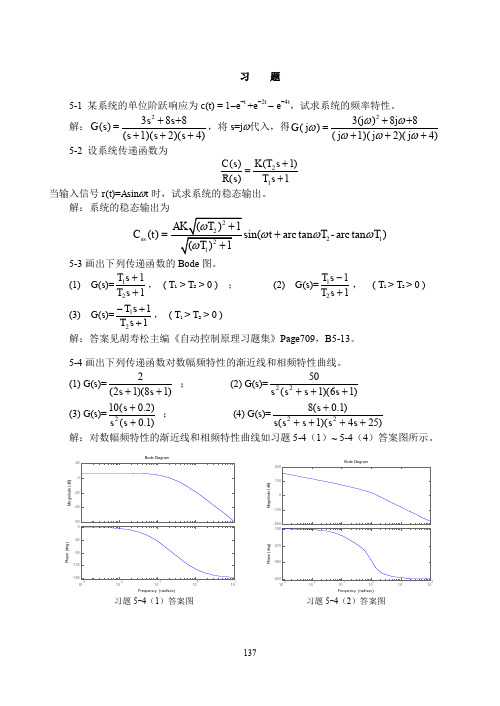
5-4画出下列传递函数对数幅频特性的渐近线和相频特性曲线。

(1) G (s )=)18)(12(2++s s ； (2) G (s )=)16)(1(5022+++s s s s(3) G (s )=)1.0()2.0(102++s s s ； (4) G (s )=)254)(1()1.0(822+++++s s s s s s解：对数幅频特性的渐近线和相频特性曲线如习题5-4（1）~ 5-4（4）答案图所示。

M a g n i t u d e (d B )1010101010P h a s e (d e g )Frequency (rad/sec)M a g n i t u d e (d B )101010101010P h a s e (d e g )Frequency (rad/sec)习题5-4（1）答案图习题5-4（2）答案图138M a g n i t u d e (d B )10101010P h a s e (d e g )Frequency (rad/sec)M a g n i t u d e (d B )10101010101010P h a s e (d e g )Frequency (rad/sec)习题5-4（3）答案图习题5-4（4）答案图5-5系统开环传递函数如下。

《自动控制原理》课后习题答案(5章)

《自动控制原理》课后习题答案（5章）5.1 系统的结构图如图5-68所示。

试依据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出ss c 和稳态误差ss e 。

⑴()t t r 2sin =⑵()()()︒︒--+=452cos 230sin t t t r图5-1解系统的传递函数：()()()21+==Φs s R s C s ()()()21++==Φs s s R s E s e 幅频特性及相频特性：()()2,2122ωωωωarctgj j -=Φ+=Φ()()2,21222ωωωωωωarctgarctg j e e -=Φ++=Φ（1）()2,2sin ==ωt t r 稳态输出：()()︒︒-=-+=452sin 221452sin 441t t c ss()︒-≈452sin 354.0t稳态误差：⎪⎭⎫ ⎝⎛-+++=2222sin 2221222arctg arctg t e ss()()︒︒+≈+=43.182sin 791.043.182sin 225t t（2）()()()()()︒︒︒︒+-+=--+=452sin 230sin 452cos 230sin t t t t t r⎪⎪⎭⎫ ⎝⎛+∠+++•-⎪⎪⎭⎫ ⎝⎛+∠+++=︒︒221452sin 221212130sin 211222j t j t c ss ()t t 2sin 225.3sin 55-+=︒ ()t t 2sin 708.05.3sin 447.0-+≈︒⎪⎭⎫ ⎝⎛-++++•-⎪⎭⎫ ⎝⎛-++++=︒︒222452sin 2221221130sin 12112222222arctg arctg t arctg arctg t e ss ()()︒︒︒︒︒︒-++•--++=4543.63452sin 410257.264530sin 510t t ()()︒︒+-+≈43.632sin 582.143.48sin 632.0t t ()()︒︒--+=57.1162sin 582.143.48sin 632.0t t5.2 若系统的单位阶跃响应：()t t e e t h 948.08.11--+-=()0≥t 试求系统的频率特性。

自动控制原理参考答案-第5章

第五章题5-1：试绘制下列开环传递函数的幅相频率特性曲线。

(1) 10G(s)H(s)(s 1)(0.2s 1)=++ (2) 25(s 1)G(s)H(s)(s 3)(s 2s 2)+=+++(3) 100G(s)H(s)(s 1)(s 3)(s 4)=+++ 题5-6：试绘制题5-1各开环传递函数的对数幅频特性渐近线和半对数相频特性曲线。

(1) 2221010122()()(1)(0.21)(1)(10.04)j G j H j j j ωωωωωωωω--==++++实频特性：)04.01)(1(210)(222ωωωω++-=P虚频特性：)04.01)(1(12)(22ωωωω++-=Q 相频特性：()arctan arctan 0.2ϕωωω=-- Nyqist 曲线：起点：0ω=(0)10P ⇒=，(0)0Q =，(0)0ϕ=终点：ω=∞()0P ⇒∞=，()0Q ∞=，()180ϕ∞=- 与虚轴交点：()0P ω= 2.236ω⇒=() 3.73Q ω⇒=- Nyqist 曲线如下：转折频率1：111T ω==；转折频率2：215T ω==对数幅频特性：()20lg ()20lg10L A ωω==-半对数相频特性：()arctan arctan 0.2ϕωωω=-- Bode 图如下：(2) 25(1)()()(3)(22)j G j H j j j ωωωωωω+=+-+ 222222225(3)(2)202(12)(9)[(2)4]j ωωωωωωωω+-+-+=+-+ 实频特性：]4)2)[(9(20)2)(3(5)(2222222ωωωωωωω+-++-+=P 虚频特性：]4)2)[(9()21(10)(22222ωωωωωω+-++-=Q相频特性：2()arctan arctan arctan 310.5ωωϕωωω=--- Nyqist 曲线：起点：0ω=5(0)6P ⇒=，(0)0Q =，(0)0ϕ=终点：ω=∞()0P ⇒∞=，()0Q ∞=，()180ϕ∞=-与虚轴交点：()0P ω= 2.09ω⇒=()0.66Q ω⇒=- Nyqist 曲线如下：225(1)0.83(1)()()(3)(22)(0.331)[(0.7)1]j j G j H j j j j j j ωωωωωωωωωω++==+-++++ 转折频率1：11 1.414T ω==；转折频率2：213T ω==对数幅频特性：5()20lg ()20lg 6L A ωω==+半对数相频特性：2()arctan arctanarctan310.5ωωϕωωω=---Bode 图如下：(3) 23222100100[128(19)]()()(1)(3)(4)(1)(3)(4)j G j H j j j j ωωωωωωωωωωω-+-==++++++实频特性：)4)(3)(1()812(100)(2222ωωωωω+++-=P虚频特性：)4)(3)(1()19(100)(2223ωωωωωω+++-=Q 相频特性：()arctan arctan 0.33arctan 0.25ϕωωωω=--- Nyqist 曲线：起点：0ω=(0)8.33P ⇒=，(0)0Q =，(0)0ϕ= 终点：ω=∞()0P ⇒∞=，()0Q ∞=，()270ϕ∞=- 与虚轴交点：()0P ω= 1.22ω⇒=() 4.77Q ω⇒=- 与实轴交点：()0Q ω= 4.36ω⇒=()0.71P ω⇒=- Nyqist 曲线如下：8.33()()(1)(0.331)(0.251)G j H j j j j ωωωωω=+++转折频率1：111T ω==；转折频率2：213T ω==；转折频率3：314T ω==对数幅频特性：()20lg ()18.4L A ωω==-半对数相频特性：()arctan arctan 0.33arctan 0.25ϕωωωω=--- Bode 图如下：题5-2：已知某一控制系统的单位阶跃响应为4t 9t c(t)1 1.8e 0.8e --=-+试求该系统的开环频率特性。

中文版教材习题五答案

z
*

30 199
30
（2）分离点为： d 0.4 ，分离角为： (2k 1)
l
2
起始角： p4 268 ， p5 268
与虚轴的交点：
K1*

0 0
K2,3*

1.034 73.04
K4*,5165.553104
K(3s 1)
s(2s 1) K(3s 1)
闭环特征方程： 2s 2 (1 3K)s K 0
闭环特征根： s1,2 (1 3K)
(1 3K)2 8K (1 3K) 9K 2 2K 1

4
4
当
K＝0
时，特征根
s1

0, s2

1 2
(1 3K ) (3K 1)2 8
(1)
G(s)

K s(s 1)2
(2)
G(s)

K(s s(s2 4s
4) 29)
(3) G(s)
K
s(s 2 4s 8)
试概略画出闭环系统根轨迹图。 5-4 参考答案：
(a) G(s)H (s) K s(s 1)2
(4) G(s) K (s 5)(s 4) s(s 1)(s 3)
-4 -3
Im
-1
0
Re 5
44
“自动控制原理”第五章习题参考答案
5-5
已知开环传递函数为 G(s)H (s)
K s(s 4)(s2 4s 20)
，请概略画出闭环系统根轨。
5-5 参考答案：
与虚轴交点：

K

自动控制原理第五章习题及答案

第五章习题与解答5-1 试求题5-1图(a)、(b)网络的频率特性。

u rR 1u cR 2CCR 2R 1u ru c(a) (b)题5-1图 R-C 网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R RR R K s T s K sCR sC R R R s U s U r c ττ ωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sC R s U s U r c )(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2 某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(t c s 和稳态误差)(t e s （1） t t r 2sin )(=（2） )452cos(2)30sin()(︒--︒+=t t t r题5-2图反馈控制系统结构图解系统闭环传递函数为: 21)(+=Φs s 频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则 )2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时, 2=ω，r m =1则 ,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2(-=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2(+=-Φ=t t j r e e e m ss ϕ（2）当 )452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ )]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ=)902cos(7.0)4.3sin(4.0--+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0--+=t t5-3 若系统单位阶跃响应h t e e t tt()..=-+≥--11808049试求系统频率特性。

自动控制原理课后习题答案第五章

自控原理第五章习题参考答案

《自动控制原理》5章课后习题参考答案.

《自动控制原理》 胡寿松第五章习题解答

自动控制原理第五章课后答案

自动控制原理及其应用课后习题第五章答案

自动控制原理卢京潮主编课后习题答案西北工业大学出版社

自动控制原理第五章课后习题答案(免费)[1]

《自动控制原理》第5章习题答案

自动控制原理课后习题答案第五章

自控原理习题解答第五章

自动控制原理_第5章习题解答-

《自动控制原理》答案 李红星 第五章

自动控制原理(孟华)第5章习题解答

《自动控制原理》课后习题答案(5章)

自动控制原理参考答案-第5章

中文版教材习题五答案

自动控制原理第五章习题及答案

《自动控制原理》胡寿松第五章习题解答

《自动控制原理》答案李红星第五章