透视图画法
透视图的基本画法1

C°
j° k° l°
c°
Fy H
g'
2
a°
1 g'
利用迹点和灭点确定直线的 全线透视,然后借助视线的 水平投影求作直线段的透视 画法,称为建筑师法。
bp
f
s N A°
B°
F
b°
a° n
L
画法几何与阴影透视讲义-透视篇
(四)用建筑师法求矩 形平面的透视(1)
第九章 建筑透视图的基本画法
fx
bp
dp
fy
n
Fx
Fy
C°
B° N
D° A
画法几何与阴影透视讲义-透视篇
x
d
b 1
g
c
4
e
3
2
fx
bp 1p
2p
3p 4p
fy
cp n
D°
E° G°
Fx
Fy
B° 1°
d° 2°
g° e°A°3°4°C°
b°
c°
a
n
画法几何与阴影透视讲义-透视篇
第九章 建筑透视图的基本画法
(三)纪念碑的二点透视
c m
d e
b
fx
n
mp
cp
bp a ep
fy
N1
C°
B° D°
Fx
c° M°
用建筑师法求矩形 平面的透视(2)
第九章 建筑透视图的基本画法
fx
bp
dp
fy
Fx
Fy
C° B°
D° A
画法几何与阴影透视讲义-透视篇
第九章 建筑透视图的基本画法
二、用建筑师法作建筑形体透视图
管道工程图画法中的透视图示

为了改进自己的学习成果,我将加强对透视图绘制技巧的 练习,多阅读相关教材和资料,加深对透视规律的理解和 掌握。
对未来学习建议
加强实践练习
拓展应用领域
关注新技术发展
建议在未来的学习中,加强对 透视图绘制技巧的实践练习, 通过大量的练习提高自己的绘 图能力和水平。
除了管道工程图外,透视图在 其他领域也有广泛的应用,如 建筑设计、机械设计等。建议 同学们在未来的学习中,拓展 透视图的应用领域,提高自己 的综合能力和竞争力。
随着科技的不断发展,新的绘 图技术和工具不断涌现。建议 同学们关注新技术的发展动态 ,及时学习和掌握新的绘图技 术和工具,提高自己的适应能 力和创新能力。
THANKS
感谢观看
透视技巧
02
运用斜线、交点等透视技巧,准确表现管道的走向和连接关系
。
细节处理
03
对阀门、法兰等连接部件进行详细绘制,提高图纸的准确性和
可读性。
实例三:特殊管道系统透视图探讨
特殊材质管道
如不锈钢、塑料等材质的管道,在透视图中表现出其独特的光泽 和质感。
非标准件处理
对于非标准件或定制件,通过透视图展示其形状、尺寸和安装方 式。
05
管道工程图实例分析与解读
实例一:简单管道系统透视图分析
管道布局
简单直线型布局,易于理解和绘制。
透视效果
通过线条的透视变化,表现出管道的远近感和立 体感。
标注与说明
包括管道直径、材质、连接方式等关键信息的标 注。
实例二:复杂管道系统透视图解读
管道交错
01
多条管道在空间中交错,形成复杂的网络结构。
透视投影要素
透视投影的主要要素包括视点、视平线、心点、基线、灭点等。视点是观察者的眼睛位置;视平线是与观察者眼 睛等高的水平线;心点是视点在投影面上的垂直投影;基线是画面上与视平线平行的线;灭点是物体上各平行线 在透视图中延伸后相交的点。
第三节 平面立体的透视图画法
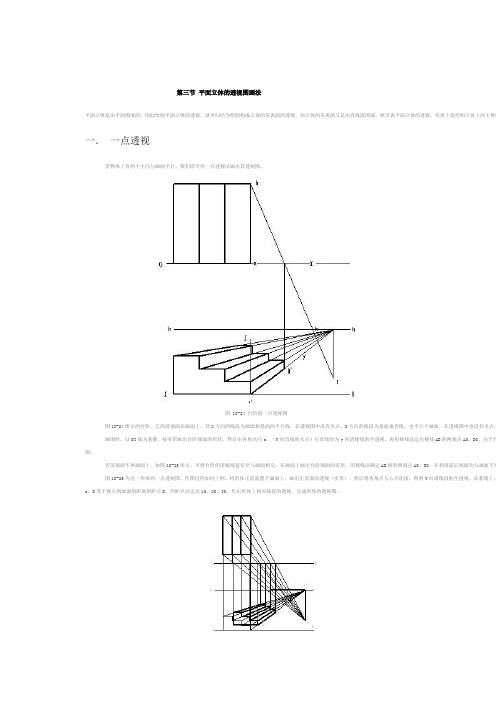
第三节平面立体的透视图画法平面立体是由平面围成的,因此绘制平面立体的透视,就可归结为绘制构成立体的各表面的透视,而立体的各表面又是由直线段围成,所以说平面立体的透视,实质上是绘制立体上的主要线一.一点透视若物体上有两个主向与画面平行,我们即可用一点透视法画出其透视图。
图 10-24 台阶的一点透视图图10-24所示的台阶,它的前端面在画面上,其X方向的线段为画面和基面的平行线,在透视图中没有灭点;Z方向的线段为基面垂直线,也平行于画面,在透视图中也没有灭点;画图时,以OX线为基准,按实形画出台阶端面的形状,然后由各角点向s,(Y向直线的灭点)引直线即为y向诸棱线的全透视,再用视线法定出棱线AB的两端点A0、B0。
由于台图。
若前端面不再画面上,如图10-25所示,可将台阶的诸棱线延长至与画面相交,在画面上画出台阶端面的实形,用视线法确定AB棱的两端点A0、B0,在利用前后端面均与画面平行图10-26为另一形体的一点透视图,作图过程如同上例。
将形体正前面置于画面上,画出正前面的透视(实形),然后将各角点与心点连接,得到Y向诸线段的全透视。
在基线上,s,D等于视点到画面的距离得距点D。
用距点法定出10、20、30,作出形体上相应线段的透视,完成形体的透视图。
图 10-25 前端面不在画面上的台阶一点透视图 10-26 建筑形体一点透视由上述作图过程可知,竖直棱线AB、CD长度相同且与画面平行、等距,其透视长度A0B0与C0D0长度也相同。
画面上的直线A10B10和C10D10分别为AB、CD的实长,虽然三角形定的透视长度A0B0与C0D0相等。
利用这一特性,在作透视图时,可将画面上的真高线平移到任何适当的位置,以便作图。
二.两点透视当物体上X、Y两个主向不与画面平行时,则物体上各个立面与画面不平行而成一定角度,因而所画出的透视图称为成角透视。
又因为X、Y方向的直线在透视中都具有灭点,故又称图 10-27 视线法画房屋的两点的透视图作两点透视时,通常采用视线法或量点法。
平行透视成角透视作图法

成角透视作图法
起点法 测点法 视线迹点法
左余点 高 度
右余点
左余点
右余点 视点
左余点 视点
右余点
视平线 基线
画面
侧视图
右余点 视点
透视图 顶视图
视平线 基线
视点
透视图 顶视图
视平线 视点
透视圆的画法
心点
视平线
距点
灯光阴影作图法
光线角度
日光阴影作图法
心点
光线角度
余点
视平线
画面
心点
基线
高1
2
视点
透视图 顶视图
视平线 基线 画面 视点
距点
心点
距点
心点
距点
心点
距点法室内景作图
距点
侧视图 正视图 高 度
宽度 长度 宽度 间距 长度
心点
距点
侧视图 正视图 高 度
宽度
长度
宽度 间距 长度
心点
视平线 基线 画面
视点
平视二点消失单视域空间的形成与特点
透视图画法PPT课件

GL
hL
f
y
f
X
PL
PL
s
真高线
F
x
F
y
(6) 作出房屋的透视图
看清题意
右立面图
平面图
正立面图
s
FX
FY
确定站点
定视平线
h
h
确定画面 位置
找灭点的 投影
(6) 作出房屋的透视图
右立面图
平面图
正立面图
s
FX
FY
h
h
(6) 作出房屋的透视图(续1)
改变作图条件--将画面线转为水平。
先画屋盖、外墙和柱子的透视。
PL
PL
a
b
c
d
GL
GL
h
PL
PL
GL
GL
HL
HL
a
FX
FY
a0
S
S
S
FY
FX
S
FY
FX
课后练习:(1)作形体的透视图。
PL
PL
画面线
hL
hL
GL
GL
基线
视平线
a
fx
a
fY
FX
FY
A
s
(2) 求形体的两点透视
立面图
平面图
PL
PL
画面线
hL
hL
视平线
GL
GL
基 线
s
站点
Fx
Fy
(3) 求形体的 两点透视
PL
GL
GL
HL
HL
S
F
(a)
(b)
(c)
(a) 已知两面投影; (b) 作基透视; (c) 作高度透视
透视图画法入门学习

F2
F1
F2
三点透视是由于产品的表面与地面倾斜形成的。产品倾斜面的平行线组的消失点不在视平线上。
三点透视的画面也是倾斜的。三组平行线分别消失于三个灭点。
壹
贰
(3)三点透视
一点透视作图法(平行透视) 例题1. 设长方体:长×高×宽=40×20×30cm,放在视点下方,视高60cm,物体正面在画面上,左边中点偏离30cm,画面离视点80cm,求透视图。
03
视点:观察点。
04
基线:基面与画面的交线。
05
视平面:过视点的水平面。
06
视距:视点到画面的距离。
07
视高:视点到基面的距离。
08
视线:视点与物体任意点的连线。
2、透视图常用术语:
透视图和轴侧图一样,都是单面投影,但二者有很大区别:轴侧图是用平行投影原理,物体上平行的线条在轴侧图上仍然平行;而透视图是用中心投影原理,物体上平行的直线在透视图上不一定平行。等长的线段有近长远短的特点。平行线组在远处消失于一点。
大型物体(建筑物)
在物体下部
向内靠近
中型产品,视平线应放在物体高度内偏上位置,俩灭点稍向内靠近,且在画面之外。
大型物体,视平线在物体下部,两灭点向内靠拢,体现雄伟壮观形象。
物体立面与画面之间的偏角每改变一个角度,其透视形象也随着改变。
物体立面与画面之间的偏角越小,透视收敛越慢,该面越宽。
水平线的灭点落在视平线上。 根据物体与画面的相对位置,以及观察者与物体的角度不同,透视图可分为:一点透视,两点透视,三点透视。
3、透视投影的规律
一点透视 当物体的主要面或主要轮廓线平行于画面时,只有与画面垂直的那一组平行线的透视有灭点(就在心点),灭点必在视平线上。如图:
04透视图的基本画法及视点

F2 Mx Fx=S Fx ※由此可得到求作斜
s g
由量点Mx作直线,与h-h的夹角为 a,此直线与通 线灭点的具体方法:过Fx的铅垂线相交,交点F1就是斜线AB的灭点。
二、用斜线灭点作透视图的实例
例:求作双坡房屋的透视图
p
h-h
d
c b a c′
b a
d′
b′
a′
g-g
s
p
作图步骤:
1、用建筑师法或量点法求 出房屋的透视平面图。
a
b
g
d
c
sg
g
a 1 A B
60
b 2
g
D
s′
z
h
D
h
g
dp sg
ap 1
bp
z1
g
2
§4-2
一、与画面相交的水平线的量点 和分量点的概念
1、量点、分量点、量线
量点法——建筑透视图 h 画法之二
g
P
M
Bp Ap T B
F
h
F
h
A1
B1
g
P
B
A g T
M Bp Ap
h
g
S
p
A
B1 A1
s
G
T m A1
§4-4 网格法——建筑透视图画法之三
一、网格法的概念 二、网格法画透视图实例 已知建筑物的平、立面图,用网格法完成其透视(放大 一倍画出) 作图步骤: (1)把建筑平面置于特定的网格中。 (2)用降下基面画网格透视。 (3)利用网格透视画建筑平面的透视。 (4)回升基面,确定高度,完成外形轮廓的透视。 (5) 用定比分割画门、窗及墙面划格线……等细部。 (6) 墨线加深,作出配景,完成全图。
景观制图——透视图画法课件

SketchUp是一款直观易用的3D建模软件,也常用于透视 图的绘制。其内置的渲染和视角工具可以帮助用户快速生 成高质量的透视图像。
Adobe Illustrator
作为一款专业的矢量绘图软件,Adobe Illustrator也支持 透视图的绘制。它提供了丰富的绘图工具和精确的测量功 能,满足绘制者的各种需求。
03
透视图的应用
景观设计中的透视图应用
场景表现
透视图能够直观地展现景观设计 的场景,包括地形、植被、水体 、建筑等各个要素,使观察者更
好地理解和感受设计意图。
空间感表现
透视图通过线条和阴影的运用,能 够准确地表达景观设计中的空间感 和层次感,有助于观察者对空间进 行感知和把握。
设计评估
透视图可以作为评估景观设计效果 的重要工具,通过观察和分析透视 图,可以对设计方案进行优化和改 进,提高设计质量。
建筑设计中的透视图应用
01 02
建筑外观表现
透视图能够真实地展现建筑的外观造型和设计风格,包括建筑的立面、 屋顶、门窗、装饰等细节,使观察者更好地了解建筑设计的特点和亮点 。
室内空间表现
透视图可以表达建筑室内空间的设计和布局,包括房间的大小、高度、 采光、家具摆放等,有助于观察者对室内环境进行感知和评价。
透视图的分类
01
02
03
一点透视
也称为平行透视,在这种 透视中,所有平行的线条 在远方汇聚于一个消失点 。
两点透视
也称为成角透视,在这种 透视中,平行的线条在两 个方向上汇聚于两个消失 点。
三点透视
也称为倾斜透视或鸟瞰透 视,用于表现高大建筑物 或场景的仰视或俯视效果 。
透视图的基本元素
透视PPT课件

a Pb
例4 作纪念碑的透视图。
例 4
(
两
点
透
视)
画面线 PH
s h
基线 s P
例5 求形体的透视图和其底面在降低基面后的透视图。
例
5 ( 两 点 透
视)
PH
A
a(b)
真高线
h
B P
P1
s
画面线 PH
视平线 h 基线 P
基线1 P1
例6 作形体的透视图。
PH 画面线
vx
h
视平线 VX
P
P
例11 作出房屋的透视图
例11(两点透 视)
h
看清题意
确定画面 位置 确定站点 定视平线
找灭点的 投影
正立面图
h
右立面图
vY
平面图
vX
s
例11 作出房屋的透视图(续1) 改变作图条件--将画面 线转为水平。 先画屋盖、外墙和柱子 的透视。
PH
h 正立面图 P
(续1)
PH
h P s
例11 作出房屋的透视图(续2) 画走廊 画门窗
透视图的分类
透视图的分 类
1. 一点透视 画面与筑物的长度和高度两组棱线的方向平行, 此时,宽度方向的棱线有一个灭点。
2. 两点透视 画面与建筑物的高度方向的棱线平行,而与另外两组 棱线的方向倾斜,此时,长度方向和宽度方向的棱线各有一个灭点。
3. 三点透视 画面与建筑物的
长、宽、高三组方向倾斜,此时, 灭点一
a
例
6 ( 两 点 透 视)
a
vY PH
s VY h
A 基线 P
例7 求形体的两点透视
PH
透视图的画法

2.视距: 建筑物与画面的位置不变,视高已定,在室内一点透视图中 ,当视距近时,画面小;当视距远时 ,画面大。在立方体的两点透视中, 当视距近时,消失点Vx、 Vy距离较 小;当视距远时,Vx’、Vy’距离大。 即视距越近,立方体的两垂直面缩 短越多,透视角度越陡。 建筑物与视点的位置不变,视高已定, 若视距近(En和P.P.的距离),则 两消失点的间距亦小,透视图形小; 若视距远(En和P’.P’.的距离), 则两消失点的间距大,透视图形大, 两图形相似(图12、13、14)。
1.视角: 在画透视图时,人的视野可假设为以视点E为顶 点圆锥体,它和画面垂直相交,其交线是以C.V .为圆心的圆,圆锥பைடு நூலகம்角的水平,垂直角为60° ,这是正常视野作的图,不会失真。在平面图上 ,在视角为60°范围以内 的立方体,球体的透视形 象真实,在此范围以外的 立方体,球体失真变形 (图10、11)。
室内透视
• • • • •
透视的画法总结

用交线法求线段的透视
在H面上过A点任 如图所示,已知H面上直线AB的画面迹 点、灭点及透视方向NF,确定A、B两点的 作一辅助线AA1与画 透视A°、B° 面相交,则辅助线 AA1的灭点为F1,因 此AA1 的透视方向为 A1F1。A点是AB与AA1 的交点,故NF、A1 F1的交点即为A点的 透视A°。 同理,可作出B 点的透视B°。过B 点所作的辅助线, 可取与AA1平行,则 可利用同一灭点F1 作图。
真高线及辅助线灭点的位置与K的方向有关。
6.2.3 集中真高线
在绘制建筑形体透视图时,一般是首 先画出建筑形体的基透视,然后求出各点 的透视高度,依次连线完成透视图的绘制。 若在量取高度时,每一点均取一条真高线, 则所取的真高线数量太多,不利于作图。 此时,可采用集中真高线量取建筑形体各 轮廓线的透视高度。
分析: AB为正 垂线,所 以灭点就 是主点s′。
作图步骤: 1.求出AB的全透视。 2.连接sa 、 sb分别交ox轴于a1、b1点。 基面位于画面的上方
3.分别过a1、b1作竖直线交Fn′于A°、B°,则A°B°即为所求。
6.3.2 交线法
两直线交点的透视,必为两直线透视的交点。
如图所示,AB、CD两线段 交于K点,在画面V上的透视 A°B°、C°D°相交于K°点, 则K°必定为K点的透视。 由此 ,若空间一点为某 两线段的交点,要求该空间 点的透视,可以先求出两线 段的透视,则它们透视的交 点即为空间点的透视。
集中真高线
如图所示,A、B两点等高,A1a1是A点的真高线。
若把B点平移到AA1上 的B1点处,则b平移到 aa1上b1处
根据直线上点的透视 性质,B1°在FA1上、 b1°在Fa1上,则 B1°b1°为 B1的透视 高度。 由于BB1平行于基线, 所以B° B1°、 b° b1°也平行于基线。 因此可在A点的真高线A1a1上量取B点的真高,返回即可 求出B点的透视高度B°b°。
《透视图画法》课件

简介
探索透视图画法,介绍其概念、作用,以及本课件内容的总结。
透视原理
1
基本透视法
深入了解基本透视原理,如单点和两点透视法。
2
中心投影法
学习如何利用中心投影法绘制更真实的透视图。
3
平行投影法
了解平行投影法,
透视坐标系的建立
学习如何建立透视坐标系,确 保透视图的准确性。
透视线的绘制
掌握绘制透视线的技巧,使透 视图更具立体感。
透视图的投影部分
了解透视图的投影原理,绘制 透视图的投影部分。
基本图形的绘制
1 正方形和长方形的透视图绘制
掌握绘制正方形和长方形的透视图的技巧和方法。
2 圆形和椭圆的透视图绘制
学习如何绘制圆形和椭圆的透视图,使其具有立体感。
3 右棱柱、右圆柱、右圆锥和右棱锥的透视图绘制
探索绘制右棱柱、右圆柱、右圆锥和右棱锥的透视图的技巧。
高级应用
多点透视法
学习利用多点透视法创造出更复 杂的透视效果。
空间环境的透视处理
探索如何运用透视处理技巧绘制 逼真的城市景观。
透视图的应用案例
欣赏一些以透视图为基础的独特 艺术案例,启发你的创作灵感。
总结
强调透视图画法的应用及其重要性,分享经验和技巧总结。
参考资料
推荐相关书籍和参考网站,帮助进一步学习透视图画法。
《园林制图与设计初步》课件——13 透视图基础

35
36
37
38
39
40
41
42
43
44
一点透视鸟瞰效果图
45
46
两点透视与一点透视的差别
47
两点透视
• 物体上的主要表面与画面倾斜,但其上的 铅垂线与画面平行,所作的透视图有两个 灭点,称为两点透视。
48
网格画法
49
50
画法2
51
52
53
54
量点法绘制体块两点透视
园
林
制
图
与
设 计
初
步
透视图基础
透视原理
3
透视图的特点
• 近大远小 • 近高远低 • 近长远短 • 近疏远密 • 互相平行的直线的透视交汇于一点
4
一点透视
• 物体上的主要立面(长度与高度方向)与 画面平行,宽度方向的直线垂直于画面所 作的透视图,只有一个灭点,称为一点透 视。
7
主点
55
56
57
58
59
60
61
两点透视效果图欣赏
62
63
64
65
66
67
68
69
70
71
小鸟瞰
72
鸟瞰
73Biblioteka 74一点变两点透视
75
76
视高
画面线 视平线
基线
站点
12
长度、高度方向无灭点 宽度方向有灭点
站点
画面线 视平线 基线
13
请同学们随意画一个网格,及自由图形
14
15
16
17
透视网格的作用
18
19
20
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 7 ( 两 点 透 视 )
平面图 PL
站点 s
Fy hL GL
(3) 求形体的
例 8
(
两
点
透
视
两点透视
)
PL
hL Vx
GL 立面图
画面线
PL
视平线
hL
Vy
基线
GL
s 站点
(4) 作台阶的两点透视
先画两边 挡板的透视。
再画右挡板 内侧台阶轮廓 线的透视。
PL
hL
Fx
a(b)
真高线
a
b P
s
例9(台阶 的两点透 视)
d
俯视图
c
PH
画面线
h主点s'
视平线 bp
例
b
3 (
一
点
透 视
)
a
PH ap
h
Do
Bo Ao
Co c' (d') a'(b')
P
左视图 基 线
P
主视图
s 站点
第三节 透视图的作法
一、一点透视 (二)量点法(距点法)
所谓量点法,就是利用量点求作透视长度的作 图方法。
(1)量点法作图原理
平行于直线AA1何BB1
b
透视
图的
H 基面
画图 步骤
1. 求灭点。
2. 求各直线的透视
方向。
PL
3. 求端点的透视。
4. 连各端点的透视 并加粗。
画图时 不需画外框线 hL
视 高
GL
a ap
n
N Ao L 画面交点
bp
v
画
PL 面
线
视
距
站点 s
Bo
灭点 V
视
hL
平 线
透视方向
P
画面
GL
基 线
例1 作出基面上的方形 网格的一点透视。
基透视a0
点的透视与基透视的连线必位于同一条铅垂 线上。
点的透视作图
GL A0
GL
ax0
VP GL
A0 GL
(二)画面上点的透视
A0
A0 VP
(三)基面上点的透视
HL
s´
HL
A0
A
A0
GL a
GL
VP
A
PL
PL
(四)画面后空间中点的透视
GL A0
GL
ax0
VP GL
A0 GL
(四)画面前空间中点的透视
7(6)
PL PL
2(3)
F HL GL PL
(a)
(b)
S
(c)
S
(a) 已知两面投影; (b) 作基透视; (c) 作高度透视
例: 作四棱柱的一点透视
HL
HL
GL
GL
Hale Waihona Puke PLPL课堂练习1: 求水平线的一
点透视。
PL
b a
H 基面 PL
站点 s
视
hL
hL
平 线
GL
P 画面 GL
水平线的透视的 画图步骤
HL
FY
h
GL d
a
GL
c
GL
a0
b
PL a
S
FX HL GL PL
FY
FX
S S
FY
FX
S
课后练习:(1)作形体的透视图。
PL 画面线
fx
例
6 ( 两 点 透 视)
a
fY PL
hL
视平线 FX
GL
a
s FY hL
A 基线 GL
(2) 求形体的两点透视
PL
画面线
hL Fx
视平线
GL
立面图
基线
s
(6) 作出房屋的透视图
h
正立面图
例12(两点透视)
h
右立面图
FY
平面图
FX
s
(6) 作出房屋的透视图(续1) 改变作图条件--将画面 线转为水平。 先画屋盖、外墙和柱子 的透视。
PL
hL 正立面图 GL
(续1)
PL
hL GL s
PL
hL
正立面图
GL
(续1)
PL
hL GL
S
(6) 作出房屋的透视图(续2) 画走廊 画门窗
C0
B0
GL
c
A0
GL
立体俯视图
d b
PL fx
fy
d0
a b0
PL
S
视线法绘制不与画面相交的形体的透视图的作法
HL
FX
HL
FY
立体主视图
GL
A0
c
T
GL
立体俯视图
d b
PL
fx
a
d0 a0 t fy
PL
S
例2 作出基面上的方形 网格的两点透视。
延长这些线至画面
PL hL Fx
灭点
画面线 视平线
1、视线法的作图原理
Vc
A
A0
VP
a
ax
HL A0
a
PP
Vc
HL
A
GL a ax
GL
GP
视线法求基面上点的透视
2、视线法作一点透视方法
1´(8´) 4´(5´)
8(5) 1(4)
2´(7´)
3´(6´)
HL
7(6) 2(3)
50
GL 40
8(5)
PL1(4) 5´
F HL
HL
10
60
30
GL GL
b1
(c)透视图
d1
c1
a1 b1
三点透视
第二节
一、灭点
透视规律
Pp F
直线的透视求法
D0
D
C0
C B B0
A
Vp
s Gp
推论:
画面上的直线,其透视为直线本身。
平行于画面的直线没有灭点
两相互平行的画面平行线
与画面相交的平行线有共同的灭点,亦即它们的透视都相 交于这个灭点
F
迹点和灭点
迹点N 灭点V 全透视NV
F
T
第二节 透视规律
求柱列的透视 S
h X
PH
作 室 内 的 一 点 透 视 图 ( 续 3 )
(7) 作室内的一点透视图(续4)
作室内的一点透 视图(续4)
室内的一点透视
用量点法求建筑形体的透视
立面图
x 10 9
8
平面图 my
y 5
4
3
mx
2
n2
7
6
n1 1
(a)已知条件
立面图
x 10 9
8
平面图 my
y 5
4
二、迹点 不与画面平行的空间直线与画面的交点称为
直线的画面迹点。
F
T
第二节 透视规律
三、各种位置点的透视求法 (一)点的透视规律
点的透视仍为一个点,点位于画面上时, 其透视为其本身。
点的透视与基透视的连线必位于同一条 铅垂线上。
点的透视——点与视点连线和画面的交点
视线SA
透视A0
基投影a
A0
x d 10 9
8
my n1
y
5
4
c
3
72
mx
a
n2
16
b
fy Pl
Hl Fx
My
s
Mx
Fy Hl
gl'
101 91
81
n11 71a121 n12 31 41 51
g‘l
b
用量点法求建筑形体的透视
D° d°
d° d°
N1
B° N2
n1
A
b°
n2
C° c°
n1 a
n2 c°
n1
b° n2
d1
c1
a1
视点(S)—人眼所在的位置,即 投影中心。
站点 (s)—人站立的位置,即视 点在基面上正透影。
主点(s')—视点在画面上的正投
影。 视高 (Ss)—视点至基面的距离。
视距 (Ss')—视点至画面的距离。
画面 P
基面H 视 高 P
s'
视 距
P 视点 S
视 s高
站点
透视术语
透视术语(续)
视平线(h-h)—过视点的水平面与画面的交线。
物体上的主要表面与画面倾斜,但其上 的铅垂线与画面平行,所作的透视图有两个 灭点,称为两点透视,如图3-8所示。
五、透视图的分类
图3-8 两点透视
五、透视图的分类
(三) 三点透视
物体上长、宽、高三个方向与画面均不 平行时,所作的透视图有三个灭点,称为 三点透视。在这三种透视图中,两点透视 应用最多,三点透视因作图复杂,很少采 用。
FAB
心点s′ 量点M
VP
A0
A
B0
A1
B
s
B
1
TAB
图3-21 量点法求取直线的透视
量点法
FAB
s′ M
hL
A0 B0
a1
gL
b1
TAB
a
b
fab
a1 m b1 tab
pL
s (1)灭点F到量点M的距离等于灭点到视点的距离。因此,在实际绘图中, 量点M的求法:在视平线上过灭点F量取长度为视点到灭点的距离处即为量点 M。 (2)在平行透视中,量点与灭点的距离恰好就是视距,所以,平行透视中 的量点通常为距点,利用它来左图也就是距点法。
