系统辨识实验报告1
系统辨识实验报告
i=1:800; figure(1) plot(i,Theta(1,:),i,Theta(2,:),i,Theta(3,:),i,Theta(4,:),i,Theta(5,:),i,T title('待估参数过渡过程') figure(2) plot(i,Pstore(1,:),i,Pstore(2,:),i,Pstore(3,:),i,Pstore(4,:),i,Pstore(5,: title('估计方差变化过程')
最小二乘法建模:
二、三次实验 本次实验要完成的内容: 1.参照index2,设计对象,从workspace空间获取数据,取二阶,三阶 对象实现最小二乘法的一次完成算法和最小二乘法的递推算法(LS and RLS); 2.对设计好的对象,在时间为200-300之间,设计一个阶跃扰动,用最 小二乘法和带遗忘因子的最小二乘法实现,对这两种算法的特点进行说 明; 实验内容结果与程序代码: 利用LS和RLS得到的二阶,三阶参数 算法 阶次 A1 A2 A3 B0 B1 B2 B3 LS 二阶 -0.78420.1373 -0.00360.5668 0.3157 RLS 二阶 -0.78240.1373 -0.00360.5668 0.3157 LS 三阶 -0.4381-0.12280.0407 -0.00780.5652 0.5106 0.1160
测试对象流程图 实验结果为:
2、加入噪声干扰 搭建对象
实验结果:
加入噪声干扰之后水箱输出不平稳,有波动。
实验二:相关分析法 搭建对象:
处理程序: for i=1:15 m(i,:)=UY(32-i:46-i,1);
end y=UY(31:45,2); gg=ones(15)+eye(15); g=1/(25*16*2)*gg*m*y; plot(g); hold on; stem(g); 实验结果: 相关分析法
系统辨识实验报告

系统辨识仿真实验根据系统已知的输入输出测量值(200个),进行最小二乘递推辨识(三阶)。
解:假设33221111)(----+++=z a z a z a z A221101)(---++=z b z b b z B 选择数据输入输出为:19510.26463 28.59951801 19621.976 34.33532814 19742.25396 35.76927848 20026.74433 38.3185258 19956.81167 40.23046349 19678.31876 44.21366407 19823.0536 45.32895813 19903.22043 47.08156767 20017.90925 47.08156767 20068.86682 47.71888023 20330.54353 56.00393622 20235.55444 61.73974343 20371.11527 61.42108715 20267.92301 63.49235151 20354.37094 63.65167965 20313.237 65.08563145 20378.58646 66.83823953 20430.65934 67.31622395 20354.91136 69.06883204 20596.50492 67.63488023 20584.24921 68.75017575 20539.29139 70.18412756 20413.59405 72.41472006 20461.48464 72.89270375 20588.68067 72.5740482 20429.32533 75.12329625 20491.1173 75.4419518 20616.40139 75.12329625 20486.99974 77.35388802 20451.52196 78.62851168 20510.68495 78.94716796 20489.94502 80.06246349 20516.16691 80.69977605 20605.64208 80.69977605 20567.65474 81.97440117 20544.64453 83.08969523 20488.93193 84.52364849 20543.67357 84.84230477 20534.4451 85.79827215 20476.70122 87.23222395 20545.34424 87.39155209 20550.1365 88.18819279 20522.46566 89.30348978 20525.82397 90.10013048 20783.50983 88.34752094 20516.72757 91.8527371 20502.24143 92.80870302 20582.6349 92.80870302 20503.70023 94.40198442 20551.03311 94.7206407 20518.46294 95.83593768 20532.85473 96.47325024 20514.9032 97.42921616 20480.30159 98.54451315 20508.59476 99.02249757 20663.99196 98.22585686 20533.19627 100.2971198 20464.57811 101.731073 20490.48136 102.2090574 20516.02613 102.6870419 20493.41425 103.6430078 20438.21948 104.9176329 20493.59845 105.0769611 20453.26103 106.192258 20475.81868 106.6702395 20450.21912 107.6262084 20423.90258 108.5821772 20412.80188 109.3788179 20401.10398 110.1754557 20404.74114 110.8127683 20391.96749 111.609409 20378.59636 112.406049720380.56057 113.0433622 20397.9799 113.5213437 20351.30919 114.6366407 20399.3989 114.7959688 20351.77222 115.9112658 20351.1081 116.5485725 20349.96542 117.1858851 20332.41135 117.9825316 20330.19319 118.6198442 20295.63143 119.575813 20308.15171 120.0537916 20288.4473 120.8504323 20300.01103 121.3284167 20263.41783 122.2843856 20273.9061 122.76237 20268.10307 123.3996826 20245.88924 124.1963233 20239.01074 124.8336358 20215.72202 125.6302707 20207.76807 126.2675833 20151.53768 127.3828802 20174.13489 127.7015365 20180.5603 128.1795209 20170.6944 128.8168335 20144.4177 129.6134742 20133.47634 130.2507868 20153.92262 130.569443 20110.39866 131.5254119 20129.88956 131.8440623 20117.27525 132.4813749 20072.31734 133.4373437 20074.44089 133.9153281 20028.40751 134.871297 20013.52278 135.5086095 19998.16007 136.1459221 19998.25218 136.6239065 19982.053 137.2612191 19965.37583 137.8985316 19996.01911 138.0578598 19946.87942 139.0138228 19928.88779 139.6511353 19910.41819 140.2884479 19891.4706 140.9257605 19872.04502 141.563073 19852.14146 142.2003856 19831.75991 142.8376982 19826.8332 143.3156826 19805.61518 143.9529951 19783.91918 144.5903077 19761.74519 145.2276203 19739.0938 145.864927 19731.89667 146.3429114 19708.40823 146.980224 19700.37462 147.4582084 19691.98252 147.9361928 19667.29912 148.5735054 19642.13773 149.2108179 19616.49836 149.8481305 19606.31382 150.3261149 19595.77079 150.8040993 19568.93646 151.4414119 19541.62415 152.0787244 19513.83443 152.7160312 19517.43178 153.0346874 19488.92451 153.672 19444.00644 154.4686407 19414.4237 155.1059533 19400.2958 155.5839377 19401.74221 155.902594 19387.01683 156.3805784 19340.06732 157.1772191 19340.31878 157.4958754 19308.46562 158.1331879 19276.13447 158.7705005 19259.25874 159.2484791 19242.02394 159.7264635 19224.43065 160.2044479 19222.41168 160.5231042 19188.2881 161.1604167 19169.61934 161.6384012 19166.52492 161.9570574 19131.32528 162.5943759 19111.58164 163.0723544 19107.41175 163.3910107 19071.13723 164.0283233 19066.25036 164.3469796 19045.19227 164.8249581 19007.8423 165.4622707 19001.87997 165.780927 18979.74524 166.2589172 18973.1866 166.5775618 18934.52217 167.214874418911.31199 167.6928647 18887.74331 168.1708549 18879.75071 168.4894995 18855.58456 168.9674898 18862.92671 169.1268121 18838.28258 169.6048023 18813.27995 170.0827926 18787.92 170.5607712 18762.20156 171.0387498 18736.12347 171.51674 18725.62029 171.8353963 18698.94588 172.3133749 18687.84523 172.6320312 18660.57218 173.1100214 18648.87403 173.4286777 18621.00467 173.9066563 18608.70905 174.2253126 18580.24103 174.7033028 18551.4157 175.1812814 18554.09634 175.3406154 18540.72525 175.6592717 18511.18294 176.1372502 18497.21437 176.4559065 18467.07459 176.9338851 18436.57515 177.4118754 18437.58401 177.5711977 18422.53998 177.8898539 18407.25696 178.2085102 18375.80156 178.6865005 18343.98882 179.1644791 18343.68206 179.323813 18327.32358 179.6424693 18294.79387 180.1204479 18293.77013 180.2797819 18260.76244 180.7577605 18259.26072 180.9170945保存为shuju.txt 文件。
系统辨识实验1实验报告

实验报告--实验1.基于matlab的4阶系统辨识实验课程:系统辨识题目:基于matlab的4阶系统辨识实验作者:专业:自动化学号:11351014目录实验报告 (1)1.引言 (2)2.实验方法和步骤 (2)3.实验数据和结果 (2)4.实验分析 (4)1、 引言系统辨识是研究如何确定系统的数学模型及其参数的理论。
而模型化是进行系统分析、仿真、设计、预测、控制和决策的前提和基础。
本次实验利用matlab 工具对一个简单的4阶系统进行辨识,以此熟悉系统辨识的基本步骤,和matlab 里的一些系统辨识常用工具箱和函数。
这次实验所采取的基本方法是对系统输入两个特定的激励信号,分别反映系统的动态特性和稳态特性。
通过对输入和输出两个系统信号的比较,来验证系统的正确性。
2、 实验方法和步骤2.1 实验方法利用matlab 对一个系统进行辨识,选取的输入信号必须能够反映系统的动态和稳态两个方面的特性,才能更好地确定系统的参数。
本次实验采取了两种输入信号,为反映动态特性,第一个选的是正弦扫频信号,由下面公式产生:选定频率范围 ,w(t)是时间t 的线性函数,具有扫频性质,可以反映系统的动态特性。
为反映稳态特性,选的输入信号是阶跃信号。
以上的到两组数据,利用matlab 的merge()函数,对两组数据融合,然后用matlab 系统辨识工具箱中的基于子空间方法的状态空间模型辨识函数n4sid()来对系统进行辨识2.2 实验步骤(1)建立一个4阶的线性系统,作为被辨识的系统,传递函数为3243211548765()125410865s s s G s s s s s -+-+=++++(2)产生扫频信号u1和阶跃信号u2(3)u1、u2作为输入对系统进行激励,分别产生输出y1和y2 (4)画出稳态测试输入信号u1-t 的曲线,和y1-t 的曲线 画出动态测试输入信号u2-t 的曲线,和y2-t 的曲线(5)使用merge()函数对u1-y1数据和u2-y2数据进行融合,并使用n4sid()函数对系统进行辨识。
系统辨识实验
实验一:系统辨识的经典方法实验目的:掌握系统的数学模型与系统的输入、输出信号之间的关系,掌握经典辨识的实验测试方法和数据处理方法。
熟悉MATLAB/Simulink环境。
实验内容:1.用阶跃响应发测试给定系统的数学模型在系统没有噪声干扰的条件下通过测试系统的阶跃响应获得系统的一阶加纯滞后或者二阶加纯滞后模型,对模型进行验证。
2.在被辨识系统中加入噪声干扰,重复上述1的实验过程。
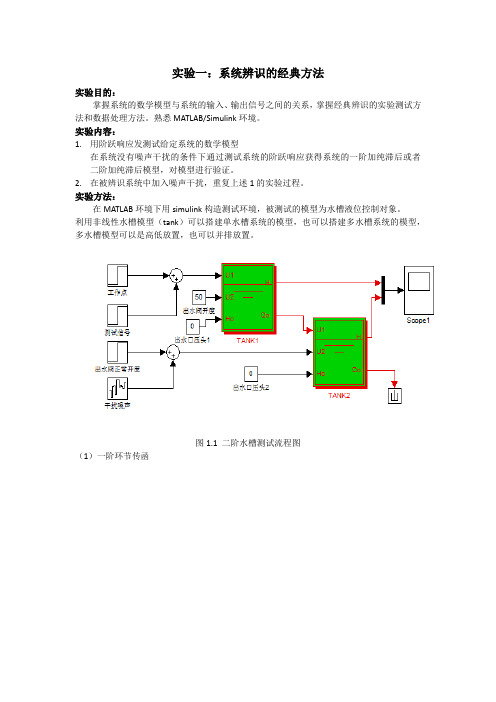
实验方法:在MATLAB环境下用simulink构造测试环境,被测试的模型为水槽液位控制对象。
利用非线性水槽模型(tank)可以搭建单水槽系统的模型,也可以搭建多水槽系统的模型,多水槽模型可以是高低放置,也可以并排放置。
图1.1 二阶水槽测试流程图(1)一阶环节传函利用两点法,找到 , 的点,对应得到 , ; 运用公式得到所以确定(2)二阶环节传函确定找到 , 的点,对应得到 , ;运用公式求的所以确定思考题1()=0.39y t 2()=0.63y t 122=2 1.1-2.3=-0.1t t τ=-⨯212()T t t =-1=1.1t 2=2.3t 122t t τ=-212()=2(2.3 1.1) 2.4T t t =-⨯-=()y y 27.1K ==2.71u u 10∞∆==∆∆1()=0.4y t=9.1t20.909T =1 2.121T =()y y 26.6K ==2.66u u 10∞∆==∆∆实验二相关分析法实验目的:掌握相关分析法测试系统数学模型的过程和方法。
掌握应用移位计数器设计M序列信号发生器的方法。
实验内容:1.设计并实现PRBS伪随机序列信号(M序列)发生器;2.应用相关分析法测试给定系统的数学模型。
使用伪随机序列信号测试系统在有噪声情况下的输出,用相关分析法辨识系统的数学模型。
3.模型验证。
实验方法:测试对象可以与实验一相同。
应用MATLAB/Simulink设计PRBS伪随机信号(M序列)发生器,可以用JK触发器构造的移位计数器实现,也可以用程序实现。
系统辨识实验报告

系统的数学建模与辨识实验报告编号:8姓名:学号: 1电加热炉动态特性辨识实验报告一.实验目的通过实验了解辨识方法在工程应用中的一些实际问题;了解数据获取和数据处理的各种方法和手段,掌握各种辨识方法的应用特点。
二.实验内容1.数据获取按照电加热计算机控制系统使用说明,加热温箱并实时监测温度。
当温度升高到一定高度基本不再发生变化时,加入辨识信号。
本设计辨识信号采用伪随机二维序列中的M序列,由于设计的M序列过长,从中截取部分作为辨识信号。
设定辨识信号的采样周期和整个辨识信号循环次数,加入辨识信号记录温度随电压变化的数据结果。
2.数据处理观察实验数据,可发现扰动较严重,需要对数据进行预处理以便进行后续辨识。
对采集数据进行滤波等处理,实验输入为M序列长度为30,由于实际采集周期为2秒,所得数据远大于需要用到的数据,同时为了提高精度,减少扰动因素影响,数据处理过程中,当输入一个M序列元素后,采集到的数据中取最后5个数据求其平均作为该输入的输出结果。
数据处理最终结果为30组输入和输出,将其生成为.mat文件以供后续离线辨识使用。
3.离线辨识利用处理过的数据选择某种辨识方法进行参数估计,并判断阶次及迟滞。
辨识完成后,进行模型验证。
三.实验操作1.设定相关实验参数,启动试验设备。
本实验设置的加热电压为60V,温度采样间隔为2s,开始实验,加热温箱系统,并通过客户端软件实时观察温箱温度,并记录,等待温箱温度升高到一定高度不再有明显上升变化。
2. 设计辨识信号考虑到实验加热电压为60V,整个系统的加热电压为之前设置的系统加热电压与辨识信号电压的和,为了在较短时间内也能产生一定的变化,辨识电压值不宜过小,选取辨识信号电压为10V 。
此时,加入辨识信号后的整个系统电压在50V 和70V 来回跳动。
辨识序列采用M 序列,并使用庞中华系统辨识程序中的M 序列生成程序,序列长度设置为31,结果如下图所示:3. 当第一步的温箱电压升高到一定高度,不再有明显升上变化时,便可认为系统已经稳定。
系统辨识实验报告30288
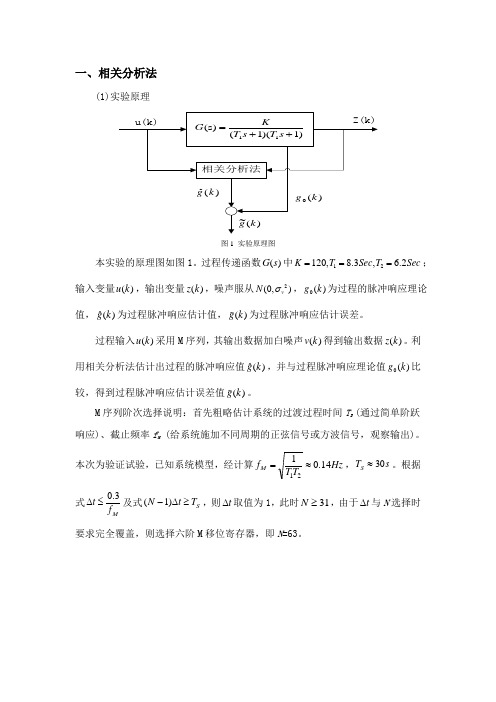
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===;输入变量()u k ,输出变量()z k ,噪声服从2(0,)v N σ,0()g k 为过程的脉冲响应理论值,ˆ()gk 为过程脉冲响应估计值,()g k 为过程脉冲响应估计误差。
过程输入()u k 采用M 序列,其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()gk ,并与过程脉冲响应理论值0()g k 比较,得到过程脉冲响应估计误差值()g k 。
M 序列阶次选择说明:首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号,观察输出)。
本次为验证试验,已知系统模型,经计算Hz T T f M 14.0121≈=,s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(,则t ∆取值为1,此时31≥N ,由于t ∆与N 选择时要求完全覆盖,则选择六阶M 移位寄存器,即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列:M 序列的循环周期63126=-=N ,时钟节拍1t Sec ∆=,幅度1a =,移位寄存器中第5、6位的内容按“模二相加”,反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下:② 生成白噪声序列: 程序如下:③ 过程仿真得到输出数据:如图2所示的过程传递函数串联,可以写成形如121211()1/1/K Gs TT s T s T =++,其中112KK TT =。
图2 过程仿真方框图程序如下:④ 计算脉冲响应估计值:互相关函数采用公式)()(1)(10k i y i x Nr k R N r i xy +⋅⋅=∑-⋅=,互相关函数所用的数据是从第二个周期开始的,其中r 为周期数,取1-3之间。
系统辨识实验报告
实验一:系统辨识的经典方法一、实验目的掌握系统的数学模型与输入、输出信号之间的关系,掌握经辨辨识的实验测试方法和数据处理方法,熟悉MATLAB/Simulink环境。
二、实验内容1、用阶跃响应法测试给定系统的数学模型在系统没有噪声干扰的条件下通过测试系统的阶跃响应获得系统的一阶加纯滞后或二阶加纯滞后模型,对模型进行验证。
2、在被辨识系统中加入噪声干扰,重复上述1的实验过程。
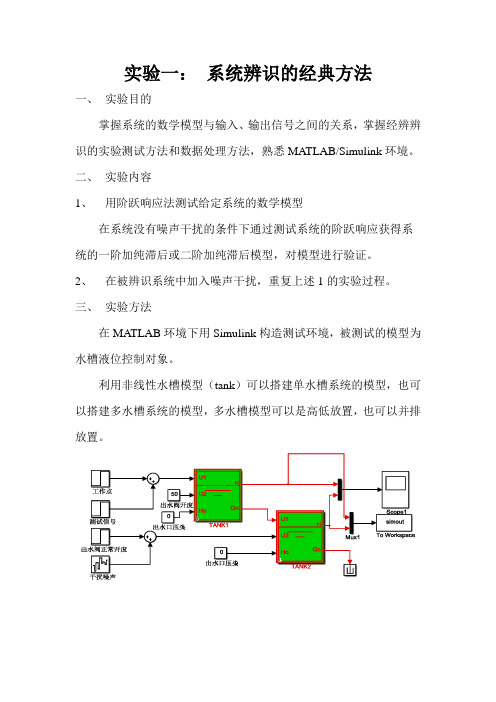
三、实验方法在MATLAB环境下用Simulink构造测试环境,被测试的模型为水槽液位控制对象。
利用非线性水槽模型(tank)可以搭建单水槽系统的模型,也可以搭建多水槽系统的模型,多水槽模型可以是高低放置,也可以并排放置。
1.噪声强度0.5,在t = 20的时候加入阶跃测试信号相应曲线2.乘同余法产生白噪声A=19;N=200;x0=37;f=2;M=512; %初始化;for k=1: N %乘同余法递推100次;x2=A*x0; %分别用x2和x0表示xi+1和xi-1;x1=mod(x2,M); %取x2存储器的数除以M的余数放x1(xi)中;v1=x1/M; %将x1存储器中的数除以256得到小于1的随v(:,k)=(v1-0.5 )*f;x0=x1; % xi-1= xi;v0=v1;end %递推100次结束;v2=v;k1=k;h=k1;%以下是绘图程序;k=1:1:k1;plot(k,v,'r');grid onset(gca,'GridLineStyle','*');grid(gca,'minor')3.白噪声序列图像020406080100120140160180200-1-0.8-0.6-0.4-0.20.20.40.60.81四、 思考题(1) 阶跃响应法测试系统数学模型的局限性。
答:只适用于某些特殊对象或者低阶简单系统;参数估计的精度有限,估计方法缺乏一般性。
系统辨识实验报告xjtu

系统辨识实验报告高海南 硕037一、实验问题单输入单输出系统:111()()()()()()A z y t B z u t C z e t ---=+其中:11231123112()1 2.851 2.7170.865()()10.70.22A z z z z B z z z z C z z z -----------=-+-=++=++()~(0,1)e t N1.产生必要随机数;2.设计实验,产生输出数据;3.用最小二乘辨识系统模型;4.任用一种适合有色噪声辨识算法辨识系统模型。
二、实验原理1.递推最小二乘递推最小二乘辨识算法可减少运算量和数据在计算机中所占的存储量,同时也能实时辨识出系统的特性,将最小二乘转化为递推估计。
最小二乘递推算法RLS 的基本思想是ˆˆ1k k θθ新的估计值()=老的估计值(-)+修正项算法迭代方程为1ˆˆˆ()(1)()[()()(1)]()(1)()[()(1)()1]()(1)()()(1)T T T k k K k z k h k k K k P k h k h k P k h k P k P k K k h k P k θθθ-⎧=-+--⎪=--+⎨⎪=---⎩(1)2.增广最小二乘增广最小二乘递推算法,扩充了最小二乘法的参数向量θ和数据向量)(k h 的维数,把噪声模型的辨识同时考虑进去,因此被称为增广最小二乘法。
最小二乘法的许多结论对它都是适用的,但最小二乘法只能获得模型的参数估计。
如果噪声模型必须用)()(1k v z D -表示时,只能用RELS 算法,方可获得无偏估计,这是RLS 算法所不能代替的。
考虑SISO 的动态系统,输入)(k u 和输出)(k z 是可以观测的;)z (G 1-是系统模型,用来描述系统的输入输出特性,)(k y 是系统的实际输出。
)z (N 1-是噪声模型,)(k v 是均值为零的不相关随机噪声。
通常 )z (A )z (B )z (G 1-11--=,)z (C )z (D )z (N 111---= (2)式中⎪⎩⎪⎨⎧++++=++++=⎪⎩⎪⎨⎧+++=++++=---------------d d c c b b a a n n 22111n n 22111n n 22111-n n 22111z z z 1)z (z z z 1)z (z z z )z (z z z 1)z (d d d D c c c C b b b B a a a A (3)若SISO 系统采用平均滑动模型,即 )z (A )z (C -1-1= (4))()(D )()z (B )(z )z (A 111k v z k u k ---+=若假定模型阶次a n 、b n 、d n 已经确定,则这类问题的辨识可用增广最小二乘法,以便获得满意的结果。
系统认识实验报告心得

系统认识实验报告心得引言在这次系统认识实验中,我通过使用不同的操作系统和学习操作系统的基本功能,对计算机操作系统有了更深入的了解。
在实验过程中,我不仅巩固了之前学到的理论知识,还提高了自己的实践能力。
在本次实验报告中,我将分享我在实验中所获得的收获和心得体会。
实验背景操作系统是计算机系统的核心组成部分,它负责协调和管理计算机硬件和软件资源。
通过本次实验,我们学习了不同类型的操作系统,包括Windows、Linux和MacOS,了解了它们的功能和特点,并掌握了基本的操作和管理方法。
实验过程第一阶段:Windows我首先开始了Windows系统的实验。
在这个阶段,我学习了Windows操作系统的基本功能和操作技巧,包括文件管理、进程管理、网络配置等。
我发现Windows操作系统的界面友好,操作简单易懂。
通过实际操作,我能够快速地创建、复制、移动和删除文件,管理多个应用程序,调整系统设置。
这个阶段的实验帮助我进一步熟悉了Windows系统,并提高了我的操作技能。
第二阶段:Linux接着是Linux系统的实验。
与Windows系统相比,Linux系统更加灵活和强大。
在这个阶段,我学习了Linux系统的基本命令和操作方法,并在终端中进行了实践操作。
我发现Linux系统可以通过命令行界面实现更多的操作,如文件管理、用户管理、软件安装等。
虽然刚开始接触Linux 系统时,我对命令行操作并不熟悉,但通过不断的练习,我逐渐掌握了基本的命令和操作技巧。
这个阶段的实验帮助我了解了Linux系统的优势和特点,并培养了我独立解决问题的能力。
第三阶段:MacOS最后是MacOS系统的实验。
MacOS是苹果公司开发的操作系统,与Windows和Linux有很大的差异。
在这个阶段,我学习了MacOS系统的基本操作和特色功能,如Launchpad、Mission Control、时间机器等。
我发现MacOS系统注重用户体验,提供了简洁、美观的界面和强大的功能。
系统辨识实验报告

系统辨识实验报告SA08157051 杜鹏超一 选择的系统模型类选择系统模型如下:se TsK τ-=G(S)然后多系统模型离散化,即;⎩⎨⎧⎭⎬⎫=--s s e TsK s e z ττG(z)二 辨识的原理,方法和公式 y(i)=-a*y(i-1)+b*u(i-1)⎪⎪⎩⎪⎪⎨⎧-+--=+-=+-=)1()1()()2()2()3()1()1()2(n bu n ay n y bu ay y bu ay y 令 T θ=[-a b] x(k)=[y(k-1) u(k-1)]或⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=)1()1()2()2()1()1(X n u n y u y u y⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()3()2(y(N) n y y y 即y=x θ+e1.批量最小二乘估计算法最小二乘估计准则:模型拟合残差为θϕε)()()(k k y k T-=则有目标函数J 为:∑==ki i k J 12)()(ε把数据代入拟合残差得:θϕε)()()(n n y n T-=下面从最小二乘准则推导正规方程。
根据术极值原理可知,最小二乘估计θ满足⎪⎪⎩⎪⎪⎨⎧∂∂∂∂=∂∂-为正定T J J LS )(0θθθθθJ 还可写成)()()(k k k J T εε=θφφθθφθφεε T T T T Ty y y y k k k J 2)()()()(-=--==)(上式中为简单起见,略去了有关各项的(n)。
⎪⎪⎩⎪⎪⎨⎧=∂∂∂∂=+-=∂∂-为正定φφθθθφφφθθθTT LS TT J y J LS 2)(022于是得:y TT ls φφφθ1)(-=的最小二乘估计为)()())()(()(1k y k x k x k x k T T -=θ2.递推最小二乘估计算法原式为)()1()1(1k e k xk y T ++=++θ得新解)1()1())1()1(()1(1++++=+-k y k x k x k x k TTθ其中:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+=+)1()()1()1()()1(k y k y k y k x k x k x T T 令:2)]1()1([)1(++=+k x k x k p T可求得)1()()1(1)1()()1(++++=+k X k p k X k x k p k k T T)]()1()1()[1()()1(k k x k y k K k k Tθθθ +-+++=+)]()1(1[)1(k x k K k p T θ++=+3 渐消记忆递推最小二乘估计算法修改目标两数J ,对残差平方加指数权λ∑=-=ki ik i k J 12)()(ελ其巾λ=0.9—0.999愈大遗忘愈慢。
系统辨识及自适应控制实验报告

系统辨识及自适应控制实验报告实验报告:系统辨识及自适应控制1.引言系统辨识和自适应控制是现代自动控制领域中的重要研究内容。
系统辨识是通过采集系统输入输出数据,建立数学模型描述系统的动态行为。
自适应控制则是根据系统辨识得到的模型,调整控制器参数以适应系统的变化和外部干扰。
本实验旨在通过实际操作,掌握系统辨识和自适应控制的基本原理和方法。
2.实验目的1)了解系统辨识的基本原理和方法;2)掌握常见的系统辨识方法,包括参数辨识和频域辨识;3)理解自适应控制的基本原理和方法;4)熟悉自适应控制的实现过程;5)通过实验验证系统辨识和自适应控制的有效性。
3.实验原理3.1系统辨识原理系统辨识的目标是通过采集系统输入输出数据,建立数学模型来描述系统的动态特性。
常见的系统辨识方法包括参数辨识和频域辨识两种。
参数辨识是通过拟合实际测量数据,找到最佳的模型参数。
常用的参数辨识方法有最小二乘法、极大似然法和最小误差平方等。
频域辨识则是通过对输入输出信号的频谱分析,得到系统的频率响应特性。
常用的频域辨识方法有傅里叶变换法、相关分析法和谱估计法等。
3.2自适应控制原理自适应控制是根据系统辨识得到的模型,调整控制器参数以适应系统的变化和外部干扰。
自适应控制分为基于模型的自适应控制和模型无关的自适应控制。
基于模型的自适应控制利用系统辨识得到的模型参数,设计相应的控制器来实现自适应控制。
常见的基于模型的自适应控制方法有模型参考自适应控制和模型预测自适应控制等。
模型无关的自适应控制则不依赖于系统辨识的模型,而是根据实际测量数据直接调整控制器参数。
常见的模型无关的自适应控制方法有自适应滑模控制和神经网络控制等。
4.实验内容4.1系统辨识实验在实验中,我们通过采集系统输入输出数据,根据最小二乘法进行参数辨识。
首先设置系统的输入信号,如阶跃信号或正弦信号,并记录对应的输出数据。
然后根据采集到的数据,选取适当的模型结构,通过最小二乘法求解最佳的模型参数。
系统辨识实验报告 中科大

1.5 预处理后检验
把原始数据分成两部分,一部分用来辨识,一部分用来检验模型。 预处理后便是部分输入的图像
预处理后便是部分输出的图像
预处理后检验数据部分输入图像
预处理后检验部分输出部分
2 辨识算法
以下 n 的取值均为 2,在以下部分为给出为什么 n 取 2 最好
2.1 批量最小二乘
2.1.1 源代码 %批量最小二乘算法 dafi=ones(N,2*n); for i=0:N-1 dafi(i+1,:)=[-vo_iden(i+1:i+n)' vi_iden(i+1:i+n)']; end cta=inv(dafi'*dafi)*dafi'*vo_iden(n+1:n+N); Y1=test*cta; %plot(Y1); E1=Y1-vo_test(n+1:n+N); En1(1,n)=E1'*E1; cta 2.1.2 辨识结果
2.3.2 辨识结果
2.3.3 模型检验 (1)用测试数据输入后得到的图像
(2)和实际偏差的曲线
2.4 增广最小二乘法
2.4.1源代码 %增广最小二乘算法 p=eye(3*n)*1000; cta=ones(3*n,1); w=zeros(n,1); W=ones(N,n); for i=0:N-1 fi=[-vo_iden(i+1:i+n)' vi_iden(i+1:i+n)' w']; k=(p*fi')/(1+fi*p*fi'); cta=cta+k*(vo_iden(i+1)-fi*cta); p=p-k*fi*p; for j=1:n-1 w(j,1)=w(j+1,1); end w(n,1)=vo_iden(i+1)-fi*cta; end w=zeros(n,1); for i=0:N-1 W(i+1,:)=w; s=[-vo_test(i+1:i+n)' vi_test(i+1:i+n)' w']; for j=1:n-1 w(j,1)=w(j+1,1); end w(n,1)=vo_test(i+1)-fi*cta; end teste=[test W]; Y4=teste*cta; %plot(Y4); E4=Y4-vi_test(n+1:n+N); En4(1,n)=E4'*E4; cta 2.4.2 辨识结果
系统辨识实验报告

系统辨识实验报告——C语言版目录实验一 .......................................................错误!未定义书签。
实验分析..................................................错误!未定义书签。
实验代码..................................................错误!未定义书签。
运行结果..................................................错误!未定义书签。
实验二 .......................................................错误!未定义书签。
实验分析..................................................错误!未定义书签。
实验代码..................................................错误!未定义书签。
运行结果..................................................错误!未定义书签。
实验三 .......................................................错误!未定义书签。
实验分析..................................................错误!未定义书签。
实验代码..................................................错误!未定义书签。
运行结果..................................................错误!未定义书签。
实验四 .......................................................错误!未定义书签。
系统辩识实验报告

一、实验目的1. 理解系统辨识的基本概念和原理。
2. 掌握递推最小二乘算法在系统辨识中的应用。
3. 通过实验,验证算法的有效性,并分析参数估计误差。
二、实验原理系统辨识是利用系统输入输出数据,对系统模型进行估计和识别的过程。
在本实验中,我们采用递推最小二乘算法对系统进行辨识。
递推最小二乘算法是一种参数估计方法,其基本思想是利用当前观测值对系统参数进行修正,使参数估计值与实际值之间的误差最小。
递推最小二乘算法具有计算简单、收敛速度快等优点。
三、实验设备1. 电脑一台,装有MATLAB软件。
2. 系统辨识实验模块。
四、实验步骤1. 打开MATLAB软件,运行系统辨识实验模块。
2. 在模块中输入已知的系数a1、a2、b1、b2。
3. 生成输入序列u(t)和噪声序列v(t)。
4. 将输入序列u(t)和噪声序列v(t)加入系统,产生输出序列y(t)。
5. 利用递推最小二乘算法对系统参数进行辨识。
6. 将得到的参数估计值代入公式计算参数估计误差。
7. 仿真出参数估计误差随时间的变化曲线。
五、实验结果与分析1. 实验结果根据实验步骤,我们得到了参数估计值和参数估计误差随时间的变化曲线。
2. 结果分析(1)参数估计值:通过递推最小二乘算法,我们得到了系统参数的估计值。
这些估计值与实际参数存在一定的误差,这是由于噪声和系统模型的不确定性所导致的。
(2)参数估计误差:从参数估计误差随时间的变化曲线可以看出,递推最小二乘算法在短时间内就能使参数估计误差达到较低水平。
这说明递推最小二乘算法具有较好的收敛性能。
(3)参数估计误差曲线:在实验过程中,我们发现参数估计误差曲线在初期变化较快,随后逐渐趋于平稳。
这表明系统辨识过程在初期具有较高的灵敏度,但随着时间的推移,参数估计误差逐渐减小,系统辨识过程逐渐稳定。
六、实验结论1. 递推最小二乘算法在系统辨识中具有较好的收敛性能,能够快速、准确地估计系统参数。
2. 实验结果表明,递推最小二乘算法能够有效减小参数估计误差,提高系统辨识精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14
四.实验运行结果:
函数界面示意图: 6. 只显示结果界面: 7. 显示过程的参考界面:
15
心得体会
我很喜欢这个课程的期末考核方式,不用再拘泥于在题目当中对该课程的了 解,而是通过 4 个 C 语言设计的练习来达到学习的目的,而且对以后的学习还有 很大的帮助。
在编写 C 语言的过程中,也遇到了一些阻碍,特别是在编写第 3,4 个的时候。 比如:用的数组太多,并且未将其初始化,运行出来的结果经常是很长的一段随 机数;或者一模一样的程序有时候就可以正常运行,有时候就总是出现报错…… 这些都是让我心塞了两周的问题。在这些问题解决之后,运行出来的结果却与实 际模型参数的出入有点大,于是又重新查找第 2 个实验是否是 M 序列产生的方式 有问题。通过对初始化寄存器赋给不同的值,可以让结果与真实模型参数之间的 误差达到最小。
实验 4 ................................................ 错误!未定义书签。 一.实验内容及要求: ............................... 错误!未定义书签。 二.实验原理: ..................................... 错误!未定义书签。 三.数据递推关系图: ............................... 错误!未定义书签。
编写并调试动态离散时间模型 LS 成批算法程序。 要求:(1)原始数据由 DU 和 DY 读出。 (2)调用求逆及相乘子程序。 (3)显示参数辨识结果。
二.实验原理:
1.批次处理的方法就是把所有的数据采集到一次性进行处理,但前提是 白色噪声、及 M 序列所共同作用而产生的输出,才能使用最小二乘法。虽然 这种方法的计算量庞大,但经常用于处理时不变系统,方法简单。
1. 基本模型:y(k)=-a1y(k-1)-a2y(k-2)+b1u(k-1)+b2u(k-2)+v(k)。 2. 引入信息矩阵 P(k),维数为 4*4,初始化为 10^5~10^12*E 的一单位 阵。gama(k)为修正系数,为无穷小标量。x(k+1)=[-y(k) -y(k-1) u(k) u(k-1)]。sita'=[a1 a2 b1 b2]。y(k+1)=DY[k+3]。 3. sita'(k+1)=sita'(k)+gama(k+1)*P(k)*x(k+1)*[y(k+1)-x'(K=1)* sita'(k)]; 4. P(k+1)=P(k)-gama(k+1)*P(k)*x(k+1)*x'(k+1)*P(k); 5. gama(k+1)=1/[1+x'(k+1)*P(k)*x(k+1)];
1
四.实验运行结果: ................................. 错误!未定义书签。 心得体会 ............................................. 错误!未定义书签。 附录(实验代码) ..................................... 错误!未定义书签。
M 序列的长度为
L=500
i
=1
Y
i
<L
N
输出 M 序列
M 序列 DU(i)=a(i)
寄存器向前移 1位
三.软件设计思想:
1. 该软件的主要功能是:产生 M 序列赋给 u(k)保存在文件中;由 u(k) 和 v(k)求得 y(k)保存在文件中。
2. 在 main 函数中给出 3 个选择:求 u(k);求 y(k);退出程序。其相 对应的函数名称为 gener,ouput,exit。
通过这学期对系统辨识这个课程的学习,让我了解到系统辨识在建立数学模 型的方面的重要性。对于不了解系统的工作机理的人来说,也有了一个可以知道 系统模型的构建方法。但是也必须要我们对所构建模型有一个较为清醒的认识, 比如要知道模型的类型,如果是动态模型,则要知道模型的参数或者阶次(但是 权函数模型就不需要事前知道模型的参数或者阶次,不知道这种方法有没有什么 我们不知道的缺陷)。在处理数据上,又一次让我了解到世上没有两全其美的事 情,计算的复杂程度和精度就好像鱼和熊掌不能兼得。也正是因为这样,才会成 为促使人们在这方面的不断寻找最优化算法的动力。在对模型进行研究时,都是 从最简单的模型开始研究,比如在没有噪声的情况下,所得到的模型参数就为系 统模型真实参数。进一步,在白色噪声的情况下,所得到的参数就为系统模型真 实参数的估计……通过这样的推理,就可以得到 LS 在系统辨识问题上的普适性, 不管系统受怎样的干扰,只要通过一系列的变换,最后还是通过 LS 来解决模型 参数的确定工作。
1. ............................................................. LabWork1 错误!未定义书签。 2. ............................................................. LabWork2 错误!未定义书签。 3. ............................................................. LabWork3 错误!未定义书签。 4. ............................................................. LabWork4 错误!未定义书签。
3. 在 MulOp(a,b,c)子函数中,有两种输入矩阵的方式:way1,way2。 相对应的功能为键盘输入,文本输入。并且两者在处理矩阵时,都调用了 Mul 函数。
4. 在 Inv()子函数中,输入和显示原矩阵,和其相应的逆矩阵。调用 qiuni(double FangZ[][M],double FZNi[][M],int n)子函数,可以都得 到原矩阵的逆矩阵。但当原矩阵不可逆时,系统输出为”The array is not
三.软件设计思想:
1. 确定该软件的功能主要有:键盘输入两个矩阵然后相乘;文本 data 输入两个矩阵将结果放在文本 result 中;键盘输入一个方阵求得其逆矩阵。 其中前两个的矩阵相乘运算部分设置为一个函数 Mul。
2. 在 main 函 数 中 提 供 两 个 关 于 矩 阵 的 选 择 : multiplitation ; invertion。其相对应的子函数为 MulOp(a,b,c),Inv()。
9
四.程序设计框图:
main 函 数
gener 子 函数
产生 DU
output 子 函数
产生 DY
退出程序
五.程序运行流程图:
1. main 函数:
input 子 函数
输入 DU, DV
deal er 函数:
3. output 函数:
10
11
实验 3
一.实验内容及要求:
3. 在 gener 子函数中产生 M 序列 u(k)保存到文本文件中。 4. 在 output 子函数中,通过对 input 子函数(读入 v(k),u(k)的数据)、 deal 子函数(由公式 y(k)(k-1)+(k-2)=u(k-1)+(k-2)+v(k)求 y(k))的调用 来达到生成 y(k)序列并保存到文本文件中。
5
3. Inv 子函数的界面: 4. 通过键盘操作计算两个矩阵的乘积:
5. 求方阵的逆矩阵:
6
7
实验 2
一.实验内容及要求:
编写并调试动态模型仿真程序: 模型:y(k)(k-1)+(k-2)=u(k-1)+(k-2)+v(k) 已知:白噪声{v(k)}数据文件为 DV,数据长度为 L=500 要求:(1) 产生长度为 L 的 M 序列数据文件 DU
4
invertible!“。
四.程序结构框图:
main 函 数
MulOp 子 函数
矩阵乘积
Inv 子 函 数
矩阵求逆
退出程序
way1 键 盘 输入矩阵
way2 文 本 输入
矩阵
qiuni 子函 数
Mul 矩阵乘 积子函数
五.运行示意图:
1. main 函数的主界面:
2. MulOp 子函数的界面:
系统辨识实验报告
学院:信息科学与技术学院 专业:自动化 日期:2016/4/26
0
目录
实验 1 ................................................ 错误!未定义书签。 一.实验内容及要求: ............................... 错误!未定义书签。 二.实验原理: ..................................... 错误!未定义书签。 三.软件设计思想: ................................. 错误!未定义书签。 四.程序结构框图: ................................. 错误!未定义书签。 五.运行示意图: ................................... 错误!未定义书签。
实验 3 ................................................ 错误!未定义书签。 一.实验内容及要求: ............................... 错误!未定义书签。 二.实验原理: ..................................... 错误!未定义书签。 三.程序数据流程图: ............................... 错误!未定义书签。 四.实验运行结果: ................................. 错误!未定义书签。
